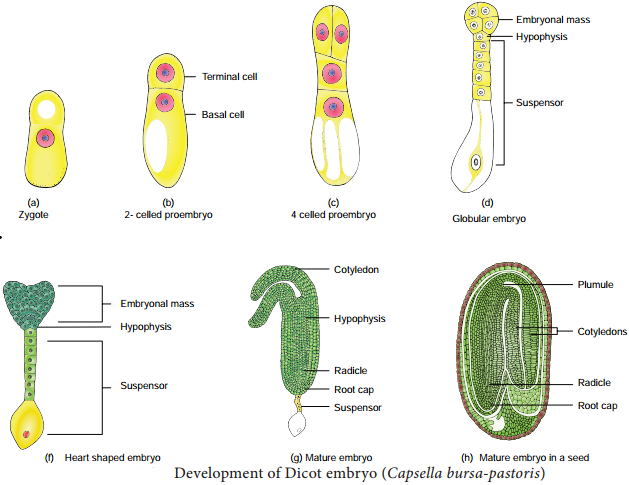
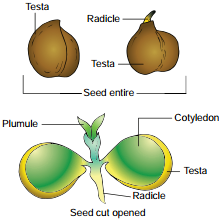
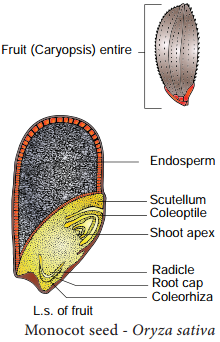
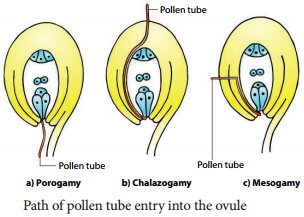
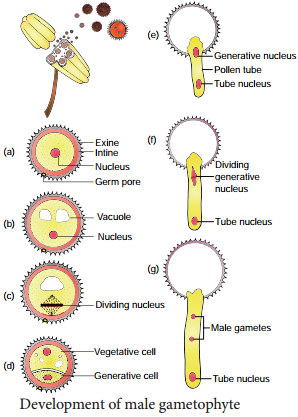
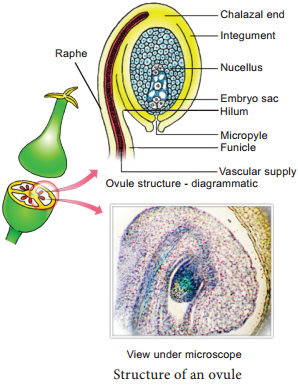
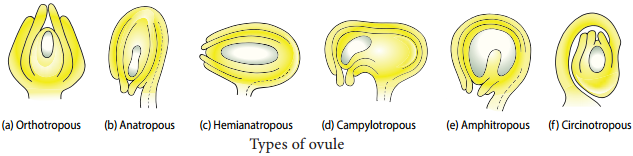
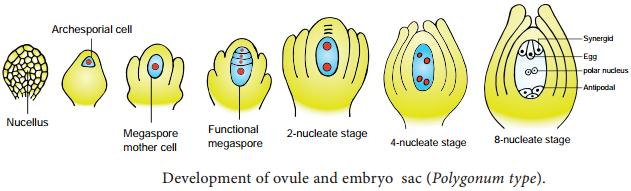
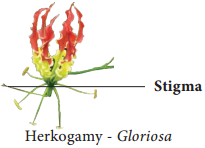
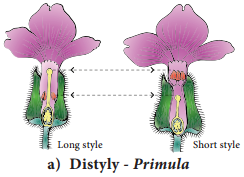
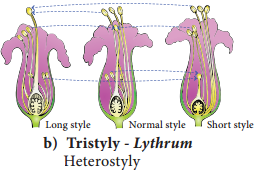
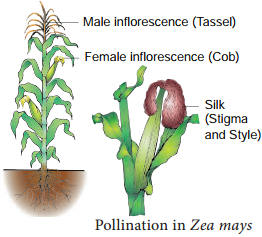
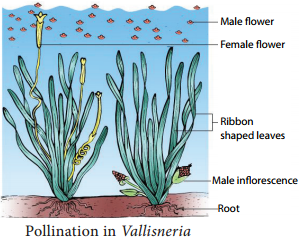
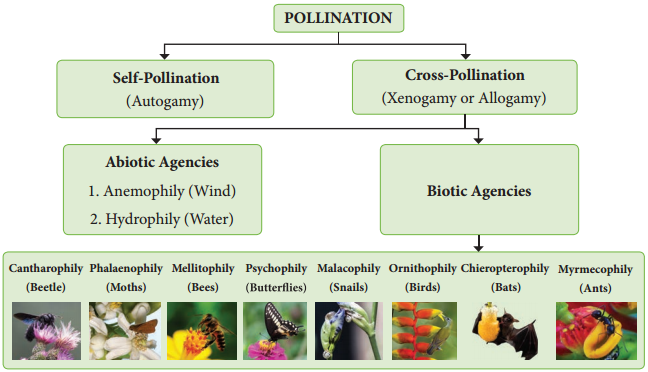
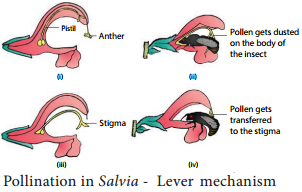
Learninsta presents the core concepts of Biology with high-quality research papers and topical review articles.
Polyembryony Types and its Occurence
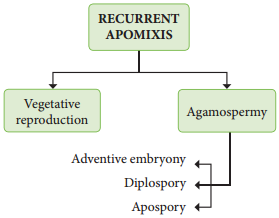
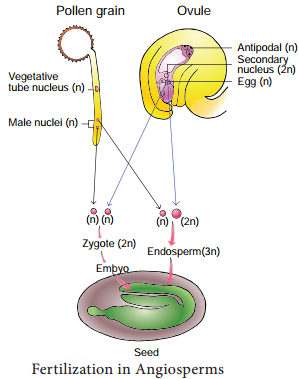
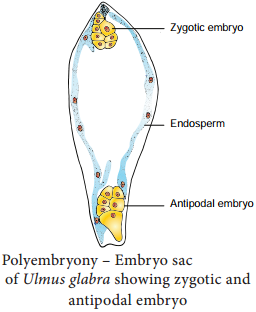
Occurrence of more than one embryo in a seed is called polyembryony (Figure 1.24). The first case of polyembryony was reported in certain oranges by Anton von Leeuwenhoek in the year 1719. Polyembryony is divided into four categories based on its origin.
1. Cleavage polyembryony (Example: Orchids)
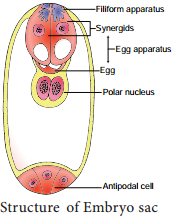
2. Formation of embryo by cells of the Embryo sac other than egg (Synergids – Aristolochia; antipodals – Ulmus and endosperm – Balanophora)
3. Development of more than one Embryo sac within the same ovule.
(Derivatives of same MMC, derivatives of two or more MMC – Casuarina)
4. Activation of some sporophytic cells of the ovule (Nucellus / integuments-Citrus and Syzygium).
Practical applications
The seedlings formed from the nucellar tissue in Citrus are found better clones for Orchards. Embryos derived through polyembryony are found virus free.