NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.5 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.5.
- Practical Geometry Class 8 Ex 4.1
- Practical Geometry Class 8 Ex 4.2
- Practical Geometry Class 8 Ex 4.3
- Practical Geometry Class 8 Ex 4.4
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 4 |
| Chapter Name | Practical Geometry |
| Exercise | Ex 4.5 |
| Number of Questions Solved | 1 |
| Category | NCERT Solutions |
NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.5
Question 1.
Draw the following:
1. The square READ with RE = 5.1 cm.
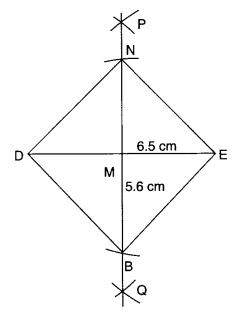
2. A rhombus whose diagonals are 5.2 cm and 6.4 cm long.
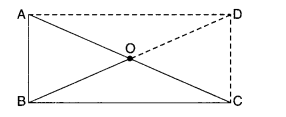
3. A rectangle with adjacent sides of lengths 5 cm and 4 cm.
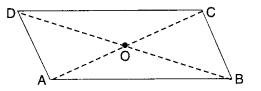
4. A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm. Is it unique?
Solution.
1. Steps of Construction
- Draw RE = 5.1 cm.
- At R, draw a ray RX such that ∠ERX
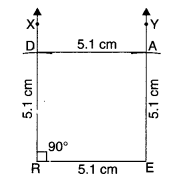
- From ray RX, cut RD = 5.1 cm.
- At E, draw a ray EY such that ∠REY = 90°.
- From ray EY, cut EA = 5.1 cm.
- Join AD.
Then, READ is the required square.
2. Steps of Construction
[We know that the diagonals of a rhombus bisect each other at right angles. So in rhombus ABCD, the diagonals AC and BD will bisect each other at right angles.]
- Draw AC = 5.2 cm.
- Construct its perpendicular bisector. Let it intersect AC at O.
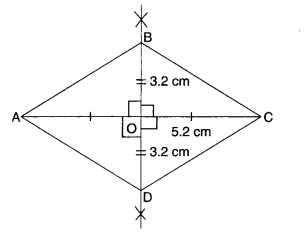
- Cut off \(\frac { 6.4 }{ 2 } \)= 3.2 cm lengths on either side of the bisector drawn in step 2, we get B and D.
- Join AB, BC, CD, and DA.
Then, ABCD is the required rhombus.
3. Steps of Construction
[We know that each angle of a rectangle is 90°. So, in rectangle PQRS,
∠P=∠Q=∠R=∠S= 90°.
Also, opposite sides of a rectangle are parallel.
So, in rectangle PQRS,
PQ || SR and PS || QR]
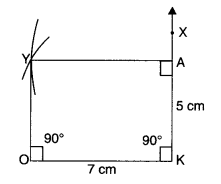
- Draw PQ = 5 cm.
- At Q, draw a ray QX such that ∠PQX = 90°.
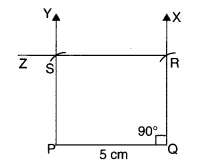
- From ray QX, cut QR = 4 cm.
- At P, draw a ray PY parallel to QR.
- At R, draw a ray RZ parallel to QP to meet the ray drawn in step 4 at S.
Then, PQRS is the required rectangle.
4. Steps of Construction
[We know that in a parallelogram, opposite sides are parallel and equal. So,
OK = YA and OK || YA;
KA = OY and KA || OY]
- Draw OK = 5.5 cm.
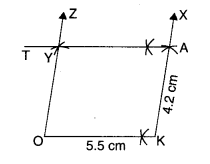
- At K, draw a ray KX at any suitable angle from OK.
- From ray KX, cut KA = 4.2 cm.
- A, draw a ray AT parallel to KO.
- At O, draw a ray OZ parallel to KA to cut the ray drawn in step 4 at Y.
Then, OKAY is the required parallelogram.
This is not unique.
Note: We can construct countless parallelograms with these dimensions by varying ∠OKA
We hope the NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.5 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.5, drop a comment below and we will get back to you at the earliest.