Dattu

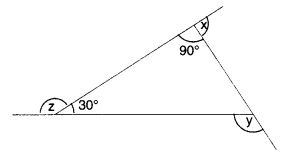
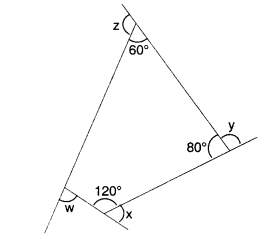
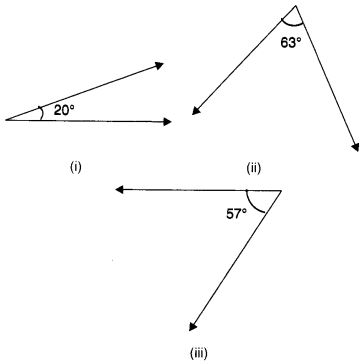
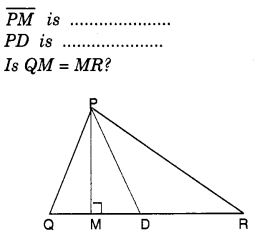
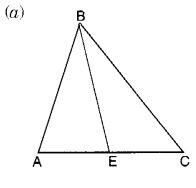
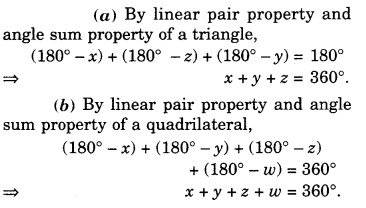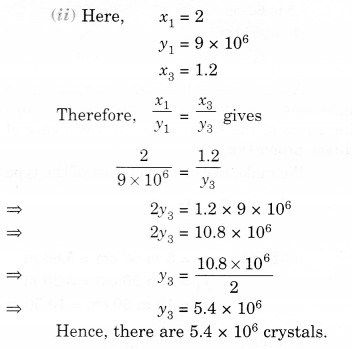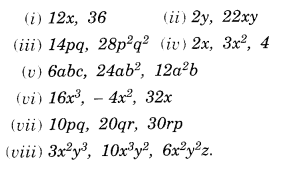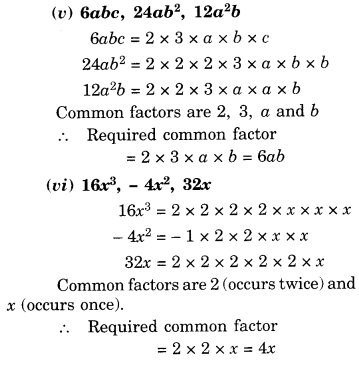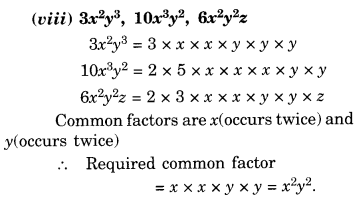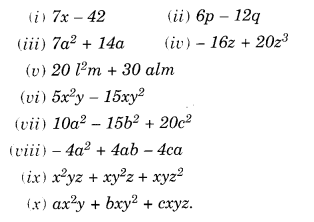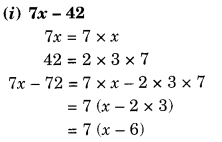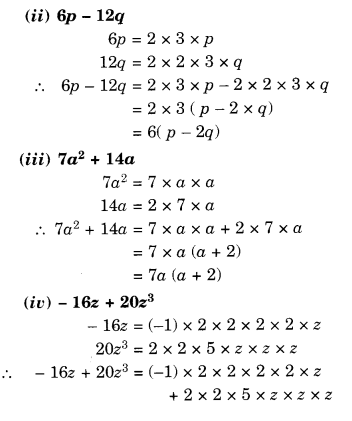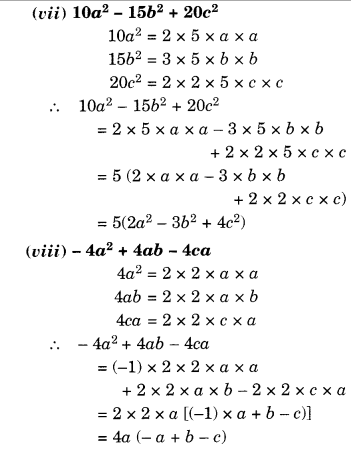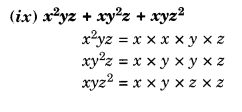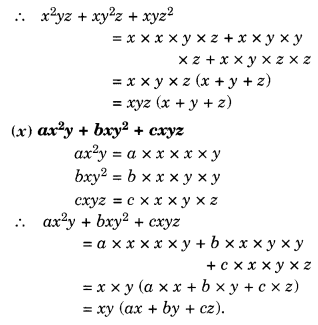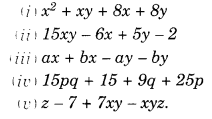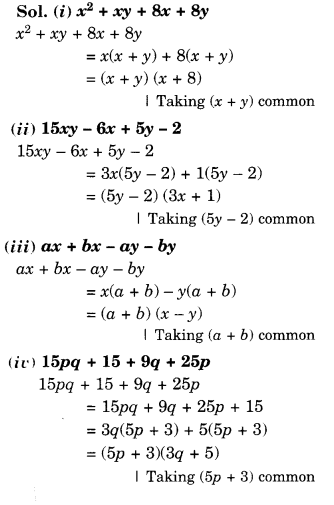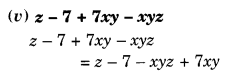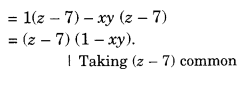NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1.

• Visualising Solid Shapes Class 8 Ex 10.2
• Visualising Solid Shapes Class 8 Ex 10.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 10
Chapter Name	Visualising Solid Shapes
Exercise	Ex 10.1
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1

Question 1.
For each of the given solid, the two views are given. Match for each solid the corresponding top and front views. The first one is done for you.

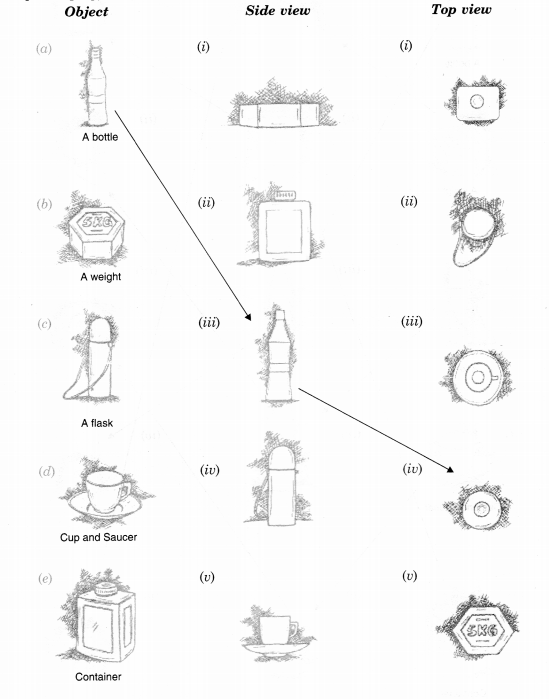
Solution.

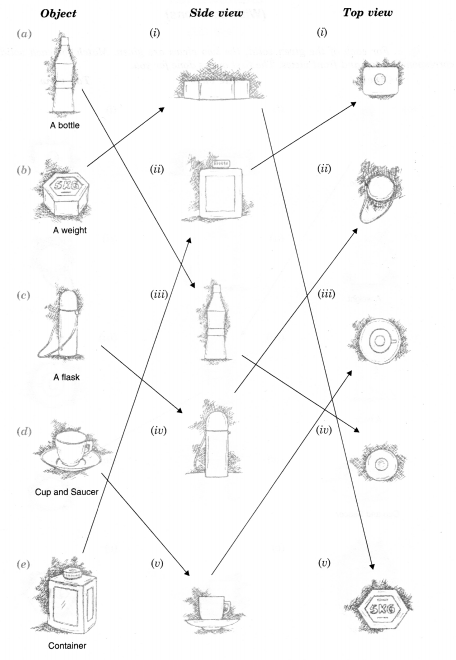
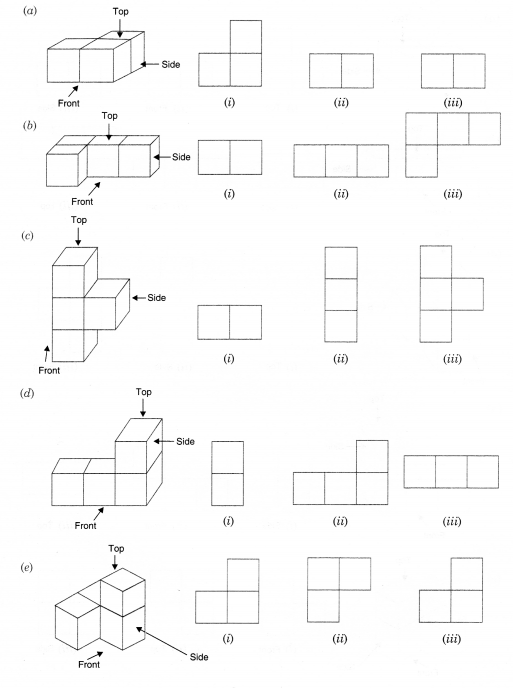
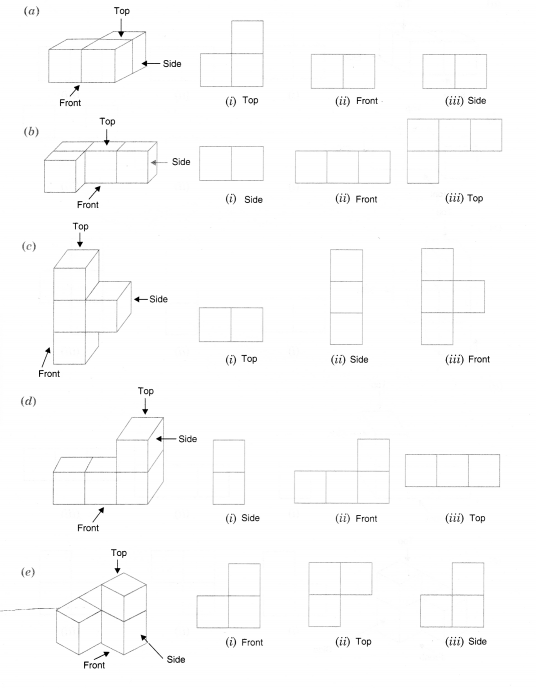
Question 2.
For each of the given solid, the three views are given. Identify for each solid the corresponding top, front and side views.

Solution.

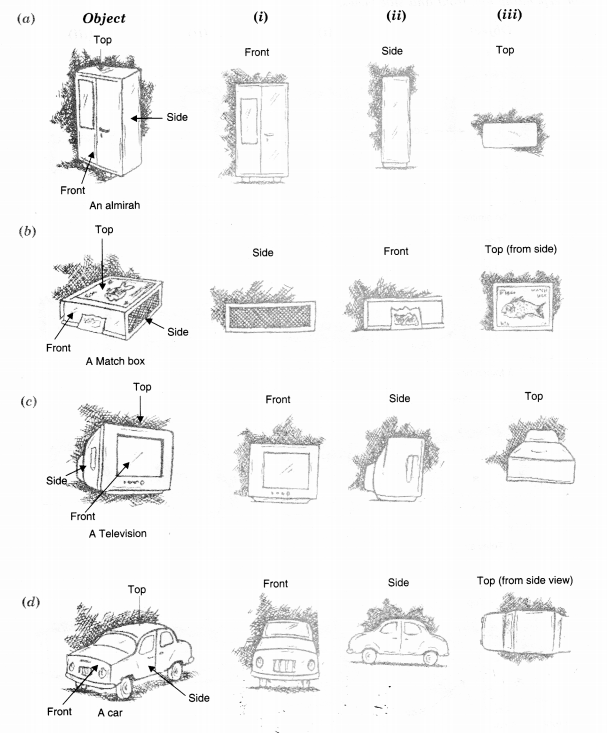
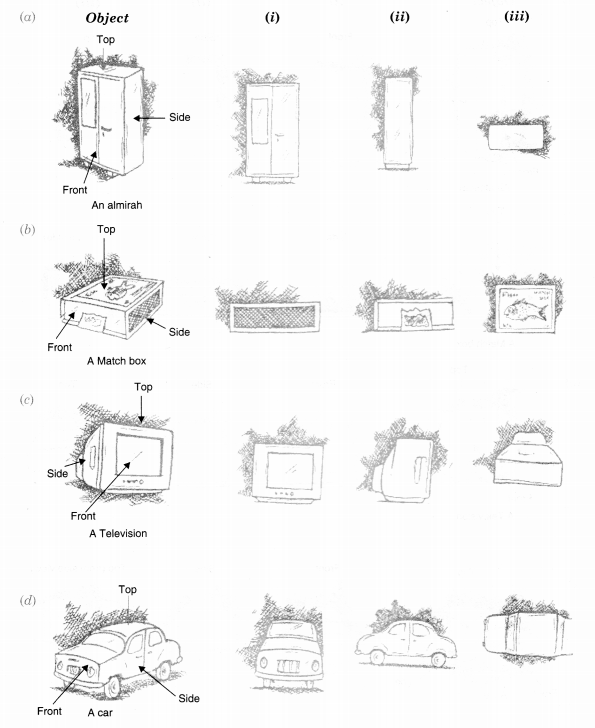
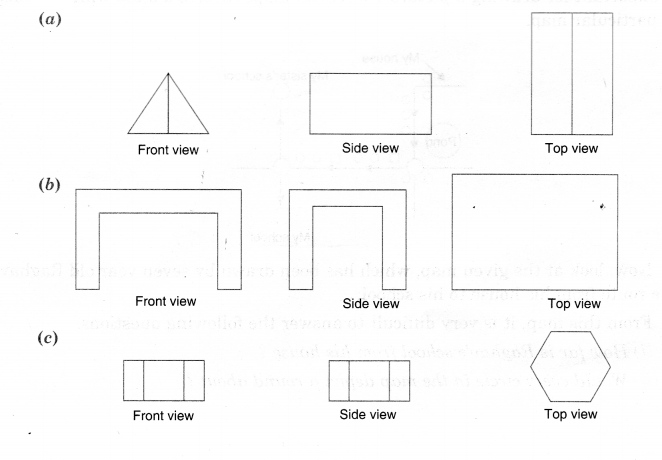
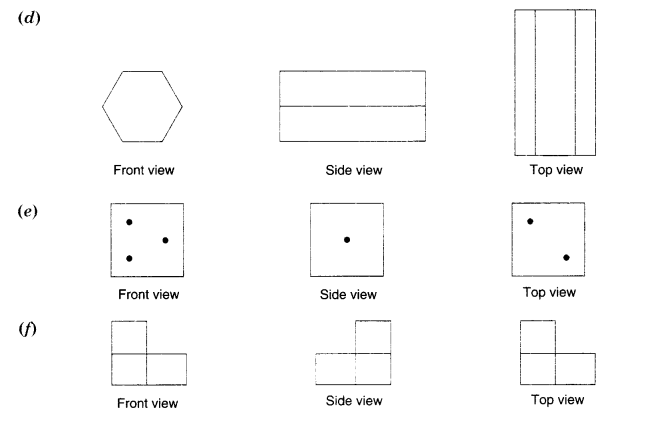
Question 3.
For each given solid, identify the top view, front view, and side view.

Solution.

Question 4.
Draw the front view, side view and top view of the given objects,

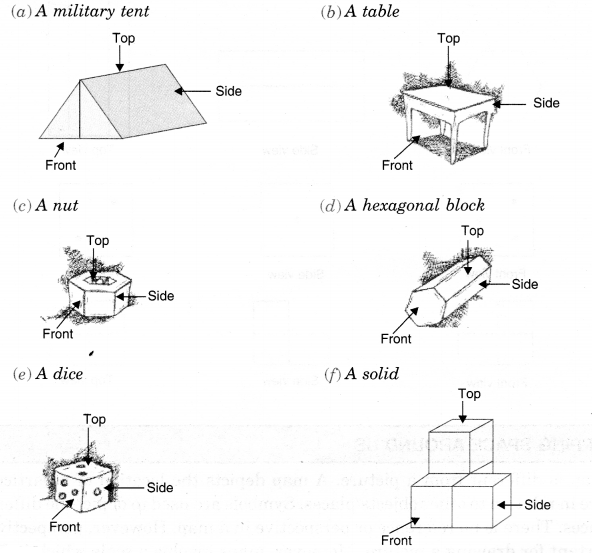
Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1.

• Congruence of Triangles Class 7 Ex 7.2
• Congruence of Triangles Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 7
Chapter Name	Congruence of Triangles
Exercise	Ex 7.1
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1

Question 1.
Complete the following statements:
(a) Two line segments are congruent if……..
(b) Among two congruent angles, one has a measure of 70°; the measure of the other angle is…….
(c) When we write ∠A = ∠B, we actually mean….
Solution:
(a) they have the same length
(b) 70°
(c) m∠A = m∠B

Question 2.
Give any two real-life examples for congruent shapes.
Solution:

1. Two coins or notes of the same denomination.
2. Two keys of the same lock.

Question 3.
If ∆ ABC = ∆ FED under the correspondence ABC ↔ FED, write all the corresponding congruent parts of the triangles.
Solution:
Corresponding vertices: A and F; B and E; C and D.
Corresponding sides : \(\overline { AB } \) and \(\overline { FE } \) ; \(\overline { BC } \) and \(\overline { ED } \); \(\overline { CA } \) and \(\overline { DF } \).
Corresponding angles: ∠A and ∠F; ∠B and ∠E; ∠C and ∠D.

Question 4.
If ∆ DEF = ∆ BCA, write the part(s) of ∆ BCA that correspond to

1. ∠E
2. \(\overline { EF } \)
3. ∠F
4. \(\overline { DF } \)

Solution:

1. ∠C
2. \(\overline { CA } \)
3. ∠A
4. \(\overline { BA } \)

We hope the NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1.

• Understanding Quadrilaterals Class 8 Ex 3.2
• Understanding Quadrilaterals Class 8 Ex 3.3
• Understanding Quadrilaterals Class 8 Ex 3.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 3
Chapter Name	Understanding Quadrilaterals
Exercise	Ex 3.1
Number of Questions Solved	7
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1

Question 1.
Given here are some figures :

Classify each of them on the basis of the following :
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Solution.
(a) ⟷ 1, 2, 5, 6, 7
(b) ⟷ 1, 2, 5, 6, 7

Question 2.
How many diagonals does each of the following have?
(a) A convex quadrilateral
(b) A regular hexagon
(c) A triangle.
Solution.
(a) → 2
(b) → 9
(c) → 0

Question 3.
What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and j try!)
Solution.
The sum of the measures of the angles of a convex quadrilateral is 360°.
Yes! this property will hold if the; quadrilateral is not convex.
If the quadrilateral is not convex, then it will be concave.
Split the concave quadrilateral ABCD into two triangles ABD and CBD by joining BD.

Question 4.
Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)

What can you say about the angle sum of a convex polygon with number of sides ?
(a) 7
(b) 8
(c) 10
(d) n
Solution.
(a) 7
Angle sum = \(\left( 7-2 \right) \times { 180 }^{ \circ }\)
= \(5\times { 180 }^{ \circ }={ 900 }^{ \circ }\)

(b) 8
Angle sum = \(\left( 8-2 \right) \times { 180 }^{ \circ }\)
= \(6\times { 180 }^{ \circ }={ 1080 }^{ \circ }\)

(c) 10
Angle sum = \(\left( 10-2 \right) \times { 180 }^{ \circ }\)
= \(8\times { 180 }^{ \circ }={ 1440 }^{ \circ }\)

(d) n
Angle sum = \(\left( n-2 \right) \times { 180 }^{ \circ }\)

Question 5.
What is a regular polygon? State the name of a regular polygon of
(i) 3 slides
(ii) 4 slides
(iii) 6 slides
Solution.
A polygon, which is both ‘equilateral’ and ‘equiangular’, is called a regular polygon.
(i) 3 slides
The name of the regular polygon of 3 slides is an equilateral triangle.
(ii) 4 slides
The name of the regular polygon of 4 slides is square
(iii) 6 slides
The name of the regular polygon of 6 slides is a regular hexagon

Question 6.
Find the angle measure x in the following figures.

Solution.

Question 7.

(a) Find x+y+z

(b) Find x+y+z+w.
Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1.

• Lines and Angles Class  7 Ex 5.2
• Lines and Angles Class  7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 5
Chapter Name	Lines and Angles
Exercise	Ex 5.1, Ex 5.2.
Number of Questions Solved	14
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1

Question 1.
Find the complement of each of the following angles:

Solution:
Since, the sum of the measures of an angle and its complement is 90°, therefore,

1. The complement of an angle of measure 20° is the angle of (90° – 20°), f.e., 70°.
2. The complement of an angle of measure 63° is the angle of (90° – 63°), i.e., 27°.
3. The complement of an angle of measure 57° is the angle of (90° – 57°), i.e., 33°.

Question 2.
Find the supplement of each of the following angles:

Solution:

1. Supplement of the angle 105° = 180° – 105° = 75°
2. Supplement of the angle 87° = 180° – 87° = 93°
3. Supplement of the angle 154° = 180° – 154° = 26°

Question 3.
Identify which of the following pairs of angles are complementary and which are supplementary.

1. 65°, 115°
2. 63°, 27°
3. 112°, 68°
4. 130°, 50°
5. 45°,45°
6. 80°, 10°.

Solution:

1. Since, 65°+ 115° = 180°
   So, this pair of angles are supplementary.
2. Since, 63°+ 27° = 90°
   So, this pair of angles are complementary.
3. Since, 112° + 68° = 180°
   So, this pair of angles are supplementary.
4. Since, 130°+50° = 180°
   So, this pair of angles are supplementary.
5. Since, 45°+ 45° = 90°
   So, this pair of angles are complementary.
6. Since, 80°+ 10° = 90°
   So, this pair of angles are complementary.

Question 4.
Find the angle which is equal to its complement.
Solution:
Let the measure of the angle be x°. Then, the measure of its complement is given to be x°.
Since, the sum of the measures of an angle and its complement is 90°, therefore,
x° + x° = 90°
⇒ 2x° = 90°
⇒ x° = 45°
Thus, the required angle is 45°.

Question 5.
Find the angle which is equal to its supplement.
Solution:
Let the measure of the angle be x°. Then,
a measure of its supplement = x°
Since, the sum of the measures of an angle and its supplement is 180°, therefore,
x° + x° = 180°
⇒ 2x° =180°
⇒ x° = 90°
Hence, the required angle is 90°.

Question 6.
In the given figure, ∠ 1 and ∠ 2 are supplementary angles.

If ∠1 is decreased, what changes should take place in ∠ 2 so that both the angles still remain supplementary?
Solution:
∠ 2 will increase as much as ∠ 1 decreases.

Question 7.
Can two angles be supplementary if both of them are:

1. acute?
2. obtuse?
3. right?

Solution:

1. No! two acute angles cannot be a supplement.
2. No! Two obtuse angles cannot be supplementary.
3. Yes! Two right angles are always supplementary.

Question 8.
An angle is greater than 45°. Is its complementary angle greater than 45° or equal to 45° or less than 45°.
Solution:
Since the sum of the measure of ah angle and its complement is 90°.
∴ The complement of an angle of measures 45° + x°,
where x > 0 is the angle of [90° – (45° + x°)] = 90° – 45° – x°= 45° – x°.
Clearly, 45° + x° > 45° – x°
Hence, the complement of an angle > 45° is less than 45°.

Question 9.
In the adjoining figure:

1. Is ∠1 adjacent to ∠2 ?
2. Is ∠ AOC adjacent to ∠ AOE?
3. Do ∠ COE and ∠ EOD form a linear pair?
4. Are ∠ BOD and ∠ DOA supplementary?
5. Is ∠ 1 vertically opposite to ∠ 4?
6. What is the vertically opposite angle of ∠ 5?

Solution:

1. Yes ! ∠ 1 is adjacent to ∠ 2.
2. No ! ∠ AOC is not adjacent to ∠ AOE.
3. Yes! ∠ COE and ∠ EOD form a linear pair.
4. Yes ! ∠ BOD and ∠ DOA are supplementary.
5. Yes ! ∠ 1 is vertically opposite to ∠ 4.
6. The vertically opposite angle of ∠ 5 is ∠ 2 + ∠ 3, i.e., ∠ COB.

Question 10.
Indicate which pairs of angles are:

1. Vertically opposite angles.
2. Linear pairs.

Solution:

1. The pair of vertically opposite angles are ∠1, ∠4; ∠5, ∠2 + ∠3.
2. The pair of linear angles are ∠1, ∠5; ∠4, ∠5.

Question 11.
In the following figure, is ∠ 1 adjacent to ∠ 2? Give reasons.

Solution:
∠1 is not adjacent to ∠2 because they have no common vertex.

Question 12.
Find the values of the angles x, y, and z in each of the following:

Solution:

Question 13.
Fill in the blanks:

1. If two angles are complementary, then the sum of their measures is
2. If two angles are supplementary, then the sum of their measures is
3. Two angles forming a linear pair are
4. If two adjacent angles are supplementary, they form a
5. If two lines intersect at a point, then the vertically opposite angles are always
6. If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are

Solution:

1. 90°
2. 180°
3. supplementary
4. linear pair
5. equal
6. obtuse angles

Question 14.
In the adjoining figure, name the following pairs of angles.

1. Obtuse vertically opposite angles
2. Adjacent complementary angles
3. Equal supplementary angles
4. Unequal supplementary angles
5. Adjacent angles that do not form a linear pair.

Solution:

1. Obtuse vertically opposite angles are ∠AOD and ∠BOC.
2. Adjacent complementary angles are ∠BOA and ∠AOE.
3. Equal supplementary angles are ∠BOE and ∠EOD.
4. Unequal supplementary angles are ∠BOA and ∠AOD, ∠BOC and ∠COD, ∠EOA, and ∠EOC.
5. Adjacent angles that do not form a linear pair are ∠AOB and ∠AOE, ∠AOE and ∠EOD; ∠EOD and ∠COD.

We hope the NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1.

• Playing with Numbers Class 8 Ex 16.2

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 16
Chapter Name	Playing with Numbers
Exercise	Ex 16.1
Number of Questions Solved	1
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1

Question 1.
Find the values of the letters in each of the following and give reasons for the steps involved.

Solution.
1.
Here, there are two letters A and B whose values are to be found out.
Let us see the sum in unit’s column. It is A + 5 and we get 2 from this. So,

2.
Here, there are three letters A, B and C whose values are to be found out.
Let us see the sum in unit’s column. It is A + 8 and we get 3 from this. So A has to be 5

That is, A = 5, B = 4 and C = 1.

4.
Here, there are two letters A and B whose values are to be found out.

5.
Here, there are three letters A, B and C whose values are to be found out.

∴ A = 5, B = 0 and C = 1

6.
Here, there are three letters A, B and C, whose values are to be found out.

7.
Here, there are two letters A and B whose values are to be found out. We have

8.
Here, there are two letters A and B whose values are to be found out.

10.
We are to find out values of A and B

We hope the NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Ex 8.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Ex 8.1.

• Comparing Quantities Class 7 Ex 8.2
• Comparing Quantities Class 7 Ex 8.3
• Comparing Quantities Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 8
Chapter Name	Comparing Quantities
Exercise	Ex 8.1
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Ex 8.1

Question 1.
Find the ratio of:
(a) ₹ 5 to 50 paise
(b) 15 kg to 210 g
(c) 9 m to 27 cm
(d) 30 days to 36 hour

Solution:
(a) ₹ 5 : 50 paise
= ₹ 5 : 50 paise
= 5 × 100 paise : 50 paise
= 500 paise : 50 paise
= 10 : 1.

(b) 15 kg to 210g
= 15 kg : 210g
= 15 × 1000 g : 210g
= 15000 g : 210g = 500:7.

(c) 9 m to 27 cm
= 9m : 27 cm = 9 × 100 cm : 27 cm
= 900 cm : 27 cm
900 : 27 = 100 : 3.

(d) 30 days to 36 hours
= 30 days : 36 hours
30 × 24 hours : 36 hours
= 720 hours : 36 hours
= 720 : 36 = 20 : 1.

Question 2.
In a computer lab, there are 3 computers for every 6 students. How many computers will be needed for 24 students?
Solution:
Let x computers be needed for 24 students.

Hence, 12 computers will be needed for
24 students.
Aliter:
In a computer lab,
Every 6 students need 3 computers.
∴ Every 1 student needs \(\frac { 3 }{ 6 } \) computers.
∴ Every 24 students need \(\frac { 3 }{ 6 } \) × 24 = 3 × 4 = 12 computers

Question 3.
Population of Rajasthan = 570 lakhs
and population of UP = 1660 lakhs.
Area of Rajasthan =3 lakh km2
and area of UP = 2 lakh km2.
(i) How many people are there per km2 in both these States?
(ii) Which State is less populated?
Solution:
(i) Number of people per sq. km. in Rajasthan state

(ii) The Rajasthan State is less populated.

We hope the NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Ex 8.1 helps you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Ex 8.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1.

• Introduction to Graphs Class 8 Ex 15.2
• Introduction to Graphs Class 8 Ex 15.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 15
Chapter Name	Introduction to Graphs
Exercise	Ex 15.1
Number of Questions Solved	7
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1

Question 1.
The following graph shows the temperature of a patient in a hospital, recorded every hour.
(a) What was the patient’s temperature at 1 p.m.?
(b) When was the patient’s temperature 38.5°C?
(c) The patient’s temperature was the same two times during the period given. What were these two times?
(d) What was the temperature at 1.30 p.m.? How did you arrive at your answer?
(e) During which periods did the patient’s temperature showed an upward trend?

Solution.
(а) The patient’s temperature at 1 p.m. was 36.5°C.
(b) The patient’s temperature was 38.5°C at 10.50 a.m. and 12 noon.
(c) The two times when the patient’s temperature was the same were 1 p.m. and 2 p.m.
(d) The temperature at 1.30 p.m. was 36.5°C.
From the graph, we see that the temperature was constant from 1 p.m. to 2 p.m. Since 1.30 p.m. comes in between 1 p.m. and 2 p.m., therefore we arrived at our answer.
(e) The patient’s temperature showed an upward trend during the periods 9 a.m. to 10 a.m., 10 a.m. to 11 a.m. and 2 p.m. to 3 p.m.

Question 2.
The following line graph shows the yearly sales figures for a manufacturing company.
(a) What were the sales in
(i) 2002
(ii) 2006?

(b) What were the sales in
(i) 2003
(ii) 2005?

(c) Compute the difference between sales in 2002 and 2006.
(d) In which year was there the greatest difference between the sales as compared to its previous year?

Solution.
(а) The sales in
(i) 2002 were ₹ 4 crores and in
(ii) 2006 were ₹ 8 crores.

(b) The sales in
(i) 2003 were ₹ 7 crores and in
(ii) 2005 were ₹ 10 crores.

(c) The difference between the sales in 2002 and 2006
= ₹ 8 crores – ₹ 4 crores = ₹ 4 crores

(d) The difference between sales in 2002 and 2003
= ₹ 7 crores – ₹ 4 crores = ₹ 3 crores
The difference between sales in 2003 and 2004
= ₹ 7 crores – ₹ 6 crores = ₹ 1 crore
The difference between the sales in 2004 and 2005
= ₹ 10 crores – ₹ 6 crores = ₹ 4 crores
The difference between sales in 2005 and 2006
= ₹ 10 crores – ₹ 8 crores = ₹ 2 crores
Therefore, in year 2005 the difference between the sales as compared to its previous year was the greatest.

Question 3.
For an experiment in Botany, two different plants, plant A and plant B were grown under similar laboratory conditions. Their heights were measured at the end of each week for 3 weeks. The results are shown by the following graph.

(a) How high was Plant A after
(i) 2 weeks
(ii) 3 weeks?

(b) How high was Plant B after
(i) 2 weeks
(ii) 3 weeks?

(c) How much did Plant A grow during
(d) How much did Plant B grow from the end of the 2nd week to the end of the 3rd week?
(e) During which week did Plant A grow most?
(f) During which week did Plant B grow least?
(g) Were the two plants of the same height during any week shown here? Specify.
Solution.
(а) The Plant A
after (i) 2 weeks was 7 cm high and
after (ii) 3 weeks was 9 cm high.

(b) The Plant B
after (i) 2 weeks was 7 cm high and
after (ii) 3 weeks was 10 cm high.

(c) The Plant A grew 9 cm – 7 cm = 2 cm during the 3rd week.

(d) From the end of the 2nd week to the end of the 3rd week, Plant B grew
= 10 cm – 7 cm = 3 cm.

(e) The Plant A grew in 1st week
= 2 cm – 0 cm = 2 cm
The Plant A grew in 2nd week
= 7 cm – 2 cm = 5 cm
The Plant A grew in 3rd week
= 9 cm – 7 cm = 2 cm
Therefore, Plant A grew mostly in the second week.

(f) Plant B grew in 1st week
= 1 cm – 0 cm = 1 cm
Plant B grew in 2nd week
= 7 cm – 1 cm = 6 cm
Plant B grew in 3rd week
= 10 cm – 7 cm = 3 cm
Therefore, Plant B grew least in the first week.

(g) At the end of 2nd week, the two plants shown here were of the same height.

Question 4.
The following graph shows the temperature forecast and the actual temperature for each day of a week:

(a) On which days was the forecast temperature the same as the actual temperature?
(b) What was the maximum forecast temperature during the week?
(c) What was the minimum actual temperature during the week?
(d) On which day did the actual temperature differ the most from the forecast temperature?
Solution.
(a) The forecast temperature was the same as the actual temperature on Tuesday, Friday and Sunday.
(b) The maximum forecast temperature during the week was 35°C.
(c) The minimum actual temperature during the week was 15°C.
(d)

Therefore, the actual temperature differed the most from the forecast temperature on Thursday.

Question 5.
Use the tables below to draw linear graphs.
(a) The number of days a hill side city received snow in different years.

(b) Population (in thousands) of men and women in a village in different years.

Solution.
(a)

(b)

Question 6.
Courier-person cycles from a town to a neighboring suburban area to deliver a parcel to a merchant. His distance from the town at different times is shown by the following graph.
(a) What is the scale taken for the time axis?
(b) How much time did the person take for the travel?
(c) How far is the place of the merchant from the town?
(d) Did the person stop on his way? Explain.
(e) During which period did he ride fastest?

Solution.
(a) The scale taken for the time axis is 4 units = 1 hour.
(b) The time taken by the person for the travel 8 a.m. to 11.30 a.m. = \(3\frac { 1 }{ 2 } \) hours.
(c) The place of the merchant from the town in 22 km.
(d) Yes. This is indicated by the hori¬zontal part of the graph (10 a.m. – 10.30 a.m.)
(e) He rides fastest between 8 a.m. and 9 a.m. (As line is more steep in this period).

Question 7.
Can there be a time-temperature graph as follows ? Justify your answer.


Solution.
(i) Yes; it can be
It shows a time-temperature graph. It shows an increase in temperature with an increase in time.
(ii) Yes; it can be
It shows a time-temperature graph.
It shows a decrease in temperature with increase in time.
(iii) It cannot be a time-temperature graph because it shows infinitely many different temperatures at one particular time which is not possible.
(iv) Yes; it can be
It shows a time-temperature graph,
It shows a fixed temperature at different times.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1.

• Algebraic Expressions and Identities Class 8 Ex 9.2
• Algebraic Expressions and Identities Class 8 Ex 9.3
• Algebraic Expressions and Identities Class 8 Ex 9.4
• Algebraic Expressions and Identities Class 8 Ex 9.5

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 9
Chapter Name	Algebraic Expressions and Identities
Exercise	Ex 9.1
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1

Question 1.
Identify the terms, their coefficients for each of the following expressions:
(i) \({ 5xyz }^{ 2 }-3zy\)
(ii) \(1+x+{ x }^{ 2 }\)
(iii) \(4{ x }^{ 2 }{ y }^{ 2 }-4{ x }^{ 2 }{ y }^{ 2 }{ z }^{ 2 }+{ z }^{ 2 }\)
(iv) 3 – pq + qr – rp
(v) \(\frac { x }{ 2 } +\frac { y }{ 2 } -xy\)
(vi) 0.3a – 0.6ab + 0.5b.
Solution.
(i) \({ 5xyz }^{ 2 }-3zy\)

(ii) \(1+x+{ x }^{ 2 }\)

(iii) \(4{ x }^{ 2 }{ y }^{ 2 }-4{ x }^{ 2 }{ y }^{ 2 }{ z }^{ 2 }+{ z }^{ 2 }\)

(iv) 3 – pq + qr – rp

(v) \(\frac { x }{ 2 } +\frac { y }{ 2 } -xy\)

(vi)0.3a – 0.6ab + 0.5b.

Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?

Solution.

Question 3.
Add the following.
(i) ab – be, be – ca, ca – ab
(ii) a -b + ab, b – c + be, c – a + ac
(iii) \(2{ p }^{ 2 }{ q }^{ 2 }-3pq+4,\quad 5+7pq-3{ p }^{ 2 }{ q }^{ 2 }\)
(iv) \({ l }^{ 2 }+{ m }^{ 2 },\quad { m }^{ 2 }+{ n }^{ 2 },\quad { n }^{ 2 }+{ l }^{ 2 }\), 2lm + 2mn + 2nl.
Solution.
(i) ab – be, be – ca, ca – ab

(ii) a -b + ab, b – c + be, c – a + ac

(iii) \(2{ p }^{ 2 }{ q }^{ 2 }-3pq+4,\quad 5+7pq-3{ p }^{ 2 }{ q }^{ 2 }\)

(iv) \({ l }^{ 2 }+{ m }^{ 2 },\quad { m }^{ 2 }+{ n }^{ 2 },\quad { n }^{ 2 }+{ l }^{ 2 }\), 2lm + 2mn + 2nl.

Question 4.
(a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 56 – 3
(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract \(4{ p }^{ 2 }q-3pq+5p{ q }^{ 2 }-8p+7q-10\) from \(18-3p-11q+5pq-2p{ q }^{ 2 }+5{ p }^{ 2 }q\)
Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1.

• Direct and Indirect Proportions Class 8 Ex 13.2

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 13
Chapter Name	Direct and Indirect Proportions
Exercise	Ex 13.1
Number of Questions Solved	10
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1

Question 1.
Following are the car parking charges near a railway station up to
4 hours ₹ 60
8 hours ₹ 100
12 hours ₹ 140
24 hours ₹ 180
Check if the parking charges are in direct proportion to the parking time.
Solution.
We have
\(\frac { 60 }{ 4 } =\frac { 15 }{ 1 } \)
\(\frac { 100 }{ 8 } =\frac { 25 }{ 2 } \)
\(\frac { 140 }{ 12 } =\frac { 35 }{ 3 } \)
\(\frac { 180 }{ 24 } =\frac { 15 }{ 2 } \)
Since all the values are not the same, therefore, the parking charges are not in direct proportion to the parking time.

Question 2.
A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of the base. In the following table, find the parts othe f base that need to be added.

Solution.
Sol. Let the number of parts of red pigment is x and the number of parts of the base is y.
As the number of parts of red pigment increases, a number of parts of the base also increases in the same ratio. So it is a case of direct proportion.
We make use of the relation of the type

Question 3.
In Question 2 above, if 1 part of a red pigment requires 75 mL of the base, how much red pigment should we mix with 1800 mL of base?
Solution.
Let the number of parts of red pigment is x and the amount of base be y mL.
As the number of parts of red pigment increases, the amount of base also increases in the same ratio. So it is a case of direct proportion. We make use of the relation of the type.

Question 4.
A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
Solution.
Let the machine fill x bottles in five hours. We put the given information in the form of a table as shown below :
Number of bottles filled 840 x2
Number of hours 6 5
More the number of hours, more the number of bottles would be filled. So, the number of bottles filled and the number of hours are directly proportional to each other.
So, \(\frac { { x }_{ 1 } }{ { x }_{ 2 } } =\frac { { y }_{ 1 } }{ { y }_{ 2 } } \)
⇒ \(\frac { 840 }{ { x }_{ 2 } } =\frac { 6 }{ 5 } \)
⇒ \(6{ x }_{ 2 }=840\times 5\)
⇒ \({ x }_{ 2 }=\frac { 840\times 5 }{ 6 } \)
⇒ \({ x }_{ 2 }=700\)
Hence, 700 bottles will be filled.

Question 5.
A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm as shown in the diagram. What is the actual length of the bacteria ? If the photograph is enlarged 20,000 times only, what would be its enlarged length?

Solution.
Actual length of the bacteria
= \(\frac { 5 }{ 50000 } \)cm
= \(\frac { 1 }{ 10000 } \) = \({ 10 }^{ -4 }\)cm
10000
Let the enlarged length be y2 cm. We put the given information in the form of a table as shown below:
Number of times Length attained
photograph enlarged (in cm)
50.000 5
20.000 y₂
More the number of times a photograph of a bacteria is enlarged, more the length attained. So, the number of times a photograph of a bacteria is enlarged and the length attained are directly proportional to each other.
So,\(\frac { { x }_{ 2 } }{ { y }_{ 2 } } =\frac { { x }_{ 2 } }{ { y }_{ 2 } } \)
⇒ \(\frac { 50000 }{ 5 } =\frac { 20000 }{ { y }_{ 2 } } \)
⇒ \(50000{ y }_{ 2 }=5\times 20000\)
⇒ \({ y }_{ 2 }=\frac { 5\times 20000 }{ 50000 } \)
⇒ \({ y }_{ 2 }=2\)
Hence, its enlarged length would be
2 cm.

Question 6.
In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship ?

Solution.

Question 7.
Suppose 2 kg of sugar contains 9 x 106 crystals. How many sugar crystals are there in
(i) 5 kg of sugar?
(ii) 1.2 kg of sugar?
Solution.
Suppose the amount of sugar is x kg and the number of crystals is y.
We put the given information in the form of a table as shown below:

As the amount of sugar increases, the number of crystals also increases in the same ratio. So it is a case of direct proportion. We make use of the relation of the type \(\frac { { x }_{ 1 } }{ { y }_{ 1 } } =\frac { { x }_{ 2 } }{ { y }_{ 2 } } \)

Question 8.
Rashmi has a roadmap with a scale of 1 cm representing 18 km. She drives on a T’oad for 72 km. What would be her distance covered in the map?
Solution.
Let the distance covered in the map be x cm. Then,
1 : 18 = x : 72
⇒ \(\frac { 1 }{ 18 } =\frac { x }{ 72 }\)
⇒ \(x=\frac { 72 }{ 18 } \)
⇒ x = 4
Hence, the distance covered in the map would be 4 cm.

Question 9.
A5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time
(i) the length of the shadow cast by another pole 10 m 50 cm high
(ii) the height of a pole which casts a shadow 5 m long.
Solution.
Let the height of the vertical pole be x m and the length of the shadow be y m.
We put the given information in the form of a table as shown below:

Question 10.
A loaded truck travels 14 km. in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Solution.
Two quantities x and y which vary in direct proportion have the relation

 

We hope the NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1.

• Factorisation Class 8 Ex 14.2
• Factorisation Class 8 Ex 14.3
• Factorisation Class 8 Ex 14.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 14
Chapter Name	Factorisation
Exercise	Ex 14.1, Ex 14.2, Ex 14.3, Ex 14.4
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1

Question 1.
Find the common factors of the given terms:

Solution.

Question 2.
Factorise the following expressions:

Solution.

Question 3.
Factorise:

Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.1.

• The Triangle and its Properties Class 7 Ex 6.2
• The Triangle and its Properties Class 7 Ex 6.3
• The Triangle and its Properties Class 7 Ex 6.4
• The Triangle and its Properties Class 7 Ex 6.5
• The Triangle and its Properties Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 6
Chapter Name	The Triangle and its Properties
Exercise	Ex 6.1
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.1

Question 1.
In ∆PQR, D is the mid-point of \(\overline { QR } \).

Solution:
\(\overline { PM } \) is the altitude.
PD is the median.
No! QM ≠ MR.

Question 2.
Draw rough sketches for the following:

(a) In ∆ ABC, BE is a median.
(b) In ∆ PQR, PQ and PR are altitudes of the triangle.
(c) In ∆ XYZ, YL is an altitude in the exterior of the triangle.

Solution:

Question 3.
Verify by drawing a diagram if the median and altitude of an isosceles triangle can be the same.
Solution:
AD is the median.
AL is the altitude.

Draw a line segment BC. By paper folding, locate the perpendicular bisector of BC. The folded crease meets BC at D, its mid-point.
Take any point A on this perpendicular bisector. Join AB and AC. The triangle thus obtained is an isosceles ∆ABC in which AB = AC.
Since D is the mid-point of BC, so AD is its median. Also, AD is the perpendicular bisector of BC. So, AD is the altitude of ∆ABC.
Thus, it is verified that the median and altitude of an isosceles triangle are the same.

We hope the NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and it’s Properties Ex 6.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.1, drop a comment below and we will get back to you at the earliest.