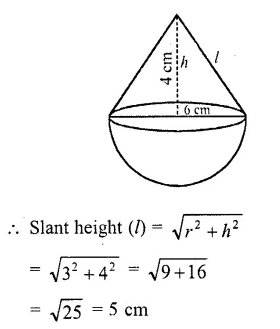
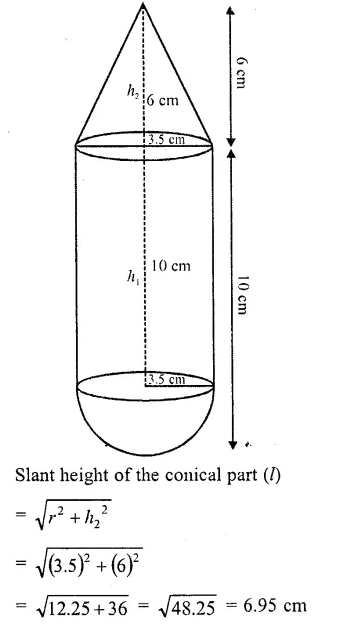
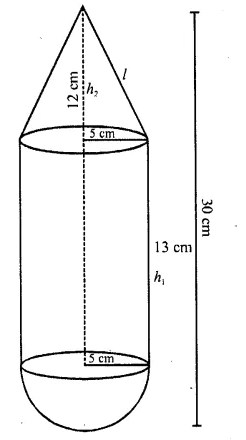
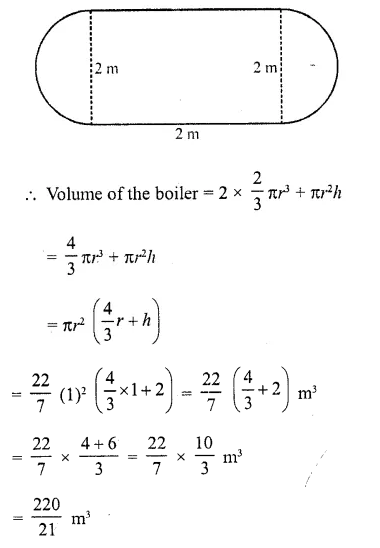
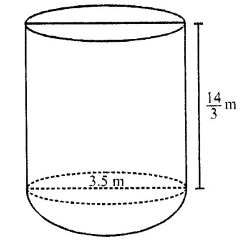
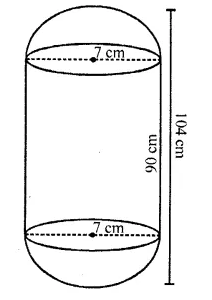
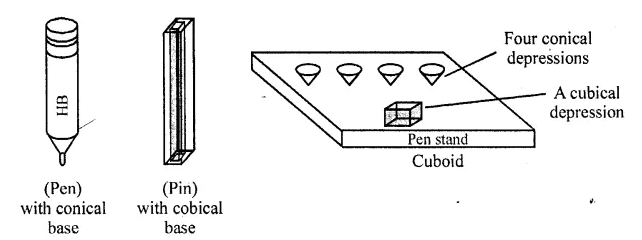
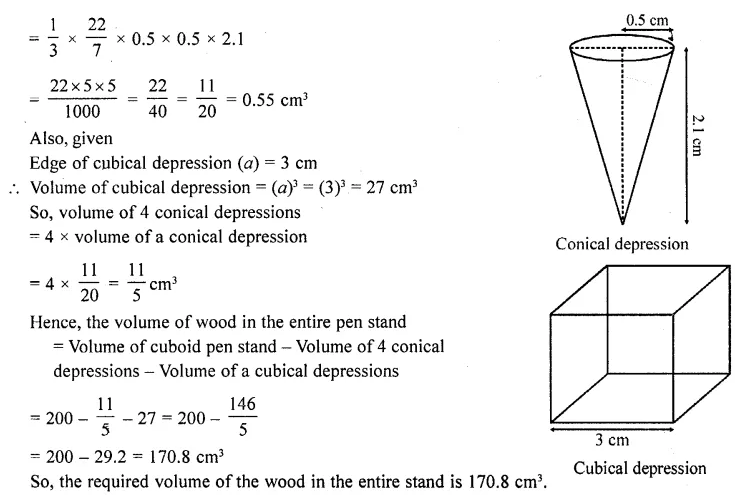
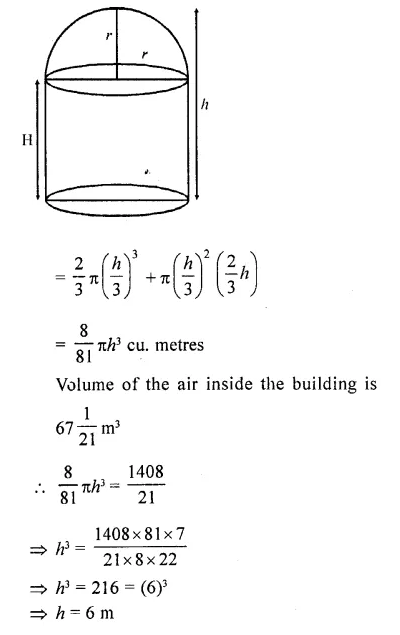
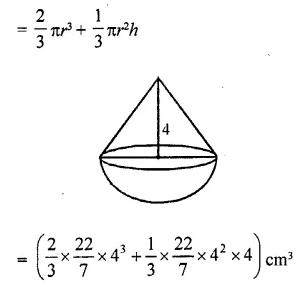
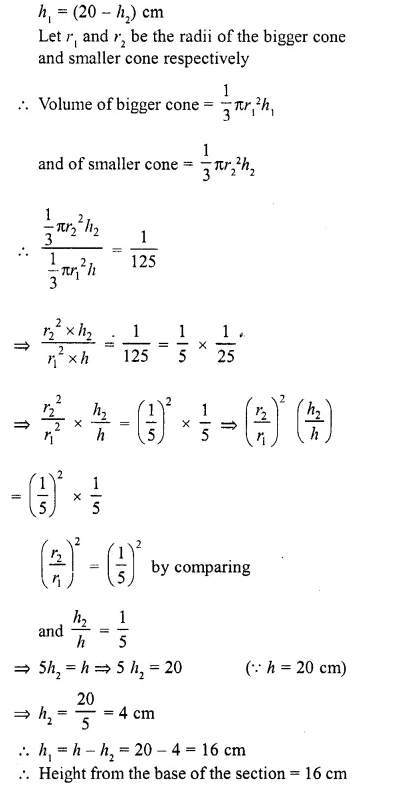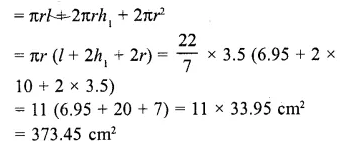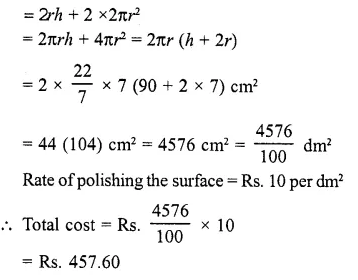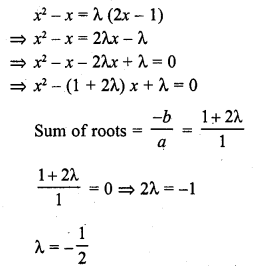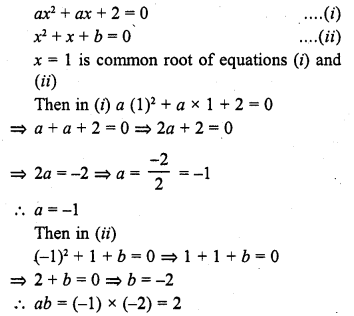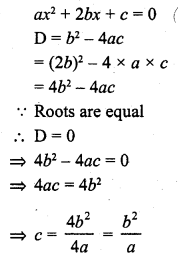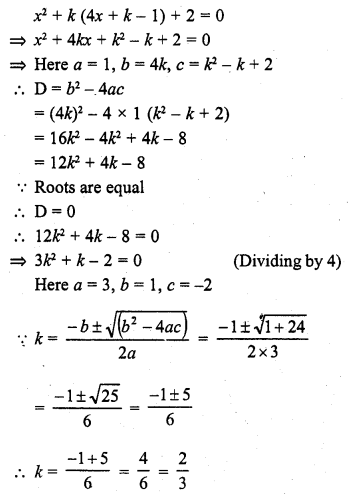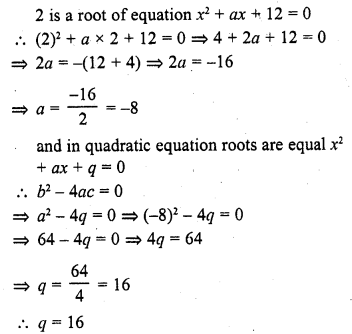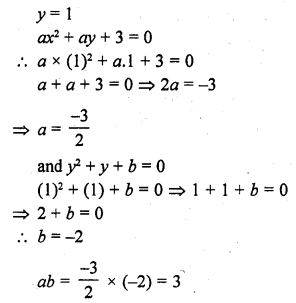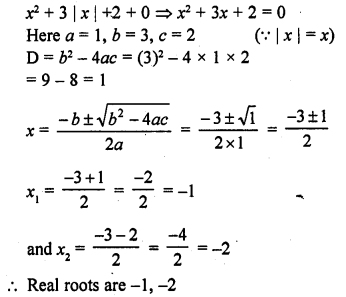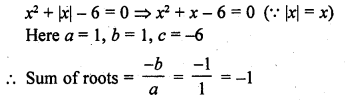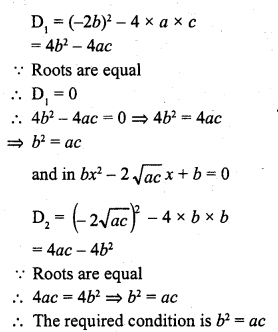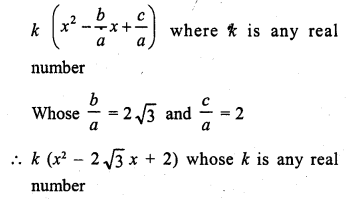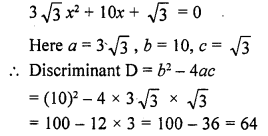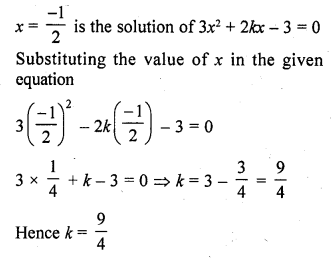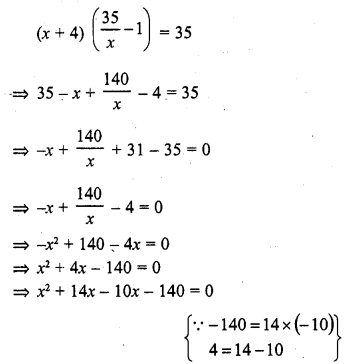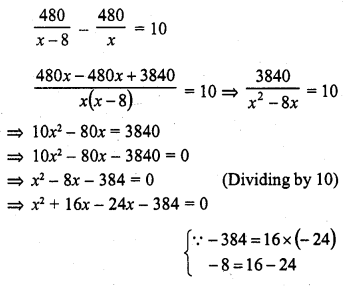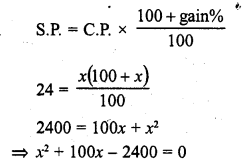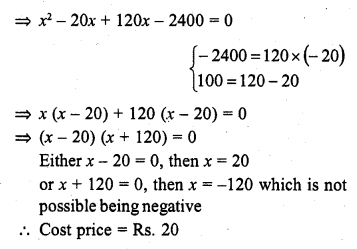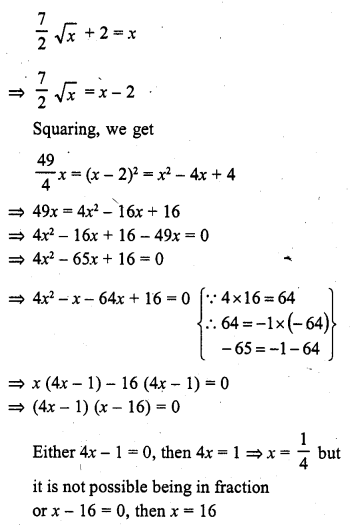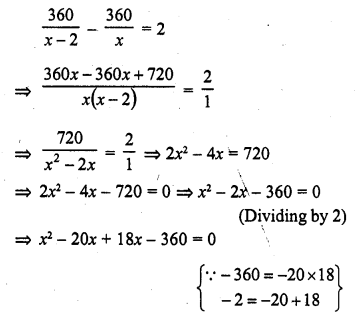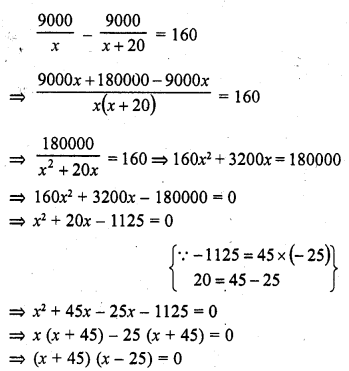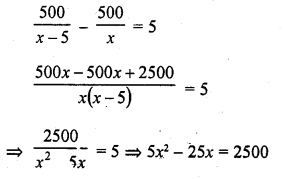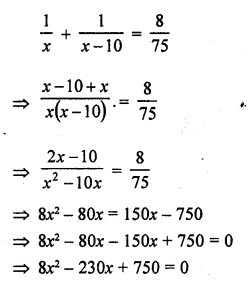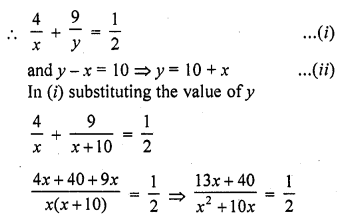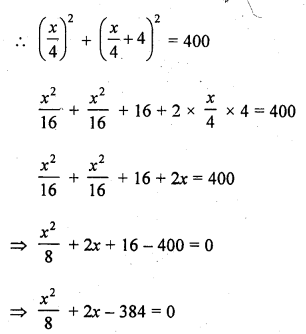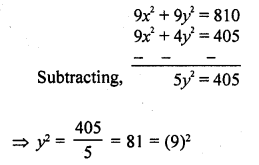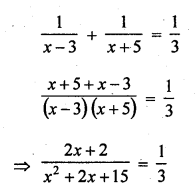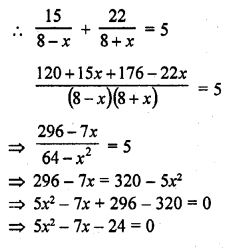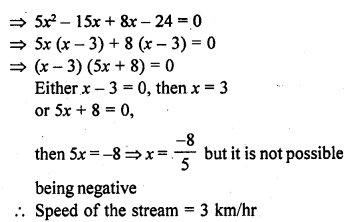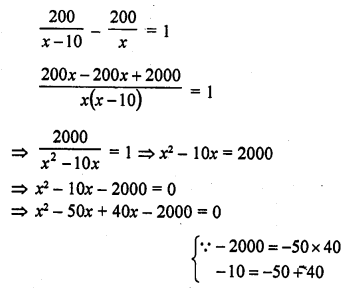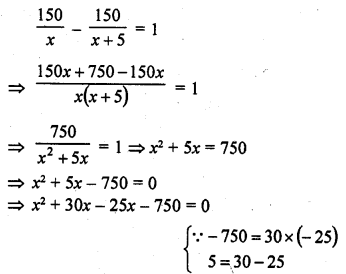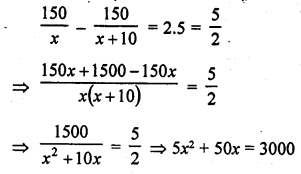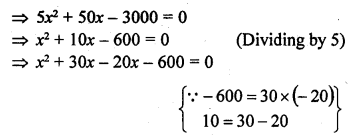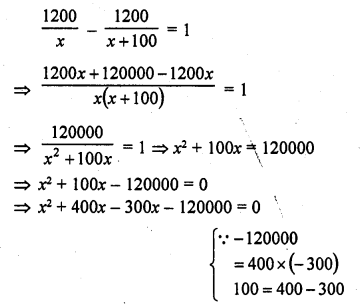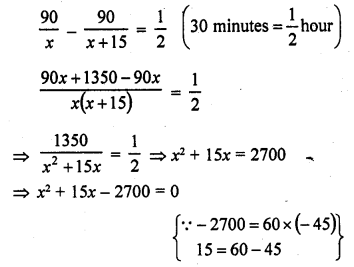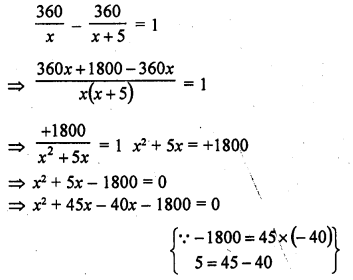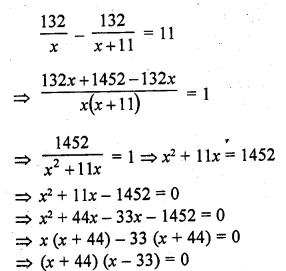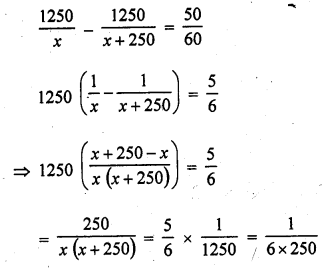RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1
Other Exercises
- RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1
- RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2
- RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.3
- RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.4
- RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.5
- RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6
- RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS
- RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS
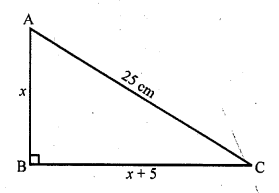
Question 1.
Write the first five terms of each of the following sequences whose nth terms are:
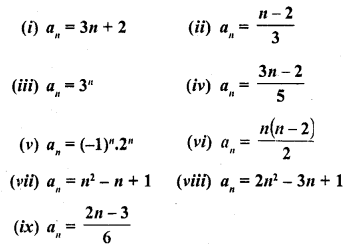
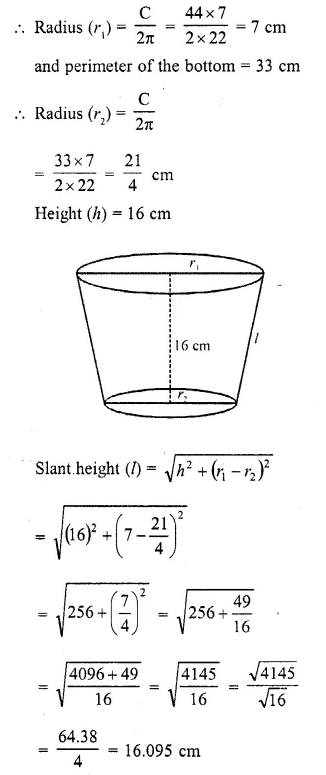
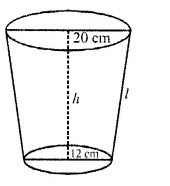
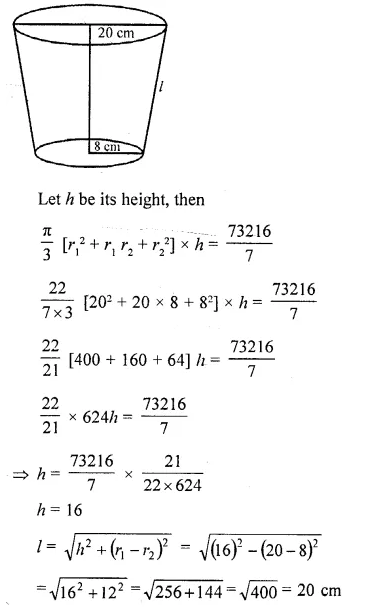
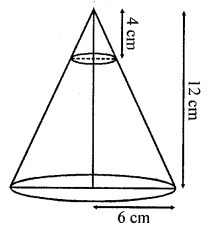
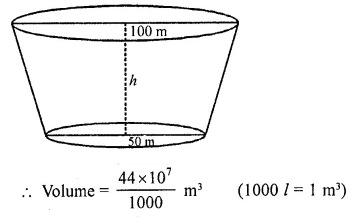
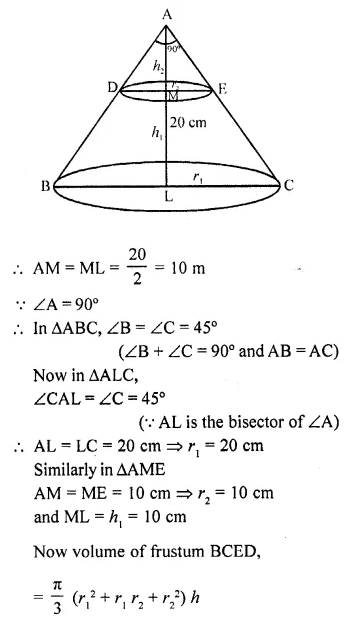
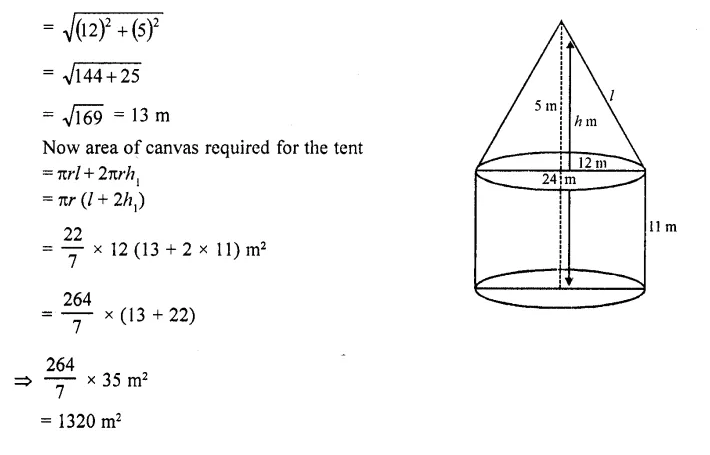
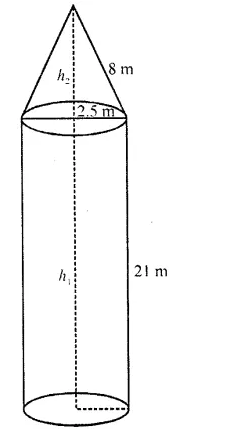
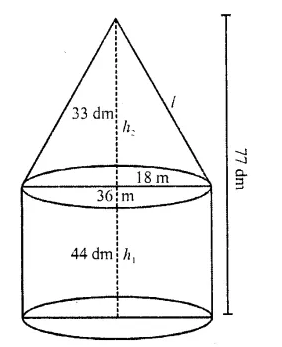
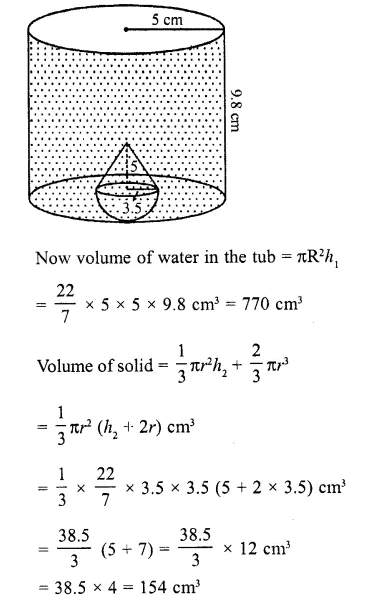
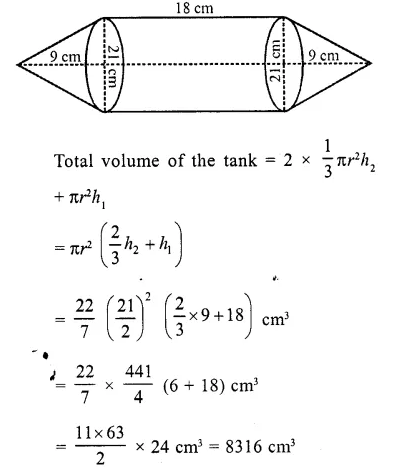
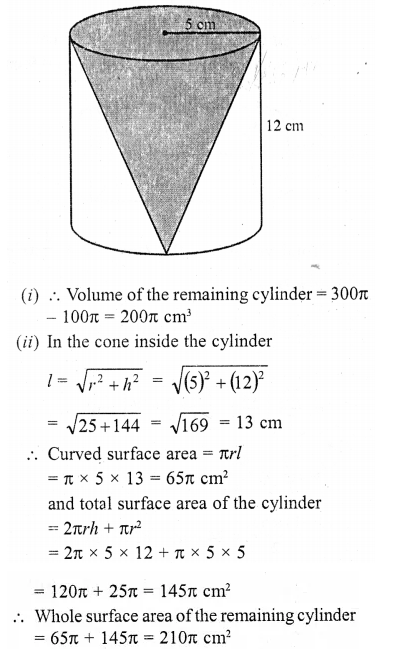
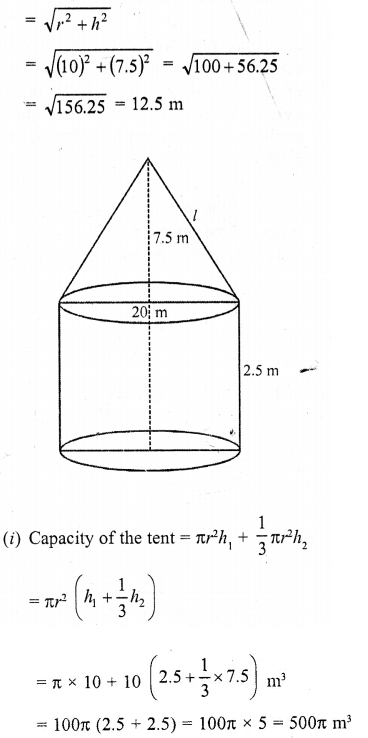
Solution:
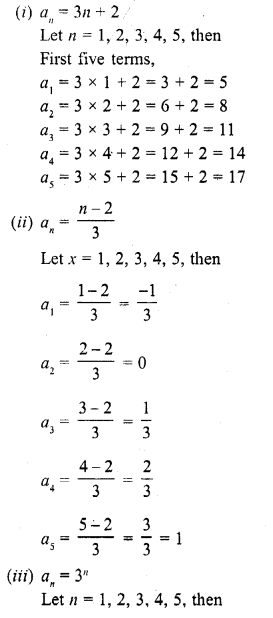
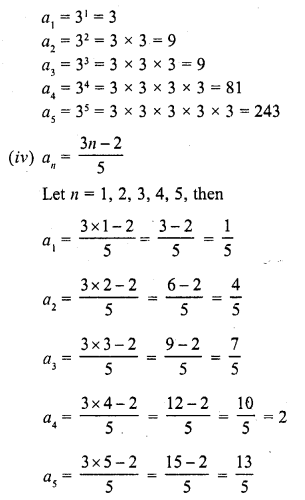
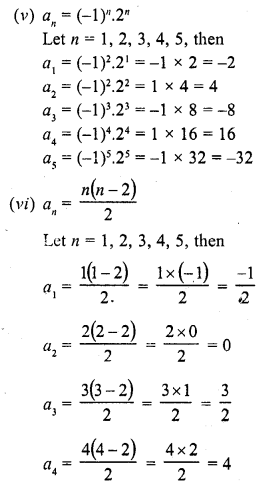
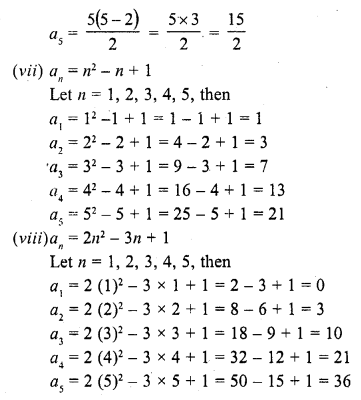
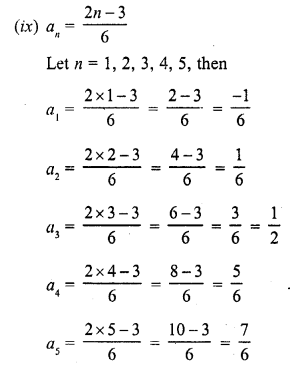
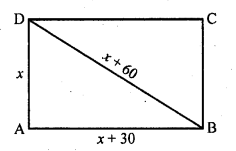
Question 2.
Find the indicated terms in each of the following sequences whose nth terms are:
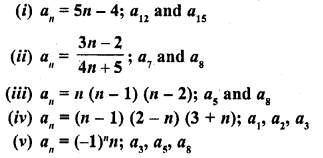
Solution:
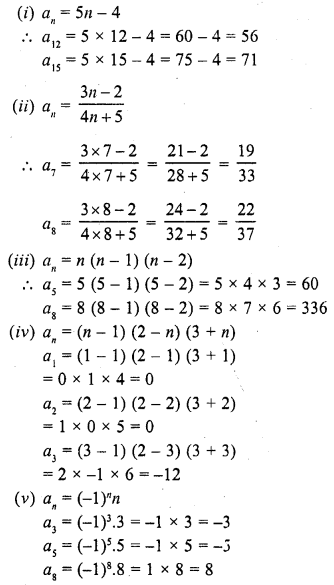
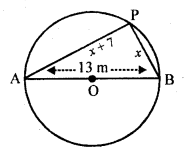
Question 3.
Find the next five terms of each of the following sequences given by :
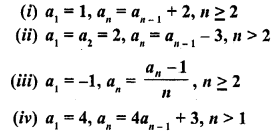
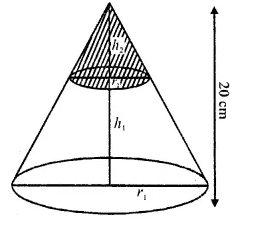
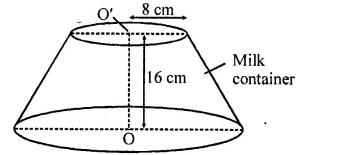
Solution:
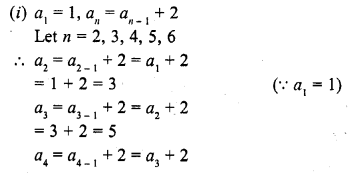
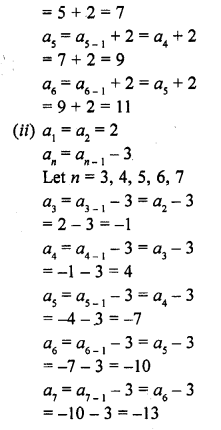
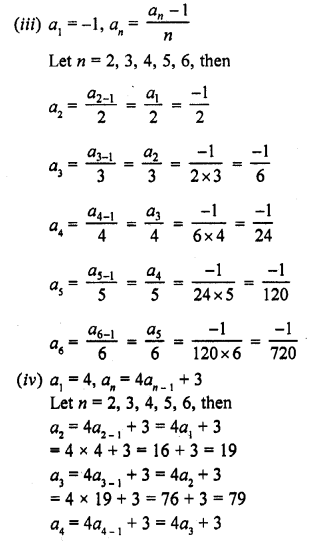
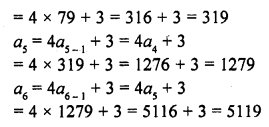
Hope given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.