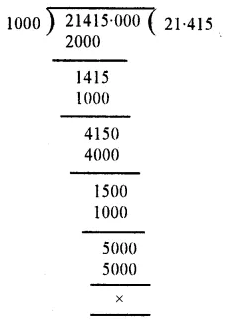
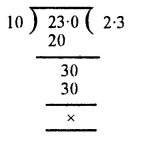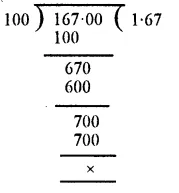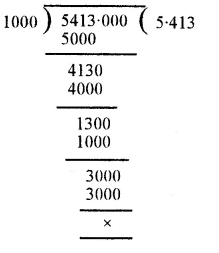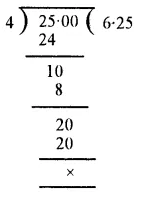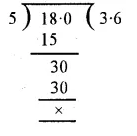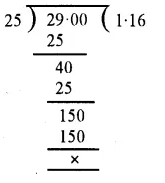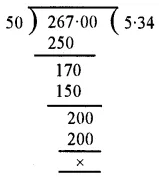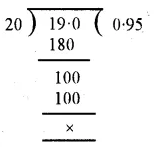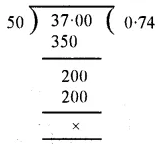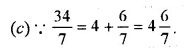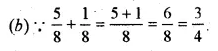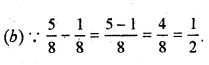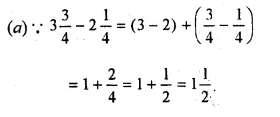RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C

RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 7 Decimals Ex 7C.

Other Exercises

Add the following decimals :

Question 1.
Solution:
9.6, 14.8, 37 and 5.9
Converting these decimals into like decimals and then adding 9.6 + 14.8 + 37.0 + 5.9
= 67.3 Ans.
Working :
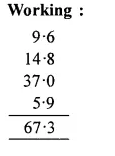
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q1.1

Question 2.
Solution:
23.7, 106.94, 68.9 and 29.5
Converting them into like decimals and then adding
23.70 + 106.94 + 68.90 + 29.50
= 229.04 Ans.
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q2.1

Question 3.
Solution:
72.8, 7.68, 16.23 and 0.7
Converting them into like decimals and then adding
72.80 + 7.68 + 16.23 + 0.70
= 97.41 Ans.
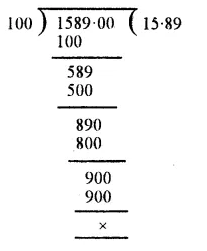
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q3.1

Question 4.
Solution:
18.6, 84.75, 8.345 and 9.7
Converting them into like decimals and then adding
18.600 + 84.750 + 8.345 + 9.700
= 121.395 Ans.
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q4.1

Question 5.
Solution:
8.236, 16.064, 63.8 and 27.53
Converting them into like decimals and then adding
8.236 + 16.064 + 63.800 + 27.530
= 115.630 Ans.
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q5.1

Question 6.
Solution:
28.9, 19.64, 123.697 and 0.354
Converting them into like decimals and then adding
28.900 + 19.640 + 123.697 + 0.354
= 172.591 Ans.
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q6.1

Question 7.
Solution:
4.37, 9.638, 17.007 and 6.8
Converting them into like decimals and then adding
4. 370 + 9.638 + 17.007 + 6.800
= 37.815 Ans.
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q7.1

Question 8.
Solution:
14.5, 0.038, 118.573 and 6.84
Converting them into like decimals and then adding
14.500 + 0.038 + 118.573 + 6.840
= 139.951 Ans.
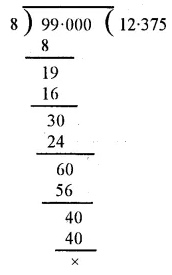
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q8.1

Question 9.
Solution:
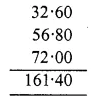
Earning for the first day = 32.60 rupees
Earning for the second day = 56.80 rupees
Earning for the third day = 72 rupees
Total earning = Rs. 32.60 + Rs. 56.80 + Rs. 72
= Rs. 161.40 Ans.
Working
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q9.1

Question 10.
Solution:
Cost of almirah = Rs. 11025
Cartage = Rs. 172.50
Cost on repair = Rs. 64.80
Total cost = Rs. 11025 + Rs. 172.50 + Rs. 64.80
= Rs. 11262.30 Ans.
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q10.1

Question 11.
Solution:
Distance covered by taxi = 36 km 235 m
= 36.235 km
Distance covered by Rickshaw = 4 km 85 m
= 4.085 km
and distance covered on foot
= 1 km 80 m
= 1.080 m
Total distance covered = 36.235 km + 4.085 km + 1.080 km
= 41.400 km
= 41 km 400 m Ans.
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q11.1

Question 12.
Solution:
Weight of sugar in a bag = 45 kg 80 g
= 45.080 kg
Mass (weight) of empty bag = 950 g
= 0.950 kg
Total weight of the bag with sugar = 45 kg 80 g + 950 g
= 45.080 kg + 0.950 kg
= 46.030 kg
= 46 kg 30 g Ans.
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q12.1

Question 13.
Solution:
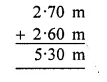
Length of cloth for shirt = 2 m 70 cm
= 2.70 m
Length of cloth for pyjamas = 2 m 60 cm
= 2.60 m
Total length of cloth = 2.70 m + 2.60 m
= 5.30 m
= 5 m 30 cm Ans.
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q13.1

Question 14.
Solution:
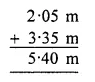
Cloth of salwar = 2 m 5 cm = 2.05 m
Cloth for shirt = 3 m 35 cm = 3.35 m
Total length of cloth = 2.05 m + 3.35 m
= 5.4.0 m
= 5 m 40 cm Ans.
Working :
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7C Q14.1

Hope given RS Aggarwal Solutions Class 6 Chapter 7 Decimals Ex 7C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B

RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 7 Decimals Ex 7B.

Other Exercises

Convert each of the following into a fraction in its simplest form :

Question 1.
Solution:
.9 = \(\\ \frac { 9 }{ 10 } \)

Question 2.
Solution:
0.6
= \(\\ \frac { 6 }{ 10 } \)
= \(\frac { 6\div 2 }{ 10\div 2 }\)
= \(\\ \frac { 3 }{ 5 } \)
(Dividing by 2, the HCF of 6, 10)

Question 3.
Solution:
.08
= \(\\ \frac { 8 }{ 100 } \)
= \(\frac { 8\div 4 }{ 100\div 4 }\)
= \(\\ \frac { 2 }{ 25 } \)
(Dividing by 4, the HCF of 7, 100)

Question 4.
Solution:
0.15
= \(\\ \frac { 15 }{ 100 } \)
= \(\frac { 15\div 5 }{ 100\div 5 }\)
= \(\\ \frac { 3 }{ 20 } \)
(Dividing by 5, the HCF of 15, 100)

Question 5.
Solution:
0.48
= \(\\ \frac { 48 }{ 100 } \)
= \(\frac { 48\div 4 }{ 100\div 4 }\)
= \(\\ \frac { 12 }{ 25 } \)
(Dividing by 4, the HCF of 48, 100)

Question 6.
Solution:
0.53
= \(\\ \frac { 53 }{ 1000 } \)

Question 7.
Solution:
= \(\\ \frac { 125 }{ 1000 } \)
= \(\frac { 125\div 125 }{ 1000\div 125 }\)
= \(\\ \frac { 1 }{ 8 } \)
(Dividing by 125, the HCF of 125, 1000)

Question 8.
Solution:
.224
= \(\\ \frac { 224 }{ 1000 } \)
= \(\frac { 224\div 8 }{ 1000\div 8 }\)
= \(\\ \frac { 28 }{ 125 } \)
(Dividing by 8, the HCF of 224, 1000)

Convert each of the following as a mixed fraction

Question 9.
Solution:
6.4
= \(\\ \frac { 64 }{ 10 } \)
= \(\frac { 64\div 2 }{ 10\div 2 }\)
= \(\\ \frac { 32 }{ 6 } \)
= \(6 \frac { 2 }{ 5 } \)
(Dividing by 2, the HCF of 64, 10)

Question 10.
Solution:
16.5
= \(\\ \frac { 165 }{ 10 } \)
= \(\frac { 165\div 5 }{ 10\div 5 }\)
= \(\\ \frac { 33 }{ 2 } \)
= \(16 \frac { 1 }{ 2 } \)
(Dividing by 5, the HCF of 165, 10)

Question 11.
Solution:
8.36
= \(\\ \frac { 836 }{ 100 } \)
= \(\frac { 836\div 4 }{ 100\div 4 }\)
= \(\\ \frac { 209 }{ 25 } \)
= \(8 \frac { 9 }{ 25 } \)
(Dividing by 4, the HCF of 836, 100)

Question 12.
Solution:
4.275
= \(\\ \frac { 4275 }{ 1000 } \)
= \(\frac { 4275\div 25 }{ 1000\div 25 }\)
= \(\\ \frac { 171 }{ 40 } \)
= \(4 \frac { 11 }{ 40 } \)
(Dividing by 25 )

Question 13.
Solution:
25.06
= \(\\ \frac { 2506 }{ 100 } \)
= \(\frac { 2506\div 2 }{ 100\div 2 }\)
= \(\\ \frac { 1253 }{ 50 } \)
= \(25 \frac { 3 }{ 50 } \)
(Dividing by 2 )

Question 14.
Solution:
7.004
= \(\\ \frac { 7004 }{ 1000 } \)
= \(\frac { 7004\div 4 }{ 1000\div 4 }\)
= \(\\ \frac { 1751 }{ 250 } \)
= \(7 \frac { 1 }{ 250 } \)
(Dividing by 4)

Question 15.
Solution:
2.052
= \(\\ \frac { 2052 }{ 1000 } \)
= \(\frac { 2052\div 4 }{ 1000\div 4 }\)
= \(\\ \frac { 513 }{ 250 } \)
= \(2 \frac { 13 }{ 250 } \)
(Dividing by 4)

Question 16.
Solution:
3.108
= \(\\ \frac { 3108 }{ 1000 } \)
= \(\frac { 3108\div 4 }{ 1000\div 4 }\)
= \(\\ \frac { 777 }{ 250 } \)
= \(3 \frac { 27 }{ 250 } \)
(Dividing by 4)

Question 17.
Solution:
\(\\ \frac { 23 }{ 10 } \)
= 2.3
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q17.1

Question 18.
Solution:
\(\\ \frac { 167 }{ 100 } \)
= 1.67
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q18.1

Question 19.
Solution:
\(\\ \frac { 1589 }{ 100 } \)
= 15.89
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q19.1

Question 20.
Solution:
\(\\ \frac { 5413 }{ 1000 } \)
= 5.413
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q20.1

Question 21.
Solution:
\(\\ \frac { 21415 }{ 1000 } \)
= 21.415
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q21.1

Question 22.
Solution:
\(\\ \frac { 25 }{ 4 } \)
= 6.25
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q22.1

Question 23.
Solution:
\(3 \frac { 3 }{ 5 } \)
= \(\\ \frac { 3\times 5+3 }{ 5 } \)
= \(\\ \frac { 15+3 }{ 5 } \)
= \(\\ \frac { 18 }{ 5 } \)
= 3.6
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q23.1

Question 24.
Solution:
\(1 \frac { 4 }{ 25 } \)
= \(\\ \frac { 1\times 25+4 }{ 25 } \)
= \(\\ \frac { 25+4 }{ 25 } \)
= \(\\ \frac { 29 }{ 25 } \)
= 1.16
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q24.1

Question 25.
Solution:
\(5 \frac { 17 }{ 50 } \)
= \(\\ \frac { 5\times 50+17 }{ 50 } \)
= \(\\ \frac { 250+17 }{ 50 } \)
= \(\\ \frac { 267 }{ 50 } \)
= 5.34
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q25.1

Question 26.
Solution:
\(12 \frac { 3 }{ 8 } \)
= \(\\ \frac { 12\times 8+3 }{ 8 } \)
= \(\\ \frac { 96+3 }{ 8 } \)
= \(\\ \frac { 99 }{ 8 } \)
= 12.375
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q26.1

Question 27.
Solution:
\(2 \frac { 19 }{ 40 } \)
= \(\\ \frac { 2\times 40+19 }{ 40 } \)
= \(\\ \frac { 80+19 }{ 40 } \)
= \(\\ \frac { 99 }{ 40 } \)
= 2.475
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q27.1

Question 28.
Solution:
\(\\ \frac { 19 }{ 20 } \)
= 0.95
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q28.1

Question 29.
Solution:
\(\\ \frac { 37 }{ 50 } \)
= 0.74
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q29.1

Question 30.
Solution:
\(\\ \frac { 107 }{ 250 } \)
= 0.428
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q30.1

Question 31.
Solution:
\(\\ \frac { 3 }{ 40 } \)
= 0.075
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q31.1

Question 32.
Solution:
\(\\ \frac { 7 }{ 8 } \)
= 0.875
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q32.1

Question 33.
Solution:
(i) 8 kg 640 g in kilograms
= \(8 \frac { 640 }{ 1000 } \) kg
= 8.640kg
(ii) 9 kg 37 g in kilograms
= \(9 \frac { 37 }{ 1000 } \) kg
= 9.037 kg.
(iii) 6 kg 8 g in kilograms
= \(6 \frac { 8 }{ 1000 } \) kg
= 6.008 kg Ans.

Question 34.
Solution:
(i) 4 km 365 m in kilometres
= \(4 \frac { 365 }{ 1000 } \) km
= 4.365 km
(ii) 5 km 87 m in kilometres
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q34.1

Question 35.
Solution:
(i) 15 kg 850 g in kilograms
= \(15 \frac { 850 }{ 1000 } \) kg
= 15.850 kg
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q35.1

Question 36.
Solution:
(i) Rs. 18 and 25 paise in rupees
= \(18 \frac { 25 }{ 100 } \)
= 18.25 rupees
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7B Q36.1

Hope given RS Aggarwal Solutions Class 6 Chapter 7 Decimals Ex 7B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7A

RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 7 Decimals Ex 7A.

Other Exercises

Question 1.
Solution:
(i)Fifty eight point six three = 58.63
(ii)One hundred twenty four point four two five = 124.425
(iii)Seven point seven six = 7.76
(iv)Nineteen point eight = 19.8
(v)Four hundred four point zero four four = 404.044
(vi)Point one seven three = 173
(v)Point zero one five = .015 Ans.

Question 2.
Solution:
(i) 14.83
Place value of 1 = 10,
Place value of 4 = 4,
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7A Q2.1
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7A Q2.2
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7A Q2.3

Question 3.
Solution:
(i) 67.83 = (6 x 10) + (7 x 1)
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7A Q3.1

Question 4.
Solution:
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7A Q4.1

Question 5.
Solution:
(i) 7.5, 64.23, 0.074 = 7.500, 64.230, 0.074
(Here, at the most 0.074 has 3 places)
(ii) 0.6, 5.937, 2.36, 4.2 = 0.600, 5.937, 2.360, 4.200
(Here, 5.937 has at most 3 places)
(iii) 1.6, 0.07, 3.58, 2.9 = 1.60, 0.07, 3.58, 2. 90
(Here, at the most are two places)
(iv) 2.5. 0.63, 14.08, 1.637 = 2.500, 0.630. 14.080, 1.637 Ans.
(Here, at the most are three places)

Question 6.
Solution:
Making like decimals where ever it is necessary,
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7A Q6.1

Question 7.
Solution:
First of all making them in like decimals,
(i) 5.8, 7.2, 5.69, 7.14, 5.06
=> 5.80, 7.20, 5.69, 7.14, 5.06
Arranging in ascending order,
5:06 <5.69 <5.80 <7.14 <7.20
=> 5.06 < 5.69 < 5.8 < 7.14 < 7.2 Ans.
(ii) 0.6, 6.6, 6.06, 66.6, 0.06
=>0.60, 6.60, 6.06, 66.60, 0.06
Arranging in ascending order,
0.06 < 0.60 < 6.06 < 6.60 < 66.60
=> 0.06 < 0.6 < 6.06 < 6.6 < 66.6 Ans.
(iii) 6.54, 6.45, 6.4, 6.5, 6.05
=> 6.54, 6.45, 6.4, 6.5, 6.05
Arranging in ascending order,
6. 05 < 6.40 < 6.45 < 6.50 < 6.54
=> 6.05 < 6.4 < 6.45 < 6.5 < 6.54 Ans.
(iv) 3.3,3.303, 3.033, 0.33, 3.003
=> 3.300, 3.303, 3.033, 0.330, 3.003
Arranging in descending order,
0.330 < 3.003 < 3.033 < 3.300 < 3.303
=> 0.33 < 3.003 < 3.033 < 3.3 < 3.303 Ans.

Question 8.
Solution:
Making them in like decimals and them comparing
(i) 7.3, 8.73, 73.03, 7.33, 8.073
=> 7.300, 8.730, 73.030, 7.330, 8.073
Arranging in descending order
73.030 > 8.730 > 8.073 > 7.330 > 7.300
=> 73.03 > 8.73 > 8.073 > 7.33 > 7.3 Ans.
(ii) 3.3, 3.03, 30.3, 30.03, 3.003
=> 3.300, 3.030, 30.300, 30.030, 3.003
Arranging in descending order
30.300> 30.030 >3.300 >3.030 > 3.003
=> 30.3 > 30.03 > 3.3 > 3.03 > 3.003 Ans.
(iii) 2.7, 7.2, 2.27, 2.72, 2.02, 2.007
=> 2.700, 7.200, 2.270, 2.720, 2.020, 2.007
Arranging in descending order
7. 200 > 2.720 > 2.700 > 2.270 > 2.020 > 2.007
=> 7.2 > 2.72 > 2.7 > 2.27 > 2.02 > 2.007 Ans.
(iv) 8.88, 8.088, 88.8, 88.08, ,8.008
=> 8.880, 8.088, 88.800, 88.080, 8.008
Arranging in descending order,
88.800 > 88.080 > 8.880 > 8.088 > 8.008
=> 88.8 > 88.08 > 8.88 > 8.088 > 8.008

 

Hope given RS Aggarwal Solutions Class 6 Chapter 7 Decimals Ex 7A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 6 Simplification Ex 6B

RS Aggarwal Class 6 Solutions Chapter 6 Simplification Ex 6B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 6 Simplification Ex 6B.

Other Exercises

OBJECTIVE QUESTIONS
Mark against the correct answer in each of the following :

Question 1.
Solution:
(c) 8 + 4 ÷ 2 x 5
= 8 + 4 x \(\\ \frac { 1 }{ 2 } \) x 5
= 8 + 10
= 18.

Question 2.
Solution:
(b) 54 ÷ 3 of 6 + 9 = 54 ÷ 18 + 9
= 54 x \(\\ \frac { 1 }{ 18 } \) + 9
= 3 + 9
= 12.

Question 3.
Solution:
(b) 13 – (12 – 6 ÷ 3)
= 13 – (12 – 2)
= 13 – 10
= 3

Question 4.
Solution:
(a) 1001 ÷ 11 of 13
= 1001 ÷ 143
= 1001 x \(\\ \frac { 1 }{ 143 } \)
= 7.

Question 5.
Solution:
(b) 133 + 28 ÷ 7 – 8 x 2
= 133 + 4 – 16
= 137 – 16
= 121.

Question 6.
Solution:
(a) 3640 – 14 ÷ 7 x 2
= 3640 – 2 x 2
= 3640 – 4
= 3636.

Question 7.
Solution:
(b) 100 x 10 – 100 + 2000 ÷ 100
= 1000 – 100 + 20
= 920.

Question 8.
Solution:
(b) \(27-\left[ 18-\left\{ 16-\left( 5-\overline { 4-1 } \right) \right\} \right] \)
= 27 – [18 – {16 – (5 – 4 + 1)}]
= 27 – [18 – {16 – 5 + 4 – 1}]
= 27 – [18 – 16 + 5 – 4 + 1]
= 27 – 18 + 16 – 5 + 4 – 1
= 23

Question 9.
Solution:
\(32-\left[ 48\div \left\{ 36-\left( 27-\overline { 16-9 } \right) \right\} \right] \)
= 32 – [48 ÷ {36 – (27 – 16 + 9)}]
= 32 – [48 ÷ {36 – 27 + 16 – 9}]
= 32 – [48 ÷ 16]
= 32 – 3
= 29

Question 10.
Solution:
(a) 8 – [28 ÷ {34 – (36 – 18 ÷ 9 x 8)}]
\(8-\left[ 28\div \left\{ 34-\left( 36-18\times \frac { 1 }{ 9 } \times 8 \right) \right\} \right] \)
= 8 – [28 ÷ {34 – (36 – 16)}]
= 8 – [28 ÷ {34 – 20}]
= 8 – {28 ÷ 14}
= 8 – 2
= 6.

Hope given RS Aggarwal Solutions Class 6 Chapter 6 Simplification Ex 6B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G

RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G.

Other Exercises

Objective Questions :
Tick the correct answer in each of the following :

Question 1.
Solution:
(c) ∴ canceling the common factor 2, we get \(\\ \frac { 3 }{ 5 } \)

Question 2.
Solution:
(c) ∴ multiplying numerator and denominator by 4, we get \(\\ \frac { 8 }{ 12 } \)

Question 3.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 3.1

Question 4.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 4.1

Question 5.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 5.1

Question 6.
Solution:
(c) each of the fractions has the same denominator.

Question 7.
Solution:
(d) none of these has greater denominator than its numerator.

Question 8.
Solution:
(a) its denominator is greater than its numerator.

Question 9.
Solution:
(b) their numerators are same and 4 < 5 , \(\frac { 3 }{ 4 } >\frac { 3 }{ 5 } \)

Question 10.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 10.1

Question 11.
Solution:
(b) In \(\frac { 4 }{ 5 } ,\frac { 2 }{ 7 } ,\frac { 4 }{ 9 } ,\frac { 4 }{ 11 } \) numerator is same then the smallest denominator’s fraction is greater.

Question 12.
Solution:
(a) Denominators are same, then fraction of smallest numerator will be smallest.

Question 13.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 13.1

Question 14.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 14.1

Question 15.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 15.1

Question 16.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 16.1

Question 17.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 17.1

Question 18.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 18.1

Question 19.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 19.1

Question 20.
Solution:
RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5G 20.1

Hope given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.9

NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.9 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.9.

Board CBSE
Textbook NCERT
Class Class 6
Subject Maths
Chapter Chapter 5
Chapter Name Understanding Elementary Shapes
Exercise  Ex 5.9
Number of Questions Solved 2
Category NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.9

Chapter 5 Understanding Elementary Shapes Ex 5.9

Question 1.
Match the following :
(a) Cone
NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes 31
(b) Sphere
NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes 32
(c) Cylinder
NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes 33
(d) Cuboid
NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes 34
(e) Pyramid
NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes 35
Give two new examples of each shape.
Solution :
(a) ↔ (ii)
(b) ↔ (iv)
(c) ↔ (v)
(d) ↔ (iii)
(e) ↔ (i).
(i) Birthday cap, ice-cream cone
(ii) Tennis Ball, laddu
(iii) Road-roller, gas cylinder
(iv) Brick, book
(v) Pyramids of Egypt, right pyramid.

Question 2.
What shape is
(a) Your installments box?
(b) A brick?
(c) A matchbox?
(d) A road-roller?
(e) A sweet laddu?
Solution :
(a) Cuboid
(b) Cuboid
(c) Cuboid
(d) Cylinder
(e) Sphere.

We hope the NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.9 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.9, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6.

Board CBSE
Textbook NCERT
Class Class 6
Subject Maths
Chapter Chapter 14
Chapter Name Practical Geometry
Exercise  Ex 14.6
Number of Questions Solved 9
Category NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6

Question 1.
Draw ∠POQ of measure 75° and find its line of symmetry.
Solution :
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 25
Step 1. Draw a ray \(\overline { OQ }\).
Step 2. Place the center of the protractor at O and the ∠ero edge along \(\overline { OQ }\).
Step 3. Start with 0 near Q. Mark point P at 75°
Step 4. Join \(\overline { OP }\). Then, ∠POQ = 75°.
Step 5. With O as center and using compasses, draw an arc that cuts both rays of ∠POQ. Label the points of intersection as F and Q’.
Step 6. With Q’ as center, draw (in the interior of ∠POQ) an arc whose radius is more than half the length Q’F.
Step 7. With the same radius and with F as center, draw another arc in the interior of ∠POQ. Let
the two arcs intersect at R. Then, \(\overline { OR }\) is the bisector of ∠POQ which is also the line of symmetry of ∠POQ as ∠POR = ∠ROQ.

Question 2.
Draw an angle of measure 147° and construct its bisector.
Solution :
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 26
Step 1. Draw \(\overline { OQ }\) of any length.
Step 2. Place the center of the protractor at O and the ∠ero edge along \(\overline { OQ }\).
Step 3. Start with 0 near Q. Mark a point P at 147°.
Step 4. Join OP. Then, ∠POQ = 147°.
Step 5. With O as center and using compasses, draw an arc that cuts both rays of ∠POQ. Label the points of intersection as F and Q’.
Step 6. With Q’ as center, draw (in the interior of ∠POQ) an arc whose radius is more than half the length Q’F.
Step 7. With the same radius and with F as center, draw another arc in the interior of ∠POQ. Let the two arcs intersect at R. Then, \(\overline { OR }\) is the bisector of ∠POQ.

Question 3.
Draw a right angle and construct its bisector.
Solution :
Step 1. Draw a ray OQ.
Step 2. Place the center of the protractor at O and the ∠ero edge along \(\overline { OQ }\).
Step 3. Start with 0 near Q. Mark point P at 90°.
Step 4. Join \(\overline { OP }\). Then, ∠POQ = 90°.
Step 5. With O as center and using compasses, draw an arc that cuts both rays of ∠POQ. Label the points of intersection as F and Q’.
Step 6. With Q’ as center, draw (in the interior of ∠POQ) an arc whose radius is more than half th length Q’F.
Step 7. With the same radius and with P center, draw another arc in the interior of ∠POQ the two arcs intersect at R. Then, \(\overline { OR }\) is the bisector of ∠POQ.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 27
Question 4.
Draw an angle of measure 153° and divide it into four equal parts.
Solution :
Step 1. Draw a ray \(\overline { OQ }\).
Step 2. Place the center of the protractor at O and the ∠ero edge along \(\overline { OQ }\).
Step 3. Start with 0 near Q. Mark a point P at 153°.
Step 4. Join OP. Then, ∠POQ = 153°.
Step 5. With O as the center and using compasses, draw an arc that cuts both rays of ∠POQ. Label the points of intersection as F and Q.
Step 6. With Q’ as the center, draw (in the interior of ∠POQ) an arc whose radius is more than half the length Q’F.
Step 7. With the same radius and with F as a center, draw another arc in the interior of ∠POQ. Let the two arcs intersect at R. Then, \(\overline { OR }\) is the bisector of ∠POQ.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 28
Step 8. With O as a center and using compasses, draw an arc that cuts both rays of ∠ROQ. Label the points of intersection as B and A.
Step 9. With A as a center, draw (in the interior of ∠ROQ) an arc whose radius is more than half the length AB.
Step 10. With the same radius and with B as a center, draw another arc in the interior of ∠ROQ. Let the two arcs intersect at S. Then, \(\overline { OS }\) is the bisector of ∠ROQ.
Step 11. With O as a center and using compasses, draw an arc that cuts both rays of ∠POR. Label the points of intersection as D and C.
Step 12. With C as a center, draw (in the interior of ∠POR) an arc whose radius is more than half the length CD.
Step 13. With the same radius and with D as centre, draw another arc in the interior of ∠POR. Let the two arcs intersect at T. Then, \(\overline { OT }\) is the bisector of ∠POR. Thus, \(\overline { OS }\), \(\overline { OR }\) and \(\overline { OT }\) divide ∠POQ = 153° into four equal parts.

Question 5.
Construct with ruler and compasses, angles of following measures:
(a) 60°
(b) 30°
(c) 90°
(d) 120°
(e) 45°
(f) 135°.
Solution :
(a) Construction of an angle of measure 60°
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 29
Step 1. Draw a line PQ and mark a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line PQ at a point say A.
Step 3. With the pointer at A (as center), now draw an arc that passes through O.
Step 4. Let the two arcs intersect at B. Join OB. We get ∠BOA whose measure is 60°.

(b) Construction of an angle of measure 30°
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 30
Step 1. Draw a line PQ and mark a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line PQ at a point say A.
Step 3. With the pointer at A (as center), now draw an arc that passes through O.
Step 4. Let the two arcs intersect at B. Join OB. We get ∠BOA whose measure is 60°.
Step 5. With O as a center and using compasses, draw an arc that cuts both rays of ∠BOA. Label the points of intersection as D and C.
Step 6. With C as a center, draw (in the interior of ∠BOA) an arc whose radius is more than half the length CD.
Step 7. With the same radius and with D as a center, draw another arc in the interior of ∠BOA. Let the two arcs intersect at E. Then, \(\overline { OE }\) is the bisector of ∠BOA, i.e., ∠BOE = ∠EOA = 30°.

(c) Construction of an angle of measure 90°
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 31
Step 1. Draw any line PQ and take a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line at A.
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the radius on the compasses and with B as a center, draw an arc which cuts the first arc at C.
Step 5. Join OB and OC.
Step 6. With O as a center and using compasses, draw an arc that cuts both rays of ∠COB. Label the points of intersection as D and E.
Step 7. With E as a center, draw (in the interior of ∠COB) an arc where the radius is more than half the length ED.
Step 8. With the same radius and with D as a center, draw another arc in the interior of ∠COL. Let
the two arcs intersect at F. Join \(\overline { OF }\). Then, \(\overline { OF }\) is the bisector of ∠COB, i.e., ∠COF = ∠FOB. Now, ∠ FOQ = 90°.

(d) Construction of an angle of measure 120°
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 32
Step 1. Draw any line PQ and take a point O on it.
Step 2. Place the pointer of the compass es at O and draw an arc of convenient radius which puts the line at A. • ‘
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the i alius > on the compasses and with B as a center, draw an arc which cuts the first arc at C. .
Step 5. Join OC. Then, ∠COA is the required angle whose measure is 120°.

(e) Construction of an angle of measure 45°
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 33
Step 1. Draw any line PQ and take a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line at A.
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the radius on the compasses and with B as a center, draw an arc which cuts the first arc at C.
Step 5. Join OB and OC.
Step 6. With O as a center and using compasses, draw an arc that cuts both rays of ∠COB. Label the points of intersection as D and E.
Step 7. With E as a center, draw (in the interior of ∠COB) an arc whose radius is more than half the length ED.
Step 8. With the same radius and with D as a center, draw another arc in the interior of ∠COB. Let the two arcs intersect at F. Join OF. Then, ∠FOQ = 90°.
Step 9. With O as a center and using compasses, draw an arc that cuts both rays to ∠FOQ. Label the points of the intersection as G and H.
Step 10. With H as a center, draw (in the interior of. ∠FOQ) an arc whose radius is more than half the length HG.
Step 11. With the same radius and with G as a center, draw another arc in the interior of ∠FOQ. Let the two arcs intersect at I. Join OI. Then, OI is the bisector of ∠FOH, i.e., ∠FOI = ∠IOH. Now,
∠FOI = ∠IOH = 45°.

(f) Construction of an angle of measure 135° it.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 34
Step 1. Draw any line PQ and take a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line at A.
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the radius on the compasses and with B as a center, draw an arc which cuts the first arc at C.
Step 5. Join OB and OC.
Step 6. With O as a center and using compasses, draw an arc that cuts both rays of ∠COB. Label the points of intersection as D and E.
Step 7. With E as the center, draw (in the interior of ∠COB) an arc whose radius is more than half the length ED.
Step 8. With the same radius and with D as the center, draw another arc in the interior of ∠COB. Let the two arcs intersect at F. Join \(\overline { OF }\). Then, \(\overline { OF }\) is the bisector of ∠COB, i.e., ∠COF = ∠FOB. Now, ∠FOQ = 90°.
Step 9. With O as a center and using compasses, draw an arc that cuts both rays of ∠POF. Label the points of intersection as G and H.
Step 10. With H as center draw (in the interior of ∠POF) an arc whose radius is more than half the length HG.
Step 11. With the same radius and with G as a center, draw another arc in the interior of ∠POF. Let
the two arcs intersect at I. Join 01. Then, \(\overline { OI }\) is the bisector of ∠POF, i.e., ∠GOI = ∠IOF. Now, ∠IOQ = 135°.

Question 6.
Draw an angle of measure 45° and bisect it.
Solution :
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 35
Step 1. Draw any line PQ and take a point O on it.
Step 2. Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line at A. ’
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the radius on the compasses and with B as a center, draw an arc which cuts the first arc at C.
Step 5. Join OB and OC.
Step 6. With O as a center and using compasses, draw an arc that cuts both rays of ∠COB. Label the points of intersection as D and E.
Step 7. With E as a center, draw (in the interior of ∠COB) an arc whose radius is more than half the length ED.
Step 8. With the same radius and with D as a center, draw another arc in the interior of ∠COB. Let
the two arcs intersect at F. Join OF. Then ∠FOQ = 90°.
Step 9. With O as a center and using compasses, draw an arc that cuts both rays of ∠FOQ. Label the points of intersection on G and H.
Step 10. With G as a center, draw in the interior of ∠FOQ) an arc whose radius is more than half the length HG.
Step 11. With the same radius and with G as a center, draw another arc in the interior of ∠FOQ. Let the two arcs intersect at I. Join OI. Then OI is the bisector of ∠FOQ, i.e., ∠FOI = ∠IOH. Now, ∠FOI = ∠IOH = 45°.
Step 12. With O as a center and using compasses, draw an arc that cuts both rays of ∠IOH. Label the points of intersection as J and K.
Step 13. With K as a center, draw (in the interior of ∠IOH) an arc whose radius is more than half the length KJ.
Step 14. With the same radius and with J as a center, draw another arc in the interior of ∠IOH. Let the two arcs intersect at L. Join OL. Then OL is the bisector of ∠IOH, i.e., ∠IOL = ∠LOK \(22\frac { 1^{ \circ } }{ 2 }\) .

Question 7.
Draw an angle of measure 135° and bisect it.
Solution :
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 36
Step 1. Draw any line PQ and take a point O on.
Step 2. Place the pointer of the compasses at’ and draw an arc of convenient radius which cul line at A.
Step 3. Without disturbing the radius on the compasses, draw an arc with A as a center which cuts the first arc at B.
Step 4. Again without disturbing the radius on the compasses and with B as a center, draw an arc which cuts the first arc at C.
Step 5. Join OB and OC.
Step 6. With O as a center and using compasses, draw an arc that cuts both rays of ∠COB. Label the points of intersection as D and E.
Step 7. With E as a center, draw (in the interior of ∠COB) an arc whose radius is more than half the length ED.
Step 8. With the same radius and with D as a center, draw another arc in the interior of ∠COB. Let
the two arcs intersect at F. Join \(\overline { OF }\). Then \(\overline { OF }\) is the bisector of ∠COB, i.e., ∠COF = ∠FOB. Now, ∠FOQ = 90°.
Step 9. With O as a center and using compasses, draw an arc that cuts both rays of ∠POF. Label the points of intersection as G and H.
Step 10. With G as a center, draw in the interior of ∠POF an arc whose radius is more than half the length HG.
Step 11. With the same radius and with H as a centre, draw another arc in the interior of ∠POF. Let
the two arcs intersect at I. Join \(\overline { OI }\). Then \(\overline { OI }\) is the bisector of ∠POF, i.e., ∠POI = ∠IOF. Now, ∠IOQ = 135°. .
Step 12. With O as centre and using compasses, draw an arc that cuts both rays of ∠IOQ. Label the points of intersection as J and K.
Step 13. With K as centre, draw (in the interior of ∠IOQ) an arc whose radius is more than half the length KJ.
Step 14. With the same radius and with J as centre, draw another arc in the interior of ∠IOQ. Let the two arcs intersect at L. Join \(\overline { OL }\). Then \(\overline { OL }\) is the bisector of ∠IOQ, i.e., ∠IOL = ∠LOQ.

Question 8.
Draw an angle of 70°. Make a copy of it using only a straight edge and compasses.
Solution :
Steps of construction
1. Construct an angle ABC = 70°.
2. Take a line z and mark a point D on it.
3. Fix the compasses pointer on B and draw an arc which cuts the sides of ∠ABC at D and E.
4. Without changing the compasses setting, place the pointer on P and draw an arc which cuts ∠ at Q.
5. Open the compasses equal to length DE.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 37
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 38
6. Without disturbing the radius on compasses, place its pointer at Q and draw an arc which cuts the previous arc at R.
7. Join PR and draw ray PR. It gives ∠RPQ which is the required angle whose measure is equal to the measure of ∠ABC.

Question 9.
Draw an angle of 40°. Copy its supplementary angle.
Solution :
Steps of construction
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 39
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 40
1. Draw ∠CAB = 40°.
2. Draw a line I and mark a point P on it.
3. Place the pointer of the compasses on A and draw an arc which cuts extended BA at E and AC at F.
4. Without changing the radius on compasses, place its pointer at P and draw an arc which cuts l at Q.
5. Open the length of compasses equal to EF.
6. Without disturbing the radius on compasses, place its pointer at Q and draw an arc which cuts the previous arc at R.
7. Join QR and draw ray QR. It gives ∠RQS which is the required angle whose measure

We hope the NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.6, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5.

Board CBSE
Textbook NCERT
Class Class 6
Subject Maths
Chapter Chapter 14
Chapter Name Practical Geometry
Exercise  Ex 14.5
Number of Questions Solved 9
Category NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5

Question 1.
Draw \(\overline { AB }\) of length 7.3 cm and find its axis of symmetry.
Solution :
Step 1. Draw a line segment \(\overline { AB }\) of length 7.3 cm.
Step 2. With A ascentere, using compasses, drawthe circle. The radius of this circle should be more than half of the length of \(\overline { AB }\).
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 16
Step 3. With the same radius and with B as a centre, draw another circle using compasses. Let it cut the previous circle at C and D.
Step 4. Join CD. Then, \(\overline { CD }\) is the axis of symmetry of \(\overline { AB }\).

Question 2.
Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
Solution :
Step 1. Draw a line segment \(\overline { AB }\) of length 9.5 cm.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 17
Step 2. With A as a centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { AB }\).
Step 3. With the same radius and with B as a centre, draw another circle using compasses. Let it cut the previous circle at C and D.
Step 4. Join CD. Then \(\overline { CD }\) is the perpendicular bisector of the line segment \(\overline { AB }\).

Question 3.
Draw the perpendicular bisector of \(\overline { XY }\) whose length is 10.3 cm.
(a) Take any point P on the bisector drawn. Examine whether PX = PY.
(b) If M is the midpoint of \(\overline { XY }\), what can you say about the lengths MX and XY ?
Solution :
Step 1. Draw a line segment \(\overline { XY }\) of length 10.3 cm.
Step 2. With X as a centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { XY }\).
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 18
Step 3. With the same radius and with Y as a centre, draw another circle using compasses. Let it cuts the previous circle at A and B.
Step 4. Join AB. Then \(\overline { AB }\) is the perpendicular bisector of the line segment \(\overline { XY }\).
(a) On examination, we find that PX = PY.
(b) We can say that the lengths of MX is half of the length of XY.

Question 4.
Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 19
Solution :
Step 1. Draw a line segment \(\overline { AB }\) of length 12.8 cm.
Step 2. With A as centre, using compasses, draw two arcs on either side of AB. The radius of this arc should be more than fialf of the length of \(\overline { AB }\).
Step 3. With the same radius and with B as centre, draw another arcs using compasses. Let it cut the previous arcs at C and D.
Step 4. Join \(\overline { CD }\). It cuts \(\overline { AB }\) at E. Then \(\overline { CD }\) is the perpendicular bisector of the line segment \(\overline { AB }\).
Step 5. With A as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of AE.
Step 6. With the same radius and with E as centre, draw another circle using compasses; Let it cut the previous circle at F and G.
Step 7. Join \(\overline { FG }\). It cuts \(\overline { AE }\) at H. Then \(\overline { FG }\) is the perpendicular bisector of the line segment \(\overline { AE }\).
Step 8. With E as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of EB.
Step 9. With the same radius and with B as centre, draw another circle using compasses. Let it cut the previous circle at I and J.
Step 10. Join \(\overline { IJ }\). It cuts \(\overline { EB }\) at K. Then \(\overline { IJ }\) is the perpendicular bisector of the line segment \(\overline { EB }\). Now, the points H, E and K divide AB into four equal parts, i.e., \(\overline { AH }\) = \(\overline { HE }\) = \(\overline { EK }\) = \(\overline { KB }\) By measurement, \(\overline { AH }\) = \(\overline { HE }\) = \(\overline { EK }\) = \(\overline { KB }\) = 3.2 cm.

Question 5.
With \(\overline { PQ }\) of length 6.1 cm as diameter draw a circle.
Solution :
Step 1. Draw a line segment \(\overline { PQ }\) of length 6.1 cm.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 20
Step 2. With P as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { PQ }\).
Step 3. With the same radius and with Q as centre, draw another circle using compasses. Let it cut the previous circle at A and B.
Step 4. Join \(\overline { AB }\). It cuts \(\overline { PQ }\) at C. Then \(\overline { AB }\) is
the perpendicular bisector of the line segment PQ .
Step 5. Place the pointer of the compasses at C and open the pencil upto P.
Step 6. Turn the compasses slowly to draw the circle.

Question 6.
Draw a circle with centre C and radius, 3.4 cm. Draw any chord \(\overline { AB }\). Construct the perpendicular bisector of \(\overline { AB }\) and examine if it passes through C.
Solution :
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 21
Step 1. Draw a point with a sharp pencil and mark it as C.
Step 2. Open the compasses for the required radius 3.4 cm, by putting the pointer on 0 and opening the pencil upto 3.4 cm.
Step 3. Place the pointer of the compasses at C. Step 4. Turn the compasses slowly to draw the
circle.
Step 5. Draw any chord \(\overline { AB }\) of this circle.
Step 6. With A as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { AB }\).
Step 7. With the same radius and with B as centre, draw another circle using compasses. Let it cut the previous circle at D and E.
Step 8. Join \(\overline { DE }\) . Then \(\overline { DE }\) is the perpendicular bisector of the line segment \(\overline { AB }\). On examination, we find that it passes through C.

Question 7.
Repeat Question 6, if \(\overline { AB }\) happens to be a diameter.
Solution :
Step 1. Draw a point with a sharp pencil and mark it as C.
Step 2. Open the compasses for the required radius 3.4 cm, by putting the pdinter of compasses on 0 of the scale and opening the pencil upto 3.4 cm.
Step 3. Place the pointer of the compasses at C.
Step 4. Turn the compasses slowly to draw the circle.
Step 5. Draw any diameter \(\overline { AB }\).
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 22
Step 6. With A as centre, using compasses, draw arcs on either side. The radius of this arc should be more than half of the length of \(\overline { AB }\).
Step 7. With the same radius and with B as centre, draw another arcs using compasses. Let it cut the previous arcs at D and E.
Step 8. Join \(\overline { DE }\) . Then \(\overline { DE }\) is the perpendicular bisector of the line segment \(\overline { AB }\). On examination, we find that it passes through C.

Question 8.
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
Solution :
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 23
Step 1. Draw a point with a sharp pencil and mark it as O.
Step 2. Open the compasses for the required radius of 4 cm. by putting the pointer on 0 and opening the pencil upto 4 cm.
Step 3. Place the pointer of the compasses at O.
Step 4. Turn the compasses slowly to draw the circle.
Step 5. Draw any two chords \(\overline { AB }\) and \(\overline { CD }\) of this circle.
Step 6. With A as centre, using compasses, draw two arcs on either side of AB. The radius of this arc should be more than half of the length of \(\overline { AB }\).
Step 7. With the same radius and with B as centre, draw another two arcs using compasses. Let it cut the previous circle at E and F.
Step 8. Join \(\overline { EF }\). Then \(\overline { EF }\) is the perpendicular bisector of the chord \(\overline { AB }\).
Step 9. With C a< centre, using compasses, draw two arcs on either side of CD. The radius of this arc should be more than half of the length of \(\overline { CD }\).
Step 10. With the same radius and with D as centre, draw another two arcs using compasses. Let it cut the previous circle at G and H.
Step 11. Join \(\overline { GH }\). Then \(\overline { GH }\) is the perpendi¬cular bisector of the chord \(\overline { CD }\). We find that the perpendicular bisectors \(\overline { EF }\) and \(\overline { GH }\) meet at O, the centre of the circle.

Question 9.
Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA- OB. Draw the perpendicular bisectors of \(\overline { OA }\) and \(\overline { OB }\). Let them meet at P. Is PA = PB?
Solution :
Step 1. Draw any angle POQ with vertex O.
Step 2. Take a point A on the arm OQ and another point B on the arm OP such that \(\overline { OA }\) = \(\overline { OB }\).
Step 3. With O as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { OA }\).
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 24
Step 4. With the same radius and with A as centre, draw another circle using compasses. Let it cut the previous circle at C and D.
Step 5. Join \(\overline { CD }\). Then \(\overline { CD }\) is the perpendicular bisector of the line segment \(\overline { OA }\).
Step 6. With O as centre, using compasses, draw a circle. The radius of this circle should be more than half of the length of \(\overline { OB }\).
Step 7. With the same radius and with B as centre, draw another circle using compasses. Let it cut the previous circle at E and F.
Step 8. Join \(\overline { EF }\). Then \(\overline { EF }\) is the perpendicular bisector of the line segment OB. The two perpendicu¬lar bisectors meet at P.
Step 9. Join \(\overline { PA }\) and \(\overline { PB }\). We find that \(\overline { PA }\) = \(\overline { PB }\).

 

We hope the NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.5, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.4

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.4 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.4.

Board CBSE
Textbook NCERT
Class Class 6
Subject Maths
Chapter Chapter 14
Chapter Name Practical Geometry
Exercise  Ex 14.4
Number of Questions Solved 3
Category NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.4

Question 1.
Draw any line segment \(\overline { AB }\) . Mark any point M on it. Through M draw a perpendicular to \(\overline { AB }\). (use ruler and compasses).
Solution :
Step 1. Given a point M on any line \(\overline { AB }\).
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 13
Step 2. With M as centre and a convenient radius, construct a part circle (arc) intersecting the line segment \(\overline { AB }\) at two points C and D.
Step 3. With C and D as centres and a radius greater than CM, construct two arcs which cut each other at N.
Step 4. Join \(\overline { MN }\). Then \(\overline { MN }\) is perpendicular to \(\overline { AB }\) at M, i.e., \(\overline { MN }\) \(\overline { AB }\).

Question 2.
Draw any’line segment \(\overline { PQ }\). Take any point R not on it. Through R draw a perpendicular to \(\overline { PQ }\). (use ruler and set-square).
Solution :
Step 1. Let \(\overline { PQ }\) be the given line segment and R be a point not on it.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 14
Step 2. Place a set-square on \(\overline { PQ }\) such that one arm of the right angle aligns along \(\overline { PQ }\).
Step 3. Place a ruler along the edge opposite of the right angle.
Step 4. Hold the ruler fixed. Slide the set-square along the ruler all the point R touches the arm of the set-square.
Step 5. Join RS along the edge through R, meeting \(\overline { PQ }\) at S. Now \(\overline { RS }\) \(\overline { PQ }\).

Question 3.
Draw a line l and a point X on it. Through X, draw a line segment \(\overline { XY }\) perpendicular to l. Now draw a perpendicular to XY at Y. (use ruler and compasses)
Solution :
Step 1. Given a point X on a line l.
Step 2. With X as centre and a convenient radius, construct a part circle (arc) intersecting the line l at two points A and B.
Step 3. With A and B as centres and a radius greater than AX, construct two arcs which cut each other at Y.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 15
Step 4. Join \(\overline { XY }\). Then \(\overline { XY }\) is perpendicular to l atX, i.e., \(\overline { XY }\) l.

 

We hope the NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.4 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.4, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.3

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.3 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.3.

Board CBSE
Textbook NCERT
Class Class 6
Subject Maths
Chapter Chapter 14
Chapter Name Practical Geometry
Exercise  Ex 14.3
Number of Questions Solved 2
Category NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.3

Question 1.
Draw any line segment \(\overline { PQ }\). Without measuring \(\overline { PQ }\) . construct a copy of \(\overline { PQ }\).
Solution :
Step 1. Given \(\overline { PQ }\) whose length is not known.
Step 2. Fix the compasses pointer on P and the pencil end on Q. The opening of the instrument now
gives the length of \(\overline { PQ }\).
Step 3. Draw any line l. Choose a point A on /. Without changing the compasses setting, place the pointer on A.
Step 4. Swing an arc that cuts l at a point, say, B. Now \(\overline { AB }\) is a copy of \(\overline { PQ }\).

Question 2.
Given some line segment \(\overline { AB }\), whose length you do not know, construct \(\overline { PQ }\) such that the length of \(\overline { PQ }\) is twice that of \(\overline { AB }\).
Solution :
Step 1. Given \(\overline { AB }\) whose length is not known.
Step 2. Fix the compasses pointer on A and the pencil end on B. The opening of the instrument now gives the length of \(\overline { AB }\).
Step 3. Draw any line l. Choose a point P on l. Without changing the compasses setting, place the pointer on P.
Step 4. Strike an arc that cuts l at a point, say, X.
Step 5. Now fix the compasses pointer on X. Strike an arc away from P that cuts l at a point, say, Q. Now, the length of \(\overline { PQ }\) is twice that of \(\overline { AB }\).

 

We hope the NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.3 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2.

Board CBSE
Textbook NCERT
Class Class 6
Subject Maths
Chapter Chapter 14
Chapter Name Practical Geometry
Exercise  Ex 14.2
Number of Questions Solved 5
Category NCERT Solutions

NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2

Question 1.
Draw a line segment of length 7.3 cm. using a ruler.
Solution :
Using ruler, we mark two points A and B which are 7.3 cm apart. Join A and B and get AB. \(\overline { AB }\) is a line segment of length 7.3 cm.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 7

Question 2.
Construct a line segment of length 5.6 cm using ruler and compasses.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 8
Solution :
Step 1. Draw a line l. Mak a point A on line l.
Step 2. Place the compasses pointer on the ∠ero mark on the ruler. Open it to place the pencil point upto the 5.6 cm mark.
Step 3. Without changing the opening of the compasses, place the pointer on A and swing an arc to cut / at B.
Step 4. AB is a line segment of required length.

Question 3.
Construct \(\overline { AB }\) of length 7.8 cm. From this cut off \(\overline { AC }\) of length 4.7 cm. Measure \(\overline { BC }\).
Solution :
Steps of Construction
Step 1. Draw a line l. Mark a point A on line l.
Step 2. Place the compasses pointer on the ∠ero mark on the ruler. Open it to place the pencil point upto the 7.8 cm mark.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 9
Step 3. Without changing the opening of the compasses, place the pointer on A and swing an arc to cut / at B.
Step 4. \(\overline { AB }\) is a line segment of length 7.8 cm.
Step 5. Place the compasses pointer on the ∠ero mark on the ruler. Open it to place the pencil point upto 4.7 cm mark.
Step 6. Without changing the opening of the compasses, place the pointer on A and swing an arc to cut / at C.
Step 7. \(\overline { AC }\) is a line segment of length 4.7 cm. On measurement. \(\overline { BC }\) =3.1 cm.

Question 4.
Given \(\overline { AB }\) of length 3.9 cm, construct \(\overline { PQ }\) such that the length of \(\overline { PQ }\) is twice that of AB Verify by measurement.
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 10
(Hint : Construct \(\overline { PX }\) such that length of PX = length of \(\overline { AB }\); then cut off \(\overline { XQ }\) such that \(\overline { XQ }\) also has the length of \(\overline { AB }\)).
Solution :
Steps of Construction
Step 1. Draw a line I. Mark a point P on line l.
Step 2. Place the compasses pointer on the A mark of the given line segment \(\overline { AB }\) . Open it to place the pencil point upto B mark of the given line segment \(\overline { AB }\).
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 11
Step 3. Without changing the opening of the compasses, place the pointer on P and swing an arc to cut l at X.
Step 4. Again without changing the opening of the compasses place the compasses pointer on the X mark of line / and swing an arc to cut / at Q.
Step 5. \(\overline { PQ }\) is a line segment of length twice that of \(\overline { AB }\). Please verify yourself by measurement.

Question 5.
Given \(\overline { AB }\) of length 7.3 cm and \(\overline { CD }\) of length 3.4 cm, construct a line segment \(\overline { XY }\) such that the length of \(\overline { XY }\) is equal to the difference between the lengths of \(\overline { AB }\) and \(\overline { CD }\) . Verify by measurement.
Solution :
Steps of Construction
Step 1. Draw a line l. Mark a point X on line l.
Step 2. Place the compasses pointer on the A mark of the given line segment \(\overline { AB }\). Open it to place the pencil point upto B mark of the given line segment \(\overline { AB }\).
Step 3. Without changing the opening of the compasses, place the pointer of compasses on X and swing an arc to cut / at ∠.
Step 4. Place the compasses pointer on the C mark of the given line segment \(\overline { CD }\). Open it to place the pencil point upto D mark of the given line segment \(\overline { CD }\).
Step 5. Without changing the opening of the compasses, place the pointer of compasses on ∠ and swing an arc towards X to cut l at Y.
Step 6. \(\overline { XY }\) is a required line segment of length = the difference between the lengths of \(\overline { AB }\) and \(\overline { CD }\).
NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry 12
Please verify yourself by measurement.

 

We hope the NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 14 Practical Geometry Ex 14.2, drop a comment below and we will get back to you at the earliest.