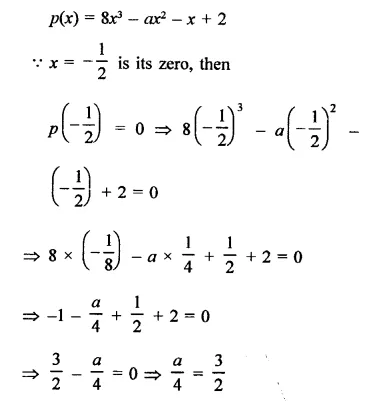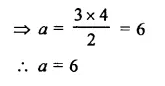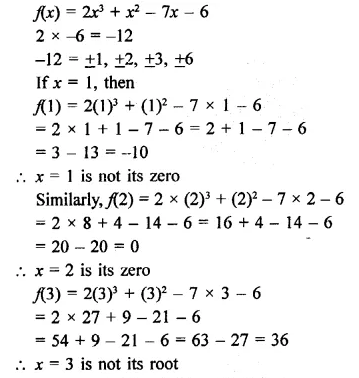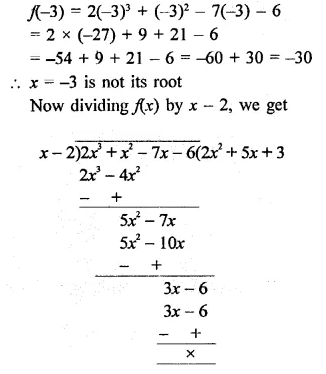RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
Other Exercises
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS
Using factor theorem, factorize each of the following polynomials:
Question 1.
x3 + 6x2 + 11x + 6
Solution:
Question 2.
x3 + 2x2 – x – 2
Solution:
Question 3.
x3 – 6x2 + 3x + 10
Solution:
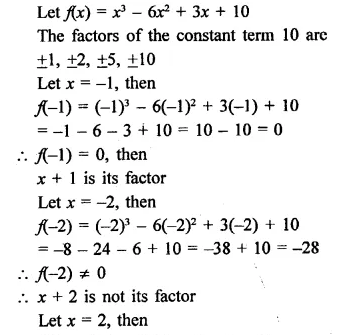
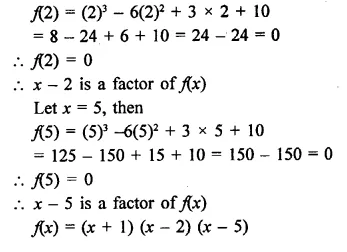
Question 4.
x4 – 7x3 + 9x2 + x- 10
Solution:
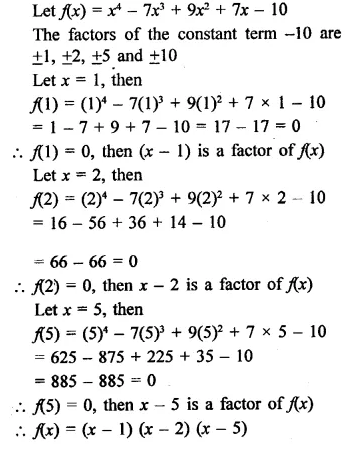
Question 5.
3x3 – x2 – 3x + 1
Solution:
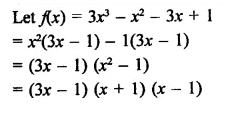
Question 6.
x3 – 23x2 + 142x – 120 [NCERT]
Solution:
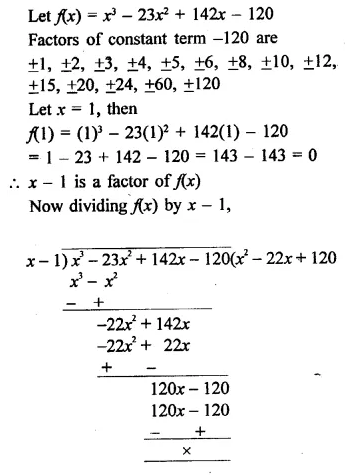
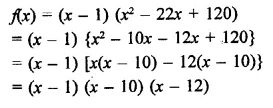
Question 7.
y3 – 7y + 6
Solution:
Let f(y) = y3 – 7y + 6
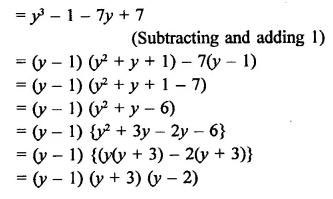
Question 8.
X3 -10x2 – 53x – 42
Solution:
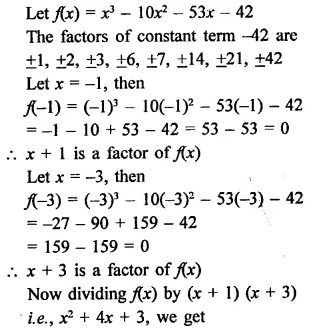
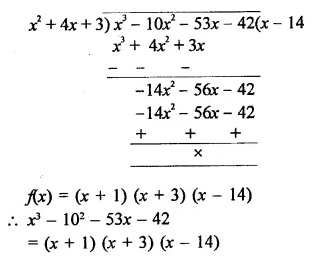
Question 9.
y3 – 2y2– 29y – 42
Solution:
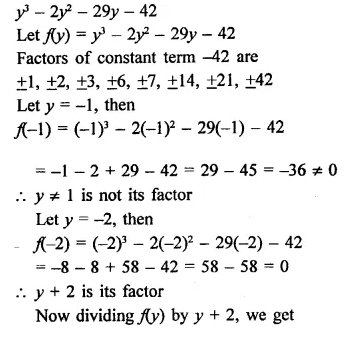
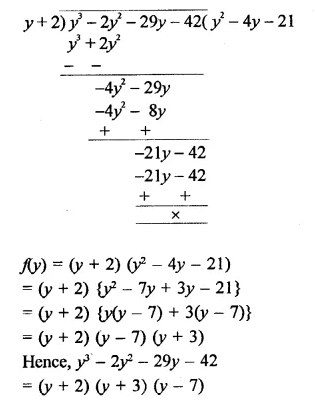
Question 10.
2y3 – 5y2 – 19y + 42
Solution:
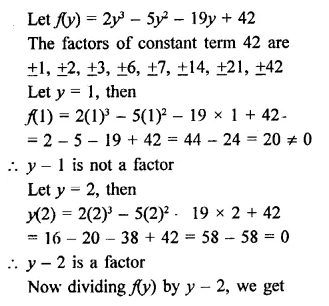
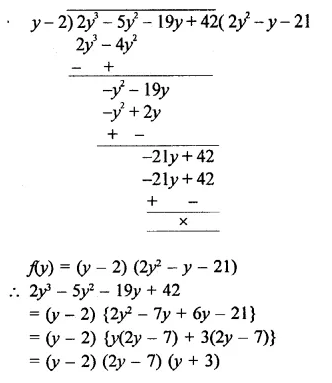
Question 11.
x3 + 132 + 32x + 20 [NCERT]
Solution:
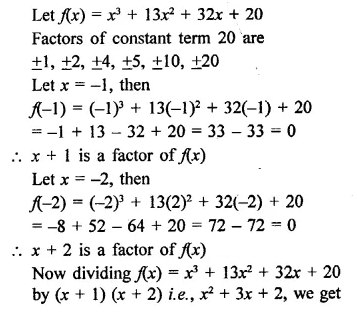
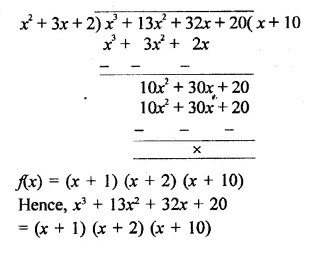
Question 12.
x3 – 3x2 – 9x – 5 [NCERT]
Solution:
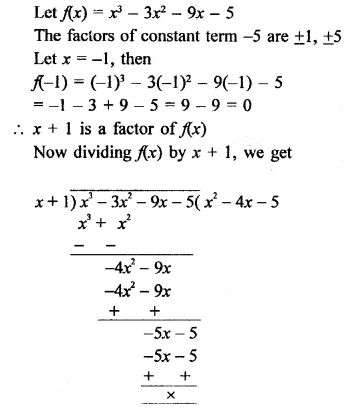
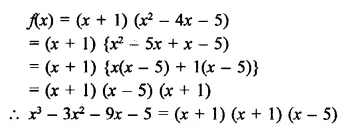
Question 13.
2y3+ y2 – 2y – 1 [NCERT]
Solution:
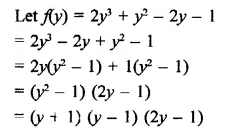
Question 14.
x3 – 2x2 – x + 2
Solution:
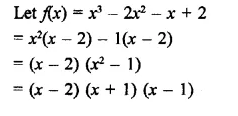
Question 15.
Factorize each of the following polynomials:
(i) x3 + 13x2 + 31x – 45 given that x + 9 is a factor
(ii) 4x3 + 20x2 + 33x + 18 given that 2x + 3 is a factor
Solution:
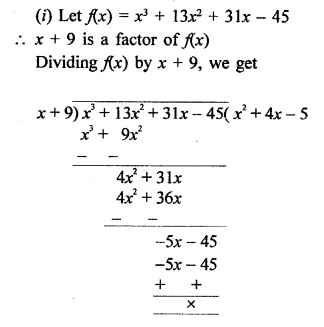
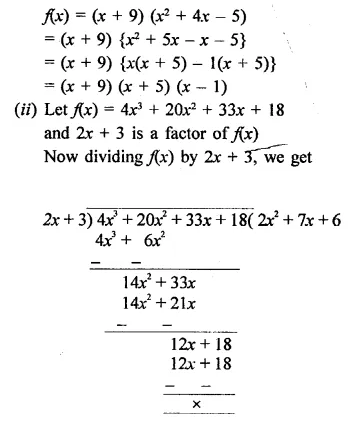
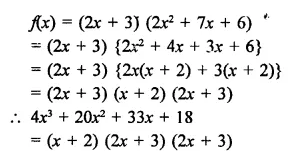
Question 16.
x4 – 2x3 – 7x2 + 8x + 12
Solution:
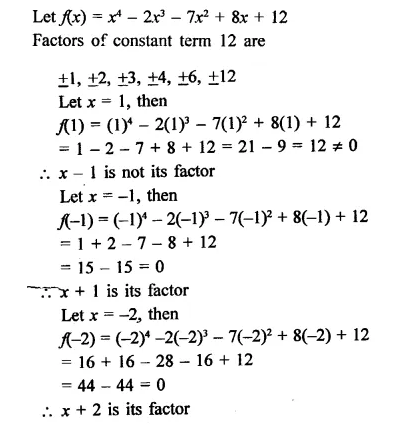
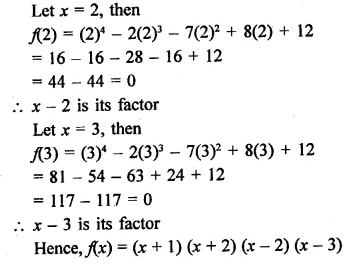
Question 17.
x4 + 10x3 + 35x2 + 50x + 24
Solution:
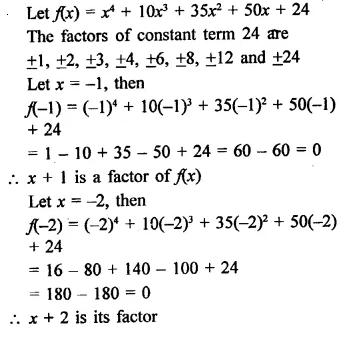
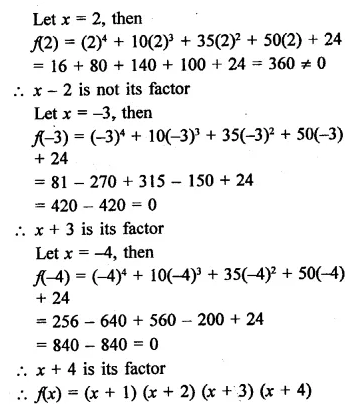
Question 18.
2x4 – 7x3 – 13x2 + 63x – 45
Solution:
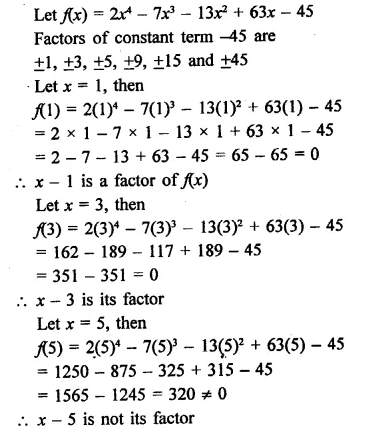
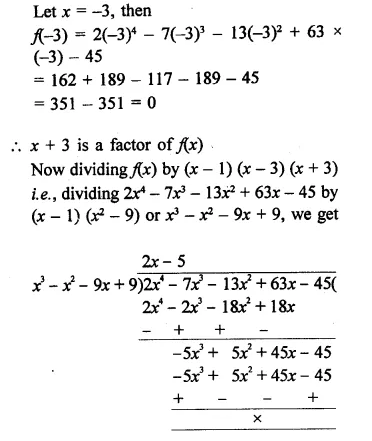
![]()
Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.