Category: CBSE Sample Papers

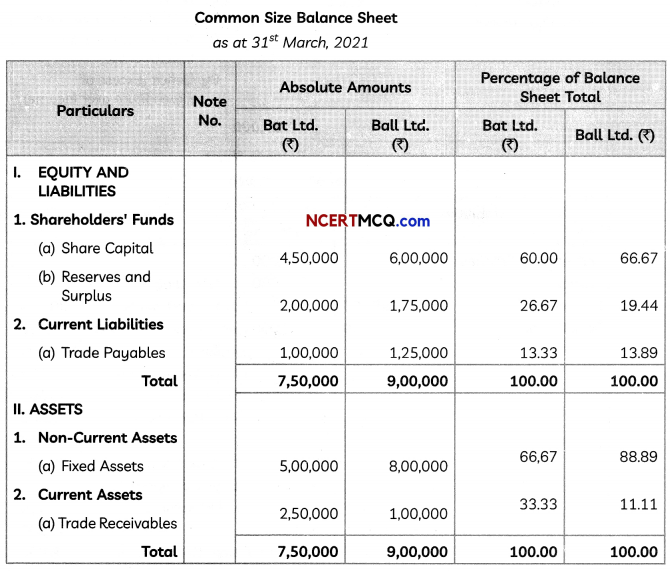
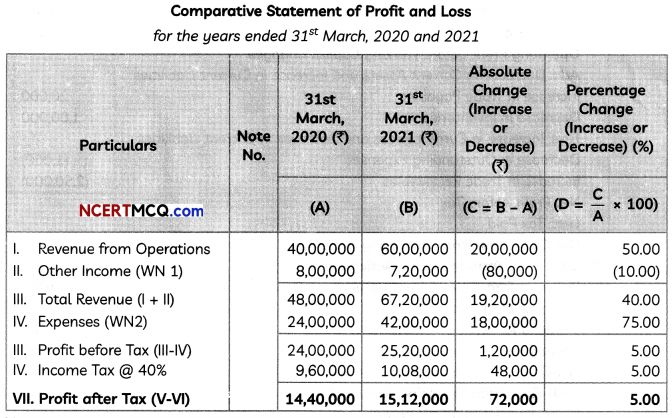
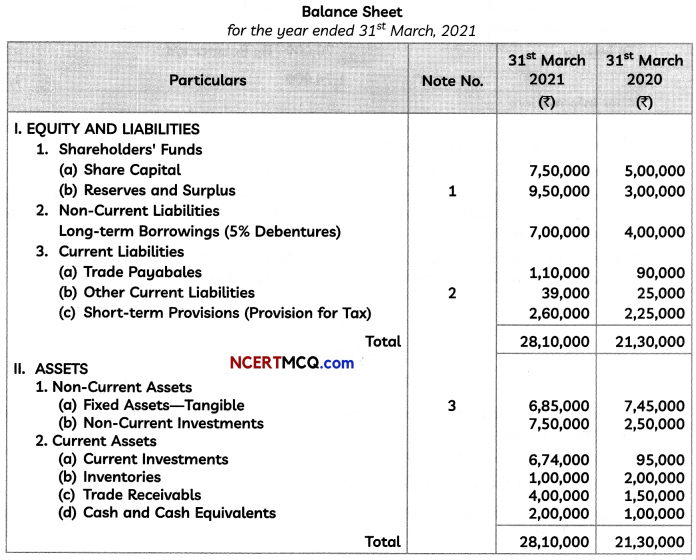
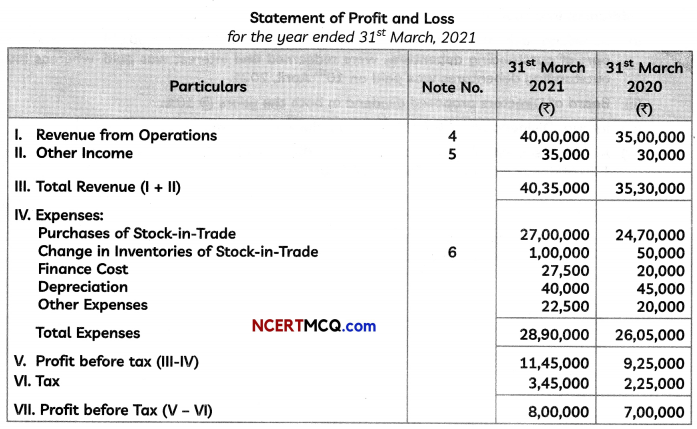
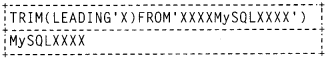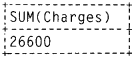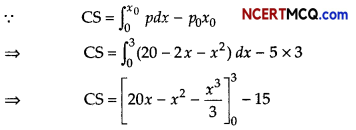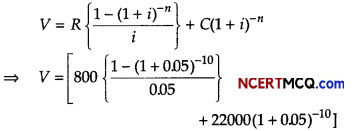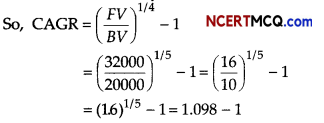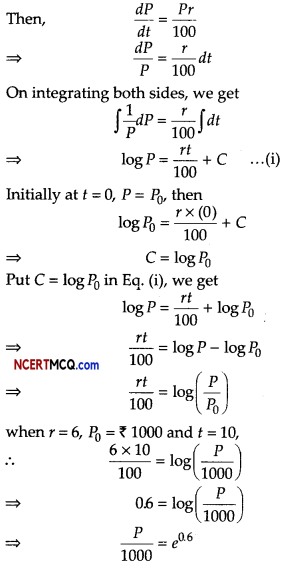Students can access the CBSE Sample Papers for Class 12 Informatics Practices with Solutions and marking scheme Term 2 Set 7 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Informatics Practices Term 2 Set 7 with Solutions

Maximum Marks : 35
Time : 2 hours

Instructions:

• The question paper is divided into 3 sections – A, B and C.
• Section A, consists of 7 questions (1-7). Each question carries 2 marks.
• Section B, consists of 3 questions (8-10). Each question carries 3 marks.
• Section C, consists of 3 questions (11-13). Each question carries 4 marks.
• Internal choices have been given for question numbers -1, 3, 8 and 12.

Section – A
(Each question carries 2 Marks)

Question 1.
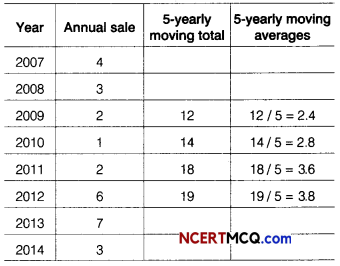
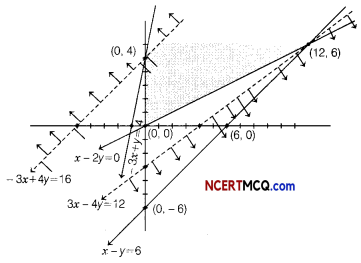
Jatin is learning networks and has come across various terms related to networks , such as MAN, URL, WWW, WAN etc. Before going into the detailed description of the terms he wants to know their expansions. Provide him the expansions of the following terms (any two in each option).
(i) MAN
(ii) URL
(iii) WWW
Or
(i) WAN
(ii) VoIP
(iii) ARPANET
Answer:
(i) Metropolitan Area network
(ii) Uniform Resource Locator
(iii) World Wide Web

Or

(i) Wide Area Network
(ii) Voice over Internet Protocol
(iii) Advanced Research Projects Agency Network

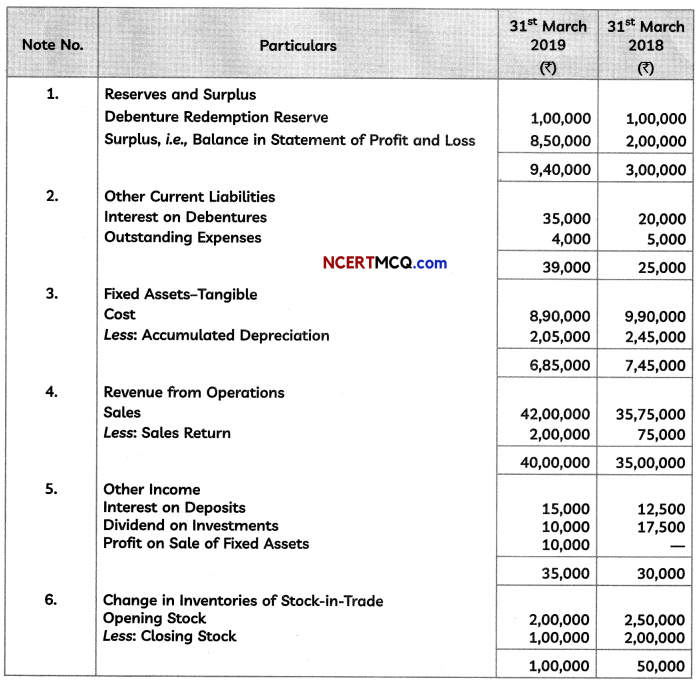
Question 2.
(i) Susmita could not recall the exact term for softwares used to view web pages or browse the web. Can you help her with the term?
Answer:
A web browser is a software that is the platform to view web pages. It also acts as an E-mail and chat client. It even helps users in browsing the web.

(ii) Alex was trying to connect the computers in his office in a specific topology. He wanted to know the advantages of the ring topology. Suggest him the advantages.
Answer:
There are some reasons, why ring topology should be used
(a) It has better performance than bus topology, even when the nodes are increased.
(b) Ring network can handle high volume of nodes in a network (robust).
(c) Reduced chances of data collision as each node release a data packet after receiving the token.
(d) Token passing makes ring topology perform better than bus topology under heavy traffic.
(e) No need of server to control connectivity among the nodes. Equal access to the resources.

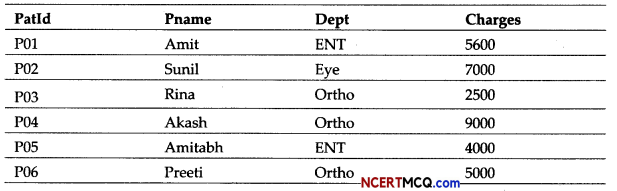
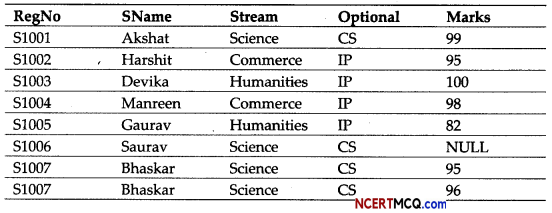
Question 3.
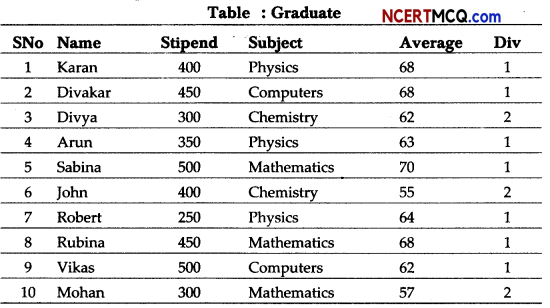
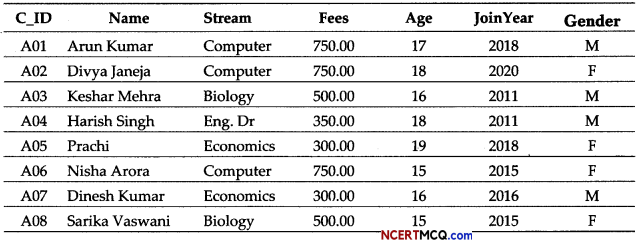
Govind was given a table Defense storing details of Defense personnel, by his teacher. His teacher taught him the string functions and told him to produce certain outputs from the table. The teacher told that the outputs may require use of more than one function. Help him in production of the outputs as required.
Table: Defense

(i) To display the PerName(Person name) along with the Wing joined in lowercase.
(ii) To display the last 4 characters of the HQ(Headquarter).
Or
(i) To display the count of Airforce personnel.
(ii) To display the 1st three characters of the wing in uppercase.
Answer:
(i) SELECT LOWERCCONCAT (PerName.Wing)) FROM Defense;
(ii) SELECT RIGHT (HQ,4) FROM Defense;
Or
(i) SELECT COUNT(*) FROM Defense WHERE Wing=“Airforce”;
(ii) SELECT UCASE( Left (Wi ng, 3)) FROM Defense;

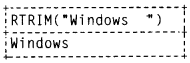
Question 4.
Param has heard that E-mail services are much easier and faster than postal systems. Provide him information and advantages of E-mail. Also, compare E-mail with chat services.
Answer:

• Electronic mail is a method of exchanging messages between people using electronic devices. E-mail entered limited use in the 1960s, but users could only send to users of the same computer. Some systems also supported a form of instant messaging, where sender and receiver needed to be online.
• E-mail is a very popular way of communicating with others over the Internet. An application that allows users to send, receive and read E-mail is called an E-mail client.
• E-mail operates across computer networks, primarily the Internet. Today’s E-mail systems are based on a store-and-forward model.
• E-mail servers accept, forward, deliver and store messages.
• Neither the users nor their computers are required to be online simultaneously. They need to connect, typically to a mail server or a webmail interface to send or receive messages or download it.

Applications: People have come to rely on E-mail for any number of functions, in addition to communication, including but not limited to reference, collaboration, storage, task management, mobile access, calendars & planning and covering your bleep.

Differences between E-mail and chat are as follows

E-mail	Chat
Large amount of data can be transferred.	Small text conversations.
Sender and receiver need not be online.	Sender and receiver need to be online.
Can carry file attachments.	Usually does not carry file attachments.

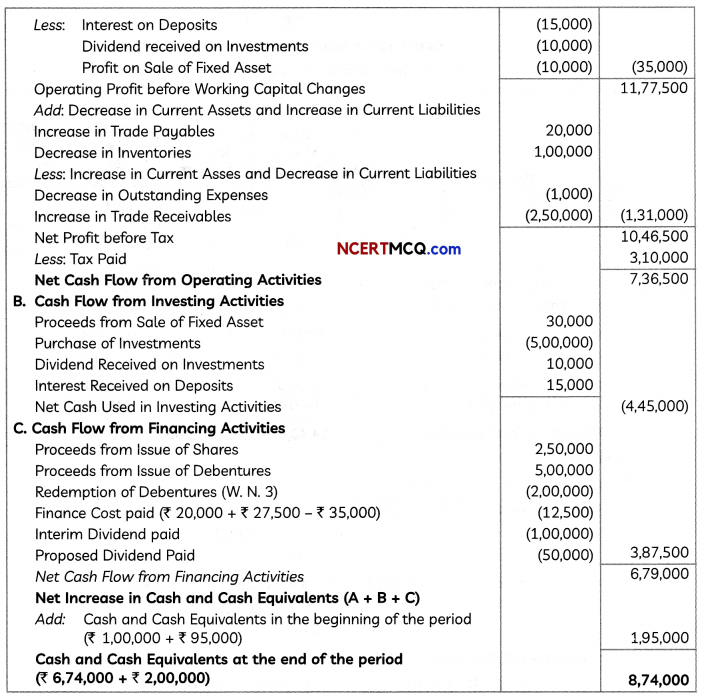
Question 5.
Mr. Johnson, teacher of a school asked the following outputs in viva of his school. Piyali a student could not answer the questions. Help her in finding the outputs.
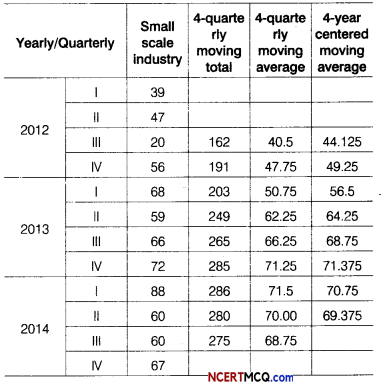
Write the outputs of following SQL statements.
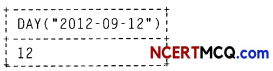
(i) SELECT DAY (‘2016-09-11 ’);
Answer:

(ii) SELECT 34%5;
Answer:

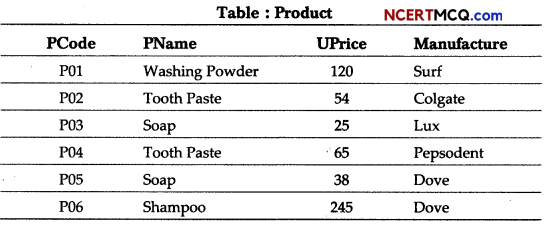
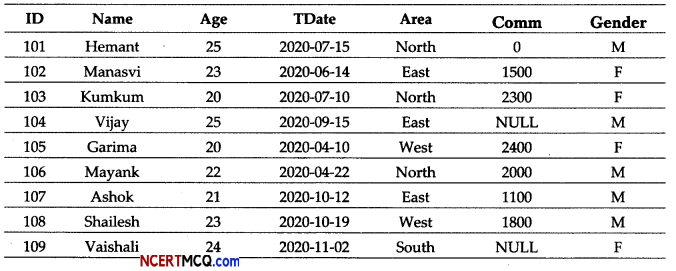
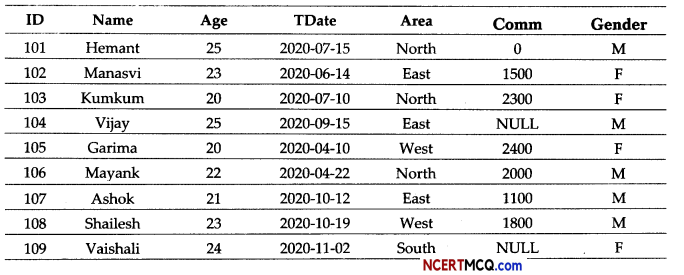
Question 6.
Anurag a database operator is not quite conversant about the usage of GROUP BY clause of SQL . Tell him how it can be used in the following cases?
Table: Automobile

(i) Which column can be used for grouping the records?
Answer:
The Type column can be used for grouping the records.

(ii) Display each type and number of vehicles in the category.
Answer:
SELECT Type, COUNT(*) FROM Automobile GROUP BY Type;

Question 7.
Help Natasha in finding the outputs of the following commands using MySQL functions with respect to the table Automobile given in previous question.
(i) SELECT CONCAT(Aname.Type) FROM Automobile WHERE Type=“Heavy”;
(ii) SELECT UCASE(Type) FROM Automobile WHERE Qty>50;
Or
(i) SELECT M0D(Qty,5) FROM Automobile WHERE Type=“Heavy”;
(ii) SELECT LEFT (Aname, 3) FROM Automobile WHERE Type=‘‘Small” ;
Answer:
(i)

(ii)

Or

(i)

The MOD() function returns the remainder of division. In the question here, the quantities for “Heavy” type are 30 and 90, hence mod returns 0 for both.

(ii)

The LEFT() function extracts certain number of characters from left of a string. In the question here, for “Small” category the 3 names are “Scooter”,”Bike” and “Jeep” from which 3 characters are extracted from left.

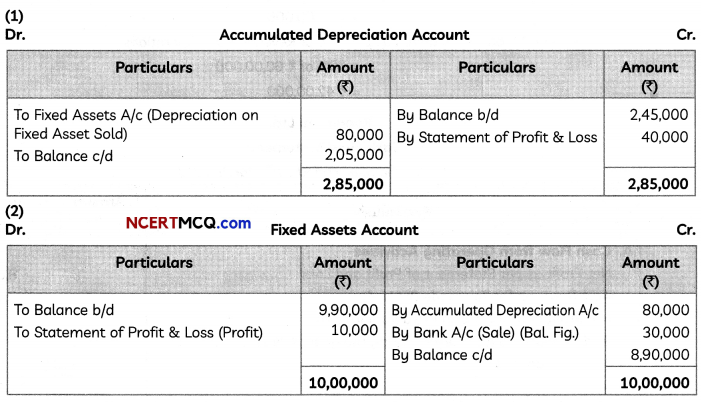
Section – B
(Each question carries 3 Marks)

Question 8.
Prakash is using MySQL functions to generate certain outputs, but is not able to guess the outputs properly. Provide him your support in finding the outputs of the following queries.
(i) SELECT MONTHNAME(‘2020-11-15’);
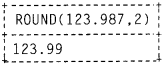
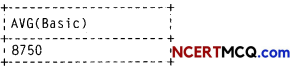
(ii) SELECT ROUND! 199.9);
(iii) SELECT INSTR(‘Hollywood’,‘oow’);
Or
After preparing a table Emp with columns Eno, Ename, Dept and Salary Rachana wanted to produce certain outputs from the table, but she was facing problems in writing the queries. Help her
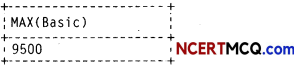
(i) To get the sum of salaries of “Salary” column of Emp table.
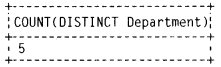
(ii) To get the count of unique department names.
(iii) To get the maximum salary from Emp table.
Answer:

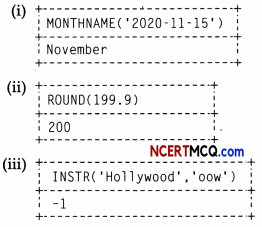
Or

(i) SELECT SUM(Sal)FROM Emp;
(ii) SELECT COLJNT(DISTINCT Dept) FROM Emp;
(iii) SELECT MAX(Salary) FROM Emp;

Question 9.
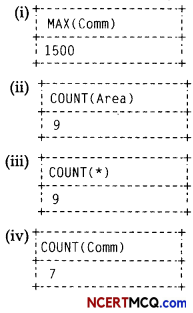
Help Anindita in finding the outputs produced from following statements using MySQL functions INSTR(), DAYNAME() and YEAR().
(i) SELECT INSTR(“Development”,“Dev”);
Answer:
Searches for the position of “Dey” in “Development”.

(ii) SELECT DAYNAME( “2019-09-11” );
Answer:
Displays the name of the weekday for the date mentioned.

(iii) SELECT YEAR( “2012 -11 – 02” );
Answer:
Displays the year part of the date in argument.

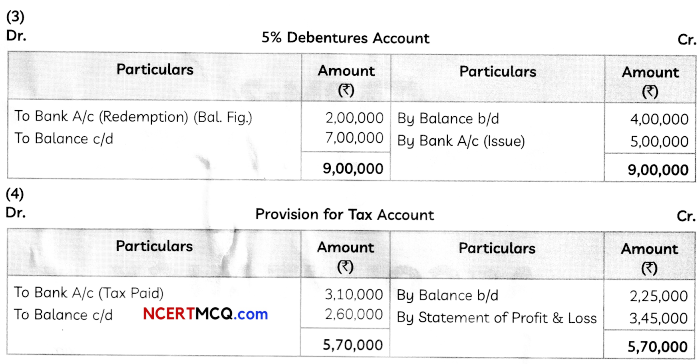
Question 10.
After writing the following SQL statements Mr. Kaustubh, ended up with errors indicating wrong function names. Suggest him with proper function names.
(i) SELECT CAPITAL( “abed”);
To convert the text to uppercase.
Answer:
SELECT UCASE(”abcd”):

(ii) SELECT EXTRACT( “abedef ”, 3,2);
To extract 2 characters from position 3 of the string.
Answer:
SELECT MID(”abcdef’3,2);

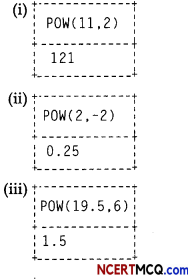
(iii) SELECT EXPONENT( 12,3);
To calculate 12³
Answer:
SELECT POW(12.3);

Section – C
(Each question carries 4 Marks)

Question 11.
Help Sunaina with proper statements to get the outputs required in the following cases with respect to the table Emp given with columns Eno, Ename, Dept and Salary.
(i) To get the 1st three letters from the Ename column from Emp table.
Answer:
SELECT LEFT(Ename. 3) FROM Emp;

(ii) To get 12³.
Answer:
SELECT POW(12.3);

(iii) To get the string “TIGER” in lowercase.
Answer:
SELECT IOWER(”TIGER”);

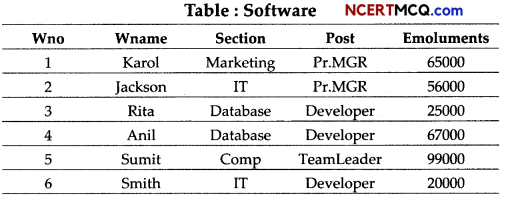
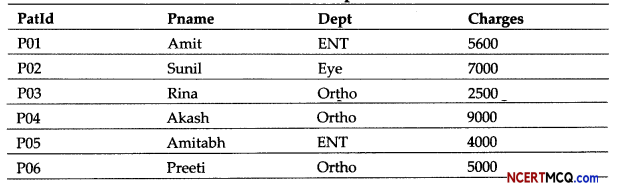
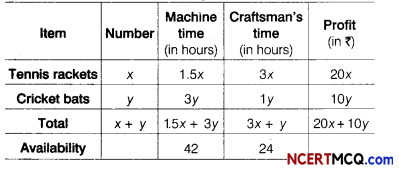
Question 12.
Akriti a student of class XII did not attend the classes on GROUP BY and aggregate functions and is now not able to solve the following assignment given by her teacher. Help her in the solutions.
Write SQL commands with respect to the table Army given below.
Table: Army

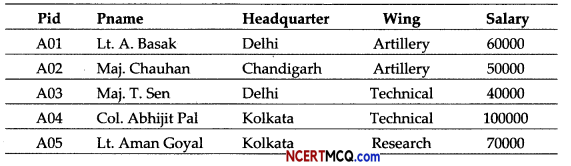
(i) To display the wing wise count of persons.
(ii) To display the total salary of majors.
(iii) To display the maximum salary among people whose Headquarter is in “Kolkata”.
(iv) To display the headquarter wise minimum salary.
Or
Write the outputs of SQL commands given with respect to the table Army given above.
(i) SELECT Wing, COUNT!*) FROM Army;
(ii) SELECT SUM(Salary) FROM Army WHERE LEFT! Pname, 3 )=“Ma j ” ;
(iii) SELECT MAX(Salary) FROM Army WHERE Headqua rter=“Kol kata”;
(iv) SELECT Headquarter, MIN(Salary) FROM Army GROUP BY Headquarter;
Answer:
(i) SELECT Wing, COUNT(*) FROM Army;
(ii) SELECT SUM(Salary) FROM Army WHERE LEFT(Pname,3)”Maj”:
(üi) SELECT MAX(Salary) FROM Army WHERE Headquarter=”Kolkata”;
(iv) SELECT Headquarter, MIN(Salary) FROM Army GROUP BY Headquarter;

Or

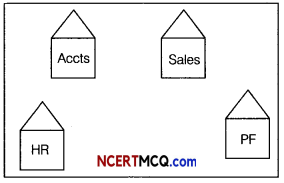
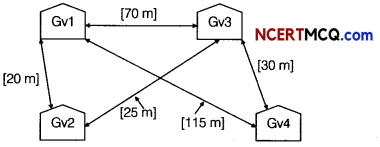
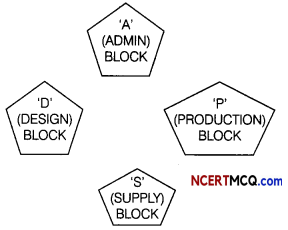
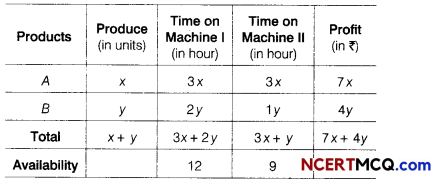
Question 13.
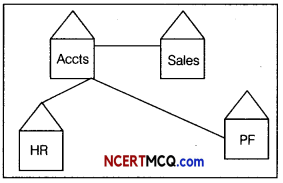
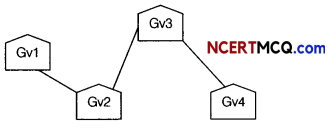
Arun Plastics has the following setup of buildings, with each building equipped with multiple computers. The distance between the buildings and the number of computers in each is given below:

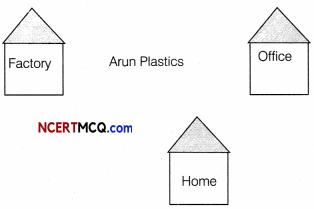
Building	Number of Computers
Factory	125
Office	30
Home	20

 

Building	Distance
Factory-Office	45m
Factory-Home	15m
Office-Home	120m

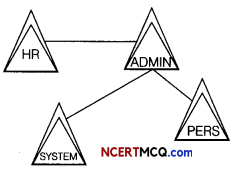
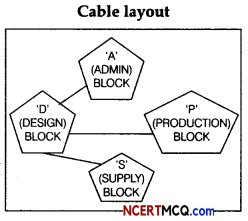
(i) Suggest a suitable cable layout of connectivity between the buildings.
Answer:
Since the smallest distances are between Factory-Office and Factory- Home, the following layout will be economical

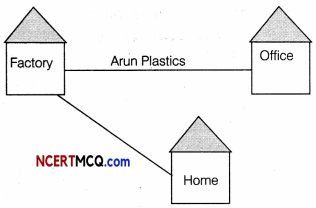
(ii) Suggest placement of server in the network.
Answer:
(ii) Server should be plaœd in the Factory as it has the maximum number of computers.

(iii) What kind of network(LAN/MAN/WAN) is formed here?
Answer:
A LAN network is formed as the distances between the buildings are small.

(iv) Which, topology should be used to connect the computers in each of the buildings?
Answer:
Star topology, as it is the best topology and it has multiple positive features in comparision to other topologies.

Students can access the CBSE Sample Papers for Class 12 Informatics Practices with Solutions and marking scheme Term 2 Set 6 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Informatics Practices Term 2 Set 6 with Solutions

Maximum Marks : 35
Time : 2 hours

Instructions

• The question paper is divided into 3 sections -A, B and C.
• Section A, consists of 7 questions (1-7). Each question carries 2 marks
• Section B, consists of 3 questions (8-10). Each question carries 3 marks.
• Section C, consists of 3 questions (11-13). Each question carries 4 marks.
• Internal choices have been given for question numbers -1, 3, 8 and 12.

Section-A
(Each question carries 2 Marks)

Question 1.
Arun is a newly appointed network executive at IGS technologies. He is well comfortable with local area networks and network systems, but is not very comfortable with the Internet concepts . He heard that Internet is called ‘Network of Networks’ and wants to know why is this so called. Clarify his doubt.
Or
Ms. Sangita wanted to connect the computers of her office with Internet facilities. Also, her network administrator told her that two devices modem and repeater will be required. Help her to understand the roles of the two devices.
Answer:
Internet is called ‘Network of Networks’ because it is global network of computers that are linked together by cables and telephone lines making communication possible among them. It can be defined as a global network over a million of smaller heterogeneous computer networks. The network which consists of thousands of network spanning the entire globe is known as Internet. The Internet is a world wide collection of networked computers, which are able to exchange information with each other very quickly.

In Internet, most computers are not connected directly, they are connected to smaller networks, which in turn are connected through gateways to the Internet backbone. A gateway is a device that connects dissimilar networks.
A backbone is central interconnecting structure that connects one or more networks.

Or

A modem is a device that modulates and demodulates signals. A modem converts signals from analog to digital and from digital to analog.
A repeater is a device that amplifies signals so that they can travel longer distances.

Question 2.
(i) Rakesh has designed a new website for a school and now wants to make it public.
Help him to understand the concept web hosting.
Answer:
A web hosting service is a type of Internet hosting service that allows you to publish your website files onto the Internet. So, anyone who will access to the Internet will access to your website. In practice, it usually refers to the service you get from a web hosting provider like one.com.

Web hosting is a service that makes your site or web application accessible on the Internet. It’s also one of the most essential elements to consider when building a website. Web hosting is typically provided by web hosts, which are businesses that maintain, configure and ran physical servers that house websites.

(ii) Remona, an in experienced web designer, wanted to design web pages and could not fix her mind whether she should prepare static or dynamic web pages. Help her with the concepts.
Answer:
A dynamic web page changes its content and appearance every time they are requested and fetched.
A static web page has always the same content and appearance every time they are fetched.

Question 3.
Biswajit a database operator came to know that certain functions in SQL have alternatives and wanted to know the alternatives for following functions
(i) SUBSTR()
(ii) POW()
Or
Sunita is a database operator and is confused about the operations of certain functions. Suggest her with proper function names for the following cases.
(i) To get the current date and time
(ii) To round a number to certain decimal places
Answer:
(i) SUBSTR() Both the SUBSTR() and the MID() functions return a part of a string. They take the parameters as the string, start position and the number of characters to extract.
(ii) POWERO The POW() or POWER() function help to calculate power of a number raised to an exponent.
Or
(i) NOW() The NOW() function of MySQL returns the current date and time.
(ii) ROUNDO The ROUND() function rounds a number to certain decimal places as per the usual rounding rules.

Question 4.
ABC Incorporation is installing networked systems for their office. They learnt that the star configuration is the best one. Write any three advantages and disadvantages of star topology.
Answer:
There are three advantages of star topology are as follows

1. Installation of star topology is very easy as all the nodes are directly connected to the central node or server.
2. Easy to detect faults and remove it.
3. Failure of single system will not bring down the entire network.

There are three disadvantages of star topology are as follows

1. Requires more cable length than bus topology.
2. If hub or server fails, the entire network will be disabled.
3. Difficult to expand, as the new node has to connect all the way to central node.

Question 5.
Gitanjali, is a database user and wants to know the proper working of the ROUND() function. Help her to understand its working, by the following statements.
(i) SELECT R0UND(893.94,1);
Answer:

The ROUND() function rounds a number to certain decimal places as per the normal rounding rules. So, ROUND(893.94,l) rounds up to 1 decimal place as 893.9, since next digit is 4, no changes to the previous digit.

(ii) SELECT R0UND( 199.99);
Answer:

Since no decimal places are indicated, decimal place is 0, so as per normal rounding rules, 199.99 becomes 200.

Question 6.
Rishi wants to know the utility of the GROUP BY and HAVING clauses of SQL . Make his concepts clear.
Answer:
The GROUP BY clause in SQL is used to arrange identical data into groups with the help of some functions, i.e. if a particular column has the same values in different rows, then it will arrange these rows in a group.

A HAVING clause in SQL specifies that an SQL SELECT statement must only return rows, where aggregate values meet the specified conditions.

A HAVING clause is like a WHERE clause, but applies only to groups as a whole (that is, to the rows in the result set representing groups), whereas the WHERE clause applies to individual rows. A query can contain both a WHERE clause and a HAVING clause.

Question 7.
Abhijit has prepared a table Graduate storing the details of some students of graduation with the subjects and division. He wants certain outputs from the table. Help him to write the queries.

(i) List the names of those students who obtained Div 1.
(ii) Display a report, listing Name, Stipend, Subject and amount of Stipend received in a year assuming that the Stipend is paid every month.
Or
Abhijit’s system is temporary down and hence he wants to predict the output of the following queries. Help him in the same.
(i) SELECT LEFT(NAME,3) FROM Graduate WHERE SNo>7;
(ii) SELECT Name, Stipend FROM Graduate WHERE Subject=”Chemistry” OR Subject=”Physics”;
Answer:
(i) SELECT Name FROM Graduate WHERE Div = 1;
(ii) SELECT Name, Stipend, Subject, Stipend *12 FROM Graduate;
Or

Section – B
(Each question carries 3 Marks)

Question 8.
Sudhir has confusions in working of INSTR(), MOD() and POWER() functions. Help him in getting outputs of the following queries and understand the functions.
(i) SELECT INSTR( ‘ keyboardandmouse ’, ‘ ad ’);
(ii) SELECT M0D( 121.5,10);
(iii) SELECT P0WER( 144,0.5);
Or
Mr. Rahman wants to know what kind of values will the following functions return, help him.
(i) SELECT UCASE (SUBSTR(‘Sofasets’.3));
(ii) SELECT INSTR ( ‘ abcdefgh ’, ‘ ef ’);
(iii) SELECT M0D (345,14);
Answer:
(i)

Or

(i) char/varchar/string
(ii) integer
(iii) integer

Question 9.
Sikha has written the following SQL statements but is not getting expected outputs. Help her to correct the queries.
(i) SELECT MODULUS(98, 7);
To get the remainder of division of 98 by 7.
Answer:
SELECT M0D(98, 7);

(ii) SELECT SEARCH( “mobile” , “ob”);
To find the position of “ob” in “mobile”.
Answer:
SELECT INSTR(“mobi1e”,“ob”);

(iii) SELECT LEFT( “SweetsandSnacks”);
To get the 1st five characters from the string.
Answer:
SELECT LEFT(“SweetsandSnacks”,5);

Question 10.
Mr. Das wants to know what corrections are required for the following SQL statements.
(i) SELECT RIGHT(“Wool engarments”, “merits”);
To extract 4 characters from right of the string.
Answer:
SELECT RIGHT(“Woolengarments”, 4);

(ii) SELECT EXPONENT(2, 5);
To get 2⁵.
Answer:
SELECT POW(2, 5);

(iii) SELECT MIDDLE(“Umbrella”.4);
To extract characters from position 4 to the end of the string.
Answer:
SELECT MID(“Umbrella”,4);

Section-C
(Each question carries 4 Marks)

Question 11.
Chandmal Stores has the following table of products sold in their store. They want certain aggregate/summative outputs for their business reports. Help them finding the following

(i) Display each manufacture and total number of products of each.
Answer:
SELECT Manufacture, C0UNT(*) FROM Product GROUP BY Manufacture;

(ii) Display the average price manufacture wise.
Answer:
Product GROUP BY Manufacture; SELECT Manufacture, AVG(UPrice) FROM Product GROUP BY Manufacture;

(iii) Display the count of different product names.
Answer:
SELECT COUNT(DISTINCT PName) FROM Product;

(iv) Display the maximum and minimum UPrice.
Answer:
SELECT MAX(UPrice), MIN(UPrice) FROM Product;

Question 12.
MT Systems has the following details of software staff members. They want certain grouped outputs from the table. Help them writing the SQL queries for the same.

(i) To display the section wise total emoluments paid.
(ii) To display number of distinct posts.
(iii) To display total emoluments paid to Pr.MGRs.
(iv) To display the average salary paid to database developers.
Or
The company MT Systems also wants to get the outputs of the following queries that use GROUP BY and aggregate functions. Help them for the operation.
(i) SELECT Section, MAX(Emoluments) FROM Software GROUP BY Section;
(ii) SELECT Post, C0UNT( *) FROM Software GROUP BY Post;
(iii) SELECT MAX( Emol uments ) FROM Software;
(iv) SELECT SUM(Emol uments) FROM Software WHERE Post=“Developer”;
Answer:
(i) SELECT Section, SUM(Emoluments ) FROM Software GROUP BY Section;
(ii) SELECT COUNT(DISTINCT Post) FROM Software;
(iii) SELECT SUM( Emoluments) FROM Software WHERE Post=“Pr.MGR”;
(iv) SELECT AVG(Emoluments) FROM Software WHERE Section=“Database’ AND Post=“Developer”;

Or

Question 13.
Bias Methodologies is planning to expand their network in India, starting with three cities in India to build infrastructure for research and development of their chemical products.

The company has planned to set up their main office in Pondicherry at three different locations and have named their offices as Back Office, Research Lab and Development Unit. The company has one more research office namely Corporate Unit in Mumbai. A rough layout of the same is as follows

(i) Suggest the type of network required (out of LAN, MAN, WAN) for connecting each of the following office units.
(a) Research Lab and Back Office
(b) Research Lab and Development Unit
Answer:
(a) LAN
(b) MAN

(ii) Which one of the following device, will you suggest for connecting all the computers with in each of their office units?
(a) Switch/Hub
(b) Modem
(c) Telephone
Answer:
(a) Switch/Hub

(iii) Which of the following communication medium, will you suggest to be procured by the company for connecting their local office units in Pondicherry for very effective (high speed) communication?
(a) Telephone cable
(b) Optical fibre
(c) Ethernet cable
Answer:
(b) Optical fibre

(iv) Suggest a cable/wiring layout for connecting the company’s local office units located in Pondicherry. Also, suggest an effective method/technology for connecting the company’s office unit located in Mumbai.
Answer:

Students can access the CBSE Sample Papers for Class 12 Informatics Practices with Solutions and marking scheme Term 2 Set 5 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Informatics Practices Term 2 Set 5 with Solutions

Maximum Marks : 35
Time : 2 hours

Instructions:

• The question paper is divided into 3 sections – A, B and C.
• Section A, consists of 7 questions (1-7). Each question carries 2 marks.
• Section B, consists of 3 questions (8-10). Each question carries 3 marks.
• Section C, consists of 3 questions (11-13). Each question carries 4 marks.
• Internal choices have been given for question numbers -1, 3, 8 and 12.

Section – A
(Each question carries 2 Marks)

Question 1.
Alakhya is new to networks. He has learnt various terms like server, client, MAC and IP address. He also came to know about the transmission mediums like radio waves, coaxial cables etc. He understood that certain devices are also important role players in a network . Explain him in short, the roles of following devices.
(i) Modem
(ii) Repeater
Or
(i) Hub
(ii) Switch
Answer:
(i) Modem (MOdulator DEModulator): It is a device that converts digital signal to analog signal (modulator) at the sender’s site and converts back analog signal to digital signal (demodulator) at the receiver’s and, in order to make communication possible via telephone lines.

(ii) Repeater: It is a network device that amplifies the signals, so that they can travel to a larger distance. Repeaters are amplifiers that help to carry forward the signals to larger distances.

Or

(i) Hub It is a multiport concentrator that connects multiple computers in a local area network.
(ii) Switch It is a network device that connects multiple segments of a LAN. It can filter network traffic and it also shares the bandwidth.

Question 2.
(i) Ashok steel industries was suggested by their network partners to install a switch in place of the previous hub installation. Explain them the use of a switch and why is a switch called an intelligent hub?
Answer:
A switch is a networking device which is used to connect different LAN segments of a network. A switch also supports packet filtering and forwarding between LAN segments.
A switch is called an intelligent hub because before simply forwarding a packet it checks for the intended destination for the packet and forwards it to that destination only, this is called packet filtering. While a hub forwards a packet to all the workstations in a network but only destination computer keeps it, rest all the computers drops that packet.

(ii) Ravi frequently listens that certain add-ons or plug-ins are required for looking at certain contents of web page. Help him to understand what are add-ons and plug-ins to a browser ?
Answer:
Add-ons or extension are tools which integrate into your browser. They are similar to regular apps or programs, but only run when the browser runs. Add-ons can allow the viewing of certain types of web content, such as Adobe Flash Player, necessary for Netflix movies and YouTube Videos respectively.
Plug-ins is a piece of software that acts as an add-on to a web browser and gives the browser additional functionality. Plug-ins can allow a web browser to display additional content, it was not originally designed to display.

Question 3.
Ms. Sudha is not clear about the proper use of TRIM() function. Help her to understand the same with one example.
Or
She is also not very conversant with the use of LCASEQ function. Explain her the working of LCASE() function with one example.
Answer:
The TRIM() function removes extra spaces from both sides of a string.
e.g.

SELECT TRIM (“ Double space ”);

Output:

Or

The LCASE() function converts a string to lowercase.
e.g.

SELECT LCASE (“CELLPHONE”);

Output:

Question 4.
Ms. Sumita understands that the data that is fetched in a browser in the form of pages comes from some remote computers that are called as web servers. Help her understand web server better with its types.
Answer:
A web server is a computer that runs websites. It’s a computer program that distributes web pages as they are requisitioned.
The basic objective of the web server is to store, process and deliver web pages to the users. This intercommunication is done using HyperText Transfer Protocol (HTTP).

A web server connects to the Internet and supports physical data interchange with other devices connected to the web.

There are various types of web server, which are available for different platforms.

• Apache Web Server
• Microsoft Internet Information Server
• NetScape Enterprise Web Server
• lighttpd
• Sun Java System Web Server
• Jigsaw Server

Question 5.
Neeraj wants to be more clear about where to use the HAVING clause and where to use the WHERE clause of SQL.
Differentiate between WHERE clause and HAVING clause in SQL and help him understand.
Answer:
Differences between WHERE clause and HAVING clause are as follows:

WHERE Clause	HAVING Clause
WHERE clause is used to filter the records from the table based on the specified condition.	HAVING clause is used to filter record from the groups based on the specified condition.
WHERE clause implements in row operations.	HAVING clause implements in column operations.
WHERE clause cannot contain aggregate function.	HAVING clause can contain aggregate function.
WHERE clause can be used with SELECT, UPDATE, DELETE statement.	HAVING clause can only be used with SELECT statement.
WHERE clause is used before GROUP BY clause.	HAVING clause is used after GROUP BY clause.
WHERE clause is used with single-row functions like UPPER, LOWER, etc.	HAVING clause is used with multiple-row functions like SUM, COUNT, etc.

Question 6.
Mr. Nandi wants to get grouped aggregate results from a table of employees of his office.
Explain him, how to use GROUP BY clause in SQL to get the desired results.
Answer:
The GROUP BY statement in SQL is used to arrange identical data into groups with the help of some functions, i.e. if a particular column has same values in different rows, then it will arrange these rows in a group. In the query, GROUP BY clause is placed after the WHERE clause.

The GROUP BY clause is used in the SELECT statement. Optionally, it is used in conjunction with aggregate functions to produce summary reports from the database.
e.g.

SELECT SUM(Sal) FROM Emp GROUP BY Desig;

The above command groups the records of the ‘Emp’ table on ‘Desig’ column and displays sum of salaries paid in each.

Question 7.
ABC advertising has the following record of their salesmen . They want to get certain aggregate results on analysing all the records together. Help them to find these results.
Table: Salesmen

(i) Display maximum commission from the salesmen.
(ii) Display the total commission earned by salesmen.
Or
(i) Display the average commission from the table.
(ii) Find the difference between maximum and minimum commission.
Answer:
(i) SELECT MAX(Conim) FROM Salesmen;
(ii) SELECT SUM(Conim) FROM Salesmen;

Or

(i) SELECT AVG(Conim) FROM Salesmen:
(ii) SELECT MAX(Cor,im)-MIN(Comm) FROM Salesmen;

Section – B
(Each question carries 3 Marks)

Question 8.
Write the statements for the following cases.
(i) Anil wants to see the dayname of a date 15th September 2016.
(ii) Riya wants to see the names of her friends in uppercase. The names are stored in a column Fname of a table FriendTab.
(iii) Bishakha wants to find the square root of 167.
Or
Write the correct SQL statements for the following situations.
Assume a table “Electronics” with fields (Itemld integer, Itemname varchar, Type varchar, Price float)
(i) To extract the last 4 characters of the Itemname in uppercase.
(ii) To round up the price upto 1 decimal place.
(iii) To search the position of the string “sc” in Itemname.
Answer:
(i) SELECT DAYNAME(”2016-09-15”);
(ii) SELECT UCASE(Fnarne) FROM FriendTab;
(iii) SELECT POW(167.O.5);

Or

(i) SELECT UCASE(RIGHT(Itemname.4)) FROM Electronics;
(ii) SELECT ROUNO(Price1) FROM Electronics;
(iii) SELECT INSTR(Itemname,”sc”) FROM Electronics;

Question 9.
Raj has written certain queries using MySQL functions and is not sure about the outputs . Help him to get the outputs for the following queries.
(i) SELECT P0W(M0D( 11.3) ,2);
Answer:

The MOD(11, 3) returns remainder of dividing 11 by 3 which is 2. The next process is POW(2,2) that returns (2)² = 4.

(ii) SELECT SUBSTR( “Antarcti cl ce”, 2,5);
Answer:

The SUBSTR(“Antarcticlce”, 2, 5) function extracts 5 characters from position 2 from the string.

(iii) SELECT YEAR( “2011-09-02”);
Answer:

The YEAR() function returns the year part of a date.

Question 10.
Rituja is trying to produce certain outputs using the INSTR(), POW() and MOD() functions. Help her to produce the desired results for the following statements.
Write the outputs of following SQL statements.
(i) SELECT I NSTR( “Honeybees” , ’’ey”);
(ii) SELECT POW (I NSTR( “Corporate”, ”ra”), 2);
(iii) SELECT M0D(120,2);
Answer:

Section – C
(Each question carries 4 Marks)

Question 11.
Army hospital Patna maintains the following table for its patients . They want certain outputs department wise – like the average charges, total number of patients department wise etc. As a database programmer help them to get the required outputs.

(i) Display each Dept and the total number of patients in each.
Answer:
SELECT Dept . COUNT(*) FROM Hospital GROUP BY Dept;

(ii) Display the department wise average charges.
Answer:
SELECT Dept. AVG(Charges) FROM Hospital GROUP BY Dept:

(iii) Display the total number of unique departments.
Answer:
SELECT COUNT(DISTINCT Dept) FROM Hospital ;

(iv) Display the minimum charges among patients whose name starts with “S” or “R”.
Answer:
SELECT MIN(Charges) FROM Hospital WHERE Pname LIKE “S%” OR Pnanie LIKE “R%”:

Question 12.
A Salesmen table of Excel sales company stores the details of salesman and their commission earned. ‘They want to produce certain aggregate reports areawise and gender wise.What queries do you think will be correct for the following requirements?
Table: Salesmen

(i) Display minimum commission earned by male salesmen.
(ii) Display maximum commission earned by female salesmen.
(iii) Find the average commission by male salesmen.
(iv) Find the sum of the commission of north area.
Or
The organisation wants to find the outputs of some of the queries as stated below, what do think will be the outputs ?
(i) SELECT MAX(Comm) FROM Salesmen WHERE Area=“East”;
(ii) SELECT COUNT(Area) FROM Salesmen;
(iii) SELECT COUNT!*) FROM Salesmen;
(iv) SELECT COUNT(Comm) FROM Salesmen;
Answer:
(i) SELECT MIN(Comm) FROM Salesmen WHERE Gender=”M”;
(ii) SELECT MAX(Comm) FROM Salesmen WHERE Gencler=”F”;
(iii) SELECT AVG(Comm) FROM Salesmen WHERE Gender=”W”;
(iv) SELECT SUM(Comm) FROM Salesmen WHERE Area=”North”;

Or

Question 13.
Mittal Steels have their following buildings as shown in the diagram . The number of computers and the distances between the buildings is given below.

Building	Number of Computers
Accts	100
Sales	15
HR	25
PF	30

 

Building	Distance
Accts-Sales	10m
Accts-HR	50 m
Accts-PF	750 m
Sales -HR	400m
Sales-PF	20m
HR-PF	900m

(i) Suggest a suitable cable layout of connectivity.
Answer:
The cable layout will be as follows:

(ii) Which building should have the server?
Answer:
Accts building should have the server as it has the maximum number of computers.

(iii) Which building should have hub/switch?
Answer:
All the buildings should have hub/switch as there are multiple computers in each of the buildings.

(iv) The company wants to connect these buildings with another office in a hilly area of the same city. What kind of network will be formed?
Answer:
MAN (Metropolitan Area Network) will be formed.

Students can access the CBSE Sample Papers for Class 12 Informatics Practices with Solutions and marking scheme Term 2 Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Informatics Practices Term 2 Set 4 with Solutions

Maximum Marks : 35
Time : 2 hours

Instructions

• The question paper is divided into 3 sections -A, B and C.
• Section A, consists of 7 questions (1-7). Each question carries 2 marks
• Section B, consists of 3 questions (8-10). Each question carries 3 marks.
• Section C, consists of 3 questions (11-13). Each question carries 4 marks.
• Internal choices have been given for question numbers -1, 3, 8 and 12.

Section-A
(Each question carries 2 Marks)

Question 1.
Mr. Akash is new to computer networks. Although he is conversant with different terms like server, client, web etc., he is confused about the types of networks on the basis of configuration and distances . Help him to understand the different types of networks on the basis of distances through which they are separated. Explain different types of networks.
Or
Mr. Akash also does not well know the different parts/components of a network and is thereby not able to properly implement a new network for his organisation . Explain him the different components of a network.
Answer:
There are many types of networks. Networks can be classified according to span of their geographical area. They can be classified into three categories.

1. Local Area Network: A LAN network interconnects computers within a limited area. This area can be a residence, school, library or office building. LAN is relatively smaller than MAN and WAN. It is privately owned network. It provides local connectivity.
In offices, LAN is used to share resources.
It can also be used to exchange information. A LAN is made up of many components.

2. Metropolitan Area Network MAN networks are larger than a local area networks. It covers a large geographical area as compared to LAN. It can be the area of an entire city. MAN may be a single network like cable TV network. It may be interconnection of many LANs.

3. Wide Area Network WAN networks are the largest networks. These networks have no limit of geographical distance. This geographical area can be a country, a continent or the whole world. Public networks can be used to connect computers in a Wide Area network.

Or

There are various components of a computer network, which are as follows

• Host /Node / Workstation It refers to the computers that are attached to a network.
• Server Computer that facilities sharing of data,software and hardware resources (e.g. printers, modems etc.) on a network is called server.
• Client A client computer is a computer that can request for some services from a server.
• NIU (Network Interface Unit) It is also known as NIC(Network Interface Card) or LAN card. It is a device that works as an intermediator between computer and the network. LAN card can be wired as well as wireless.
• Hub/Switch Hub/ Switch is a device used to interconnect computers on a network.
• Communication channel It is a way/ method to provide communication between computers and devices on a network.

Question 2.
(i) Jatin heard that a switch is a better device than a hub and can perform better in communications of a network.
Suggest him one point of difference between switch and hub.
Answer:
A hub is a networking device that allows you to connect multiple PCs to a single network, whereas a switch connects various devices together on a single computer network.

(ii) Rahul knows that the best topology is the star topology. Point out to him the negative characteristics of the star topology.
Answer:
(a) Increased cost due to independent cables.
(b) Central node dependency.

Question 3.
Briefly state descriptions for Smita, who is a database operator. The role of the following MySQL functions
(i) NOW()
(ii) RTRIM()
Or
Write the uses of following functions
(i) MID()
(ii) DATE()
Answer:
NOW() function returns the current date and time both.
The date is returned in YYYY-MM-DD format and the time is returned in HH:MM:SS format.

(ii) RTRIM() function removes extra spaces from the right of a string. .
e.g.
SELECT RTRIM(“Windows ”);

Output

OR

(i) MID() function extracts characters from any position of a string just like the SUBSTRQ function . It takes the string, start position and the number of characters to extract.

(ii) DATE() function returns the date part from a date and time given as parameter, e.g. SELECT DATE(“2021-09-08 05 : 46 : 50”);

Output

Question 4.
Before implementing a network for their web based activities ITC Ltd., IT manager wanted to be conversant about the data sharing facilities of a network . How will you make him/her understand the data sharing facilities of a network?
Answer:
Data sharing is considered as an important application of networking. There are many reasons. Users can share data easily with the help of networks.

For example. In an organization, users of different departments can share files easily with the help of network. Networking helps to increase the speed and accuracy of data communication.

Data can be transferred to others within seconds using networks. Besides this, cost of data transfer using networks is also very low.

Using networks, a single task can be performed by dividing the work into team groups. It increases the productivity of work.

Question 5.
Jessica wants to understand the working of INSTR, CONCAT, LEFT and RIGHT functions. Explain her the working of the functions by giving the outputs for following SQL statements.
(i) SELECT INSTR(“HimgiriExpress”,”px”);
Answer:

INSTR() function returns the position of a sub-string in a string. If not found returns 0. Here “px” is not present in “HimgiriExpress”. So it returns 0.

(ii) SELECT C0NCAT( LEFT( “Banana”, 3), RIGHTC “AppT e”, 2));
Answer:

LEFT(“Banana”, 3) extracts 3 characters from left of the string, i.e. “Ban” and RIGHT(“Apple”,2) extracts 2 characters from right of the string, i.e. le. CONCATf) function is used to add two strings, i.e. Banle.

Question 6.
Rita forgot the clauses that help to group records of a table and to apply conditions on such grouped records. Help her with the proper clauses.
(i) To group the records of a table on common values of a column.
Answer:
Group BY clause

(ii) To give a condition on grouped records.
Answer:
HAVING clause

Question 7.
A table CollegeStudents is prepared for students of MKC Commerce College. The college committee wants to get certain outputs. Help them with SQL commands for the following requirements.

(i) To display Name, Fee, Gender, Join Year about the CollegeStudents, who have joined before 2010.
(ii) To display the names of CollegeStudents, who are paying Fee more than 30000.
Or
The MKC Commerce College also wants certain more outputs on the basis of the joining year of the students. Provide them proper SQL commands for the following
(i) To display the names of all CollegeStudents in ascending order of their joinyear.
(ii) To display the year and the total number of CollegeStudents joined in each year from the table College Students.
Answer:
(i) SELECT Name, Fee, Gender, JoinYear FROM CollegeStudents WHERE JoinYear<2010;
(ii) SELECT Name FROM CollegeStudents WHERE Fee>30000;
Or
(i) SELECT Name FROM CollegeStudents ORDER BY JoinYear;
(ii) SELECT JoinYear, COUNT(*) FROM CollegeStudents GROUP BY JoinYear;

Section-B
(Each question carries 3 Marks)

Question 8.
Mr. Bansal, the sports instructor of Greenage school wants certain outputs from the Sports table using functions of SQL. Which SQL statements will give the outputs as specified in the following statements ?

(i) To get the date when each sport is played.
(ii) To get the sportnames in uppercase.
(iii) To get the last 3 characters of each sportname.
Or
Mr. Bansal is also not very comfortable with MID,MOD and RIGHT functions. Help him to write alternative commands for the following statements.
(i) SELECT MID( ‘Aniket’ ,1,4);
(ii) SELECT M0D( 11,2);
(iii) SELECT RIGHT(‘Movie’,3);
Answer:
(i) SELECT DAY (Dtof Play) FROM Sports;
(ii) SELECT UCASE(Sportname) FROM Sports;
(iii) SELECT RIGHT(Sportname,3) FROM . Sports;
Or
(i) SELECT LEFT(‘ Ani ket ’ ,4);
(ii) SELECT 11 % 2;
(iii) SELECT SUBSTR( ‘Movie’ , – 3,3);

Question 9.
Nitin is getting confused with the working of some MySQL functions . Giving an example illustrate to him the use of the following functions.
Write the uses of following MySQL functions
(i) MONTH()
Answer:
MONTH() function returns the month part of a date.
e.g. SELECT MONTH(“2021-09-11”);

Output

(ii) ROUND()
Answer:
ROUND() function returns the month part of a date.
e.g. SELECT ROUND( 123.987,2);

Output

(iii) LEADING clause with TRIM()
Answer:
LEADING clause with TRIM() function removes extra spaces or characters from both sides of a string. The LEADING clause with TRIM() function removes some leading characters from a string.
e.g. SELECT TRIM (LEADING ’X’ FROM ‘XXXXMySQLXXXX’);

Output

Question 10.
While learning uses of MySQL functions, Jasminder was not properly understanding the uses of the following functions. Explain her the uses with one example of each.
(i) MONTHNAME()
Answer:
MONTHNAME() function returns the name of the month for the date specified, e.g. SELECT MONTHNAME(“2022-09-02”);

Output

(ii) UCASE()
Answer:
UCASE() function converts a string to uppercase.
e.g. SELECT UCASE(“return”);

Output

(iii) DAY()
Answer:
DAY() function returns the day part from the date specified as argument.
e.g. SELECT DAY( “2012-09 -12” );

Output

Section – C
(Each question carries k Marks)

Question 11.
Indian railways maintains the following table of its emloyees . They want to get certain summative results department wise and on the basis of male and female employees working . Help the IT staff to predict the outputs of the statements given, before implementing them.

(i) SELECT SUM(Basic) FROM Employee WHERE Department=’Personnel’;
Answer:

(ii) SELECT AVG(Basic) FROM Employee WHERE Sex=’F’;
Answer:

(iii) SELECT MAX(Basic) FROM Employee WHERE Sex=’M’;
Answer:

(iv) SELECT COUNT (DISTINCT Department) FROM Employee;
Answer:

Question 12.
The Staff table of GI systems maintains the details of its staff, with their monthly CTC . They want to find certain results like department wise total CTC, designation wise averages etc. The requirements are given in the following statements. Suggest them proper SQL statements for the same.

(i) To display the total MCTC (Monthly Cost To Company) of sales department.
(ii) To display average MCTC of staff who have a joining date.
(iii) To display the maximum MCTC among officers.
(iv) To display the sum of MCTC of staff whose name has “a” somewhere .
Or
They want to know the outputs such as total, average, maximum etc., of CTCs of the staffs of certain posts and departments . The following commands are written. Help them to predict the outputs.
(i) SELECT MIN(MCTC) FROM Staff WHERE Dept=“Pers”;
(ii) SELECT COUNTCDISTINCT Dept) FROM Staff;
(iii) SELECT SUM(MCTC) FROM Staff WHERE JoinDt IS NULL;
(iv) SELECT COUNT(JoinDt) FROM Staff;
Answer:
(i) SELECT SUM(MCTC) FROM Staff WHERE Dept=”Sales”;
(ii) SELECT AVG(MCTC) FROM Staff WHERE JoinDt IS NOT NULL;
(iii) SELECT MAX(MCTC) FROM Staff WHERE Post=”Offi cer”;
(iv) SELECT SUM(MCTC) FROM Staff WHERE Staffname LIKE “%a%”:

Or

(i)

The MIN() function returns the minimum value from the records that match the condition.

(ii)

COUNT(DISTINCT) function returns the count of unique values in a column.

(iii)

The SUM () function returns the sum of values for the records that match the condition.

(iv)

COUNT(JoinDt) function counts the number of NON NULL values.

Question 13.
Global Village Enterprises has following four buildings in Hyderabad city.

The distance between the buildings is given in metres. Also, the number of computers in each of the buildings is given below.

Building	Number of computers
Gvl	35
Gv2	25
Gv3	80
Gv4	60

Computers in each building are networked but buildings are not networked so far. The
company has now decided to connect building also.
(i) Suggest a cable layout for these buildings.
Answer:
Cable layout

(ii) In each of the buildings, the management wants that each LAN segment gets a dedicated bandwidth, i.e. bandwidth must not be shared. How can this be achieved?
Answer:
To give dedicated bandwidth, the computers in each building should be connected via switches as switches offer dedicated bandwidth.

(iii) The company also wants to make available shared Internet access for each ot the buildings. How can this be achieved?
Answer:
By installing routers in each building, shared Internet access can be made possible.

(iv) The company wants to link its head office in GV1 building to its another office in Japan.
Answer:
Satellite, as it can connect offices across globe.

Students can access the CBSE Sample Papers for Class 12 Informatics Practices with Solutions and marking scheme Term 2 Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Informatics Practices Term 2 Set 3 with Solutions

Maximum Marks : 35
Time : 2 hours

Instructions:

• The question paper is divided into 3 sections – A, B and C.
• Section A, consists of 7 questions (1-7). Each question carries 2 marks.
• Section B, consists of 3 questions (8-10). Each question carries 3 marks.
• Section C, consists of 3 questions (11-13). Each question carries 4 marks.
• Internal choices have been given for question numbers -1, 3, 8 and 12.

Section – A
(Each question carries 2 Marks)

Question 1.
Jitendra, while looking at a web page found that some of the components were not working . The website prompted to install certain plug-ins to the browser. Explain the term plug-ins and why they are needed?
Or
Mr. Navneet found that his login id and password are automatically appearing on keypress in the login page. Explain him how cookies are responsible for this and how they are useful?
Answer:
Browser extensions and plug-ins are generally similar. They are software components (sometimes called “add-ons”) that add features to an existing computer program. These plug-ins allow you to do things in your browser such as view PDF files or watch videos on sites such as Netflix.

Or

Cookies are files created by websites you visit. They make your online experience easier by saving browsing information.
With cookies, sites can keep you signed in, remember your site preferences and give you locally relevant content. The purpose of the computer cookie is to help the website keep track of your visits and activity.

Question 2.
(i) Looking for network devices that are required for running of a computer network Ms. Rashmi found a device called Modem. Explain her the role of Modem in a network.
Answer:
Modem is abbreviation for Modulator Demodulator. Modems are used for data transfer from one computer network to another computer network through telephone lines. The computer network works in digital mode, while analog technology is used for carrying messages across phone lines. Modem converts from analog to digital and digital to analog.

(ii) The employees of WoodCorp Ltd. were steadily facing the problem of weak signals. The network engineer suggested installation of repeaters. Explain them the use of repeater in a network.
Answer:
Repeater is a network device that retransmits the data from sender to the receiver side of the network. The incoming data can be in the form of wireless, electrical signals and optical signals. The repeaters transfer the data through a large area distance. The repeaters ensures the security and quality of the data and retransmits the data by securely preserving the signals. For the longer distance data transmission, the repeaters are used without compromising the security and quality of data.

Question 3.
Mahi wanted to find the data from a student table with certain formattings on the data using some MySQL functions.
The table structure is as follows
STUDENT (RollNo, Name, Class, Stream, Percentage)
(i) To display the 3rd to 7th characters of name attribute.
(ii) To display the name of each student in uppercase letters with their RollNo, whose percentage is greater than 70.
Or
Snigdha has some confusions regarding the working of LEFT() and RTRIM() functions. Help her in finding the outputs of following statements.
(i) mysql >SELECT LEFT (’Swati’,4);
(ii) mysql>SELECT RTRIM (‘!!!!!Study is important!!!!!’);
Answer:
(i) SELECT SUBSTR( Name, 3,5) FROM STUDENT;

(ii) SELECT UCASE( Name), Roll No FROM
STUDENT WHERE Percentage>70;

Or

(i)

(ii)

Question 4.
Jim heard the term topology and could not make out how this term is related to networks. Explain him the term topology, its types and various topologies used.
Answer:
In networking, topology refers to the layout of a computer network. Physical topology means the placement of the elements of the network, including the location of the devices or the layout of the cables. Logical topology maps the flow of data, regardless of the physical layout.
Few topologies are – Star, Bus, Ring, Tree, etc.

Question 5.
(i) Ms. Sudha a database operator wants to find the maximum and minimum values from a column test_score of a table. Explain how the MAX() and MIN() functions can help her ?
(ii) She also wants to find the average of the test_score and the count of records in the table, provide her the explanation of AVG() and COUNT() functions, so that she can get her desired results.
Answer:
MAX([DISTINCT I All] expr) It returns the maximum value of expr. MAX() may take a string argument, in such cases, it returns the maximum string value. The DISTINCT keyword can be used to find the maximum of the distinct values of expr, however this produces the same result as omitting DISTINCT. MAX() returns NULL, if there were no matching rows,
e.g.

mysql> SELECT MAX(test_score) FROM STUDENT;

MIN([DISTINCTI All]expr) It returns the minimum value of expr. MIN() may take a string argument, in such cases, it returns the minimum string value. The DISTINCT keyword can be used to find the minimum of the distinct values of expr, however this produces the same result as omitting DISTINCT. MIN() returns NULL, if there were no matching rows.
e.g.

mysql> SELECT MIN(test_score) FROM STUDENT;

(ii) AVG ([DISTINCT]expr) It returns the average value of expr. The DISTINCT option can be used as of MySQL to return the average of the distinct values of expr. AVG() returns NULL, if there were no matching rows.
e.g.

mysql> SELECT AVG(test_score) FROM STUDENT;

COUNT(expr) It returns a count of the number of non NULL values of expr in the rows retrieved by a SELECT statement. The result is a BIGINT value.
COUNT() returns 0, if there were no matching rows. COUNT(*) is somewhat different in that it returns a count of the number of rows retrieved, whether or not they contain NULL values.
e.g.

mysql > SELECT COUNT (*) FROM STUDENT;

The query would give the output, total number of rows in STUDENT table. COUNT( [DISTINCT] expr) It returns a count of the number of rows with different non NULL expr values.

COUNT(DISTINCT) returns 0, if there were no matching rows,
e.g.

mysql> SELECT COUNT(DI ST INCT results) FROM STUDENT; .

Question 6.
Shyam was interrogated by his teacher in a viva about the differences between single-row functions and multiple-row functions. He could not answer the questions. Help shyam in figuring out four differences.
Answer:

Single-row functions	Multiple-row functions / Aggregate functions
1. It operates on a single row at a time.	1. It operates on multiple rows.
2. It returns one result per row.	2. It returns one result for multiple rows.
3. It can be used in SELECT, WHERE and ORDER BY clause.	3. It can be used in the SELECT clause only.
4. Mathematical, String and Date functions are examples of single-row functions.	4. MAX(), MIN(), AVG(), SUM(), COUNT() and COUNT(*) are examples of multiple-row functions.

Question 7.
Mr. Roy is a manager in a hotel and wants to find out some data from a table where he maintains the hotel records. He is not very expert with SQL commands and functions. Help him to write the queries.
Table: Hotel

(i) Display count of the different room types from the table Hotel.
(ii) Display the average room charges of “AC” rooms.
Or
(i) Display the count of Dtof Arrival from the table Hotel.
(ii) Display the minimum charges.
Answer:
(i) SELECT COUNT(DISTINCT RoomType) FROM Hotel;
(ii) SELECT AVG(Charges) FROM Hotel WHERE RoomType=“AC”;
Or
(i) SELECT COUNT(DtofArrival ) FROM Hotel;
(ii) SELECT MIN(Charges) FROM Hotel;

Section – B
(Each question carries 3 Marks)

Question 8.
Samriddhi is a database operator at New Software Systems Inc. She wants to understand the working of certain MySQL functions. She has wrote following MySQL statements and wants to understand the outputs. Help her to predict the outputs of the following statements.
(i) SELECT SUBSTR(‘Informaticspractices’ ,-10, 2);
(ii) SELECT ROUND(1999.98, 1);
(iii) SELECT TRUNCATE(1778.89, -1 );
Or
(i) SELECT POW( 11, 2);
(ii) SELECT P0W( 2 , -2);
(iii) SELECT POW(19.5, 6);
Answer:

Or

Question 9.
Naina works for M/s Anish Steels Ltd. She has written following statements, but is not able to understand the outputs. Explain her the working of these statements and produce the outputs.
(i) SELECT INSTRC ‘computerscience’ , ‘sc’);
(ii) SELECT MID( ‘ f unandfood ’, 3,4);
(iii) SELECT ROUNDC1334.99) ;
Answer:

Question 10.
Certain Date/Time and numeric functions trouble Sunil and he is not able to understand and implement properly the functions. Help him with the outputs of the following commands.
(i) SELECT M0D( 12,7);
(ii) SELECT M0NTH(‘2012-09-12’) ;
(iii) SELECT YEAR( ‘2021 -01 -01′);
Answer:

Section – C
(Each question carries 4 Marks)

Question 11.
While working with records of students, to find aggregate results, Mr. Akashdeep wrote some queries using MySQL functions, but is not sure about the outputs produced. Help him to find the proper outputs of the statements given below.
Table: Student

(i) SELECT Name, JoinYear FROM Student WHERE Gender — ‘F’ AND C_ID=’A02’;
(ii) SELECT MIN (JoinYear) FROM Student WHERE Gender — ‘M’;
(iii) SELECT AVG(Fee) FROM Student WHERE C_ID=’AO1’ OR C_ID=’A05’;
(iv) SELECT SUM(Fee) FROM Student WHERE Stream=”Computer”;
Answer:

Question 12.
The IT department of Doctor’s Hub maintains the following Hospital table for patient records. They are in the process of producing some reports, department wise to analyse the performance and expenses of its various departments. Help them with SQL queries using aggregate functions and GROUP BY clause to get the required results.
Table: Hospital

(i) Display the department wise number of patients.
(ii) Display the unique department names.
(iii) Display the department wise maximum charges.
(iv) Display department wise average charges.
Or
Help the IT department in finding the outputs of the queries given below with respect to the table Hospital given above.
(i) SELECT Dept, MIN (Charges)FROM Hospital GROUP BY Dept;
(ii) SELECT COUNT(DISTINCt Dept) FROM Hospital;
(iii) SELECT MAX(Charges) FROM Hospital WHERE Dept=“0rtho”;
(iv) SELECT SUM(Charges)FROM Hospital WHERE Charges>4000;
Answer:
(i) SELECT Dept, COUNT!*) FROM Hospital GROUP BY Dept;
(ii) SELECT DISTINCT Dept FROM Hospital ;
(iii) SELECT Dept, MAX(Charges) FROM Hospital GROUP BY Dept;
(iv) SELECT Dept, AVG(Charges) FROM Hospital GROUP BY Dept;

Or

(i)

The records are grouped by Department and MIN(charges) finds the minimum in each group.

(ii)

COUNT (DISTINCT Dept) finds the count of unique departments.

(iii)

The MAX(Charges) finds the maximum charges in Ortho department.

(iv)

The SUM(Charges) finds the sum of the charges, where charges are more than 4000.

Question 13.
Red Pandas Infosystems has its 4 blocks of buildings . The number of computers and distances between them is given below

Building	Number of Computers
HR	15
ADMIN	100
SYSTEM	25
PERS	30

 

Building	Distance
HR-ADMIN	10m
HR- SYSTEM	50m
HR- PERS	750m
ADMIN- SYSTEM	300m
ADMIN- PERS	20m
SYSTEM-PERS	250m

Answer the following questions with respect to the above scenario.
(i) Suggest a suitable cable layout for the network.
Answer:
The cable layout is given below:

Since the ADMIN building has the maximum number of computers, connecting to it will ensure best connectivity.

(ii) Suggest the best place to house the server of the network.
Answer:
ADMIN building, as it has the maximum number of computers.

(iii) Which topology should be used to connect computers in each building?
Answer:
Star topology, as it is the topology offering best facilities.

(iv) What kind of network will be formed here (LAN/MAN/WAN)?
Answer:
LAN (Local Area Network)

Students can access the CBSE Sample Papers for Class 12 Informatics Practices with Solutions and marking scheme Term 2 Set 1 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Informatics Practices Term 2 Set 1 with Solutions

Maximum Marks : 35
Time : 2 hours

Instructions:

• The question paper is divided into 3 sections – A, B and C.
• Section A, consists of 7 questions (1-7). Each question carries 2 marks.
• Section B, consists of 3 questions (8-10). Each question carries 3 marks.
• Section C, consists of 3 questions (11-13). Each question carries 4 marks.
• Internal choices have been given for question numbers -1, 3, 8 and 12.

Section – A
(Each question carries 2 Marks)

Question 1.
Aman, a freelance website developer, has been assigned a task to design few web pages for a book shop. Help Aman in deciding out of static web page and dynamic web page, what kind of web pages should be designed by clearly differentiating between static and dynamic web pages on atleast two points?
Or
Priyanka, a beginner in IT field has just started learning web technologies. Help her in understanding the difference between website and web pages with the help of a suitable general example of each.
Answer:
He should develop dynamic web pages as they are richer with features, interactive and are better in performance.

Differentiation between static and dynamic web pages are as follows:

Page	Dynamic Web Page
In static web pages, pages will remain same until someone changes it manually.	In dynamic web pages, content of pages are different for different visitors.
Static web pages are simple in terms of complexity.	Dynamic web pages are complicated.
In static web pages, information are change rarely.	In dynamic web page, information are changed frequently.
Static web page takes less time for loading than dynamic web page.	Dynamic web page takes more time for loading.
Static web pages are written in languages such as HTML, JavaScript, CSS, etc.	Dynamic web pages are written in languages such as CGI, AJAX, ASP, ASP.NET, etc.

Or

A website is a collection of web pages. Whereas, a web page is a single page/file.
Just as a book is a collection of multiple pages.

Website	Web Page
1. Website is a collection of web pages displayed on the web with a client like browser.	1. It is part of website that includes information and content and is displayed on the browser to user or visitor.
2. It is a combination of web pages created using HTML and CSS.	2. Information is usually written in HTML language.
3. It requires more time to develop the website as compared to web pages.	3. It requires less time to develop a web page as compared to the website.
4. It includes content about Several entities.	4. It includes content or information about a single entity.
5. There is no such extension included in the URL of the website.	5. URL of web page include extension.
6. It is quite hard and complex to create the structure of the website and its programming.	6. It is quite easy and simple to develop web page after website structure is being created.

Question 2.
(i) I

• am a small text file.
• created on a user’s computer.
• contain small pieces of data – like a username, pass ward and user’s browsing history as well as preferences.
• may help to improve user’s web browsing experience.

Who am I?
Answer:
Cookie A cookie (called an Internet or web cookie) is the term given to describe a type of message that is given to a web browser by a web server. The main purpose of a cookie is to identify users and possibly prepare customised web pages or to save site login information.

When you enter a website using cookies, you may be asked to fill out a form providing personal information like your name, E-mail address and interests. This information is packaged into a cookie and sent to your web browser, which then stores the information for later use. The next time you go to the same website, your browser will send the cookie to the web server. The message is sent back to the server each time the browser requests a page from the server.

(ii) Name any two popular web browers.
Answer:
Internet Explorer, Mozilla Firefox.

Question 3.
Predict the output of the following queries.
(i) SELECT P0WER(5, 3);
(ii) SELECT M0D(5, 3);
Or
Briefly explain the purpose of the following SQL functions.
(i) POWER( )
(ii) MOD( )
Answer:
(i)

The POWER(x,y) returns x^y, hence POWER(5,3) returns 5³ = 125.

(ii)

MOD(x,y) returns the remainder of dividing x by y. Hence, MOD(5,3) returns 2.

Or

(i) POWER() function returns the value of a number raised to the power of another number.
(ii) MOD() function returns the remainder of a number dividing by another number.

Question 4.
Navya has just created a website for her company and now need to host it. Briefly discuss the role of a web server in hosting a website.
Answer:
A web server is the residence of web pages. It is also the agent that fetches the web pages when the web pages are requested by clients.
The main job of a web server is to display website content through storing, processing and delivering web pages to users. All computers that host websites must have web server software. Web servers are used in web hosting or the hosting of data for websites and web-based applications or web applications.

Question 5.
Help Reshma in predicting the output of the following queries.
(i) SELECT R0UND(8.72,3);
Answer:

ROUND() function rounds a number to certain decimal places. Here, number of decimal places is 3 and the number is 8.72 . So, the output will be 8.720

(ii) SELECT ROUND(9.8);
Answer:

ROUND() function rounds a number to certain decimal places. Here, number of decimal places is 0 . So, as per rounding rules the integer part increases by 1 to give 10.

Question 6.
Aryan, a database administrator, has grouped records of a table with the help of GROUP BY clause.
He needs to further filter groups of records generated through GROUP BY clause.
Suggest suitable clause for it and properly, explain its usage with the help of an example.
Answer:
He needs to use the HAVING clause. Just as the WHERE clause filters individual records on a condition, the HAVING clause can be used to filter groups on basis of a condition.
eg.

SELECT Dept, COUNT!*) FROM Emp GROUP BY Dept;

Groups the records on Emp table by Dept and displays count of employees in each department.

SELECT Dept, COUNT!*) FROM Emp GROUP BY Dept HAVING C0UNT(*)>5;

Groups the records on Emp table by Dept and displays count of employees in each department, but only those departments are shown whose number of employees are >5.

Question 7.
Mr. Som, a HR Manager in a multinational company “Star-X world”, has created the Emp table to store the records of employees.
Table: Emp

He has written following queries
(i) SELECT MAXCYEAR(DOB)) FROM Emp; .
(ii) SELECT EName FROM Emp WHERE M0NTH(D0J)=11;
Predict the output.
Or
Based on the table given above, help Mr. Som writing queries for the following task.
(i) To display the name of eldest employee and his/her DOB.
(ii) To display the name of those employees whose joining month is May.
Answer:
(i)

YEAR(DOB) returns the year part of each DOB and MAX() finds the maximum value among these.

(ii)

MONTH(DOJ) extracts the month part of a date which is compared to 11. Here, the only employee with 11 as DOJ is “Melinda”.

Or

(i) SELECT Ename, DOB FROM Emp WHERE DOB = (SELECT MIN (DOB) FROM Emp);
(ii) SELECT Ename FROM Emp WHERE MONTH (DOJ)= 05;

Section – B
(Each question carries 3 Marks)

Question 8.
Predict the output of the following queries.
(i) SELECT INSTRC’exams@cbse.nic.in’,’.’):
(ii) SELECT SUBSTR(‘exams@cbse.nic. in’,7.4);
(iii) SELECT LEFT(‘ exams@cbse. nic. i n’, 5);
Or
Ms.Saumya is working on a MySQL table named ‘Hotel’ having following structure
Table: Hotel

She need to perform following task on the table.
(i) To fetch last 2 characters from the user_id column.
(ii) To display the values of name column in lower case.
(iii) To display 3 characters from 3rd place from the column city.
Suggest suitable SQL function for the same. Also, write the query to achieve the desired task.
Answer:
(i)

The INSTR() function returns the position of String2 in Stringl. Hereis present in position 11 of the string exams@cbse.nic.in.

(ii)

The SUBSTR() function extracts certain number of characters from a start position and number of characters specified. Here SUBSTR(exams@cbse.nic.in,7,4) extracts 4 characters from position 7 of the string.

(iii)

The LEFT() function extracts certain number of characters from left of a string. Here, LEFT(exams@cbse.nic.in, 5) extracts 5 characters from left of the string.

Or

(i) Function RIGHT()
Quay SELECT RIGHT(user_id,2) FROM Hotel;

(ii) Function LCASEQ
Query SELECT LCASE(name) FROM Hotel;

(iii) Function SUBSTR()
Query SELECT SUBSTR(city, 3, 3) FROM

Question 9.
Reena is working with functions of MySQL. Explain her following
(i) What is the purpose of NOW() function?
Answer:
The NOW( )function returns the system date and time.

(ii) How many parameters does it accept?
Answer:
0 parameters

(iii) What is the general format of its return type?
Answer:
“YYYY-MM-DD HH: MM : SS”.

Question 10.
While dealing with string data type in MySQL, its observed that sometimes unnecessary space character comes in between which hampers the successful executing of a string manipulation module. Name the suitable MySQL function(s) to remove leading, trailing and both type of space characters from a string. Also, give MySQL queries to depict the same.
Answer:
(i) To remove leading spaces – LTRIM()

e.g. SELECT LTRIM( “Spaces”);

Output:

(ii) To remove trailing spaces — RTRIM()

e.g. SELECT RTRIMC’Spaces”);

Output:

(iii) To remove spaces in both sides— TRIM()

e.g. SELECT TRIM(” Spaces ”);

Output:

Section -C
(Each question carries A Marks)

Question 11.
Carefully, observe the following table named ‘stock’
Table: Stock

Write SQL queries for the following
(i) To display the records in decreasing order of Price.
Answer:
SELECT * FROM Stock ORDER BY Price DESC;

(ii) To display Category and Category wise total Quantities of products.
Answer:
SELECT Category, SUM(Qty) FROM Stock GROUP BY Category;

(iii) To display the Category and its average Price.
Answer:
SELECT Category, AVG(Price) FROM Stock GROUP BY Category;

(iv) To display Category and Category wise highest Price of the products.
Answer:
SELECT Category, MAX(Price) FROM Stock GROUP BY Category;

Question 12.
Satyam, a database analyst has created the following table
Table: Student

He has written following queries
(i) SELECT SUM(Marks) FROM Student WHERE Optional= IP’ AND Stream= ‘Commerce’;
(ii) SELECT MAX(Marks)+MIN(Marks) FROM Student WHERE Optional= ‘CS’:
(iii) SELECT AVG(Marks) FROM Student WHERE Optional ‘IP’;
(iv) SELECT LENGTH(SName) FROM Student WHERE Marks IS NULL;
Help him in predicting the output of the above given queries.
Or
Based on the above given table named ‘Student’, Satyam has executed following queries
SELECT COUNT(*) FROM Student;
SELECT COUNT(Marks) FROM Student;
Predict the output of the above given queries.
Also, give proper justifications of the output generated through each query.
Answer:
(i)

The SUM() function returns sum of values in a column. Here, the condition is Optional = “IP” and Stream=”Commerce”, sum of marks of these records gives 193.

(ii)

The MAX() and MIN() functions return the maximum and minimum values in a column. Here, the maximum and minimum values are 99 and 95 for Optional=”CS”. Sum of the two gives 194.

(iii)

The AVG() function returns the average of values in a column. Here, the condition is optional=”IP”. Average of these values of marks gives 93.75.

(iv)

The LENGTH() function returns the length of a string value. Here the condition is Marks IS NULL, for which there is only 1 matching name that is “Saurav” whose length is 6.

Or

(i)

COUNT(*) function counts the number of records in a table. Here, the number of records is 8.

(ii)

COUNT(Marks) returns the number of NON NULL values in the marks column. Here, we have 7 values.

Question 13.
“Anutulya Creations”-A start-up fashion house has set up its main centre at Kanpur, Uttar Pradesh for its dress designing, production and dress supplying activities. It has 4 blocks of buildings.

Numbers of computers in each block:

Block A	20
Block D	80
Block P	15
Block S	8

Based on the above specifications, answer the following questions. .
(i) Out of LAN, WAN and MAN, what type of network will be formed if we interconnect different computers of the campus? Justify.
Answer:
A LAN network is formed. LAN or Local Area Network is a network of systems spread in a small area thar spans for 500m to lKm approx. Here the distances between the offices is maximum 150m.

(ii) Suggest the topology, which should be used to efficiently connect various blocks of buildings within Kanpur centre for fast communication.
Also, draw the cable layout for the same.
Answer:
Star topology should be used.

Star topology has the best features such as error detection, easy attachment of nodes etc.
Since Block D has the maximum number of computers, if the other buildings are connected to it, the communication will be faster.

(iii) Suggest the placement of the following device with justification.
(a) Repeater
(b) Hub/Switch
Answer:
(a) Repeater A to S and P to D.
Since the distances between the blocks are 110m and 150m respectively a repeater will be required to amplify the signals.

(b) Switch/Hub Its will be required in all the buildings to connect multiple computers present in them.

(iv) Nowadays, video-conferencing software is being used frequently by the company to discuss the product details with the clients. Name any one video conferencing software.
Also, mention the protocol which is used internally in video conferencing software.
Answer:
Video conferencing softwares Zoom, Google Meet
Protocol VoIP (Voice over Internet Protocol)

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 10 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 10 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
The marginal revenue function of a commodity is given by MR = 6 – 5x + x².
Find the demand function.
Or

Answer:
We have, MR = 6 – 5x + x²
Now, R = ∫(MR) dx + K
= ∫(6 – 5x + x²)dx + K
= 6x – \(\frac{5 x^{2}}{2}\) + \(\frac{x^{3}}{3}\) + k
When x = 0, then R = 0.
∴ K = 0
Thus, R = 6x – \(\frac{5}{2}\)x² + \(\frac{x^{3}}{3}\) and the
corresponding demand function is given by

where p is the price, when the number of units sold x.

OR

Here, redefined the given integrand in given interval (0, 4).
For, 0 < x < 4, |x| = x
0 < x ≤ 2 , |x – 2| = – (x – 2)
2 ≤ x < 4 , |x – 2| = (x – 2)
0 < x < 4, |x – 4| = – (x – 4)

= 8 + 2 + 2 + (16 – 8)
= 8 + 2 + 2 + 8 = 20

Question 2.
A group of 5 patients treated with medicines P weigh 10, 8, 12, 6, 4 (in kg). Second group of 7 patients treated with medicine Q weigh 14, 12, 8,10, 6, 2,11 (in kg). Comment on rejection of hypothesis with significance level 5%. [given, t_(10,0.05) = 1.812]
Answer:
Consider,
H₀: µ₁ = µ₂ and H₁: µ₁ > µ₂
[where, µ₁ and µ₂ denotes population means for given two groups]


Given, t_(10,0.05) = 1812
Since, t_cal value < t_tab value
Hence, null hypothesis (H₀) may be accepted with 5% significance.

Question 3.
A machine, the useful life of which is estimated to be 12 yr, cost ₹ 15000. Calculate the scrap value at the end of its life, depreciation being charged at 8% per annum [given, (0.92)¹² = 0.3676].
Or
What sum of money is needed to invest now, so as to get ₹ 8000 at the beginning of every month forever, if the money is worth 6% per annum compounded monthly?
Answer:
We have,
C = ₹ 15000, n = 12 yr and r = 8% = 0.08.
We know that S = C (1 – r)ⁿ
S = 15000(1 – 0.08)¹²
= 15000 (0.92 )¹²
= 15000 × 0.3676
= ₹ 5514
∴ The scrap value is ₹ 5514.

Or

Given, R = ₹ 8000 and r = \(\frac{6}{12}\) % = 0.5% per month.
So, i = \(\frac{0.5}{100}\) = 0.005
The given annuity is a perpetuity of second type.
So, P = R + \(\frac{R}{i}\) = 8000 + \(\frac{8000}{0.005}\)
= 8000 + 1600000
=1608000
Hence, ₹ 1608000 are needed to invest now to get ₹ 8000 at the beginning of every month forever

Question 4.
A firm has to transport 1200 packages using large vans, which can carry 200 packages each and small vans which can take 80 packages each. The cost for engaging each large van is ₹ 400 and each small van is ₹ 200. Not more than ₹ 3000 is to be spent on the job and the number of large vans cannot exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimise cost.
Answer:
Let the firm has x number of large vans and y number of small vans. From the given information, we have following corresponding constraint table.

Thus, we see that objective function for minimum cost is Z = 400 x + 200y.
Subject to constraints are,
200x + 80y ≥ 1200 [package constraint]
⇒ 5x + 2y ≥ 30 …(i)
and 400x + 200y ≤ 3000 [cost constraint]
⇒ 2x + y ≤ 15 …(ii)
and x ≤ y [van constraint] …(iii)
and x ≥ 0, y ≥ 0
[non-negative constraints] …(iv)
Thus, required LPP to minimise cost is minimise Z = 400x + 200y
Subject to constraints are,
5x + 2y ≥ 30, 2x + y ≤ 15, x ≤ y, x ≥ 0 and y ≥ 0

Question 5.
Construct 3-yearly moving averages from the following data.

Answer:
Calculate of 3-yearly moving averages

Question 6.
Find the effective rate that is equivalent to a nomial rate of 8% compounded semi-annually.
Answer:
We have,

⇒ r_e = (1 + 0.04)² – 1
⇒ r_e = (1.04)² – 1
= 1.0816 – 1
= 0.0816
Hence, the effective rate is 8.16%.

Section – B [12 marks]

Question 7.
The time series given below shows the number of TV sold by a company since 2003.

Find the linear equation that describes the trend in the number of TV sold.
Also, estimate the sale of TV in 2014.
Answer:
Here, n = 10 (even)
So, origin is mean of two middle years
i.e., \(\frac{2007+2008}{2}\) = 2007.5

Table for fitting linear equation

The linear equation would be of the form
y_t = a + bx
The two normal equations shall be
Σy = m + bΣx
Σxy = aΣx + bΣx²
Since, Σx = 0, a = \(\frac{\Sigma y}{n}=\frac{956}{10}\) = 95.6
and b = \(\frac{\Sigma x y}{\Sigma x^{2}}=\frac{1978}{330}\) = 5.994
Thus, the linear equation is y_t = 95.6 + 5.994 x
For 2014, x would be + 13
y₂₀₁₄ = 95.6+ 5.994(13)
= 95.6 + 77.92 = 173.52 thousand
Hence, the expected number of TV that would be sold in 2014 shall be ₹ 173520.

Question 8.
Consider the following hypothesis
H₀ : µ = 275
H₀ : µ ≠ 275
A sample of 60 provided a sample mean of 287.6. The population standard deviation is 15 and level of significance α = 0.05. Check the hypothesis test, given above using interval estimation.
Answer:
Given, µ₀ = 275, n = 60, x̄ = 287.6, σ = 15
and α = 005. So, Z_α/2 = Z_0.025 = 1.96
Confidence interval = x̄ ± Z_α/2. \(\frac{\sigma}{\sqrt{n}}\)
= 287.6 ± 1.96 × \(\frac{15}{\sqrt{60}}\)
= 287.6 ± 3.8
So, confidence interval is
(287.6 – 38,287.6 + 38) i.e. (2838,291.4).
Since, the hypothesized value of population mean µ₀ = 275 lies in the confidence interval (2838, 291.4), so H₀ cannot be rejected.

Question 9.
The present value of a perpetual income of ₹ R at the end of every month, the first being received at the end of 3 yr is ₹ 75000. Find the value of R, if money is worth 15% per annum compounded monthly [given, (1.0125)^-35 = 0.6474]
OR
A bond of face value of ₹ 1200 has a coupon rate 10% per annum paid semi-annually and matures in 6 yr. If the present value of the bond is ₹ 1560, find the yield to maturity.
Answer:
Clearly, it is the case of deferred perpetuity.
Present value (P) = ₹ 75000
Periodic payment = ₹ R
Rate of interest (r) = 15% = 0.15
Interest is compounded monthly, so we have
i = \(\frac{r}{12}=\frac{0.15}{12}\) = 0.0125
Since, the first payment is receivable at the end of 3 yr, the period of deferment (n) = 35.

∴ Approximate yield to maturity (YTM) = 0.0217
or 2% per half year or 4% per annum.

Question 10.
The demand functions for a commodity is given by p = 20 – 2x – x². Find the consumed surplus, when market demand is 3.
Answer:
It is given that x₀ = 3
On substituting x = 3 and p = p₀ in demand function
p = 20 – 2x – x², we get
p₀ = 20 – 6 – 9 = 5

⇒ CS = (60 – 9 – 9) -15
⇒ CS = 27
Hence, consumer’s surplus is 27.

Section – C [16 Marks]

Question 11.
Mr. Taneja purchase a house of ₹ 4500000 with a down payment of ₹ 500000 and balance in EMI for 25 yr. If bank charges 6% per annum compounded monthly. Calculate the EMI. [given, (1.005)³⁰⁰ = 4.4650].
OR
Find the purchase price of a ₹ 20000 bond, redeemable at the end of 10 yr at 110 and paying annual dividends at 4%, if the yield rate is to be 5% effective.
[given, (1.05)^-10 = 0.6139]
Answer:
Cost of house = ₹ 4500000
Down payment = ₹ 500000
∴ Balance = ₹(4500000 – 500000) = ₹ 4000000
So, p = ₹ 4000000, i = \(\frac{6}{1200}\) = 0.005 and n = 25 × 12 = 300 months

Hence, EMI of Mr. Taneja is ₹ 25772.
Total interest paid = x(EMI) – P
= 300(25772) – 4000000
= 7731600 – 4000000
= 3731600
Hence, total interest paid is ₹ 3731600

Or

We have, n = Number of period = 10
and i yield rate = \(\frac{5}{100}\) = 0.05
R = Annual dividend
= 4% of face value
= ₹ \(\left(\frac{4}{100} \times 20000\right)\) = ₹ 800
The bond is redeemed at 110.
Therefore, the redemption price of the bond is 110% of its face value.
Thus, C = Redemption price
= ₹\(\left(20000 \times \frac{110}{100}\right)\) = ₹ 22000
Let V be the purchase price of the bond. Then,

= [16000(1- (1.05)^-10] + 22000(1.05)^-10]
= [16000(1 – 0.6139) + 22000 (0.6139)]
= [16000(0.3861) +1350500]
= (617700 +1350500)
= ₹ 19683.40
∴ The purchase price of bond is 119683.40

Question 12.
A population grows at the rate of 10% per year. How long does it take for the population to double? Use differential equation for it.
Answer:
Let P₀ be the initial population and P be the population after t yr.

Question 13.
Diwakar invested ₹ 20000 in a mutual fund in year 2010. The value of mutual fund increased to ₹ 32000 in year 2015. Calculate the compound annual growth rate (CAGR) of his investment, [given, (1.6)^1/5 = 1.098]
Answer:
Given, the begining value of the investment = ₹20000
Fund value of the investment = ₹ 32000
Number of years = 5 yr

= 0.098 = (0.098 × 100)% = 9.8%
Hence, CAGR is 9.8%.

Case Based/Data Based

Question 14.
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 h of machine time and 3 h of craftman’s time in its making, while a cricket bat takes 3 h of machine’s time and 1 h of craftman’s time. In a day, the factory has the availability of not more than 42 h of machine’s time and 24 h of craftman’s time.

(i) What number of rackets and bats must be made, if the factory is to work at full capacity?
(ii) If the profits on rackets and on bats is ₹ 20 and ₹ 10, respectively. Find the maximum profit of the factory, when it works at full capacity.
Answer:
Let the number of rackets and the number of cricket bats to be made in a day be x and y, respectively. Construct the following table.

Construct the following table.

The machine time is not available for more than 42 h.
∴ 1.5x + 3y ≤ 42
The craftman’s time is not available for more than 24 h.
∴ 3x + y ≤ 24
The profit on rackets is ₹ 20 and on bats is ₹ 10.
∴ Maximum Z = 20x + 10y …(i)
Subject to constraints are,
15x + 3y ≤ 42 ……(ii)
3x + y ≤ 24
and x, y ≥ 0 ……. (iv)
Firstly draw the graph of the line
1.5x + 3y = 42

X	0	28
y	14	0

On putting (0, 0) in the inequality 1.5x + 3y ≤ 42, we have
1.5 × 0 + 3 × 0 ≤ 42
⇒ 0 ≤ 42 (which is true)
So, the half plane is towards the origin.
Since, x, y ≥ 0
So, the feasible region lies in the first quadrant. Secondly, draw the graph of the line
3x + y = 24

X	0	8
y	24	0

On putting (0, 0) in the inequality 3x + y ≤ 24, we have
3 × 0 + 0 ≤ 24 ⇒ 0 ≤ 24 (which is true)
So, the half plane is towards the origin.
On solving equations 1.5x + 3y = 42 and 3x + y = 24, we get B (4,12).
∴ Feasible region is OABCO.
The comer points of the feasible region are
0 (0, 0), A (8, 0), B(4,12) and C (0,14).
The values of Z at these points are as follows.

Corner point	Value of Z = 20x + 10y
0(0, 0)	0
A(8, 0)	160
6(4, 12)	200 (Maximum)
C(0, 14)	140

Thus, the maximum profit of the factory, when it works to its full capacity is ₹ 200.
Hence, 4 tennis rackets and 12 cricket bats must be made, if the factory is to work at full capacity.

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 11 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 11 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
Evaluate ∫\(\frac{d x}{x\left(x^{3}+8\right)}\)
Or
The supply function of a producer is given by p = \(\frac{2}{5}\)e^2x, where x denotes thousand units.
Find producer’s surplus when sales are 2000 units.
Answer:
Let I = ∫\(\frac{d x}{x\left(x^{3}+8\right)}\) = ∫\(\frac{x^{2}}{x^{3}\left(x^{3}+8\right)}\)dx
Now, put x³ + 8 = t

[adding and substracting by (4)² in denominator]

Or

Given, the supply function, p = \(\frac{2}{5}\)e^2x
When sales are 2000 units i.e. x₀ = 2, then we get
p₀ = \(\frac{2}{5}\)e⁴ [when x = 2 then p = latex]\frac{2}{5}[/latex]e⁴]

Question 2.
Find a linear trend to the following data by the least squares method,

Or
Find seasonal variations by ratio-to-trend method from the data given below.

Answer:
Here, n = 5 is odd.
Hence, middle year i.e. 1989 taken as origin.

We construct the table as

Let trend line of y (production) on x be
y_t = a + bx (origin 1989) ………(i)

The normal equation for estimating a and b in Eq. (i) are Σy = na + b Σx
⇒ 103 = 5a + b × 0
⇒ 5a = 103 ⇒ a = \(\frac{103}{5}\) = 20.6
and Σxy = aΣx + bΣx²
26 = a x O + b x 40
b = \(\frac{26}{40}\) = 0.65

The linear trend
y_t = a + bx
y_t = 20.6 + 0.65x

Or

For determining seasonal variation by ratio-to-trend method, first we will determine the trend of yearly data and then convert it to quarterly data.
Table for calculating trend values

The equation of the straight line trend is y_t = a + bx.
Since, Σx = 0, a = \(\frac{\Sigma y}{n}=\frac{280}{5}\) = 56
and b = \(\frac{\Sigma x y}{\Sigma x^{2}}=\frac{120}{10}\) = 12
Quarterly increment = \(\frac{12}{4}\) = 3.

Question 3.
What sum of money invested, now would establish a scholarship of ₹ 20000 to be awarded at the starting of each year to a deserving student, if money is worth 8% compounded annually?
Answer:
Since, the payments are made at the starting of each year forever, it is a perpetuity due. Periodic payment (R) = ₹ 20000 Interest is compounded annually, so i = 8% = 0.08
Present value (P) of a perpetuity due is given as, P= R(1 + \(\frac{1}{i}\)) ⇒ P = 20000(1 + \(\frac{1}{0.08}\))
⇒ P = 20000 × 13.5 = 270000

∴ Amount to be invested is ₹ 270000.

Question 4.
A desktop computer costing ₹ 60000 has a useful life of 18 yr. If annual depreciation is ₹ 3000, find its scrap value, using linear method.
Answer:
Given, original cost of desktop computer = ₹ 60000
Useful life = 18 yr
Annual depreciation = ₹ 3000
Let the scrap, value of the desktop computer be ₹ S. Then, using annual depreciation
= \(\frac{\text { Original cost }-\text { Scrap value }}{\text { Useful life in years }}\)
3000 = \(\frac{60000-S}{18}\)
⇒ 54000 = 60000 – S ⇒ S = 6000
Hence, the scrap value of desktop computer is ₹ 6000.

Question 5.
Consider the following hypothesis test.
H₀ : µ ≤ 30
H₁ : µ > 30
A sample of 45 provided a sample mean of 32.4. The population standard deviation is 6.
(i) Compute the value of the test statistic.
(ii) What is the p-value?
Answer:
Given, µ₀ = 30, n = 45, x̄ = 32.4, σ = 6 and α = 0.01
(i) Test statistics,

(ii) ∵ Z = 2.68 > 0
So, p-value of 2.68 = Area under the standard normal curve to the right of Z
= 1 – 0.9963 (using table) = 0.0037
∴ p-value = 0.0037

Question 6.
Find the maximum value of Z = 4x + 2y, subject to constraints are
2x + 3y ≤ 18, x + y ≥ 10 and x, y ≥ 0.
Answer:
The given LPP’s maximize Z = 4x + 2y
Subject to constraints are
2x + 3y ≤ 18, x + y ≥ 10 and x, y ≥ 0
The graph of the above LPP is

From the above graph, we see that for the feasible solutions there is no common area in the first quadrant. Hence, the objective function Z cannot be maximized.

Section – B [12 Marks]

Question 7.
You are given the following data about the life of two brands of bulbs.

Do you think, there is a significant difference in the quality of the two brands of bulbs? (the table value of t for 25 degree of freedom at 5% level of significance is 1.708).
Answer:
Given, x̄₁ = 2100, s₁ = 250 and n₁ = 12,
x̄₂ = 2180, s₂ = 300 and n₂ = 15
Consider, null hypothesis : There is no significant difference in the quality of the two brands of bulbs.

Since, the computed value of t = 0739 is less than the table value of t = 1.708 [at 5% for 25 degree of freedom], we accept the null hypothesis.

Question 8.
The quarterly profits of a small scale industry (? in thousands) is as follows.

Calculate 4-quarterly moving averages, display these and the original figures graphically on the same graph sheet.
Answer:


We draw the following graph from the above data.

A kink is shown near origin on the Y-axis to indicate that the scale on Y-axis starts with 20. The dark curve represents quarterly profits of a small scale industry and dotted curve represents 4-quarterly centered moving averages.

Question 9.
If the interest is compounded continuously at 6% per annum, how much worth ₹ 1000 will be 10 yr? (given, e^0.6 = 1.822)
Answer:
Let P be the principal amount at any time t and the rate of interest be r% per annum compounded continuously.

⇒ P = 1000 × 1.822
= 1822
Hence, in 10 yr, the worth of ₹ 1000 will become ₹ 1822.

Question 10.
The value of a car depreciates by 12.5% every year. By what percent will the value of the car decrease after 3 yr?
Or
A firm anticipates a capital expenditure of ₹ 80000 for a new equipment in 5 yr. How much should be deposited quarterly in sinking fund carrying 12% per annum compounded quarterly to provide for the purchase? [given (1.03)²⁰ = 1.8061]
Answer:
Let the present value of the car be ₹ P, then value of the car after 3 yr
= P(1 – i)ⁱ
= P(1 – \(\frac{12.5}{100}\))³
= P(1 – \(\frac{1}{8}\))³ = P\(\left(\frac{7}{8}\right)^{3}\)

Decrease in the value of the car after 3 yr
= P – P\(\left(\frac{7}{8}\right)^{3}\)
= P(1 – \(\frac{343}{512}\)) = \(\frac{169P}{512}\)

∴ Percentage decrease in the value of the car after 3 yr

Thus, ₹ 2977.29 deposited quarterly in a sinking fund.

Section – C [16 Marks]

Question 11.
The marginal cost function for a product is given by MC = \(\frac{5}{\sqrt{2 x+9}}\) and fixed cost ₹ 20 find the average cost for 10 units of output.
Answer:

It is given that x = 0 and C = 20
From Eq. (i) we get
20 = 5\(\sqrt{2 \times 0+9}\) + K
⇒ 20 = 15 + K
⇒ K = 5

Substituting K = 5 in Eq (i) we get
C = 5\(\sqrt{2 x+9}\) + 5
Now, AC = \(\frac{C}{x}\)

Hence, average cost for 10 units of outputs is ₹ 3.195

Question 12.
An aeroplane can carry a maximum of 200 passengers. A profit of ₹ 1000 is made on each executive class ticket and a profit of ₹ 600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?
Or
A toy company manufactures two types of dolls A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is almost half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of type B by atmost 600 units. If the company makes profit of ₹ 12 and ₹ 16 per doll respectively, on dolls A and B, how many of each should be produced weekly in order to maximise the profit?
Answer:
Let x passengers travel by executive class and y passengers travel by economy class.

We construct the following table:

Class	Number of tickets	Profit (in ₹)
Executive	x	1000x
Economy	y	600y
Total	x+y	1000x+ 600y

So, our problem is to maximise
Z = 1000x + 600y …(i)
Subject to constraints,
x + y ≤ 200 …(ii)
x ≥ 20 …(iii)
y – 4x ≥ 0 ⇒ y ≥ 4x …(iv)
and x, y ≥ 0 ……….(v)

Firstly, draw the graph of the line x + y = 200

x	0	200
y	200	0

Putting (0, 0) in the inequality x + y ≤ 200, we have
0 + 0 ≤ 200 ⇒ 0 ≤ 200 (which is true)

So, the half plane is towards the origin. Secondly, draw the graph of the line y = 4x

x	0	20
y	0	80

Putting (10,0) in the inequality y ≥ 4x, we have
0 ≥ 4 x 10 ⇒ 0 ≥ 40 (which is false)

So, the half plane is towards Y-axis.
Thirdly, draw the graph of the line x = 20

Putting (0, 0) in the inequality x ≥ 20, we have 0 ≥ 20 (which is false)
So, the half plane is away from the origin. Since, x,y ≥ 0
So, the feasible region lies in the first quadrant.

On solving the equations, we get
A (20, 80), B(40, 160) and C (20, 180).
∴ Feasible region is ABCA

The corner points of the feasible region are A(20, 80), B(40,160) and C(20,180). The value of Z at these points are as follows:

Corner point	Value of Z = 1000x + 600y
.4(20, 80)	68000
8(40, 160)	136000 (Maximum)
C(20, 180)	128000

Thus, the maximum value of Z is 136000 at B(40, 160).

Thus, 40 tickets of executive class and 160 tickets of economy class should be sold to maximise the profit and the maximum profit is ₹ 136000.
Or
Let the company manufactures x dolls of type A and y dolls of type B, then
x,y ≥ 0 …(i)
x + y ≤ 1200 …(ii)
y ≤ x/2 ⇒ x – 2y ≥ 0 …(iii)
and x ≤ 3y + 600 ⇒ x -3y ≤ 600 …(iv)

Firstly, draw the graph of the line x + y = 1200

x	1200	0
y	0	1200

Putting (0, 0) in the inequality x + y ≤ 1200, we have
0 + 0 ≤ 1200 ⇒ 0 ≤ 1200 (which is true)

So, the half plane is towards the origin. Secondly, draw the graph of the line x – 2y = 0
Putting (200, 0) in the inequality x – 2y ≥ 0, we have
200 – 2 × 0 ≥ 0 ⇒ 200 ≥ 0 (which is true)

So, the half plane is towards the X-axis.

Thirdly draw the graph of the line x – 3y = 600

x	600	0
y	0	-200

Putting (0, 0) in the inequality x – 3y≤ 600, we have
0 – 3 x 0 ≤ 600 ⇒ 0 ≤ 600 (which is true)

So, the half plane is towards the origin.
Since, x,y ≥ 0, so the feasible region lies in the first quadrant.

The point of intersection of lines x – 3y = 600 and x + y = 1200 is B(1050,150), of lines x = 2 y and x + y = 1200 is C (800,400).
Let Z be the total profit, then Z = 12 x +16y

Feasible region is OABCO.
The comer points of the feasible region are A (600,0), B(1050,150) and C(800,400).

The values of Z at these points are as follows.

Corner point	Value of Z = 12x + 16y
4(600, 0)	7200
fi{1050, 150)	15000
C(800, 400)	16000 (Maximum)

The maximum value of Z is 16000 at C(800,400).

Thus, 800 and 400 dolls of types A and type B should be produced respectively to get the maximum profit of ₹ 16000.

Question 13.
Face value of bond is 1 1000, coupon rate 4.25% per annum paid semi-annually and matures in 10 yr. If present value of bond is ₹ 918.23. What is the yield to maturity.
Answer:
Given, F = ₹ 1000, r = 4.25%
and i = \(\frac{4.25}{2}\)% = \(\frac{4.25}{200}\) (semi-annually)
So, C = ₹ 1000 × \(\frac{4.25}{200}\) = ₹ 21.25 200
N = 10 × 2 = 20 yr and PV = ₹ 918.23

Approximate Yield to Maturity (YTM)

Approximate YTM = 2.64% (semi-annually)
= 5.28% per annum

Hence, yield to maturity is 5.28 per annum.

Case Based/Data Based

Question 14.
A loan is the leading of money by one or more individual, organisations or other entities to other individuals, organisations etc. The recepient incurs a debt and is usually liable to pay interest on that debt untill it is repaid as well as to repay the principle amount borrowed.

A loan of ₹ 400000 at the interest rate of 6.75% per annum compounded monthly is to be amortized by equal payment at the end of each month for 10 yr, find
(i) the size of each monthly payment
(ii) the principal outstanding at the beginning of 61st month. [given (1.005625)¹²⁰ = 1.9603 and (1.005625)⁶⁰ =1.4001]
Answer:
Given, P = ₹ 400000, n = 12 × 10 = 120 675
and i = \(\frac{6.75}{1200}\) = 0.005625

(i) ∴ Size of monthly payment (EMI)

Hence, monthly payment is ₹ 4593

(ii) We know that principal outstanding at beginning of kth period
= \(\frac{\operatorname{EMI}\left[(1+i)^{n-k+1}-1\right]}{i(1+i)^{n-k+1}}\)
So, principal outstanding at beginning of 61st month

Hence, principal outstanding at beginning of 61st month is ₹ 233336.89

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 8 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 8 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
The feasible region (shaded) for a LPP is shown in the following figure

Find the maximum value of Z = 3x + 4y.
Answer:
As clear from the graph comer points are O, A, E, D with coordinates (0, 0), (52, 0), (44, 16) and (0, 38).

Corner points	Z = 3x + 4y
0(0,0)	0
4(52, 0)	156
£(44,16)	196 (Maximum)
D(0, 38)	152

Hence, the maximum value of Z is 196 at E(44, 16)

Question 2.
Find the force of interest corresponding to the effective rate 11%.
[given, log(1.11) = 0.0453 and log e = 0.4342]
Answer:
Given, r_e = 11% = 0.11
We know that, r_e = e^r – 1
∴ 0.11 = e^r – 1
⇒ e^r = 1.11
Taking log on both sides,
r log e = log(1.11)
⇒ r(0.4342) = 0.0453
⇒ r = \(\frac{0.0453}{0.4342}\)
= 0.1043 = 10.43%
∴ The force of interest is 10.43%.

Question 3.
An asset costing ₹ 95000 is expected to have a useful life of 8 yr, has final annual depreciation of ₹ 8000. Find the final scrap value of asset.
Answer:
Given, D = ₹ 8000, C = ₹ 95000 and n = 8 yr
We know that, D = \(\frac{C-S}{n}\)
∴ 8000 = \(\frac{95000-S}{8}\)
⇒ 95000 – S = 8000 × 8
⇒ 95000 – S = 64000
⇒ S = 95000 – 64000
⇒ S = ₹ 31000
∴ Final scrap value of the asset is ₹ 31000.

Question 4.
A manufacturer’s marginal cost is \(\frac{600}{\sqrt{5 x+36}}\). Find the cost involved to increase production from 150 units to 450 units.
Or
The marginal revenue function of a commodity is given MR = 12 – 3x² + 4x.
Find the total revenue from the sale of 4 units.
Answer:
Given, marginal cost (MC) = \(\frac{600}{\sqrt{5 x+36}}\)
⇒ \(\frac{d C}{d x}=\frac{600}{\sqrt{5 x+36}}\)
⇒ \(\frac{600}{\sqrt{5 x+36}}\)
Cost involved to increases production from 150 units to 450 units is,

= 240 [√2286 – √786]
= 240 (47.81 – 28D3)
= 240 × 1978
= ₹ 4747.2
Or
We have, MR = 12 – 3x² + 4x
∵ ∫dr = ∫MR dx [∵ MR = \(\frac{d R}{d x}\)
We know that when x = 0, then R = 0
∵ K = 0
R = 12x – x³ + 2x² [from Eq. (i)]
Now, the total revenue from the sale of 4 units is given by put x = 4
R = 48 – 64 + 32 = 16

Question 5.
Consider the following hypothesis
H_o: μ = 315 and H_a: μ ≠ 315
A sample of 60 provided a sample mean of 324.6. The population standard is 14 and level of significance α = 0.05. Check the hypothesis test given above, using interval estimation.
Answer:
Given, μ_o = 315, n = 60, x̄ = 324b
σ = 14 and α = 0.05
∴ Confidence interval = x̄ ± Z_α/2\(\frac{\sigma}{\sqrt{n}}\)
= 324.6 ± 1.96 × \(\frac{14}{\sqrt{60}}\) [∵ Z_α/2 = Z_0.025 = 1.96]
∴ Confidence interval
= 324.6 ± 1.96 × 131
= 324.6 ± 3.54
= (324.6 – 3.54,324b + 3.54)
= (32136, 328.14)
Since, the hypothesis value of population mean p0 = 315 does not lies in confidence interval, so H₀ rejected.

Question 6.
For the following series of observations

Calculate 5- yearly moving averages.
Or
The data below shows the figures of income of a municipal corporation over the years.

Calculate 4-yearly centred moving averages.
Answer:

∴ 5-yearly moving averages are 2.4, 2.8, 3.6 and 3.8
OR

∴ 4-yearly centred moving averages are 5.375, 5.125 and 4.875.

Section – B [12 Marks]

Question 7.
The average nicotine content of a particular brand of cigarette is supposed to be 2.2 mg per cigarette. A smoker of this brand wants to see, if it is really 2.2 mg or more. With this purpose the nicotine contents of 50 cigarettes are measured. The sample mean based on 50 cigarettes is 2.95 mg per cigarette. The population standard deviation is 0.8 mg. Do the data provide enough evidence that the average nicotine content exceeds 2.2 mg? Test at 5% level using p-value approach and critical value approach, [given, Z_0.05 = 1.645]
Answer:
Consider H₀ : μ = 2.2
H_a :μ > 2.2
x̄ = 2.95, μ₀ = 2.2,
n = 50 and σ = 0.8
∴ Test statistics,

Since, |t| > Z_0.05
So, reject H₀ at 5% level.
Means provide sufficient evidence to conclude that average nicotine content exceeds 1.5 mg per cigarette.

Question 8.
Fit a straight line trend for the following data and find the trend values. Estimate the sales for 2018.

Answer:
Table for fitting straight line trend

The equation of the straight line trend is
y_t = a + bx
∴ a = \(\frac{\Sigma y}{n}=\frac{435}{7}\) = 62.143
∴ b = \(\frac{\Sigma x y}{x^{2}}=\frac{273}{28}\) = 9.75
y = 62.143 + 9.75x
Hence, y₂₀₀₆ = 62.143 + 9.75(-3)
= 62.143 – 29.25 = 32893
y₂₀₀₇ = 62.143 + 9.75 (- 2)
= 62.143 – 19.5 = 42.643, etc.
For 2018, x shall be + 9,
y₂₀₁₈ = 62.143 + 9.75(9)
= 62.143 + 87.75 = 149.893
The estimated sales for the year 2018 is ₹ 149.893 lakh.

Question 9.
Rohit has taken a loan of ₹ 600000 with interest rate 10% for the period of 12 yr. Find (reducing) EMI for the above data. [given (1.0083)¹² = 1.1043]
Or
What nominal rate compounded quarterly will be equivalent to 12% compounded continuously? [given e^0.12 = 1.1274]
Answer:
Given, P = ₹ 600000, n = 12 yr
Interest rate = 10% (per annum)
Monthly interest rate (r) = \(\)
= \(\frac{0.10}{12}\) = 0.0083

OR

⇒ \(\left(1+\frac{r}{4}\right)\) = antilog (0.0134)
= 1.031
⇒ \(\frac{r}{4}\) = 0.031
⇒ r = 0.124
⇒ r = 12.4%

Question 10.
A manufacturer’s marginal revenue function is given by MR = 275 – x – 0.3x². Find the increase in the manufacturer’s total increase in revenue, if the production is increased from 10 to 20 units.
Answer:
We have
⇒ MR = 275 – x – 0.3x²
⇒ \(\frac{d R}{d x}\) = MR
⇒ \(\frac{d R}{d x}\) = 275 – x – 0.3x²
We have to find the total increase in revenue, if the production is increased from 10 to 20 units i.e. we have to
R(20) – R(10)

Hence, increase in revenue is ₹ 1900

Section – C [16 Marks]

Question 11.
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 h and that of second machine is 9 h per day.
Each unit of product A requires 3 h on both machines and each unit of product B requires 2 h on first machine and 1 h on second machine. Each unit of product A is sold at a profit of ₹ 7 and B at a profit of ₹ 4. Find the production level per day for maximum profit graphically.
Answer:
Let the manufacturer produces the products A and B be x and y units, respectively.
We construct the following table

Here, total profit Z = 7x + 4y
i.e. maximise Z = 7x + 4y …(i)
Subject to the constraints are
3x + 2y ≤ 12
3x + y ≤ 9 and x ≥ 0, y ≥ 0
Now, consider the given inequations as equations
3x + 2y = 12 …(ii)
3x + y = 9 …….. (iii)
Table for line 3x + 2y = 12 or y = \(\frac{12-3 x}{2}\) is

X	0	4
y	6	0

It passes through the points (0, 6) and (4, 0).
On putting (0, 0) in the inequality 3x + 2 y ≤ 12,
we get
0 + 0 ≤ 12 ⇒ 0 < 12 [true]
So, the half plane is towards the origin.
Table for line 3x + y = 9 or y = 9 – 3x is

X	0	3
y	9	0

It passes through the points (0, 9) and (3, 0).
On putting (0, 0) in the inequality 3x + y ≤ 9, we get
0 + 0 ≤ 9 ⇒ 0 ≤ 9 [true]
So, the half plane is towards the origin.
Also, x ≥ 0 and y ≥ 0, so the region lies in 1st quadrant.
Now, the intersection point of lines (i) and (ii) is
(3x + 2y) – (3x + y) = 12 – 9
⇒ y = 3
and 3x = 12 – 2 × 3
⇒ 3x = 12 – 6
⇒ x = 2
Thus, the point of intersection is B (2, 3).
The graph of inequations is shown below

Here, we see that OABC is a required feasible region, whose comer points are O(0,0), A(3, 0), B(2, 3) and C(0, 6).
The values of Z at these comer points are as follows

Corner points	Value of Z = 7x + 4y
0(0,0)	Z = 0+ 0= 0
4(3,0)	Z = 7×3+0 = 21
8(2,3)	Z =7×2+4×3 = 26 (maximum)
C(0,6)	Z =7×0+ 4×6 = 24

Hence, for maximum profit, manufacturer produce 2 units of product A and 3 units of product B.

Question 12.
A machine costs a company ₹ 52000 and its effective life is estimated to be 25 yr. A sinking fund is created for replacing the machine by a new model at the end of its life time, when its scrap realizes a sum of ₹ 2500 only. The price of the new model is estimated to be 25% more than the price of present one. Find what amount should be set aside at the end of each year out of the profit for the sinking fund, if it accumulates at 3.5% compound annually? [given (1.035)²⁵ = 23632]
Answer:
Let ₹ R be the amount set aside each year. Since, the cost of new machine is 25% more than the cost of present.
Cost of machine = ₹ 52000
Cost of new machine after increasing the 25% of the cost of machine,
i.e. 52000 + 25% of 52000
= 52000 \(\left(1+\frac{25}{100}\right)\)
= 52000 × \(\frac{5}{4}\) = ₹ 65000
Scrap value of the present machine = ₹ 2500
So, net amount required at the end of 25 yr to purchase the new model = ₹ (65000 – 2500)
= ₹ 62500
We know that, R = \(\frac{i \times S}{(1+i)^{n}-1}\)
Here, S = ₹ 62500, n = 25 yr and i = \(\frac{3.5}{100}\) = 0.035

Thus, ₹ 1604.68 are set aside each year out of the profit to purchase the new model of the machine.

Question 13.
A bond of face value of ₹ 1000 matures in 5 yr. Interest is paid semi-annually and bond is priced to yield 8% per annum. If the present value of bond is ₹ 1100, find the annual coupon rate, [given (1.04)^-10 = 0.6761]
Or
A person buys a house for which be agrees to pay ₹ 25000 at the end of each month for 8 yr. If money is worth 12% converted monthly, what is the cash price of house? [given (1.01)^-96 = 0.3847]
Answer:
Let the annual coupon rate is 6%.
Given, F = ₹ 1000, then C = ₹ 1000 × \(\frac{r}{200}\) = ₹ 5 r
d = 8% per annum or 4% per half-year
i = \(\frac{4}{100}\) = 0.04
N = 5 × 2 = 10 yr and PV = ₹ 1100
∴ PV = \(\frac{C\left[1-(1+i)^{-N}\right]}{i}\) + F(1 + i)^-N

Hence, coupon rate is 10.47%.
Or
Given, EMI = ₹ 25000, n = 12 × 8 = 96 and
i = \(\frac{12}{1200}\) = 0.01
Let P be the cash price of house.

Hence, the cash price of house is ₹ 1538250.

Case Based/Data Based

Question 14.
Suppose the height and radius of cylindrical pot be 10 cm and ‘r’ cm. The volume of a cylindrical pot changes at a constant rate. At initial time, the radius of the pot is 3 cm. On the basis of above information, answer the following questions.
(i) Write the solution of differential equation formed by the given statement.
Answer:
According to the given statement,
\(\frac{d}{d t}\) (volume of cylinder) = k,
where k is some positive constant.
\(\frac{d}{d t}\) (πr²h) = k
⇒ \(\frac{d}{d t}\) [πr²(10)] = k [∵ h = 10 cm given]
⇒ 10π dr² = kdt
On integrating both sides, we get
10π ∫d(r²) = k∫dt
⇒ 10π(r²) = k(0) + C …(i)
Initially at t = 0, r = 3, then
10π(3)² = k(0) + C
⇒ C = 90π
Put C = 907t in Eq. (i), we get
10πr² = kt + 90π

(ii) After 5 s, the radius of pot becomes 6 cm. Then, find the value of constant.
Answer:
When t = 5 s, r = 6 cm, then
10π(6)² = k( 5) + 90π [∵ 10πr² = kt + 90π]
⇒ 5k= 360π – 90π
⇒ 5 k = 270π
⇒ k = 54π

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 9 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 9 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
Evaluate ∫\(\frac{1}{x^{2}\left(x^{4}+1\right)^{3 / 4}}\) dx
Or
The supply function for a commodity is p = 7 + x. Determine producer’s surplus, if 15 units of goods are sold.
Answer:

Or
Given, p = 7 + x and x₀ = 15
When x₀ = 15, then p₀ = 7 + 15 = 22

Question 2.
Find the f-test value for the following two samples from a populations

Or
Out of 250 clusters 10 clusters are selected randomly as given below:

Estimate the population mean.
Answer:
We have, x̄ = \(\frac{5+7+4+9}{4}=\frac{25}{4}\) = 6.25
and ȳ = \(\frac{4+3+2+8}{4}=\frac{17}{4}\) = 4.25
Σ(x – x̄)² = (5 – 6.25)² + (7 – 6.25)² + (4 – 6.25)² + (9 – 6.25)²
= 1.5625 + 0.5625 + 5.0625 + 7.5625 = 14.75
and Σ(y – ȳ)² = (4 – 4.25)² + (3 – 4.25)² + (2 – 4.25)² + (8 – 4.25)²
= 0.0625 + 1.5625 + 5.0625 + 14.0625
= 20.75

We know that

Or

From the above table,
Σx_i = 96 + 121 + 42 + 49 + 53 + 50 + 39 + 47 + 41 + 75 = 613
and Σx_i = 8 + 12 + 4 + 10 + 9 + 3 + 7 + 3 + 8 + 7 = 71
∴ Population (x) = \(\frac{\Sigma x_{i}}{\Sigma n_{i}}=\frac{613}{71}\) = 8.63

Question 3.
Find the present value of perpetuity of ₹ 800 at the end of each quarter, if money is worth 10% compounded quarterly.
Answer:
Given, R = 800 and r = 10% = 0.10
∴ i = \(\frac{0.10}{4}\) = 0.025
∴ Present value of perpetuity,
P = \(\frac{R}{i}=\frac{800}{0.025}\) = ₹ 32000

Question 4.
The demand of a product over 6 weeks is 90, 110, 105, 130, 85 and 102. If 3 months moving average is x and 5 month morving average is y, find x + y.
Answer:
We know that
3 months moving average
= \(=\frac{\text { Sum of latest } 3 \text { trend }}{3}\)
and similarly for 5 months moving average
Now, x = \(\frac{130+85+102}{3}=\frac{317}{3}\) = 10567
and y = \(\frac{110+105+130+85+102}{5}=\frac{532}{5}\) = 1069
∴ x + y = 105.67 + 106.4 = 212.07

Question 5.
Find the effective rate, which is equivalent to a stated rate of 5% compounded semi-annually.
Answer:
Given, r = 5% and p = 2 (half-year)
So, effective rate (per rupee)
= (1 + \(\frac{r}{100 p}\))^p – 1
= (1 + \(\frac{5}{200}\))² – 1
= (1 + 0.025)² – 1
= (1.025)² – 1
= 1.0506 – 1
= 0.0506
∴ The effective rate = (0.0506) × 100% = 5.06%

Question 6.
Maximise Z = x + y, subject to constraints are
x + 4y ≤8, 2x + 3y ≤ 12, 3x + y ≤ 9 and x, y ≥ 0.
Answer:
Here, the given LPP is,

Maximise Z = x + y
Subject to constraints are,
x + 4y ≤8, 2x + 3y ≤ 12, 3x + y ≤ 9 and x, y ≥ 0
On solving x + 4y = 8 and 3x + y = 9, we get
x = \(\frac{28}{11}\) and y = \(\frac{15}{11}\)
From the feasible region, it is clear that coordinates of comer points are (0, 0), (3, 0), \(\left(\frac{28}{11}, \frac{15}{11}\right)\) and (0,2).

Corner points	Value of Z = x + y
(0,0)	0
(3,0)	3
\( \left(\frac{28}{11}, \frac{15}{11}\right) \)	\( \frac{43}{11}=3 \frac{10}{11} \)(maximum)
(0, 2)	2

Hence, the maximum value is 3 \(\frac{10}{11}\) at \(\left(\frac{28}{11}, \frac{5}{11}\right)\)

Section – B [12 Marks]

Question 7.
The population of a town grows at the rate of 10% per year. Using differential equation, find how long it will take for the population to grow 2 times.
Or
The marginal revenue function for a commodity is given by MR = 8 + 3x – 5x². Find the demand function.
Answer:
Let P0 be the population initially and P be the population after t yr.

According to question,
\(\frac{d}{d t}\)(P) = 10% of P ⇒ \(\frac{d P}{d t}=\frac{1}{10}\) P
⇒ \(\frac{1}{P}\) dP = \(\frac{1}{10}\)dt

On integration both sides, we get
∫\(\frac{1}{P}\) dP = ∫\(\frac{1}{10}\)dt
⇒ log P = \(\frac{1}{10}\)t + C

When t = 0, then P = P₀
∴ logP₀ = 0 + C ⇒ C = log P₀

From Eq.(i)
log P = \(\frac{1}{10}\)t + log P₀
⇒ log\(\frac{P}{P_{0}}=\frac{1}{10}\)t ……….(ii)

When the population grows 2 times, then
P = 2P₀
∴ log\(\left(\frac{2 P_{0}}{P_{0}}\right)=\frac{1}{10}\)t
⇒ t = 10log2
Hence, it takes 10 log 2 yr for the population to grow 2 times.

Or

Given MR = 8 + 3x – 5x²

Question 8.
10 students are selected at random from a college and their heights are found to be 100, 104,108,110,118,120,122,124,126 and 128 cm. In the light of these data, discuss the suggestion that the mean height of the students of the college is 110 cm. [given, t₉ (0.05) = 2.262].
Answer:
Consider, table for the sample mean (x̄) and S. Computation of x̄ and S

We have, \(\sum_{i=1}^{10}\) x_i = 1160 and n= 10
= \(\frac{1}{n} \sum_{i=1}^{10}\)x_i
= \(\frac{1160}{10}\) = 116

From the table, we find that

We have degree of freedom = (10 -1) = 9 It is given that t₉(0.05) = 2.262
∴ Calculated |t| = 1.94 < 2.262 = t₉(005)
i.e. Calculated |t| < tabulated t₉(0.05)
So, we accept the null hypothesis. Hence, the sample mean is same as the population mean. Consequently, the mean height of the students of the college is 110 cm.

Question 9.
From the following data compute 4-yearly moving averages and determine the trend values. Also, find the short-term fluctuations.

Answer:
Table for 4-yearly moving averages.

Question 10.
Mr. Kapoor invested ₹ 25000 in a mutual fund in year 2012. The value of mutual fund increased to ₹ 30000 in year 2016. Calculate the compound annual growth rate (CAGR) of his investment. [given, (1.2)^1/4 = 1.0466]
Answer:
Given, 13V = ₹ 25000, EV = ₹ 30000
and number of year (n) =4 yr
∴ CAGR = \(\left(\frac{\mathrm{EV}}{\mathrm{BV}}\right)^{1 / n}\) – 1
= \(\left(\frac{30000}{25000}\right)^{1 / 4}\) – 1 = \(\left(\frac{6}{5}\right)^{1 / 4}\) – 1
= (1.2)^1/4 – 1 = 1.0466 – 1 = 0.0466
∴ CAGR = (00466 × 100)% = 4.66%

Section – C [16 Marks]

Question 11.
Maximise and minimise Z = 3x – 4y, subject to constraints are
x – 2y ≤ 0, -3x + y ≤ 4, x – y ≤ 6 and x, y ≥ 0.
Answer:
Given, LPP is,
Maximise and minimise Z = 3x – 4y

Subject to constraints are
x – 2y ≤ 0, -3x + y ≤ 4, x – y ≤ 6 and x, y ≥ 0.
[on solving x – y = 6 and x – 2y = 0, we get x = 12 and y = 6]

From the shown graph, for the feasible region, we see that it is unbounded and coordinates of comer points are (0, 0), (12, 6) and (0, 4).

Corner points	Value of Z = 3x – 4y
(0.0)	0
(0,4)	-16 (minimum)
(12,6)	12 (maximum)

For given unbounded region the minimum value of Z may or may not be -16. So, for deciding this, we graph the inequality.
3x – 4y < -16 and check whether the resulting open half plane has common points with feasible region or not. Thus, from the figure it shows it has common points with feasible region, so it does not have any minimum value. Also, similarly for maximum value, we graph the inequality 3x – 4y > 12 and see that resulting open half plane has no common points with the feasible region and hence maximum value 12 exist for Z = 3x – 4y.

Question 12.
A couple wishes to purchase a house for ₹ 1000000 with a down payment of ₹ 200000. If they can amortize the balance at an interest rate 8% per annum compounded monthly for 10 yr. Find the monthly installment (EMI). [given, (1.006)^-120 = 0.4878]
Answer:
Amortized amount, P = Cost of house – Cash down payment
= 1000000 – 200000 = ₹ 800000
i = \(\frac{0.08}{12}\) = 0.006
n = 10 × 12 = 120 months

Question 13.
Mr. Shiv Chandra wants to know the amount, he should pay for a goldmine expected to yield an annual return of 400000 for the next 10 yr, after which it will be worthless. Find the amount, he should pay for the mine, if he wants to yield 18% annual return on his investment and also set up a sinking fund to replace the purchase price. Assume that the sinking fund earns 10% annually. [given (1.1)¹⁰ = 2.5937]
Or
A bond has a face value of ₹ 1000, matures in 4 yr coupon rate is 4% per annum. The bond makes annual payments. If the yield to maturity is 4%. Find the fair value of bond, [given (1.04)^-4 =0.8551]
Answer:
Given, rate of return on investment = 18% = 0.18
Let x be the purchase price of the mine.
Return on investment of ₹ x per year = 0.18+
Life of mine (n) = 10 yr
Net annual return = ₹ 400000

Sinking fund is created to replace the purchase price.
∴ Amount to be placed into sinking fund each year is ₹ (400000 – 0.18x).
These payments must accumulate to ₹ x at the end of 10 yr.
∴ Amount A = ₹ x,
i = r = 10% = 0.10
Here, n = 10 and R = ₹ (400000 – 0.18.x)

We know that

∴ Purchase price of the goldmine is ₹ 1648125.25

Or

Here, F = ₹ 1000, r = 4%, N = 4 yr and d = 4%

Case Based/Data Based

Question 14.
A long lasting company produces biscuits. Whose marginal revenue functions of a commodity is given by MR = 6x² – 5x + 2.

On the basis of the above information, answer the following questions.
(i) Find the total revenue functions.
Answer:
Given, marginal revenue functions
MR = 6x² – 5x + 2
⇒ \(\frac{d R}{d x}\) = MR = 6x² – 5x + 2
R = ∫(6x² – 5x + 2)dx
R = \(\frac{6 x^{3}}{3}-\frac{5 x^{2}}{2}\) + 2x + K
R = 2x³ – \(\frac{5 x^{2}}{2}\) + 2x + K

(ii) If the productions increases from 10 to 20. Find the increase in their revenue.
Answer:
The increase in revenue, when productions increase from 10 to 20, is

Students can access the CBSE Sample Papers for Class 12 Accountancy with Solutions and marking scheme Term 2 Set 5 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Accountancy Standard Term 2 Set 5 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper comprises two Parts – A and B. There are 12 questions in the question paper. Alt1 questions are compulsory.
• Part-A is compulsory for all candidates.
• Part-B has two options i.e., (i) Analysis of Financial Statements and (ii) Computerized Accounting. Students must attempt only one. of the given options.
• There is no overall choice. However, an internal choice has been provided in 3 questions of three marks and 1 question of five marks.

PART-A
(Accounting for Not-for-Profit Organisations, Partnership Firms and Companies)

Question 1.
From the following information provided by Reunion Club, calculate the amount of subscriptions which will be treated as income for the year ended 31^st March, 2021:
(i) Subscriptions collected during the year ended 31^st March, 2021 amounted to ₹ 49,000.
(ii) Subscriptions for the year ended 31^st March, 2021 collected in the year ended 31^stMarch, 2020 amounted to ₹ 3,000.
(iii) Subscriptions unpaid for the year ended 31^st March, 2021 amounted to ₹ 2,000. (2)
Answer:

Question 2.
On dissolution, how will you deal with Partner’s Loan if it appears on:
(A) Assets side of company’s Balance Sheet
(B) Liabilities side of company’s Balance Sheet (2)
Answer:
(A) If Partner’s Loan appears on the Assets side of the Balance Sheet, it indicates that partner has taken loan from the firm. In that case, at the time of dissolution the amount of loan will be transferred to the concerned Partner’s Capital Account. The following Journal Entry will be passed:

(B) If Partner’s Loan appears on the Liabilities side of the Balance Sheet, it indicates that the respective partner or partners have given loan to the firm. In this case, partner’s loan will be paid off after paying all the external liabilities first. The following accounting entry will be passed:

Question 3.
Tanmay, Gautam and Jagat were partners in a partnership firm ‘Jagatam Limited’ sharing profits and losses in the ratio of 6 : 5 : 4. Gautam retired and his capital after making adjustments on account of reserves, revaluation of assets and reassessment of liabilities stood at ₹ 10,01,600. Tanmay and Jagat agreed to pay him ₹ 11,60,000 in full settlement of his claim.

Pass necessary journal entry for the treatment of goodwill at the time of retirement of Gautam. Also show your workings clearly. (2)
Answer:

Working Notes:
(1) Calculation of Profit Sharing Ratio:
Old Profit Sharing Ratio of Tanmay, Gautam and Jagat = 6 : 5 : 4
New Profit Sharing Ratio and Gaining Ratio of Tanmay and Jagat will be 6 : 4 or 3 : 2, as no information provided of future profit sharing ratio between Tanmay and Jagat.

(2) Calculation of Gautam’s Share of Goodwill:
Gautam’s Share of Goodwill = Amount Paid – Gautam’s Capital after Adjustments
= ₹ 11,60,000 – ₹ 10,01,600
= ₹ 1,58,400

Gautam’s share of goodwill will be compensated by gaining partners, Tanmay and Jagat in their Gaining Ratio, i.e., 3 : 2.
Tanmay Will compansate = ₹ 1,58,400 × \(\frac{3}{5}\) = ₹ 95,040
Jagat Will compansate = ₹ 1,58,400 × \(\frac{2}{5}\) = ₹ 63,360

Question 4.
Show how are the following items dealt with while preparing the final accounts of Khadagpur Sports Club for the year ended 31^st March, 2020:
Case I:
(i) Expenditure on construction of Stadium is ₹ 6,00,000.
(ii) The construction work is in progress and has not yet completed.
(iii) Capital Fund as at 31st March, 2019 is ₹ 20,00,000.

Case II:
(i) Expenditure on construction of Stadium is ₹ 6,00,000.
(ii) The construction work is in progress and has not yet completed.
(iii) Stadium Fund as at 31^st March, 2019 is ₹ 10,00,000.
(iv) Capital Fund as at 31^st March, 2019 is ₹ 20,00,000.
OR
How will you treat the following items while preparing Income and Expenditure Account and Balance Sheet of a Not-for-Profit Organisation ?
(A) Donation for Building
(B) Sale of Newspapers
(C) Investment purchased. (3)
Answer:
Case I:

Case II:

OR
(A) Donation for Building: Donation for Building means that the donation received can only be used as a specific donation for building. Specific donation is capitalised and is shown on the Liabilities side of the Balance Sheet of Not-for-Profit Organisation.

(B) Sale of Newspapers: The money paid for newspapers, magazines, periodicals, etc. is a revenue expense and is debited to Income and Expenditure Account. Thus, the amount realised from the sale of newspapers, magazines, periodicals, etc. will be credited to Income and Expenditure Account.

(C) Investment Purchased: Investments purchased are viewed as capital spending and are shown on the Assets side of the Balance Sheet of Not-for-Profit Organisation.

Question 5.
Alpha, Beta and Gamma were partern in a firm sharing profit and losses is the ratio of 2 : 2 : 1. On 31^st March, 2021, their Balance Sheet was as follows:

On 30^th June, 2021, Beta died. The partnership Deed of the firm provided for the folloiwng on the death of a partner:

(i) Goodwill of the firm was to be calculated on the basis of two times the average profit of he
past five years. The profite for the years ended:
31^st March, 2020 – ₹ 1,00,000
31^st March, 2019 – ₹ 1,60,000
31^st March, 2018 – ₹ 22,20,000
31^st March, 2017 – ₹ 2,40,000

(ii) Beta’s share of profit on loss from 1^st April, 2021 till he death was to be calculated on the basis of the profit or loss for the year ended 31^st March, 2021.

You are required to prepare Beta’s Capital Account at the time of her death to be presented to his executors. (3)
Answer:

Working Notes:
(1) Calculation of Beta’s Share of Goodwill:
Average Profit of 5 years = \(\frac{₹ 1,00,000+₹ 1,60,000+₹ 2,20,000+₹ 4,40,000-₹ 3,20,000}{5}\)
= \(\frac{₹ 6,00,000}{5}\) = ₹ 1,20,000
Goodwill of Firm = Average profit × 2
= ₹ 1,20,000 × 2
= ₹ 2,40,000
Beta’s Share of Goodwill = 22,40,000 × \(\frac{2}{5}\)
= ₹ 96,000
which will be contributed by Alpha and Gamma is their gaining ratio, 2 : 1.
Alpha will contribute = ₹ 96,000 × \(\frac{2}{3}\) = ₹ 64,000
Gamma and contribute = ₹ 96,000 × \(\frac{1}{3}\) = ₹ 32,000

(2) Calculation of Beta’s share of profit or loss upto his date of Death:
Beta’s share of loss upto his Date of Death = 3,20,000 × \(\frac{2}{5} \times \frac{3}{12}\)
= ₹ 32,000

Question 6.
On 1^st June, 2019, Rilco Energy Ltd. issued 10,000, 7% Debentures of ₹ 100 each at a discount of 10% redeemable at a premium of 10% at the end of five years. All the debentures were subscribed and allotment was made.
Prepare the Balance Sheet (extract) as at 31^st March, 2020.
OR
Relco India Ltd. purchased machinery costing ₹ 1,35,000. It was agreed that the purchase consideration be paid by issuing 9% Debentures of ₹ 100 each. Give necessary journal entries if the debentures have been issued:
(A) at par
(B) at a discount of 10%. (3)
Answer:

Notes to Accounts:

OR

Working Note:

= \(\frac{1,35,000}{100-10}\)
= 1,350

Question 7.
A and B are partners in a firm sharing profits and losses in the ratio of 3 : 2. On 31st March, 2020, their Balance Sheet was as follows:

The firm was dissolved on 31^st March, 2020 and both the partners agreed to the following:
(i) Investments were taken over by A at an agreed value of ₹ 4,000. He also agreed to settle Mrs. A’s Loan.
(ii) Other assets realised as: Stock – ₹ 2,500; Debtors – ₹ 9,250; Furniture – ₹ 2,250; Plant – ₹ 12,500.
(iii) Expenses of dissolution amounted to ₹ 800.
(iv) Creditors agreed to accept ₹ 18,500 in full settlement of their claim.
You are required to prepare Realisation Account and Partners’ Capital Account of the firm dissolved.
OR
Alka, Binod and Cheenu are partners in a firm ABC Limited, sharing profits and losses as Alka 1/3, Binod 1/2 and Cheenu 1/6 respectively. The Balance Sheet of the firm as on 31^st March, 2019 was as follows:

It was agreed that:
(i) Goodwill will be valued at ₹ 27,000.
(ii) Depreciation of 10% was to be provided on Machinery.
(iii) Patents were to be reduced by 20%.
(iv) Liability on account of Provident Fund was estimated at ₹ 2,400.
(v) Chander took over Investments for ₹ 15,800.
(vi) Amit and Balan decided to adjust their capitals in proportion of their profit sharing ratio by opening Current Accounts.
Prepare Revaluation Account and Partners’ Capital Accounts on Chander’s retirement. (5)
Answer:

OR


Working Notes:
(1) Calcuation of Gaining Ratio:
Old Radio of Alka,Binod anid Cheenu = \(\frac{1}{3}: \frac{1}{2}: \frac{1}{6}\) or 2 : 3 : 1
Cheenu retires from the firm
New Ratio of Alka and Binod = 3 : 2
Gaining Ratio = New Radio – Old Radio
Alka’s Gain = \(\frac{3}{5}-\frac{2}{6}\) = \(\frac{18-10}{30}\) = \(\frac{8}{30}\) (Gain)
Binod’s Gain = \(\frac{2}{5}-\frac{3}{6}\) = \(\frac{12-15}{30}\) = –\(\frac{3}{30}\) (Sacrifice)

(2) Adjustment of Goodwill:
Goodwill of the Firm = ₹ 24,000
Cheenu’s Share of Goodwill = ₹ 24,000 × \(\frac{1}{6}\) = ₹ 4,000
Alka’s Gain in Goodwill = ₹ 24,000 × \(\frac{8}{30}\) = ₹ 6,400
Binod’s Sacrifice in Goodwill = ₹ 24,000 × \(\frac{3}{30}\) = ₹ 2,400

Question 8.
Jagannath Hotels Co. engaged in business of hotels, having chain of hotels in Andhra Pradesh decided to expand their business in other states also. For that the directors of the company decided to start their hotels in nearby states viz. Karnataka, Maharashtra and Goa.
For their underway hotels in Goa, Jagannath Hotels Co. purchased furniture of ₹ 88,00,000 from Deluxxe Furniture Store.
Jagannath Hotels Co. paid 50% of the amount by accepting a bill of exchange in favour of Deluxxe Furniture Store payable after five months. For the balance amount the company issued 10% Debentures of ₹ 100 each at a premium of 10% in favour of Deluxxe Furniture Store.

You are required to answer the following questions:
(A) Pass journal entry which will be passed at the time of purchase of furniture in the books of Jagannath Hotels Co.
(B) Pass journal entry for the payment made through bill of exchange.
(C) Calculate the number of debentures issued to Deluxxe Furniture Store.
(D) Calculate the amount to be transferred to Securities Premium Reserve Account.
(E) Pass journal entry for the allotment of debentures. (5)
Answer:

Working Note:
Purchase Price of Furniture = ₹ 88,00,000
Amount Paid by Bill of Exchange = 50% of ₹ 88,00,000
= \(\frac{50}{100}\) × ₹ 88,00,000 = ₹ 44,00,000

(C) Balance Amount due to Deluxxe Furniture Store = Purchase Price of Furniture – Amount Paid by Bill of Exchange
= ₹ 88,00,000 – (50% of ₹ 88,00,000)
= ₹ 44,00,000
Number of Debentures Issued to Deluxxe Furniture Store

= \(\frac{44,00,000}{₹ 100+(10 \% \text { of } ₹ 100)}\)
= \(\frac{44,00,000}{₹ 110}\) = 40,000
Number of Debentures Issued to Deluxxe Furniture Store = 40,000
Premium per debenture = 10% of ₹ 100 = ₹ 10

(E) Amount transferred to Securities Premium Reserve Account
= Number of Debentures × Premium per debenture = 40,000 × ₹ 10 = ₹ 4,00,000

(E)

Question 9.
Following is the Receipts and Payments of Bengaluru Sports Club for the year ended 31^st March, 2021:

(i) On 31^st March, 2020 subscriptions outstanding was ₹ 6,000 and on 31^st March, 2021 subscriptions outstanding was ₹ 8,000.
(ii) Salary outstanding on 31^st March, 2021 was ₹ 4,000.
(iii) On 1^st April, 2020 the club had Building of ₹ 1,60,000, Furniture of ₹ 40,000,10% Investments of ₹ 90,000 and Sports Equipments of ₹ 50,000. Depreciation charged on these items including purchases was 10%.

Prepare Income and Expenditure Account of Bengaluru Sports Club for the year ended 31^st March, 2021. Also prepare Balance Sheet of the club as at 31^st March, 2021. (5)
Answer:

Workin Note:

PART-B
Option-1
(Analysis of Financial Statements)

Question 10.
State whether the following transactions will result in inflow, outflow or no flow of cash while preparing Cash Flow Statement:
(A) Increase in Marketable Securities by ₹ 5,000.
(B) Decrease in Sundry Debtors by ₹ 15,000. (2)
Answer:
(A) Increase in Marketable Securities by ₹ 5,000 wilL result in no fLow of cash while preparing Cash Flow Statement.
(B) Decrease in Sundry Debtors by ₹ 15,000 will result in inflow of cash while preparing Cash Flow Statement

Question 11.
Prepare Common Size Balance Sheet from the Balance Sheets of Bat Ltd. and Ball Ltd. as at 31^st March, 2021 are:

OR
Prepare Comparative Statement of Profit and Loss from the followng figures:

Particulars	31st March, 2021	31st March, 2020
Revenue from Operations	₹ 60,00,000	₹ 40,00,000
Other Income (% of Revenue from Operations)	12%	20%
Expenses (% of Revenue from Operations)	70%	60%
Tax Rate	40%	40%

Answer:

OR

Working Notes:
(1) Computation of Other Income:
Other Income on 31^st March, 2020 = 20% of Revenue from Operations
= 20% of ₹ 40,00,000
= ₹ 8,00,000
Other Income on 31^st March, 2021 = 12% of Revenue from Operations
= 12% of ₹ 60,00,000
= ₹ 7,20,000

(2) Computation of Expenses:
Expenses on 31^st March, 2020 = 60% of Revenue from Operations
= 60% of ₹ 40,00,000
= ₹ 24,00,000
Expenses on 31^st March, 2021 = 70% of Revenue from Operations
= 70% of ₹ 60,00,000
= ₹ 42,00,000

Question 12.
From the following Balance Sheet as at 31^st March, 2021 and Statement of Profit and Loss for the year ended 31^st March, 2021 of Roopakshi Ltd. and additional information, prepare Cash Flow Statement for the year ended 31^st March, 2021:


Notes to Accounts:

Additional Information:
(i) Additional debentures were issued on 1^st October, 2020 of ₹ 5,00,000. On the same date, part of outstanding debentures were redeemed and interest was paid, whereas interest on outstanding debentures was paid on 10^th April, 2021.
(ii) Board of Directors proposed dividend in both the years @ 10%.
(iii) Interim Dividend of ₹ 1,00,000 was paid during the year.
(iv) A fixed asset with original cost of ₹ 1,00,000, on which depreciation till date was provided of
₹ 80,000 was sold at a profit of ₹ 10,000. (5)
Answer:


Working Notes: