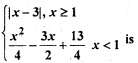MCQ Questions – Page 3

MCQ Questions for Class 12 Maths Chapter 12 Linear Programming with Answers

Linear Programming Class 12 MCQ Online Test With Answers Questions

October 24, 2024

Check the below NCERT MCQ Questions for Class 12 Maths Chapter 12 Linear Programming with Answers Pdf free download. MCQ Questions for Class 12 Maths with Answers were prepared based on the latest exam pattern. We have provided Linear Programming Class 12 Maths MCQs Questions with Answers to help students understand the concept very well.

Class 12 Maths Chapter 12 MCQ With Answers

Maths Class 12 Chapter 12 MCQs On Linear Programming

Linear Programming Class 12 MCQ Question 1.
Feasible region in the set of points which satisfy
(a) The objective functions
(b) Some the given constraints
(c) All of the given constraints
(d) None of these

Answer

Answer: (c) All of the given constraints

MCQ Questions On Linear Programming Class 12 Question 2.
Of all the points of the feasible region for maximum or minimum of objective function the points
(a) Inside the feasible region
(b) At the boundary line of the feasible region
(c) Vertex point of the boundary of the feasible region
(d) None of these

Answer

Answer: (c) Vertex point of the boundary of the feasible region

Linear Programming MCQ With Answers Pdf Question 3.
Objective function of a linear programming problem is
(a) a constraint
(b) function to be obtimized
(c) A relation between the variables
(d) None of these

Answer

Answer: (b) function to be obtimized

Linear Programming MCQ Class 12 Question 4.
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of a L.P.P. is called its
(a) Unbounded solution
(b) Optimum solution
(c) Feasible solution
(d) None of these

Answer

Answer: (c) Feasible solution

Lpp MCQ Class 12 Question 5.
The maximum value of the object function Z = 5x + 10 y subject to the constraints x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0 is
(a) 300
(b) 600
(c) 400
(d) 800

Answer

Answer: (b) 600

Lpp MCQ Questions Class 12 Question 6.
The maximum value of Z = 4x + 2y subject to the constraints 2x + 3y ≤ 18, x + y ≥ 10, x, y ≤ 0 is
(a) 36
(b) 40
(c) 30
(d) None of these

Answer

Answer: (d) None of these

Lpp Class 12 MCQ Question 7.
In equation 3x – y ≥ 3 and 4x – 4y > 4
(a) Have solution for positive x and y
(b) Have no solution for positive x and y
(c) Have solution for all x
(d) Have solution for all y

Answer

Answer: (a) Have solution for positive x and y

Linear Programming Is A MCQ Question 8.
The maximum value of Z = 3x + 4y subjected to contraints x + y ≤ 40, x + 2y ≤ 60, x ≥ 0 and y ≥ 0 is
(a) 120
(b) 140
(c) 100
(d) 160

Answer

Answer: (b) 140

MCQ On Lpp Class 12 Question 9.
Maximize Z = 11 x + 8y subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0.
(a) 44 at (4, 2)
(b) 60 at (4, 2)
(c) 62 at (4, 0)
(d) 48 at (4, 2)

Answer

Answer: (b) 60 at (4, 2)

MCQ Of Linear Programming Class 12 Question 10.
Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0
(a) 20 at (1, 0)
(b) 30 at (0, 6)
(c) 37 at (4, 5)
(d) 33 at (6, 3)

Answer

Answer: (c) 37 at (4, 5)

MCQ On Linear Programming Question 11.
Maximize Z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0
(a) 16 at (4, 0)
(b) 24 at (0, 4)
(c) 24 at (6, 0)
(d) 36 at (0, 6)

Answer

Answer: (d) 36 at (0, 6)

MCQ On Linear Programming Class 12 Question 12.
Maximize Z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0
(a) 59 at (\(\frac{9}{2}\), \(\frac{5}{2}\))
(b) 42 at (6, 0)
(c) 49 at (7, 0)
(d) 57.2 at (0, 5.2)

Answer

Answer: (a) 59 at (\(\frac{9}{2}\), \(\frac{5}{2}\))

MCQ Of Lpp Class 12 Question 13.
Maximize Z = 6x + 4y, subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0
(a) 12 at (2, 0)
(b) \(\frac{140}{3}\) at (\(\frac{2}{3}\), \(\frac{1}{3}\))
(c) 16 at (2, 1)
(d) 4 at (0, 1)

Answer

Answer: (c) 16 at (2, 1)

Class 12 Maths Chapter 12 MCQ Question 14.
Maximize Z = 10 x₁ + 25 x₂, subject to 0 ≤ x₁ ≤ 3, 0 ≤ x₂ ≤ 3, x₁ + x₂ ≤ 5
(a) 80 at (3, 2)
(b) 75 at (0, 3)
(c) 30 at (3, 0)
(d) 95 at (2, 3)

Answer

Answer: (d) 95 at (2, 3)

Linear Programming MCQs Question 15.
Z = 20x₁ + 20₂, subject to x₁ ≥ 0, x₂ ≥ 0, x₁ + 2x₂ ≥ 8, 3x₁ + 2x₂ ≥ 15, 5x₁ + 2x₂ ≥ 20. The minimum value of Z occurs at
(a) (8, 0)
(b) (\(\frac{5}{2}\), \(\frac{15}{4}\))
(c) (\(\frac{7}{2}\), \(\frac{9}{4}\))
(d) (0, 10)

Answer

Answer: (c) (\(\frac{7}{2}\), \(\frac{9}{4}\))

Linear Programming MCQ Class 12 Question 16.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at
(a) (4, 0)
(b) (28, 8)
(c) (2, \(\frac{7}{2}\))
(d) (0, 3)

Answer

Answer: (c) (2, \(\frac{7}{2}\))

Linear Programming Class 12 MCQ Questions Question 17.
The corner point of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y.
Compare the quantity in Column A and Column B

Column A	Column B
Maximum of Z	325

(a) The quantity in column A is greater
(b) The quantity in column B is greater
(c) The two quantities are equal
(d) The relationship cannot be determined On the basis of the information supplied

Answer

Answer: (b) The quantity in column B is greater

Question 18.
The feasible region for a LPP is shown shaded in the figure. Let Z = 3x – 4y be the objective function. Minimum of Z occurs at

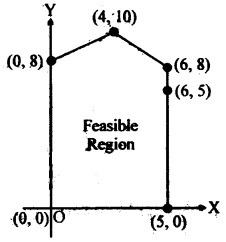
(a) (0, 0)
(b) (0, 8)
(c) (5, 0)
(d) (4, 10)

Answer

Answer: (b) (0, 8)

Question 19.
Refer to Question 18 maximum of Z occurs at
(a) (5, 0)
(b) (6, 5)
(c) (6, 8)
(d) (4, 10)

Answer

Answer: (a) (5, 0)

Question 20.
Refer to Question 18 (Maximum value of Z+ Minimum value of Z) is equal to
(a) 13
(b) 1
(c) -13
(d) -17

Answer

Answer: (d) -17

We hope the given NCERT MCQ Questions for Class 12 Maths Chapter 12 Linear Programming with Answers Pdf free download will help you. If you have any queries regarding Linear Programming CBSE Class 12 Maths MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 12 Maths MCQ:

MCQ Questions for Class 12 Maths Chapter 13 Probability with Answers

Probability Class 12 MCQ Online Test With Answers Questions

October 24, 2024

Check the below NCERT MCQ Questions for Class 12 Maths Chapter 13 Probability with Answers Pdf free download. MCQ Questions for Class 12 Maths with Answers were prepared based on the latest exam pattern. We have provided Probability Class 12 Maths MCQs Questions with Answers to help students understand the concept very well.

Class 12 Maths Chapter 13 MCQ With Answers

Maths Class 12 Chapter 13 MCQs On Probability

MCQ On Probability Class 12 Question 1.
If A and B are two independent events, then
(a) P(A∩B) = P(a) × P(b)
(b) P(AB) = 1 – P(A’) P(B’)
(c) P(AB) = 1 + P (A’) P(B’) P(A’)
(d) P (AB) = \(\frac{P(A’)}{P(B’)}\)

Answer

Answer: (a) P(A∩B) = P(a) × P(b)

Probability MCQ Class 12 Question 2.
The probability of an event is \(\frac{3}{7}\). Then odd against the event is
(a) 4 : 3
(b) 7 : 3
(c) 3 : 7
(d) 3 : 4

Answer

Answer: (a) 4 : 3

MCQ On Probability Class 12 Pdf Question 3.
A pair of dice are rolled. The probability of obtaining an even prime number on each die is
(a) \(\frac{1}{36}\)
(b) \(\frac{1}{12}\)
(c) \(\frac{1}{6}\)
(d) 0

Answer

Answer: (a) \(\frac{1}{36}\)

Probability Class 12 MCQ Question 4
If P(a) = \(\frac{3}{8}\), P(b) = \(\frac{1}{3}\) and P(A∩B) = — then P (A’ ∩B’)
(a) \(\frac{13}{24}\)
(b) \(\frac{13}{8}\)
(c) \(\frac{13}{9}\)
(d) \(\frac{13}{4}\)

Answer

Answer: (a) \(\frac{13}{24}\)

MCQ Of Probability Class 12 Question 5.
P(A∩B) = \(\frac{3}{8}\), P(b) = \(\frac{1}{2}\) and P(a) = \(\frac{1}{4}\) then P(\(\frac{B’}{A’}\)) =
(a) \(\frac{3}{5}\)
(b) \(\frac{5}{8}\)
(c) \(\frac{3}{8}\)
(d) \(\frac{5}{6}\)

Answer

Answer: (d) \(\frac{5}{6}\)

Probability MCQs With Answers Pdf Class 12 Question 6.
If A and B are two events such that P(a) ≠ 0 and P(\(\frac{B}{A}\)) = 1 then
(a) P(\(\frac{A}{B}\)) = 1
(b) P(\(\frac{B}{A}\)) = 1
(c) P(\(\frac{A}{B}\)) = 0
(d) P(\(\frac{B}{A}\)) = 0

Answer

Answer: (b) P(\(\frac{B}{A}\)) = 1

Probability Class 12 MCQ Questions Question 7.
If P (a) = \(\frac{3}{8}\), P(b) = \(\frac{1}{2}\) and P(A∩B) = \(\frac{1}{4}\) then P(\(\frac{A’}{B’}\)) =
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{3}{4}\)
(d) \(\frac{3}{8}\)

Answer

Answer: (b) \(\frac{1}{3}\)

Probability Questions And Answers Pdf Class 12 Question 8.
If A and B are two events such that P(a) ≠ 0 and P(\(\frac{B}{A}\)) = 1, then
(a) B ⊂ A
(b) B = φ
(c) A ⊂ B
(d) A ∩ B = φ

Answer

Answer: (c) A ⊂ B

Probability Class 12 Applied Mathematics MCQ Question 9.
If A and B are any two events such that P(a) + P(b) – P(A∩B) = P(a) then
(a) P(\(\frac{B}{A}\)) = 1
(b) P(\(\frac{B}{A}\)) = 0
(c) P(\(\frac{A}{B}\)) = 1
(d) P(\(\frac{A}{B}\)) = 0

Answer

Answer: (c) P(\(\frac{A}{B}\)) = 1

Class 12 Probability MCQ Question 10.
If A and B are events such that P (A∪B) = \(\frac{3}{4}\). P(A∩B) = \(\frac{1}{4}\), P(a) = \(\frac{2}{3}\) then P(AB) is
(a) \(\frac{3}{8}\)
(b) \(\frac{5}{8}\)
(c) \(\frac{5}{12}\)
(d) \(\frac{1}{4}\)

Answer

Answer: (b) \(\frac{5}{8}\)

Probability Class 12 Questions And Answers Question 11.
If one card is drawn out of 52 playing cards, the probability that it is an dice is
(a) \(\frac{1}{26}\)
(b) \(\frac{1}{13}\)
(c) \(\frac{1}{52}\)
(d) \(\frac{1}{4}\)

Answer

Answer: (b) \(\frac{1}{13}\)

Probability Class 12 Important Questions Question 12.
The chance of getting a doublet with 2 dice is
(a) \(\frac{2}{3}\)
(b) \(\frac{1}{6}\)
(c) \(\frac{5}{6}\)
(d) \(\frac{5}{36}\)

Answer

Answer: (b) \(\frac{1}{6}\)

Question 13.
Two number are chosen, one by one without replacement from the set of number A = {1, 2, 3, 4, 5, 6} then the probability that minimum value of two number chosen is less than 4 is
(a) \(\frac{14}{15}\)
(b) \(\frac{1}{15}\)
(c) \(\frac{1}{5}\)
(d) \(\frac{8}{5}\)

Answer

Answer: (b) \(\frac{1}{15}\)

Question 14.
If P(x) = \(\frac{2}{15}\); y = 1, 2, 3, 4, 5, 0 otherwise then P|x = 1 or 2| is
(a) \(\frac{1}{15}\)
(b) \(\frac{2}{15}\)
(c) \(\frac{1}{5}\)
(d) None of these

Answer

Answer: (c) \(\frac{1}{5}\)

Question 15.
Five horse are in a race. Mr. A select two of the horses at random and best on them. The probability that Mr. A select the winning horses is
(a) \(\frac{4}{5}\)
(b) \(\frac{3}{5}\)
(c) \(\frac{1}{5}\)
(d) \(\frac{2}{5}\)

Answer

Answer: (d) \(\frac{2}{5}\)

Question 16.
The probability of India w inning a test match against. West Indies is \(\frac{1}{2}\). Assuming independence from match to match the probability that in a match series India second win occurs at the third test is
(a) \(\frac{1}{6}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{2}{3}\)

Answer

Answer: (b) \(\frac{1}{4}\)

Question 17.
Three distinct numbers.are selected from First 100 natural numbers. The probability divisible by 2 and 3 is
(a) \(\frac{9}{25}\)
(b) \(\frac{4}{35}\)
(c) \(\frac{4}{55}\)
(d) \(\frac{4}{1155}\)

Answer

Answer: (d) \(\frac{4}{1155}\)

Question 18.
The probability that A speaks truth is \(\frac{4}{5}\) while this probability for B is \(\frac{3}{4}\). The probability that they contradict each others when asked to speak ana fact is
(a) \(\frac{7}{20}\)
(b) \(\frac{1}{5}\)
(c) \(\frac{3}{20}\)
(d) \(\frac{4}{5}\)

Answer

Answer: (d) \(\frac{4}{5}\)

Question 19.
Two dice are tossed once. The probability of getting an even number at the first dice ora total of 8 is
(a) \(\frac{1}{36}\)
(b) \(\frac{3}{36}\)
(c) \(\frac{11}{36}\)
(d) \(\frac{5}{9}\)

Answer

Answer: (d) \(\frac{5}{9}\)

Question 20.
The mean and the variance of binomial distribution are 4 and 2, respectively. Then the probability of 2 success
(a) \(\frac{128}{256}\)
(b) \(\frac{219}{256}\)
(c) \(\frac{7}{64}\)
(d) \(\frac{28}{256}\)

Answer

Answer: (c) \(\frac{7}{64}\)

Question 21.
A pair of dice are rolled. The probability of obtaining an even prime number on each dice is
(a) \(\frac{1}{36}\)
(b) \(\frac{1}{12}\)
(c) \(\frac{1}{6}\)
(d) 0

Answer

Answer: (a) \(\frac{1}{36}\)

Question 22.
If A, B are two events associated with same random experiment such that P(a) = 0.4, P(b) = 0.8 and P(B/A) = 0.6 then P(A/B) is
(a) 0.3
(b) 0.4
(c) 0.5
(d) 0.6

Answer

Answer: (a) 0.3

Question 23.
If P(a) = \(\frac{3}{8}\), P(b) = \(\frac{5}{8}\), P(A∪B) = \(\frac{3}{4}\) then p(\(\frac{B}{A}\)) is
(a) \(\frac{3}{47}\)
(b) \(\frac{5}{49}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{1}{4}\)

Answer

Answer: (c) \(\frac{2}{3}\)

Question 24.
An urn contain’s balls of which 3 are red, 4 are blue and 2 are green, 3 balls are drawn at random without replacement from the urn. The probability that the 3 balls haye different colours is
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{7}\)
(c) \(\frac{1}{21}\)
(d) \(\frac{2}{23}\)

Answer

Answer: (b) \(\frac{2}{7}\)

Question 25.
An experiment has 10 equally likely outcomes. Let A and B be two non-empty events of the experiment. A consists 4 outcomes, the number of outcomes that B must have so that A and B are independent is
(a) 2, 4 or 8
(b) 36 or 9
(c) 4 or 8
(d) 5 or 10

Answer

Answer: (d) 5 or 10

Question 28.
If P(a) = \(\frac{4}{5}\) and P(A∩B) = \(\frac{7}{10}\), then P(B/A) is equal
(a) \(\frac{1}{10}\)
(b) \(\frac{1}{8}\)
(c) \(\frac{7}{8}\)
(d) \(\frac{17}{20}\)

Answer

Answer: (d) \(\frac{17}{20}\)

Question 29.
If P(A∩B) = \(\frac{7}{10}\) and P(b) = \(\frac{17}{20}\), then P(A|B) equals
(a) \(\frac{14}{17}\)
(b) \(\frac{17}{20}\)
(c) \(\frac{7}{8}\)
(d) \(\frac{1}{8}\)

Answer

Answer: (a) \(\frac{14}{17}\)

Question 30.
If P(a) = \(\frac{7}{10}\) P(b) = \(\frac{7}{10}\) and P(A∪B) = \(\frac{7}{10}\) then P (B|A) + P(A|B) equals
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{5}{12}\)
(d) \(\frac{7}{12}\)

Answer

Answer: (d) \(\frac{7}{12}\)

Question 31.
If P(a) = \(\frac{2}{5}\), P(b) = \(\frac{3}{10}\) and P (A∩B) = \(\frac{1}{5}\), then P (A’|B’). P(B’|A’) is equal to
(a) \(\frac{5}{6}\)
(b) \(\frac{5}{7}\)
(c) \(\frac{25}{42}\)
(d) 1

Answer

Answer: (c) \(\frac{25}{42}\)

Question 32.
If P(a) = 0,4, P(b) = 0.8 and P(B|A) = 0.6 then P(A∪B) is equal to
(a) 0.24
(b) 0.3
(c) 0.48
(d) 0.96

Answer

Answer: (d) 0.96

Question 33.
If A and B are two events and A ≠ Φ, B ≠ Φ, then
(a) P (A|B) = P (a). P (b)
(b) P (A|B) = \(\frac{P(A∩B)}{P(B)}\)
(c) P (A + B). P (B|A) = 1
(d) P (A|B) = P (a) | P (b)

Answer

Answer: (b) P (A|B) = \(\frac{P(A∩B)}{P(B)}\)

Question 34.
A and B are events such that P(a) = 0.4, P(b) = 0.3 and P(A∪B) = 0.5. Then P(B∩A) equals
(a) \(\frac{2}{3}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{3}{10}\)
(d) \(\frac{1}{5}\)

Answer

Answer: (d) \(\frac{1}{5}\)

Question 35.
You are given that A and B are two events such that P(b) = \(\frac{3}{5}\), P(A|B) = \(\frac{1}{2}\) and P (A∪B) = \(\frac{4}{5}\), then P(a) equals
(a) \(\frac{3}{10}\)
(b) \(\frac{1}{5}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{3}{5}\)

Answer

Answer: (c) \(\frac{1}{2}\)

Question 36.
You are given that A and B are two events such that P(b) = \(\frac{3}{5}\), P(A|B) = \(\frac{1}{2}\) and P (A∪B) = then P(B|A’) equals
(a) \(\frac{1}{5}\)
(b) \(\frac{3}{10}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{3}{5}\)

Answer

Answer: (d) \(\frac{3}{5}\)

Question 37.
If P(b) = \(\frac{1}{5}\), P(A|B) = \(\frac{1}{2}\) and P(A∪B) = \(\frac{4}{5}\) then P (A∪B)’ + P (A’∪B) =
(a) \(\frac{1}{5}\)
(b) \(\frac{4}{5}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{3}{5}\)

Answer

Answer: (d) \(\frac{3}{5}\)

Question 38.
Let P (a) = \(\frac{7}{13}\), P(b) = \(\frac{9}{13}\) and P (A∪B) = \(\frac{9}{13}\), Then P(A’|B) is equal to
(a) \(\frac{6}{13}\)
(b) \(\frac{4}{13}\)
(c) \(\frac{4}{9}\)
(d) \(\frac{5}{9}\)

Answer

Answer: (d) \(\frac{5}{9}\)

Question 39.
If A and B are such that events that P(a) > 0 and P(b) ≠ 1, then P (A’|B’) equal
(a) 1 – P (A|B)
(b) 1 – P(A’|B)
(c) \(\frac{1-P(A∪B)}{P(B’)}\)
(d) p(A’) | P(B’)

Answer

Answer: (c) \(\frac{1-P(A∪B)}{P(B’)}\)

Question 40.
If two events are independent, then
(a) they must be mutually exclusive
(b) the sum of their probabilities must be equal to 1
(c) (a) and (b) both are correct
(d) None of the above is correct

Answer

Answer: (d) None of the above is correct

Question 41.
If A and B are two independent events with P(a) = \(\frac{3}{5}\) and P (b) = \(\frac{4}{9}\), then P (A’∩B’) equals
(a) \(\frac{4}{15}\)
(b) \(\frac{8}{15}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{2}{9}\)

Answer

Answer: (d) \(\frac{2}{9}\)

Question 42.
Let A and B two event such that P(a) = \(\frac{3}{8}\), P(b) = \(\frac{5}{8}\) and P(A∪B) = \(\frac{3}{4}\). Then P(A|B).P(A’|B) is equal to
(a) \(\frac{2}{5}\)
(b) \(\frac{3}{8}\)
(c) \(\frac{3}{20}\)
(d) \(\frac{6}{25}\)
Ans. (d)

Answer

Answer: (d) \(\frac{6}{25}\)

Question 43.
If the event A and B are independent, then P(A∩B) is equal to
(a) P(a) + P(b)
(b) P(a) – P(b)
(c) P(a). P(b)
(d) P(a) | P(b)

Answer

Answer: (c) P(a). P(b)

We hope the given NCERT MCQ Questions for Class 12 Maths Chapter 13 Probability with Answers Pdf free download will help you. If you have any queries regarding Probability CBSE Class 12 Maths MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 12 Maths MCQ:

MCQ Questions for Class 12 Maths Chapter 9 Differential Equations with Answers

Differential Equations Class 12 MCQ Online Test With Answers Questions

October 24, 2024

Check the below NCERT MCQ Questions for Class 12 Maths Chapter 9 Differential Equations with Answers Pdf free download. MCQ Questions for Class 12 Maths with Answers were prepared based on the latest exam pattern. We have provided Differential Equations Class 12 Maths MCQs Questions with Answers to help students understand the concept very well.

Class 12 Maths Chapter 9 MCQ With Answers

Maths Class 12 Chapter 9 MCQs On Differential Equations

MCQ On Differential Equations Class 12 Chapter 9 Question 1.
Integration factor of differential equation \(\frac{dy}{dx}\) + py = Q, where P and IQ are functions of x is
(a) ∫e^pdx
(b) \(_{e}\)∫pdx
(c) \(_{e}\)-∫pdx
(d) None of these

Answer

Answer: (d) None of these

Differential Equations Class 12 MCQ Chapter 9 Question 2.
The radius of a circle is increasing at the rate of 0.4 cm/ s. The rate of increasing of its circumference is
(a) 0.4 π cm/s
(b) 0.8 π cm/s
(c) 0.8 cm/s
(d) None of these

Answer

Answer: (b) 0.8 π cm/s

Differential Equations MCQ Class 12 Chapter 9 Question 3.
The solution of \(\frac{dy}{dx}\) = 1 + x + y + xy is
(a) x – y = k(1 + xy)
(b) log (1 + y) = x + \(\frac{x^2}{2}\) + k
(c) log (1 + x) + y + \(\frac{y^2}{2}\) = k
(d) None of these

Answer

Answer: (b) log (1 + y) = x + \(\frac{x^2}{2}\) + k

MCQ On Differential Equations Class 12 Chapter 9 Question 4.
The degree of the differential equation
(\(\frac{d^2y}{dx}\))² + (\(\frac{dy}{dx}\))² = x sin \(\frac{dy}{dx}\) is
(a) 1
(b) 2
(c) 3
(d) not defined

Answer

Answer: (d) not defined

Differential Equations MCQ Questions And Answers Class 12 Chapter 9 Question 5.
The degree of differential equation
[1 + (\(\frac{dy}{dx}\))²]^{\(\frac{3}{2}\)} = \(\frac{d^2y}{dx^2}\) is
(a) 4
(b) \(\frac{3}{2}\)
(c) 2
(d) not defined

Answer

Answer: (c) 2

Differential Equation MCQ Class 12 Chapter 9 Question 6.
The order and degree of the differential equation
\(\frac{d^2y}{dx^2}\) + (\(\frac{dy}{dx}\))^{\(\frac{1}{4}\)} + x^{\(\frac{1}{3}\)} = 0 respectvely, are
(a) 2 and not defined
(b) 2 and 2
(c) 2 and 3
(d) 3 and 3

Answer

Answer: (a) 2 and not defined

Differential Equations MCQ With Answers Class 12 Chapter 9 Question 7.
If y = e^-x (A cos x + B sin x), then y is a solution of
(a) \(\frac{d^2y}{dx^2}\) + 2\(\frac{dy}{dx}\) = 0
(b) \(\frac{d^2y}{dx^2}\) – 2\(\frac{dy}{dx}\) + 2y = 0
(c) \(\frac{d^2y}{dx^2}\) + 2\(\frac{dy}{dx}\) + 2y = 0
(d) \(\frac{d^2y}{dx^2}\) + 2y = 0

Answer

Answer: (c) \(\frac{d^2y}{dx^2}\) + 2\(\frac{dy}{dx}\) + 2y = 0

Differential Equations MCQ Questions Class 12 Chapter 9 Question 8.
The differential equation for y = A cos αx + B sin αx where A and B are arbitary constants is
(a) \(\frac{d^2y}{dx^2}\) – α²y = 0
(b) \(\frac{d^2y}{dx^2}\) + α²y = 0
(c) \(\frac{d^2y}{dx^2}\) + αy = 0
(d) \(\frac{d^2y}{dx^2}\) – αy = 0

Answer

Answer: (b) \(\frac{d^2y}{dx^2}\) + α²y = 0

MCQ Differential Equations Class 12 Chapter 9 Question 9.
Solution of differential equation xdy – ydx = Q represents
(a) a rectangular hyperbola
(b) parabola whose vertex is at origin
(c) straight line passing through origin
(d) a circle whose centre is at origin

Answer

Answer: (c) straight line passing through origin

Integrating Factor MCQ Class 12 Chapter 9 Question 10.
Integrating factor of the differential equation cos x \(\frac{dy}{dx}\) + y sin x = 1 is
(a) cos x
(b) tan x
(c) sec x
(d) sin x

Answer

Answer: (c) sec x

Differential Equations MCQ With Solution Pdf Class 12 Chapter 9 Question 11.
Solution of the differential equation tan y sec² x dx + tan x sec² y dy + 0 is .
(a) tan x + tan y = k
(b) tan x – tan y = k
(c) \(\frac{tan x}{tan y}\) = k
(d) tan x.tan y = k

Answer

Answer: (d) tan x.tan y = k

Differential Equation MCQs Class 12 Chapter 9 Question 12.
Family r = Ax + A³ of curves is represented by the differential equation of degree
(a) 1
(b) 2
(c) 3
(d) 4

Answer

Answer: (b) 2

MCQ Of Differential Equation Class 12 Chapter 9 Question 13.
Integrating factor of \(\frac{xdy}{dx}\) – y = x⁴ – 3x is
(a) x
(b) log x
(c) \(\frac{1}{2}\)
(d) -x

Answer

Answer: (c) \(\frac{1}{2}\)

Linear Differential Equations MCQs With Answers Class 12 Chapter 9 Question 14.
Solution of \(\frac{dy}{dx}\) – y = 1 y(0) = 1 is given by
(a) xy = -e^x
(b) xy = -e^-x
(c) xy = -1
(d) y = 2e^x – 1

Answer

Answer: (d) y = 2e^x – 1

MCQs On Differential Equations Class 12 Chapter 9 Question 15.
The number of solutions of \(\frac{dy}{dx}\) = \(\frac{y+1}{x-1}\) when y(1) = 2 is
(a) none
(b) one
(c) two
(d) infinite

Answer

Answer: (b) one

Differential Equations MCQs Class 12 Chapter 9 Question 16.
Which of the following is a second order differential equation?
(a) (y’)² + x = y²
(b) y’y” + y = sin x
(c) y” + (y”)² + y = 0
(d) y’ = y²

Answer

Answer: (b) y’y” + y = sin x

MCQ Questions On Differential Equations Class 12 Chapter 9 Question 17.
Integrating factor of the differential equation
(1 – x²) \(\frac{dy}{dx}\) – xy = 1 is
(a) -x
(b) \(\frac{x}{1+x^2}\)
(c) \(\sqrt{1-x^2}\)
(d) \(\frac{1}{2}\) log(1 – x²)

Answer

Answer: (c) \(\sqrt{1-x^2}\)

MCQ On Differential Calculus Class 12 Chapter 9 Question 18.
tan^-1 x + tan^-1 y = c is the general solution of the differential equation
(a) \(\frac{dy}{dx}\) = \(\frac{1+y^2}{1+x^2}\)
(b) \(\frac{dy}{dx}\) = \(\frac{1+x^2}{1+y^2}\)
(c) (1 + x²)dy + (1 + y²)dx = 0
(d) (1 +x²2)dx+(1 + y²)dy = 0

Answer

Answer: (c) (1 + x²)dy + (1 + y²)dx = 0

Maths MCQ Questions Class 12 Chapter 9 Question 19.
The differential equation y \(\frac{dy}{dx}\) + x = c represents
(a) Family of hyperbolas
(b) Family of parabolas
(c) Family of ellipses
(d) Family of circles

Answer

Answer: (d) Family of circles

MCQ Questions For Class 12 Maths With Answers Chapter 9 Question 20.
The general solution of e^x cos y dx – e^x sin y dy = 0 is
(a) e^x cos y = k
(b) e^x sin y = k
(c) e^x = k cos y
(d) e^x = k sin y

Answer

Answer: (a) e^x cos y = k

Question 21.
The degree of the differential equation
\(\frac{d^2y}{dx^2}\) + (\(\frac{dy}{dx}\))³ + 6y⁵ = 0 is
(a) 1
(b) 2
(c) 3
(d) 5

Answer

Answer: (a) 1

Question 22.
The solution of \(\frac{dy}{dx}\) + y = e^-x, y (0) = 0 is
(a) y = e^x(x – 1)
(b) y = xe^-x
(c) y = xe^-x + 1
(d) y = (x + 1 )e^-x

Answer

Answer: (b) y = xe^-x

Question 23.
Integrating factor of the differential equation \(\frac{dy}{dx}\) + y tan x – sec x = 0 is
(a) cos x
(b) sec x
(c) e^{cos x}
(d) e^{sec x}

Answer

Answer: (b) sec x

Question 24.
The solution of the differential equation \(\frac{dy}{dx}\) = \(\frac{1+y^2}{1+x^2}\)
(a) y = tan^-1 x
(b) y – x = k(1 + xy)
(c) x = tan^-1 y
(d) tan (xy) = k

Answer

Answer: (b) y – x = k(1 + xy)

Question 25.
The integrating factor of the differential equation \(\frac{dy}{dx}\) + y = \(\frac{1+y}{x}\) is
(a) \(\frac{x}{e^x}\)
(b) \(\frac{e^x}{x}\)
(c) xe^x
(d) e^x

Answer

Answer: (b) \(\frac{e^x}{x}\)

Question 26.
y = ae^mx + be^-mx satisfies which of the following differential equation?
(a) \(\frac{dy}{dx}\) + my = 0
(b) \(\frac{dy}{dx}\) – my = 0
(c) \(\frac{d^2y}{dx^2}\) – m²y = 0
(d) \(\frac{d^2y}{dx^2}\) +m²y = 0

Answer

Answer: (c) \(\frac{d^2y}{dx^2}\) – m²y = 0

Question 27.
The solution of the differential equation cos x sin y dx + sin x cos y dy = 0 is
(a) \(\frac{sin x}{sin y}\) = c
(b) sin x sin y = c
(c) sin x + sin y = z
(d) cos x cos y = c

Answer

Answer: (b) sin x sin y = c

Question 28.
The solution of x \(\frac{dy}{dx}\) + y = e^x is
(a) y = \(\frac{e^x}{x}\) + \(\frac{k}{x}\)
(b) y = xe^x + cx
(c) y = xe^x + k
(d) x = \(\frac{e^vy}{y}\) + \(\frac{k}{y}\)

Answer

Answer: (a) y = \(\frac{e^x}{x}\) + \(\frac{k}{x}\)

Question 29.
The differential equation of the family of cuves x² + y² – 2ay = 0, where a is arbitrary constant is
(a) (x² – y²)\(\frac{dy}{dx}\) = 2xy
(b) 2 (x² + y²)\(\frac{dy}{dx}\) = xy
(c) 2(x² – y²)\(\frac{dy}{dx}\) = xy
(d) (x² + y²) \(\frac{dy}{dx}\) = 2xy

Answer

Answer: (a) (x² – y²)\(\frac{dy}{dx}\) = 2xy

Question 30.
Family y = Ax + A³ of curves will correspond to a differential equation of order
(a) 3
(b) 2
(c) 1
(d) not finite

Answer

Answer: (b) 2

Question 31.
The general solution of \(\frac{dy}{dx}\) = 2x e^x²-y is
(a) e^x²-y = c
(b) e^-y + e^x² = c
(c) e^y = e^x² + c
(d) e^x²+y = c

Answer

Answer: (c) e^y = e^x² + c

Question 32.
The curve for which the slope of the tangent at any point is equal to the ratio of the abcissa to the ordinate of the point is
(a) an ellipse
(b) parabola
(c) circle
(d) rectangular hyperbola

Answer

Answer: (d) rectangular hyperbola

Question 33.
The general solution of the differential equation \(\frac{dy}{dx}\) = e^{\(\frac{x^2}{2}\)} + xy is
(a) y = ce^{\(\frac{-x^2}{2}\)}
(b) y = ce^{\(\frac{x^2}{2}\)}
(c) y = (x + c)e^{\(\frac{x^2}{2}\)}
(d) y = (c – x)e^{\(\frac{x^2}{2}\)}

Answer

Answer: (c) y = (x + c)e^{\(\frac{x^2}{2}\)}

Question 34.
The solution of the equation (2y – 1) dx-(2x + 3)dy = 0 is
(a) \(\frac{2x-1}{2y+3}\) = k
(b) \(\frac{2y+1}{2x-3}\) = k
(c) \(\frac{2x+3}{2y-1}\) = k
(d) \(\frac{2x-1}{2y-1}\) = k

Answer

Answer: (c) \(\frac{2x+3}{2y-1}\) = k

Question 35.
The differential equation for which y = a cos x + b sin x is a solution is
(a) \(\frac{d^2y}{dx^2}\) + y = 0
(b) \(\frac{d^2y}{dx^2}\) – y = 0
(c) \(\frac{d^2y}{dx^2}\) + (a + b)y = 0
(d) \(\frac{d^2y}{dx^2}\) + (a – b)y = 0

Answer

Answer: (a) \(\frac{d^2y}{dx^2}\) + y = 0

Question 36.
The solution of \(\frac{dy}{dx}\) + y = e^-x, y (0) = 0 is
(a) y = e^-x (x – 1)
(b) y = xe^x
(c) y = xe^-x + 1
(d) y = xe^-x

Answer

Answer: (d) y = xe^-x

Question 37.
The order and degree of the differential equation
(\(\frac{d^2y}{dx^3}\))² – 3\(\frac{d^2y}{dx^2}\) + 2(\(\frac{dy}{dx}\))⁴ = y⁴ are
(a) 1, 4
(b) 3, 4
(c) 2, 4
(d) 3, 2

Answer

Answer: (d) 3, 2

Question 38.
The order and degree of the differential equation
[1 + (\(\frac{dy}{dx}\))²] = \(\frac{d^2y}{dx^2}\) are
(a) 1, \(\frac{3}{2}\)
(b) 2, 3
(c) 2, 1
(d) 3, 4

Answer

Answer: (c) 2, 1

Question 39.
The differential equation of the family of curves y² = 4a (x + a) is
(a) y² = 4\(\frac{dy}{dx}\) (x + \(\frac{dy}{dx}\))
(b) 2y\(\frac{dy}{dx}\) = 4a
(c) y\(\frac{d^2y}{dx^2}\) + (\(\frac{dy}{dx}\))² = 0
(d) 2x\(\frac{dy}{dx}\) + y(\(\frac{dy}{dx}\))² – y

Answer

Answer: (c) y\(\frac{d^2y}{dx^2}\) + (\(\frac{dy}{dx}\))² = 0

Question 40.
Which of the following is the general solution of \(\frac{d^2y}{dx^2}\) – 2\(\frac{dy}{dx}\) + y = 0
(a) y = (Ax + B)e^x
(b) y = (Ax + B)e^-x
(c) y = Ae^x + Be^-x
(d) y = A cos x + B sin x

Answer

Answer: (a) y = (Ax + B)e^x

We hope the given NCERT MCQ Questions for Class 12 Maths Chapter 9 Differential Equations with Answers Pdf free download will help you. If you have any queries regarding Differential Equations CBSE Class 12 Maths MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 12 Maths MCQ:

MCQ Questions for Class 12 Maths Chapter 8 Application of Integrals with Answers

Application of Integrals Class 12 MCQ Online Test With Answers Questions

October 24, 2024

Check the below NCERT MCQ Questions for Class 12 Maths Chapter 8 Application of Integrals with Answers Pdf free download. MCQ Questions for Class 12 Maths with Answers were prepared based on the latest exam pattern. We have provided Application of Integrals Class 12 Maths MCQs Questions with Answers to help students understand the concept very well.

Class 12 Maths Chapter 8 MCQ With Answers

Maths Class 12 Chapter 8 MCQs On Application of Integrals

MCQ On Application Of Integration Chapter 8 Question 1.
The area of the region bounded by the y-axis, y = cos x and y = sin x, 0 ≤ x ≤ \(\frac{π}{2}\) is
(a) √2 sq.units
(b) (√2 + 1) sq. units
(c) (√2 – 1) sq. units
(d) (2√2 – 1) sq.units

Answer

Answer: (c) (√2 – 1) sq. units

Application Of Integration MCQ Chapter 8 Question 2.
The area of the region bounded by the curve x² = 4y and the straight line x = 4y – 2 is
(a) \(\frac{3}{8}\) sq.units
(b) \(\frac{5}{8}\) sq.units
(c) \(\frac{7}{8}\) sq.units
(d) \(\frac{9}{8}\) sq. units

Answer

Answer: (d) \(\frac{9}{8}\) sq. units

Application Of Integrals MCQ Chapter 8 Question 3.
The area of the region bounded by the curve y = \(\sqrt{16-x^2}\) and x-axis is
(a) 8π sq.units
(b) 20π sq. units
(c) 16π sq. units
(d) 256π sq. units

Answer

Answer: (a) 8π sq.units

Application Of Integration Important Questions Chapter 8 Question 4.
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x² + y² = 32 is
(a) 16π sq.units
(b) 4π sq. units
(c) 32π sq. units
(d) 24π sq. units

Answer

Answer: (b) 4π sq. units

Application Of Integrals Class 12 Chapter 8 Question 5.
Area of the region bounded by the curve y = cos x between x = 0 and x = π is
(a) 2 sq. units
(b) 4 sq, units
(c) 3 sq.units
(d) 1 sq. units

Answer

Answer: (a) 2 sq. units

MCQ On Line Integral Chapter 8 Question 6.
The area of the region bounded by parabola y² = x and the straight line 2y = x is
(a) \(\frac{4}{3}\) sq. unit
(b) 1 sq. unit
(c) \(\frac{2}{3}\) sq. units
(d) \(\frac{1}{3}\) sq. units

Answer

Answer: (a) \(\frac{4}{3}\) sq. unit

Question 7.
The area of the region bounded by the curve y = sin x between the ordinates x = 0, x = \(\frac{π}{2}\) and the x-axis is
(a) 2 sq. units
(b) 4 sq. units
(c) 3 sq. units
(d) 1 sq, unit

Answer

Answer: (d) 1 sq, unit

Question 8.
The area of the region bounded by the ellipse \(\frac{x²}{25}\) + \(\frac{y²}{16}\) = 1 is
(a) 20π sq. units
(b) 20π² sq. units
(c) 16π² sq. units
(d) 25π sq. units

Answer

Answer: (a) 20π sq. units

Question 9.
The area of the region bounded by the circle x² + y² = 1 is
(a) 2π sq. units
(b) 7π sq. units
(c) 3π sq. units
(d) 4π sq. units

Answer

Answer: (b) 7π sq. units

Question 10.
The area of the region bounded by the and the lines x = 2 and x = 3
(a) \(\frac{7}{2}\) sq. unit
(b) \(\frac{9}{2}\) sq. unit
(c) \(\frac{11}{2}\) sq. units
(d) \(\frac{13}{2}\) sq. units

Answer

Answer: (a) \(\frac{7}{2}\) sq. unit

Question 11.
The area of the region bounded by the curve x = 2y + 3 and the lines y = 1 and y = -1 is
(a) 4 sq. units
(b) \(\frac{3}{2}\) sq. units
(c) 6 sq. units
(d) 8 sq, units

Answer

Answer: (c) 6 sq. units

Question 12.
If y = 2 sin x + sin 2x for 0 ≤ x ≤ 2π, then the area enclosed by the curve and x-axis is
(a) \(\frac{9}{2}\) sq. units
(b) 8 sq. units
(c) 12 sq. units
(d) 4 sq. unjts

Answer

Answer: (c) 12 sq. units

Question 13.
Tne area bounded by the curve y = x² – 1 and the straight line x + y = 3 is
(a) \(\frac{9}{2}\) sq. units
(b) 4 sq. units
(c) \(\frac{7\sqrt{17}}{6}\) sq. units
(d) \(\frac{17\sqrt{17}}{6}\) sq. unjts

Answer

Answer: (d) \(\frac{17\sqrt{17}}{6}\) sq. unjts

Question 14.
Area bounded by the lines y = |x| – 2 and y = 1 – |x – 1| is equal to
(a) 4 sq. units
(b) 6 sq. units
(c) 2 sq. units
(d) 8 sq. units

Answer

Answer: (a) 4 sq. units

Question 15.
The area bounded by the lines y = |x| – 1 and y = -|x| + 1 is
(a) 1 sq. unit
(b) 2 sq. unit
(c) 2√2 sq. units
(d) 4 sq. units

Answer

Answer: (b) 2 sq. unit

Question 16.
The area of the region bounded by the line y = | x – 2 |, x = 1, x = 3 and x-axis is
(a) 4 sq. units
(b) 2 sq, units
(c) 3 sq. units
(d) 1 sq. unit

Answer

Answer: (d) 1 sq. unit

Question 17.
Area bounded by the ellipse \(\frac{x^2}{4}\) + \(\frac{y^2}{9}\) = 1 is
(a) 6π sq. units
(b) 3π sq. units
(c) 12π sq. units
(d) None of these

Answer

Answer: (a) 6π sq. units

Question 18.
Area of triangle whose two vertices formed from the x-axis and line y = 3 – |x| is,
(a) 9 sq. units
(b) \(\frac{3}{2}\) sq. units
(c) 3 sq. units
(d) None of these

Answer

Answer: (d) None of these

Question 19.
The area of ellipse \(\frac{x^2}{4^2}\) + \(\frac{y^2}{9^2}\) = 1 is
(a) 6π sq. units
(b) \(\frac{π(a^2+b^2)}{4}\) sq. units
(c) π(a + b) sq. units
(d) None of these

Answer

Answer: (d) None of these

Question 20.
The area bounded by the lines |x| + |y| = 1 is
(a) 1 sq. unit
(b) 2 sq. units
(c) 2√2 sq. units
(d) 4 sq. units

Answer

Answer: (b) 2 sq. units

Question 21.
The area bounded by the curve 2x² + y² = 2 is
(a) π sq. units
(b) √2π sq. units
(c) \(\frac{π}{2}\) sq. units
(d) 2π sq. units

Answer

Answer: (b) √2π sq. units

Question 22.
The area bounded by the curve x² = 4y + 4 and line 3x + 4y = 0 is
(a) \(\frac{25}{4}\) sq. units
(b) \(\frac{125}{8}\) sq. units
(c) \(\frac{125}{16}\) sq. units
(d) \(\frac{124}{4}\) sq. units

Answer

Answer: (d) \(\frac{124}{4}\) sq. units

Question 23.
Area of the ellipse \(\frac{x^2}{a^2}\) + \(\frac{y^2}{b^2}\) = 1 is
(a) 4π ab sq. units
(b) 2π ab sq. units
(c) π ab sq. units.
(d) \(\frac{π ab}{2}\) sq. units

Answer

Answer: (c) π ab sq. units.

Question 24.
Area bounded between the parabola y² = 4ax and its latus rectum is
(a) \(\frac{1}{3}\) a sq. units
(b) \(\frac{1}{3}\) a² sq. units
(c) \(\frac{8}{3}\) a sq. units
(d) \(\frac{8}{3}\) a² sq. units

Answer

Answer: (d) \(\frac{8}{3}\) a² sq. units

Question 25.
The area bounded by the line y = 2x – 2, y = -x and x-axis is given by
(a) \(\frac{9}{2}\) sq. units
(b) \(\frac{43}{6}\) sq. units
(c) \(\frac{35}{6}\) sq. units
(d) None pf these

Answer

Answer: (d) None pf these

We hope the given NCERT MCQ Questions for Class 12 Maths Chapter 8 Application of Integrals with Answers Pdf free download will help you. If you have any queries regarding Application of Integrals CBSE Class 12 Maths MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 12 Maths MCQ:

MCQ Questions for Class 12 Maths Chapter 6 Application of Derivatives with Answers

Application of Derivatives Class 12 MCQ Online Test With Answers Questions

October 24, 2024

Check the below NCERT MCQ Questions for Class 12 Maths Chapter 6 Application of Derivatives with Answers Pdf free download. MCQ Questions for Class 12 Maths with Answers were prepared based on the latest exam pattern. We have provided Application of Derivatives Class 12 Maths MCQs Questions with Answers to help students understand the concept very well.

Class 12 Maths Chapter 6 MCQ With Answers

Maths Class 12 Chapter 6 MCQs On Application of Derivatives

Question 1.
The sides of an equilateral triangle are increasing at the rate of 2cm/sec. The rate at which the are increases, when side is 10 cm is
(a) 10 cm²/s
(b) √3 cm²/s
(c) 10√3 cm²/s
(d) \(\frac{10}{3}\) cm²/s

Answer

Answer: (c) 10√3 cm²/s

Question 2.
A ladder, 5 meter long, standing oh a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is
(a) \(\frac{1}{10}\) radian/sec
(b) \(\frac{1}{20}\) radian/sec
(c) 20 radiah/sec
(d) 10 radiah/sec

Answer

Answer: (b) \(\frac{1}{20}\) radian/sec

Question 3.
The curve y – x^1/5 at (0, 0) has
(a) a vertical tangent (parallel to y-axis)
(b) a horizontal tangent (parallel to x-axis)
(c) an oblique tangent
(d) no tangent

Answer

Answer: (b) a horizontal tangent (parallel to x-axis)

Question 4.
The equation of normal to the curve 3x² – y² = 8 which is parallel to the line ,x + 3y = 8 is
(a) 3x – y = 8
(b) 3x + y + 8 = 0
(c) x + 3y ± 8 = 0
(d) x + 3y = 0

Answer

Answer: (c) x + 3y ± 8 = 0

Question 5.
If the curve ay + x² = 7 and x³ = y, cut orthogonally at (1, 1) then the value of a is
(a) 1
(b) 0
(c) -6
(d) 6

Answer

Answer: (d) 6

Question 6.
If y = x⁴ – 10 and if x changes from 2 to 1.99 what is the change in y
(a) 0.32
(b) 0.032
(c) 5.68
(d) 5.968

Answer

Answer: (a) 0.32

Question 7.
The equation of tangent to the curve y (1 + x²) = 2 – x, w here it crosses x-axis is:
(a) x + 5y = 2
(b) x – 5y = 2
(c) 5x – y = 2
(d) 5x + y = 2

Answer

Answer: (a) x + 5y = 2

Question 8.
The points at which the tangents to the curve y = x² – 12x +18 are parallel to x-axis are
(a) (2, – 2), (- 2, -34)
(b) (2, 34), (- 2, 0)
(c) (0, 34), (-2, 0)
(d) (2, 2),(-2, 34).

Answer

Answer: (d) (2, 2),(-2, 34).

Question 9.
The tangent to the curve y = e^2x at the point (0, 1) meets x-axis at
(a) (0, 1)
(b) (-\(\frac{1}{2}\), 0)
(c) (2, 0)
(d) (0, 2)

Answer

Answer: (b) (-\(\frac{1}{2}\), 0)

Question 10.
The slope of tangent to the curve x = t² + 3t – 8, y = 2t² – 2t – 5 at the point (2, -1) is
(a) \(\frac{22}{7}\)
(b) \(\frac{6}{7}\)
(c) \(\frac{-6}{7}\)
(d) -6

Answer

Answer: (c) \(\frac{-6}{7}\)

Question 11.
The two curves; x³ – 3xy² + 2 = 0 and 3x²y – y³ – 2 = 0 intersect at an angle of
(a) \(\frac{π}{4}\)
(b) \(\frac{π}{3}\)
(c) \(\frac{π}{2}\)
(d) \(\frac{π}{6}\)

Answer

Answer: (a) \(\frac{π}{4}\)

Question 12.
The interval on which the function f (x) = 2x³ + 9x² + 12x – 1 is decreasing is
(a) [-1, ∞]
(b) [-2, -1]
(c) [-∞, -2]
(d) [-1, 1]

Answer

Answer: (b) [-2, -1]

Question 13.
Let the f: R → R be defined by f (x) = 2x + cos x, then f
(a) has a minimum at x = 3t
(b) has a maximum, at x = 0
(c) is a decreasing function
(d) is an increasing function

Answer

Answer: (d) is an increasing function

Question 14.
y = x (x – 3)² decreases for the values of x given by
(a) 1 < x < 3
(b) x < 0
(c) x > 0
(d) 0 < x <\(\frac{3}{2}\)

Answer

Answer: (a) 1 < x < 3

Question 15.
The function f(x) = 4 sin³ x – 6 sin²x + 12 sin x + 100 is strictly
(a) increasing in (π, \(\frac{3π}{2}\))
(b) decreasing in (\(\frac{π}{2}\), π)
(c) decreasing in [\(\frac{-π}{2}\),\(\frac{π}{2}\)]
(d) decreasing in [0, \(\frac{π}{2}\)]

Answer

Answer: (c) decreasing in [\(\frac{-π}{2}\),\(\frac{π}{2}\)]

Question 16.
Which of the following functions is decreasing on(0, \(\frac{π}{2}\))?
(a) sin 2x
(b) tan x
(c) cos x
(d) cos 3x

Answer

Answer: (c) cos x

Question 17.
The function f(x) = tan x – x
(a) always increases
(b) always decreases
(c) sometimes increases and sometimes decreases
(d) never increases

Answer

Answer: (a) always increases

Question 18.
If x is real, the minimum value of x² – 8x + 17 is
(a) -1
(b) 0
(c) 1
(d) 2

Answer

Answer: (d) 2

Question 19.
The smallest value of the polynomial x³ – 18x² + 96x in [0, 9] is
(a) 126
(b) 0
(c) 135
(d) 160

Answer

Answer: (b) 0

Question 20.
The function f(x) = 2x³ – 3x² – 12x + 4 has
(a) two points of local maximum
(b) two points of local minimum
(c) one maxima and one minima
(d) no maxima or minima

Answer

Answer: (c) one maxima and one minima

Question 21.
The maximum value of sin x . cos x is
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{2}\)
(c) √2
(d) 2√2

Answer

Answer: (b) \(\frac{1}{2}\)

Question 22.
At x = \(\frac{5π}{6}\), f (x) = 2 sin 3x + 3 cos 3x is
(a) maximum
(b) minimum
(c) zero
(d) neither maximum nor minimum

Answer

Answer: (d) neither maximum nor minimum

Question 23.
Maximum slope of the curve y = -x³ + 3x² + 9x – 27 is
(a) 0
(b) 12
(c) 16
(d) 32

Answer

Answer: (a) 0

Question 24.
f(x) = x^x has a stationary point at
(a) x = e
(b) x = \(\frac{1}{e}\)
(c) x = 1
(d) x = √e

Answer

Answer: (b) x = \(\frac{1}{e}\)

Question 25.
The maximum value of (\(\frac{1}{x}\))^x is
(a) e
(b) e²
(c) e^1/x
(d) (\(\frac{1}{e}\))^1/e

Answer

Answer: (d) (\(\frac{1}{e}\))^1/e

Question 26.
If the volume of a sphere is increasing at a constant rate, then the rate at which its radius is increasing is
(a) a constant
(b) proportional to the radius
(c) inversely proportional to the radius
(d) inversely proportional to the surface area

Answer

Answer: (d) inversely proportional to the surface area

Question 27.
A particle is moving along the curve x = at² + bt + c. If ac = b², then particle would be moving with uniform
(a) rotation
(b) velocity
(c) acceleration
(d) retardation

Answer

Answer: (c) acceleration

Question 28.
The distance Y metres covered by a body in t seconds, is given by s = 3t² – 8t + 5. The body will stop after
(a) 1 s
(b) \(\frac{3}{4}\) s
(c) \(\frac{4}{3}\) s
(d) 4 s

Answer

Answer: (c) \(\frac{4}{3}\) s

Question 29.
The position of a point in time Y is given by x = a + bt + ct², y = at + bt². Its acceleration at timet Y is
(a) b – c
(b) b + c
(c) 2b – 2c
(d) 2\(\sqrt{b^2+c^2}\)

Answer

Answer: (d) 2\(\sqrt{b^2+c^2}\)

Question 30.
The function f(x) = log (1 + x) – \(\frac{2x}{2+x}\) is increasing on
(a) (-1, ∞)
(b) (-∞, 0)
(b) (-∞, ∞)
(d) None of these

Answer

Answer: (a) (-1, ∞)

Question 31.
f(x) = (\(\frac{e^{2x}-1}{e^{2x}+1}\)) is
(a) an increasing function
(b) a decreasing function
(c) an even function
(d) None of these

Answer

Answer: (a) an increasing function

Question 32.
If f (x) = \(\frac{x}{sin x}\) and g (x) = \(\frac{x}{tan x}\), 0 < x ≤ 1, then in the interval
(a) both f (x) and g (x) are increasing functions
(b) both f (x) and g (x) are decreasing functions
(c) f(x) is an increasing function
(d) g (x) is an increasing function

Answer

Answer: (c) f(x) is an increasing function

Question 33.
The function f(x) = cot^-1 x + x increases in the interval
(a) (1, ∞)
(b) (-1, ∞)
(c) (0, ∞)
(d) (-∞, ∞)

Answer

Answer: (d) (-∞, ∞)

Question 34.
The function f(x) = \(\frac{x}{log x}\) increases on the interval
(a) (0, ∞)
(b) (0, e)
(c) (e, ∞)
(d) None of these

Answer

Answer: (c) (e, ∞)

Question 35.
The value of b for which the function f (x) = sin x – bx + c is decreasing for x ∈ R is given by
(a) b < 1
(b) b ≥ 1
(c) b > 1
(d) b ≤ 1

Answer

Answer: (c) b > 1

Question 36.
If f (x) = x³ – 6x² + 9x + 3 be a decreasing function, then x lies in
(a) (-∞, -1) ∩ (3, ∞)
(b) (1, 3)
(c) (3, ∞)
(d) None of these

Answer

Answer: (b) (1, 3)

Question 37.
The function f (x) = 1 – x³ – x⁵ is decreasing for
(a) 1 < x < 5
(b) x < 1
(c) x > 1
(d) all values of x

Answer

Answer: (d) all values of x

Question 38.
Function, f (x) = \(\frac{λ sin x+ 6 cos x}{2 sin x + 3 cos x}\) is monotonic increasing, if
(a) λ > 1
(b) λ < 1
(c) λ < 4
(d) λ > 4

Answer

Answer: (d) λ > 4

Question 39.
The length of the longest interval, in which the function 3 sin x – 4 sin³ x is increasing is
(a) \(\frac{π}{3}\)
(b) \(\frac{π}{2}\)
(c) \(\frac{3π}{2}\)
(d) π

Answer

Answer: (d) π

Question 40.
2x³ – 6x + 5 is an increasing function, if
(a) 0 < x < 1
(b) -1 < x < 1
(c) x < -1 or x > 1
(d) -1 < x < –\(\frac{1}{2}\)

Answer

Answer: (c) x < -1 or x > 1

Question 41.
The function f(x) = x + cos x is
(a) always increasing
(b) always decreasing
(c) increasing for certain range of x
(d) None of these

Answer

Answer: (a) always increasing

Question 42.
The function which is neither decreasing nor increasing in (\(\frac{π}{2}\), \(\frac{3π}{2}\)) is
(a) cosec x
(b) tan x
(c) x²
(d) |x – 1|

Answer

Answer: (b) tan x

Question 43.
The function /’defined by f(x) = 4⁴ – 2x + 1 is increasing for
(a) x < 1
(b) x > 0
(c) x < \(\frac{1}{2}\)
(d) x > \(\frac{1}{2}\)

Answer

Answer: (d) x > \(\frac{1}{2}\)

Question 44.
The interval in which the function y = x³ + 5x² – 1 is decreasing, is
(a) (0, \(\frac{1}{3}\))
(b) (0, 10)
(c) (\(\frac{-10}{3}\), 0)
(d) None of these

Answer

Answer: (c) (\(\frac{-10}{3}\), 0)

We hope the given NCERT MCQ Questions for Class 12 Maths Chapter 6 Application of Derivatives with Answers Pdf free download will help you. If you have any queries regarding Application of Derivatives CBSE Class 12 Maths MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 12 Maths MCQ:

MCQ Questions for Class 12 Maths Chapter 5 Continuity and Differentiability with Answers

Continuity and Differentiability Class 12 MCQ Online Test With Answers Questions

October 24, 2024

Check the below NCERT MCQ Questions for Class 12 Maths Chapter 5 Continuity and Differentiability with Answers Pdf free download. MCQ Questions for Class 12 Maths with Answers were prepared based on the latest exam pattern. We have provided Continuity and Differentiability Class 12 Maths MCQs Questions with Answers to help students understand the concept very well.

Class 12 Maths Chapter 5 MCQ With Answers

Maths Class 12 Chapter 5 MCQs On Continuity and Differentiability

Continuity And Differentiability Class 12 MCQ Question 1.
If f (x) = 2x and g (x) = \(\frac{x^2}{2}\) + 1, then’which of the following can be a discontinuous function
(a) f(x) + g(x)
(b) f(x) – g(x)
(c) f(x).g(x)
(d) \(\frac{g(x)}{f(x)}\)

Answer

Answer: (d) \(\frac{g(x)}{f(x)}\)

Continuity And Differentiability MCQ Question 2.
The function f(x) = \(\frac{4-x^2}{4x-x^3}\) is
(a) discontinuous at only one point at x = 0
(b) discontinuous at exactly two points
(c) discontinuous at exactly three points
(d) None of these

Answer

Answer: (a) discontinuous at only one point at x = 0

Differentiation MCQ Class 12 Question 3.
The set of points where the function f given by f (x) =| 2x – 1| sin x is differentiable is
(a) R
(b) R = {\(\frac{1}{2}\)}
(c) (0, ∞)
(d) None of these

Answer

Answer: (b) R = {\(\frac{1}{2}\)}

MCQ On Continuity And Differentiability Question 4.
The function f(x) = cot x is discontinuous on the set
(a) {x = nπ, n ∈ Z}
(b) {x = 2nπ, n ∈ Z}
(c) {x = (2n + 1) \(\frac{π}{2}\) n ∈ Z}
(d) {x – \(\frac{nπ}{2}\) n ∈ Z}

Answer

Answer: (a) {x = nπ, n ∈ Z}

Class 12 Maths Chapter 5 MCQ Question 5.
The function f(x) = e^|x| is
(a) continuous everywhere but not differentiable at x = 0
(b) continuous and differentiable everywhere
(c) not continuous at x = 0
(d) None of these

Answer

Answer: (a) continuous everywhere but not differentiable at x = 0

Continuity And Differentiability Class 12 MCQ Term 1 Question 6.
If f(x) = x² sin\(\frac{1}{x}\), where x ≠ 0, then the value of the function f(x) at x = 0, so that the function is continuous at x = 0 is
(a) 0
(b) -1
(c) 1
(d) None of these

Answer

Answer: (a) 0

Continuity And Differentiability Class 12 MCQ With Solutions Question 7.
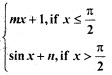If f(x) =is continuous at x = \(\frac{π}{2}\), then
(a) m = 1, n = 0
(b) m = \(\frac{nπ}{2}\) + 1
(c) n = \(\frac{mπ}{2}\)
(d) m = n = \(\frac{π}{2}\)

Answer

Answer: (c) n = \(\frac{mπ}{2}\)

MCQ Of Continuity And Differentiability Question 8.
If y = log(\(\frac{1-x^2}{1+x^2}\)), then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{4x^3}{1-x^4}\)
(b) \(\frac{-4x}{1-x^4}\)
(c) \(\frac{1}{4-x^4}\)
(d) \(\frac{-4x^3}{1-x^4}\)

Answer

Answer: (b) \(\frac{-4x}{1-x^4}\)

Class 12 Continuity And Differentiability MCQ Question 9.
Let f(x) = |sin x| Then
(a) f is everywhere differentiable
(b) f is everywhere continuous but not differentiable at x = nπ, n ∈ Z
(c) f is everywhere continuous but no differentiable at x = (2n + 1) \(\frac{π}{2}\) n ∈ Z
(d) None of these

Answer

Answer: (b) f is everywhere continuous but not differentiable at x = nπ, n ∈ Z

MCQ Of Differentiation Class 12 Question 10.
If y = \(\sqrt{sin x+y}\) then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{cosx}{2y-1}\)
(b) \(\frac{cosx}{1-2y}\)
(c) \(\frac{sinx}{1-xy}\)
(d) \(\frac{sinx}{2y-1}\)

Answer

Answer: (a) \(\frac{cosx}{2y-1}\)

MCQ Of Continuity And Differentiability Class 12 Question 11.
The derivative of cos^-1 (2x² – 1) w.r.t cos^-1 x is
(a) 2
(b) \(\frac{-1}{2\sqrt{1-x^2}}\)
(c) \(\frac{2}{x}\)
(d) 1 – x²

Answer

Answer: (a) 2

MCQ On Differentiation Class 12 Question 12.
If x = t², y = t³, then \(\frac{d^2y}{dx^2}\)
(a) \(\frac{3}{2}\)
(b) \(\frac{3}{4t}\)
(c) \(\frac{3}{2t}\)
(d) \(\frac{3}{4t}\)

Answer

Answer: (b) \(\frac{3}{4t}\)

MCQ On Differentiation Class 12 Pdf Question 13.
The value of c in Rolle’s theorem for the function f(x) = x³ – 3x in the interval [o, √3] is
(a) 1
(b) -1
(c) \(\frac{3}{2}\)
(d) \(\frac{1}{3}\)

Answer

Answer: (a) 1

MCQ Questions On Differentiation Class 12 Question 14.
For the function f(x) = x + \(\frac{1}{x}\), x ∈ [1, 3] the value of c for mean value theorem is
(a) 1
(b) √3
(c) 2
(d) None of these

Answer

Answer: (b) √3

MCQ On Continuity And Differentiability With Solutions Question 15.
Let f be defined on [-5, 5] as
f(x) = {\(_{-x, if x is irrational}^{x, if x is rational}\) Then f(x) is
(a) continuous at every x except x = 0
(b) discontinuous at everyx except x = 0
(c) continuous everywhere
(d) discontinuous everywhere

Answer

Answer: (b) discontinuous at everyx except x = 0

Class 12 Maths Ch 5 MCQ Question 16.
Let function f (x) =
(a) continuous at x = 1
(b) differentiable at x = 1
(c) continuous at x = -3
(d) All of these

Answer

Answer: (d) All of these

Class 12 Maths Continuity And Differentiability MCQ Question 17.
If f(x) = \(\frac{\sqrt{4+x}-2}{x}\) x ≠ 0 be continuous at x = 0, then f(o) =
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) 2
(d) \(\frac{3}{2}\)

Answer

Answer: (b) \(\frac{1}{4}\)

MCQ Of Chapter 5 Maths Class 12 Question 18.
let f(2) = 4 then f”(2) = 4 then \(_{x→2}^{lim}\) \(\frac{xf(2)-2f(x)}{x-2}\) is given by
(a) 2
(b) -2
(c) -4
(d) 3

Answer

Answer: (c) -4

Ch 5 Maths Class 12 MCQ Question 19.
It is given that f'(a) exists, then \(_{x→2}^{lim}\) [/latex] \(\frac{xf(a)-af(x)}{(x-a)}\) is equal to
(a) f(a) – af'(a)
(b) f'(a)
(c) -f’(a)
(d) f (a) + af'(a)

Answer

Answer: (a) f(a) – af'(a)

Class 12 Maths Chapter 5 MCQ Questions With Solutions Question 20.
If f(x) = \(\sqrt{25-x^2}\), then \(_{x→2}^{lim}\)\(\frac{f(x)-f(1)}{x-1}\) is equal to
(a) \(\frac{1}{24}\)
(b) \(\frac{1}{5}\)
(c) –\(\sqrt{24}\)
(d) \(\frac{1}{\sqrt{24}}\)

Answer

Answer: (d) \(\frac{1}{\sqrt{24}}\)

Question 21.
If y = ax² + b, then \(\frac{dy}{dx}\) at x = 2 is equal to ax
(a) 4a
(b) 3a
(c) 2a
(d) None of these

Answer

Answer: (a) 4a

Question 22.
If x sin (a + y) = sin y, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{sin^2(a+y)}{sin a}\)
(b) \(\frac{sin a}{sin^2(a+y)}\)
(c) \(\frac{sin(a+y)}{sin a}\)
(d) \(\frac{sin a}{sin(a+y)}\)

Answer

Answer: (a) \(\frac{sin^2(a+y)}{sin a}\)

Question 23.
If x \(\sqrt{1+y}+y\sqrt{1+x}\) = 0, then \(\frac{dy}{dx}\) =
(a) \(\frac{x+1}{x}\)
(b) \(\frac{1}{1+x}\)
(c) \(\frac{-1}{(1+x)^2}\)
(d) \(\frac{x}{1+x}\)

Answer

Answer: (c) \(\frac{-1}{(1+x)^2}\)

Question 24.
If y = x tan y, then \(\frac{dy}{dx}\) =
(a) \(\frac{tan x}{x-x^2-y^2}\)
(b) \(\frac{y}{x-x^2-y^2}\)
(c) \(\frac{tan y}{y-x}\)
(d) \(\frac{tan x}{x-y^2}\)

Answer

Answer: (b) \(\frac{y}{x-x^2-y^2}\)

Question 25.
If y = (1 + x) (1 + x²) (1 + x⁴) …….. (1 + x²ⁿ), then the value of \(\frac{dy}{dx}\) at x = 0 is
(a) 0
(b) -1
(c) 1
(d) None of these

Answer

Answer: (c) 1

Question 26.
If f(x) = \(\frac{5x}{(1-x)^{2/3}}\) + cos² (2x + 1), then f'(0) =
(a) 5 + 2 sin 2
(b) 5 + 2 cos 2
(c) 5 – 2 sin 2
(d) 5 – 2 cos 2

Answer

Answer: (c) 5 – 2 sin 2

Question 27.
If sec(\(\frac{x^2-2x}{x^2+1}\)) – y then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{y*2}{x^2}\)
(b) \(\frac{2y\sqrt{y^2-1}(x^2+x-1)}{(x^2+1)^2}\)
(c) \(\frac{(x^2+x-1)}{y\sqrt{y^2-1}}\)
(d) \(\frac{x^2-y^2}{x^2+y^2}\)

Answer

Answer: (b) \(\frac{2y\sqrt{y^2-1}(x^2+x-1)}{(x^2+1)^2}\)

Question 28.
If f(x) = \(\sqrt{1+cos^2(x^2)}\), then the value of f’ (\(\frac{√π}{2}\)) is
(a) \(\frac{√π}{6}\)
(b) –\(\frac{√π}{6}\)
(c) \(\frac{1}{√6}\)
(d) \(\frac{π}{√6}\)

Answer

Answer: (b) –\(\frac{√π}{6}\)

Question 29.
Differential coefficient of \(\sqrt{sec√x}\) is
(a) \(\frac{1}{4√x}\) = sec √x sin √x
(b) \(\frac{1}{4√x}\) = (sec√x)^3/2 sin√x
(c) \(\frac{1}{2}\) √x sec√x sin √x.
(d) \(\frac{1}{2}\)√x (sec√x)^3/2 sin√x

Answer

Answer: (b) \(\frac{1}{4√x}\) = (sec√x)^3/2 sin√x

Question 30.
Let f(x)={\(_{1-cos x, for x ≤ 0}^{sin x, for x > 0}\) and g (x) = e^x. Then the value of (g o f)’ (0) is
(a) 1
(b) -1
(c) 0
(d) None of these

Answer

Answer: (c) 0

Question 31.
If x^myⁿ = (x + y)^m+n, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{x+y}{xy}\)
(b) xy
(c) \(\frac{x}{y}\)
(d) \(\frac{y}{x}\)

Answer

Answer: (d) \(\frac{y}{x}\)

Question 32.
If \(\sqrt{(x+y)}\) + \(\sqrt{(y-x)}\) = a, then \(\frac{dy}{dx}\)

Answer

Answer: (a) \(\frac{\sqrt{(x+y)}-\sqrt{(y-x)}}{\sqrt{y-x}+\sqrt{x+y}}\)

Question 33.
If ax² + 2hxy + by² = 1, then \(\frac{dy}{dx}\)equals
(a) \(\frac{hx+by}{ax+by}\)
(b) \(\frac{ax+by}{hx+by}\)
(c) \(\frac{ax+hy}{hx+hy}\)
(d) \(\frac{-(ax+hy)}{hx+by}\)

Answer

Answer: (d) \(\frac{-(ax+hy)}{hx+by}\)

Question 34.
If sec (\(\frac{x-y}{x+y}\)) = a then \(\frac{dy}{dx}\) is
(a) –\(\frac{y}{x}\)
(b) \(\frac{x}{y}\)
(c) –\(\frac{x}{y}\)
(d) \(\frac{y}{x}\)

Answer

Answer: (d) \(\frac{y}{x}\)

Question 35.
If y = tan^-1(\(\frac{sinx+cosx}{cox-sinx}\)) then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{1}{2}\)
(b) \(\frac{π}{4}\)
(c) 0
(d) 1

Answer

Answer: (d) 1

Question 36.
If y = tan^-1(\(\frac{√x-x}{1+x^{3/2}}\)), then y'(1) is equal to
(a) 0
(b) (\(\frac{√x-x}{1+x^{3/2}}\))
(c) -1
(d) –\(\frac{1}{4}\)

Answer

Answer: (d) –\(\frac{1}{4}\)

Question 37.
The differential coefficient of tan^-1(\(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\)) is
(a) \(\sqrt{1-x^2}\)
(b) \(\frac{1}{\sqrt{1-x^2}}\)
(c) \(\frac{1}{2\sqrt{1-x^2}}\)
(d) x

Answer

Answer: (c) \(\frac{1}{2\sqrt{1-x^2}}\)

Question 38.
\(\frac{d}{dx}\)[tan^-1(\(\frac{a-x}{1+ax}\))] is equal to

Answer

Answer: (a) –\(\frac{1}{1+x^2}\)

Question 39.
\(\frac{d}{dx}\)(x\(\sqrt{a^2-x^2}+a^2 sin^{-1}(\frac{x}{a})\)) is equal to
(a) \(\sqrt{a^2-x^2}\)
(b) 2\(\sqrt{a^2-x^2}\)
(c) \(\frac{1}{\sqrt{a^2-x^2}}\)
(d) None of these

Answer

Answer: (b) 2\(\sqrt{a^2-x^2}\)

Question 40.
If f(x) = tan^-1(\(\sqrt{\frac{1+sinx}{1-sinx}}\)), 0 ≤ x ≤ \(\frac{π}{2}\), then f'(\(\frac{π}{6}\)) is
(a) –\(\frac{1}{4}\)
(b) –\(\frac{1}{2}\)
(c) \(\frac{1}{4}\)
(d) \(\frac{1}{2}\)

Answer

Answer: (d) \(\frac{1}{2}\)

Question 41.
If y = sin^-1(\(\frac{√x-1}{√x+1}\)) + sec^-1(\(\frac{√x+1}{√x-1}\)), x > 0, then \(\frac{dy}{dx}\) is equal to
(a) 1
(b) 0
(c) \(\frac{π}{2}\)
(d) None of these

Answer

Answer: (b) 0

Question 42.
If x = exp {tan^-1(\(\frac{y-x^2}{x^2}\))}, then \(\frac{dy}{dx}\) equals
(a) 2x [1 + tan (log x)] + x sec² (log x)
(b) x [1 + tan (log x)] + sec² (log x)
(c) 2x [1 + tan (logx)] + x² sec² (log x)
(d) 2x [1 + tan (log x)] + sec² (log x)

Answer

Answer: (a) 2x [1 + tan (log x)] + x sec² (log x)

Question 43.
If y = e^3x+n, then the value of \(\frac{dy}{dx}\)|_x=0 is
(a) 1
(b) 0
(c) -1
(d) 3e⁷

Answer

Answer: (d) 3e⁷

Question 44.
Let f (x) = e^x, g (x) = sin^-1 x and h (x) = f |g(x)|, then \(\frac{h'(x)}{h(x)}\) is equal to
(a) e^{sin^-1x}
(b) \(\frac{1}{\sqrt{1-x^2}}\)
(c) sin^-1x
(d) \(\frac{1}{(1-x^2)}\)

Answer

Answer: (b) \(\frac{1}{\sqrt{1-x^2}}\)

Question 45.
If y = ae^x+ be^-x + c Where a, b, c are parameters, they y’ is equal to
(a) ae^x – be^-x
(b) ae^x + be^-x
(c) -(ae^x + be^-x)
(d) ae^x – be^x

Answer

Answer: (a) ae^x – be^-x

Question 46.
If sin y + e^{-xcos y} = e, then \(\frac{dy}{dx}\) at (1, π) is equal to
(a) sin y
(b) -x cos y
(c) e
(d) sin y – x cos y

Answer

Answer: (c) e

Question 47.
Derivative of the function f (x) = log₅ (Iog,x), x > 7 is
(a) \(\frac{1}{x(log5)(log7)(log7-x)}\)
(b) \(\frac{1}{x(log5)(log7)}\)
(c) \(\frac{1}{x(logx)}\)
(d) None of these

Answer

Answer: (a) \(\frac{1}{x(log5)(log7)(log7-x)}\)

Question 48.
If y = log₁₀x + log y, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{y}{y-1}\)
(b) \(\frac{y}{x}\)
(c) \(\frac{log_{10}e}{x}\)(\(\frac{y}{y-1}\))
(d) None of these

Answer

Answer: (c) \(\frac{log_{10}e}{x}\)(\(\frac{y}{y-1}\))

Question 49.
If y = log [e^x(\(\frac{x-1}{x-2}\))\(^{1/2}\)], then \(\frac{dy}{dx}\) is equal to
(a) 7
(b) \(\frac{3}{x-2}\)
(c) \(\frac{3}{(x-1)}\)
(d) None of these

Answer

Answer: (d) None of these

Question 50.
If y = e^{\(\frac{1}{2}\) log(1+tan²x)}, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{1}{2}\) sec² x
(b) sec² x
(c) sec x tan x
(d) e^{\(\frac{1}{2}\) log(1+tan²x)}

Answer

Answer: (c) sec x tan x

Question 51.
If y = 2^x3^2x-1 then \(\frac{dy}{dx}\) is equal to dx
(a) (log 2) (log 3)
(b) (log lg)
(c) (log 18²) y²
(d) y (log 18)

Answer

Answer: (d) y (log 18)

Question 52.
If x^x = y^y, then \(\frac{dy}{dx}\) is equal to
(a) –\(\frac{y}{x}\)
(b) –\(\frac{x}{y}\)
(c) 1 + log (\(\frac{x}{y}\) )
(d) \(\frac{1+logx}{1+logy}\)

Answer

Answer: (d) \(\frac{1+logx}{1+logy}\)

Question 53.
If y = (tan x)^{sin x}, then \(\frac{dy}{dx}\) is equal to
(a) sec x + cos x
(b) sec x+ log tan x
(c) (tan x)^{sin x}
(d) None of these

Answer

Answer: (d) None of these

Question 54.
If x^y = e^x-y then \(\frac{dy}{dx}\) is
(a) \(\frac{1+x}{1+log x}\)
(b) \(\frac{1-log x}{1+log y}\)
(c) not defined
(d) \(\frac{-y}{(1+log x)^2}\)

Answer

Answer: (d) \(\frac{-y}{(1+log x)^2}\)

Question 55.
The derivative of y = (1 – x) (2 – x)…. (n – x) at x = 1 is equal to
(a) 0
(b) (-1) (n – 1)!
(c) n ! – 1
(d) (-1)^n-1 (n – 1)!

Answer

Answer: (b) (-1) (n – 1)!

Question 56.
If f(x) = cos x, cos 2 x, cos 4 x, cos 8 x, cos 16 x, then the value of'(\(\frac{π}{4}\)) is
(a) 1
(b) √2
(c) \(\frac{1}{√2}\)
(d) 0

Answer

Answer: (b) (-1) (n – 1)!

Question 57.
x^y. y^x = 16, then the value of \(\frac{dy}{dx}\) at (2, 2) is
(a) -1
(b) 0
(c) -1
(d) None of these

Answer

Answer: (a) -1

Question 58.
If y = e^{x+e^{x+e^x+….to∞}} find \(\frac{dy}{dx}\) =
(a) \(\frac{y^2}{1-y}\)
(b) \(\frac{y^2}{y-1}\)
(c) \(\frac{y}{y-1}\)
(d) \(\frac{-y}{y-1}\)

Answer

Answer: (c) \(\frac{y}{y-1}\)

Question 59.
If x = \(\frac{1-t^2}{1+t^2}\) and y = \(\frac{2t}{1+t^2}\) then \(\frac{dy}{dx}\) is equal to dx
(a) –\(\frac{y}{x}\)
(b) \(\frac{y}{x}\)
(c) –\(\frac{x}{y}\)
(d) \(\frac{x}{y}\)

Answer

Answer: (c) –\(\frac{x}{y}\)

Question 60.
If x = a cos⁴ θ, y = a sin⁴ θ. then \(\frac{dy}{dx}\) at θ = \(\frac{3π}{4}\) is
(a) -1
(b) 1
(c) -a²
(d) a²

Answer

Answer: (a) -1

Question 61.
If x = sin^-1 (3t – 4t³) and y = cos^-1 (\(\sqrt{1-t^2}\)) then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{1}{2}\)
(b) \(\frac{2}{5}\)
(c) \(\frac{3}{2}\)
(d) \(\frac{1}{3}\)

Answer

Answer: (d) \(\frac{1}{3}\)

Question 62.
Let y = t¹⁰ + 1 and x = t⁸ + 1, then \(\frac{d^2y}{dx^2}\), is equal to
(a) \(\frac{d^2y}{dx^2}\)
(b) 20t⁸
(c) \(\frac{5}{16t^6}\)
(d) None of these

Answer

Answer: (d) \(\frac{1}{3}\)

Question 63.
The derivative of e^x³ with respect to log x is
(a) e^e³
(b) 3x²2e^x³
(c) 3x³e^x³
(d) 3x²e^x³+ 3x²

Answer

Answer: (c) 3x³e^x³

Question 64.
If x = e^t sin t, y = e^tcos t, t is a parameter, then \(\frac{dy}{dx}\) at (1, 1) is equal to
(a) –\(\frac{1}{2}\)
(b) –\(\frac{1}{4}\)
(c) 0
(d) \(\frac{1}{2}\)

Answer

Answer: (c) 0

Question 65.
The derivative of sin^-1 (\(\frac{2x}{1+x^2}\)) with respect to cos^-1 (\(\frac{1-x^2}{1+x^2}\)) is
(a) -1
(b) 1
(c) 2
(d) 4

Answer

Answer: (b) 1

We hope the given NCERT MCQ Questions for Class 12 Maths Chapter 5 Continuity and Differentiability with Answers Pdf free download will help you. If you have any queries regarding Continuity and Differentiability CBSE Class 12 Maths MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 12 Maths MCQ:

MCQ Questions for Class 11 Maths Chapter 8 Binomial Theorem with Answers

Binomial Theorem Class 11 MCQ Online Test With Answers Questions

October 24, 2024

Check the below NCERT MCQ Questions for Class 11 Maths Chapter 8 Binomial Theorem with Answers Pdf free download. MCQ Questions for Class 11 Maths with Answers were prepared based on the latest exam pattern. We have provided Binomial Theorem Class 11 Maths MCQs Questions with Answers to help students understand the concept very well.

Online Binomial Expansion Calculator and find the expansion of the given binomial term.

Class 11 Maths Chapter 8 MCQ With Answers

Maths Class 11 Chapter 8 MCQs On Binomial Theorem

MCQ On Binomial Theorem Class 11 Question 1.
The coefficient of y in the expansion of (y² + c/y)⁵ is
(a) 10c
(b) 10c²
(c) 10c³
(d) None of these

Answer

Answer: (c) 10c³
Hint:
Given, binomial expression is (y² + c/y)⁵
Now, T_r+1 = ⁵C_r × (y²)^5-r × (c/y)^r
= ⁵C_r × y^10-3r × C^r
Now, 10 – 3r = 1
⇒ 3r = 9
⇒ r = 3
So, the coefficient of y = ⁵C₃ × c³ = 10c³

Binomial Theorem MCQ Question 2:
(1.1)¹⁰⁰⁰⁰ is _____ 1000
(a) greater than
(b) less than
(c) equal to
(d) None of these

Answer

Answer: (a) greater than
Hint:
Given, (1.1)¹⁰⁰⁰⁰ = (1 + 0.1)¹⁰⁰⁰⁰
¹⁰⁰⁰⁰C₀ + ¹⁰⁰⁰⁰C₁ × (0.1) + ¹⁰⁰⁰⁰C₂ ×(0.1)² + other +ve terms
= 1 + 10000×(0.1) + other +ve terms
= 1 + 1000 + other +ve terms
> 1000
So, (1.1)¹⁰⁰⁰⁰ is greater than 1000

The Chebyshev’s Theorem Calculator calculator shows steps for finding the smallest percentage of data values within ‘k’ standard deviations

MCQ On Binomial Theorem Question 3.
The fourth term in the expansion (x – 2y)¹² is
(a) -1670 x⁹ × y³
(b) -7160 x⁹ × y³
(c) -1760 x⁹ × y³
(d) -1607 x⁹ × y³

Answer

Answer: (c) -1760 x⁹ × y³
Hint:
4th term in (x – 2y)¹² = T₄
= T₃₊₁
= ¹²C₃ (x)^12-3 ×(-2y)³
= ¹²C₃ x⁹ ×(-8y³)
= {(12×11×10)/(3×2×1)} × x⁹ ×(-8y³)
= -(2×11×10×8) × x⁹ × y³
= -1760 x⁹ × y³

MCQs On Binomial Theorem Question 4.
If n is a positive integer, then (√3+1)²ⁿ⁺¹ + (√3−1)²ⁿ⁺¹ is
(a) an even positive integer
(b) a rational number
(c) an odd positive integer
(d) an irrational number

Answer

Answer: (d) an irrational number
Hint:
Since n is a positive integer, assume n = 1
(√3+1)³ + (√3−1)³
= {3√3 + 1 + 3√3(√3 + 1)} + {3√3 – 1 – 3√3(√3 – 1)}
= 3√3 + 1 + 9 + 3√3 + 3√3 – 1 – 9 + 3√3
= 12√3, which is an irrational number.

Binomial Theorem Class 11 MCQ Question 5.
If the third term in the binomial expansion of (1 + x)^m is (-1/8)x² then the rational value of m is
(a) 2
(b) 1/2
(c) 3
(d) 4

Answer

Answer: (b) 1/2
Hint:
(1 + x)^m = 1 + mx + {m(m – 1)/2}x² + ……..
Now, {m(m – 1)/2}x² = (-1/8)x²
⇒ m(m – 1)/2 = -1/8
⇒ 4m² – 4m = -1
⇒ 4m² – 4m + 1 = 0
⇒ (2m – 1)² = 0
⇒ 2m – 1 = 0
⇒ m = 1/2

Binomial Theorem MCQ Pdf Question 6.
The greatest coefficient in the expansion of (1 + x)¹⁰ is
(a) 10!/(5!)
(b) 10!/(5!)²
(c) 10!/(5! × 4!)²
(d) 10!/(5! × 4!)

Answer

Answer: (b) 10!/(5!)²
Hint:
The coefficient of x^r in the expansion of (1 + x)¹⁰ is ¹⁰C_r and ¹⁰C_r is maximum for
r = 10/ = 5
Hence, the greatest coefficient = ¹⁰C₅
= 10!/(5!)²

Binomial Theorem MCQs With Answers Pdf Question 7.
The coefficient of xⁿ in the expansion of (1 – 2x + 3x² – 4x³ + ……..)^-n is
(a) (2n)!/n!
(b) (2n)!/(n!)²
(c) (2n)!/{2×(n!)²}
(d) None of these

Answer

Answer: (b) (2n)!/(n!)²
Hint:
We have,
(1 – 2x + 3x² – 4x³ + ……..)^-n = {(1 + x)^-2}^-n
= (1 + x)²ⁿ
So, the coefficient of xⁿC₃ = ²ⁿC_n = (2n)!/(n!)²

Binomial Theorem MCQ With Solution Question 8.
The value of n in the expansion of (a + b)ⁿ if the first three terms of the expansion are 729, 7290 and 30375, respectively is
(a) 2
(b) 4
(c) 6
(d) 8

Answer

Answer: (c) 6
Hint:
Given that the first three terms of the expansion are 729, 7290 and 30375 respectively.
Now T₁ = ⁿC₀ × a^n-0 × b⁰ = 729
⇒ aⁿ = 729 ……………. 1
T₂ = ⁿC₁ × a^n-1 × b¹ = 7290
⇒ n
a^n-1 × b = 7290 ……. 2
T₃ = ⁿC₂ × a^n-2 × b² = 30375
⇒ {n(n-1)/2}
a^n-2 × b² = 30375 ……. 3
Now equation 2/equation 1
n
a^n-1 × b/aⁿ = 7290/729
⇒ n×b/n = 10 ……. 4
Now equation 3/equation 2
{n(n-1)/2}
a^n-2 × b² /n
a^n-1 × b = 30375/7290
⇒ b(n-1)/2a = 30375/7290
⇒ b(n-1)/a = (30375×2)/7290
⇒ bn/a – b/a = 60750/7290
⇒ 10 – b/a = 6075/729 (60750 and 7290 is divided by 10)
⇒ 10 – b/a = 25/3 (6075 and 729 is divided by 243)
⇒ 10 – 25/3 = b/a
⇒ (30-25)/3 = b/a
⇒ 5/3 = b/a
⇒ b/a = 5/3 …………….. 5
Put this value in equation 4, we get
n × 5/3 = 10
⇒ 5n = 30
⇒ n = 30/5
⇒ n = 6
So, the value of n is 6

Maths MCQs For Class 11 With Answers Pdf Question 9.
If α and β are the roots of the equation x² – x + 1 = 0 then the value of α²⁰⁰⁹ + β²⁰⁰⁹ is
(a) 0
(b) 1
(c) -1
(d) 10

Answer

Answer: (b) 1
Hint:
Given, x² – x + 1 = 0
Now, by Shridharacharya formula, we get
x = {1 ± √(1 – 4×1×1) }/2
⇒ x = {1 ± √(1 – 4) }/2
⇒ x = {1 ± √(-3)}/2
⇒ x = {1 ± √(3 × -1)}/2
⇒ x = {1 ± √3 × √-1}/2
⇒ x = {1 ± i√3}/2 {since i = √-1}
⇒ x = {1 + i√3}/2, {–1 – i√3}/2
⇒ x = -{-1 – i√3}/2, -{-1 + i√3}/2
⇒ x = w, w² {since w = {-1 + i√3}/2 and w² = {-1 – i√3}/2 }
Hence, α = -w, β = w²
Again we know that w³ = 1 and 1 + w + w² = 0
Now, α²⁰⁰⁹ + β²⁰⁰⁹ = α²⁰⁰⁷ × α² + β²⁰⁰⁷ × β²
= (-w)²⁰⁰⁷ × (-w)² + (-w²)²⁰⁰⁷ × (-w²)² {since 2007 is multiple of 3}
= -(w)²⁰⁰⁷ × (w)² – (w²)²⁰⁰⁷ × (w⁴)
= -1 × w² – 1 × w³ × w
= -1 × w² – 1 × 1 × w
= -w² – w
= 1 {since 1 + w + w² = 0}
So, α²⁰⁰⁹ + β²⁰⁰⁹ = 1

MCQ Questions For Class 11 Maths With Answers Pdf Question 10.
The general term of the expansion (a + b)ⁿ is
(a) T_r+1 = ⁿC_r × a^r × b^r
(b) T_r+1 = ⁿC_r × a^r × b^n-r
(c) T_r+1 = ⁿC_r × a^n-r × b^n-r
(d) T_r+1 = ⁿC_r × a^n-r × b^r

Answer

Answer: (d) T_r+1 = ⁿC_r × a^n-r × b^r
Hint:
The general term of the expansion (a + b)ⁿ is
T_r+1 = ⁿC_r × a^n-r × b^r

MCQ Questions For Class 11 Maths With Answers Question 11.
The coefficient of xⁿ in the expansion (1 + x + x² + …..)^-n is
(a) 1
(b) (-1)ⁿ
(c) n
(d) n+1

Answer

Answer: (b) (-1)ⁿ
Hint:
We know that
(1 + x + x² + …..)^-n = (1 – x)^-n
Now, the coefficient of x = (-1)ⁿ × ⁿC_n
= (-1)ⁿ

Question 12.
If n is a positive integer, then (√5+1)²ⁿ + 1 − (√5−1)²ⁿ + 1 is
(a) an odd positive integer
(b) not an integer
(c) none of these
(d) an even positive integer

Answer

Answer: (b) not an integer
Hint:
Since n is a positive integer, assume n = 1
(√5+1)² + 1 − (√5−1)² + 1
= (5 + 2√5 + 1) + 1 – (5 – 2√5 + 1) + 1 {since (x+y)² = x² + 2xy + y²}
= 4√5 + 2, which is not an integer

Question 13.
In the expansion of (a + b)ⁿ, if n is even then the middle term is
(a) (n/2 + 1)^th term
(b) (n/2)^th term
(c) n^th term
(d) (n/2 – 1)^th term

Answer

Answer: (a) (n/2 + 1)^th term
Hint:
In the expansion of (a + b)ⁿ,
if n is even then the middle term is (n/2 + 1)^th term

Question 14.
In the expansion of (a + b)ⁿ, if n is odd then the number of middle term is/are
(a) 0
(b) 1
(c) 2
(d) More than 2

Answer

Answer: (c) 2
Hint:
In the expansion of (a + b)ⁿ,
if n is odd then there are two middle terms which are
{(n + 1)/2}^th term and {(n+1)/2 + 1}^th term

Question 15.
if n is a positive ineger then 2³ⁿn – 7n – 1 is divisible by
(a) 7
(b) 9
(c) 49
(d) 81

Answer

Answer: (c) 49
Hint:
Given, 2³ⁿ – 7n – 1 = 2^3×n – 7n – 1
= 8ⁿ – 7n – 1
= (1 + 7)ⁿ – 7n – 1
= {ⁿC₀ + ⁿC₁ 7 + ⁿC₂ 7² + …….. + ⁿC_n 7ⁿ} – 7n – 1
= {1 + 7n + ⁿC₂ 7² + …….. + ⁿC_n 7ⁿ} – 7n – 1
= ⁿC₂ 7² + …….. + ⁿC_n 7ⁿ
= 49(ⁿC₂ + …….. + ⁿC_n 7^n-2)
which is divisible by 49
So, 2³ⁿ – 7n – 1 is divisible by 49

Question 16.
In the binomial expansion of (7^1/2 + 5^1/3)³⁷, the number of integers are
(a) 2
(b) 4
(c) 6
(d) 8

Answer

Answer: (c) 6
Hint:
Given, (7^1/2 + 5^1/3)³⁷
Now, general term of this binomial T_r+1 = ³⁷C_r × (7^1/2)^37-r × (5^1/3)^r
⇒ T_r+1 = ³⁷C_r × 7(^37-r)^/2 × (5)^r/3
This General term will be an integer if ³⁷C_r is an integer, 7(^37-r)^/2 is an integer and (5)^r/3 is an integer.
Now, ³⁷C_r will always be a positive integer.
Since ³⁷C_r denotes the number of ways of selecting r things out of 37 things, it can not be a fraction.
So, ³⁷C_r is an integer.
Again, 7(^37-r)^/2C_r will be an integer if (37 – r)/2 is an integer.
So, r = 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37 …………. 1
And if (5)^r/3 is an integer, then r/3 should be an integer.
So, r = 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36 ………….2
Now, take intersection of 1 and 2, we get
r = 3, 9, 15, 21, 27, 33
So, total possible value of r is 6
Hence, there are 6 integers are in the binomial expansion of (7^1/2 + 5^1/3)³⁷

Question 17.
The number of ordered triplets of positive integers which are solution of the equation x + y + z = 100 is
(a) 4815
(b) 4851
(c) 8451
(d) 8415

Answer

Answer: (b) 4851
Hint:
Given, x + y + z = 100;
where x ≥ 1, y ≥ 1, z ≥ 1
Let u = x – 1, v = y – 1, w = z – 1
where u ≥ 0, v ≥ 0, w ≥ 0
Now, equation becomes
u + v + w = 97
So, the total number of solution = ^97+3-1C_3-1
= ⁹⁹C₂
= (99 × 98)/2
= 4851

Question 18.
The greatest coefficient in the expansion of (1 + x)¹⁰ is
(a) 10!/(5!)
(b) 10!/(5!)²
(c) 10!/(5! × 4!)²
(d) 10!/(5! × 4!)

Answer

Answer: (b) 10!/(5!)²
Hint:
The coefficient of x^r in the expansion of (1 + x)¹⁰ is ¹⁰C_r and ¹⁰C_r is maximum for
r = 10/2 = 5
Hence, the greatest coefficient = ¹⁰C₅
= 10!/(5!)²

Question 19.
If the third term in the binomial expansion of (1 + x)^m is (-1/8)x² then the rational value of m is
(a) 2
(b) 1/2
(c) 3
(d) 4

Answer

Question 20.
In the binomial expansion of (a + b)ⁿ, the coefficient of fourth and thirteenth terms are equal to each other, then the value of n is
(a) 10
(b) 15
(c) 20
(d) 25

Answer

Answer: (b) 15
Hint:
Given, in the binomial expansion of (a + b)ⁿ, the coefficient of fourth and thirteenth terms are equal to each other
⇒ ⁿC₃ = ⁿC₁₂
This is possible when n = 15
Because ¹⁵C₁₃ = ¹⁵C₁₂

We hope the given NCERT MCQ Questions for Class 11 Maths Chapter 8 Binomial Theorem with Answers Pdf free download will help you. If you have any queries regarding CBSE Class 11 Maths Binomial Theorem MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 11 Maths MCQ:

MCQ Questions for Class 12 Maths Chapter 4 Determinants with Answers

Determinants Class 12 MCQ Online Test With Answers Questions

October 24, 2024

Check the below NCERT MCQ Questions for Class 12 Maths Chapter 4 Determinants with Answers Pdf free download. MCQ Questions for Class 12 Maths with Answers were prepared based on the latest exam pattern. We have provided Determinants Class 12 Maths MCQs Questions with Answers to help students understand the concept very well.

Class 12 Maths Chapter 4 MCQ With Answers

Maths Class 12 Chapter 4 MCQs On Determinants

Determinants Class 12 MCQ Questions Question 1.
\(\left[\begin{array}{ccc}
1 & x & x^{2} \\
1 & y & y^{2} \\
1 & z & z^{2}
\end{array}\right]\)
(a) (x – y) (y + z)(z + x)
(b) (x + y) (y – z)(z – x)
(c) (x – y) (y – z)(z + x)
(d) (x – y) (y – z) (z – x)

Answer

Answer: (d) (x – y) (y – z) (z – x)

Determinants Class 12 MCQ Question 2.
The value of the determinant
\(\left[\begin{array}{ccc}
3 & 1 & 7 \\
5 & 0 & 2 \\
2 & 5 & 3
\end{array}\right]\)
(a) 124
(b) 125
(c) 134
(d) 144

Answer

Answer: (c) 134

MCQ Of Determinants Class 12 Question 3.
If a, b, c are in A.P. then the determinant
\(\left[\begin{array}{ccc}
x+2 & x+3 & x+2a \\
x+3 & x+4 & x+2b \\
x+4 & x+5 & x+2c
\end{array}\right]\)
(a) 1
(b) x
(c) 0
(d) 2x

Answer

Answer: (c) 0

Class 12 Maths Chapter 4 MCQ Question 4.
If w is a non-real root of the equation x² – 1 = 0. then
\(\left[\begin{array}{ccc}
1 & ω & ω^{2} \\
ω & ω^{2} & 1 \\
ω^{2} & 1 & ω
\end{array}\right]\) =
(a) 0
(b) 1
(c) ω
(d) ω²

Answer

Answer: (a) 0

Determinants MCQ Class 12 Question 5.
If Δ = \(\left[\begin{array}{cc}
10 & 2 \\
30 & 6
\end{array}\right]\) then A =
(a) 0
(b) 10
(c) 12
(d) 60

Answer

Answer: (a) 0

MCQ On Determinants Class 12 Question 6.
If 7 and 2 are two roots of the equation \(\left[\begin{array}{ccc}
x & 3 & 7 \\
2 & x & 2 \\
7 & 6 & x
\end{array}\right]\) then the third root is
(a) -9
(b) 14
(c) \(\frac{1}{2}\)
(d) None of these

Answer

Answer: (a) -9

Determinants MCQs Class 12 Question 7.
If \(\left[\begin{array}{cc}
x & 2 \\
18 & x
\end{array}\right]\) = \(\left[\begin{array}{cc}
6 & 2 \\
18 & 6
\end{array}\right]\) x is equal to
(a) 6
(b) ±6
(c) -1
(d) -6

Answer

Answer: (b) ±6

Determinants MCQs With Answers Class 12 Question 8.
\(\left[\begin{array}{ccc}
1 & a & a^{2}-bc \\
1 & b & b^{2}-ca \\
1 & c & c^{2}-ab
\end{array}\right]\) is equal to
(a) abc
(b) ab + bc + ca
(c) 0
(d) (a – b)(b – c)(c – a)

Answer

Answer: (c) 0

Determinant MCQ Class 12 Question 9.
A = \(\left[\begin{array}{ll}
\alpha & q \\
q & \alpha
\end{array}\right]\) |A³| = 125 then α =
(a) ±3
(b) ±2
(c) ±5
(d) 0

Answer

Answer: (a) ±3

Class 12 Determinants MCQ Question 10.
If a ≠ 0 and \(\left[\begin{array}{ccc}
1+a & 1 & 1 \\
1 & 1+a & 1 \\
1 & 1 & 1+a
\end{array}\right]\) = 0 then a =
(a) a = -3
(b) a = 0
(c) a = 1
(d) a = 3

Answer

Answer: (a) a = -3

MCQ Questions On Determinants Class 12 Question 11.
If x > 0 and x ≠ 1. y > 0. and y ≠ 1, z > 0 and z ≠ 1 then
\(\left[\begin{array}{ccc}
1 & log_{x}y & log_{x}z \\
log_{y}x & 1 & log_{y}z \\
log_{z}x & log_{z}y & 1
\end{array}\right]\) is equal to
(a) 1
(b) -1
(c) 0
(d) None of these

Answer

Answer: (c) 0

Determinants MCQs Class 12 Question 12.
\(\left[\begin{array}{ccc}
y+z & z & x \\
y & z+x & y \\
z & z & x+y
\end{array}\right]\) is equal to
(a) 6xyz
(b) xyz
(c) 4xyz
(d) xy + yz + zx

Answer

Answer: (c) 4xyz

MCQ Of Chapter 4 Maths Class 12 Question 13.
If \(\left[\begin{array}{cc}
2 & 4 \\
5 & 1
\end{array}\right]\) = \(\left[\begin{array}{cc}
2x & 4 \\
6 & x
\end{array}\right]\) then the value of x is
(a) ±2
(b) ±\(\frac{1}{3}\)
(c) ±√3
(d) ± (0.5)

Answer

Answer: (c) ±√3

MCQs On Determinants Class 12 Question 14.
If \(\left[\begin{array}{cc}
2x & 5 \\
8 & x
\end{array}\right]\) = \(\left[\begin{array}{cc}
6 & -2 \\
7 & 3
\end{array}\right]\) then the value of x is
(a) 3
(b) ±3
(c) ±6
(d) 6

Answer

Answer: (c) ±6

MCQ Determinants Class 12 Question 15.
The value of determinant \(\left[\begin{array}{ccc}
a-b & b+c & a \\
b-c & c+a & b \\
c-a & a+b & c
\end{array}\right]\)
(a) a³ + b³ + c ³
(b) 3bc
(c) a³ + b³ + c³ – 3abc
(d) None of these

Answer

Answer: (c) a³ + b³ + c³ – 3abc

MCQ On Determinants Class 12 With Solutions Question 16.
The area of a triangle with vertices (-3, 0) (3, 0) and (0, k) is 9 sq. units. The value of k will be
(a) 9
(b) 3
(c) -9
(d) 6

Answer

Answer: (b) 3

Class 12 Maths Ch 4 MCQ Question 17.
The determinant \(\left[\begin{array}{ccc}
b^{2}-ab & b-c & bc-ac \\
ab-a^{2} & a-b & b^{2}-ab \\
bc-ac & c-a & ab-a^{2}
\end{array}\right]\) equals
(a) abc(b – c)(c -a)(a – b)
(b) (b – c)(c – a)(a – b)
(c) (a + b + c)(b – c)(c – a)(a – b)
(d) None of these

Answer

Answer: (d) None of these

Ch 4 Maths Class 12 MCQ Question 18.
The number of distinct real roots of \(\left[\begin{array}{ccc}
sin x & cos x & cos x \\
cos x & sin x & cos x \\
cos x & cos x & sin x
\end{array}\right]\) = 0 in the interval –\(\frac{π}{4}\) ≤ x ≤ \(\frac{π}{4}\) is
(a) 0
(b) 2
(c) 1
(d) 3

Answer

Answer: (c) 1

Chapter 4 Maths Class 12 MCQ Question 19.
If A, B and C are angles of a triangle, then the determinant
\(\left[\begin{array}{ccc}
-1 & cos C & cos B \\
cos C & -1 & cos A \\
cos B & cos A & -1
\end{array}\right]\)
(a) 0
(b) -1
(c) 1
(d) None of these

Answer

Answer: (a) 0

MCQ On Matrices And Determinants Class 12 Question 20.
Let f(t) = \(\left[\begin{array}{ccc}
cot t & t & 1 \\
2 sin t & t & 2t \\
sin t & t & t
\end{array}\right]\) then \(_{t→0}^{lim}\) \(\frac{f(t)}{t^2}\) is equal to
(a) 0
(b) -1
(c) 2
(d) 3

Answer

Answer: (a) 0

Question 21.
The maximum value of \(\left[\begin{array}{ccc}
1 & 1 & 1 \\
1 & 1+sin θ & 1 \\
1+cos θ & 1 & 1
\end{array}\right]\) is (θ is real number)
(a) \(\frac{1}{2}\)
(b) \(\frac{√3}{2}\)
(c) \(\frac{2√3}{4}\)
(d) √2

Answer

Answer: (a) \(\frac{1}{2}\)

Question 22.
If f(x) = \(\left[\begin{array}{ccc}
0 & x-a & x-b \\
x+a & 0 & x-c \\
x+b & x+c & 0
\end{array}\right]\) then
(a) f(a) = 0
(b) f(b) = 0
(c) f(0) = 0
(d) f(1) = 0

Answer

Answer: (c) f(0) = 0

Question 23.
If A = \(\left[\begin{array}{ccc}
2 & \lambda & -3 \\
0 & 2 & 5 \\
1 & 1 & 3
\end{array}\right]\) then A^-1 exists if
(a) λ = 2
(b) λ ≠ 2
(c) λ ≠ -2
(d) None of these

Answer

Answer: (d) None of these

Question 24.
If A and B are invertible matrices, then which of the following is not correct?
(a) adj A = |A|.A^-1
(b) det (a)^-1 = [det (a)]^-1
(c) (AB)^-1 = B^-1A^-1
(d) (A + B)^-1 = B^-1 + A^-1

Answer

Answer: (d) (A + B)^-1 = B^-1 + A^-1

Question 25.
If x, y, z are all different from zero and
\(\left[\begin{array}{ccc}
1+x & 1 & 1 \\
1 & 1+y & 1 \\
1 & 1 & 1+z
\end{array}\right]\) = 0, then value of x^-1 + y^-1 + z^-1 is
(a) xyz
(b) x^-1y^-1z^-1
(c) -x – y – z
(d) -1

Answer

Answer: (d) -1

Question 26.
The value of the determinant \(\left[\begin{array}{ccc}
x & x+y & x+2y \\
x+2y & x & x+y \\
x+y & x+2y & x
\end{array}\right]\) is
(a) 9x² (x + y)
(b) 9y² (x + y)
(c) 3y² (x + y)
(d) 7x² (x + y)

Answer

Answer: (b) 9y² (x + y)

Question 27.
There are two values of a which makes determinant
Δ = \(\left[\begin{array}{ccc}
1 & -2 & 5 \\
2 & a & -1 \\
0 & 4 & 2a
\end{array}\right]\) = 86, then sum of these number is
(a) 4
(b) 5
(c) -4
(d) 9

Answer

Answer: (c) -4

Question 28.
Evaluate the determinant Δ = \(\left|\begin{array}{cc}
log_{3}512 & log_{4}3 \\
log_{3}8 & log_{4}9
\end{array}\right|\)
(a) \(\frac{15}{2}\)
(b) 12
(c) \(\frac{14}{3}\)
(d) 6

Answer

Answer: (a) \(\frac{15}{2}\)

Question 29.
\(\left|\begin{array}{cc}
x & -7 \\
x & 5 x+1
\end{array}\right|\)
(a) 3x² + 4
(b) x(5x + 8)
(c) 3x + 4x²
(d) x(3x + 4)

Answer

Answer: (b) x(5x + 8)

Question 30.
\( \left|\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \alpha
\end{array}\right|\)
(a) 0
(b) 1
(c) 2
(d) 3

Answer

Answer: (b) 1

Question 31.
\( \left|\begin{array}{ll}
\cos 15^{\circ} & \sin 15^{\circ} \\
\sin 75^{\circ} & \cos 75^{\circ}
\end{array}\right|\)
(a) 0
(b) 5
(c) 3
(d) 7

Answer

Answer: (a) 0

Question 32.
\(\left|\begin{array}{cc}
a+i b & c+i d \\
-c+i d & a-i b
\end{array}\right|\)
(a) (a + b)²
(b) (a + b + c + d)²
(c) (a² + b² – c² – d²)
(d) a² + b² + c² + a²

Answer

Answer: (d) a² + b² + c² + a²

Question 33.
If \(\left|\begin{array}{lll}
b+c & c+a & a+b \\
c+a & a+b & b+c \\
a+b & b+c & c+a
\end{array}\right|\) = \(k\left|\begin{array}{lll}
a & b & c \\
b & c & a \\
c & a & b
\end{array}\right|\) then k =
(a) 0
(b) 1
(c) 2
(d) 3

Answer

Answer: (c) 2

Question 34.
If \(\left|\begin{array}{ccc}
a-b-c & 2 a & 2 a \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\) = k (a + b + c)³ then k is
(a) 0
(b) 1
(c) 2
(d) 3

Answer

Answer: (b) 1

Question 35.
\(\left|\begin{array}{lll}
a+1 & a+2 & a+4 \\
a+3 & a+5 & a+8 \\
a+7 & a+10 & a+14
\end{array}\right|\) =
(a) 2
(b) -2
(c) 4
(d) -4

Answer

Answer: (b) -2

Question 36.
If abc ≠ 0 and \(\left|\begin{array}{ccc}
1+a & 1 & 1 \\
1 & 1+b & 1 \\
1 & 1 & 1+c
\end{array}\right|\) = 0 then \(\frac{1}{a}\) + \(\frac{1}{b}\) + \(\frac{1}{c}\) =
(a) 1
(b) 2
(c) -1
(d) -3

Answer

Answer: (c) -1

Question 37.
\(\left|\begin{array}{ccc}
2 x y & x^{2} & y^{2} \\
x^{2} & y^{2} & 2 x y \\
y^{2} & 2 x y & x^{2}
\end{array}\right|\) =
(a) (x³ + y³)²
(b) (x² + y²)³
(c) -(x² + y²)³
(d) -(x³ + y³)²

Answer

Answer: (d) -(x³ + y³)²

Question 38.
\(\left|\begin{array}{ccc}
b^{2} c^{2} & b c & b+c \\
c^{2} a^{2} & c a & c+a \\
a^{2} b^{2} & a b & a+b
\end{array}\right|\) =
(a) a⁷ + b⁷ + c⁷
(b) (a + b + c)⁷
(c) (a² + b² + c²) (a⁵ + b⁵ + c⁵)
(d) 0

Answer

Answer: (d) 0

Question 39.
If a, b, c are cube roots of unity, then
\(\left|\begin{array}{lll}
e^{a} & e^{2 a} & e^{3 a}-1 \\
e^{b} & e^{2 b} & e^{3 b}-1 \\
e^{c} & e^{2 c} & e^{3 c}-1
\end{array}\right|\) =
(a) 0
(b) e
(c) e²
(d) e³

Answer

Answer: (a) 0

Question 40.
The value of
\(\left|\begin{array}{ccc}
\cos (\alpha+\beta) & -\sin (\alpha+\beta) & \cos 2 \beta \\
\sin \alpha & \cos \alpha & \sin \beta \\
-\cos \alpha & \sin \alpha & \cos \beta
\end{array}\right|\)
is independent of
(a) α
(b) β
(c) α.β
(d) None of these

Answer

Answer: (a) α

Question 41.
If x is a complex root of the equation
\(\left|\begin{array}{lll}
1 & x & x \\
x & 1 & x \\
x & x & 1
\end{array}\right|\) + \(\left|\begin{array}{ccc}
1-x & 1 & 1 \\
1 & 1-x & 1 \\
1 & 1 & 1-x
\end{array}\right|\) = 0
then x²⁰⁰⁷ + x^-2007 =
(a) 1
(b) -1
(c) -2
(d) 2

Answer

Answer: (c) -2

Question 42.
\(\left|\begin{array}{lll}
b-c & c-a & a-b \\
c-a & a-b & b-c \\
a-b & b-c & c-a
\end{array}\right|\) =
(a) 0
(b) 1
(c) 2
(d) 3

Answer

Answer: (a) 0

Question 43.
Let Δ = \(\left|\begin{array}{ccc}
x & y & z \\
x^{2} & y^{2} & z^{2} \\
x^{3} & y^{3} & z^{3}
\end{array}\right|\) then the value of Δ is
(a) (x – y) (y- z)(z – x)
(b) xyz
(c) x² + y² + z²)²
(d) xyz (x – y)(y – z) (z – x)

Answer

Answer: (d) xyz (x – y)(y – z) (z – x)

Question 44.
The value of the determinant \(\left|\begin{array}{ccc}
\alpha & \beta & \gamma \\
\alpha^{2} & \beta^{2} & \gamma^{2} \\
\beta+\gamma & \gamma+\alpha & \alpha+\beta
\end{array}\right|\)
(a) (α + β)(β + γ)(γ + α)
(b) (α – β)(β – γ) (γ – α) (α + β + γ)
(c) (α + β + γ)² (α – β – γ)²
(d) αβγ (α + β + γ)

Answer

Answer: (b) (α – β)(β – γ) (γ – α) (α + β + γ)

We hope the given NCERT MCQ Questions for Class 12 Maths Chapter 4 Determinants with Answers Pdf free download will help you. If you have any queries regarding Determinants CBSE Class 12 Maths MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 12 Maths MCQ:

MCQ Questions for Class 11 Sociology Chapter 2 Social Change and Social Order in Rural and Urban Society with Answers

Social Change and Social Order in Rural and Urban Society Class 11 MCQ Online Test With Answers QuestionsSocial Structure, Stratification and Social Processes in Society Class 11 MCQ Online Test With Answers QuestionsSocial Structure, Stratification and Social Processes in Society Class 11 MCQ Online Test With Answers QuestionsSocial Structure, Stratification and Social Processes in Society Class 11 MCQ Online Test With Answers Questions Class 11 MCQ Online Test With Answers Questions Class 11 MCQ Online Test With Answers Questions

October 24, 2024

Check the below Online Education NCERT MCQ Questions for Class 11 Sociology Chapter 2 Social Change and Social Order in Rural and Urban Society with Answers Pdf free download. MCQ Questions for Class 11 Sociology with Answers were prepared based on the latest exam pattern. We have provided Social Change and Social Order in Rural and Urban Society Class 11 Sociology MCQs Questions with Answers to help students understand the concept very well.

Class 11 Sociology Chapter 2 Social Change and Social Order in Rural and Urban Society MCQ With Answers

Sociology Class 11 Chapter 2 MCQs On Social Change and Social Order in Rural and Urban Society

Question 1.
The National Rural Employment Guarantee Act was introduced in the Year _____
(a) 2002
(b) 2003
(c) 2004
(d) 2005

Answer

Answer: (d) 2005

Question 2.
Youth rebellion is an example of _____ Culture.
(a) adaptive
(b) societal
(c) counter
(d) revolutionary

Answer

Answer: (c) counter

Question 3.
The natural disaster that hit Indonesia, Sri Lanka, the Andaman Islands, and parts of Tamil Nadu in December 2004 was ______
(a) reversible
(b) irreversible
(c) counter culture
(d) revolution

Answer

Answer: (b) irreversible

Question 4.
Which term refers to an explicitly codified norm or rule?
(a) Tariffs
(b) Law
(c) Authority
(d) Evolution

Answer

Answer: (b) Law

Question 5.
The new spinning and weaving machines destroyed the ______ industry of the Indian subcontinent with technological innovations in the textile industry in Britain.
(a) transport
(b) handloom
(c) silk
(d) cotton

Answer

Answer: (b) handloom

Question 6.
Ruling families of Mewar, in Rajasthan India, is an example of ______ authority.
(a) Bureaucratic
(b) Charismatic
(c) Traditional
(d) None of the above

Answer

Answer: (c) Traditional

Question 7.
Which thinker proposed a theory where living organisms evolve-or change slowly over several centuries or even millennia, by adapting themselves to natural circumstances.
(a) Spencer
(b) Darwin
(c) Einstein
(d) Comte

Answer

Answer: (b) Darwin

Question 8.
_____ refers to landowning intermediate castes that are numerically large in number and thus enjoy political dominance in a given region.
(a) Low Castes
(b) Untouchables
(c) Dominant Castes
(d) Gentrification

Answer

Answer: (c) Dominant Castes

Question 9.
The French revolution(1789-93) and the Soviet or Russian revolution of 1917 are examples of ______
(a) Evolution
(b) Political evolution
(c) Social evolution
(d) Revolution

Answer

Answer: (d) Revolution

Question 10.
Which power considered to be justified or proper?
(a) Tariffs
(b) Charismatic
(c) Authority
(d) Evolution

Answer

Answer: (c) Authority

Question 11.
Urban communities that are sealed off by fences or walls with controlled entry and exit are called ______ communities.
(a) reversible
(b) counter
(c) gated
(d) revolution

Answer

Answer: (c) gated

Question 12.
Social Darwinism, is a theory that emphasised the importance of _____ change.
(a) revolutionary
(b) adaptive
(c) evolutionary
(d) societal

Answer

Answer: (b) adaptive

We hope the given NCERT MCQ Questions for Class 11 Sociology Chapter 2 Social Change and Social Order in Rural and Urban Society with Answers Pdf free download will help you. If you have any queries regarding CBSE Class 11 Sociology Social Change and Social Order in Rural and Urban Society MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 11 Sociology with Answers MCQ:

MCQ Questions for Class 12 Maths Chapter 3 Matrices with Answers

Matrices Class 12 MCQ Online Test With Answers Questions

October 24, 2024

Check the below NCERT MCQ Questions for Class 12 Maths Chapter 3 Matrices with Answers Pdf free download. MCQ Questions for Class 12 Maths with Answers were prepared based on the latest exam pattern. We have provided Matrices Class 12 Maths MCQs Questions with Answers to help students understand the concept very well.

Class 12 Maths Chapter 3 MCQ With Answers

Maths Class 12 Chapter 3 MCQs On Matrices

Matrices Class 12 MCQ Questions Chapter 3 Question 1.
\(\left|\begin{array}{lll}
3 & 4 & 5 \\
0 & 2 & 3 \\
0 & 0 & 7
\end{array}\right|\) = A then |A| = ?
(a) 40
(b) 50
(c) 42
(d) 15

Answer

Answer: (c) 42

Matrices Class 12 MCQ Chapter 3 Question 2.
The inverse of A = \(\left|\begin{array}{ll}
2 & 3 \\
5 & k
\end{array}\right|\) will not be obtained if A has the value
(a) 2
(b) \(\frac{3}{2}\)
(c) \(\frac{5}{2}\)
(d) \(\frac{15}{2}\)

Answer

Answer: (d) \(\frac{15}{2}\)

Matrices MCQ Questions Class 12 Question 3.
For any unit matrix I
(a) I² = I
(b) |I| = 0
(c) |I| = 2
(d) |I| = 5

Answer

Answer: (a) I² = I

Matrix Class 12 MCQ Chapter 3 Question 4.
A matrix A = [a_ij]_m×n is said to be symmetric if
(a) a_ij = 0
(b) a_ij = a_ji
(c) a_ij = a_ij
(d) a_ij = 1

Answer

Answer: (b) a_ij = a_ji

Class 12 Maths Chapter 3 MCQ Question 5.
If A = \(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right|\) then A² is
(a) 27 A
(b) 2 A
(c) 3 A
(d) 1

Answer

Answer: (c) 3 A

MCQ Of Matrices Class 12 Question 6.
A matrix A = [a_ij]_m×n is said to be skew symmetric if
(a) a_ij = 0
(b) a_ij = a_ji
(c) a_ij = -a_ji
(d) a_ij = 1

Answer

Answer: (b) a_ij = a_ji

Matrices MCQ Class 12 Chapter 3 Question 7.
A = [a_ij]_m×n is a square matrix if
(a) m = n
(b) m < n
(c) m > n
(d) None of these

Answer

Answer: (a) m = n

Matrix MCQ Class 12 Chapter 3 Question 8.
If A and B are square matrices then (AB)’ =
(a) B’A’
(b) A’B’
(c) AB’
(d) A’B’

Answer

Answer: (a) B’A’

MCQ On Matrices Class 12 Chapter 3 Question 9.
If A = \(\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\) and adj A is
(a) \(\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\)

Answer

Answer: (c) \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\)

Class 12 Matrices MCQ Chapter 3 Question 10.
If \(\left[\begin{array}{cc}
1-x & 2 \\
18 & 6
\end{array}\right]\) = \(\left[\begin{array}{cc}
6 & 2 \\
18 & 6
\end{array}\right]\) then x =
(a) ±6
(b) 6
(c) -5
(d) 7

Answer

Answer: (c) -5

Matrix MCQ Questions Chapter 3 Question 11.
If \(\left|\begin{array}{ll}
x & 8 \\
3 & 3
\end{array}\right|\) = 0, the value of x is
(a) 3
(b) 8
(c) 24
(d) 0

Answer

Answer: (b) 8

MCQ Of Matrix Class 12 Chapter 3 Question 12.
If A = \(\left[\begin{array}{cc}
i & 0 \\
0 & i
\end{array}\right]\) then A² =
(a) \(\left[\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
-1 & 0 \\
0 & 1
\end{array}\right]\)

Answer

Answer: (b) \(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\)

Matrices MCQ With Answers Pdf Chapter 3 Question 13.
Let A be a non-singular matrix of the order 2 × 2 then |A^-1|=
(a) |A|
(b) \(\frac{1}{|A|}\)
(c) 0
(d) 1

Answer

Answer: (b) \(\frac{1}{|A|}\)

MCQ On Matrices Class 12 Pdf Download Question 14.
If A = \(\left[\begin{array}{cc}
1 & 2 \\
2 & 1
\end{array}\right]\) then adj A =
(a) \(\left[\begin{array}{cc}
1 & -2 \\
-2 & 1
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
2 & 1 \\
1 & 1
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
1 & -2 \\
-2 & -1
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
-1 & 2 \\
-2 & -1
\end{array}\right]\)

Answer

Answer: (a) \(\left[\begin{array}{cc}
1 & -2 \\
-2 & 1
\end{array}\right]\)

Class 12 Matrix MCQ Questions Chapter 3 Question 15.
If A = \(\left[\begin{array}{cc}
1 & 1 \\
0 & 1
\end{array}\right]\) B = \(\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]\) then AB =
(a) \(\left[\begin{array}{cc}
0 & 0 \\
0 & 0
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
1 & 1 \\
1 & 0
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]\)
(d) 10

Answer

Answer: (b) \(\left[\begin{array}{cc}
1 & 1 \\
1 & 0
\end{array}\right]\)

Matrices Class 12 MCQs Chapter 3 Question 16.
If \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
a & b & -1
\end{array}\right]\) then A² =
(a) a unit matrix
(b) A
(c) a null matrix
(d) -A

Answer

Answer: (a) a unit matrix

Chapter 3 Maths Class 12 MCQ Question 17.
If A = \(\left[\begin{array}{cc}
α & 0 \\
1 & 1
\end{array}\right]\) B = \(\left[\begin{array}{cc}
1 & 0 \\
5 & 1
\end{array}\right]\) where A² = B then the value of α is
(a) 1
(b) -1
(c) 4
(d) we cant calculate the value of α

Answer

Answer: (d) we cant calculate the value of α

Class 12 Maths Ch 3 MCQ Question 18.
If A = \(\left[\begin{array}{cc}
1 & 2 \\
3 & 4
\end{array}\right]\) then
(a) |A| = 0
(b) A^-1 exists
(c) A^-1 does not exist
(d) None of these

Answer

Answer: (b) A^-1 exists

MCQ Class 12 Maths Chapter 3 Question 19.
If A = \(\left[\begin{array}{cc}
2x & 5 \\
8 & x
\end{array}\right]\) = \(\left[\begin{array}{cc}
6 & -2 \\
7 & 3
\end{array}\right]\) then the value of x is
(a) 3
(b) ±3
(c) ±6
(d) 6

Answer

Answer: (a) 3

Matrix MCQ Questions And Answers Chapter 3 Question 20.
Let A = \(\left[\begin{array}{cc}
1 & -1 \\
2 & 3
\end{array}\right]\) then
(a) A^-1 = \(\left[\begin{array}{cc}
\frac{3}{5} & \frac{1}{5} \\
\frac{-2}{5} & \frac{1}{5}
\end{array}\right]\)
(b) |A| = 0
(c) |A| = 5
(d) A² = 1

Answer

Answer: (a) A^-1 = \(\left[\begin{array}{cc}
\frac{3}{5} & \frac{1}{5} \\
\frac{-2}{5} & \frac{1}{5}
\end{array}\right]\)

Question 21.
If A = \( \left[\begin{array}{ccc}
2 & \lambda & -3 \\
0 & 2 & 5 \\
1 & 1 & 3
\end{array}\right]\) yhen A^-1 exists if
(a) λ = 2
(b) λ ≠ 2
(c) λ ≠ -2
(d) none of these

Answer

Answer: (d) none of these

Question 22.
If A = \(\left[\begin{array}{cc}
α & 2 \\
2 & α
\end{array}\right]\) and |A³| = 25 then α is
(a) ±3
(b) ±2
(c) ±5
(d) 0

Answer

Answer: (a) ±3

Question 23.
A² – A + I = 0 then the inverse of A
(a) A
(b) A + I
(c) I – A
(d) A – I

Answer

Answer: (c) I – A

Question 24.
If A = \(\left[\begin{array}{cc}
2 & 3 \\
1 & -4
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
1 & -2 \\
-1 & 3
\end{array}\right]\) then find (AB)^-1
(a) \(\frac{1}{11}\) \(\left[\begin{array}{cc}
14 & 5 \\
5 & 1
\end{array}\right]\)
(b) \(\frac{1}{11}\) \(\left[\begin{array}{cc}
14 & -5 \\
-5 & 1
\end{array}\right]\)
(c) \(\frac{1}{11}\) \(\left[\begin{array}{cc}
1 & 5 \\
5 & 14
\end{array}\right]\)
(d) \(\frac{1}{11}\) \(\left[\begin{array}{cc}
1 & -5 \\
-5 & 14
\end{array}\right]\)

Answer

Answer: (a) \(\frac{1}{11}\) \(\left[\begin{array}{cc}
14 & 5 \\
5 & 1
\end{array}\right]\)

Question 25.
If A = \(\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\) then A² – 5A – 7I is
(a) zero matrix
(b) a diagonal matrix
(c) identity matrix
(d) None of these

Answer

Answer: (b) a diagonal matrix

Question 26.
If A = \(\left[\begin{array}{cc}
\cos x & -\sin x \\
\sin x & \cos x
\end{array}\right]\) then A + A^T = I if the value of x is
(a) \(\frac{π}{6}\)
(b) \(\frac{π}{3}\)
(c) π
(d) 0

Answer

Answer: (b) \(\frac{π}{3}\)

Question 27.
If \(\left[\begin{array}{cc}
x+y & y \\
2x & x-y
\end{array}\right]\) \(\left[\begin{array}{c}
2 \\
-1
\end{array}\right]\) \(\left[\begin{array}{c}
3 \\
2
\end{array}\right]\) then xy equal to
(a) -5
(b) -4
(c) 4
(d) 5

Answer

Answer: (a) -5

Question 28.
If A = \(\left[\begin{array}{cc}
1 & 2 \\
4 & 2
\end{array}\right]\) then |2A| =
(a) 2|A|
(b) 4|A|
(c) 8|A|
(d) None of these

Answer

Answer: (b) 4|A|

Question 29.
If A = \(\left[\begin{array}{cc}
a & b \\
c & d
\end{array}\right]\) then A² is equal to
(a) \(\left[\begin{array}{cc}
a^{2} & b^{2} \\
c^{2} & d^{2}
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
b^{2}+bc & ab+bd \\
ac+dc & dc+d^{2}
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
a^{3} & b^{3} \\
c^{3} & d^{3}
\end{array}\right]\)
(d) None of these

Answer

Answer: (b) \(\left[\begin{array}{cc}
b^{2}+bc & ab+bd \\
ac+dc & dc+d^{2}
\end{array}\right]\)

Question 30.
\(\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\) is inverse of
(a) \(\left[\begin{array}{cc}
-\cos \theta & -\sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
\sin \theta & -\cos \theta
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\)
(d) None of these

Answer

Answer: (c) \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\)

Question 31.
A = \(\left[\begin{array}{cc}
a & b \\
b & a
\end{array}\right]\) and A² = \(\left[\begin{array}{cc}
α & β \\
β & α
\end{array}\right]\) then
(a) α = a² + b², β = ab
(b) α = a² + b², β = 2ab
(c) α = a² + b², β = a² – b²
(d) α = 2ab, β = a² + b²

Answer

Answer: (b) α = a² + b², β = 2ab

Question 32.
The matrix \(\left[\begin{array}{ccc}
2 & -1 & 4 \\
1 & 0 & -5 \\
-4 & 5 & 7
\end{array}\right]\) is
(a) a symmetric matix
(b) a skew-sybtmetric matrix
(c) a diagonal matrix
(d) None of these

Answer

Answer: (d) None of these

Question 33.
If a matrix is both symmetric matrix and skew symmetric matrix then
(a) A is a diagonal matrix
(b) A is zero matrix
(c) A is scalar matrix
(d) None of these

Answer

Answer: (b) A is zero matrix

Question 34.
If \(\left[\begin{array}{cc}
x+y & 3 \\
4 & x-y
\end{array}\right]\) = \(\left[\begin{array}{cc}
1 & 3 \\
4 & -3
\end{array}\right]\) then (x, y) is
(a) (-1, 2)
(b) (-1, -2)
(c) (-2, -1)
(d) (1, -2)

Answer

Answer: (a) (-1, 2)

Question 35.
The matrix P = \(\left[\begin{array}{ccc}
0 & 0 & 4 \\
0 & 4 & 0 \\
4 & 0 & 0
\end{array}\right]\) is
(a) square matrix
(b) diagonal matrix
(c) unit matrix
(d) None of these

Answer

Answer: (a) square matrix

Question 36.
Total number of possible matrices of order 3 × 3 with each entry 2 or 0 is
(a) 9
(b) 27
(c) 81
(d) 512

Answer

Answer: (d) 512

Question 37.
If \(\left[\begin{array}{cc}
2x+y & 4x \\
5x-7 & 4x
\end{array}\right]\) = \(\left[\begin{array}{cc}
7 & 7y-13 \\
y & x+6
\end{array}\right]\) then the value of x, y is
(a) 3, 1
(b) 2, 3
(c) 2, 4
(d) 3, 3

Answer

Answer: (b) 2, 3

Question 38.
If A and B are two matrices of the order 3 × m and 3 × n, respectively, and m = n, then the order of matrix (5A – 2B) is
(a) m × 3
(b) 3 × 3
(c) m × n
(d) 3 × n

Answer

Answer: (d) 3 × n

Question 39.
If A = \(\frac{1}{π}\) \(\left[\begin{array}{cc}
\sin ^{-1}(x \pi) & \tan^{1}\left(\frac{x}{\pi}\right) \\
\sin ^{-1}\left(\frac{x}{\pi}\right) & \cot ^{-1}(\pi x)
\end{array}\right]\)
B = \(\frac{1}{π}\) \(\left[\begin{array}{cc}
\cos ^{-1}(x \pi) & \tan ^{-1}\left(\frac{x}{\pi}\right) \\
\sin ^{-1}\left(\frac{x}{\pi}\right) & -\tan ^{-1}(\pi x)
\end{array}\right]\)
then A – B equal to
(a) I
(b) O
(c) 1
(d) \(\frac{3}{2}\) I

Answer

Answer: (d) \(\frac{3}{2}\) I

Question 40.
If A = \(\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]\) then A² is equal to
(a) \(\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
1 & 0 \\
1 & 0
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
0 & 1 \\
0 & 1
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]\)

Answer

Answer: (d) \(\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]\)

Question 41.
If matrix A = [a_ij]_2×2 where a_ij = {\(_{0 if i = j}^{1 if i ≠ j}\) then A² is equal to
(a) I
(b) A
(c) O
(d) None of these

Answer

Answer: (a) I

Question 42.
The matrix \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 0
\end{array}\right]\) is a
(a) identity matrix
(b) symmetric matrix
(c) skew symmetric matrix
(d) None of these

Answer

Answer: (b) symmetric matrix

Question 43.
The matrix \(\left[\begin{array}{ccc}
0 & -5 & 8 \\
5 & 0 & 12 \\
-8 & -12 & 0
\end{array}\right]\) is a
(a) diagonal matrix
(b) symmetric matrix
(c) skew symmetric matrix
(d) scalar matrix

Answer

Answer: (c) skew symmetric matrix

Question 44.
If A is matrix of order m × n and B is a matrix such that AB’ and B’A are both defined, then order of matrix B is
(a) m × m
(b) n × n
(c) n × m
(d) m × n

Answer

Answer: (d) m × n

Question 45.
If A and B are matrices of same order, then (AB’ – BA’) is a
(a) skew symmetric matrix
(b) null matrix
(c) symmetric matrix
(d) unit matrix

Answer

Answer: (a) skew symmetric matrix

Question 46.
If A is a square matrix such that A² = I, then (A – I)³ + (A + I)³ – 7A is equal to
(a) A
(b) I – A
(c) I + A
(d) 3 A

Answer

Answer: (a) A

Question 47.
For any two matrices A and B, we have
(a) AB = BA
(b) AB ≠ BA
(c) AB = 0
(d) None of these

Answer

Answer: (d) None of these

Question 48.
If A = [a_ij]_2×2 where a_ij = i + j, then A is equal to
(a) \(\left[\begin{array}{cc}
1 & 2 \\
3 & 4
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
2 & 3 \\
3 & 4
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
1 & 1 \\
2 & 2
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
1 & 2 \\
1 & 2
\end{array}\right]\)

Answer

Answer: (b) \(\left[\begin{array}{cc}
2 & 3 \\
3 & 4
\end{array}\right]\)

Question 49.
The number of all possible matrices of order 3 × 3 with each entry 0 or 1 is
(a) 18
(b) 512
(c) 81
(d) None of these

Answer

Answer: (b) 512

Question 50.
The order of the single matrix obtained from
\(\left[\begin{array}{cc}
1 & -1 \\
0 & 2 \\
2 & 3
\end{array}\right]\) \(\left\{\left[\begin{array}{ccc}
-1 & 0 & 2 \\
2 & 0 & 1
\end{array}\right]-\left[\begin{array}{ccc}
0 & 1 & 23 \\
1 & 0 & 21
\end{array}\right]\right\}\) is
(a) 2 × 2
(b) 2 × 3
(c) 3 × 2
(d) 3 × 3

Answer

Answer: (d) 3 × 3

Question 51.
A square matrix A = [a_ij]_n×n is called a diagonal matrix if a_ij = 0 for
(a) i = j
(b) i < j
(c) i > j
(d) i ≠ j

Answer

Answer: (d) i ≠ j

Question 52.
A square matrix A = [a_ij]_n×n is called a lower triangular matrix if a_ij = 0 for
(a) i = j
(b) i < j
(c) i > j
(d) None of these

Answer

Answer: (b) i < j

Question 53.
The matrix A = \(\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]\) is a
(a) unit matrix
(b) diagonal matrix
(c) symmetric matrix
(d) skew symmetric matrix

Answer

Answer: (c) symmetric matrix

Question 54.
If \(\left[\begin{array}{cc}
x+y & 2x+z\\
x-y & 2z+2
\end{array}\right]\) = \(\left[\begin{array}{cc}
4 & 7 \\
0 & 10
\end{array}\right]\) then find the value of x, y, z and w respectively
(a) 2, 2, 3, 4
(b) 2, 3, 1, 2
(c) 3, 3, 0, 1
(d) None of these

Answer

Answer: (a) 2, 2, 3, 4

Question 55.
If \(\left[\begin{array}{cc}
x-y & 2x+z\\
2x-y & 3z+w
\end{array}\right]\) = \(\left[\begin{array}{cc}
-1 & 5 \\
0 & 13
\end{array}\right]\) then the value of w is
(a) 1
(b) 2
(c) 3
(d) 4

Answer

Answer: (d) 4

Question 56.
Find x, y, z and w respectively such that
\(\left[\begin{array}{cc}
x-y & 2x+z\\
2x-y & 2x+w
\end{array}\right]\) = \(\left[\begin{array}{cc}
5 & 3 \\
12 & 15
\end{array}\right]\)
(a) 7, 2, 1, 1
(b) 7, 5, 3, 8
(c) 1, 2, 5, 6
(d) 6, 3, 2, 1

Answer

Answer: (a) 7, 2, 1, 1

Question 57.
If \(\left[\begin{array}{cc}
a+b & 2\\
5 & ab
\end{array}\right]\) = \(\left[\begin{array}{cc}
6 & 2 \\
5 & 8
\end{array}\right]\) then find the value of a and b respectively
(a) 2, 4
(b) 4, 2
(c) Both (a) and (b)
(d) None of these

Answer

Answer: (c) Both (a) and (b)

Question 58.
For what values of x and y are the following matrices equal
A = \(\left[\begin{array}{cc}
2x+1 & 3y\\
0 & y^{2}-5y
\end{array}\right]\) B = \(\left[\begin{array}{cc}
x+3 & y^{2}+2 \\
0 & -6
\end{array}\right]\)
(a) 2, 3
(b) 3, 4
(c) 2, 2
(d) 3, 3

Answer

Answer: (c) 2, 2

Question 59.
If A = \(\left[\begin{array}{cc}
α & 0\\
1 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
1 & 0 \\
5 & 1
\end{array}\right]\) then find value of α for which A² = B is
(a) 1
(b) -1
(c) 4
(d) None of these

Answer

Answer: (d) None of these

Question 60.
If P = \(\left[\begin{array}{ccc}
i & 0 & -i \\
0 & -i & i \\
-i & i & 0
\end{array}\right]\) and Q = \(\left[\begin{array}{cc}
-i & i \\
0 & 0 \\
i & -i
\end{array}\right]\) then PQ is equal to
(a) \(\left[\begin{array}{cc}
-2 & 2 \\
1 & -1 \\
1 & -1
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
2 & -2 \\
-1 & 1 \\
-1 & 1
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
2 & -2\\
-1 & 1
\end{array}\right]\)
(d) \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)

Answer

Answer: (b) \(\left[\begin{array}{cc}
2 & -2 \\
-1 & 1 \\
-1 & 1
\end{array}\right]\)

Question 61.
\(\left[\begin{array}{c}
1 & x & 1
\end{array}\right]\) \(\left[\begin{array}{ccc}
1 & 3 & 2 \\
2 & 5 & 1 \\
15 & 3 & 2
\end{array}\right]\) \(\left[\begin{array}{c}
1 \\
2 \\
x
\end{array}\right]\)
(a) -7
(b) -11
(c) -2
(d) 14

Answer

Answer: (c) -2

Question 62.
If A = \(\left[\begin{array}{cc}
1 & -1\\
2 & -1
\end{array}\right]\) B = \(\left[\begin{array}{cc}
x & 1\\
y & -1
\end{array}\right]\) and (A + B)² = A² + B², then x + y is
(a) 2
(b) 3
(c) 4
(d) 5

Answer

Answer: (d) 5

Question 63.
If AB = A and BA = B, then
(a) B = 1
(b)A = I
(c) A² = A
(d) B² = I

Answer

Answer: (c) A² = A

Question 64.
If A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
a & b & -1
\end{array}\right]\) then (A – I) (A + I) = 0 for
(a) a = b = 0 only
(b) a = 0 only
(c) b = 0 only
(d) any a and b

Answer

Answer: (d) any a and b

Question 65.
If A = \(\left[\begin{array}{cc}
1 & 1\\
0 & 2
\end{array}\right]\) then A⁸ – 2⁸ (A – I)
(a) I – A
(b) 2I – A
(c) I + A
(d) A – 2I

Answer

Answer: (b) 2I – A

Question 66.
If A = \(\left[\begin{array}{ccc}
2 & 2 & 1 \\
1 & 3 & 1 \\
1 & 2 & 2
\end{array}\right]\) then A³ – 7A² + 10A =
(a) 5I + A
(b) 5I – A
(c) 5I
(d) 6I

Answer

Answer: (b) 5I – A

Question 67.
If A is a m × n matrix such that AB and BA are both defined, then B is an
(a) m × n matrix
(b) n × m matrix
(c) n × n matrix
(d) m × m matrix

Answer

Answer: (b) n × m matrix

Question 68.
If A = \(\left[\begin{array}{cc}
1 & 2\\
3 & 4
\end{array}\right]\) then A² – 5A is equal to
(a) 2I
(b) 3I
(c) -2I
(d) null matrix

Answer

Answer: (a) 2I

Question 69.
If A = \(\left[\begin{array}{cc}
-2 & 4\\
-1 & 2
\end{array}\right]\) then A² is
(a) null matrix
(b) unit matrix
(c) \(\left[\begin{array}{cc}
0 & 0\\
0 & 0
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
0 & 0\\
0 & 1
\end{array}\right]\)

Answer

Answer: (a) null matrix

Question 70.
If A and B are 2 × 2 matrices, then which of the following is true?
(a) (A + B)² = A² + B² + 2AB
(b) (A – B)² = A² + B² – 2AB
(c) (A – B)(A + B) = A² + AB – BA – B²
(d) (A + B) (A – B) = A² – B²

Answer

Answer: (c) (A – B)(A + B) = A² + AB – BA – B²

We hope the given NCERT MCQ Questions for Class 12 Maths Chapter 3 Matrices with Answers Pdf free download will help you. If you have any queries regarding Matrices CBSE Class 12 Maths MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 12 Maths MCQ:

MCQ Questions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions with Answers

Inverse Trigonometric Functions Class 12 MCQ Online Test With Answers Questions

October 24, 2024

Check the below NCERT MCQ Questions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions with Answers Pdf free download. MCQ Questions for Class 12 Maths with Answers were prepared based on the latest exam pattern. We have provided Inverse Trigonometric Functions Class 12 Maths MCQs Questions with Answers to help students understand the concept very well.

Class 12 Maths Chapter 2 MCQ With Answers

Maths Class 12 Chapter 2 MCQs On Inverse Trigonometric Functions

Inverse Trigonometric Functions Class 12 MCQ Question 1.
sin^-1 (sin\(\frac{2π}{3}\)) =
(a) \(\frac{2π}{3}\)
(b) \(\frac{π}{6}\)
(c) \(\frac{4π}{3}\)
(d) \(\frac{π}{3}\)

Answer

Answer: (d) \(\frac{π}{3}\)

Inverse Trigonometry Class 12 MCQ Question 2.
sin^-1 (1 – x) – 2 sin^-1 x = \(\frac{π}{2}\) then x = ?
(a) 0, \(\frac{1}{2}\)
(b) 1, \(\frac{1}{2}\)
(c) \(\frac{1}{2}\)
(d) 0

Answer

Answer: (d) 0

MCQ Of Inverse Trigonometry Class 12 Question 3.
tan^-1 √3 – sec^-1(-2)
(a) π
(b) –\(\frac{π}{3}\), 0
(c) \(\frac{π}{3}\)
(d) \(\frac{2π}{3}\)

Answer

Answer: (b) –\(\frac{π}{3}\), 0

Inverse Trigonometric Functions MCQ Question 4.
sin(sec^-1 x + cosec^-1x) =
(a) 1
(b) -1
(c) \(\frac{π}{2}\)
(d) \(\frac{π}{3}\)

Answer

Answer: (a) 1

Class 12 Maths Chapter 2 MCQ Question 5.
2 tan^-1 \(\frac{1}{3}\) + tan^-1 \(\frac{1}{7}\) =
(a) tan^-1 \(\frac{44}{29}\)
(b) \(\frac{π}{2}\)
(c) 0
(d) \(\frac{π}{4}\)

Answer

Answer: (d) \(\frac{π}{4}\)

MCQ On Inverse Trigonometric Functions Question 6.
The principle value of sin^-1 \(\frac{√3}{2}\) is
(a) \(\frac{2π}{3}\)
(b) \(\frac{π}{6}\)
(c) \(\frac{π}{4}\)
(d) \(\frac{π}{3}\)

Answer

Answer: (d) \(\frac{π}{3}\)

MCQ Inverse Trigonometry Class 12 Question 7.
The value of the expression tan^-1(\(\frac{1}{2}\)cos^-1\(\frac{2}{√5}\)) is
(a) 2 + √5
(b) √5 – 2
(c) \(\frac{√5+2}{4}\)
(d) √5 + 2

Answer

Answer: (d) √5 + 2

Class 12 Inverse Trigonometry MCQ Question 8.
Simplified form of cos^-1 (4x³ – 3x)
(a) 3 sin^-1x
(b) 3 cos^-1x
(c) π – 3 sin^-1x
(d) None of these

Answer

Answer: (b) 3 cos^-1x

Inverse Trigonometric Functions Class 12 MCQ With Solutions Question 9.
The value of tan(tan^-1 \(\frac{4}{5}\) + tan^-1 \(\frac{2}{3}\)) is
(a) \(\frac{6}{17}\)
(b) \(\frac{7}{16}\)
(c) \(\frac{17}{6}\)
(d) None of these

Answer

Answer: (d) None of these

MCQ On Inverse Trigonometric Functions Class 12 Question 10.
tan^-1(\(\frac{x}{y}\)) – tan^-1(\(\frac{x-y}{x+y}\)) is equal to
(a) \(\frac{π}{3}\)
(b) \(\frac{π}{4}\)
(c) \(\frac{π}{2}\)
(d) \(\frac{-3π}{4}\)

Answer

Answer: (b) \(\frac{π}{4}\)

Inverse Trigonometry MCQ Question 11.
The value of x for which sin |cot^-1(1 – x)| = cos (tan^-1 x) is
(a) \(\frac{2}{1}\)
(b) 1
(c) 0
(d) \(\frac{1}{2}\)

Answer

Answer: (d) \(\frac{1}{2}\)

Class 12 Maths Chapter 2 MCQ Questions Question 12.
Princal value of cos^-1(\(\frac{-1}{√2}\))
(a) \(\frac{3π}{4}\)
(b) \(\frac{5π}{4}\)
(c) –\(\frac{π}{4}\)
(d) None of these

Answer

Answer: (a) \(\frac{3π}{4}\)

MCQ Questions For Inverse Trigonometry Class 12 With Solutions Question 13.
tan^-1 √3 – sec^-1 (-2) is equal to
(a) π
(b) –\(\frac{π}{3}\)
(c) \(\frac{π}{3}\)
(d) \(\frac{2π}{3}\)

Answer

Answer: (b) –\(\frac{π}{3}\)

Class 12 Maths Ch 2 MCQ Question 14.
If y = sec^-1 x then
(a) 0 ≤ y ≤ π
(b) 0 ≤ y ≤ \(\frac{π}{2}\)
(c) –\(\frac{π}{2}\) < y < \(\frac{π}{2}\)
(d) None of these

Answer

Answer: (d) None of these

Ch 2 Maths Class 12 MCQ Question 15.
If x + \(\frac{1}{x}\) = 2 then the principal value of sin^-1 x is x
(a) \(\frac{π}{4}\)
(b) \(\frac{π}{2}\)
(c) π
(d) \(\frac{3π}{2}\)

Answer

Answer: (d) \(\frac{3π}{2}\)

Inverse Trigonometry MCQ Class 12 Question 16.
4 tan^-1 \(\frac{1}{5}\) – tan^-1 \(\frac{1}{239}\)
(a) π
(b) \(\frac{π}{2}\)
(c) \(\frac{π}{3}\)
(d) \(\frac{π}{4}\)

Answer

Answer: (d) \(\frac{π}{4}\)

Inverse Trigonometric Functions MCQ Pdf Question 17.
The principle value of sin^-1(sin\(\frac{2π}{3}\)) is
(a) \(\frac{2π}{3}\)
(b) \(\frac{π}{3}\)
(c) \(\frac{-π}{6}\)
(d) \(\frac{π}{6}\)

Answer

Answer: (b) \(\frac{π}{3}\)

MCQ Questions For Inverse Trigonometry Class 12 Question 18.
The value of cos^-1(\(\frac{1}{2}\)) + 2sin^-1(\(\frac{1}{2}\)) is equal to
(a) \(\frac{π}{4}\)
(b) \(\frac{π}{6}\)
(c) \(\frac{2π}{3}\)
(d) \(\frac{5π}{6}\)

Answer

Answer: (b) \(\frac{π}{6}\)

Chapter 2 Maths Class 12 MCQ Question 19.
Algebraic expression for sin (cot^-1 x) is
(a) \(\frac{1}{1+x^2}\)
(b) \(\frac{1}{\sqrt{1+x^2}}\)
(c) \(\frac{x}{\sqrt{1+x^2}}\)
(d) None of these

Answer

Answer: (b) \(\frac{1}{\sqrt{1+x^2}}\)

Inverse Trigonometry MCQs Question 20.
If sin^-1(\(\frac{2x}{1+x^2}\)) + sin^-1\(\frac{2y}{1+y^2}\) = 2 tan^-1 a then a is equal to
(a) \(\frac{x-y}{1+xy}\)
(b) \(\frac{y}{1+xy}\)
(c) \(\frac{y}{1-xy}\)
(d) \(\frac{x+y}{1-xy}\)

Answer

Answer: (d) \(\frac{x+y}{1-xy}\)

Question 21.
Princal value of tan^-1 (-1) is
(a) \(\frac{π}{4}\)
(b) \(\frac{-π}{2}\)
(c) \(\frac{5π}{4}\)
(d) \(\frac{-π}{4}\)

Answer

Answer: (d) \(\frac{-π}{4}\)

Question 22.
tan^-1(\(\frac{1}{4}\)) + tan^-1(\(\frac{2}{9}\)) equal to

Answer

Answer: (d) tan^-1(\(\frac{1}{2}\))

Question 23.
Principal value of sin^-1(\(\frac{1}{√2}\))
(a) \(\frac{π}{4}\)
(b) \(\frac{3π}{4}\)
(c) \(\frac{5π}{4}\)
(d) None of these

Answer

Answer: (a) \(\frac{π}{4}\)

Question 24.
sin^-1 x = y Then
(a) 0 ≤ y ≤ π
(b) –\(\frac{π}{2}\) ≤ y ≤ \(\frac{π}{2}\)
(c) 0 < y < π
(d) –\(\frac{π}{2}\) < y < –\(\frac{π}{2}\)

Answer

Answer: (b) –\(\frac{π}{2}\) ≤ y ≤ \(\frac{π}{2}\)

Question 25.
cos^-1(cos\(\frac{7π}{6}\)) is equal to
(a) \(\frac{7π}{6}\)
(b) \(\frac{5π}{6}\)
(c) \(\frac{π}{3}\)
(d) \(\frac{π}{6}\)

Answer

Answer: (b) \(\frac{5π}{6}\)

Question 26.
sin[\(\frac{π}{3}\) – sin^-1(-\(\frac{1}{2}\))] is equal to
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{1}{4}\)
(d) 1

Answer

Answer: (d) 1

Question 27.
tan^-1\(\frac{1}{2}\) + tan^-1\(\frac{2}{11}\) = tan^-1 a then a = ?
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{3}{4}\)
(d) 1

Answer

Answer: (c) \(\frac{3}{4}\)

Question 28.
tan^-1\(\frac{1}{2}\) + tan^-1\(\frac{1}{3}\) =
(a) \(\frac{π}{4}\)
(b) \(\frac{π}{2}\)
(c) \(\frac{π}{3}\)
(d) π

Answer

Answer: (a) \(\frac{π}{4}\)

Question 29.
If sin^-1 x + sin^-1 y = \(\frac{2π}{3}\) then cos^-1 x + cos^-1 y =
(a) \(\frac{2π}{3}\)
(b) \(\frac{π}{4}\)
(c) \(\frac{π}{3}\)
(d) \(\frac{π}{2}\)

Answer

Answer: (c) \(\frac{π}{3}\)

Question 30.
The principal value of cosec^-1 (-2) is
(a) –\(\frac{2π}{3}\)
(b) \(\frac{π}{6}\)
(c) \(\frac{2π}{3}\)
(d) –\(\frac{π}{6}\)

Answer

Answer: (d) –\(\frac{π}{6}\)

Question 31.
The domain of the following f(x) = \(\sqrt{sin^{-1}x}\) is
(a) [0, 1]
(b) [-1, 1]
(c) [-, 0]
(d) [0, 1]

Answer

Answer: (a) [0, 1]

Question 32.
Which of the following is the principal value branch of cos^-1 x?
(a) [\(\frac{-π}{2}\), \(\frac{π}{2}\)]
(b) (0, π)
(c) (0, π)
(d) (0, π) – {\(\frac{π}{2}\)}

Answer

Answer: (c) (0, π)

Question 33.
Which of the following is the principal value branch of cosec^-1 x?
(a) (\(\frac{-π}{2}\), \(\frac{π}{2}\))
(b) (0, π) – {\(\frac{π}{2}\)}
(c) [\(\frac{-π}{2}\), \(\frac{π}{2}\)]
(d) [\(\frac{-π}{2}\), \(\frac{π}{2}\)] – [0]

Answer

Answer: (d) [\(\frac{-π}{2}\), \(\frac{π}{2}\)] – [0]

Question 34.
If 3 tan^-1 x + cot^-1 x = π, then x equals
(a) 0
(b) 1
(c) -1
(d) \(\frac{1}{2}\)

Answer

Answer: (b) 1

Question 35.
The value of cos^-1[cos(\(\frac{33π}{5}\))] is
(a) \(\frac{3π}{5}\)
(b) \(\frac{-3π}{5}\)
(c) \(\frac{π}{10}\)
(d) –\(\frac{-π}{10}\)

Answer

Answer: (a) \(\frac{3π}{5}\)

Question 36.
The domain of the function cos^-1 (2x – 1) is
(a) [0, 1]
(b) [-1, 1]
(c) [-1, -1]
(d) [0, π]

Answer

Answer: (a) [0, 1]

Question 37.
The domain of the function defined by f (x) = sin^-1 \(\sqrt{x-1}\) is
(a) [1, 2]
(b) [-1, 1]
(c) [0, 1]
(d) None of these

Answer

Answer: (a) [1, 2]

Question 38.
If cos(sin^-1\(\frac{2}{5}\) + cos^-1 x) = 0 then x is equal to
(a) \(\frac{1}{5}\)
(b) \(\frac{2}{5}\)
(c) 0
(d) 1

Answer

Answer: (b) \(\frac{2}{5}\)

Question 39.
The value of sin (2 tan^-1 (.75)) is equal to
(a) .75
(b) 1.5
(c) .96
(d) sin 1.5

Answer

Answer: (c) .96

Question 40.
The value of cos^-1 (cos\(\frac{3π}{2}\)) is equal to
(a) \(\frac{π}{2}\)
(b) \(\frac{3π}{2}\)
(c) \(\frac{5π}{2}\)
(d) –\(\frac{7π}{2}\)

Answer

Answer: (a) \(\frac{π}{2}\)

Question 41.
The value of expression 2 sec^-1 2 + sin^-1 (\(\frac{1}{2}\)) is
(a) \(\frac{π}{6}\)
(b) \(\frac{5π}{6}\)
(c) \(\frac{7π}{6}\)
(d) 1

Answer

Answer: (b) \(\frac{5π}{6}\)

Question 42.
If tan^-1 x + tan^-1 y = \(\frac{4π}{5}\) then cot^-1 x + cot^-1 y equals
(a) \(\frac{π}{5}\)
(b) \(\frac{2π}{5}\)
(c) \(\frac{3π}{5}\)
(d) π

Answer

Answer: (a) \(\frac{π}{5}\)

Question 43.
If sin^-1(\(\frac{2a}{1+a^2}\)) + cos^-1(\(\frac{1-a^2}{1+a^2}\)) = tan^-1(\(\frac{2x}{1-x^2}\)) where a, x ∈ |0, 1| then the value of x is
(a) 0
(b) \(\frac{a}{2}\)
(c) a
(d) \(\frac{2a}{1-a^2}\)

Answer

Answer: (d) \(\frac{2a}{1-a^2}\)

Question 44.
The value of sin [cos^-1(\(\frac{7}{25}\))] is
(a) \(\frac{25}{24}\)
(b) \(\frac{25}{7}\)
(c) \(\frac{24}{25}\)
(d) \(\frac{7}{24}\)

Answer

Answer: (c) \(\frac{24}{25}\)

Question 45.
If |x| ≤ 1, then 2 tan^-1 x + sin^-1(\(\frac{2x}{1+x^2}\)) is equal to
(a) 4 tan^-1 x
(b) \(\frac{π}{2}\)
(c) 0
(d) π

Answer

Answer: (a) 4 tan^-1 x

Question 46.
If cos^-1 α + cos^-1 β + cos^-1 γ = 3π, then α(β + γ) + β (γ + α) + γ(α + β) equals
(a) 0
(b) 1
(c) 6
(d) 12

Answer

Answer: (c) 6

Question 47.
The number of real solution of the equation is
\(\sqrt{1+cos 2x}\) = √2 cos^-1(cos x) in [\(\frac{π}{2}\), π] is
(a) 0
(b) 1
(c) 2
(d) None of these

Answer

Answer: (c) 2

Question 48.
If cos^-1 x > sin^-1 x, then
(a) \(\frac{1}{√2}\) < x ≤ 1
(b) 0 ≤ x < \(\frac{1}{√2}\)
(c) -1 ≤ x < \(\frac{1}{√2}\) (d) x > 0

Answer

Answer: (b) 0 ≤ x < \(\frac{1}{√2}\)

Question 49.
sin^-1(\(\frac{-1}{2}\))
(a) \(\frac{π}{3}\)
(b) –\(\frac{π}{3}\)
(c) \(\frac{π}{6}\)
(d) –\(\frac{π}{6}\)

Answer

Answer: (d) –\(\frac{π}{6}\)

Question 50.
sec^-1(\(\frac{-2}{√3}\))
(a) \(\frac{π}{6}\)
(b) \(\frac{π}{3}\)
(c) \(\frac{5π}{6}\)
(d) –\(\frac{2π}{3}\)

Answer

Answer: (c) \(\frac{5π}{6}\)

Question 51.
cos^-1(\(\frac{1}{2}\))
(a) –\(\frac{π}{3}\)
(b) \(\frac{π}{3}\)
(c) \(\frac{π}{2}\)
(d) \(\frac{2π}{3}\)

Answer

Answer: (b) \(\frac{π}{3}\)

Question 52.
cosec^-1(\(\frac{-2}{√3}\))
(a) –\(\frac{π}{3}\)
(b) \(\frac{π}{3}\)
(c) \(\frac{π}{2}\)
(d) –\(\frac{π}{2}\)

Answer

Answer: (a) –\(\frac{π}{3}\)

Question 53.
cot^-1(1)
(a) \(\frac{π}{3}\)
(b) \(\frac{π}{4}\)
(c) \(\frac{π}{2}\)
(d) 0

Answer

Answer: (b) \(\frac{π}{4}\)

Question 54.
cos^-1(\(\frac{√3}{2}\))
(a) \(\frac{5π}{6}\)
(b) \(\frac{π}{6}\)
(c) \(\frac{4π}{9}\)
(d) \(\frac{2π}{3}\)

Answer

Answer: (a) \(\frac{5π}{6}\)

Question 55.
cosec^-1(2)
(a) \(\frac{π}{6}\)
(b) \(\frac{2π}{3}\)
(c) \(\frac{5π}{6}\)
(d) 0

Answer

Answer: (a) \(\frac{π}{6}\)

Question 56.
sec^-1(2)
(a) \(\frac{π}{6}\)
(b) \(\frac{π}{3}\)
(c) \(\frac{2π}{3}\)
(d) \(\frac{5π}{6}\)

Answer

Answer: (b) \(\frac{π}{3}\)

Question 57.
tan^-1(√3)
(a) \(\frac{π}{6}\)
(b) \(\frac{π}{3}\)
(c) \(\frac{2π}{3}\)
(d) \(\frac{5π}{6}\)

Answer

Answer: (b) \(\frac{π}{3}\)

Question 58.
cot^-1(-√3)
(a) \(\frac{5π}{6}\)
(b) \(\frac{π}{3}\)
(c) \(\frac{π}{2}\)
(d) \(\frac{π}{4}\)

Answer

Answer: (a) \(\frac{5π}{6}\)

Question 59.
tan^-1 + cos^-1 (\(\frac{-1}{2}\)) + sin^-1 (\(\frac{-1}{2}\))
(a) \(\frac{2π}{3}\)
(b) \(\frac{3π}{4}\)
(c) \(\frac{π}{2}\)
(d) 6π

Answer

Answer: (b) \(\frac{3π}{4}\)

Question 60.
tan^-1 (√3) + sec^-1 (-2) – cosec^-1 (\(\frac{2}{√3}\))
(a) \(\frac{5π}{6}\)
(b) \(\frac{2π}{3}\)
(c) \(\frac{π}{3}\)
(d) 0

Answer

Answer: (d) 0

Question 61.
cos^-1 (\(\frac{-1}{2}\)) + 2sin^-1 (\(\frac{-1}{2}\))
(a) \(\frac{π}{3}\)
(b) \(\frac{2π}{3}\)
(c) \(\frac{3π}{4}\)
(d) \(\frac{5π}{8}\)

Answer

Answer: (a) \(\frac{π}{3}\)

Question 62.
If cot^-1 (\(\sqrt{cosα}\)) – tan^-1 (\(\sqrt{cosα}\)) = x then sin x is equal to
(a) tan² (\(\frac{α}{2}\))
(b) cot² (\(\frac{α}{2}\))
(c) tan α
(d) cot (\(\frac{α}{2}\))

Answer

Answer: (a) tan² (\(\frac{α}{2}\))

Question 63.
4 tan^-1 \(\frac{1}{5}\) – tan^-1 \(\frac{1}{70}\) + tan^-1 \(\frac{1}{99}\) is equal to
(a) \(\frac{π}{6}\)
(b) \(\frac{π}{4}\)
(c) \(\frac{π}{3}\)
(d) \(\frac{π}{2}\)

Answer

Answer: (b) \(\frac{π}{4}\)

Question 64.
If 6 sin^-1 (x² – 6x + 8.5) = π, then x is equal to
(a) 1
(b) 2
(c) 3
(d) 8

Answer

Answer: (b) 2

Question 65.
Number of solutions of the equation
tan^-1 (\(\frac{1}{2x+1}\)) + tan^-1 (\(\frac{1}{4x+1}\)) = tan^-1 (\(\frac{2}{x^2}\))
(a) 1
(b) 2
(c) 3
(d) 4

Answer

Answer: (b) 2

We hope the given NCERT MCQ Questions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions with Answers Pdf free download will help you. If you have any queries regarding Inverse Trigonometric Functions CBSE Class 12 Maths MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 12 Maths MCQ:

Category: MCQ Questions

Class 12 Maths Chapter 12 MCQ With Answers

Maths Class 12 Chapter 12 MCQs On Linear Programming

Class 12 Maths Chapter 13 MCQ With Answers

Maths Class 12 Chapter 13 MCQs On Probability

Class 12 Maths Chapter 9 MCQ With Answers

Maths Class 12 Chapter 9 MCQs On Differential Equations

Class 12 Maths Chapter 8 MCQ With Answers

Maths Class 12 Chapter 8 MCQs On Application of Integrals

Class 12 Maths Chapter 6 MCQ With Answers

Maths Class 12 Chapter 6 MCQs On Application of Derivatives

Class 12 Maths Chapter 5 MCQ With Answers

Maths Class 12 Chapter 5 MCQs On Continuity and Differentiability

Class 11 Maths Chapter 8 MCQ With Answers

Maths Class 11 Chapter 8 MCQs On Binomial Theorem

Class 12 Maths Chapter 4 MCQ With Answers

Maths Class 12 Chapter 4 MCQs On Determinants

Class 11 Sociology Chapter 2 Social Change and Social Order in Rural and Urban Society MCQ With Answers

Sociology Class 11 Chapter 2 MCQs On Social Change and Social Order in Rural and Urban Society

Class 12 Maths Chapter 3 MCQ With Answers

Maths Class 12 Chapter 3 MCQs On Matrices

Class 12 Maths Chapter 2 MCQ With Answers

Maths Class 12 Chapter 2 MCQs On Inverse Trigonometric Functions