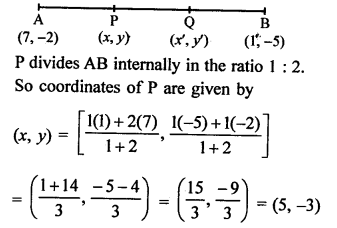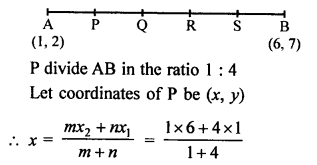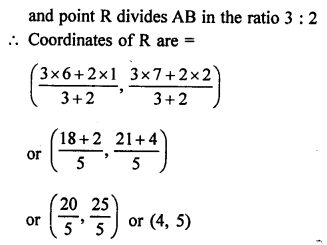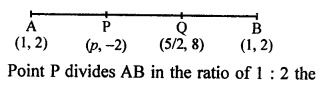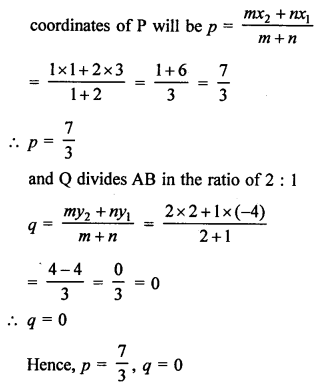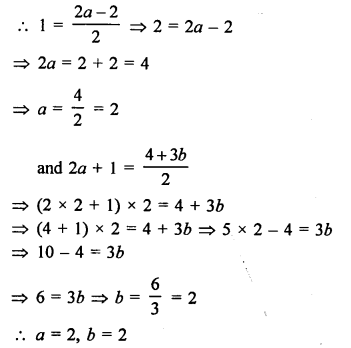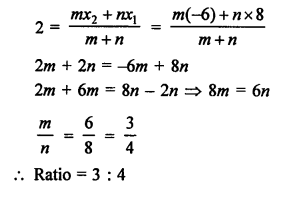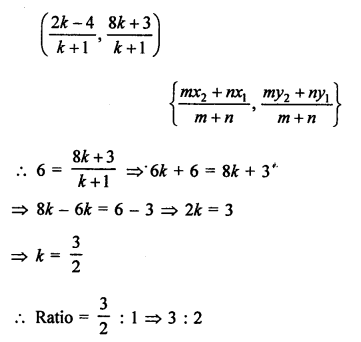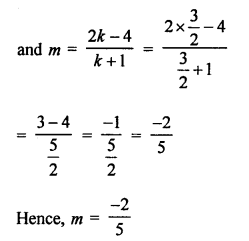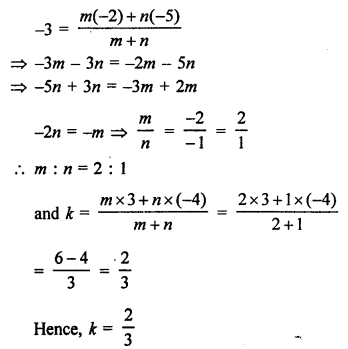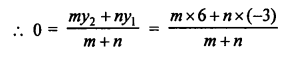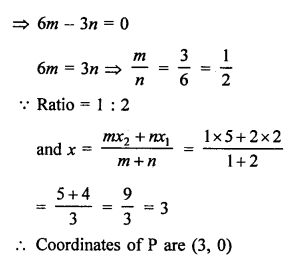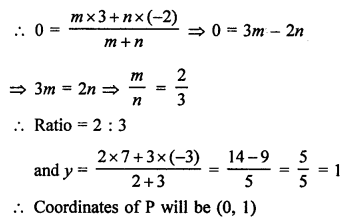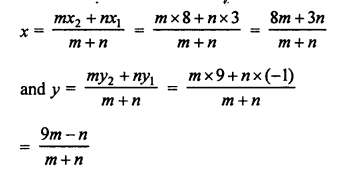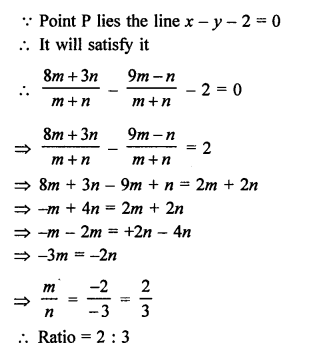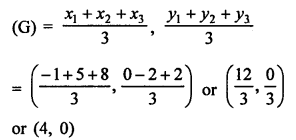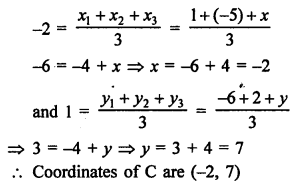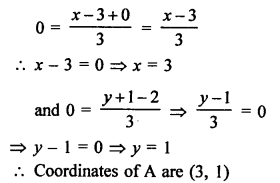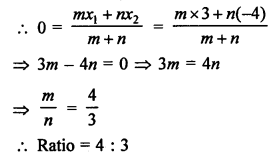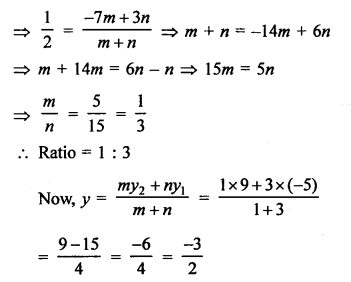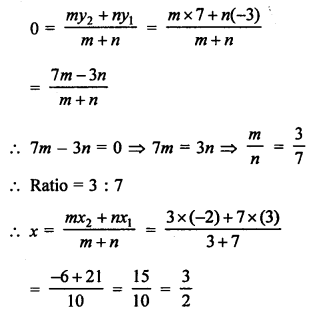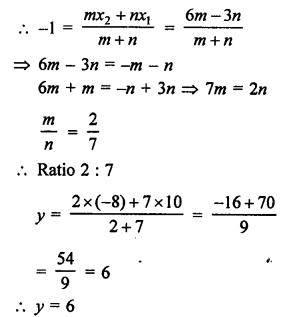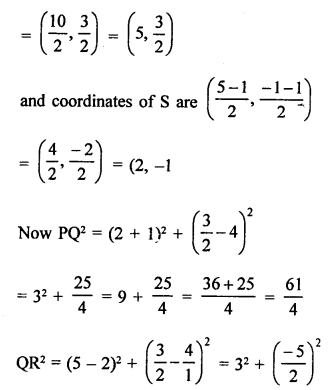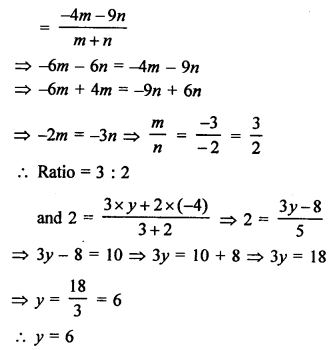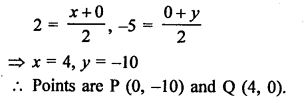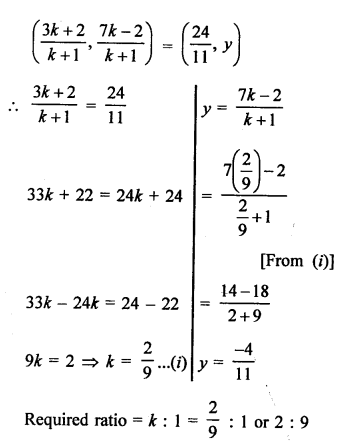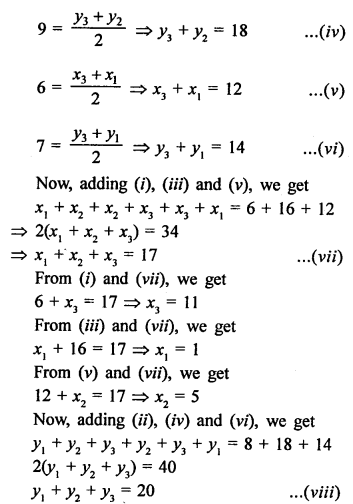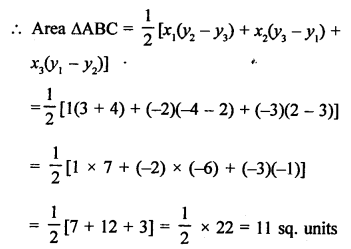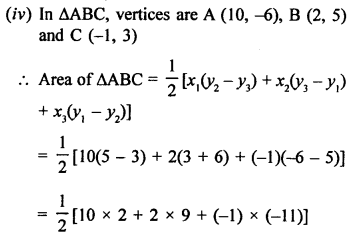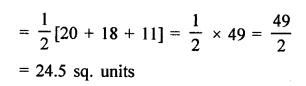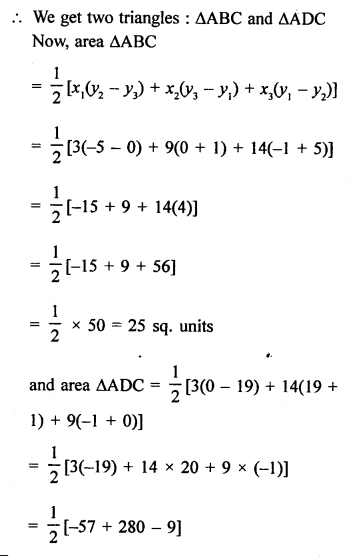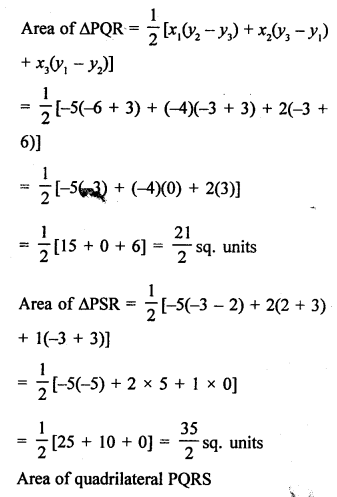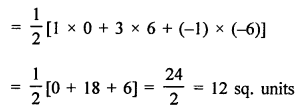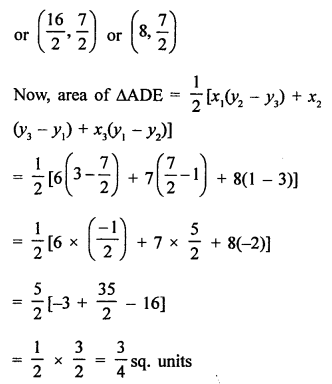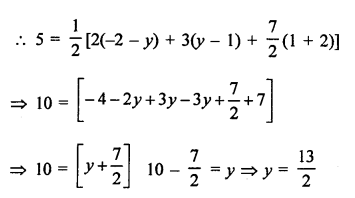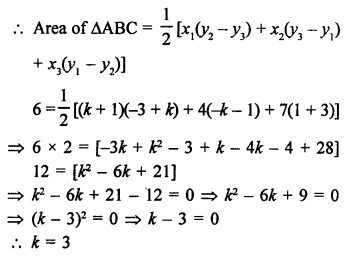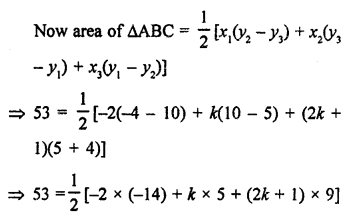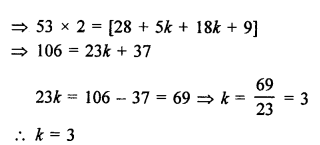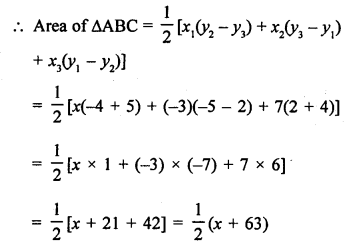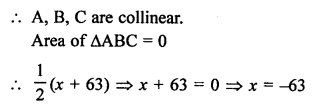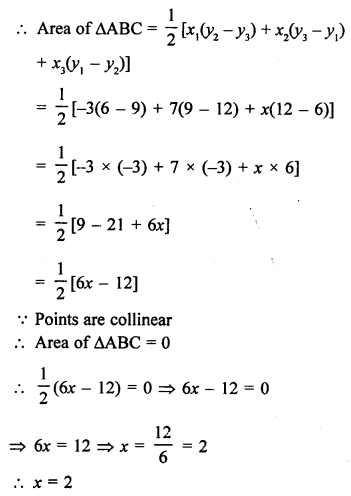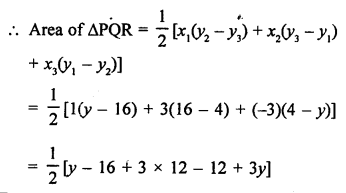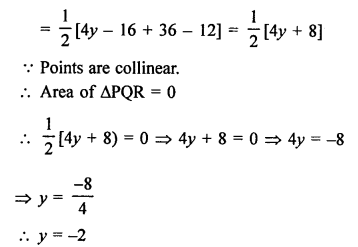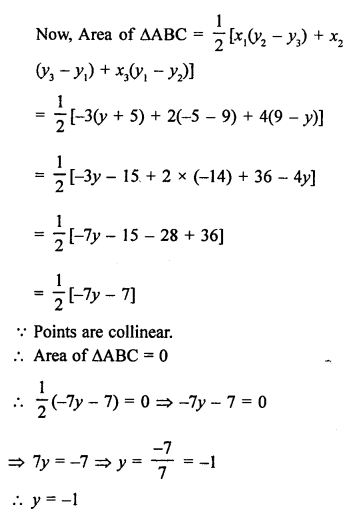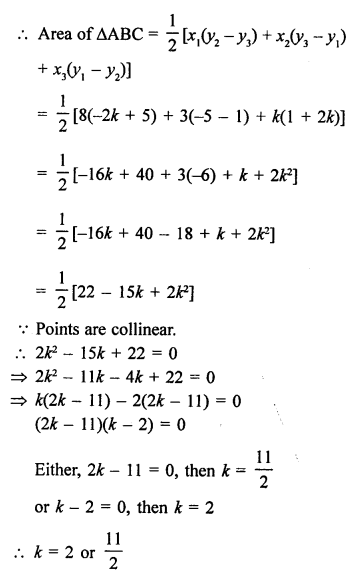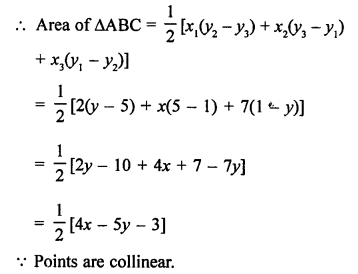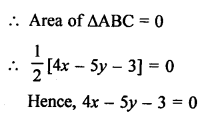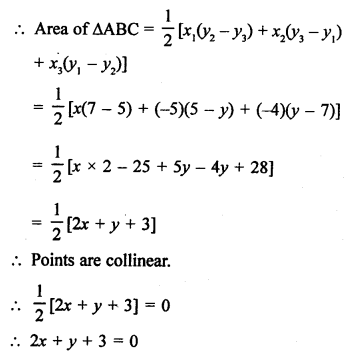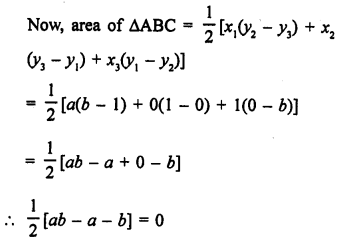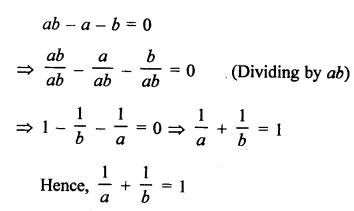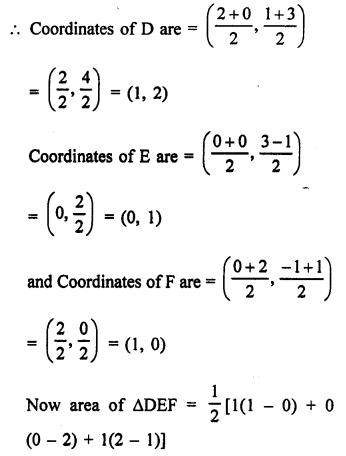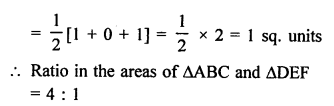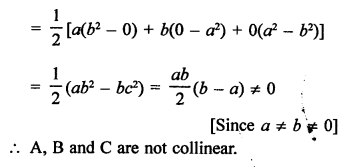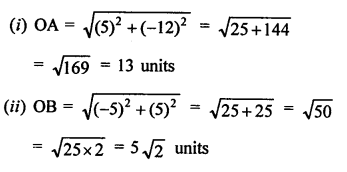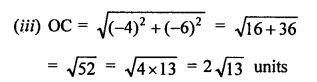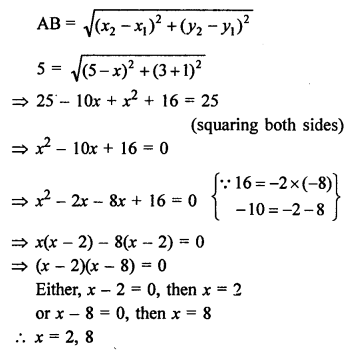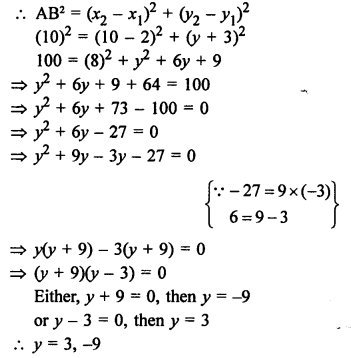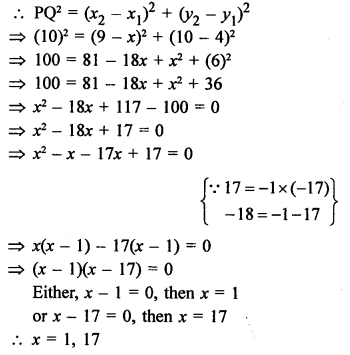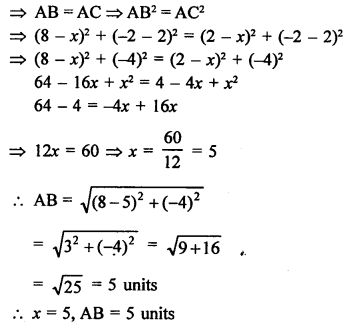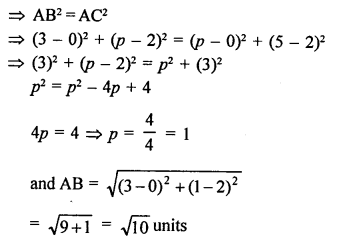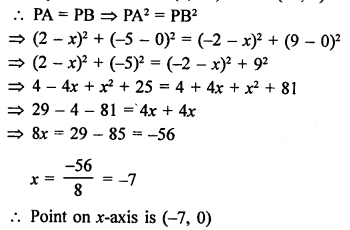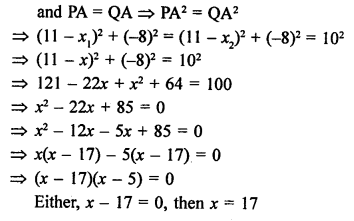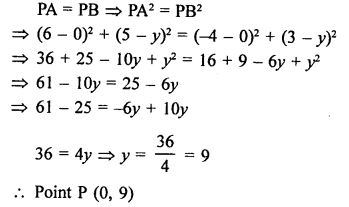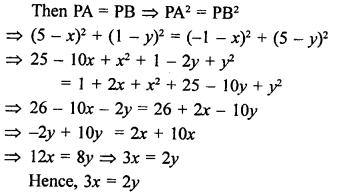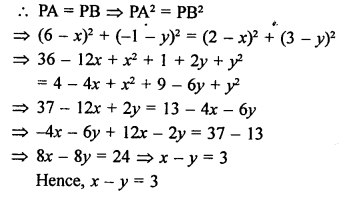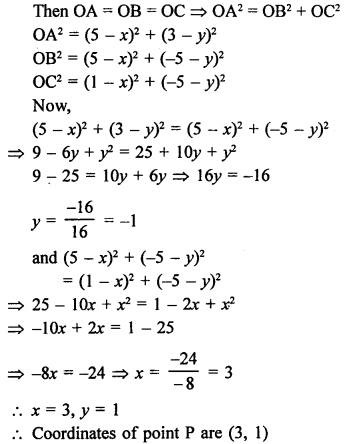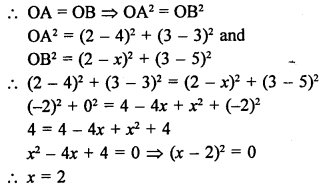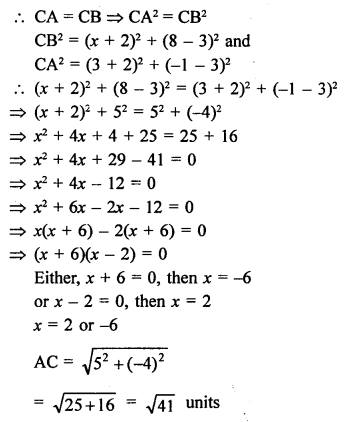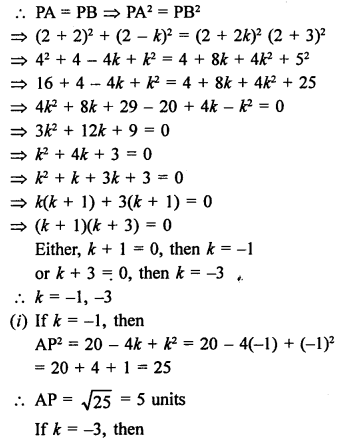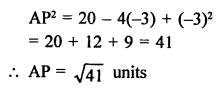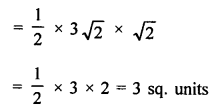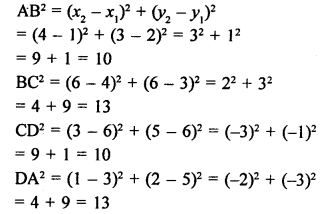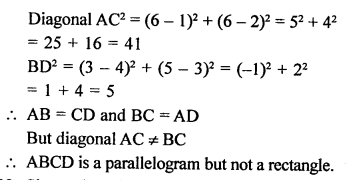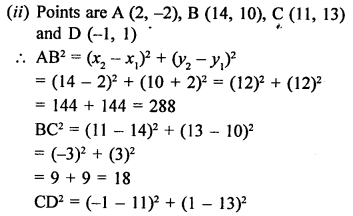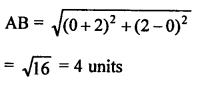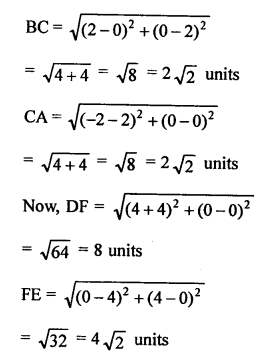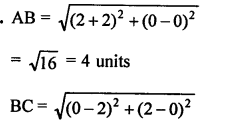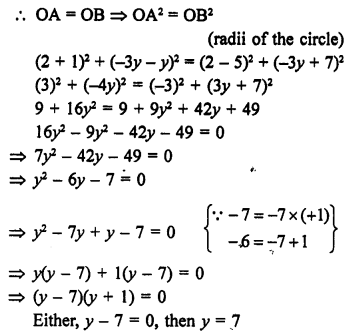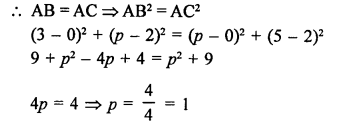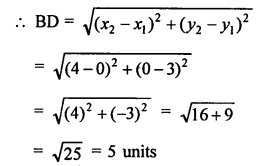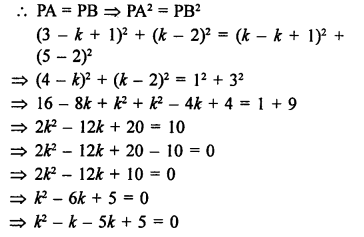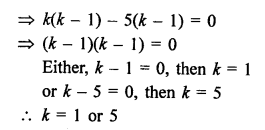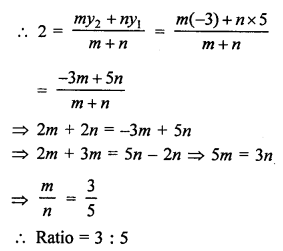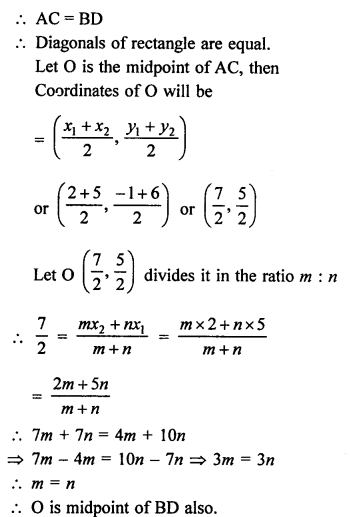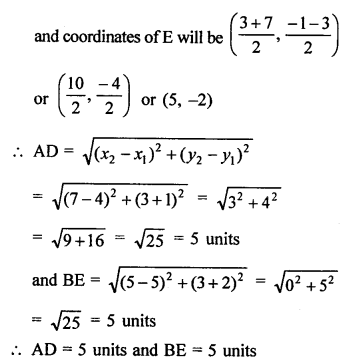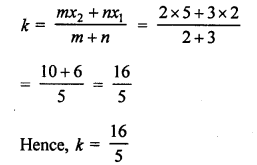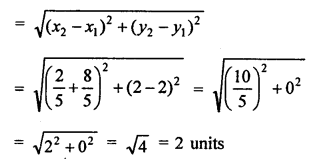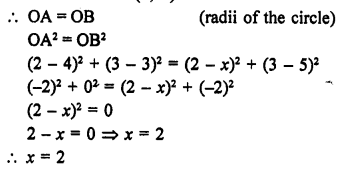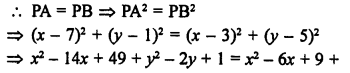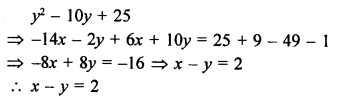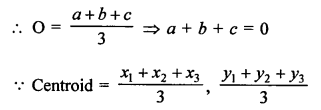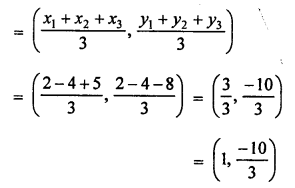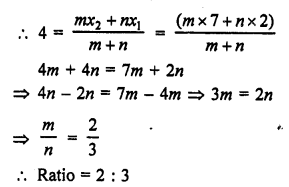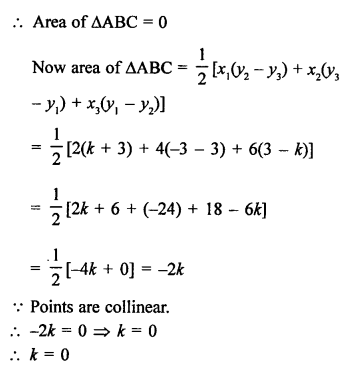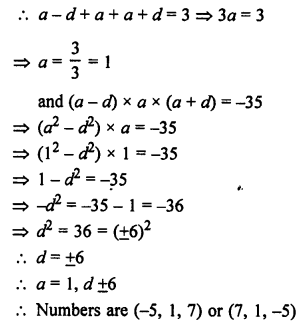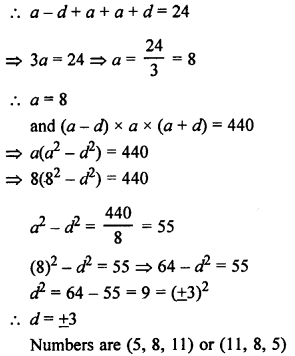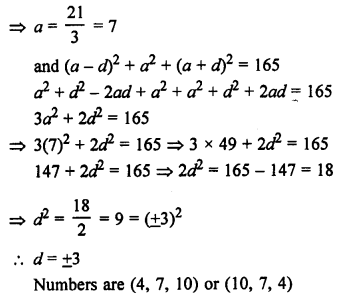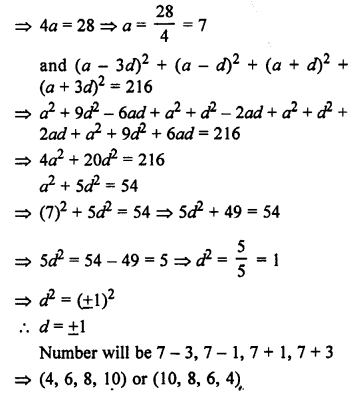RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry MCQS
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry MCQS.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16A
- RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16B
- RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16C
- RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16D
- RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry MCQS
Choose the correct answer in each of the following questions.
Question 1.
Solution:
Distance between P (-6, 8) and origin O (0, 0)
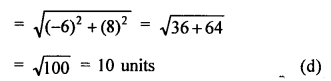
Question 2.
Solution:
Distance of the point (-3, 4) from x-axis = 4 (c)
Question 3.
Solution:
Let point P (x, 0) is on x-axis which is equidistant from points A (-1, 0) and B (5, 0)
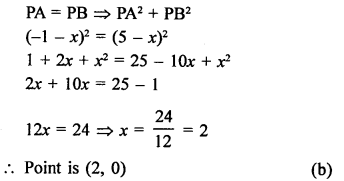
Question 4.
Solution:
R (5, 6) is the midpoint of the line segment joining the points A (6, 5) and B (4, y)
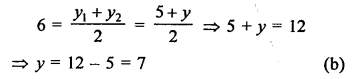
Question 5.
Solution:
Point C (k, 4) divides the join of points A (2, 6) and B (5, 1) in the ratio 2 : 3
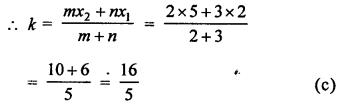
Question 6.
Solution:
Vertices of ∆ABC are A (0, 4), B (0, 0) and C (3, 0)
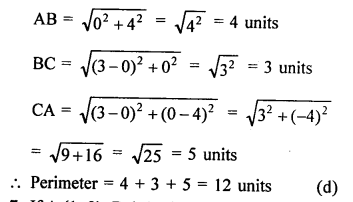
Question 7.
Solution:
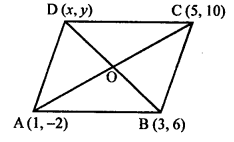
A (1, 3), B (-1, 2), C (2, 5) and D (x, 4) are the vertices of a ||gm ABCD.
AB = CD

Question 8.
Solution:
Points A (x, 2), B (-3, -4) and C (7, -5) are collinear
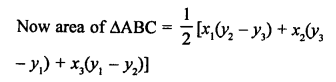
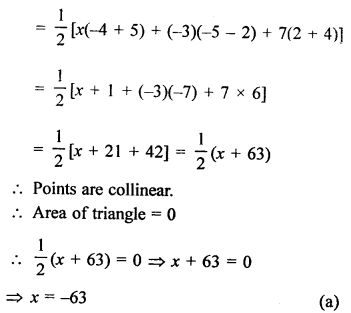
Question 9.
Solution:
Area of ∆ABC whose vertices are A (5, 0), B (8, 0) and C (8, 4)
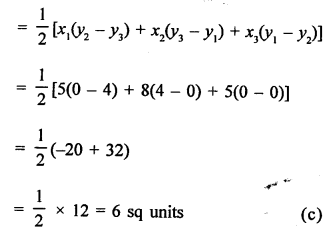
Question 10.
Solution:
Area of ∆ABC with vertices A (a, 0), O (0, 0) and B (0, b)
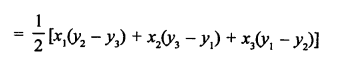
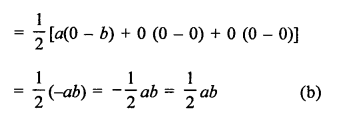
Question 11.
Solution:
P( \(\frac { a }{ 2 }\), 4) is midpoint of the line segment joining the points A (-6, 5) and B (-2, 3)
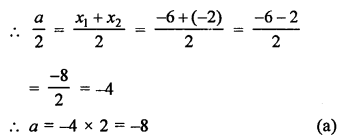
Question 12.
Solution:
ABCD is a rectangle whose three vertices are B (4, 0), C (4, 3) and D (0, 3)
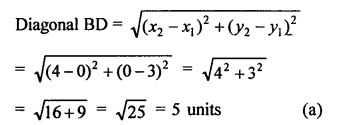
Question 13.
Solution:
Let coordinates of P be (x, 7)
P divides the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1
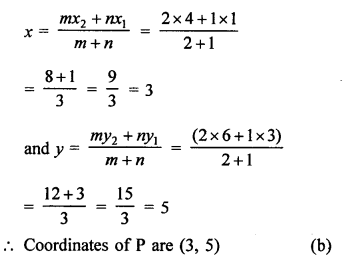
Question 14.
Solution:
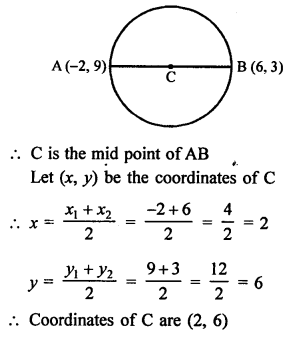
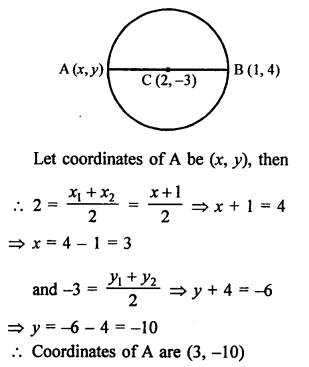
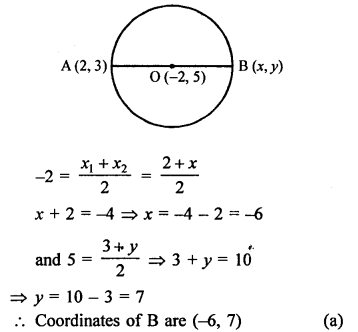
Let coordinates of one end of diameter of a circle are A (2, 3) coordinates of centre are (-2, 5)
Let coordinates of other end B of the diameter be (x, y)
Question 15.
Solution:
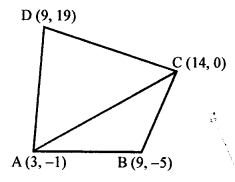
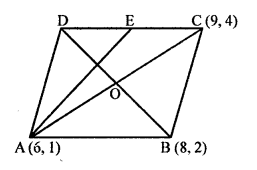
In the given figure, P (5, -3) and Q (3, y) are the points of trisection of the line segment joining A (7, -2) and B (1, -5)
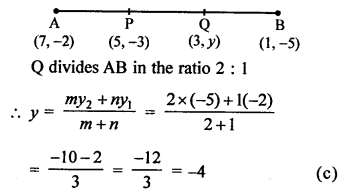
Question 16.
Solution:
Midpoint of AB is P (0, 4) coordinates of B are (-2, 3)

Question 17.
Solution:
Let point P (x, y) divides AB with vertices A(2, -5) and B (5, 2) in the ratio 2 : 3

Question 18.
Solution:
A (-6, 7) and B (-1, -5) two points, then
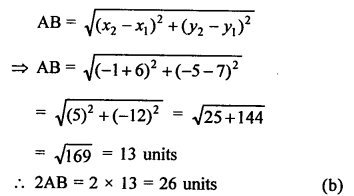
Question 19.
Solution:
Let point P (x, 0) on x-axis is equidistant from A (7, 6) and B (-3, 4)
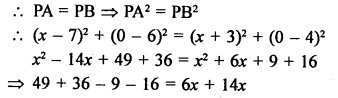
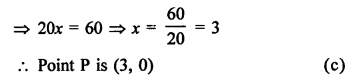
Question 20.
Solution:
Distance of P (3, 4) from the x-axis = 4 units. (b)
Question 21.
Solution:
Let a point P (x, 0) on x-axis divides the line segment.
AB joining the points A (2, -3) and B (5, 6) in the ratio m : n.
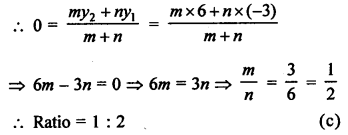
Question 22.
Solution:
Let a point A (0, y) on y-axis divides the line segment PQ joining the points P (-4, 2) and Q (8, 3) in the ratio of m : n.
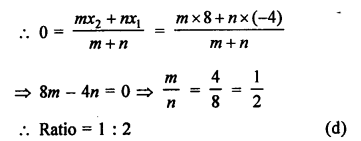
Question 23.
Solution:
P (-1, 1) is the midpoint of line segment joining the points A (-3, b) and B (1, b + 4)
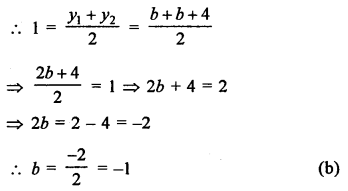
Question 24.
Solution:
Let the point P (x, y) divides the line segment joining the points A (2, -2) and B (3, 7) in the ratio k : 1, then
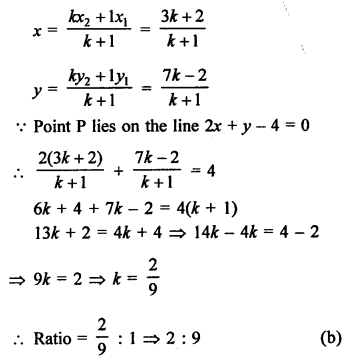
Question 25.
Solution:
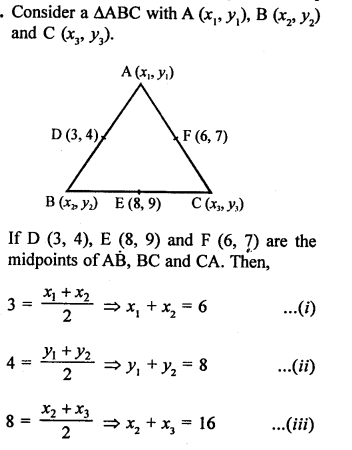
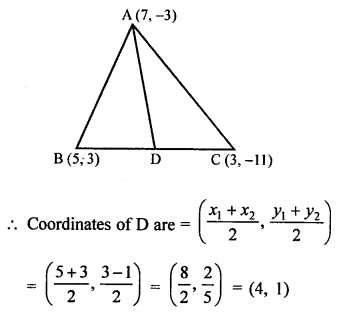
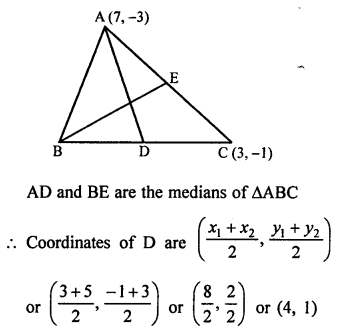
AD is the median of ∆ABC with vertices A (4, 2), B (6, 5) and C (1, 4)
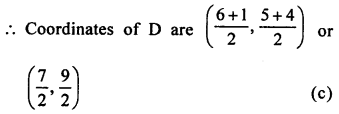
Question 26.
Solution:
A (-1, 0), B (5, -2) and C (8, 2) are the vertices of a ∆ABC then centroid
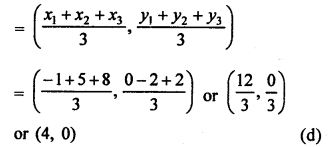
Question 27.
Solution:
Two vertices A (-1, 4), B (5, 2) of a ∆ABC and its centroid G is (0, -3)
Let (x, y) be the co-ordinates of vertex C, then
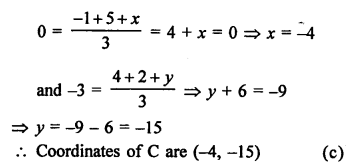
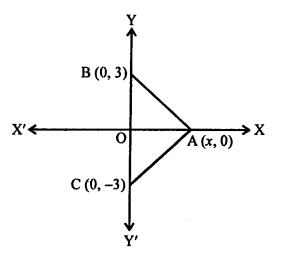
Question 28.
Solution:
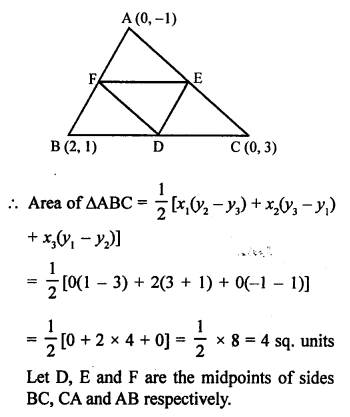
Points A (-4, 0), B (4, 0) and C (0, 3) are vertices of a ∆ABC.
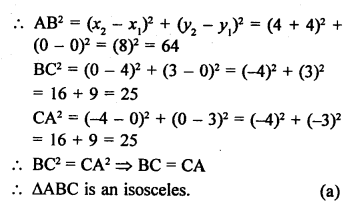
Question 29.
Solution:
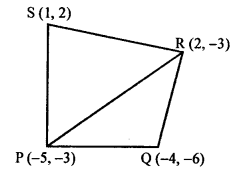
Points P (0, 6), Q (-5, 3) and R (3, 1) are the vertices of a ∆PQR

Question 30.
Solution:
Points A (2, 3), B (5, k) and C (6, 7) are collinear
Area of ∆ABC = 0
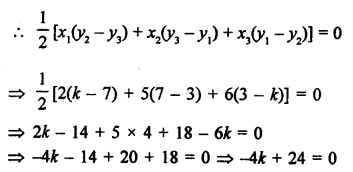
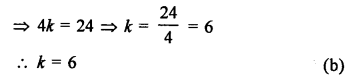
Question 31.
Solution:
Points A (1, 2), B (0, 0) and C (a, b) are collinear
Area of ∆ABC = 0
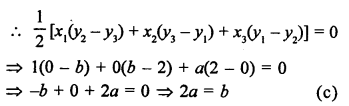
Question 32.
Solution:
A (3, 0), B (7, 0) and C (8, 4)
Area ∆ABC
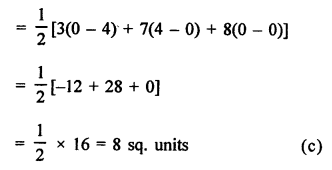
Question 33.
Solution:
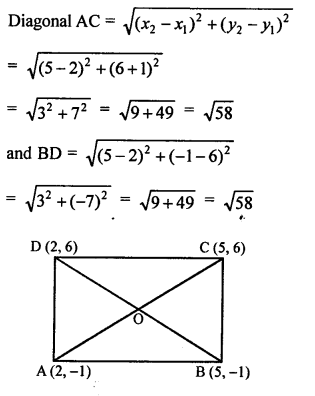
AOBC is a rectangle with vertices A (0, 3), O (0, 0) and B (5, 0) and each diagonal of rectangle are equal.
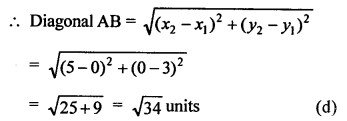
Question 34.
Solution:
Points are A (4, p) and B (1, 0)
Distance = 5 units
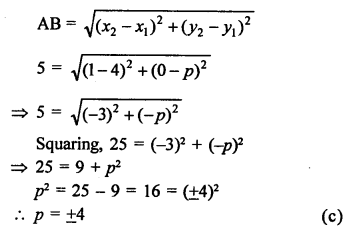
Hope given RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.