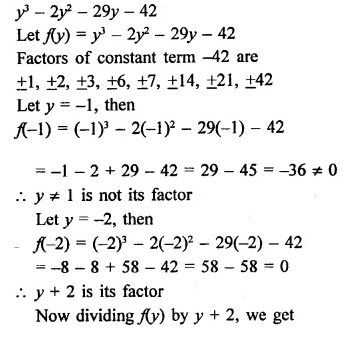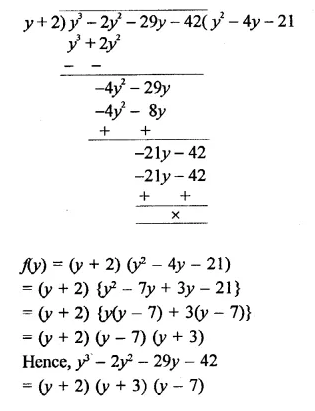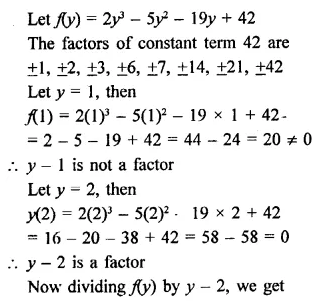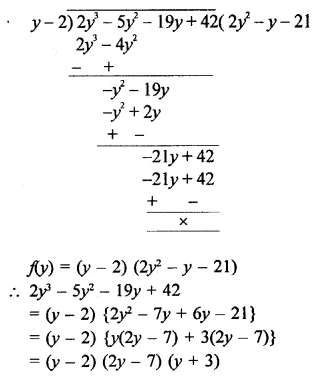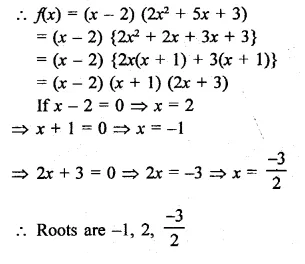Tag: Maths Class 9 RD Sharma Solutions

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

Question 1.
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
(i) -2x + 3y = 12
(ii) x-\(\frac { y }{ 2 }\) -5 = 0
(iii) 2x + 3y = 9.35
(iv) 3x = -7y
(v) 2x + 3 = 0
(vi) y – 5 = 0
(vii) 4 = 3x
(viii) y = \(\frac { x }{ 2 }\)
Solution:
(i) -2x + 3y = 12
⇒  -2x + 3y – 12 = 0
Here a -2, b = 3, c = – 12
(ii) x – \(\frac { y }{ 2 }\) -5 = 0
Here a = 1, b =\(\frac { 1 }{ 2 }\) ,c = -5
(iii) 2x + 3y = 9.35
⇒  2x + 3y – 9.35 = 0
Here a = 2, b = 3, c = – 9.35
(iv) 3x = -7y
⇒  3x + 7y + 0 = 0
Here a = 3, b = 7,c = 0
(v) 2x + 3 = 0
⇒ 2x + 0y + 3 = 0
Here a = 2, b = 0, c = 3
(vi) y-5 = 0 ⇒ ox+y-5 = 0
Here a = 0, b = 1, c = -5
(vii) 4 = 3x
⇒ 3x – 4 = 0
⇒ 3x + 0y – 4 = 0
Here a = 3, b = 0, c = -4
(Viii) y= \(\frac { x }{ 2 }\)
⇒  \(\frac { x }{ 2 }\) – y+ 0 = 0
⇒  x-2y + 0 = 0
Here a = 1, y = -2, c = 0

Question 2.
Write each of the following as an equation in two variables.
(i) 2x = -3
(ii) y = 3
(iii) 5x = \(\frac { 7 }{ 2 }\)
(iv) y =\(\frac { 3 }{ 2 }\)x
Solution:
(i) 2x = -3⇒  2x + 3 = 0
⇒ 2x + 0y + 3 = 0
(ii) y= 3 ⇒  y-3=0
⇒  0x+ y-3 = 0
(iii) 5x =\(\frac { 7 }{ 2 }\) ⇒ 10x = 7
⇒  10x + 0y – 7 = 0
(iv) y=\(\frac { 3 }{ 2 }\)x⇒2y = 3x
⇒ 3x – 2y + 0 = 0

Question 3.
The cost of ball pen is ₹5 less than half of the cost of fountain pen. Write this statement as a linear equation in two variables.
Solution:
Let cost of a fountain pen = ₹x
and cost of ball pen = ₹y
∴ According to the condition,
y = \(\frac { x }{ 2 }\) -5
⇒  2y = x – 10
⇒  x – 2y – 10 = 0

 

Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

Using factor theorem, factorize each of the following polynomials:
Question 1.
x³ + 6x² + 11x + 6
Solution:

Question 2.
x³ + 2x² – x – 2
Solution:

Question 3.
x³ – 6x² + 3x + 10
Solution:

Question 4.
x⁴ – 7x³ + 9x² + x- 10
Solution:

Question 5.
3x³ – x² – 3x + 1
Solution:

Question 6.
x³ – 23x² + 142x – 120        [NCERT]
Solution:

Question 7.
y³ – 7y + 6
Solution:
Let f(y) = y³ – 7y + 6

Question 8.
X³ -10x² – 53x – 42
Solution:

Question 9.
y³ – 2y²– 29y – 42
Solution:

Question 10.
2y³ – 5y² – 19y + 42
Solution:

Question 11.
x³ + 13² + 32x + 20      [NCERT]
Solution:

Question 12.
x³ – 3x² – 9x – 5 [NCERT]
Solution:

Question 13.
2y³+ y² – 2y – 1      [NCERT]
Solution:

Question 14.
x³ – 2x² – x + 2
Solution:

Question 15.
Factorize each of the following polynomials:
(i) x³ + 13x² + 31x – 45 given that x + 9 is a factor
(ii) 4x³ + 20x² + 33x + 18 given that 2x + 3 is a factor
Solution:

Question 16.
x⁴ – 2x³ – 7x² + 8x + 12
Solution:

Question 17.
x⁴ + 10x³ + 35x² + 50x + 24
Solution:

Question 18.
2x⁴ – 7x³ – 13x² + 63x – 45
Solution:

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

Question 1.
Define zero or root of a polynomial.
Solution:
A real number a is a zero or root of a polynomial f(x) if f(α) = 0

Question 2.
If x = \(\frac { 1 }{ 2 }\) is a zero of the polynomial f(x) =  8x³ + ax² – 4x + 2, find the value of a.
Solution:

Question 3.
Write the remainder when the polynomial f(x) = x³+x²-3x + 2is divided by x + 1.
Solution:
f(x) = x³+x²-3x + 2
Let x + 1 = 0, then x = -1
∴ Remainder =(-1)
Now,f(-1) = (-1)³ + (-1)² – 3(-1) + 2
= -1 + 1+ 3 + 2 = 5
∴ Remainder = 5

Question 4.
Find the remainder when x³ + 4x² + 4x – 3 is divided by x.
Solution:
f(x) = x³ + 4x² + 4x – 3
Dividing f(x) by x, we get
Let x = 0, then
f(x) = 0 + 0 + 0 – 3 = -3
∴  Remainder = -3

Question 5.
If x + 1 is a factor of x³ + a, then write the value of a.
Solution:
Let f(x) = x³ + a
∴ x + 1 is a factor of fx)
Let x + 1 = 0
⇒ x = -1
∴ f(-1) = x³ + a
= (-1)³ + a = -1 + a
∴  x + 1 is a factor
∴  Remainder = 0
∴  -1 + a = 0 ⇒  a = 1
Hence a = 1

Question 6.
If f(x) = x⁴-2x³ + 3x² – ax – b when divided by x – 1, the remainder is 6, then find the value of a + b.
Solution:
f(x) = x⁴ – 2x³ + 3x² – ax – b
Dividing f(x) by x – 1, the remainder = 6
Now let x – 1 = 0, then x = 1
∴  f(1) = (1)⁴ – 2(1)³ + 3(1)² -ax 1-b
= 1 -2 + 3-a-b = 2-a-b
∴ Remainder = 6
∴ 2 – a – b = 6  ⇒ a + b = 2 – 6 = -4
Hence a + b = -4

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.1
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Question 1.
In the figure, lines l₁ and l₂ intersect at O, forming angles as shown in the figure. If x = 45, find the values of y, z and n.

Solution:
Two lines l₁ and l₂ intersect each other at O ∠x = 45°
∵ ∠z = ∠x (Vertically opposite angles)
= 45°
But x + y = 180° (Linear pair)
⇒45° + y= 180°
⇒ y= 180°-45°= 135°
But u = y (Vertically opposite angles)
∴ u = 135°
Hence y = 135°, z = 45° and u = 135°

Question 2.
In the figure, three coplanar lines intersect at a point O, forming angles as shown in the figure. Find the values of x, y, z and u.

Solution:
Three lines AB, CD and EF intersect at O
∠BOD = 90°, ∠DOF = 50°
∵ AB is a line
∴ ∠BOD + ∠DOF + FOA = 180°
⇒ 90° + 50° + u = 180°
⇒ 140° + w = 180°
∴ u= 180°- 140° = 40°
But x = u (Vertically opposite angles)
∴ x = 40°
Similarly, y = 50° and z = 90°
Hence x = 40°, y = 50°, z = 90° and u = 40°

Question 3.
In the figure, find the values of x, y and z.

Solution:
Two lines l₁ and l₂ intersect each other at O
∴ Vertically opposite angles are equal,
∴ y = 25° and x = z
Now 25° + x = 180° (Linear pair)
⇒ x= 180°-25°= 155°
∴ z = x = 155°
Hence x = 155°, y = 25°, z = 155°

Question 4.
In the figure, find the value of x.

Solution:
∵ EF and CD intersect each other at O
∴ Vertically opposite angles are equal,
∴ ∠1 = 2x
AB is a line
3x + ∠1 + 5x = 180° (Angles on the same side of a line)
⇒ 3x + 2x + 5x = 180°
⇒ 10x = 180° ⇒ x = \(\frac { { 180 }^{ \circ } }{ 10 }\)  = 18°
Hence x = 18°

Question 5.
If one of the four angles formed by two intersecting lines is a right angle, then show that each of the four angles is a right angle.
Solution:
Given : Two lines AB and CD intersect each other at O. ∠AOC = 90°

To prove: ∠AOD = ∠BOC = ∠BOD = 90°
Proof : ∵ AB and CD intersect each other at O
∴ ∠AOC = ∠BOD and ∠BOC = ∠AOD (Vertically opposite angles)
∴ But ∠AOC = 90°
∴ ∠BOD = 90°
∴ ∠AOC + ∠BOC = 180° (Linear pair)
⇒ 90° + ∠BOC = 180°
∴ ∠BOC = 180° -90° = 90°
∴ ∠AOD = ∠BOC = 90°
∴ ∠AOD = ∠BOC = ∠BOD = 90°

Question 6.
In the figure, rays AB and CD intersect at O.
(i) Determine y when x = 60°
(ii) Determine x when y = 40°

Solution:
In the figure,
AB is a line
∴ 2x + y = 180° (Linear pair)
(i) If x = 60°, then
2 x 60° + y = 180°
⇒ 120° +y= 180°
∴ y= 180°- 120° = 60°
(ii) If y = 40°, then
2x + 40° = 180°
⇒ 2x = 180° – 40° = 140°
⇒ x= \(\frac { { 140 }^{ \circ } }{ 2 }\)  =70°
∴ x = 70°

Question 7.
In the figure, lines AB, CD and EF intersect at O. Find the measures of ∠AOC, ∠COF, ∠DOE and ∠BOF.

Solution:
Three lines AB, CD and EF intersect each other at O
∠AOE = 40° and ∠BOD = 35°
(i) ∠AOC = ∠BOD (Vertically opposite angles)
= 35°
AB is a line
∴ ∠AOE + ∠DOE + ∠BOD = 180°
⇒ 40° + ∠DOE + 35° = 180°
⇒ 75° + ∠DOE = 180°
⇒ ∠DOE = 180°-75° = 105°
But ∠COF = ∠DOE (Vertically opposite angles)
∴ ∠COF = 105°
Similarly, ∠BOF = ∠AOE (Vertically opposite angles)
⇒ ∠BOF = 40°
Hence ∠AOC = 35°, ∠COF = 105°, ∠DOE = 105° and ∠BOF = 40°

Question 8.
AB, CD and EF are three concurrent lines passing through the point O such that OF bisects ∠BOD. If ∠BOF = 35°, find ∠BOC and ∠AOD.
Solution:
AB, CD and EF intersect at O. Such that OF is the bisector of
∠BOD ∠BOF = 35°

∵ OF bisects ∠BOD,
∴ ∠DOF = ∠BOF = 35° (Vertically opposite angles)
∴ ∠BOD = 35° + 35° = 70°
But ∠BOC + ∠BOD = 180° (Linear pair)
⇒ ∠BOC + 70° = 180°
⇒ ∠BOC = 180°-70°= 110°
But ∠AOD = ∠BOC (Vertically opposite angles)
= 110°
Hence ∠BOC = 110° and ∠AOD =110°

Question 9.
In the figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.

Solution:
In the figure, AB and CD intersect each other at O
∠AOC + ∠BOE = 70°
∠BOD = 40°

AB is a line
∴ ∠AOC + ∠BOE + ∠COE = 180° (Angles on one side of a line)
⇒ 70° + ∠COE = 180°
⇒ ∠COE = 180°-70°= 110°
and ∠AOC = ∠BOD (Vertically opposite angles)
⇒ ∠AOC = 40°
∴ ∠BOE = 70° – 40° = 30°
and reflex ∠COE = 360° – ∠COE
= 360°- 110° = 250°

Question 10.
Which of the following statements are true (T) and which are false (F)?
(i) Angles forming a linear pair are supplementary.
(ii) If two adjacent angles are equal, then each angle measures 90°.
(iii) Angles forming a linear pair can both be acute angles.
(iv) If angles forming a linear pair are equal, then each of these angles is of measure 90°.
Solution:
(i) True.
(ii) False. It can be possible if they are a linear pair.
(iii) False. In a linear pair, if one is acute, then the other will be obtuse.
(iv) True.

Question 11.
Fill in the blanks so as to make the following statements true:
(i) If one angle of a linear pair is acute, then its other angle will be …….. .
(ii) A ray stands on a line, then the sum of the two adjacent angles so formed is ……… .
(iii) If the sum of two adjacent angles is 180°, then the …… arms of the two angles are opposite rays.
Solution:
(i) If one angle of a linear pair is acute, then its other angle will be obtuse.
(ii) A ray stands on a line, then the sum of the two adjacent angles so formed is 180°.
(iii) If the sum of two adjacent angles is 180°, then the uncommon arms of the two angles are opposite rays.

Question 12.
Prove that the bisectors of a pair of vertically opposite angles are in the same straight line.
Solution:
Given : Lines AB and CD intersect each other at O.
OE and OF are the bisectors of ∠AOC and ∠BOD respectively

To prove : OE and OF are in the same line
Proof : ∵ ∠AOC = ∠BOD (Vertically opposite angles)
∵ OE and OF are the bisectors of ∠AOC and ∠BOD
∴ ∠1 = ∠2 and ∠3 = ∠4
⇒ ∠1 = ∠2 = \(\frac { 1 }{ 2 }\) ∠AOC and
∠3 = ∠4 = \(\frac { 1 }{ 2 }\) ∠BOD
∴ ∠1 = ∠2 = ∠3 = ∠4
∵ AOB is a line
∴ ∠BOD + ∠AOD = 180° (Linear pair)
⇒ ∠3 + ∠4 + ∠AOD = 180°
⇒ ∠3 + ∠1 + ∠AOD = 180° (∵ ∠1 = ∠4)
∴ EOF is a straight line

Question 13.
If two straight lines intersect each other, prove that the ray opposite to the bisector of one of the angles thus formed bisects the vertically opposite angle.
Solution:
Given : AB and CD intersect each other at O. OE is the bisector of ∠AOD and EO is produced to F.

To prove : OF is the bisector of ∠BOC
Proof : ∵ AB and CD intersect each other at O
∴ ∠AOD = ∠BOC (Vertically opposite angles)
∵OE is the bisector of ∠AOD
∴ ∠1 = ∠2
∵ AB and EF intersect each other at O
∴∠1 = ∠4 (Vertically opposite angles) Similarly, CD and EF intersect each other at O
∴ ∠2 = ∠3
But ∠1 = ∠2
∴ ∠3 = ∠4
OF is the bisector of ∠BOC

Hope given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1
• RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles VSAQS

Question 1.
Define the following tenns :
(i) Line segment
(ii) Collinear points
(iii) Parallel lines  
(iv) Intersecting lines
(v) Concurrent lines   
(vi) Ray
(vii) Half-line.
Solution:
(i) A line segment is a part of a line which lies between two points on it and it is denoted as \(\overline { AB }\)   or only by AB. It has two end points and is measureable.

(ii) Three or more points which lie on the same straight line, are called collinear points.
(iii) Two lines which do not intersect each other at any point are called parallel lines.
(iv) If two lines have one point in common, are called intersecting lines.
(v) If two or more lines which pass through a common point are called concurrent lines.
(vi) Ray : A part of a line which has one end point.
(vii) Half line : If A, B, C, be the points on a line l, such that A lies between B and C and we delete the point from line l, two parts of l that remain are each called a half-line.

Question 2.
(i) How many lines can pass through a given point?
(ii) In how many points can two distinct lines at the most intersect?
Solution:
(i) Infinitely many lines can pass through a given point.
(ii) Two distinct lines at the most intersect at one point.

Question 3.
(i) Given two points P and Q, find how many line segments do they determine?
(ii) Name the line segments determined by the three collinear points P, Q and R.
Solution:
(i) Only one line segment can be drawn through two given points P and Q.
(ii) Three collinear points P, Q and R, three lines segments determine : \(\overline { PQ }\) , \(\overline { QR }\)  and \(\overline { PR }\) .

Question 4.
Write the truth value (T/F) of each of the following statements:
(i) Two lines intersect in a point.
(ii) Two lines may intersect in two points.
(iii) A segment has no length.
(iv) Two distinct points always determine a line.
(v) Every ray has a finite length.
(vi) A ray has one end-point only.
(vii) A segment has one end-point only.
(viii) The ray AB is same as ray BA.
(ix) Only a single line may pass through a given point.
(x) Two lines are coincident if they have only one point in common.
Solution:
(i)  False : As two lines do not intersect also any a point.
(ii) False : Two lines intersect at the most one point.
(iii) False : A line segment has definitely length.
(iv) True.
(v) False : Every ray has no definite length.
(vi) True.
(vii) False : A segment has two end point.
(viii)False : Rays AB and BA are two different rays.
(ix) False : Through a given point, infinitely many lines can pass.
(x) False : Two lines are coincident of each and every points coincide each other.

Question 5.
In the figure, name the following:


(i) Five line segments.
(ii) Five rays.
(iii) Four collinear points.
(iv) Two pairs of non-intersecting line segments.
Solution:
From the given figure,
(i) Five line segments are AC, PQ, PR, RS, QS.
(ii) Five rays : \(\xrightarrow { PA }\)  , \(\xrightarrow { RB }\)  , \(\xrightarrow { PB }\)  , \(\xrightarrow { CS }\)  , \(\xrightarrow { DS }\)  .
(iii) Four collinear points are : CDQS, APR, PQL, PRB.
(iv) Two pairs of non-intersecting line segments an AB and CD, AP and CD, AR and CS, PR and QS.

Question 6.
Fill in the blanks so as to make the following statements true:
(i) Two distinct points in a plane determine a _____ line.
(ii) Two distinct_____ in a plane cannot have more than one point in common.
(iii) Given a line and a point, not on the line, there is one and only _____  line which passes through the given point and is_____ to the given line.
(iv) A line separates a plane into ____ parts namely the____  and the____  itself.
Solution:
(i) Two distinct points in a plane determine a unique line.
(ii) Two distinct lines in a plane cannot have more than one point in common.
(iii) Given a line and a point, not on the line, there is one and only perpendicular line which passes through the given point and is perpendicular to the given line.
(iv) A line separates a plane into three parts namely the two half planes, and the one line itself.

 

Hope given RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

Question 1.
If f(x) = 2x³ – 13x² + 17x + 12, find
(i) f (2)
(ii) f (-3)
(iii) f(0)
Solution:
f(x) = 2x³ – 13x² + 17x + 12
(i) f(2) = 2(2)³ – 13(2)² + 17(2) + 12
= 2 x 8-13 x 4+17 x 2+12
= 16-52 + 34 + 12
= 62 – 52
= 10
(ii) f(-3) = 2(-3)³ – 13(-3)² + 17 x (-3) + 12
= 2 x (-27) – 13 x 9 + 17 x (-3) + 12
= -54 – 117 -51 + 12
= -222 + 12
= -210
(iii) f(0) = 2 x (0)³ – 13(0)² + 17 x 0 + 12
= 0-0 + 0+ 12 = 12

Question 2.
Verify whether the indicated numbers are zeros of the polynomials corresponding to them in the following cases: [NCERT]

Solution:

Question 3.
If x = 2 is a root of the polynomial f(x) = 2x²-3x + la, find the value of a.
Solution:
p(x) = 2x² – 3x + 7a
∵ x = 2 is its zero, then
p(0) = 0
∴ p( 2) = 2(2)² – 3×2 + la = 0
⇒2 x 4-3 x2 + 7a = 0
⇒ 8 – 6 + 7o = 0
⇒2 + 7a = 0
⇒ 7a = -2 ⇒ a =\(\frac { -2 }{ 7 }\)
∴ Hence a = \(\frac { -2 }{ 7 }\)

Question 4.
If x = –\(\frac { 1 }{ 2 }\) is a zero of the polynomial p(x) = 8x³ – ax² – x + 2, find the value of a.
Solution:

Question 5.
If x = 0 and x = -1 are the roots of the polynomial f(x) = 2x³ – 3x² + ax + b, find the value of a and b.
Solution:
f(x) = 2x³ – 3x² + ax + b
∵ x = 0 and x = -1 are its zeros
∴ f(0) = 0 and f(-1) = 0
Now, f(0) = 0
⇒  2(0)³ – 3(0)² + a x 0 + b = 0
⇒ 0-0 + 0 + b= 0
∴ b = 0
and f(-1) = 0
⇒ 2(-1)³ – 3(-1)² + a(-1) + b = 0
⇒  2 x (-1) – 3 x 1 + a x (-1) + b = 0
⇒ -2 -3-a + b = 0
⇒ -2-3-a + 0 = 0
⇒ -5- a = 0=>a =-5
Hence a = -5, b = 0

Question 6.
Find the integral roots of the polynomial f(x) = x³ + 6x² + 11x + 6.
Solution:
f(x) = x³ + 6x² + 11x + 6
Construct = 6 = ±1, ±2, +3, ±6
If x = 1, then
f(1) = (1)³ + 6(1)² + 11 x 1 + 6
= 1+ 6+11+ 6 = 24
∵  f(x) ≠ 0, +0
∴ x = 1 is not its zero
Similarly, f(-1) = (-1)³ + 6(-1)² + 11(-1) + 6
= -1 + 6 x 1-11+6
=-1+6-11+6
= 12-12 = 0
∴  x = -1 is its zero
f(-2) = (-2)³ + 6(-2)² + 11 (-2) + 6
= -8 + 24 – 22 + 6
= -30 + 30 = 0
∴ x = -2 is its zero
f(-3) = (-3)³ + 6(-3)² + 11 (-3) + 6
= -27 + 54 – 33 + 6 = 60 – 60 = 0
∴  x = -3 is its zero
x = -1, -2, -3 are zeros of f(x)
Hence roots of f(x) are -1, -2, -3

Question 7.
Find the rational roots of the polynomial f(x) = 2x³ + x² – 7x – 6.
Solution:

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1
• RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles VSAQS

Question 1.
How many least number of distinct points determine a unique line?
Solution:
At least two distinct points determine a unique line.

Question 2.
How many lines can be drawn through both of the given points?
Solution:
Through two given points, one line can be drawn.

Question 3.
How many lines can be drawn through a given point?
Solution:
Through a given point, infinitely many lines can be drawn.

Question 4.
in how many points two distinct lines can intersect?
Solution:
Two distinct lines can intersect at the most one point.

Question 5.
In how many points a line, not in a plane, can intersect the plane?
Solution:
A line not in a plane, can intersect the plane at one point.

Question 6.
In how many points two distinct planes can intersect?
Solution:
Two distinct planes can intersect each other at infinite number of points.

Question 7.
In how many lines two distinct planes can intersect?
Solution:
Two distinct planes intersect each other in one line.

Question 8.
How many least number of distinct points determine a unique plane?
Solution:
Three non-collinear points can determine a unique plane.

Question 9.
Given three distinct points in a plane, how many lines can be drawn by joining them?
Solution:
Through three given points, one line can be drawn of they are collinear and three if they are non-collinear.

Question 10.
How many planes can be made to pass through a line and a point not on the line?
Solution:
Only one plane can be made to pass through a line and a point not on the line.

Question 11.
How many planes can be made to pass through two points?
Solution:
Infinite number of planes can be made to pass through two points.

Question 12.
How many planes can be made to pass through three distinct points?
Solution:
Infinite number of planes can be made of they are collinear and only one plane, if they are non-collinear.

Hope given RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

Question 1.
Write the equation representing x-axis.
Solution:
The equation of x-axis is, y = 0.

Question 2.
Write the equation representing y-axis.
Solution:
The equation of y-axis is, x = 0.

Question 3.
Write the equation of a line passing through the point (0, 4) and parallel to x-axis.
Solution:
The equation of the line passing through the point (0,4) and parallel to x-axis will be y = 4.

Question 4.
Write the equation of a line passing through the point (3, 5) and parallel to x-axis.
Solution:
The equation of the line passing through the point (3, 5) and parallel to x-axis will be y = 5.

Question 5.
Write the equation of a line parallel toy-axis and passing through the point (-3, -7).
Solution:
The equations of the line passing through the point (-3, -7) and parallel to y-axis will be x = -3.

Question 6.
A line passes through the point (-4, 6) and is parallel to x-axis. Find its equation. A line passes through the point (-4, 6) and is parallel to x-axis. Find its equation.
Solution:
A line parallel to x-axis and passing through the point (-4, 6) will be y = 6.

Question 7.
Solve the equation 3x – 2 = 2x + 3 and represent the solution on the number line.
Solution:
3x – 2 = 2x + 3
⇒  3x – 2x = 3 + 2 (By terms formation)
⇒  x = 5
∴ x = 5
Solution on the number line is

Question 8.
Solve the equation 2y – 1 = y + 1 and represent it graphically on the coordinate plane.

Solution:
2y – 1 = y + 1
⇒ 2y – y = 1 +1
⇒  y = 2
∴ It is a line parallel to x-axis at a distance of 2 units above the x-axis is y = 2.

Question 9.
If the point (a, 2) lies on the graph of the linear equation 2x – 3y + 8 = 0, find the value of a.
Solution:
∵ Points (a, 2) lies on the equation
2x – 3y + 8 = 0
∴ It will satisfy the equation,
Now substituting the value of x = a, y = 2 in the equation
⇒ 2a – 3 x 2+ 8= 0
⇒ 2a + 2= 0
⇒ 2a = -2
⇒ a = \(\frac { -2 }{ 2 }\) = -1
∴ a = -1

Question 10.
Find the value of k for which the point (1, -2) lies on the graph of the linear equation, x – 2y + k = 0.
Solution:
∵ Point (1, -2) lies on the graph of the equation x – 2y + k = 0
∴ x = 1, y = -2 will satisfy the equation
Now substituting the value of x = 1, y = -2 in it
1-2 (-2) + k = 0
⇒  1 + 4 + k = 0
⇒  5+ k = 0 ⇒  k =-5
∴  k = -5

Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.1
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Question 1.
In the figure, OA and OB are opposite rays:
(i) If x = 25°, what is the value of y?
(ii) If y = 35°, what is the value of x?

Solution:
(i) If x = 25°
∴ 3x = 3 x 25° = 75°
But ∠AOC + ∠BOC = 180° (Linear pair)
⇒ ∠AOC + 75° = 180°
⇒ ∠AOC = 180° – 75°
⇒ ∠AOC = 105°
∴ 2y + 5 = 105° ⇒ 2y= 105° – 5° = 100°
⇒ y = \(\frac { { 100 }^{ \circ } }{ 2 }\)  = 50°
∴ If x = 25° then y = 50°
(ii) If y = 35°, then ∠AOC = 2y + 5
∴ 2y + 5 = 2 x 35° + 5 = 70° + 5 = 75°
But ∠AOC + ∠BOC = 180° (Linear pair)
⇒ 75° + ∠BOC = 180°
⇒ ∠BOC = 180°-75°= 105°
∴ 3x = 105° ⇒ x = \(\frac { { 105 }^{ \circ } }{ 3 }\) = 35°
∴ x = 35°

Question 2.
In the figure, write all pairs of adjacent angles and all the linear pairs.

Solution:
In the given figure,
(i) ∠AOD, ∠COD; ∠BOC, ∠COD; ∠AOD, ∠BOD and ∠AOC, ∠BOC are the pairs of adjacent angles.
(ii) ∠AOD, ∠BOD and ∠AOC, ∠BOC are the pairs of linear pairs.

Question 3.
In the figure, find x, further find ∠BOC, ∠COD and ∠AOD.

Solution:
In the figure,
AOB is a straight line
∴ ∠AOD + ∠DOB = 180° (Linear pair)
⇒ ∠AOD + ∠DOC + ∠COB = 180°
⇒ x+ 10° + x + x + 20 = 180°
⇒ 3x + 30° = 180°
⇒ 3x= 180° -30°= 150°
⇒ x = \(\frac { { 150 }^{ \circ } }{ 3 }\) = 50°
∴ x = 50°
Now ∠BOC =x + 20° = 50° + 20° = 70°
∠COD = x = 50°
and ∠AOD = x + 10° = 50° + 10° = 60°

Question 4.
In the figure, rays OA, OB, OC, OD and OE have the common end point O. Show that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.

Solution:
Produce AO to F such that AOF is a straight line
Now ∠AOB + ∠BOF = 180° (Linear pair)

⇒ ∠AOB + ∠BOC + ∠COF = 180° …(i)
Similarly, ∠AOE + ∠EOF = 180°
⇒ ∠AOE + ∠EOD + ∠DOF = 180° …(ii)
Adding (i) and (ii)
∠AOB + ∠BOC + ∠COF + ∠DOF + ∠EOD + ∠AOE = 180° + 180°
⇒ ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°
Hence proved.

Question 5.
In the figure, ∠AOC and ∠BOC form a linear pair. If a – 2b = 30°, find a and b.

Solution:
∠AOC + ∠BOC = 180° (Linear pair)
⇒ a + 6 = 180° …(i)
and a – 2b = 30° …(ii)
Subtracting (ii) from (i), 3b = 150°
⇒ b = \(\frac { { 150 }^{ \circ } }{ 3 }\) = 50°
and a + 50° = 180°
⇒ a= 180°-50°= 130°
∴ a = 130°, b = 50°

Question 6.
How many pairs of adjacent angles are formed when two lines intersect in a point?
Solution:
If two lines AB and CD intersect each other at a point O, then four pairs of linear pairs are formed i.e.
∠AOC, ∠BOC; ∠BOC, ∠BOD; ∠BOD, ∠AOD and ∠AOD, ∠AOC

Question 7.
How many pairs of adjacent angles, in all, can you name in the figure.

Solution:
In the given figure 10 pairs of adjacent angles are formed as given below:
∠AOB, ∠BOC; ∠AOB, ∠BOD; ∠AOC, ∠COD; ∠AOD, ∠BOE; ∠AOB, ∠BOE; ∠AOC, ∠COF; ∠BOC, ∠COD; ∠BOC, ∠COE; ∠COD, ∠DOE and ∠BOD, ∠DOE

Question 8.
In the figure, determine the value of x.

Solution:
In the figure
∠AOC + ∠COB + ∠BOD +∠AOD = 360 (angles at a point )

⇒ 3x + 3x + x + 150° = 360°
⇒ 7x – 360° – 150° = 210°
⇒ x = \(\frac { { 210 }^{ \circ } }{ 7 }\) = 30°
∴ x = 30°

Question 9.
In the figure, AOC is a line, find x.

Solution:
In the figure,
∠AOB + ∠BOC = 180° (Linear pair)
⇒ 70° + 2x = 180°
⇒ 2x = 180° – 70°
⇒ 2x = 110°⇒x = \(\frac { { 110 }^{ \circ } }{ 2 }\) = 55°
∴ x = 55°

Question 10.
In the figure, POS is a line, find x.

Solution:
In the figure, POS is a line
∴ ∠POQ + ∠QOS = 180° (Linear pair)
⇒ ∠POQ + ∠QOR + ∠ROS = 180°
⇒ 60° + 4x + 40° = 180°
⇒ 4x + 100° – 180°
⇒ 4x = 180° – 100° = 80°
⇒ x = \(\frac { { 80 }^{ \circ } }{ 4 }\) =20°
∴ x = 20°

Question 11.
In the figure, ACB is a line such that ∠DCA = 5x and ∠DCB = 4x. Find the value of x.

Solution:
ACB is a line, ∠DCA = 5x and ∠DCB = 4x
∠ACD + ∠DCB = 180° (Linear pair)
⇒ 5x + 4x = 180° ⇒ 9x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 9 }\) = 20°
∴ x = 20°
∴ ∠ACD = 5x = 5 x 20° = 100° and ∠DCB = 4x = 4 x 20° = 80°

Question 12.
Given ∠POR = 3x and ∠QOR = 2x + 10°, find the value ofx for which POQ will be a line.

Solution:
∠POR = 3x and ∠QOR = 2x + 10°
If POQ is a line, then
∠POR + ∠QOR = 180° (Linear pair)
⇒ 3x + 2x + 10° = 180°
⇒ 5x = 180° – 10° = 170°
⇒ x = \(\frac { { 170 }^{ \circ } }{ 5 }\) = 34°
∴ x = 34°

Question 13.
What value ofy would make AOB, a line in the figure, if ∠AOC = 4y and ∠BOC = (6y + 30).

Solution:
In the figure,
AOB is a line if
∠AOC + ∠BOC = 180°
⇒ 6y + 30° + 4y= 180°
⇒ 10y= 180°-30°= 150°
150°
⇒ y = \(\frac { { 150 }^{ \circ } }{ 10 }\) = 15°
∴ y = 15°

Question 14.
In the figure, OP, OQ, OR and OS are four rays. Prove that: ∠POQ + ∠QOR + ∠SOR + ∠POS = 360° [NCERT]

Solution:
In the figure, OP, OQ, OR and OS are the rays from O
To prove : ∠POQ + ∠QOR + ∠SOR + ∠POS = 360°
Construction : Produce PO to E

Proof: ∠POQ + ∠QOE = 180° (Linear pair)
Similarly, ∠EOS + ∠POS = 180°
Adding we get,
∠POQ + ∠QOR + ∠ROE + ∠EOS + ∠POS = 180° + 180° ,
⇒ ∠POQ + ∠QOR + ∠ROS + ∠POS = 360° Hence ∠POQ + ∠QOR + ∠SOR + ∠POS = 360°

Question 15.
In the figure, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ respectively. If ∠POS = x, find ∠ROT. [NCERT]

Solution:
Ray OR stands on a line POQ forming ∠POS and ∠QOS

OR and OT the angle bisects of ∠POS and ∠QOS respectively. ∠POS = x
But ∠POS + ∠QOS = 180° (Linear pair)
⇒ x + ∠QOS = 180°
⇒ ∠QOS = 180° – x
∵ OR and OT are the bisectors of angle

Question 16.
In the figure, lines PQ and RS intersect each other at point O. If ∠POR : ∠ROQ = 5 : 7. Find all the angles. [NCERT]

Solution:
Lines PQ and PR, intersect each other at O
∵ Vertically opposite angles are equal
∴ ∠POR = ∠QOS and ∠ROQ = ∠POS
∠POR : ∠ROQ = 5:7
Let ∠POR = 5x and ∠ROQ = 7x
But ∠POR + ∠ROQ = 180° (Linear pair)
∴ 5x + 7x = 180° ⇒ 12x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 12 }\) = 15°
∴ ∠POR = 5x = 5 x 15° = 75°
and ∠ROQ = 7x = 7 x 15° = 105°
But ∠QOS = POR = 75° (Vertically opposite angles)
and ∠POS = ∠ROQ = 105°

Question 17.
In the figure, a is greater than b by one third of a right-angle. Find the values of a and b.

Solution:
In the figure,
∠AOC + ∠BOC = 180° (Linear pair)
⇒ a + b =180° …(i)
But a = b + \(\frac { 1 }{ 3 }\) x 90° = b + 30°
⇒ a – b = 30° …(ii)
Adding (i) and (ii)
210°
2a = 210° ⇒ a = \(\frac { { 210 }^{ \circ } }{ 2 }\) = 105°
and 105° + b = 180°
⇒ b = 180° – 105°
∴ b = 75°
Hence a = 105°, b = 75°

Question 18.
In the figure, ∠AOF and ∠FOG form a linear pair.
∠EOB = ∠FOC = 90° and ∠DOC = ∠FOG = ∠AOB = 30°

(i) Find the measures of ∠FOE, ∠COB and ∠DOE.
(ii) Name all the right angles.
(iii) Name three pairs of adjacent complementary angles.
(iv) Name three pairs of adjacent supplementary angles.
(v) Name three pairs of adjacent angles.
Solution:
In the figure,
∠AOF and ∠FOG form a linear pair
∠EOB = ∠FOC = 90°
∠DOC = ∠FOG = ∠AOB = 30°

(i) ∠BOE = 90°, ∠AOB = 30°
But ∠BOE + ∠AOB + ∠EOG = 180°
⇒ 30° + 90° + ∠EOG = 180°
∴∠EOG = 180° – 30° – 90° = 60°
But ∠FOG = 30°
∴ ∠FOE = 60° – 30° = 30°
∠COD = 30°, ∠COF = 90°
∴ ∠DOF = 90° – 30° = 60°
∠DOE = ∠DOF – ∠EOF
= 60° – 30° = 30°
∠BOC = BOE – ∠COE
= 90° – 30° – 30° = 90° – 60° = 30°
(ii) Right angles are,
∠AOD = 30° + 30° + 30° = 90°
∠BOE = 30° + 30° + 30° = 90°
∠COF = 30° + 30° + 30° = 90°
and ∠DOG = 30° + 30° + 30° = 90°
(iii) Pairs of adjacent complementaiy angles are ∠AOB, ∠BOD; ∠AOC, ∠COD; ∠BOC, ∠COE
(iv) Pairs of adjacent supplementary angles are ∠AOB, ∠BOG; ∠AOC, ∠COG and ∠AOD, ∠DOG
(v) Pairs of adjacent angles are ∠BOC, ∠COD; ∠COD, ∠DOE and ∠DOE, ∠EOF.

Question 19.
In the figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = \(\frac { 1 }{ 2 }\)(∠QOS – ∠POS). [NCERT]

Solution:
Ray OR ⊥ ROQ. OS is another ray lying between OP and OR.

To prove : ∠ROS = \(\frac { 1 }{ 2 }\)(∠QOS – ∠POS)
Proof : ∵ RO ⊥ POQ
∴ ∠POR = 90°
⇒ ∠POS + ∠ROS = 90° …(i)
⇒ ∠ROS = 90° – ∠POS
But ∠POS + ∠QOS = 180° (Linear pair)
= 2(∠POS + ∠ROS) [From (i)]
∠POS + ∠QOS = 2∠ROS + 2∠POS
⇒ 2∠ROS = ∠POS + ∠QOS – 2∠POS
= ∠QOS – ∠POS
∴ ROS = \(\frac { 1 }{ 2 }\) (∠QOS – ∠POS)

Hope given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

Question 1.
Write two solutions for each of the following equations
(i) 3x + 4y = 7           
(ii) x = 6y
(iii) x + πy = 4           
(iv) \(\frac { 2 }{ 3 }\) x – y = 4
Solution:


(ii)  x = 6y
Let y = 0, then
x = 6 x 0 = 0
∴ x = 0, y = 0
x = 0, y = 0 are the solutions of the equation
Let y= 1, then
x = 6 x 1 = 0                          –
∴ x = 6, y = 1 are the solutions of the equation.
(iii) x + πy = 4
Let x = 4, then
4 + πy = 4
⇒ πy = 4- 4 = 0
∴ y = 0
∴ x = 4, y = 0 are the solutions of the equation
Let x = 0, then
0 + πy = 4 ⇒ πy = 4

Question 2.
Check which of the following are solutions of the equations 2x – y =6 and which are not
(i) (3, 0)                    
(ii) (0, 6)
(iii) (2,-2)                 
(iv)(\(\sqrt { 3 } \) ,0)
(v) (\(\frac { 1 }{ 2 }\) ,-5)
Solution:
Equation is 2x – y = 6
(i) Solution is (3, 0) i.e. x = 3, y = 0
Substituting the value of x and y in the equation
2 x 3 – 0 = 6 ⇒ 6 – 0 = 6
6 = 6
Which is true
∴  (3, 0) is the solutions.
(ii) (0, 6) i.e. x =0, y =6
Substituting the value of x and y in the equation
2 x 0 – 6 = 6 ⇒  0-6 = 6
⇒ -6 = 6  which is not true
∴   (0, 6) is not its solution’
(iii) (2, -2) i.e. x = 2, y = -2
Substituting the value of x and y in the equation
2 x 2 – (-2) = 6 ⇒ 4 + 2 = 6
⇒ 6 = 6 which is true.
∴   (2, -2) is the solution.
(iv) (\(\sqrt { 3 } \),0) i.e. x = \(\sqrt { 3 } \) , y = 0,
Substituting the value of x and y in the equations
2 x \(\sqrt { 3 } \)-(0) = 6
⇒ 2\(\sqrt { 3 } \)-0 = 6
⇒  2 \(\sqrt { 3 } \) =  6 which is not true
∴ (\(\sqrt { 3 } \) > 0) is not the solution.

Question 3.
If x = -1, y = 2 is a solution of the equation 3x + 4y =k  Find the value of k.
Solution:
x = -1, y = 2
The equation is 3x + 4y = k
Substituting the value of x and y in it
3 x (-1) + 4 (2) = k
⇒ -3+ 8 = k
⇒  5 = k
∴ k = 5

Question 4.
Find the value of λ if x = -λ and y = \(\frac { 5 }{ 2 }\) is a solution of the equation x + 4y – 7 = 0.
Solution:
 x = -λ, y= \(\frac { 5 }{ 2 }\)
Equation is x + 4y – 7 = 0
Substituting the value of x and y,
-λ  + 4 x \(\frac { 5 }{ 2 }\) -7 = 0
⇒  -λ + 10 – 7 = 0
⇒  -λ +3 = 0
∴  -λ = -3
⇒  λ = 3
Hence λ = 3

Question 5.
If x = 2α + 1 and y = α – 1 is a solution of the equation 2x – 3y + 5 = 0, find the value of α.
Solution:
x = 2α + 1, y = α – 1
are the solution of the equation 2x – 3y + 5 – 0
Substituting the value of x and y
2(2α + 1) -3 (α – 1) + 5 = 0
⇒  4α+ 2-3α+ 3 + 5 = 0
⇒ α+10 = 0
⇒ α = -10
Hence α = -10

Question 6.
If x = 1, and y = 6 is a solution of the equation 8x – ay + a² = 0, find the values of a.
Solution:
x = 1, y = 6 is a solution of the equation
8x – ay + a² = 0
Substituting the value of x and y,
8 x 1-a x 6 + a² = o
⇒  8 – 6a + a² = 0
⇒  a² – 6a + 8 = 0
⇒  a² – 2a -4a + 8 = 0
⇒  a (a – 2) – 4 (a – 2) = 0
⇒  (a – 2) (a – 4) = 0
Either a – 2 = 0, then a = 2
or a – 4 = 0, then a = 4
Hence a = 2, 4

Question 7.
Write two solutions of the form x = 0, y = a and x = b, y = 0 for each of the following equations.
(i) 5x – 2y = 10
(ii) -4x + 3y = 12
(iii) 2x + 3y = 24
Solution:
(i)  5x – 2y = 10
Let x = 0, then

Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 8 Lines and Angles MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 8 Lines and Angles MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 8 Lines and Angles Ex 8.1
• RD Sharma Class 9 Solutions Chapter 8 Lines and Angles MCQS

Mark the correct alternative in each of the following:
Question 1.
The point of intersect of the co-ordiante axes is
(a) ordinate
(b) abscissa
(c) quadrant                 
(d) origin
Solution:
Origin    (d)

Question 2.
The abscissa and ordinate of the origin are
(a) (0, 0)
(b) (1, 0)
(c) (0, 1)                     
(d) (1, 1)
Solution:
The abscissa and ordinate of the origin are (0, 0).     (a) 

Question 3.
The measure of the angle between the co-ordinate axes is
(a) 0°                          
(b)   90°
(c) 180°                      
(d)   360°
Solution:
The measure of the angle between the coordinates of axes is 90°.     (b)

Question 4.
A point whose abscissa and ordinate are 2 and -5 respectively, lies in
(a) First quadrant
(b) Second quadrant
(c) Third  quadrant
(d) Fourth quadrant
Solution:
The point whose abscissa is 2 and ordinate -5 will lies in fourth quadrant.     (d)

Question 5.
Points (-4, 0) and (7, 0) lie
(a) on x-axis                
(b)   y-axis
(c) in first quadrant
(d) in second quadrant
Solution:
∵ The ordinates of both the points are 0
∴ They lie on x-axis            (a)

Question 6.
The ordinate of any point on x-axis is
(a) 0                           
(b) 1
(c) -1                          
(d) any number
Solution:
The ordinate of any point lying on x-axis is 0.          (a)

Question 7.
The abscissa of any point on y-axis is
(a) 0                           
(b) 1
(c) -1                          
(d) any number
Solution:
The abscissa of any point on y-axis is 0.          (a)

Question 8.
The abscissa of a point is positive in the
(a) First and Second quadrant
(b) Second and Third quadrant
(c) Third and Fourth quadrant
(d) Fourth and First quadrant
Solution:
The abscissa of a point is positive in the fourth and First quadrant.   (d)

Question 9.
A point whose abscissa is -3 and ordinate 2 lies in
(a) First quadrant         
(b) Second quadrant
(c) Third quadrant         
(d) Fourth quadrant
Solution:
A point (-3, 2) will lies in second quadrant.         (b)

Question 10.
Two points having same abscissae but different ordinates lie on
(a) x-axis
(b) y-axis
(c) a line parallel to y-axis
(d) a line parallel to x-axis
Solution:
Two points having same abscissae but different ordinates is a line parallel to y- axis.           (c)

Question 11.
The perpendicular distance of the point P (4, 3) from x-axis is
(a) 4                          
(b) 3
(c) 5                          
(d) none   of these
Solution:
The perpendiculat distance of the point P (4, 3) from x-axis is 3.         (b)

Question 12.
The perpendicular distance of the point P (4, 3) from y-axis is
(a) 4                          
(b) 3
(c) 5                          
(d) none of these
Solution:
perpendicular distance of the point P (4, 3) from y-axis is 4.         (a)

Question 13.
The distance of the point P (4, 3) from the origin is
(a) 4                          
(b) 3
(c) 5     
(d) 7
Solution:
The distance of the point P (4, 3) from origin is \(\sqrt { { 4 }^{ 2 }+{ 3 }^{ 3 } }\)
= \(\sqrt { 16+9 }\)
= \(\sqrt { 25 }\)   = 5        (c) 

Question 14.
The area of the triangle formed by the points A (2, 0), B (6, 0) and C (4, 6) is
(a) 24 sq. units
(b) 12 sq. units
(c) 10 sq. units            
(d) none of these
Solution:

Question 15.
The area of the triangle formed by the points P (0, 1), Q (0, 5) and R (3, 4) is
(a) 16 sq. units
(b) 8 sq. units
(c) 4 sq. units             
(d) 6 sq. units
Solution:

Hope given RD Sharma Class 9 Solutions Chapter 8 Lines and Angles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.