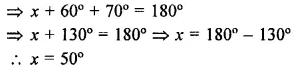RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1
Other Exercises
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.2
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.4
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS
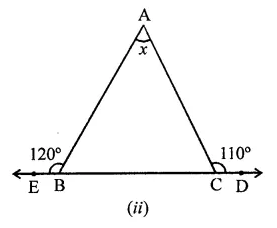
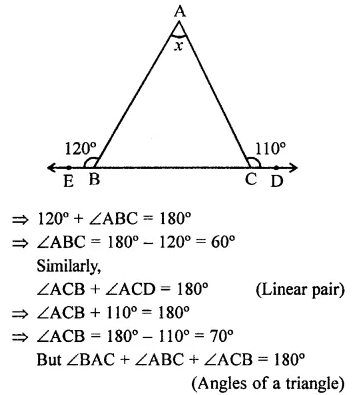
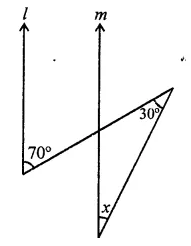
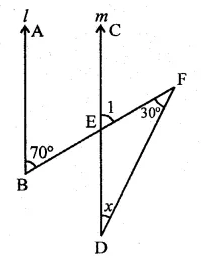
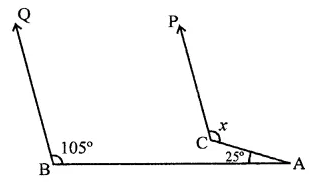
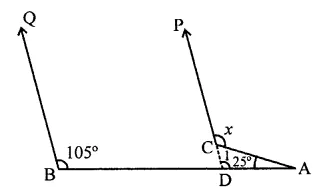
Question 1.
Three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
Solution:
Sum of four angles of a quadrilateral = 360°
Three angles are = 110°, 50° and 40°
∴ Fourth angle = 360° – (110° + 50° + 40°)
= 360° – 200° = 160°
Question 2.
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measures of each angle of the quadrilateral.
Solution:
Sum of angles of a quadrilateral ABCD = 360°
Ratio in angles = 1 : 2 : 4 : 5
Let first angle = x
Second angle = 2x
Third angle = 4x
and fourth angle = 5x
∴ x + 2x + 4x + 5x = 360°
⇒ 12x = 360° ⇒ x = \(\frac { { 360 }^{ \circ } }{ 12 }\) = 30°
∴ First angle = 30°
Second angle = 30° x 2 = 60°
Third angle = 30° x 4 = 120°
Fourth angle = 30° x 5 = 150°
Question 3.
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral. [NCERT]
Solution:
Sum of four angles of a quadrilateral = 360°
Ratio in the angles = 3 : 5 : 9 : 13
Let first angle = 3x
Then second angle = 5x
Third angle = 9x
and fourth angle = 13x
∴ 3x + 5x + 9x+ 13x = 360°
⇒ 30x = 360°
⇒ x = \(\frac { { 360 }^{ \circ } }{ 30 }\) = 12°
∴ First angle = 3x = 3 x 12° = 36°
Second angle = 5x = 5 x 12° = 60°
Third angle = 9x = 9 x 12° = 108°
Fourth angle = 13 x 12° = 156°
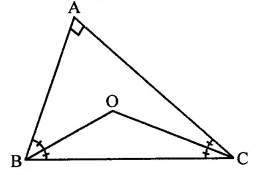
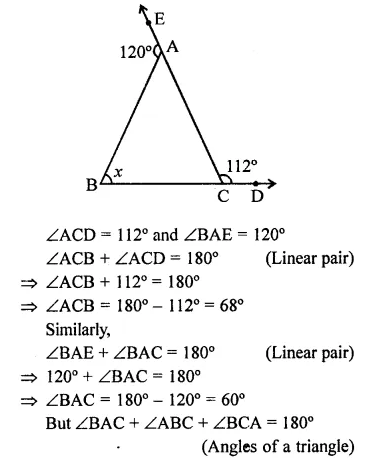
Question 4.
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively.
Prove that ∠COD = \(\frac { 1 }{ 2 }\) (∠A + ∠B).
Solution:

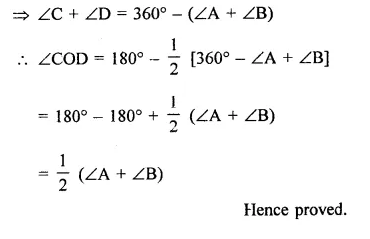
Hope given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.