RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
Other Exercises
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS
Question 1.
In ∆ABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
Solution:
In ∆ABC, ∠A = 40°, ∠B = 60°
But ∠A + ∠B + ∠C = 180°
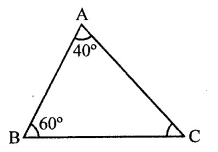
⇒ 40° + 60° + ∠C = 180°
⇒ ∠C = 180° = (40° + 60°)
= 180° – 100° = 80°
∵ ∠C = 80°, which is the greatest angle and
∠A = 40° is the smallest angle
∴ Side AB which is opposite to the greatest angle is the longest and side BC which is opposite to the smallest angle is the shortest.
Question 2.
In a ∆ABC, if ∠B = ∠C = 45°. which is the longest side?
Solution:
In ∆ABC, ∠B = ∠C = 45°
But ∠A + ∠B + ∠C = 180°
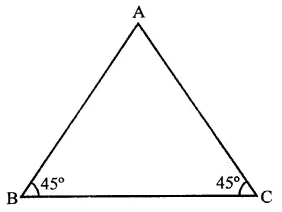
⇒ ∠A + 45° + 45° = 180°
⇒ ∠A + 90° = 180°
∴ ∠A = 180°-90° = 90°
∴∠A is the greatest
∴ Side BC opposite to it is the longest
Question 3.
In ∆ABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that :
(i) AD > CD
(ii) AD > AC
Solution:
Given : In AABC, side BC is produced to D such that BD = BC
∠A = 70° and ∠B = 60°
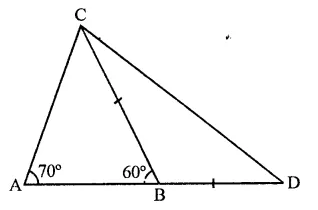
To prove :
(i) AD > CD (ii) AD > AC
Proof: In ∆ABC,
∠A = 70°, ∠B = 60°
But Ext. ∠CBD + ∠CBA = 180° (Linear pair)
∠CBD + 60° = 180° 3
⇒ ∠CBD = 180° – 60° = 120°
But in ∆BCD,
BD = BC
∴ ∠D = ∠BCD
But ∠D + ∠BCD = 180° – 120° = 60°
∴∠D = ∠BCD = \(\frac { { 60 }^{ \circ } }{ 2 }\) = 30°
and in ∆ABC,
∠A + ∠B + ∠C = 180°
⇒ 70° + 60° + ∠C = 180°
⇒ 130° + ∠C = 180°
∴ ∠C =180°- 130° = 50°
Now ∠ACD = ∠ACB + ∠BCD = 50° + 30° = 80°
(i) Now in ∆ACB,
∠ACD = 80° and ∠A = 70°
∴ Side AD > CD
(Greater angle has greatest side opposite to it)
(ii) ∵ ∠ACD = 80° and ∠D = 30°
∴ AD > AC
Question 4.
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
Solution:
We know that in a triangle, sum of any two sides is greater than the third side and 2 cm + 3 cm = 5 cm and 5 cm < 7 cm
∴ This triangle is not possible to draw
Question 5.
In ∆ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
Solution:
In ∆ABC, ∠B = 35°, ∠C = 65° and AP is the bisector of ∠BAC which meets BC in P.
Arrange PA, PB and PC in descending order In ∆ABC,
∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
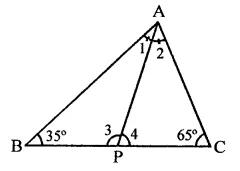
⇒ ∠A + 35° + 65° = 180°
∠A + 100°= 180°
∴ ∠A =180°- 100° = 80°
∵ PA is a bisector of ∠BAC
∴ ∠1 = ∠2 = \(\frac { { 80 }^{ \circ } }{ 2 }\) = 40°
Now in ∆ACP, ∠ACP > ∠CAP
⇒ ∠C > ∠2
∴ AP > CP …(i)
Similarly, in ∆ABP,
∠BAP > ∠ABP ⇒ ∠1 > ∠B
∴ BP > AP …(ii)
From (i) and (ii)
BP > AP > CP
Question 6.
Prove that the perimeter of a triangle is greater than the sum of its altitudes
Solution:
Given : In ∆ABC,
AD, BE and CF are altitudes
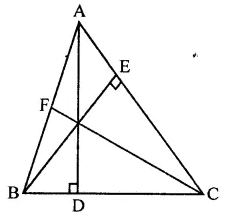
To prove : AB + BC + CA > AD + BC + CF
Proof : We know that side opposite to greater angle is greater.
In ∆ABD, ∠D = 90°
∴ ∠D > ∠B
∴ AB >AD …(i)
Similarly, we can prove that
BC > BE and
CA > CF
Adding we get,
AB + BC + CA > AD + BE + CF
Question 7.
In the figure, prove that:
(i) CD + DA + AB + BC > 2AC
(ii) CD + DA + AB > BC
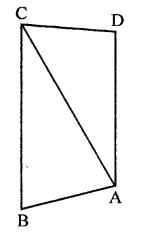
Solution:
Given : In the figure, ABCD is a quadrilateral and AC is joined
To prove :
(i) CD + DA + AB + BC > 2AC
(ii) CD + DA + AB > BC
Proof:
(i) In ∆ABC,
AB + BC > AC …(i)
(Sum of two sides of a triangle is greater than its third side)
Similarly in ∆ADC,
CD + DA > AC …(ii)
Adding (i) and (ii)
CD + DA + AB + BC > AC + AC
⇒ CD + DA + AB + BC > 2AC
(ii) In ∆ACD,
CD + DA > CA
(Sum of two sides of a triangle is greater than its third side)
Adding AB to both sides,
CD + DA + AB > CA + AB
But CA + AB > BC (in ∆ABC)
∴ CD + DA + AD > BC
Question 8.
Which of the following statements are true (T) and which are false (F)?
(i) Sum of the three sides of a triangle is less than the sum of its three altitudes.
(ii) Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
(iii) Sum of any two sides of a triangle is greater than the third side.
(iv) Difference of any two sides of a triangle is equal to the third side.
(v) If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
(vi) Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
Solution:
(i) False. Sum of three sides of a triangle is greater than the sum of its altitudes.
(ii) True.
(iii) True.
(iv) False. Difference of any two sides is less than the third side.
(v) True.
(vi) True.
Question 9.
Fill in the blanks to make the following statements true.
(i) In a right triangle, the hypotenuse is the ……. side.
(ii) The sum of three altitudes of a triangle is ……. than its perimeter.
(iii) The sum of any two sides of a triangle is …….. than the third side.
(iv) If two angles of a triangle are unequal, then the smaller angle has the ….. side opposite to it.
(v) Difference of any two sides of a triangle is……. than the third side.
(vi) If two sides of a triangle are unequal, then the larger side has ……… angle opposite to it.
Solution:
(i) In a right triangle, the hypotenuse is the longest side.
(ii) The sum of three altitudes of a triangle is less than its perimeter.
(iii) The sum of any two sides of a triangle is greater than the third side.
(iv) If two angles of a triangle are unequal, then the smaller angle has the smaller side opposite to it.
(v) Difference of any two sides of a triangle is less than the third side.
(vi) If two sides of a triangle are unequal, then the larger side has greater angle opposite to it.
Question 10.
O is any point in the interior of ∆ABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + OB + OC
(iii) OA + OB + OC > \(\frac { 1 }{ 2 }\) (AB + BC + CA)
Solution:
Given : In ∆ABC, O is any point in the interior of the ∆ABC, OA, OB and OC are joined
To prove :
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + OB + OC
(iii) OA + OB + OC > \(\frac { 1 }{ 2 }\) (AB + BC + CA)
Construction : Produce BO to meet AC in D.
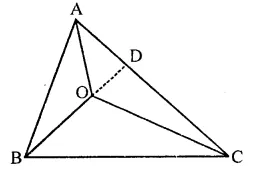
Proof: In ∆ABD,
(i) AB + AD > BD (Sum of any two sides of a triangle is greater than third)
⇒ AB + AD > BO + OD …(i)
Similarly, in ∆ODC,
OD + DC > OC …(ii)
Adding (i) and (ii)
AB + AD + OD + DC > OB + OD + OC
⇒ AB + AD + DC > OB + OC
⇒ AB + AC > OB + OC
(ii) Similarly, we can prove that
BC + AB > OA + OC
and CA + BC > OA + OB
(iii) In ∆OAB, AOBC and ∆OCA,
OA + OB > AB
OB + OC > BC
and OC + OA > CA
Adding, we get
2(OA + OB + OC) > AB + BC + CA
∴ OA + OB + OO > \(\frac { 1 }{ 2 }\) (AB + BC + CA)
Question 11.
Prove that in a quadrilateral the sum of all the sides is greater than the sum of its diagonals.
Solution:
Given : In quadrilateral ABCD, AC and BD are its diagonals,
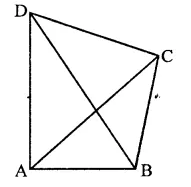
To prove : AB + BC + CD + DA > AC + BD
Proof: In ∆ABC,
AB + BC > AC …(i)
(Sum of any two sides of a triangle is greater than its third side)
Similarly, in ∆ADC,
DA + CD > AC …(ii)
In ∆ABD,
AB + DA > BD …(iii)
In ∆BCD,
BC + CD > BD …(iv)
Adding (i), (ii), (iii) and (iv)
2(AB + BC + CD + DA) > 2AC + 2BD
⇒ 2(AB + BC + CD + DA) > 2(AC + BD)
∴ AB + BC + CD + DA > AC + BD
Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.