RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS

Question 1.
Solution:
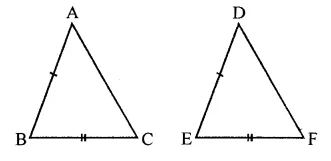
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.

In AABC and ADEF,
∆ABC ≅ ∆DEF
and AB = DE, BC = EF
∴ ∠A = ∠D, ∠B = ∠E and ∠C = ∠F

Question 2.
Solution:
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C = ∠F. Are the two triangles necessarily congruent?

No, as the triangles are equiangular, so similar.

Question 3.
Solution:
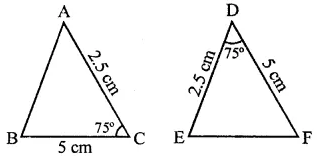
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5 cm and ∠D = 75°. Are two triangles congruent?
Yes, triangles are congruent (SAS axiom)

Question 4.
Solution:
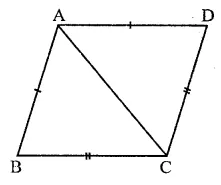
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
Yes, these are congruent
In two triangles ABC are ADC,
AB = AD (Given)
BC = CD (Given)
and AC = AC (Common)
∴ ∆sABC ≅ AADC (SSS axiom)

Question 5.
Solution:
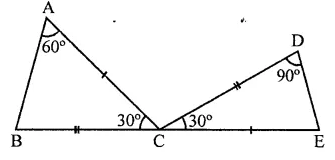
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C – 30° and ∠D = 90°. Are two triangles congruent?
Yes, triangles are congruent because,
In ∆ABC, and ∆CDE,
AC = CE
BC = CD ∠C = 30°
∴ ∆ABC ≅ ∆CDE (SAS axiom)

Question 6.
Solution:
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.

Given : In ∆ABC, AB = AC
BE and CF are two medians

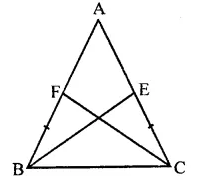
To prove : BE = CF
Proof: In ∆ABE and ∆ACF.
AB = AC (Given)
∠A = ∠A (Common)
AE = AF (Half of equal sides)
∴ ∆ABE ≅ ∆ACF (SAS axiom)
∴ BE = CF (c.p.c.t.)

Question 7.
Solution:
Find the measure of each angle of an equilateral triangle.

In ∆ABC,
AB = AC = BC

∵ AB = AC
∴ ∠C = ∠B …(i)
(Angles opposite to equal sides)
Similarly,
AC = BC
∴ ∠B = ∠A …(ii)
From (i) and (ii),
∠A = ∠B = ∠C
But ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
∴ ∠A + ∠B + ∠C = \(\frac { { 180 }^{ \circ } }{ 3 }\)  = 60°

Question 8.
Solution:
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ∆ADE ≅ ∆BCE.

Given : An equilateral ACDE is formed on the side of square ABCD. AE and BE are joined

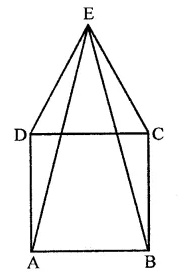
To prove : ∆ADE ≅ ∆BCE
Proof : In ∆ADE and ∆BCE,
AD = BC (Sides of a square)
DE = CE (Sides of equilateral triangle)
∠ADE = ∠BCE(Each = 90° + 60° = 150°)
∴ AADE ≅ ABCE (SAS axiom)

Question 9.
Solution:
Prove that the sum of three altitude of a triangle is less than the sum of its sides.

Given : In ∆ABC, AD, BE and CF are the altitude of ∆ABC

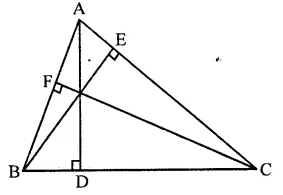
To prove : AD + BE + CF < AB + BC + CA
Proof : In right ∆ABD, ∠D = 90°
Then other two angles are acute
∵ ∠B < ∠D
∴ AD < AB …(i)
Similarly, in ∆BEC and ∆ABE we can prove thatBE and CF < CA …(iii)
Adding (i), (ii), (iii)
AD + BE -t CF < AB + BC + CA

Question 10.
Solution:
In the figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.

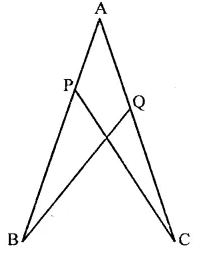
Given : In the figure, AB = AC, ∠B = ∠C
To prove : BQ = CP
Proof : In ∆ABQ and ∆ACP
AB = AC (Given)
∠A = ∠A (Common)
∠B = ∠C (Given)
∴ ∆ABQ ≅ ∆ACP (ASA axiom)
∴ BQ = CP (c.p.c.t.)

Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.