RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
Other Exercises
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS
Question 1.
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
Solution:
Given : In ∆ABC, D is mid-point of BC and DE ⊥ AB, DF ⊥ AC and DE = DF
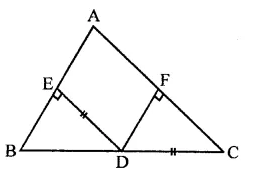
To Prove : ∆ABC is an isosceles triangle
Proof : In right ∆BDE and ∆CDF,
Side DE = DF
Hyp. BD = CD
∴ ∆BDE ≅ ∆CDF (RHS axiom)
∴ ∠B = ∠C (c.p.c.t.)
Now in ∆ABC,
∠B = ∠C (Prove)
∴ AC = AB (Sides opposite to equal angles)
∴ AABC is an isosceles triangle
Question 2.
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ∆ABC is an isosceles.
Solution:
Given : In ∆ABC,
BE ⊥ AC and CF ⊥ AB
BE = CF
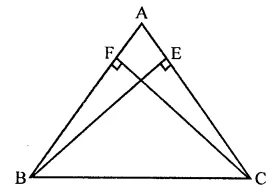
To prove : AABC is an isosceles triangle
Proof : In right ABCE and ABCF Side
BE = CF (Given)
Hyp. BC = BC (Common)
∴ ∆BCE ≅ ∆BCF (RHS axiom)
∴ ∠BCE = ∠CBF (c.p.c.t.)
∴ AB = AC (Sides opposite to equal angles)
∴ ∆ABC is an isosceles triangle
Question 3.
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
Solution:
Given : A point P lies in the angle ABC and PL ⊥ BA and PM ⊥ BC and PL = PM. PB is joined
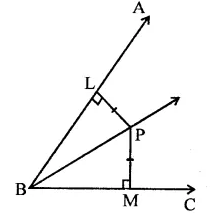
To prove : PB is the bisector ∠ABC,
Proof : In right ∆PLB and ∆PMB
Side PL = PM (Given)
Hyp. PB = PB (Common)
∴ ∆PLB ≅ ∆PMB (RHS axiom)
∴ ∆PBL = ∆PBM (c.p.c.t.)
∴ PB is the bisector of ∠ABC
Question 4.
In the figure, AD ⊥ CD and CB ⊥ CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.
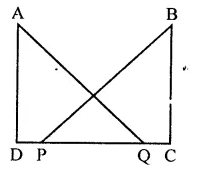
Solution:
Given : In the figure,
AD ⊥ CD and CB ⊥ CD, AQ = BP and DP = CQ
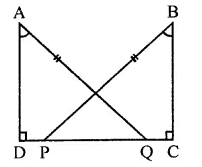
To prove : ∠DAQ = ∠CBP
Proof : ∵ DP = CQ
∴ DP + PQ = PQ + QC
⇒ DQ = PC
Now in right ∆ADQ and ∆BCP
Side DQ = PC (Proved)
Hyp. AQ = BP
∴ ∆ADQ ≅ ∆BCP (RHS axiom)
∴ ∠DAQ = ∠CBP (c.p.c.t.)
Question 5.
Which of the following statements are true (T) and which are false (F):
(i) Sides opposite to equal angles of a triangle may be unequal.
(ii) Angles opposite to equal sides of a triangle are equal.
(iii) The measure of each angle of an equilateral triangle is 60°.
(iv) If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles.
(v) The bisectors of two equal angles of a triangle are equal.
(vi) If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
(vii) The two altitudes corresponding to two equal sides of a triangle need not be equal.
(viii)If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
(ix) Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
Solution:
(i) False : Sides opposite to equal angles of a triangle are equal.
(ii) True.
(iii) True.
(iv) False : The triangle is an isosceles triangle.
(v) True.
(vi) False : The triangle is an isosceles.
(vii) False : The altitude an equal.
(viii) False : If one side and hypotenuse of one right triangle on one side and hypotenuse of the other right triangle are equal, then triangles are congruent.
(ix) True.
Question 6.
Fill in the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are …….
(ii) Angle opposite to equal sides of a triangle are …….
(iii) In an equilateral triangle all angles are …….
(iv) In a ∆ABC if ∠A = ∠C, then AB = …….
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = ……..
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is ……… CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ∆ABC ≅ ∆……
Solution:
(i) Sides opposite to equal angles of a triangle are equal.
(ii) Angle opposite to equal sides of a triangle are equal.
(iii) In an equilateral triangle all angles are equal.
(iv) In a ∆ABC, if ∠A = ∠C, then AB = BC.
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = AC.
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is equal to CE.
(vii) In right triangles ABC and DEF, it hypotenuse AB = EF and side AC = DE, then ∆ABC ≅ ∆EFD.
Question 7.
ABCD is a square, X and Y are points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
Solution:
Given : In square ABCD, X and Y are points on side AD and BC respectively and AY = BX
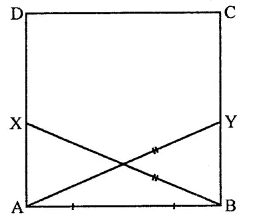
To prove : BY = AX
∠BAY = ∠ABX
Proof: In right ∆BAX and ∆ABY
AB =AB (Common)
Hyp. BX = AY (Given)
∴ ∆BAX ≅ ∆ABY (RHS axiom)
∴ AX = BY (c.p.c.t.)
∠ABX = ∠BAY (c.p.c.t.)
Hence, BY = AX and ∠BAY = ∠ABX.
Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.