RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS

Question 1.
BD and CE are bisectors of ∠B and ∠C of an isosceles ∠ABC with AB = AC. Prove that BD = CE.
Solution:
Given : In ∆ABC, AB = AC
BD and CE are the bisectors of ∠B and ∠C respectively
To prove : BD = CE
Proof: In ∆ABC, AB = AC
∴ ∠B = ∠C (Angles opposite to equal sides)
∴ \(\frac { 1 }{ 2 }\) ∠B = \(\frac { 1 }{ 2 }\) ∠C

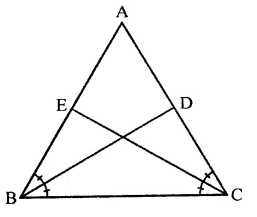
∠DBC = ∠ECB
Now, in ∆DBC and ∆EBC,
BC = BC (Common)
∠C = ∠B (Equal angles)
∠DBC = ∠ECB (Proved)
∴ ∆DBC ≅ ∆EBC (ASA axiom)
∴ BD = CE

Question 2.
In the figure, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that: ∆RBT = ∆SAT.

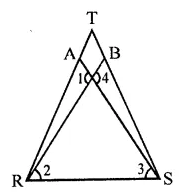
Solution:
Given : In the figure, RT = TS
∠1 = 2∠2 and ∠4 = 2∠3
To prove : ∆RBT ≅ ∆SAT
Proof : ∵ ∠1 = ∠4 (Vertically opposite angles)
But ∠1 = 2∠2 and 4 = 2∠3
∴ 2∠2 = 2∠3 ⇒ ∠2 = ∠3
∵ RT = ST (Given)
∴∠R = ∠S (Angles opposite to equal sides)
∴ ∠R – ∠2 = ∠S – ∠3
⇒ ∠TRB = ∠AST
Now in ∆RBT and ∆SAT
∠TRB = ∠SAT (prove)
RT = ST (Given)
∠T = ∠T (Common)
∴ ∆RBT ≅ ∆SAT (SAS axiom)

Question 3.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Solution:
Given : Two lines AB and CD intersect each other at O such that AD = BC and AD \(\parallel\)
BC

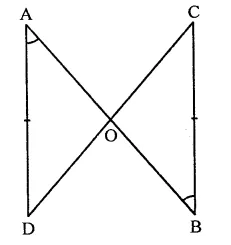
To prove : AB and CD bisect each other
i. e. AO = OB and CO = OD
Proof: In ∆AOD and ∆BOC,
AD = BC (Given)
∠A = ∠B (Alternate angles)
∠D = ∠C (Alternate angles)
∴ ∆AOD ≅ ∆BOC (ASA axiom)
AO = OB and AO = OC (c.p.c.t.)
Hence AB and CD bisect each other.

Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.