Tag: NCERT Solutions for Class 7 Maths

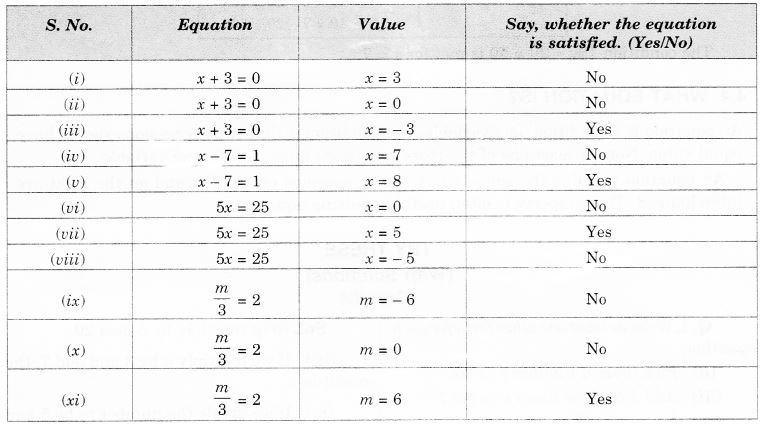
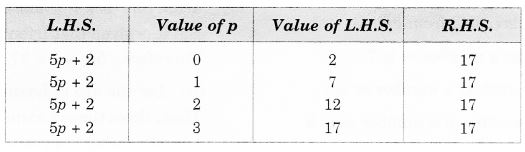
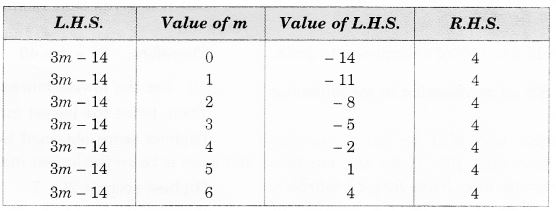
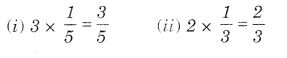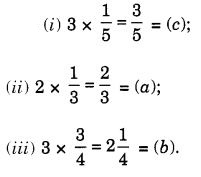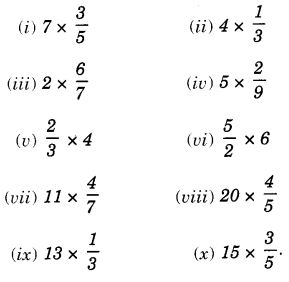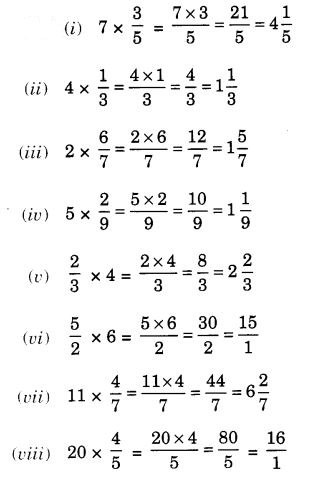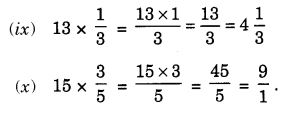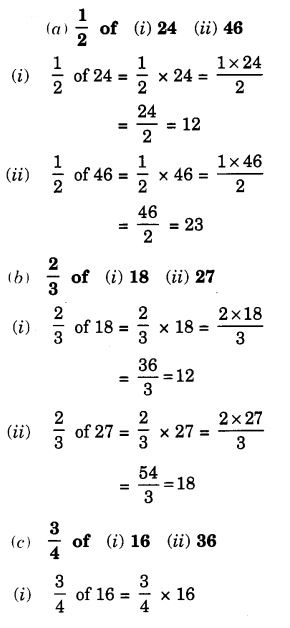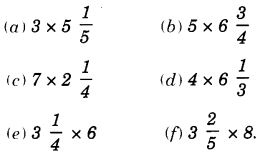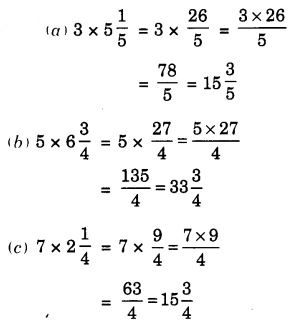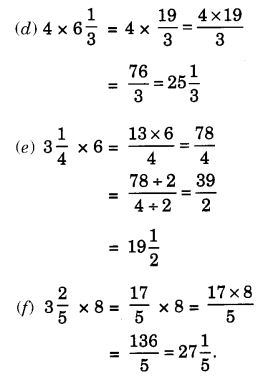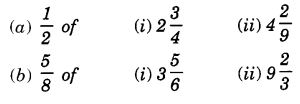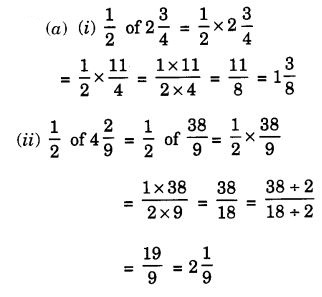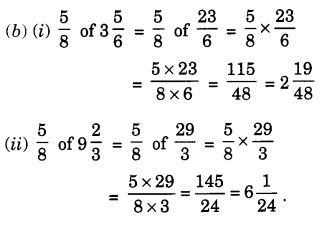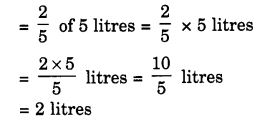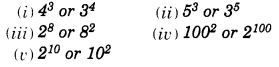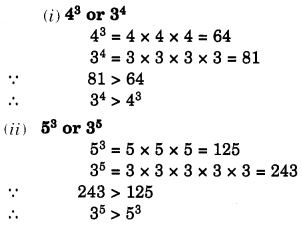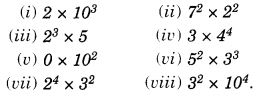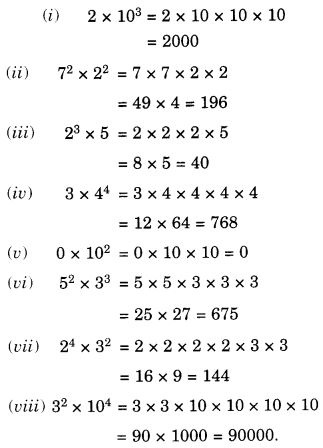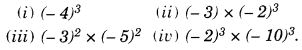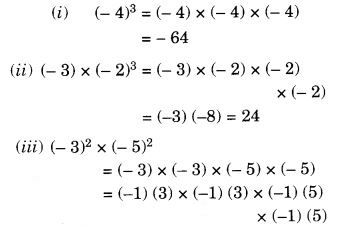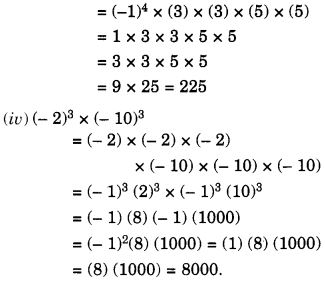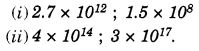NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.3 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.3.

• Fractions and Decimals Class 7 Ex 2.1
• Fractions and Decimals Class 7 Ex 2.2
• Fractions and Decimals Class 7 Ex 2.4
• Fractions and Decimals Class 7 Ex 2.5
• Fractions and Decimals Class 7 Ex 2.6
• Fractions and Decimals Class 7 Ex 2.7
• Fractions and Decimals Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.3

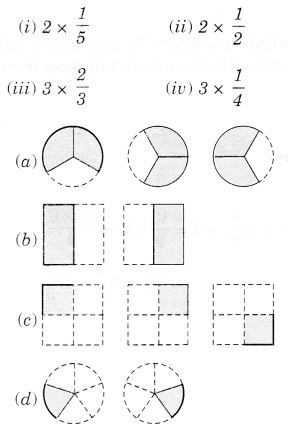
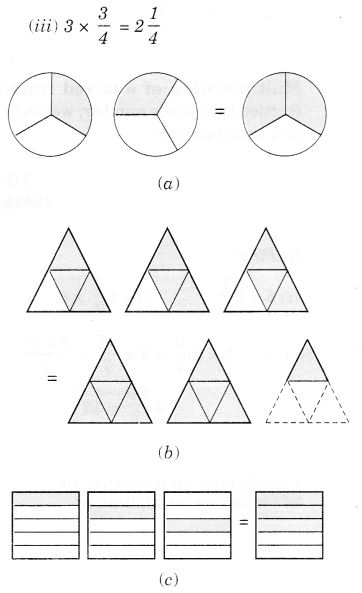
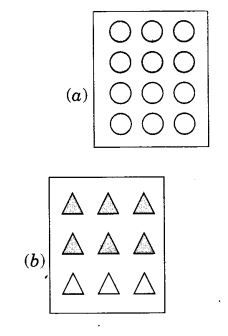
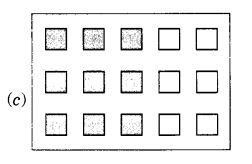
Question 1.
Find:

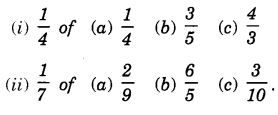
Solution:

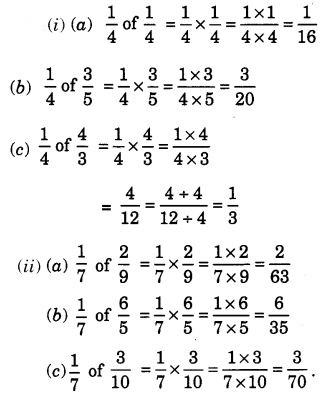
Question 2.
Multiply and reduce to lowest form (if possible):


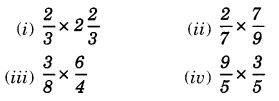
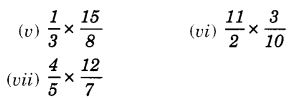
Solution:

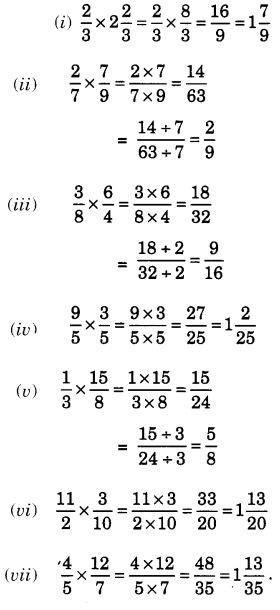
Question 3.
Multiply the following fractions:

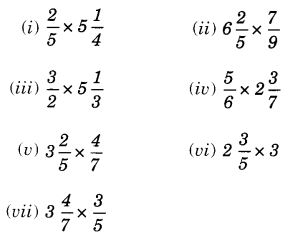
Solution:

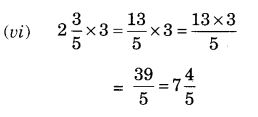
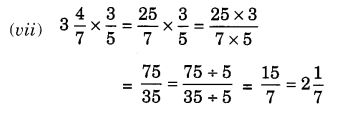
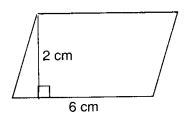
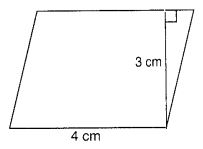
Question 4.
Which is greater:

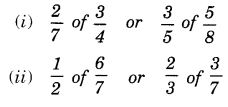
Solution:

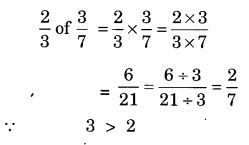
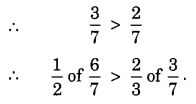
Question 5.
Saili plants 4 saplings, in a row, in her garden. The distance between two adjacent saplings is \(\frac { 3 }{ 4 } \) m. Find the distance between the first and the last sapling.
Solution:

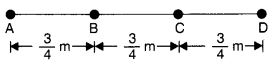
Let A, B, C and D be the four saplings planted in a row.
Distance between two adjacent saplings = \(\frac { 3 }{ 4 } \) m
∴ Distance between the first and the last sapling = AD = 3 × AB

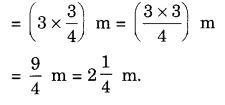
Question 6.
Lipika reads a book for 1 \(\frac { 3 }{ 4 } \) hours everyday. She reads the entire book in 6 days. How many hours in all were required by her to read the book?
Solution:
Hours in all required by Lipika to read the book

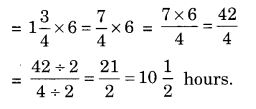
Question 7.
A car runs 16 km using 1 litre of petrol. How much distance will it cover using 2 \(\frac { 3 }{ 4 } \) litres of petrol?
Solution:
Distance covered by the car using 2 \(\frac { 3 }{ 4 } \) litres of petrol

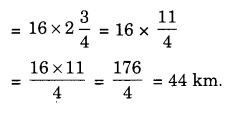
Question 8.

Solution:

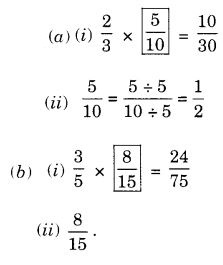
We hope the NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.3 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.2 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.2.

• Fractions and Decimals Class 7 Ex 2.1
• Fractions and Decimals Class 7 Ex 2.3
• Fractions and Decimals Class 7 Ex 2.4
• Fractions and Decimals Class 7 Ex 2.5
• Fractions and Decimals Class 7 Ex 2.6
• Fractions and Decimals Class 7 Ex 2.7
• Fractions and Decimals Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.2

Question 1.
Which of the drawings (a) to (d) show:

Solution:
(i) (d)
(ii) (b)
(iii) (a)
(iv) (c)

Question 2.
Some pictures (a) to (c) are given below. Tell which of them show:


Solution:

Question 3.
Multiply and reduce to lowest form and convert into a mixed fraction:

Solution:

Question 4.
Shade

1. \(\frac { 1 }{ 2 } \) of the circles in box (a)
2. \(\frac { 2 }{ 3 } \) of the triangles in box (b)
3. \(\frac { 3 }{ 5 } \) of the squares in box (c)

Solution:

Question 5.
Find:

Solution:

Question 6.
Multiply and express as a mixed fraction:

Solution:

Question 7.
Find

Solution:

Question 8.
Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 liters of water. Vidya consumed \(\frac { 2 }{ 5 } \) of the water. Pratap consumed the remaining water.
(i) How much water did Vidya drink?
(ii) What fraction of the total quantity of water did Pratap drink?
Solution:
(i) Quantity of water drank by Vidya

(ii) Quantity of water drank by Pratap
= 5 litres – 2 litres = 3 litres
∴ The fraction of the total quantity of water drank by Pratap

We hope the NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.2 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.4 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.4.

• Integers Class 7 Ex 1.1
• Integers Class 7 Ex 1.2
• Integers Class 7 Ex 1.3
• Integers Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.4

Question 1.
Evaluate each of the following:

(a) (-30)+ 10
(b) 50 + (-5)
(c) (-36) +(-9)
(d) (-49) + (49)
(e) 13 + [(- 2) + 1]
(f) 0 + (-12)
(g) (-31) + [(-30) + (-1)]
(h) [(-36)+ 12]+3
(i) [(- 6) + 5] + [(- 2) + 1].

Solution:

(a) (- 30) + 10 = – 3
(b) 50 +(-5) = – 10
(c) (-36) +(-9) = 4
(d) (- 49) + (49) = – 1
(e) 13 + [(- 2) + 1] = 13 + (- 1) = – 13
(f) 0 + (- 12) = 0
(g) (- 31) + [(- 30) + (- 1)] = (- 31) + (- 31) = 1
(h) [(- 36) + 12] + 3 = (- 3) + 3 = – 1
(i) [(- 6) + 5] + [(- 2) + 1] = (- 1) + (- 1) = 1.

Question 2.
Verify that
a + (b + c) ≠ (a + b) + (a ÷ c)
for each of the following values of a, b and c.
(a) a = 12, b = – 4, c = 2
(b) a = (- 10), b = 1, c = l.
Solution:
(a) a + (b + c) = 12 ÷ [(- 4) + 2] = 12 + (- 2) = – 6
(a ÷ b) + (a ÷ c) = 12 ÷ (- 4) + 12 ÷ 2 = -3 + 6 = 3
So, a + (b + c) ≠ (a + b) + (a + c)

(b) a ÷ (b + c) = (- 10) + (1 + 1) = (- 10) + 2 = – 5
a ÷ b + a ÷ c = (- 10) ÷ 1 + (- 10) ÷ 1 = (- 10) + (- 10) = – 20
So, a ÷ (b + c) ≠ (a ÷ b) + (a ÷ c).

Question 3.
Fill in the blanks:

(a) 369 ÷ …….. = 369
(b) -75 ÷ …….. = – 1
(c) (- 206) ÷ ……. = 1
(d) -87 ÷ …….. = 87
(e) ……. ÷ 1 = -87
(f) ……. ÷ 48 = -1
(g) 20 ÷ …… = -2
(h) …… ÷ (4) = – 3.

Solution:

(a) 369 ÷ 1 = 369
(b) – 75 ÷ 75 = -1
(c) (- 206) ÷ (- 206) = 1
(d) – 87 ÷ – 1 = 87
(e) – 87 ÷ 1 = – 87
(f) – 48 ÷ 48 = – 1
(g) 20 ÷ (-10) = – 2
(h) – 12 ÷ (4) = – 3.

Question 4.
Write five pairs of integers (a, b) such that a + b = -3. One such pair is (6, -2) because 6 +(-2) = (-3).
Solution:
Five pairs of integers (a, b) such that a + b = -3 are (- 6, 2), (-9, 3), (12,- 4), (21, -7), (-24, 8)
Note: We may write many such pairs of integers.

Question 5.
The temperature at 12 noon was 10°C above zero. If it decreases at the rate of 2°C per hour until mid-night, at what time would the temperature be 8°C degrees below zero? What would be the temperature at mid night?
Solution:
Difference in temperatures +10 °C and -8
= [10 – (- 8)] °C = (10 + 8)° C = 18 °C
Decrease in temperature in one hour = 2°C
Number of hours taken to have temperature 8 °C below zero \(=\frac { Total\quad decrease }{ Decrease\quad in\quad one\quad hour } \)
\(=\frac { 18 }{ 2 }\)
So, at 9 P.M., the temperature will be 8 °C below zero
Temperature at mid-night = 10 °C – (2 x 12) °C
= 10°C – 24 °C = -14 °C

Question 6.
In a class test (+3) marks are given for every correct answer and (- 2) marks are given for every incorrect answer and no marks for not attempting any question.
(i) Radhika scored 20 marks. If she has got 12 correct answers, how many questions has she attempted incorrectly?
(ii) Mohini scores – 5 marks in this test, though she has got 7 correct answers. How many questions has she attempted incorrectly?
Solution:
(i) Let ‘x’ be the number of incorrect questions attempted by Radhika.
According to the question, we get
(+ 3) × 12 + x × (-2) = 20
⇒ 36 – 2x = 20
⇒ 2x = 36 – 20
⇒ x = \(\frac { 16 }{ 2 } \) = 8
Therefore, Radhika attempted 8 incorrect questions.

(ii) Let ‘x’ be the number of incorrect question attempted by Mohini.
According to the question, we get
(+ 3) × 7 + x × (- 2) = – 5
⇒ 21 – 2x = -5
⇒ 2x = 21 + 5
⇒ x = \(\frac { 26 }{ 2 } \) = 13
Therefore, Mohini attempted 13 incorrect questions.

Question 7.
An elevator descends into a mine shaft at the rate of 6m/min. If the descent starts from 10 m above the ground level, how long will it take to reach – 350 m.
Solution:
Difference in heights at two positions = 10 m – (-350 m) = 360 m
Rate of descent = 6 m/minute
∴ Time taken \(=\left( 360 \right) \div \left( 6 \right)\) minutes = 60 minutes = 1 hour
Hence, the elevator will take 1 hour to reach = 350 m.

We hope the NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.4 helps you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.4, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.3 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.3.

• Integers Class 7 Ex 1.1
• Integers Class 7 Ex 1.2
• Integers Class 7 Ex 1.4
• Integers Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.3

Question 1.
Find each of the following products:
(a) 3 × (- 1)
(b) (- 1) × 225
(c) (-21) × (- 30)
(d) (- 316) × (- 1)
(e) (- 15) × 0 × (- 18)
(f) (- 12) × (- 11) × (10)
(g) 9 × (-3) × (-6)
(h) (- 18) ×(-5)× (- 4)
(i) (- 1) × (-2) × (-3) × 4
(j) (- 3) × (- 6) × (-2) × (- 1).
Solution:
(a) 3 x (- 1) = – (3 x 1) = – 3
(b) (- 1) x 225 = – (1 x 225) = – 225
(c) (- 21) x (- 30) = 21 x 30 = 630
(d) (- 316) x (- 1) = 316 x 1 = 316
(e) (- 15) x 0 x (- 18) = [(- 15) x 0]  x  (- 18) = 0 x (- 18) = 0
(f) (- 12) x (- 11) x (10) = [(- 12) x (- 11)] x (10) = (132) x (10) = 1320
(g) 9 x (- 3) x (- 6) = [9 x (- 3)] x (- 6) = (- 27) x (- 6) = 162
(h) (- 18) x (- 5) x (- 4) = [(- 18) x (- 5)] x (- 4) = 90 x (- 4) = – 360
(i) (- 1) x (- 2) x (- 3) x 4 = [(- 1) x (- 2)] x [(- 3) x 4] = (2)x (- 12) = -24
(j) (- 3) x (- 6) x (- 2) x (- 1) = [(- 3) x (- 6)] x [(- 2) x (- 1)] = (18) x (2) = 36

Question 2.
Verify the following:
(a) 18 × [7 + (- 3)] = [18 × 7] + [18 × (- 3)]
(b) (-21)×[(-4) + (-6)] = [(-21) × (-4)] + [(-21) × (-6)
Solution:
(a) 18 × [7 + (- 3)] = [18 × 7] + [18 × (- 3)]
L.H.S. = 18 × [7 + (- 3)]
= 18 × L(7 – 3)] = 18 × (4) = 18 × 4 = 72
R.H.S. = [18 × 7] + [18 × (- 3)]
= 126 + [- (18 × 3)] = 126 + (- 54) = 126 – 54 = 72
So, 18 × [7 + (- 3)]
= [18 × 7] + [18 × (- 3)]

(b) (- 21) × [(- 4) + (- 6)] = [(- 21) × (- 4)] + [(- 21) × (- 6)]
L.H.S. = (- 21) × [(- 4) + (- 6)]
= (- 21) × (- 10)
= 21 × 10 = 210
R. H.S. = [(- 21) × (- 4)] + [(- 21) × (- 6)]
= (21 × 4) + (21 × 6)
= 84 + 126 = 210
So, (- 21) × [(- 4) + (- 6)]
= [(- 21) × (- 4)] + [(- 21) × (- 6)].

Question 3.
(i) For any integer a, what is (-1)×a equal to?
(ii) Determine the integer whose product with (- 1) is
(a) – 22
(b) 37
(c) 0.
Solution:
(i) For any integer a, (-1) x a = -a.
(ii) We know that the product of any integer and (-1) is the additive inverse of an integer.
The integer whose product with (-1) is
(a) additive inverse of -22, t. e., 22.
(b) additive inverse of 37, i.e., -37.
(c) additive inverse of 0, i.e., 0.

Question 4.
Starting from (- 1) × 5, write various products showing some pattern to show (- 1) × (-1) – 1.
Solution:
(- 1) × 5 = – 5
(- 1) × 4 = – 4 [= (- 5) + 1]
(- 1) × 3 = – 3 [= (- 4) + 1]
(- 1) × 2 = – 2 [= (- 3) + 1]
(- 1) × 1 = – 1 [= (- 2) + 1]
(- 1) × 0 = 0 [= (- 1) + 1]
(- 1) × (- 1) = 1 [= 0 + 1]

Question 5.
Find the product, using suitable properties:
(a) 26 × (- 48) + (- 48) × (- 36)
(b) 8 × 53 × (- 125)
(c) 15×(-25)×(-4)×(- 10)
(d) (-41) × 102
(e) 625 × (-35) + (- 625) × 65
(f) 7 × (50 -2)
(g) (-17) × (-29)
(h) (- 57) ×(-19)+ 57.
Solution:
(a) We have, 26 x (-48) + (- 48) x (- 36)
= (- 48) x 26 + (- 48) x (- 36)
= (- 48) x [26 + (- 36)]
= (- 48) x (26 – 36)
=(- 48) x (- 10)= 480
(b) We have,
8 x 53 x (- 125) = [8 x (- 125)] x 53
= (- 1000) x 53 = – 53000
(c) We have,
15 x (- 25) x (- 4) x (- 10)
=15 x [(- 25) x (-4)] x (- 10)
= 15 x (100) x (- 10)
= (15 x 100) x (- 10)
= 1500 x (- 10) = – 15000
(d) We have,
(- 41) x 102 = (- 41) x (100 + 2)
= (- 41) x 100 + (- 41) x 2 = -4100 – 82 = – 4182
(e) We have, 625 x (- 35) + (- 625) x 65
= 625 x (- 35) + (625) x (- 65)
= 625 x [(- 35)+ (- 65)]
= 625 x (- 100) = – 62500
(f) 7 x (50 – 2) = 7 x 50 – 7 x 2
= 350 -14 =336
(g) (-17) x (- 29) = (-17) x [(- 30) + 1]
= (- 17) x (- 30) + (- 17) x 1 = 510 – 17 = 493
(h) (- 57) x (-19)+ 57 =57 x 19 + 57 x 1
= 57 x (19 +1)
= 57 x 20 = 1140

Question 6.
A certain freezing process requires that room temperature be lowered from 40°C at the rate of 5° C every hour. What will be the room temperature 10 hours after the process begins?
Solution:
Room temperature 10 hours after the process begins
= 40°C – 10 × 5°C
= 40°C – 50°C
= – (50 – 40)°C = – 10°C

Question 7.
In a class test containing 10 questions, 5 marks are awarded for every correct answer and (-2) marks are awarded for every incorrect answer and 0 for questions not attempted.
(i) Mohan gets four correct and si× incorrect answers. What is his score?
(ii) Reshma gets five correct answers and five incorrect answers, what is her score?
(iii) Heena gets two correct and five incorrect answers out of seven questions she attempts. What is her score?
Solution:
(i) Mohan gets for four correct answers 4 × 5 = 20 marks
He also gets for si× incorrect answers. 6 × (- 2) = – 12 marks.
Therefore, Mohan’s score = 20 + (- 12) = 20-12 = 8 marks.

(ii) Reshma gets for five correct answers 5 × 5 = 25 marks
She also gets for five incorrect answers 5 × (- 2) = – 10 marks Therefore, Reshma’s score = 25 + (- 10) = 25-10 = 15 marks.

(iii) Heena gets for two correct answers
2 × 5 = 10 marks.
She also gets for five incorrect answers 5 × (- 2) = – 10 marks
She didn’t attempt three questions. For these, she gets 3×0 = 0 marks
Therefore, Heena’s score = 10 + (- 10) + 0 = 10 – 10 + 0 = 0 marks.

Question 8.
A cement company earns a profit of ₹ 8 per bag of white cement sold and a loss of ₹ 5 per bag of grey cement sold.
(a) The company sells 3,000 bags of white cement and 5,000 bags of grey cement in a month. What is its profit or loss?
(b) What is the number of white cement bags it must sell to have neither profit nor loss if the number of grey bags sold is 6,400 bags.
Solution:
(a) The company sells 3,000 bags of white cement. So her profit = 3,000 × 8 = ₹ 24,000
Also, the company sells 5,000 bags of grey cement. So her loss = 5,000 × 5 = ₹ 25,000
Since 25,000 > 24,000
Therefore, the company is at a loss and the loss is = 25000 – 24000 = ₹ 1000

(b) Let ‘×’ be the number of white cement bags sold.
According to the question, we get
x × 8 = 6400 × 5
⇒ x = \(\frac { 6400\times 5 }{ 8 }\) = 800 × 5 = 4,000 bags.
Therefore, 4,000 bags of white cement must be sold to have neither profit nor loss.

Question 9.
Replace the blank with an integer to make it a true statement.

1. (a) (- 3) × …….. = 27
2. (b) 5 × …….. = -35
3. (c) …….. × (- 8) = – 56
4. (d) …….. × (- 12) = 132.

Solution:

1. (a) (-3) x (- 9) = 27
2. (b) 5 x (-7) = (-35)
3. (c) 7 x (-8) = (-56)
4. (d) (-11) x (-12) = 132

We hope the NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.3 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.2 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.2.

• Integers Class 7 Ex 1.1
• Integers Class 7 Ex 1.3
• Integers Class 7 Ex 1.4
• Integers Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.2

Question 1.
Write down a pair of integers whose:

(a) the sum is -7
(b) the difference is -10
(c) the sum is 0.

Solution:

(a) (-15) and 8
(b) 15 and 25.
(c) (-49) and 49

Question 2.

(a) Write a pair of negative integers whose difference gives 8.
(b) Write a negative integer and a positive integer whose sum is -5.
(c) Write a negative integer and a positive integer whose difference is -3.

Solution:

(a) (-10) and (-18)
(b) (-10) and 5
(c) (-1) and 2

Question 3.
In a quiz, team A scored – 40, 10,0 and team B scored 10, 0, – 40 in three successive rounds. Which team scored more? Can we say that we can add integers in any order?
Solution:
Total scores of team A = (- 40) + 10 + 0 = – 40 + 10 + 0 = – 30
and, total scores of team B = 10 + 0 + (- 40) = 10 + 0 – 40 = – 30
Since the total scores of each team are equal.
∴ No team scored more than the other but each has an equal score.
Yes, integers can be added in any order and the result remains unaltered.
For example, 10 + 0 + (-40) = -30 = -40 + 0 + 10

Question 4.
Fill in the blanks to make the following statements true:

1. (-5) + (-8) = (+8) + (……)
2. -53 + …… = -53.
3. 17 + …… = 0
4. [13 + (-12)] + (…… ) = 13 + [(-12) + (- 7)]
5. (- 4) + [15 + (- 3)] = [(-4) + 15] + …….

Solution:

1. (-5) + (-8) = (-8) + (- 5)
2. -53 + 0 = -53
3. 17 + (- 17) = 0
4. [13 + (- 12)] + (- 7) = 13 + [(- 12) + (-7)]
5. (- 4) + [15 + (- 3)] = [(- 4) + 15] + (- 3).

We hope the NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.2 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Ex 14.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Ex 14.1.

• Symmetry Class 7 Ex 14.2
• Symmetry Class 7 Ex 14.3
• Symmetry Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Ex 14.1

Question 1.
Copy the figures with punched holes and find the axes of symmetry for the following :


Solution:

Question 2.
Given the line(s) of symmetry, find the other hole(s):

Solution:

Question 3.
In the following figures, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete each figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?
<
Solution:

Question 4.
The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry:

Identify multiple lines of symmetry, if any, in each of the following figures:

Solution:

Question 5.
Copy the figure given here. Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?

Solution:


Yes! there is more than one way to make the figure symmetric.

• Let us take the diagonal BD and shade the squares as shown in the figure to make the figure symmetric about BD.
• Similarly, the figure is symmetric about the diagonal AC. Thus, the figure is symmetric about both the diagonals.
• The figure is symmetric about EF and GH also.

Question 6.
Copy the diagram and complete each shape to be symmetric about the mirror line(s) :

Solution:

Question 7.
State the number of lines of symmetry for the following figures :
(a) An equilateral triangle
(b) An isosceles triangle
(c) A scalene triangle
(d) A square
(e) A rectangle
(f) A rhombus
(g) A parallelogram
(h) A quadrilateral
(i) A regular hexagon
(j) A circle.
Solution:

Question 8.
What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about
(a) a vertical mirror
(b) a horizontal mirror
(c) both horizontal and vertical mirrors.
Solution:

Question 9.
Give three examples of shapes with no line of symmetry.
Solution:

(b) A scalene triangle,
(c) A parallelogram

Question 10.
What other name can you give to the line of symmetry of

1. an isosceles triangle?
2. a circle?

Solution:

1. Median
2. Diameter

We hope the NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Ex 14.1 helps you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Ex 14.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.1.

• Exponents and Powers Class 7 Ex 13.2
• Exponents and Powers Class 7 Ex 13.3
• Exponents and Powers Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.1

Question 1.
Find the value of:

1. 2⁶
2. 9³
3. 11²
4. 5⁴.

Solution:

1. 2⁶ = 2 × 2 × 2 × 2 × 2 × 2 = 64
2. 9³ = 9 × 9 × 9 = 729
3. 11² = 11 × 11 = 121
4. 5⁴ = 5 × 5 × 5 × 5 = 625.

Question 2.
Express the following in exponential form:

1. 6 × 6 × 6 × 6
2. t × t
3. b × b × b × b
4. 5 × 5 × 7 × 7 × 7
5. 2 × 2 × a × a
6. a × a × a × c × c × c × c × d.

Solution:

1. 6 × 6 × 6 × 6 = 6⁴
2. t × t = t²
3. b × b × b × b = b⁴
4. 5 × 5 × 7 × 7 × 7 = 5² × 7³
5. 2 × 2 × a × a = 2² × a²
6. a × a × a × c × c × c × c × d = a³ × c⁴ × d.

Question 3.
Express each of the following numbers using the exponential notation:
(i) 512
(ii) 343
(iii) 729
(iv) 3125.
Solution:




Question 4.
Identify wherever possible, in each of the following?

Solution:

Question 5.
Express each of the following as a product of powers of their prime factors:
(i) 648
(ii) 405
(iii) 540
(iv) 3600
Solution:

Question 6.
Simplify:

Solution:

Question 7.
Simplify:

Solution:

Question 8.
Compare the following numbers:

Solution:

We hope the NCERT Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 15 Visualising Solid Shapes Ex 15.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 15 Visualising Solid Shapes Ex 15.1.

• Visualising Solid Shapes Class 7 Ex 15.1
• Visualising Solid Shapes Class 7 Ex 15.2
• Visualising Solid Shapes Class 7 Ex 15.3
• Visualising Solid Shapes Class 7 Ex 15.4
• Visualising Solid Shapes Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 15 Visualising Solid Shapes Ex 15.1

Question 1.
Identify the nets which can be used to make cubes (cut out copies of the nets and try it):

Solution:
(ii), (iii), (iv) and (vi).

Question 2.
Dice are cubes with dots on each face. Opposite faces of a die always have a total of seven dots on them. Here are two nets to make dice (cubes); the numbers inserted in each square indicate the number of dots in that box.

Solution:
Insert suitable numbers in the blanks, remembering that the number on the opposite faces should total to 7.

Question 3.
Can this be a net for a die? Explain your answer.

Solution:
No, this cannot be a net for a die. Because one pair of opposite faces will have 1 and 4 on them and another pair of opposite faces will have 3 and 6 on them whose total is not equal to 7.

Question 4.
Here is an incomplete net for making a cube. Complete it in at least two different ways. Remember that a cube has six faces. How many are there on the net here? (Give two separate diagrams. If you like, you may use a squared sheet for easy manipulation).

Solution:
In the net given here three faces are shown.

Question 5.
Match the nets with appropriate solids:

Solution:
(a) ↔ (ii)
(b) ↔ (iii)
(c) ↔ (iv)
(d) ↔ (i)

We hope the NCERT Solutions for Class 7 Maths Chapter 15 Visualising Solid Shapes Ex 15.1 helps you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 15 Visualising Solid Shapes Ex 15.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.1.

• Simple Equations Class 7 Ex 4.2
• Simple Equations Class 7 Ex 4.3
• Simple Equations Class 7 Ex 4.4
• Simple Equations Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.1

Question 1.
Complete the last column of the table.

Solution:

Question 2.
Check whether the value given in the brackets is a solution to the given equation or not.

(a) n + 5 = 19 (n = 1)
(b) 7n + 5 = 19 (n = – 2)
(c) 7n + 5 = 19 (n = 2)
(d) 4p – 3 = 13 (p = 1)
(e) 4p – 3 = 13 (p = – 4)
(f) 4p – 3 = 13 (p = 0).

Solution:
(a) n + 5 = 19 (n = 1)
L.H.S. = n + 5 = 1 + 5 | when n = 1 = 5
R.H.S. = 19
∵ L.H.S. ≠ R.H.S.
∴ n = 1 is not a solution to the given equation n + 5 = 19.

(b) 7n + 5 = 19 (n = – 2)
L.H.S. = 7n + 5 = 7(- 2) + 5 | when n = – 2 = – 14 + 5 = – 9
R.H.S. = 19
∵ L.H.S. ≠ R.H.S.
∴ n = – 2 is not a solution to the given equation 7n + 5 = 19.

(c) 7n + 5 = 19 (n = 2)
L.H.S. = In + 5 = 7(2) + 5 | when n = 2 = 14 + 5 = 19 = R.H.S.
∴ n = 2 is a solution to the given equation 7n + 5 = 19.

(d) 4p – 3 = 13 (p = 1)
L.H.S. = 4p – 3 = 4(1) – 3 | when p = 1 = 4 – 3 = 1
R.H.S. = 13
∵ L.H.S. ≠ R.H.S.
∴ p = 1 is not a solution to the given equation 4p – 3 = 13.

(e) 4p – 3 = 13 (p = – 4)
L.H.S. = 4p – 3 = 4(- 4) – 3 , | when p = – 4 = – 16 – 3 = – 19
R.H.S. = 13
∵ L.H.S. ≠ R.H.S.
∴ p = – 4 is not a solution to the given equation
4p – 3 = 13.

(f) 4p – 3 = 13 (p = 0)
L.H.S. = 4 (p) – 3 = 4(0) – 3 | when p = 0 = 0 – 3 = – 3
R.H.S. = 13
∵ L.H.S. ≠ R.H.S.
∴ p = 0 is not a solution to the given equation 4p – 3 = 13.

Question 3.
Solve the following equations by trial and error method.

1. 5p + 2 = 17
2. 3m – 14 = 4.

Solution:
(i) 5p + 2 = 17

So, p = 3 is the solution of the given equation 5p + 2 = 17.

(ii) 3m – 14 = 4

So, m = 6 is the solution of the given equation 3m – 14 = 4.

Question 4.
Write equations for the following statements.

1. The sum of numbers x and 4 is 9.
2. 2 subtracted from y is 8.
3. Ten times a is 70.
4. The number b divided by 5 gives 6.
5. Three-fourth oft is 15.
6. Seven times m plus 7 gets you 77.
7. One-fourth of a number x minus 4 gives 4.
8. If you take away 6 from 6 times y, you get 60.
9. If you add 3 to one-third of z, you get 30.

Solution:

1. x + 4 = 9
2. y – 2 = 8
3. 10 a = 70
4. b ÷ 5 = 6
5. \(\frac { 3 }{ 4 } \) × t = 15
6. 7m + 7 = 77
7. \(\frac { 1 }{ 4 } \) × x – 4 = 4
8. 6y – 6 = 60
9. \(\frac { 1 }{ 3 } \) × z + 3 = 30

Question 5.
Write the following equations in statement forms:

1. p + 4 = 15
2. m – 7 = 3
3. 2m = 7
4. \(\frac { m }{ 5 } \) = 3
5. \(\frac { 3m }{ 5 } \) = 6
6. 3p + 4 = 25
7. 4p – 2 = 18
8. \(\frac { p }{ 2 } \) + 2 = 8.

Solution:

1. The sum of p and 4 is 15.
2. 7 subtracted from m is 3.
3. Twice a number m is 7.
4. One-fifth of a number m is 3.
5. Three-fifth of a number m is 6.
6. Three times a number p, when added to 4, gives 25.
7. 2 subtracted from four times a number p is 18.
8. Add 2 to half of a number p to get 8.

Question 6.
Set up an equation in the following cases:

1. Irfan says that he has 7 marbles more than five times the marbles Permit has. Irfan has 37 marbles. (Take m to be the number of Permit’s marbles.)
2. Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age. (Take Laxmi’s age to be y years.)
3. The teacher tells the class that the highest marks obtained by a student in her class are twice the lowest marks plus 7. The highest score is 87. (Take the lowest score to be l.)
4. In an isosceles triangle, the vertex angle is twice either base angle. (Let the base angle be b in degrees. Remember that the sum of angles of triangle is 180 degrees).

Solution:
(i) Let the number of marbles with Parmit be m.
Then, 7 added to 5 times mis 5m + 7
It is given that 7 marbles more than five times the marble is 37. Thus, the equation obtained is 5m + 7 = 37.

(ii) Let Laxmi’s age be y years. Then, 4 added to 3 times y is 3y + 4
It is given that the father is 4 years older than 3 times Laxmi’s age. His age is 49years.
Then, we have the following equation : 3y + 4 = 49

(iii) Let the lowest marks be l. Then, twice the lowest marks plus 7 is 2l +7
It is given that, the highest marks 87 obtained by a student is twice the lowest marks plus 7.
So, we have the following equation : 2l + 7 = 87

(iv) Let the base angle be b. Then, the vertex angle = 2b.
Since, sum of the angles of a triangle is 180°
∴ b + b + 2b = 180°
⇒ 4b = 180°
which is the required equation.

We hope the NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.1.

• Perimeter and Area Class 7 Ex 11.2
• Perimeter and Area Class 7 Ex 11.3
• Perimeter and Area Class 7 Ex 11.4
• Perimeter and Area Class 7 MCQ

NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.1

Question 1.
The length and the breadth of a rectangular piece of land is 500 m and 300 m respectively. Find
(i) its area
(ii) the cost of the land, if 1 m² of the land cost ₹ 10,000.
Solution:

Here, length = 500 m, breadth = 300 m
(i) Area = length × breadth = (500 × 300) m² = 1,50,000 m²
(ii) Cost of land at the rate of ₹ 10,000 per 1 m² = ₹ (10,000 × 1,50,000) = ₹ 1,50,00,00,000.

Question 2.
Find the area of a square park whose perimeter is 320 m.
Solution:

Question 3.
Find the breadth of a rectangular plot of land, if its area is 440 m² and the length is 22 m. Also, find its perimeter.
Solution:

Question 4.
The perimeter of a rectangular sheet is 100 cm. If the length is 35 cm, find its breadth. Also find the area.

Solution:

Question 5.
The area of a square park is the same as a rectangular park. If the side of the square park is 60 m and the length of the rectangular park is 90 m, find the breadth of the rectangular park.

Solution:


Hence, the breadth of the rectangular park is 40 m.

Question 6.
A wire is in the shape of a rectangle. Its length is 40 cm and breadth is 22 cm. If the same wire is rebent in the shape of a square, what will be the measure of each side? Also, find which shape encloses more area?
Solution:

Question 7.
The perimeter of a rectangle is 130 cm. If the breadth of the rectangle is 30 cm, find its length. Also, find the area of the rectangle.

Solution:

Question 8.
A door of length 2 m and breadth 1 m is fitted in a wall. The length of the wall is 4.5 m and the breadth is 3.6 m (figure). Find the cost of whitewashing the wall, if the rate of whitewashing the wall is ₹ 20 per m².
Solution:

We hope the NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.1, drop a comment below and we will get back to you at the earliest.