Prasanna

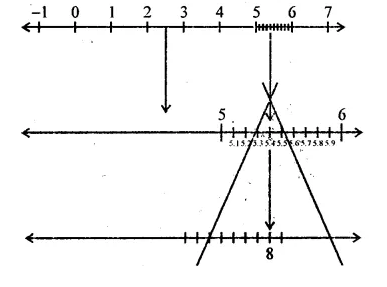
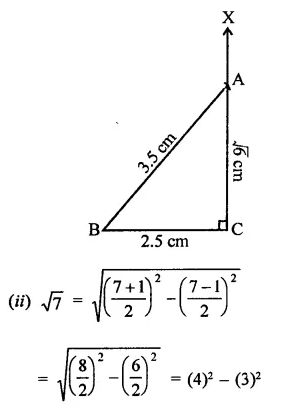
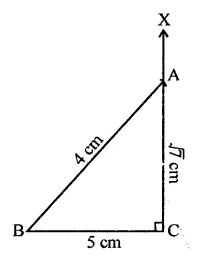
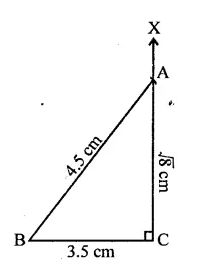
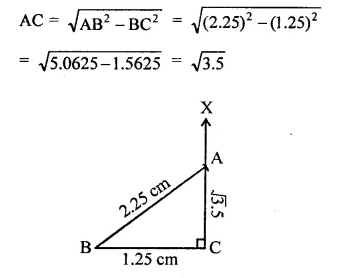
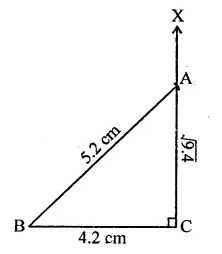
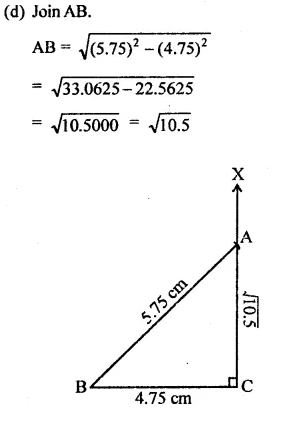
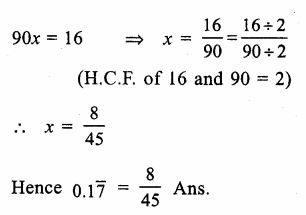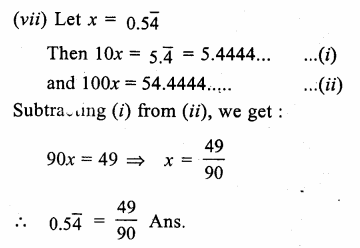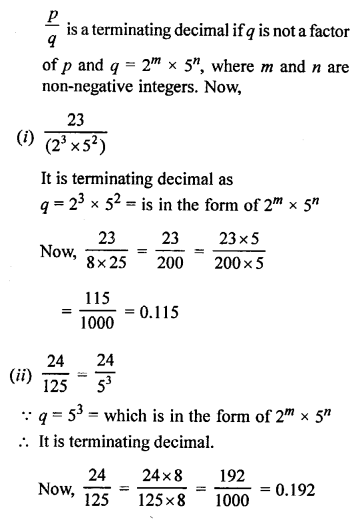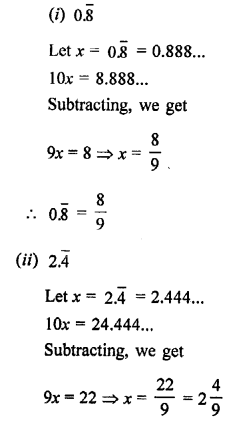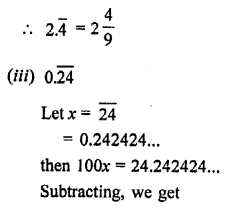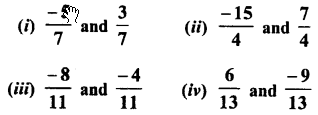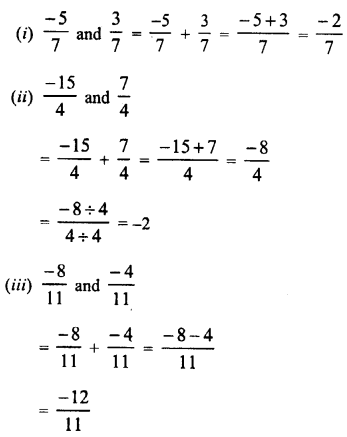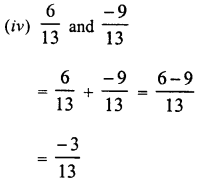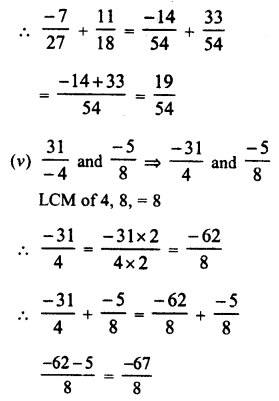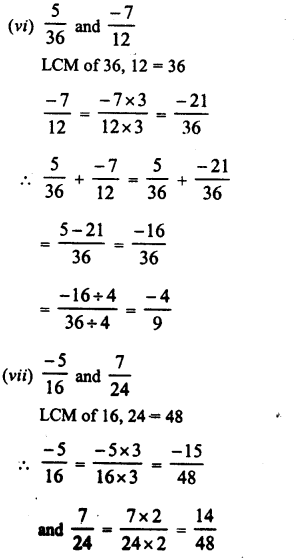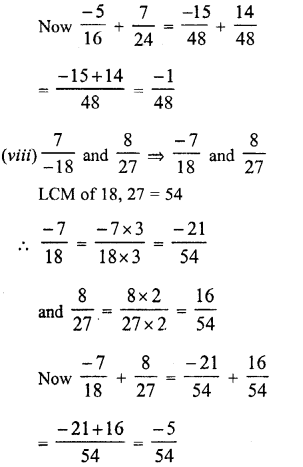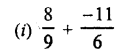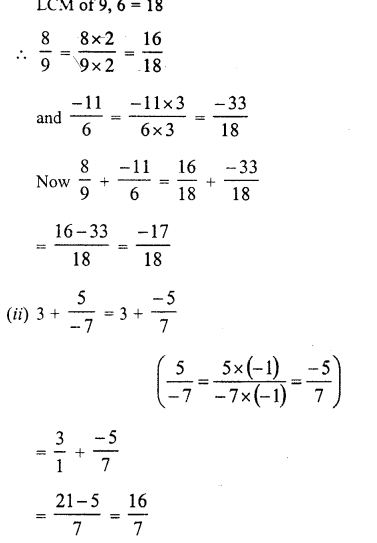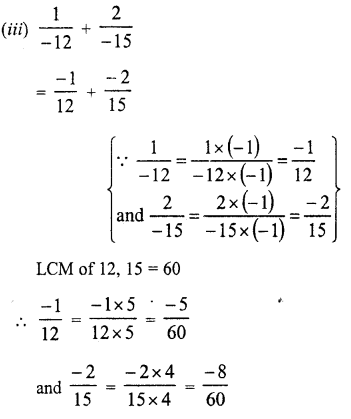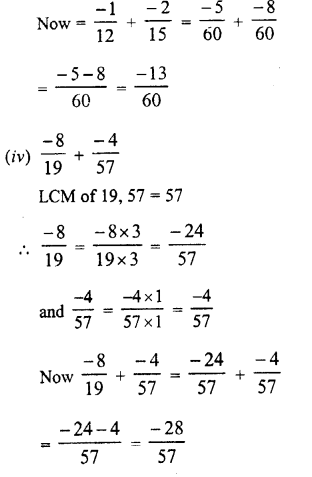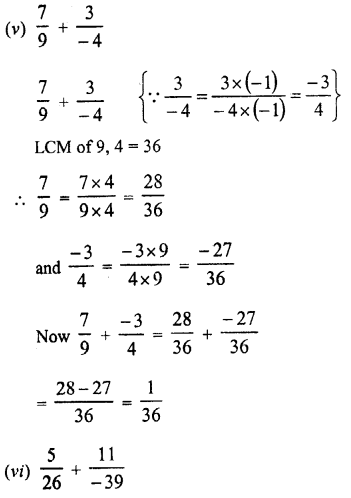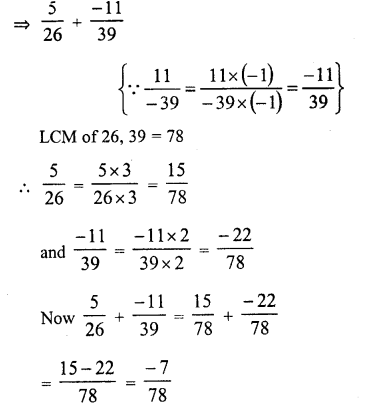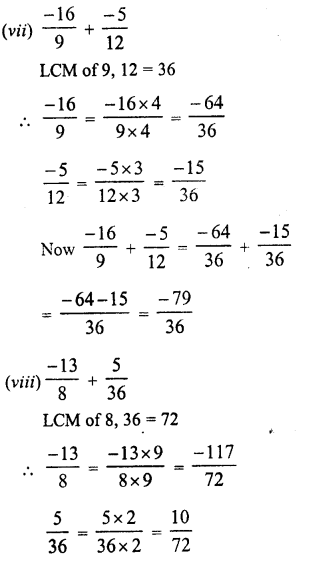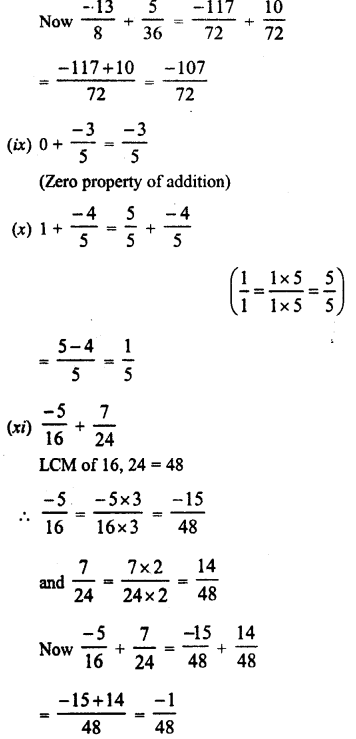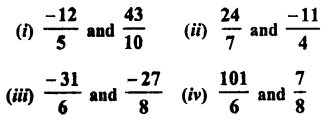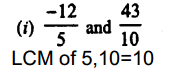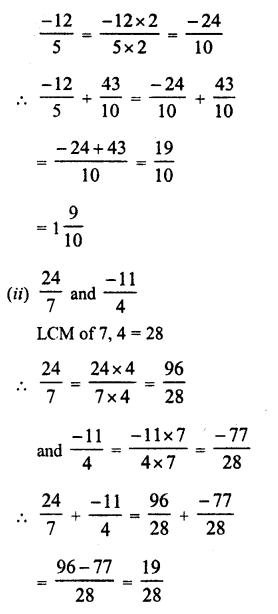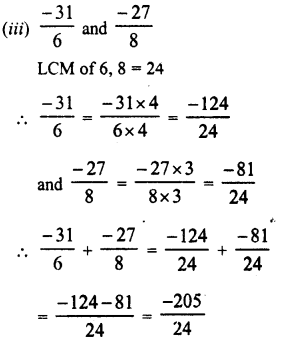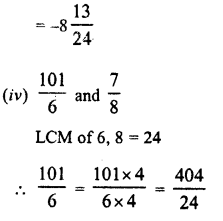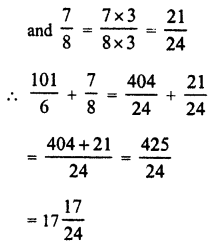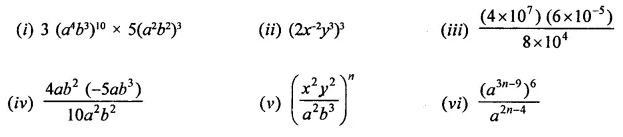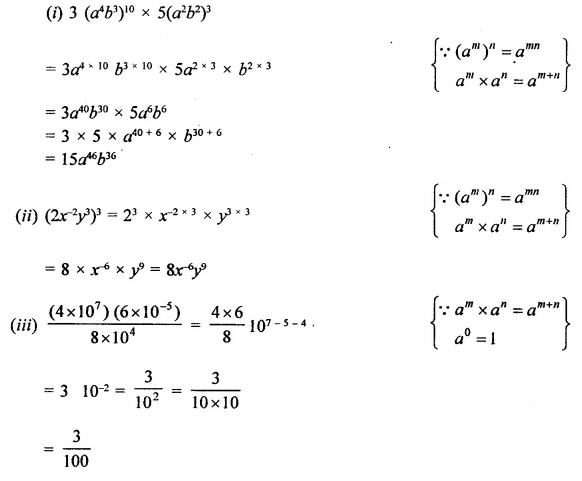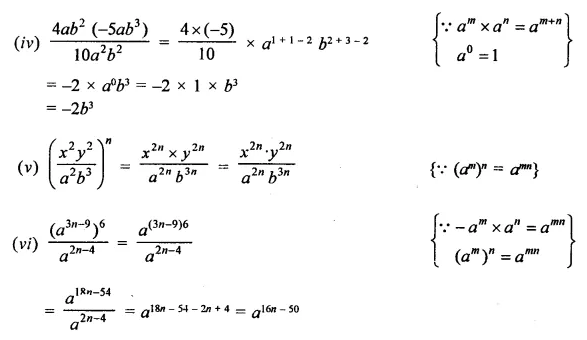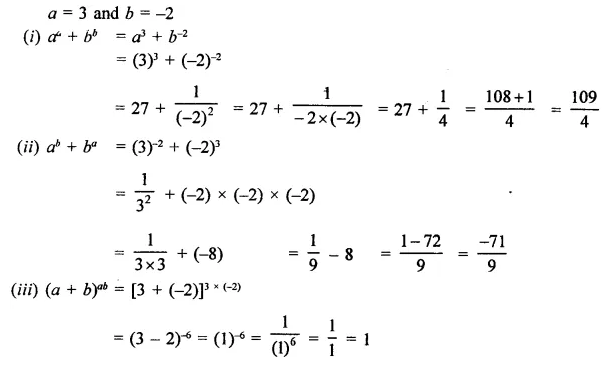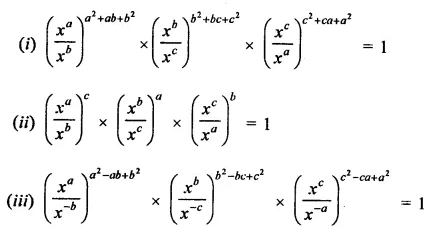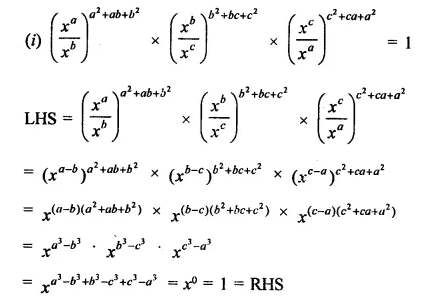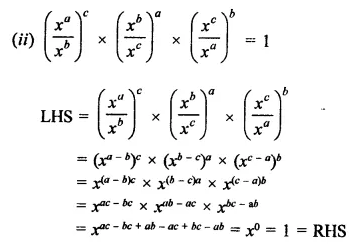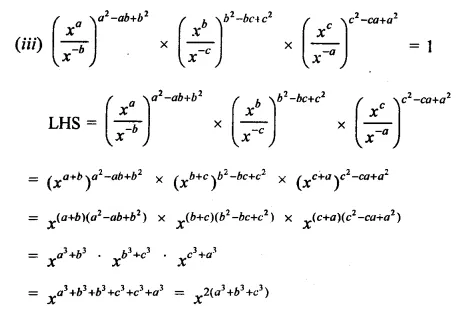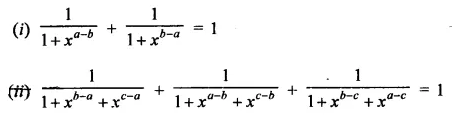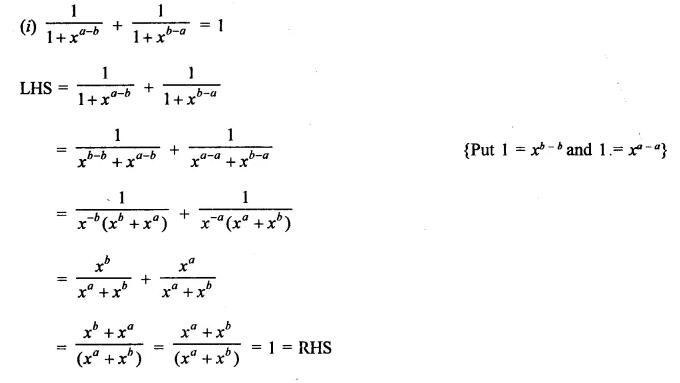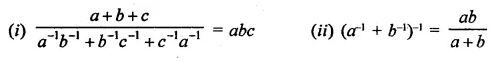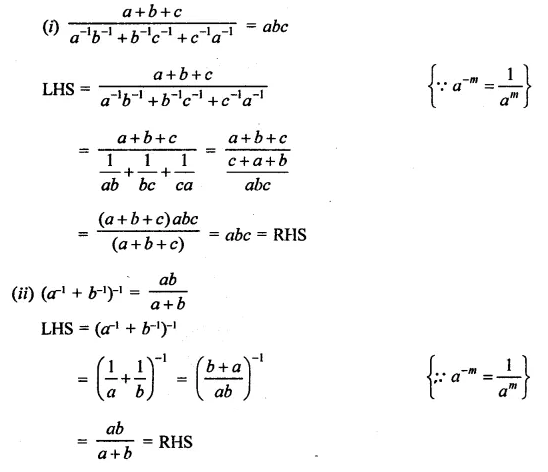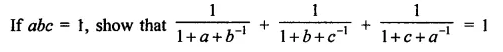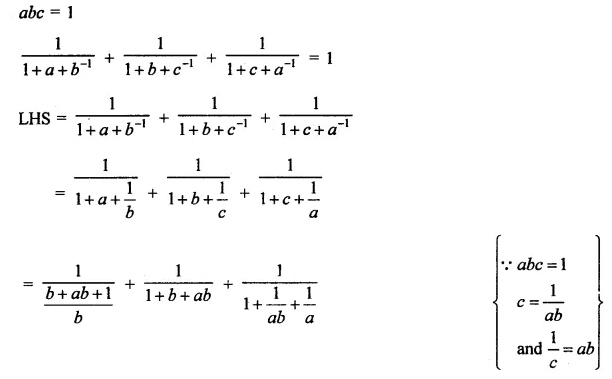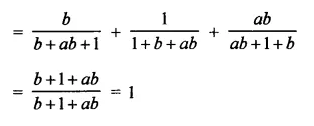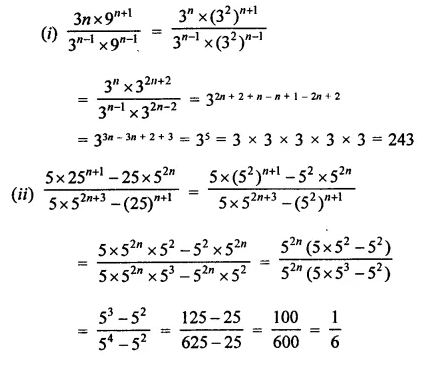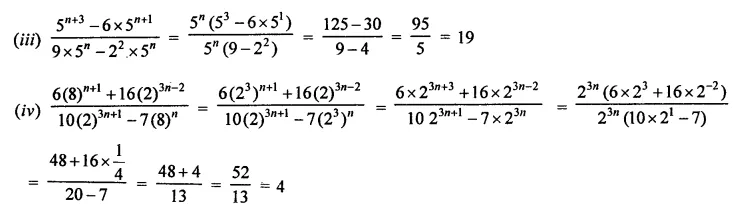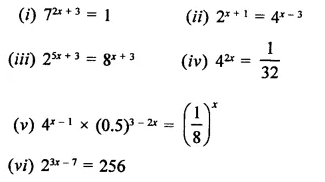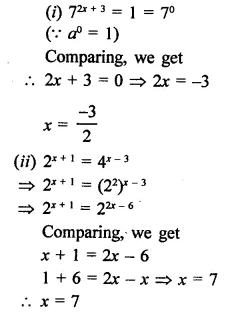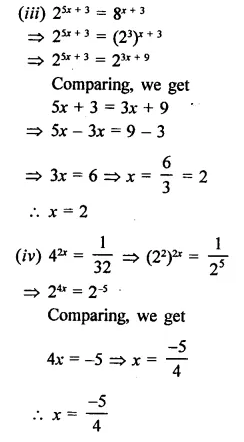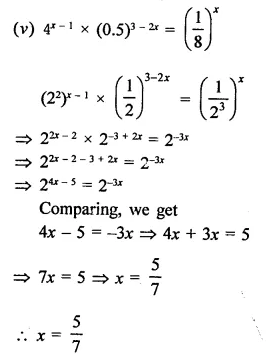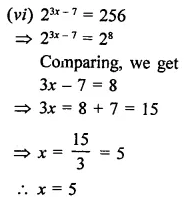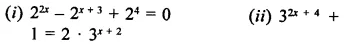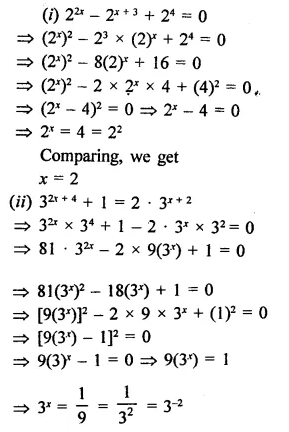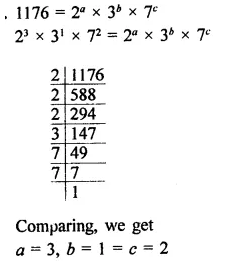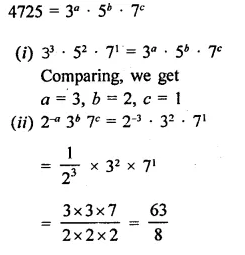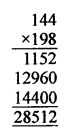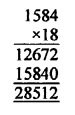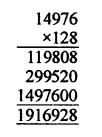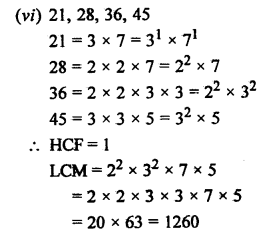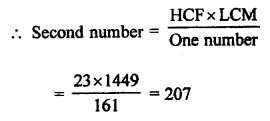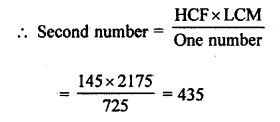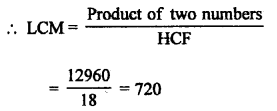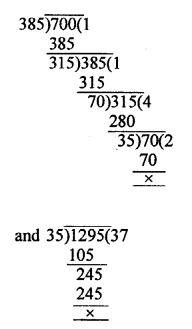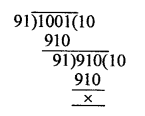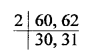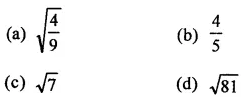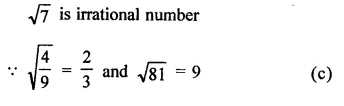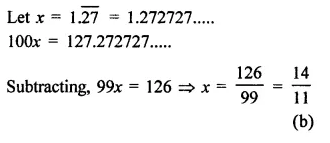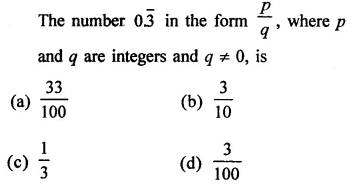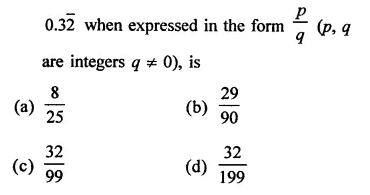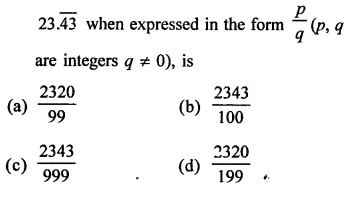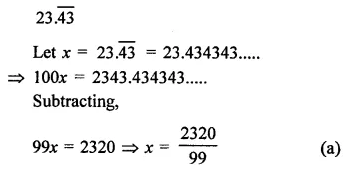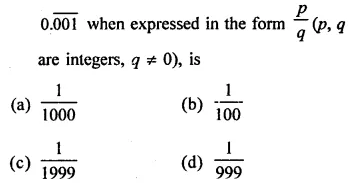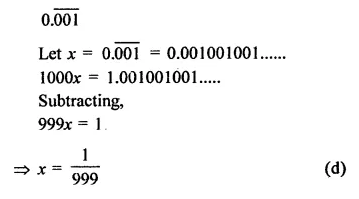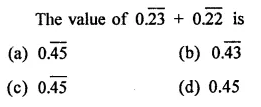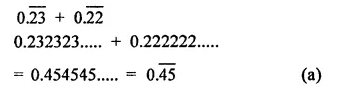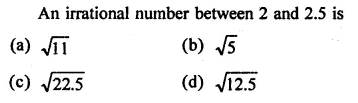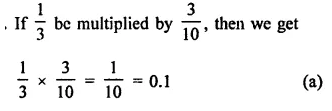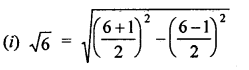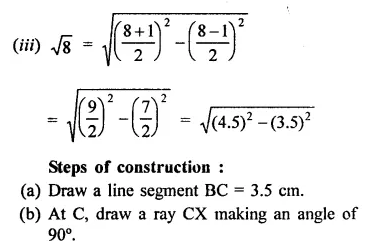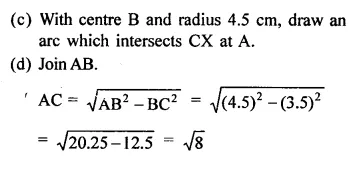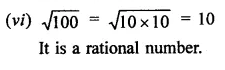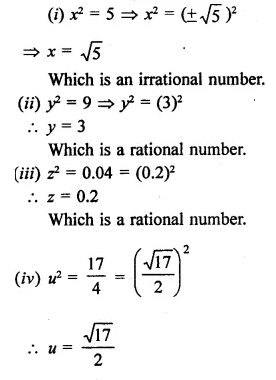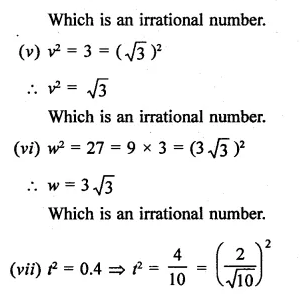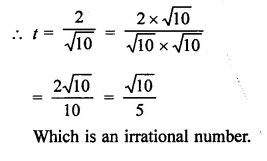RD Sharma Class 9 Solutions Chapter 2 Exponents of Real Numbers Ex 2.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 2 Exponents of Real Numbers Ex 2.2

Question 1.
Assuming that x, y, z are positive real numbers, simplify each of the following:

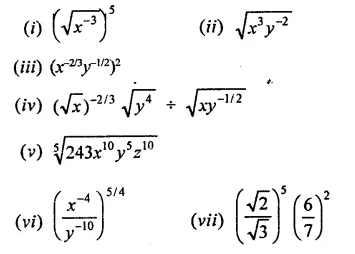
Solution:

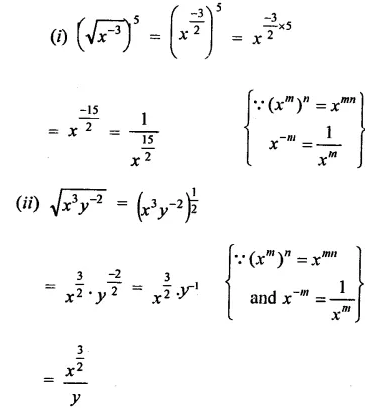
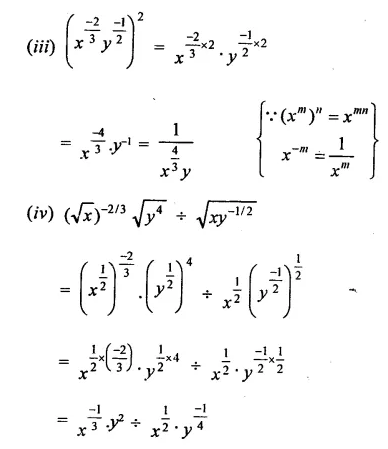
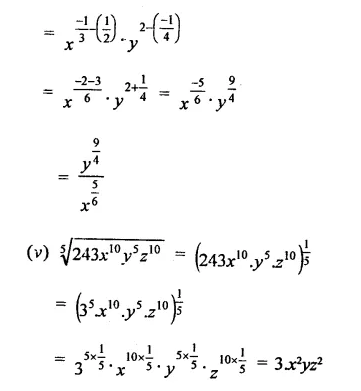
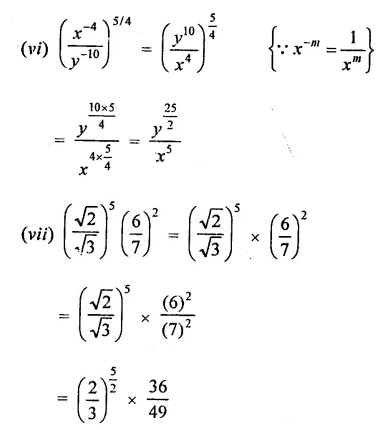
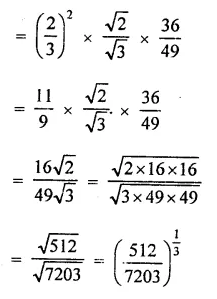
Question 2.
Simplify:

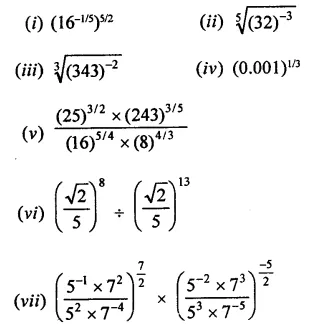
Solution:

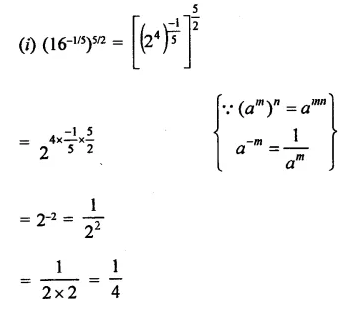
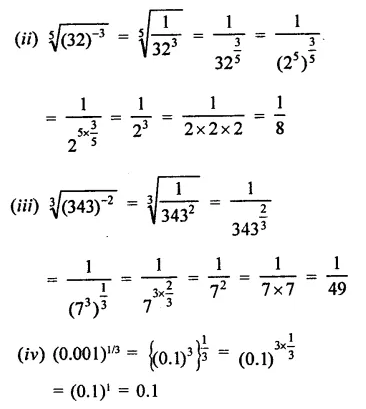
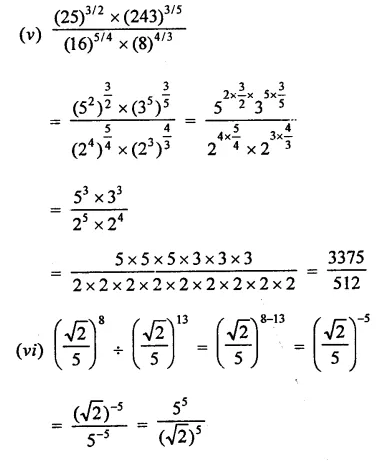
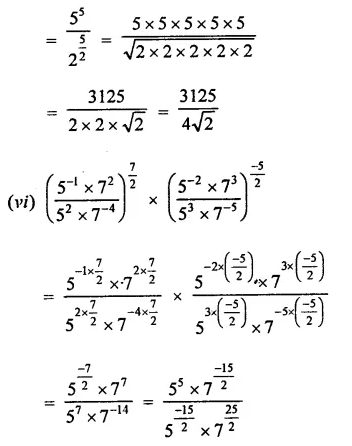
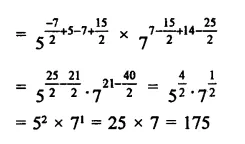
Question 3.
Prove that:

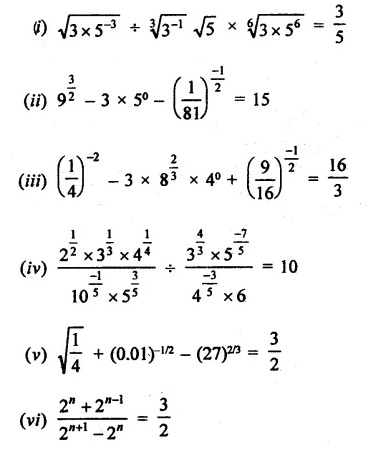
Solution:

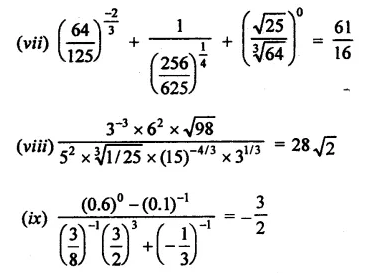
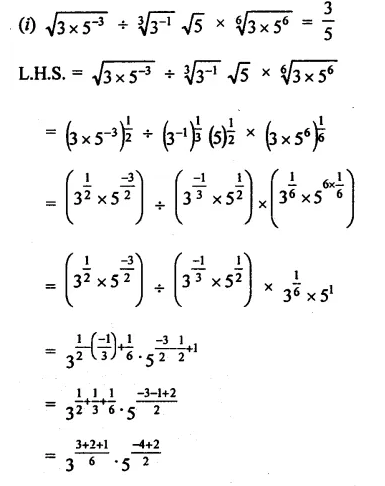
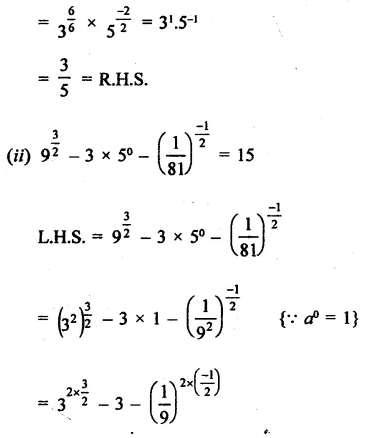
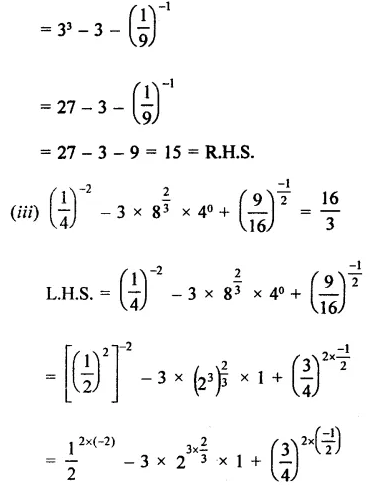
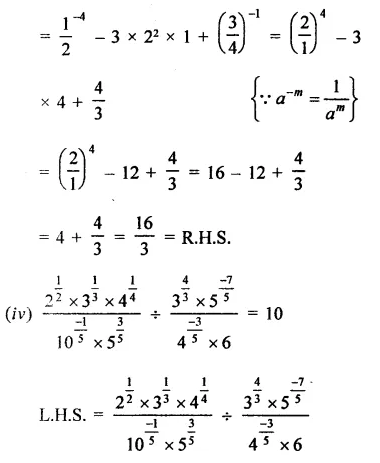
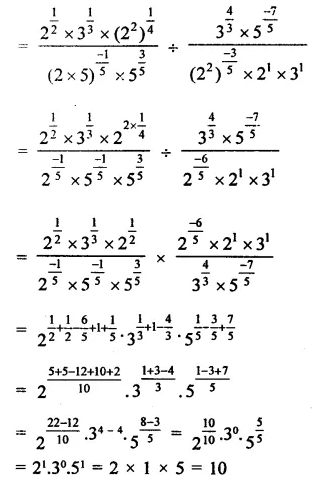
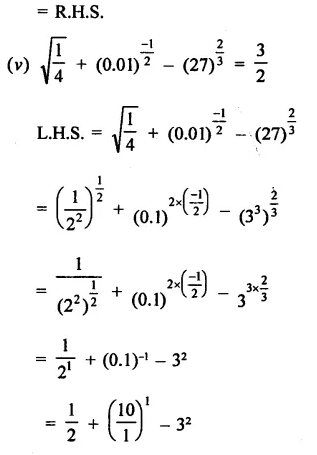
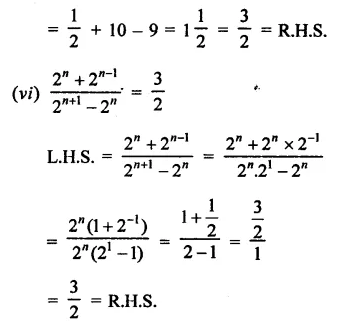
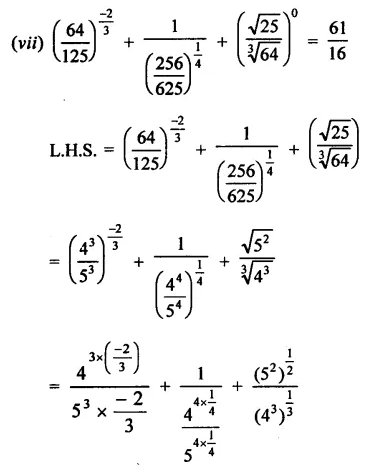
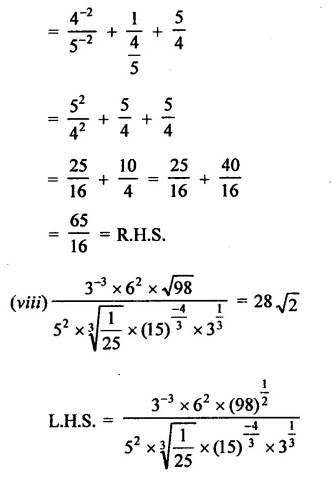
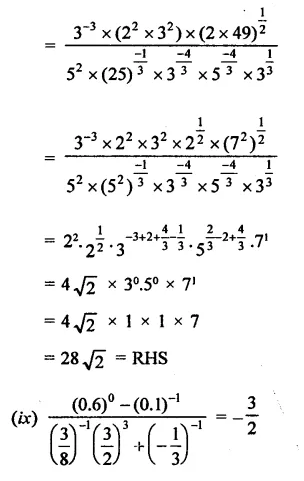
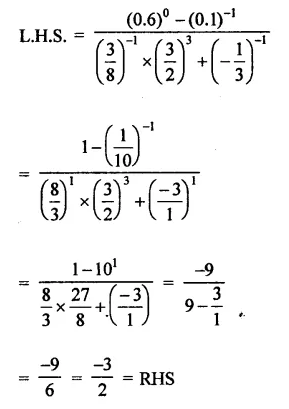
Question 4.
Show that:


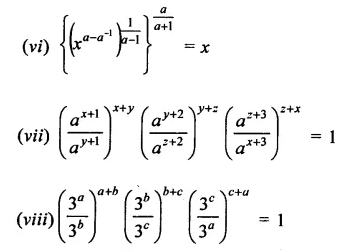
Solution:

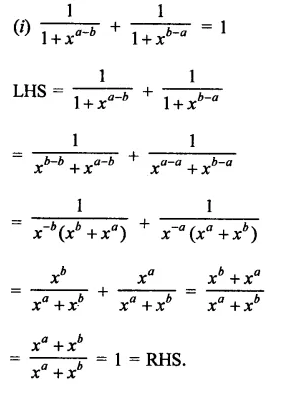
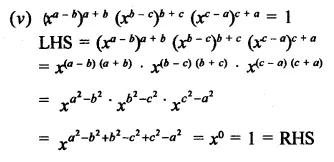
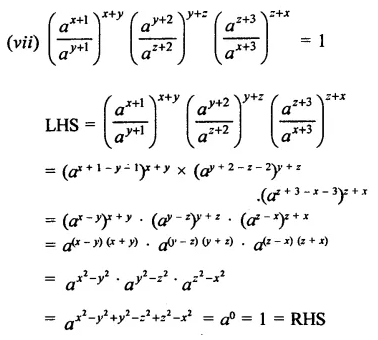
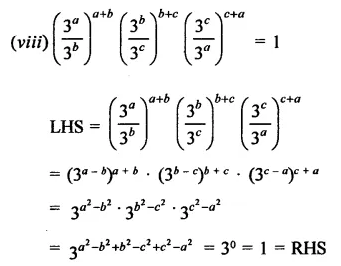
Question 5.

Solution:

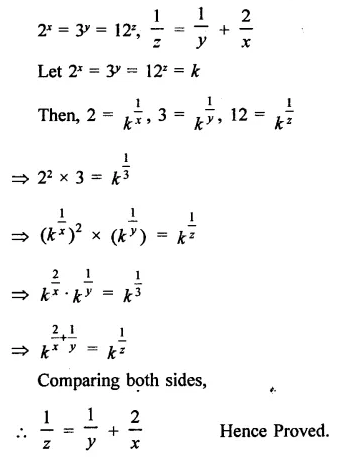
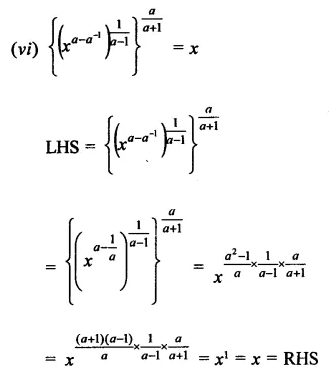
Question 6.

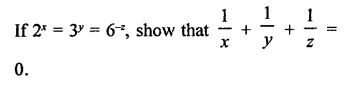
Solution:

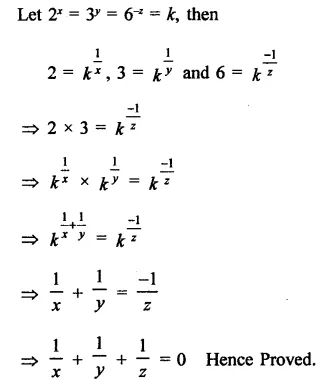
Question 7.

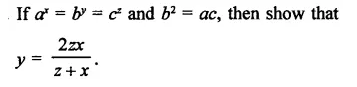
Solution:

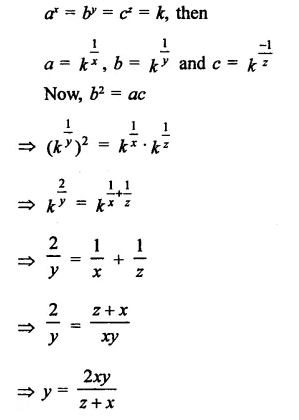
Question 8.

Solution:

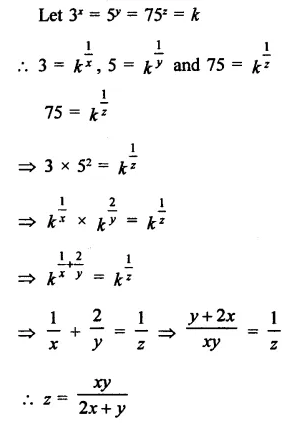
Question 9.

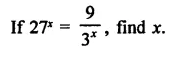
Solution:

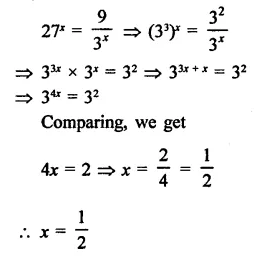
Question 10.
Find the values of x in each  of the following:

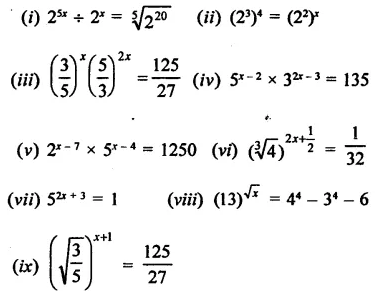
Solution:

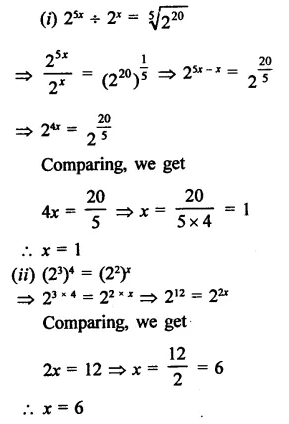
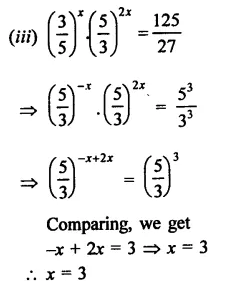
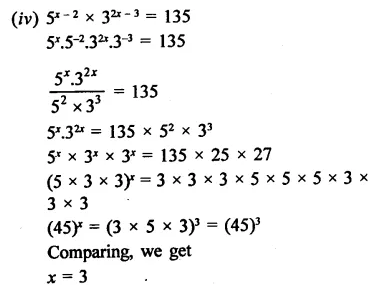
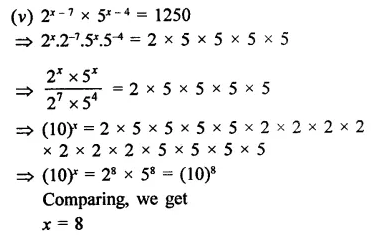
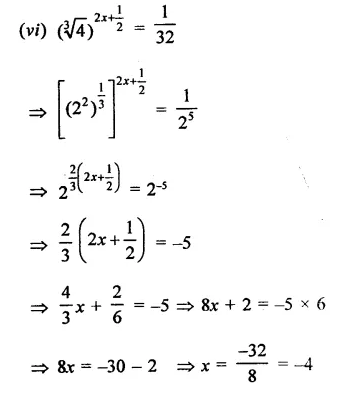
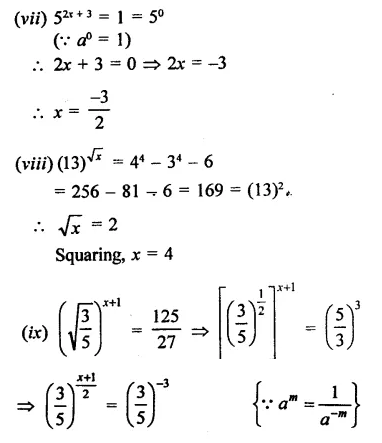
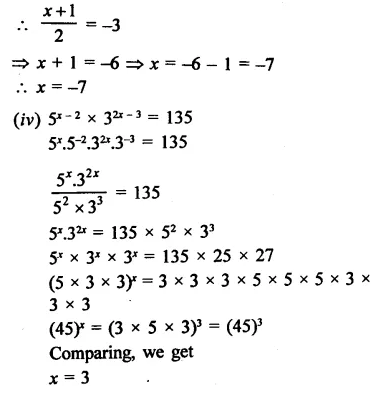
Question 11.
If x = 2^1/3 + 2^2/3, show that x³ – 6x = 6.
Solution:

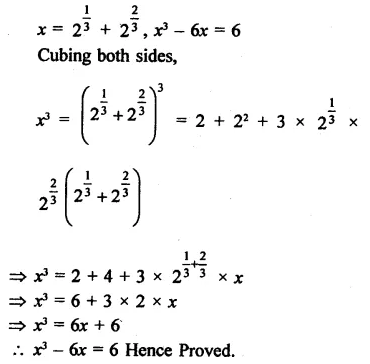
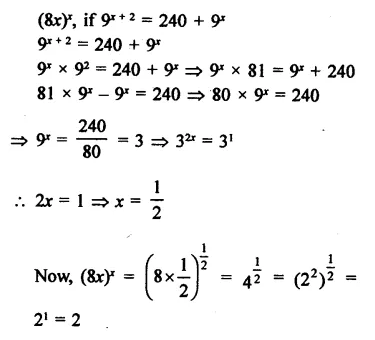
Question 12.
Determine (8x)^x, if 9^{x+ 2} = 240 + 9^x.
Solution:

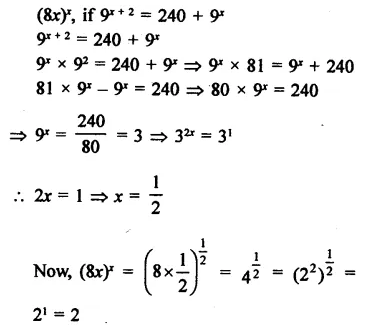
Question 13.
If 3^x+1 = 9^x-2, find the value of 2^{1 +x}.
Solution:

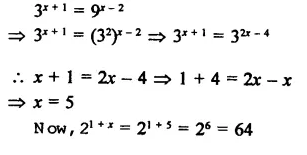
Question 14.
If 3^4x = (81)^-1 and 10^1/y = 0.0001, find the value of 2^-x+4y
Solution:

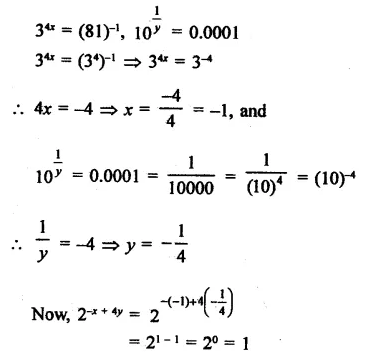
Question 15.
If 5^3x = 125 and 10^y = 0.001 find x and y.
Solution:

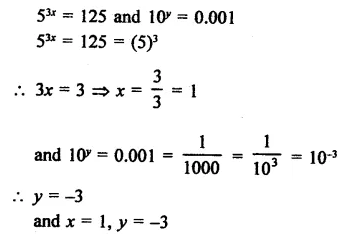
Question 16.
Solve the following equations:

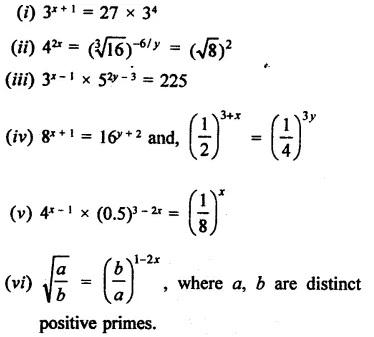
Solution:

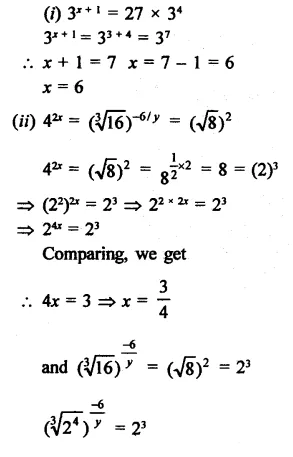
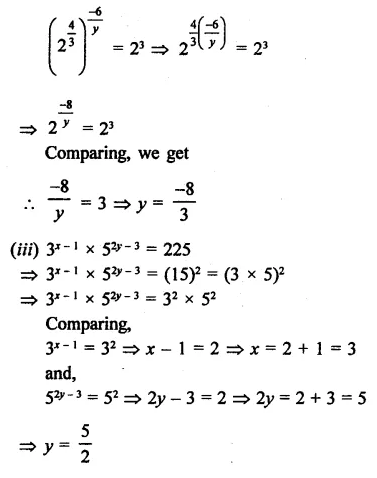
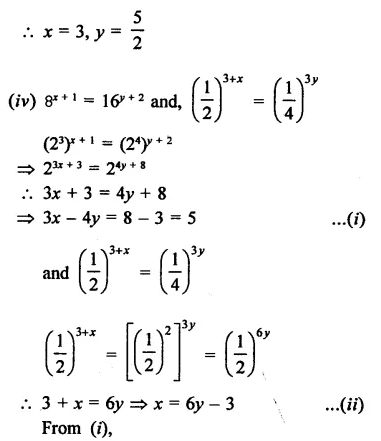
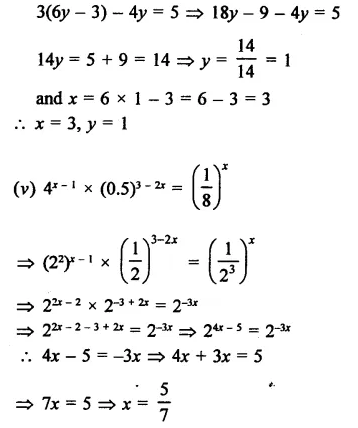
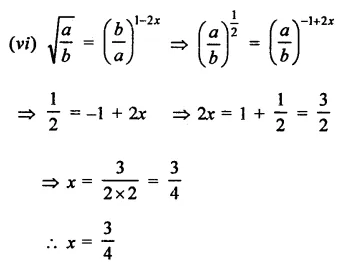
Question 17.

Solution:

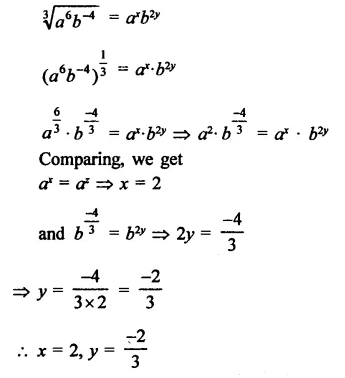
Question 18.
If a and b are different positive primes such that

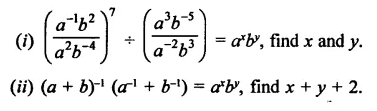
Solution:

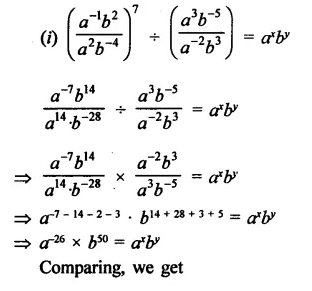
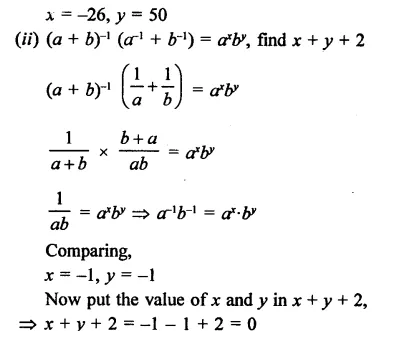
Question 19.
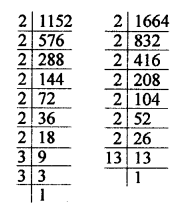
If 2^x x 3^y x 5^z = 2160, find x, y and z. Hence, compute the value of 3^x x 2^-y x 5^-z.
Solution:

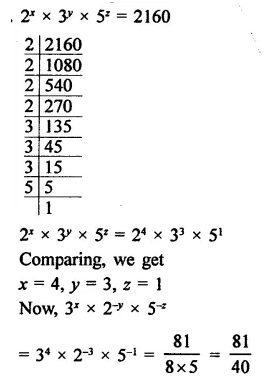
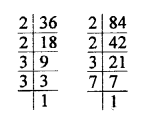
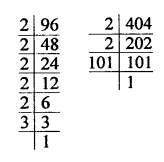
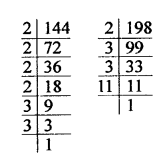
Question 20.
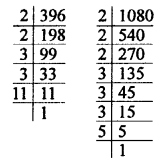
If 1176 = 2^a x 3^b x 7^c, find the values of a, b and c. Hence, compute the value of 2^a x 3^b x 7^-c as a fraction.
Solution:

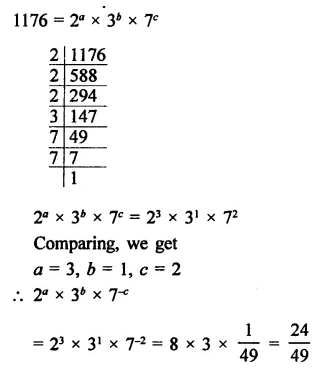
Question 21.
Simplify:

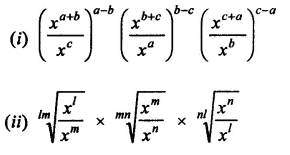
Solution:

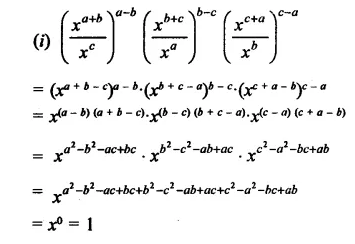
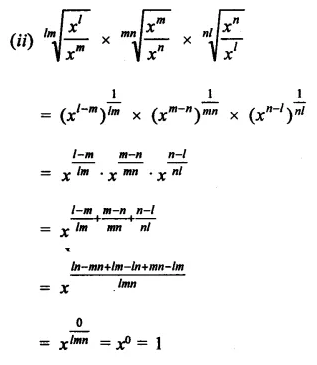
Question 22.
Show that:

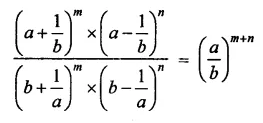
Solution:

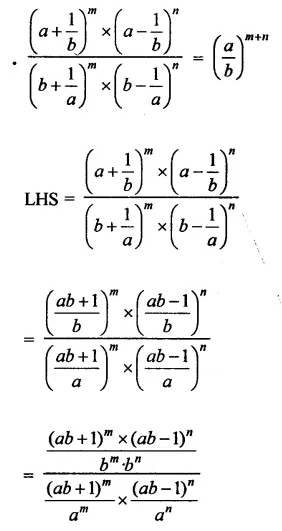
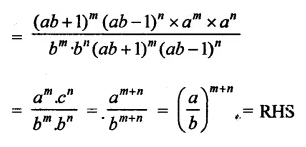
Question 23.

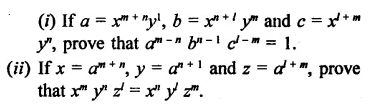
Solution:

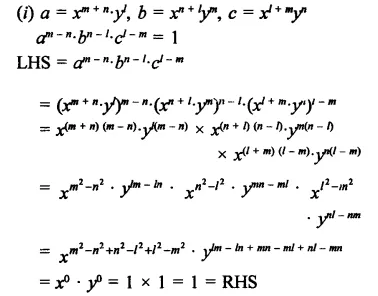
Hope given RD Sharma Class 9 Solutions Chapter 2 Exponents of Real Numbers Ex 2.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.1
• RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.2
• RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.3
• RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.4
• RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.5
• RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6
• RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.7
• RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.8

Question 1.
Add the following rational numbers:

Solution:

Question 2.
Add the following rational numbers:

Solution:

Question 3.
Simplify:

Solution:

Question 4.
Add and Express the sum as mixed fraction:

Solution:

Hope given RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 2 Exponents of Real Numbers Ex 2.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 2 Exponents of Real Numbers Ex 2.1

Question 1.
Simplify the following:

Solution:

Question 2.
If a = 3 and b =-2, find the values of:
(i) a^a+ b^b
(ii) a^b + b^a
(iii) (a+b)^ab
Solution:

Question 3.
Prove that:

Solution:

Question 4.
Prove that

Solution:

Question 5.
Prove that

Solution:

Question 6.

Solution:

Question 7.
Simplify the following:

Solution:

Question 8.
Solve the following equations for x:

Solution:

Question 9.
Solve the following equations for x:

Solution:

Question 10.
If 49392 = a⁴b²V³, find the values.of a, b and c, where a, b and c are different positive primes.
Solution:

Question 11.
If 1176 = 2^a x 3^b x T^c, find a, 6 and c.
Solution:

Question 12.
Given 4725 = 3^a5^b7^c, find:
(i) the integral values of a, b and c
(ii) the value of 2^-a 3^b 7^c
Solution:

Question 13.
If a = xy^p-1, b = xy ^q-1 and c = xy^r-1, prove that a^q-r b^r-p c^p-q = 1
Solution:

Hope given RD Sharma Class 9 Solutions Chapter 2 Exponents of Real Numbers Ex 2.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 1 Number Systems MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 1 Number Systems MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.1
• RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.2
• RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.3
• RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.4
• RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.5
• RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.6
• RD Sharma Class 9 Solutions Chapter 1 Number Systems MCQS

the correct alternative in each of the following:
Question 1.
Which one of the following is a correct statement?
(a) Decimal expansion of a rational number is terminating
(b) Decimal expansion of a rational number is non-terminating
(c) Decimal expansion of an irrational number is terminating
(d) Decimal expansion of an irrational number is non-terminating and non-repeating
Solution:
Decimal expansion of an irrational number is non-terminating and non-repeating . (d)

Question 2.
Which one of the following statements is true?
(a) The sum of two irrational numbers is always an irrational-number            
(b) The sum of two irrational numbers is always a rational number
(c) The sum of two irrational numbers may be a rational number or an irrational number
(d) The sum of two irrational numbers is always an integer
Solution:
The sum of two irrational numbers may be a rational number or an irrational number (c)

Question 3.
Which of the following is a correct statement?
(a) Sum of two irrational numbers is always irrational
(b) Sum of a rational and irrational number is always an irrational number
(c) Square of an irrational number is always a rational number
(d) Sum of two rational numbers can never be an integer
Solution:
Sum of a rational and irrational number is always an irrational number         (b)

Question 4.
Which of the following statements is true?
(a) Product of two irrational numbers is always irrational
(b) Product of a rational and an irrational number is always irrational
(c) Sum of two irrational numbers can never be irrational
(d) Sum of an integer and a rational number can never be an integer
Solution:
Product of a rational and an irrational number is always irrational    (b)

Question 5.
Which of the following is irrational?

Solution:

Question 6.
Which of the following is irrational?
(a) 14
(b)  0.14\(\overline { 16 }\)
(c)   0.\(\overline { 1416 }\)                  
(d)  0.1014001400014
Solution:
0.1014001400014…….. is irrational as it is non-terminating nor repeating decimal, (d)

Question 7.
Which of the following is rational?

Solution:

Question 8.
The number 0.318564318564318564… is:
(a) a natural number
(b) an integer
(c) a rational number
(d) an irrational number
Solution:
The number = 0.318564318564318564…………
= 0.\(\overline { 318564 }\)
∵ The decimal is non-terminating and recurring
∴ It is rational number.   (c)

Question 9.
If n is a natural number, then \(\sqrt { n } \)is
(a) always a natural number
(b) always a rational number
(c) always an irrational number
(d) sometimes a natural number and sometimes an irrational number
Solution:
If n is a natural number then \(\sqrt { n } \) may sometimes a natural number and sometime an irrational number e.g.
If n = 2 then \(\sqrt { n } \) =\(\sqrt { 2 } \) which is are irrational and if n = 4, then \(\sqrt { n } \)= \(\sqrt { 4 } \) =  2 which is a rational number.       (d)

Question 10.
Which of the following numbers can be represented as non-terminating, repeating decimals?

Solution:

Question 11.
Every point on a number line represents
(a) a unique real number
(b) a natural number
(c) a rational number
(d) an irrational number
Solution:
Every point on a number line represents a unique real number.         (a)

Question 12.
Which of the following is irrational?
(a) 0.15                     
(b) 0.01516
(c) 0.\(\overline { 1516 }\)                
(d) 0.5015001500015..
Solution:
As it is non-terminating non-repeating decimals while others are terminating or non-terminating repeating decimals. (d)

Question 13.
The number 1.\(\overline { 27 }\) in the form \(\frac { p }{ q }\)  , where p and q are integers and q ≠ 0, is

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.

Solution:

Question 19.

Solution:
An irrational number between 2 and 2.5 is \(\sqrt { 5 } \) as it has approximate value 2.236… (b)

Question 20.
The number of consecutive zeros in 2³ x 3⁴ x 5⁴ x 7, is
(a) 3                            
(b) 2
(c) 4
(d) 5
Solution:
In 2³ x 3⁴ x 5⁴ x 7, number of consecutive zero will be 3 as 2³ x 5⁴ = 2 x 2 x 2 x 5x 5 x 5 x 5 = 5000      (a)

Question 21.
The smallest rational number by which \(\frac { 1 }{ 3 }\) should be multiplied so that its decimal expansion terminates after one place of decimal, is

Solution:

Hope given RD Sharma Class 9 Solutions Chapter 1 Number Systems MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.6

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.6

Question 1.
Visualise 2.665 on the number line, using successive magnification.
Solution:
2.665
∵ It lies between 2 and 3

Question 2.
Visualise the representation of 5.3\(\overline { 7 }\) on the number line upto 5 decimal places, that is upto 5.37777.         [NCERT]
Solution:
5.37777.

Hope given RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.5

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.5

Question 1.
Complete the following sentences:
(i) Every point on the number line corresponds to a … number which many be either … or
(ii) The decimal form of an irrational number is neither … nor …
(iii) The decimal representation of a rational number is either … or …
(iv) Every real number is either … number or … number.
Solution:
(i) Every point on the number line corresponds to a real number which many be either rational or irrational.
(ii) The decimal form of an irrational number is neither terminating nor repeating.
(iii) The decimal representation of a rational number is either terminating or non­terminating, recurring.
(iv) Every real number is either rational number or an irrational number.

Question 2.
Find whether the following statements are true or false:
(i)  Every real number is either rational or irrational.
(ii) π is an irrational number.
(iii) Irrational numbers cannot be represented by points on the number line.
Solution:
(i) True. (Value of π = 3.14)
(ii) False : we can represent irrational number also.

Question 3.
Represent \(\sqrt { 6 } \), \(\sqrt { 7 } \), \(\sqrt { 8 } \) on the number line.
Solution:

Question 4.
Represent \(\sqrt { 3.5 } \) , \(\sqrt { 9.4 } \)and \(\sqrt { 10.5 } \) on the real number line.
Solution:

Hope given RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.4

Question 1.
Define an irrational number.
Solution:
A number which cannot be expressed in the form of \(\frac { p }{ q }\) where p and q are integers and q ≠ 0 is called an irrational number.

Question 2.
Explain, how irrational numbers differ from rational numbers?
Solution:
A rational number can be expressed in either terminating decimal or non-terminating recurring decimals but an irrational number is expressed in non-terminating non-recurring decimals.

Question 3.
Examine, whether the following numbers are rational or irrational:

Solution:

Question 4.
Identify the following as rational or irrational numbers. Give the decimal representation of rational numbers:

Solution:

Question 5.
In  the following equation, find which variables x, y, z etc. represent rational or irrational numbers:

Solution:

Question 6.
Given two rational numbers lying between 0.232332333233332… and 0.212112111211112.
Solution:
Two rational numbers lying between 0.232332333233332… and 0.212112111211112… will be 0.232 and 0.212

Question 7.
Give two rational numbers lying between 0.515115111511115… and 0.5353353335…
Solution:
Two rational numbers lying between 0.515115111511115… and 0.535335333533335… will be 0.515, 0.535

Question 8.
Find one irrational numbers between 0.2101 and 0.2222… = 0.\(\overline { 2 }\).
Solution:
One irrational number lying between 0.2101 and 0.2222… = 0.\(\overline { 2 }\) will be 2201.0010001…

Question 9.
Find a rational number and also an irrational number lying between the numbers, 0.3030030003… and 0.3010010001…
Solution:
Between two numbers 0.3030030003… and 0.3010010001…, a rational will be 0.301 and irrational number will be 0.3020020002…

Question 10.
Find three different irrational numbers between the rational numbers \(\frac { 5 }{ 7 }\) and \(\frac { 9 }{ 11 }\). [NCERT]
Solution:

Question 11.
Give an example of each, of two irrational numbers whose:
(i) difference is a rational number.
(ii) difference is an irrational number.
(iii) sum is a rational number.
(iv) sum is an irrational number.
(v) product is a rational number.
(vi) product is an irrational number.
(vii) quotient is a rational number.
(viii) quotient is an irrational number.
Solution:
(i) Two numbers whose difference is also a rational number, e.g. \(\sqrt { 2 } \)
, \(\sqrt { 2 } \)  which are irrational numbers.
∴ Difference = \(\sqrt { 2 } \) – \(\sqrt { 2 } \) = 0 which is also a rational number.
(ii) Two numbers whose difference is an irrational number.
e.g. \(\sqrt { 3 } \)  and \(\sqrt { 2 } \)  which are irrational numbers.
Now difference = \(\sqrt { 3 } \)  –\(\sqrt { 2 } \)  which is also an irrational number.
(iii) Let two irrational numbers be \(\sqrt { 3 } \)  and –\(\sqrt { 2 } \)  which are irrational numbers.
Now sum = \(\sqrt { 3 } \)  + (-\(\sqrt { 3 } \)) = \(\sqrt { 3 } \)
– \(\sqrt { 3 } \)  = 0 Which is a rational number.
(iv) Let two numbers be \(\sqrt { 5 } \)  , \(\sqrt { 3 } \) which are irrational numbers.
Now sum = \(\sqrt { 5 } \) + \(\sqrt { 3 } \)  which is an irrational number.
(v) Let numbers be \(\sqrt { 3 } \)  +\(\sqrt { 2 } \)and  \(\sqrt { 3 } \)  –\(\sqrt { 2 } \)which are irrational numbers.
Now product = (\(\sqrt { 3} \)  +\(\sqrt { 2 } \) ) (\(\sqrt { 3 } \) –\(\sqrt { 2 } \))
= 3-2 = 1 which is a rational number.
(vi) Let numbers be \(\sqrt { 3 } \) and \(\sqrt { 5 } \) , which are irrational number.
Now product = \(\sqrt { 3 } \) x \(\sqrt { 5 } \)  = \(\sqrt { 3×5 } \)
⁼ \(\sqrt { 15 } \)
which is an irrational number.
(vii) Let numbers be 6 \(\sqrt { 2 } \)  and 2 \(\sqrt { 2 } \) which are irrational numbers.
Quotient =\(\frac { 6\sqrt { 2 } }{ 2\sqrt { 2 } }\) = 3 which is a rational number.
(viii) Let numbers be \(\sqrt { 3 } \)and \(\sqrt { 5 } \) which are irrational numbers.
Now quotient =\(\frac { \sqrt { 3 } }{ \sqrt { 5 } }\) = \(\sqrt { \frac { 3 }{ 5 } }\) which is an  irrational number.

Question 12.
Find two irrational numbers between 0.5 and 0.55.
Solution:
Two irrational numbers between 0.5 and 0.55 will be 0.51010010001… and 52020020002…

Question 13.
Find two irrational numbers lying betwee 0.1 and 0.12.
Solution:
Two irrational numbers lying between 0.1 and 0.12 will be 0.1010010001… and 0.1020020002…

Question 14.
Prove that \(\sqrt { 3 } \)+\(\sqrt { 5 } \) is an irrational number.
Solution:

Hope given RD Sharma Class 9 Solutions Chapter 1 Number Systems Ex 1.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.