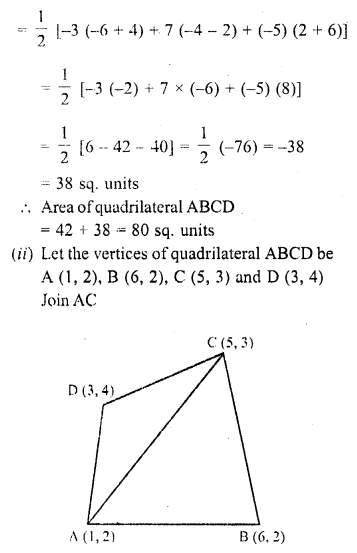
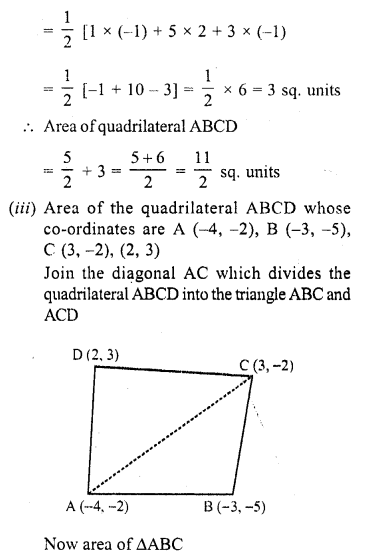
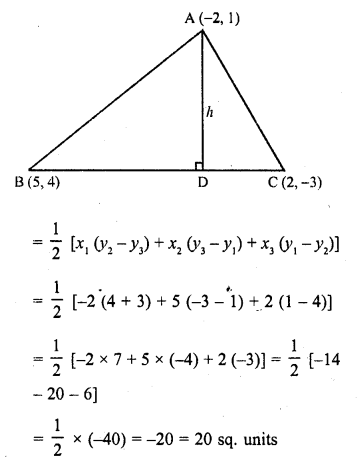
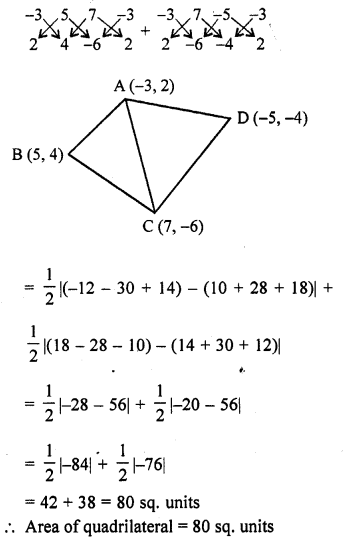
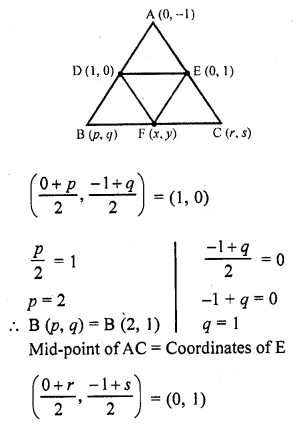
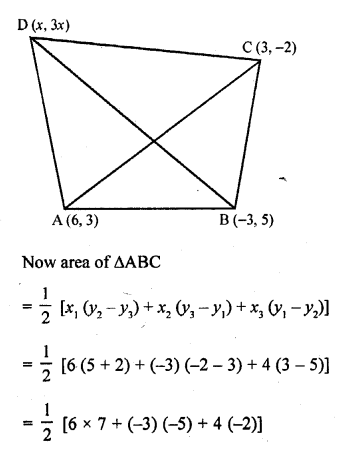
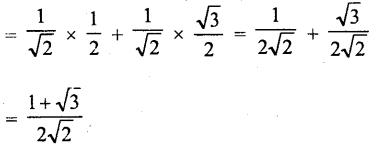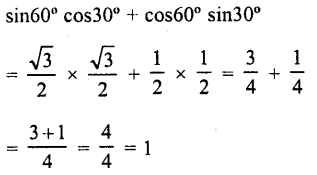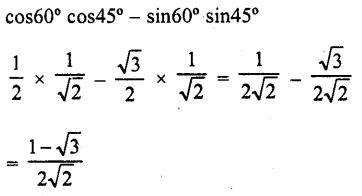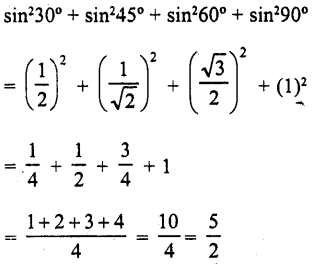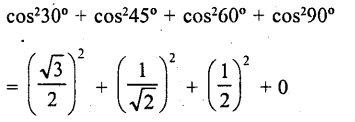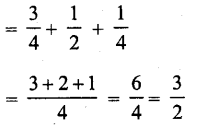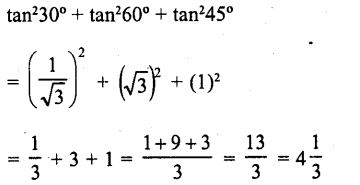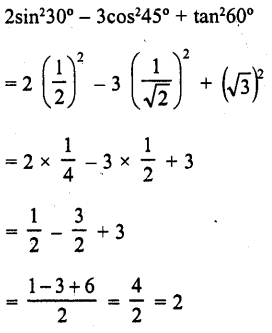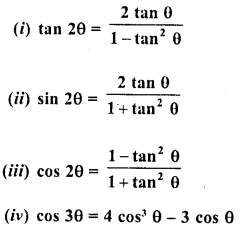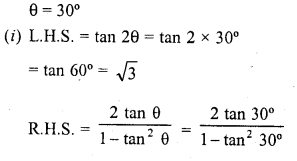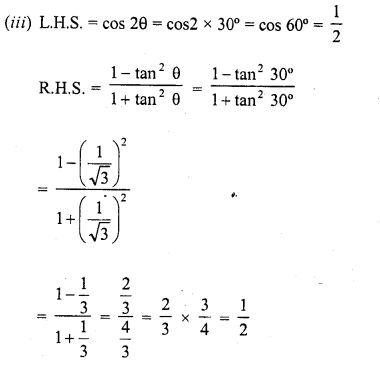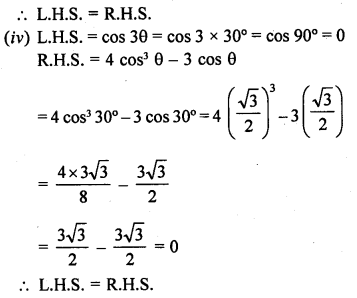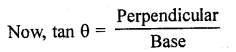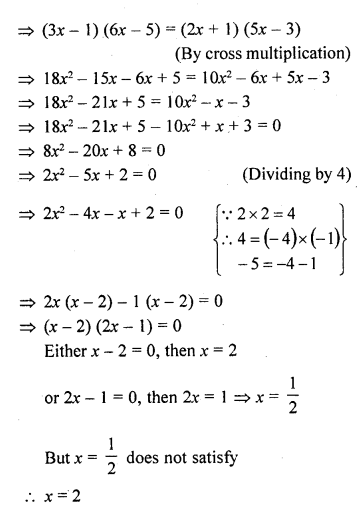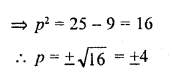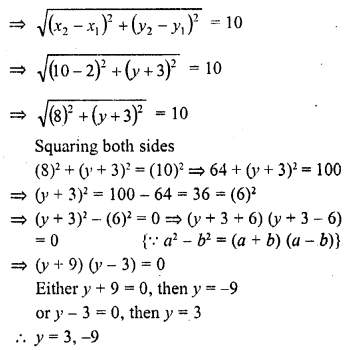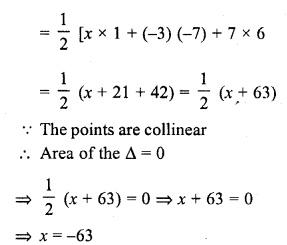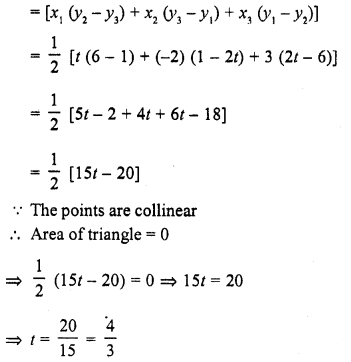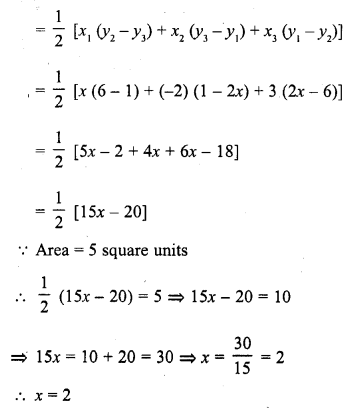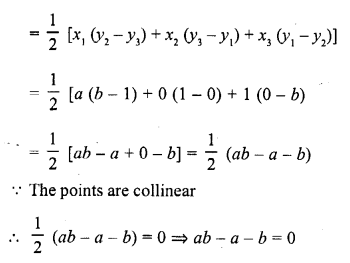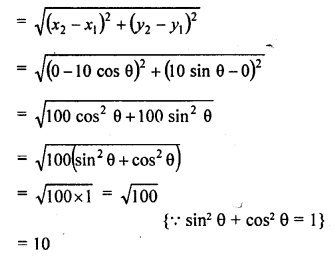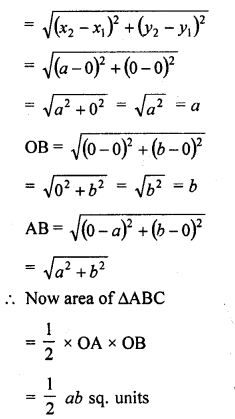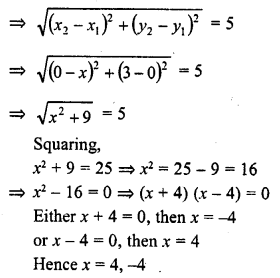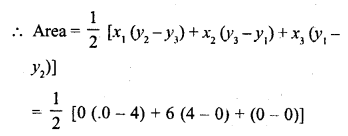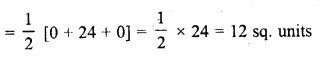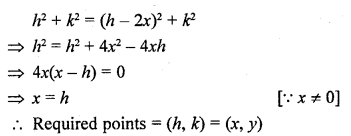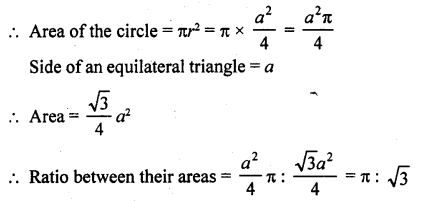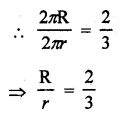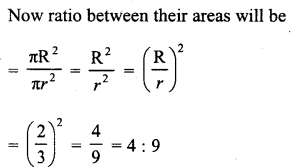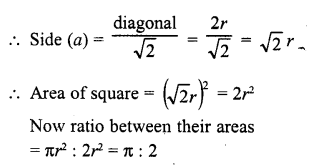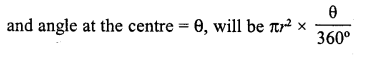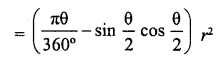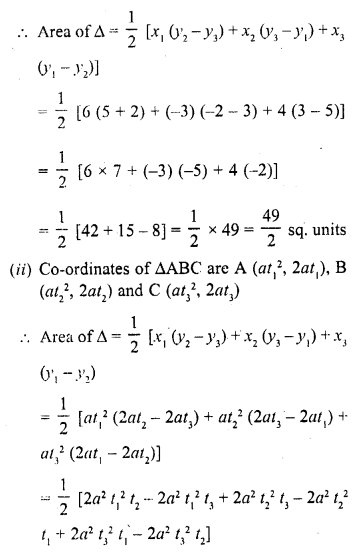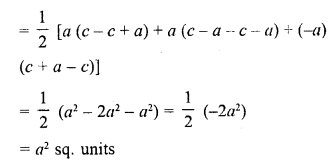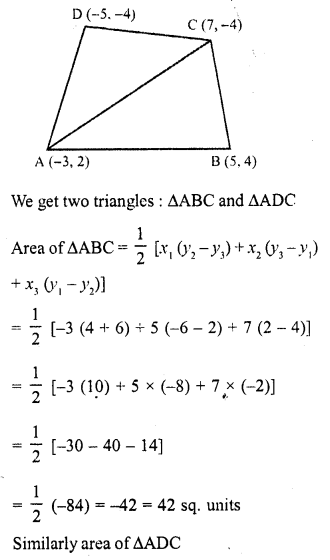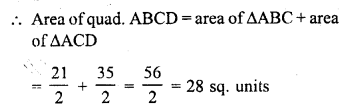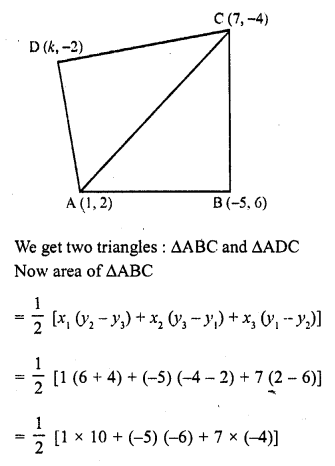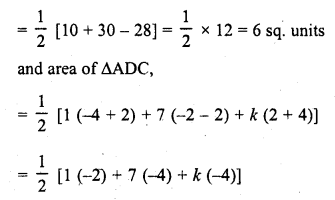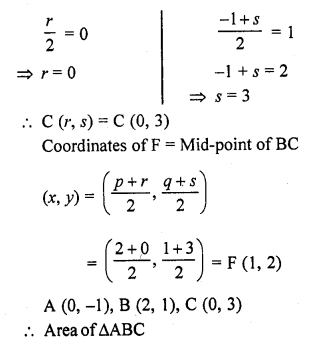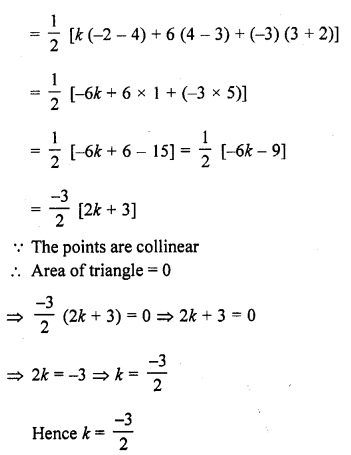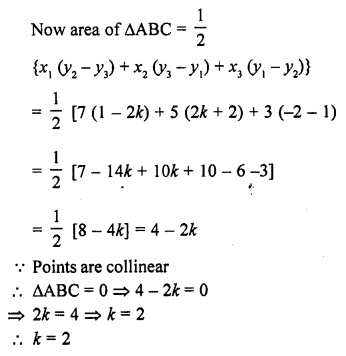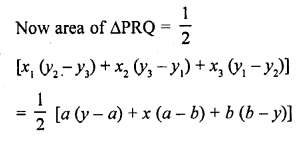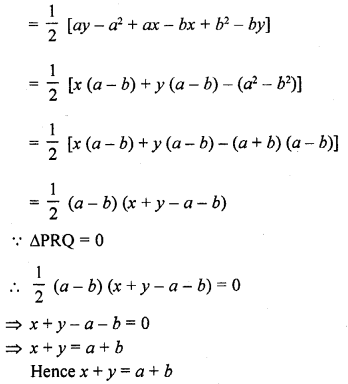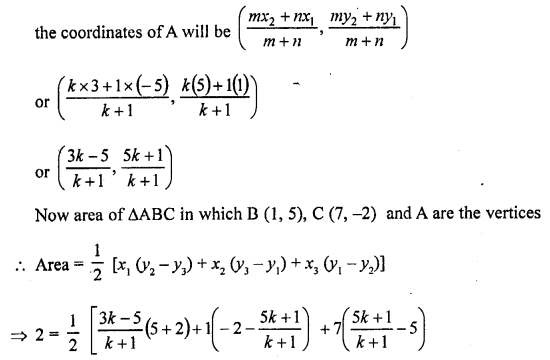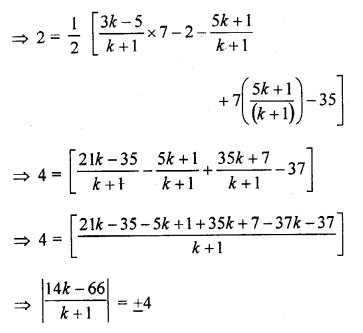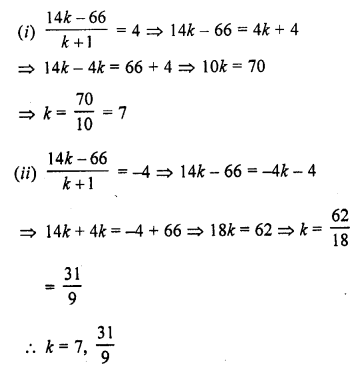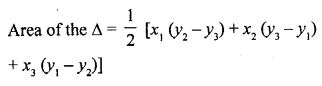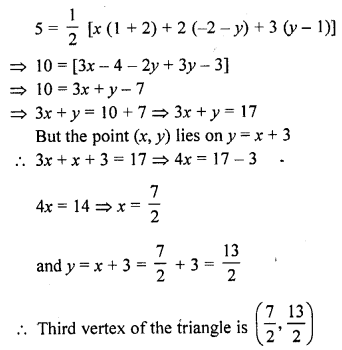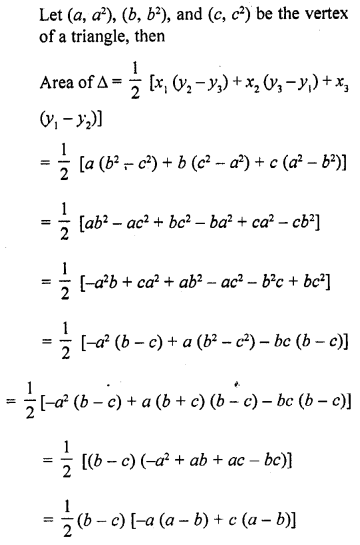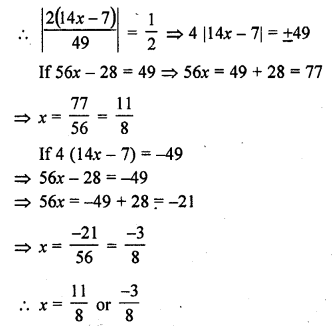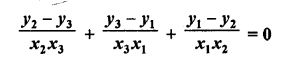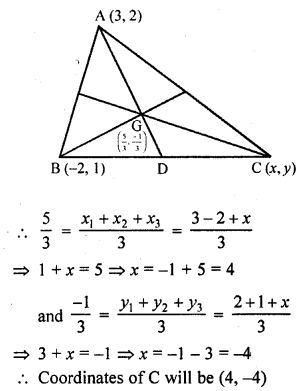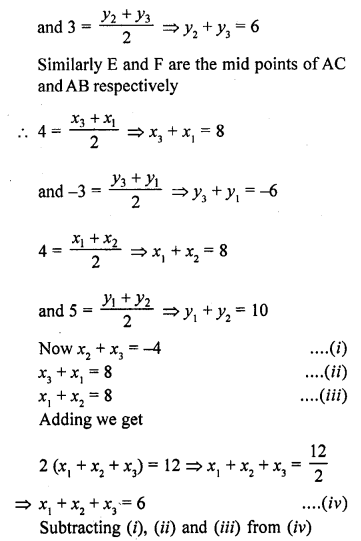Prasanna – Page 283

RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6

January 10, 2023

RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6

Other Exercises

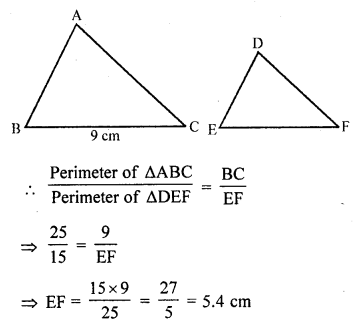
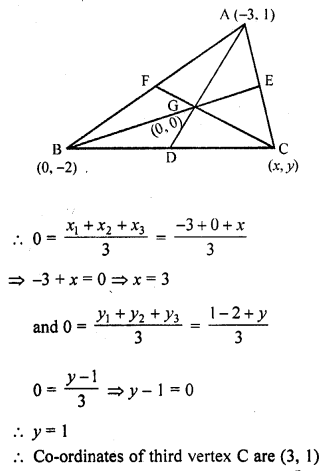
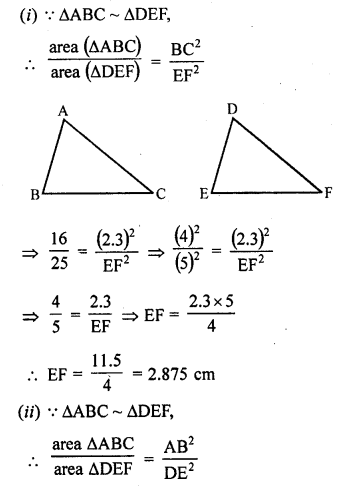
Question 1.
Triangles ABC and DEF are similar.
(i) If area (∆ABC) = 16 cm², area (∆DEF) = 25 cm² and BC = 2.3 cm, find EF. (C.B.S.E. 1992)
(ii) If area (∆ABC) = 9 cm², area (∆DEF) = 64 cm² and DE = 5.1 cm, find AB.
(iii) If AC = 19 cm and DF = 8 cm, find the ratio of the area of two triangles. (C.B.S.E. 1992C)
(iv) If area (∆ABC) = 36 cm², area (∆DEF) = 64 cm² and DE = 6.2 cm, find AB. (C.B.S.E. 1992)
(v) If AB = 1.2 cm and DE = 1.4 cm, find the ratio of the areas of ∆ABC and ∆DEF. (C.B.S.E. 1991C)
Solution:
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 1

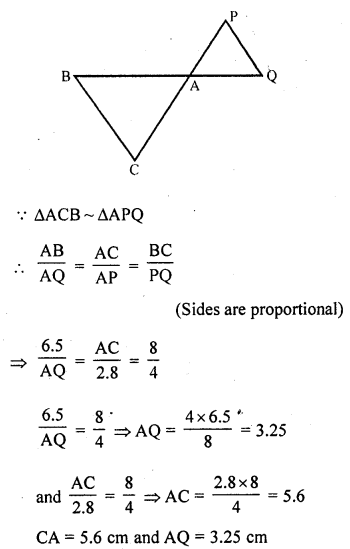
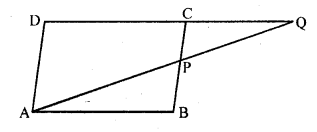
Question 2.
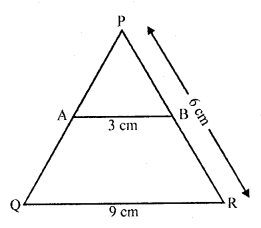
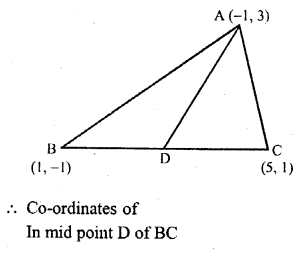
In the figure, ∆ACB ~ ∆APQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ. Also, find the area (∆ACB) : area (∆APQ).
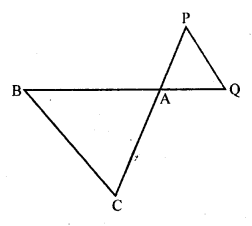
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 4
Solution:

Question 3.
The areas of two similar triangles are 81 cm² and 49 cm² respectively. Find the ratio of their corresponding heights, what is the ratio of their corresponding medians ?
Solution:
Areas of two similar triangles are 81 cm² and 49 cm²
The ratio of the areas of two similar triangles are proportion to the square of their corresponding altitudes and also squares of their corresponding medians
Ratio in their altitudes = √81 : √49 = 9 : 7
Similarly, the ratio in their medians = √81 : √49 = 9 : 7

Question 4.
The areas of two similar triangles are 169 cm² and 121 cm² respectively. If the longest side of the larger triangle is 26 cm, find the longest side of the smaller triangle.
Solution:
Triangles are similar Area of larger triangle = 169 cm²
and area of the smaller triangle =121 cm²
Length of longest sides of the larger triangles = 26 cm
Let the length of longest side of the smaller triangle = x
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 7

Question 5.
The areas of two similar triangles are 25 cm² and 36 cm² respectively. If the altitude of the first triangle is 2.4 cm, find the corresponding altitude of the other.
Solution:
Area of first triangle = 25 cm²
Area of second = 36 cm²
Altitude of the first triangle = 2.4 cm
Let altitude of the second triangle = x
The triangles are similar
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 8

Question 6.
The corresponding altitudes of two similar triangles are 6 cm and 9 cm respectively. Find the ratio of their areas.
Solution:
Length of the corresponding altitude of two triangles are 6 cm and 9 cm
triangles are similar
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 9

Question 7.
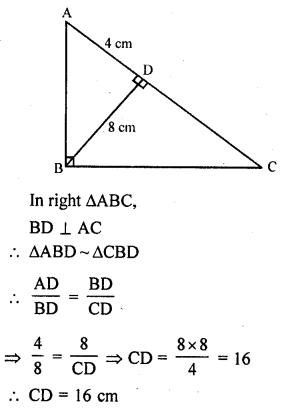
ABC is a triangle in which ∠A = 90°, AN ⊥ BC, BC = 12 cm and AC = 5 cm. Find the ratio of the areas of the ∆ANC and ∆ABC.
Solution:
In ∆ABC, ∠A = 90°
AN ⊥ BC
BC = 12 cm, AC = 5 cm
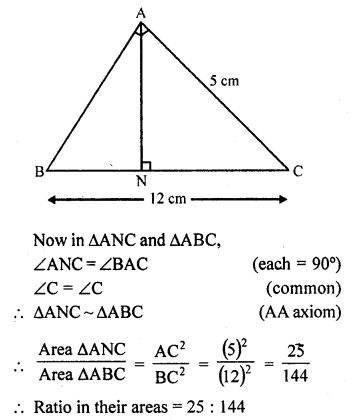
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 10

Question 8.
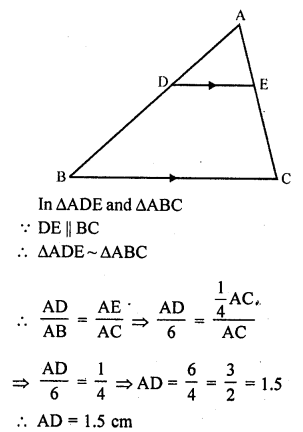
In the figure, DE || BC
(i) If DE = 4 cm, BC = 6 cm and area (∆ADE) = 16 cm², find the area of ∆ABC.
(ii) If DE = 4 cm, BC = 8 cm and area of (∆ADE) = 25 cm², find the area of ∆ABC. (C.B.S.E. 1991)
(iii) If DE : BC = 3 : 5, calculate the ratio of the areas of ∆ADE and the trapezium BCED
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 11
Solution:

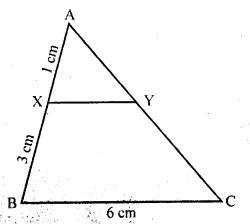
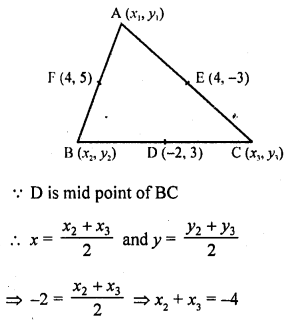
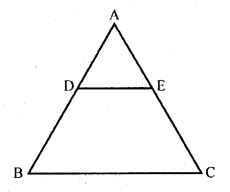
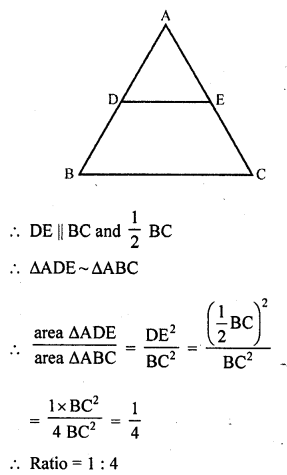
Question 9.
In ∆ABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ∆ADE and ∆ABC.
Solution:
In ∆ABC, D and E are the mid points of AB and AC respectively
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 15

Question 10.
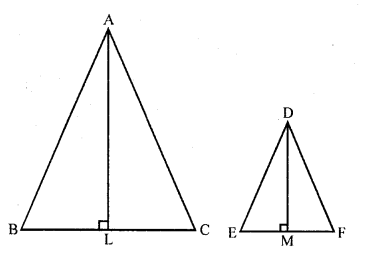
The areas of two similar triangles are 100 cm² and 49 cm² respectively. If the altitude of the bigger triangle is 5 cm, find the corresponding altitude of the other. (C.B.S.E. 2002)
Solution:
∆ABC ~ ∆DEF
area ∆ABC = 100 cm²
and area ∆DEF = 49 cm²
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 16

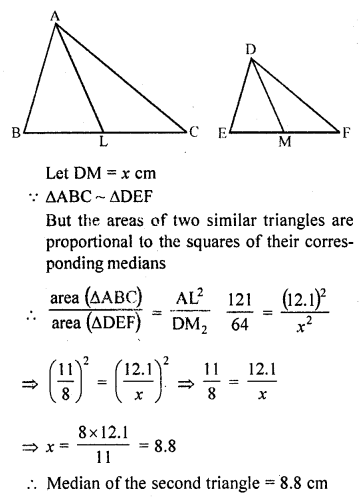
Question 11.
The areas of two similar triangles are 121 cm² and 64 cm² respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other. (C.B.S.E. 2001)
Solution:
∆ABC ~ ∆DEF
area of ∆ABC = 121 cm² area of ∆DEF = 64 cm²
AL and DM are the medians of ∆ABC and ∆DEF respectively
AL = 12.1 cm
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 18

Question 12.
In ∆ABC ~ ∆DEF such that AB = 5 cm and (∆ABC) = 20 cm² and area (∆DEF) = 45 cm², determine DE.
Solution:
∆ABC ~ ∆DEF
area (∆ABC) = 20 cm²
area (∆DEF) = 45 cm²
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 19

Question 13.
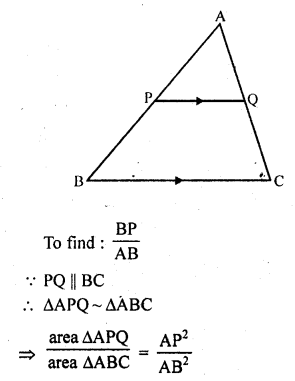
In ∆ABC, PQ is a line segment intersecting AB at P and AC at Q such that PQ || BC and PQ divides ∆ABC into two parts equal in area. Find \(\frac { BP }{ AB }\).
Solution:
In ∆ABC, PQ || BC and PQ divides ∆ABC in two parts ∆APQ and trap. BPQC of equal in area
i.e., area ∆APQ = area BPQC
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 21

Question 14.
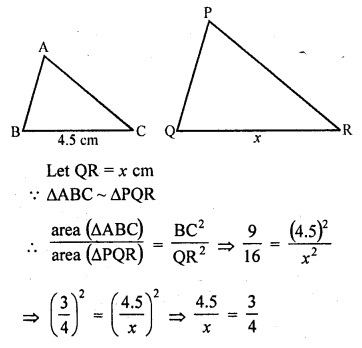
The areas of two similar triangles ABC and PQR are in the ratio 9 : 16. If BC = 4.5 cm, find the length of QR. (C.B.S.E. 2004)
Solution:
∆ABC ~ ∆PQR
area (∆ABC) : area (∆PQR) = 9 : 16
and BC = 4.5 cm
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 23

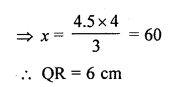
Question 15.
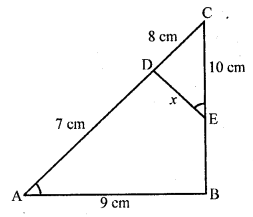
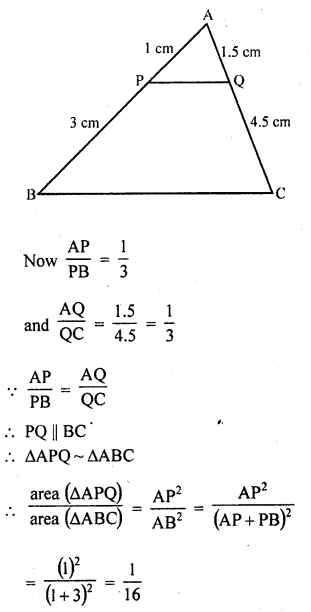
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 cm, prove that area of ∆APQ is one sixteenth of the area of ∆ABC. (C.B.S.E. 2005)
Solution:
In ∆ABC, P and Q are two points on AB and AC respectively such that
AP = 1 cm, PB = 3 cm, AQ = 1.5 cm and QC = 4.5 cm
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 25

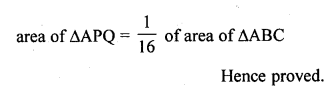
Question 16.
If D is a point on the side AB of ∆ABC such that AD : DB = 3 : 2 and E is a point on BC such that DE || AC. Find the ratio of areas of ∆ABC and ∆BDE. (C.B.S.E. 2006C)
Solution:
In ∆ABC, D is a point on AB such that AD : DB = 3 : 2
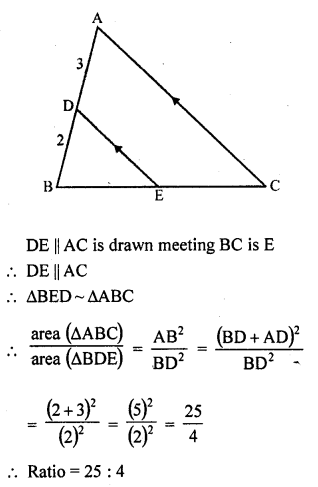
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 27

Question 17.
If ∆ABC and ∆BDE are equilateral triangles, where D is the mid point of BC, find the ratio of areas of ∆ABC and ∆BDE. [CBSE 2010]
Solution:
∆ABC and ∆DBE are equilateral triangles Where D is mid point of BC
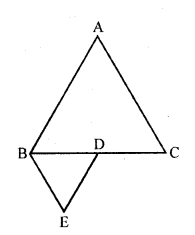
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 28

Question 18.
Two isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding heights.
Solution:
Two isosceles triangles have equal vertical angles
So their base angles will also be the equal to each other
Triangles will be similar Now, ratio in their areas = 36 : 25
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 30

Question 19.
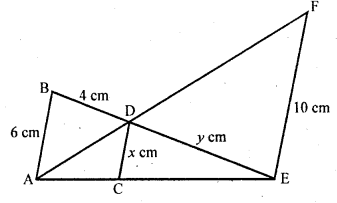
In the figure, ∆ABC and ∆DBC are on the same base BC. If AD and BC intersect
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 31
Solution:
Given : Two ∆ABC and ∆DBC are on the same base BC as shown in the figure
AC and BD intersect eachother at O

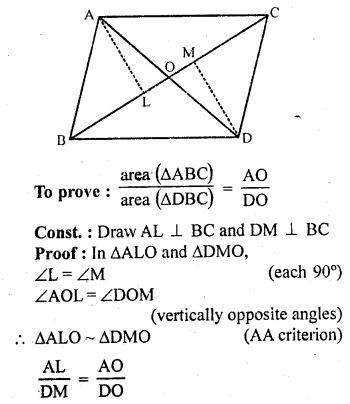
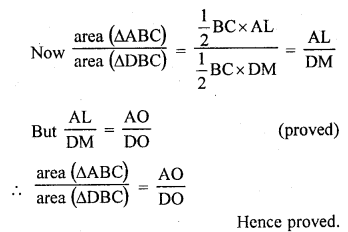
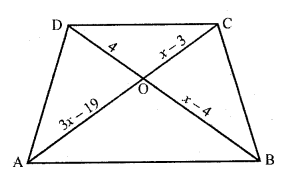
Question 20.
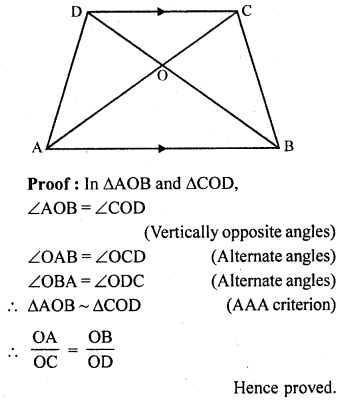
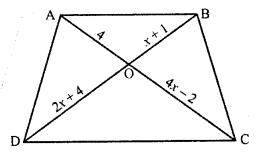
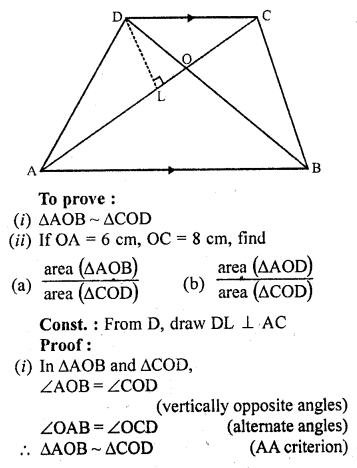
ABCD is a trapezium in which AB || CD. The diagonals AC and BD intersect at O. Prove that
(i) ∆AOB ~ ∆COD
(ii) If OA = 6 cm, OC = 8 cm, find
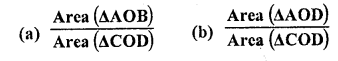
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 34
Solution:
Given : ABCD is a trapezium in which AB || CD
Diagonals AC and BD intersect each other at O

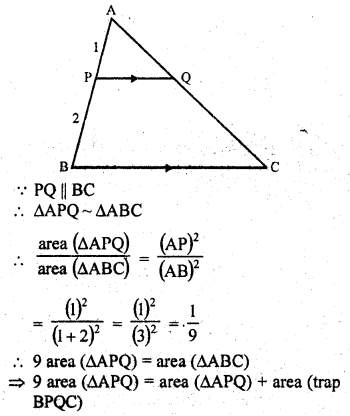
Question 21.
In ∆ABC, P divides the side AB such that AP : PB = 1 : 2. Q is a point in AC such that PQ || BC. Find the ratio of the areas of ∆APQ and trapezium BPQC.
Solution:
In ∆ABC, P is a point on AB such that AP : PQ = 1 : 2
PQ || BC
Now we have to find the ratio between area ∆APQ and area trap BPQC
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 37

Question 22.
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area (∆ADE) : Area (∆ABC) = 3 : 4. [CBSE 2010]
Solution:
Given: In equilateral ∆ABC, AD ⊥ BC and with base AD, another equilateral ∆ADE is constructed
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 39

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2

January 10, 2023

RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2

Other Exercises

Evaluate each of the following (1-19) : 1.
Question 1.
sin45° sin30° + cos45° cos30°.
Solution:
sin 45° sin 30° + cos 45° cos 30°
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 1

Question 2.
sin60° cos30° + cos60° sin30°.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 2

Question 3.
cos60° cos45° – sin60° sin45°.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 3

Question 4.
sin²30° + sin²45° + sin²60° + sin²290°.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 4

Question 5.
cos²30° + cos²45° + cos²60° + cos²90°.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 5

Question 6.
tan²30° + tan²60° + tan²45°.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 7

Question 7.
2sin²30° – 3cos²45° + tan²60°.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 8

Question 8.
sin²30°cos²4S° + 4tan²30° + \(\frac { 1 }{ 2 }\) sin²90° -2cos²90° + \(\frac { 1 }{ 24 }\) cos20°.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 9

Question 9.
4 (sin⁴ 60° + cos⁴ 30°) – 3 (tan² 60° – tan² 45°) + 5cos² 45°
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 11

Question 10.
(cosecc² 45° sec² 30°) (sin² 30° + 4cot² 45° – sec² 60°).
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 12

Question 11.
cosec³ 30° cos 60° tan³ 45° sin2 90° sec² 45° cot 30°.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 14

Question 12.
cot² 30° – 2cocs² 60° – \(\frac { 3 }{ 4 }\)sec2 45° – 4sec² 30°.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 15

Question 13.
(cos0° + sin45° + sin30°) (sin90° – cos45° + cos60°)
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 16

Question 14.
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 18
Solution:

Question 15.
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 20
Solution:

Question 16.
4 (sin⁴ 30° + cos² 60°) – 3 (cos² 45° – sin² 90°) – sin² 60°
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 22

Question 17.
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 23
Solution:

Question 18.
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 25
Solution:

Question 19.
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 28
Solution:

Find the value of x in each of the following : (20-25)

Question 20.
2sin 3x = √3
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 30

Question 21.
2sin \(\frac { x }{ 2 }\) = 1
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 31

Question 22.
√3 sin x=cos x
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 32

Question 23.
tan x = sin 45° cos 45° + sin 30°
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 33

Question 24.
√3 tan 2x = cos 60° +sin 45° cos 45°
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 34

Question 25.
cos 2x = cos 60° cos 30° + sin 60° sin 30°
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 36

Question 26.
If θ = 30°, verify that :
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 37
Solution:

Question 27.
If A = B = 60°, verify that:
(i) cos (A – B) = cos A cos B + sin A sin B
(ii) sin (A – B) = sin A cos B – cos A sin B tan A – tan B
(iii) tan (A – B) = \(\frac { tanA-tanB }{ 1+tanA-tanB }\)
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 42

Question 28.
If A = 30° and B = 60°, verify that :
(i) sin (A + B) = sin A cos B + cos A sin B
(ii) cos (A + B) = cos A cos B – sin A sin B
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 44

Question 29.
If sin (A + B) = 1 and cos (A,-B) = 1,0° < A + B < 90°, A > B find A and B.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 45

Question 30.
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 47
Solution:

Question 31.
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 49
Solution:

Question 32.
In a ∆ABC right angle at B, ∠A = ∠C. Find the values of
(i) sin A cos C + cos A sin C
(ii) sin A sin B + cos A cos B
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 52

Question 33.
Find acute angles A and B, if sin (A + 2B)=\(\frac { \sqrt { 3 } }{ 2 }\) and cos (A + 4B) = 0, A > B.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 53

Question 34.
In ΔPQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 54

Question 35.
If sin (A – B) = sin A cos B – cos A sin B and cos (A – B) = cos A cos B + sin A sin B, find the values of sin 15° and cos 15°.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 56

Question 36.
In a right triangle ABC, right angled at ∠C if ∠B = 60° and AB – 15 units. Find the remaining angles and sides.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 57

Question 37.
If ΔABC is a right triangle such that ∠C = 90°, ∠A = 45° and BC = 7 units. Find ∠B, AB and AC.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 59

Question 38.
In a rectangle ABCD, AB = 20 cm, ∠BAC = 60°, calculate side BC and diagonals AC and BD.
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 61

Question 39.
If A and B are acute angles such that
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 62
Solution:

Question 40.
Prove that (√3 + 1) (3 – cot 30°) = tan³ 60° – 2sin 60°. [NCERT Exemplar]
Solution:
RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 65

Hope given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1

January 10, 2023

RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1

Other Exercises

Question 1.
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower ?
Solution:
Let TS is the tower and P is a point which is 20 m away from the foot of the tower and angle of elevation of T is 60°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 1

Question 2.
The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 9.5 m away from the wall. Find the length of the ladder.
Solution:
Let LM is the ladder which makes an angle of 60° with the wall LM
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 2

Question 3.
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wail and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
Solution:
Let LM be the ladder which makes an angle of 60° with the wall LN and at a distance of 2 m from the foot of the wall
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 3

Question 4.
An electric pole is 10 m high. A steel wire tied to top of the pole is affixed at a point on the ground to keep the pole up right. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
Solution:
Let AB be the pole and a wire AC is tied to the top of the pole with a point C on the ground which makes an angle of 45° with the ground
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 5

Question 5.
A kite is flying at a height of 75 metres from the ground level, attached to a string inclined at 60° to the horizontal. Find the length of the string to the nearest metre.
Solution:
Let K be the kite flying in the sky at a height of 75 m from the ground LM. The string KL makes an angle of 60° to the ground
Let length of string KL = x m
KM = 75 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 7

Question 6.
A ladder 15 m long just reaches the top of a vertical wall. If the ladders makes an angle of 60° with the wall, then find the height of the wall.
Solution:
Given that, the height of the ladder = 15 m
Let the height of the vertical wall = h
and the ladder makes an angle of elevation 60° with the wall i.e., θ = 60°.
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 8

Question 7.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flag-staff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
Solution:
Let TR be the tower and FT is the flag on it. P is an point on the ground 70 m away from the foot of the tower. From P, the angle of elevation of the top and bottom of the flag are 60° and 45° respectively Let h be the height of flag staff and x be the height of the tower
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 9

Question 8.
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break ? [CBSE 1995]
Solution:
Let TR be the tree whose height is 15 m
Let it is broken from A and its top T touches the ground at B making an angle of 60° with the ground
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 11

Question 9.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 metres. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 30° and 60°. Find the height of the tower. (C.B.S.E. 1995)
Solution:
Let TR be the tower and FT is a flag staff on it. A is a point on the ground such that it makes angles of elevation of the bottom and top of the flag staff of 30° and 60° respectively
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 12

Question 10.
A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the root of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
Solution:
Let TR be the tower. A person at A on the ground observes the angle of elevation of the top T of the tower as 30° and then moves towards the foot of the tower. At a distance of 50 m at B, the angle of elevation becomes 60°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 14
Let h be the height of the tower and BR = x, then AR = (50 + x)

Question 11.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m longer than when it was 60°. Find the height of the tower.
Solution:
Let TR be we know
Let the shadow of TR at the elevation of the sun 45° be x m and at 60°, will be (x – 10) m Now in right ΔTAR,
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 17

Question 12.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° at two observing points 100 m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground from the just observation point.
Solution:
Let P be the parachutist landing to Q on the ground
A and B are two observations such that AB = 10 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 19
Let h be the height of the parachutist from the ground and x be the distance of B from Q and (100 + x) is the distance from A to Q Now in right ΔAPQ,

Question 13.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects. (C.B.S.E. 1992)
Solution:
Let TR be the tower and A, B are two objects which makes angles of elevation with top of the tower as 45° and 60° respectively
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 22

Question 14.
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use\(\sqrt { 3 } \) = 1-732). (C.B.S.E. 2006)
Solution:
Let TR be the tower. A is a point on the same level which makes an angle of elevation of 30° with the top of the tower TR, and 150 m from A towards the foot of the tower the angle of elevaton is 60°, Let TR = h m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 24

Question 15.
The angle of elevation of the top of a tower as observed from a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626] (C.B.S.E. 2001C)
Solution:
Let PQ be the tower and from a points A, and B the angles of elevations of top P of the tower are 32° and 63° respectively and AB= 100 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 26

Question 16.
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower from the point A. (C.B.S.E. 2002)
Solution:
Let CD be the tower and from a point A on the same ground, the angle of elevation of the top of the tower is 30°. B is another point such that AB = 20 m and from B, the angle of elevation is 60°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 28
Let h be the height of the tower CD and x is the length of AD
∴ BD = (x – 20) m
Now in right ΔCAD

Question 17.
From the top of a building 15 m high the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between the tower and building. (C.B.S.E. 2002)
Solution:
Let TR be the tower and AB be the building The angles of elevation of the top of the tower T, from A is 30° and from B is 60°
Height of AB = 15 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 31
Let the height of tower TR = h and the distance between the tower and building = x
In right ΔTBR,

Question 18.
On a horizontral plane there is a vertical tower with the flag pole on the top of the tower. At a point 9 metres away from the foot of the tower the angle of elevation of the top and bottom of the flag pole are 60° and 30° respectively. Find the height of the tower and the flag pole mounted on it. (C.B.S.E. 2005)
Solution:
Let TR be the tower and F is the flag pole on it. A is a point 9 m away from the foot of the tower and angles of elevation of the top and bottom of the flag pole from A are 60° and 30° respectively
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 34

Question 19.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance between the foot of the tree to the point where the top touches the ground is 8 in. Find the height of the tree.
Solution:
Let TR be the tree and it is broken from A and broken part of the tree makes an angle of 30° on the ground at B
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 36

Question 20.
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take \(\sqrt { 3 } \) = 1.732
Solution:
Let BA is the building such that BA = 10 in CB is a flag-staff on the building P is a point on the ground such that the angles of the elevation of the top of the building is 30° and that of the top of the flag-staff is 45°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 39

Question 21.
A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using
(i) trigonometric ratios
(ii) property of similar triangles.
Solution:
Let LP is the lamp-post and GR is the girl who is at a distance of 3.2 m
From the lamp-post and its shadow is AR which is 4.8 m long. Let ∠A = 0
Height of girl GR = 1.6 m and let height of lamp post = h
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 41

Question 22.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increasees from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution:
Let BA is the boy whose height is 1.5 m and CD is building whose height is 30 m Angle of elevation of C from B (eyes of the boy) is 30°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 43
and on moving some distance towards the building at L, the angle of elevation of C is 60°
Let AM = BL = x and AD = y
Then LE = MD = y – x
and CE = CD – ED = 30 – 1.5 = 28.5 m
Now in right ΔCBE

Question 23.
The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was “60°. Find the height of the tower.
Solution:
Let TR be the tower and RB and RA are its shadows at the elevation of 60° and 30° respectively. Such that BA = 40 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 45
Let h be the height of the tower and let shadow RA = x m
Then shadow RB = (x – 40) m
Now in right ΔTAR,

Question 24.
From a point on the ground the angles of elevation of the bottom and top of a transmission tower fixed at the top of 20 m high building are 45° and 60° respectively. Find the height of the transmission tower.
Solution:
BC is the building and AB is the transmission on it the height of the building is 20 m From a point P, the angles of elevation of B and A are 45° and 60° respectively
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 47
Let height of the transmission AB = h and let PC = x
Now in right ΔBPC,

Question 25.
The angles of depression of the top and bottom of 8 m tali building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance Between the two buildings.
Solution:
Let AB be the multistoried building and CD is another building. From A, the angles of depression of the top C and bottom D of the other building are 30° and 45° respectively Height of building is 8 m i.e. CD = 8 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 49

Question 26.
A statue 1.6 m tall stands on the top of pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angles of elevation of the top of thd\pedestal is 45°. Find the height of the pedestal. (C.B.S.E. 2008)
Solution:
Let AB be the statue standing on the top of a pedestal BC
From a point P on the ground the angles of elevation of the top of the statue is 60° and top of the pedestal BC is 45°
Let height of BC = h and PC = x
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 51

Question 27.
A T.V. Tower stands vertically on a bank of a river. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river.
Solution:
Let AB is the T.V. tower and CB is the,width of the river. D is a point which is 20 m away from C
Now angles of elevation from A to C and D are 60° and 30° respectively.
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 53

Question 28.
From the top of a 7 m high building, the – angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution:
Let AB be the building and CD be the cable tower
From the top of building, the angle of elevation of the top of tower is 60° and angle of depression of the foot of the tower is 45° Now AB = 7 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 55

Question 29.
As observed from the top of a 75 m tall lighthouse, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution:
Let LH is die light house and A, B are two ships From L, angles of depression of the ships A and B are 30° and 45° respectively
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 57

Question 30.
The angle of elevation of the top of the building from the foot of the tower is 30° and the angle of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution:
Let AB be the tower and CD is the building The angle of elevation of the top of the building from the foot of the tower is 30° and the angle of the top of the tower from the foot of the building is 60°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 59

Question 31.
From a point on a bridge across a river the angles of depression of the banks onopposite side of the river are 30° and 45° respectively. If bridge is at the height of 30 m from the banks, find the width of the river.
Solution:
Let BR is the bridge with a height of 30 m and angles of depression from B the top of the bridge to two given points C and D on the opposite sides of the river are 30° and 45° respectively CD is the width of the river Let CR = x and DR = y
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 61

Question 32.
Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point between them on the road the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distances of the point from the poles.
Solution:
AB and CD are two equal poles on either side of the road BD which is 80 m wide P is a point on the road such that the angles of elevation of the tops of the poles are 60° and 30° respectively
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 62
Let the length of each pole in h and let BP = x, then DP = 80 – x
In right ΔABP,

Question 33.
A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30° respectively. Find the width of the river.
Solution:
Let AB be the tree on which a man is sitting the tree is on a small island in the middle of the river. C and D are the foot of the poles on either bank of the river The angles of depression from A to the poles C and D are 60° and 30° respectively and AB = 20 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 65

Question 34.
A vertical tower stands on a horizontal plane and is surmounted by a flag-staff of height 7 m. From a point on the plane, the angle of elevation of the bottom of the flag-staff is 30° and that of the top of the flag-staff is 45°. Find the height of the tower.
Solution:
Let AB be a flag post on a building BC From a point P on the same ground, angle of elevations of A and B are 45° and 30° respectively
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 67

Question 35.
The length of the shadow of a tower standing on level plane is found to be 2x metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of tower is x (\(\sqrt { 3 } \) +1) metres.
Solution:
Let PQ be the tower whose shadow is QA at the elevation of 45° and QB at the elevation of 30° such that AB = 2x
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 69

Question 36.
A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 Find the height of the tree.
Solution:
Let TR be the tree arid it is broken at S and its broken parts touches the ground at P making ah angle of 30° elevation angle,
PR = 10 m
Let length of the tree TR = h and let TS = SP = x
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 71

Question 37.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 60° to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
Solution:
Let B is the balloon which is connected by the cable BC which is 215 m long and makes an angle of elevation of 60° with the ground Let h be the height of the balloon
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 73

Question 38.
Two men on either side of the cliff 80 m high observes the angles of elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
Solution:
Let CL is the cliff and A and B are two men on either side of the cliff making angles of elevation with C as 30“ and 60“ respectively Height of cliff CL = 80 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 74

Question 39.
Find the angle of elevation of the sun (sun’s altitutde) when the length of the shadow of a vertical pole is equal to its height.
Solution:
Let the height of pole AB = h m
Then its shadow = h m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 76

Question 40.
An aeroplane is flying at a height of 210 m. Flying at this height at some instant the angles of depression of two points in a line in opposite directions on both the banks of the river are 45° and 60°. Find the width of the river. (Use \(\sqrt { 3 } \) = 1.73) [CBSE 2015]
Solution:
Height of the aeroplane = 210 m
Let AB is the height of aeroplane and C and D are the points on the opposite banks of a river.
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 78

Question 41.
The angle of elevation of the top of a chimney from the top of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30°. If the height of the tower is 40 m, find the height of the chimney. According to pollution control norms, the minimum height of a smoke emitting chimney should be 100 m. State if the height of the above mentioned chimriey meets the pollution norms. What value is discussed in this question? [CBSE 2014]
Solution:
Let CD be the tower area AB be the chimney angle of elevation of the top of tower with the top of the chimney is 60° and foot of chimney with the top of tower is 30°
CD = 40 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 80

Question 42.
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angle of depression of two ships are observed from the top of the light house are 60° and 45° respectively. If the height of the light house is 200 m, find the distance between the two ships. (Use \(\sqrt { 3 } \) = 1.73)
Solution:
Let AB be the light house and C and D are two ships which make angle of depression with the top A of the light house of 60° and 45°
AB = 20 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 82

Question 43.
The horizontal distance between two poles is 15 m. The angle of depression of the top of the first pole as seen from the top of the second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. (\(\sqrt { 3 } \) = 1.732) [CBSE 2013]
Solution:
Let AB and CD are two poles and distance between them = 15 m, and AB = 24 m Angle of elevation from top of pole CD, to pole AB = 30°
From C, draw CE || DB
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 84

Question 44.
The angles of depression of two ships from the top of a light house and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the light house.
Solution:
Let PQ be the light house and A and B are two ships on the same side of the light house Angle of depression from top of the light house of the two ships are 30° and 45°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 86

Question 45.
The angles of elevation of the top of a tower from two points at’a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution:
Let TR be the tower. A and B are two points which make the angled of elevation with top of tower as θ and 90° – θ (∵ angles are complementary)
Let height of tower TR = h and AR = 9 m, BR = 4m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 87

Question 46.
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
Solution:
Let AB be the tower and CD is the pole. Angles of depression from the top A to the top and bottom of the pole are 45° and 60° respectively
AB = 50 m, let CD = h and BD = EC = x
∵ CE || DB
∴ EB = CD = h
and AE = 50 – h
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 88

Question 47.
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 80 m, find the height of the first tree.
Solution:
Let AB and CD be the two trees
AB = 80 m, angle of depression from A of C is 45°. Draw CE || DB
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 90

Question 48.
A flag-staff stands on the top of a^5 m high tower. From a point on the ground, the angle of elevation of the top of the flag-staff is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the flagstaff.
Solution:
Let FT is the flag-staff situated on the top of the tower TR. A is any point on the same plane which makes angles of elevation with top of the flag-staff and top of the tower are 60° and 45° respectively.
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 91

Question 49.
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
Solution:
Let TR is the tower From a point X, the angle of elevation of T is 60° and 40 m above X, from the point Y, the angle of elevation is 45°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 93

Question 50.
As observed from the top of a 150 m tall light house, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
Solution:
Let LH be the light house, A apd B ate two ships making angles of elevation with the top of the light house as 30° and 45° respectively.
LH = 150 m.
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 96

Question 51.
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
Solution:
Let RS is the rock and TP is the tower. The angles of elevation of the top of rock with the top and foot of the tower are 30° and 45° respectively
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 98
Height of TP = 100 m
Let height of rock RS = h
From T, draw TQ || PS _
Then QS = TP = 100 m ‘
and RQ = h – 100
Let PS = TQ = x
Now in right ΔRPS
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 99

Question 52.
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance between the two cars and how far is each car from the tower ?
Solution:
Let TR be the tower and A and B are two cars on the road making angles of elevation with T the top of tower as 30° and 60°
Height of the tower TR = 50 m
Let AR = x and BR = y
Now in right ΔTAR,
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 101

Question 53.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
(i) the horizontal distance between AB and CD.
(ii) the height of the lamp post
(iii) the difference between the heights of the building and the lamp post. [CBSE 2009]
Solution:
Let AB is the building and CD is the verticle lamp
From A, the top of the building angles of depression of C and D are 30° and 60° respectively
Height of building AB = 60 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 104
Let height of CD = h
Draw CE || DB || AX
∴ ∠ACE = ∠XAC = 30° and ∠ADB = ∠XAD = 60°
EB = CD = h and AE = 60 – h
Let DB = CE = x
Now in right ΔACE,

Question 54.
Two boats approach a light house in midsea from opposite directions. The angles of elevation of the top of the light house from two boats are 30° and 45° respectively. If the distance between two boats is 100 m, find the height of the light house. [CBSE 2014]
Solution:
Let LH is the light house and A and B are two boats on the opposite directions of the light house which are making angle of elevation of the top L of the light house as 30° and 45°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 107

Question 55.
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If the tower is 50 m high, what is the height of the hill ?[CBSE 2006C, 2013]
Solution:
Let TR be the tower, HL is the hill and angles of elevation of top of the hill is 60° and top of the tower is 30
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 109

Question 56.
A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h. [CBSE 2017]
Solution:
Let the distance BC be x m and CD be y m.
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 111

Question 57.
From the fop of a 120 m ifigh tower, a man observes two cars on the opposite sides of the tower and in straightline with the base of tower with angles of depression as 60° and 45°. Find the distance between the cars. (Take \(\sqrt { 3 } \) = 1.732) [CBSE 2017]
Solution:
Let BD be the tower and A and C be the two points on ground.
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 114
Then, BD, the height of the tower = 120m
∠BAD = 45°, ∠BCD = 60°

Question 58.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between these points. [CBSE2017]
Solution:
Let TR be the tower and A, B are two objects which makes angles of elevation with top of the tower as 45° and 60° respectively
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 116

Question 59.
A fire in a building B is reported on telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel ?
Solution:
Let B is the building one fire and P and Q the fire stations which are 20 km apart i.e., PQ = 20 km.

RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 119
P and Q observes the angles with B, as 60° and 45° respectively.
Draw BA ⊥ PQ
Let AB = h Now in right ΔBAQ

Question 60.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 30°. Calculate the distance of the cliff from the ship and the height of the cliff.
Solution:
Let M is a man on the deck MN such that MN = 10 m, AB is the cliff
From M the angle of elevation of A is 45°
and angle of depression of B is 30°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 124

Question 61.
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
Solution:
Let M is the man on the deck MN such that MN = 8 m. AB is the hill From M, the angle of elevation of A is 60° and angle of depression of B is 30°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 126

Question 62.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
Solution:
Let AB and CD are two temples on the banks of the river.
AB = 50 m
From A, the angles of depression of the top and botttom of the other temple are 30° and 60° respectively.
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 128

Question 63.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
Solution:
Let A is the plane flying in the sky at is height of 3000 m i.e., AB = 3000 m
P is a point on the ground which from an angle of elevation of 45° at A and then after a flight of 15 seconds at A’ the angle of elevation because 30°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 131

Question 64.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the the speed of the aeroplane in km/hr.
Solution:
Let A be the aeroplane and AB is the height which 1 km and make an angle of elevations of 60° from a point P on the ground After moving 10 second’s flight, the angle of elevation becomes 30° from P
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 133
A’B’=AB =1 km = 1000 m
Let PB = y and BB’ = x
Now in right ΔAPB,

Question 65.
A tree standing on a horizontal plane is leaning towards east. At two points situated at distance a and b exactly due west on it, the angles of elevation of the top are respectively a and p. Prove that the height of the top from the ground is
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 136
Solution:
Let CD is the tree which is leaning towardsEast and A and B are two points on the West making angles of elevation with top C of the tree as α and β
A and B are at the distance of a and b from the foot of the tree CD, then AD = a, BD = b
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 137

Question 66.
The angle of elevation of a stationery cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
Solution:
Let C is the cloud over a lake LK
From a point M which, is 2500 m above the lake level, angle of elevation of C is 15° and angle of depression of the reflection of C in the lake which is R is 45°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 140

Question 67.
If the angle of elevation of a cloud from a point h metres above a lake is a and the angle of depression of its reflection in the lake be p, prove that the distance of the cloud from the point of \(\frac { 2h\sec { \alpha } }{ \tan { \beta -\tan { \alpha } } }\) [CBSE 2004]
Solution:
Let C be the cloud and from a point M which h m is above the lake level angle of elevation is α and angle of reflection of the cloud C, is β
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 143

Question 68.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive mile stones on opposite sides of the aeroplane are observed to be a and p. Show that the height in miles of aeroplane above the road is given by \(\frac { \tan { \alpha } \tan { \beta } }{ \tan { \alpha } +\tan { \beta } }\) [CBSE 2004]
Solution:
Let A is aeroplane and C and D are two such points that the angles of depression from A are a and p respectively and CD = 1 km
Let height of the plane be h
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 146

Question 69.
PQ is a post of given height a and AB is a tower at some distance. If a and p are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
Solution:
Let PQ is post and AB is the tower Angles of elevation of B, from P and Q are a and P respectively
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 148

Question 70.
A ladder rests against a wail at an angle a to the horizontal. Its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle p with the horizontal.
Show that \(\frac { a }{ b }\) = \(\frac { \cos { \alpha } -\cos { \beta } }{ \sin { \beta } -\sin { \alpha } }\)
Solution:
In the figure, AC and ED is the same stair, so AC = ED
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 150

Question 71.
A tower subtends an angle a at a point A in the plane of its base and the angle of depression of the foot of the tower at a point b metres just above A is p. Prove that the height of the tower is b tan α cot β.
Solution:
Let TR is the tower which subtends angle α at a point A on the same plane
AB = b and angle of depression of R from B is β
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 152

Question 72.
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine theangle of elevation of the top of the tower from his eye.
Solution:
Let TR is the tower and CD is the observer who is 28.5 m away from the tower TR
Height of the tower TR = 30 m
and height of observer CD = 1.5 m
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 154

Question 73.
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
Solution:
Let AC be the leg of stool whose top in a square shaped of side AB = 0.5 m
Height of stool AL = 1.5 m, and angle of inclination by the leg of the stool = 60°
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 155

Question 74.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is standing on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
Solution:
Let K be the kite. A and B are two boys flying kites. Boy B is standing on a building 10 m high
The string AK of kite of boy A is 100 m Let h be the height of the kite and x is the length of string of kite of second boy B
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 158

Question 75.
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is \(\frac { h(\tan { \alpha } +\tan { \beta } ) }{ \tan { \alpha } \tan { \beta } }\) meters.
Solution:
Let LH be the light house and A and B are two ships which make angles of elevation with L are a and p respectively
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 160

Question 76.
From the top of a tower hmetre high, the angles of depression of two objects, which are in the line with the foot of the tower are a and β (β > α). Find the distance between the two objects. [NCERT Exemplar]
Solution:
Let the distance between two objects is x m
and CD = y m
Given that, ∠BAX = α = ∠ABD [alternate angle]
∠CAY = β = ∠ACD [alternate angle]
and the height of tower, AD = h m Now, in ΔACD,
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 162

Question 77.
A window of a house is h metre above the ground. From the window, the angles of elevation and depression of the top and bottom of another house situated on the opposite side of the lane are found to be α and β respectively. Prove that the height of the house is h( 1 + tan α tan β) metres. [NCERT Exemplar]
Solution:
Let the height of the other house = OQ = H
and OB = MW = x m
Given that, height of the first house = WB = h = MO
and ∠QWM = α, ∠OWM =β= ∠WOB [alternate angle]
Now, in ΔWOB,
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 164

Question 78.
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.[NCERT Exemplar]
Solution:
Let the height of the balloon from above the ground is H.
A and OP = w₂R = w₁Q = x
Given that, height of lower window from above the ground = w₂P = 2 m = OR
Height of upper window from above the lower window = w₁w₂ = 4 m = QR
∴ BQ = OB – (QR + RO)
BQ = H – (4 + 2)
BQ = H – 6
RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 166

Hope given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5

January 10, 2023

RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5

Other Exercises

Question 1.
In the figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ. (C.B.S.E. 1991)
Solution:
In the figure,
∆ACB ~ ∆APQ
BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 1

Question 2.
In the figure, AB || QR. Find the length of PB. (C.B.S.E. 1994)
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 2
Solution:
In the figure,
In ∆PQR, AB || QR
AB = 3 cm, QR =9 cm, PR = 6 cm
In ∆PAB and ∆PQR
∠P = ∠P (common)
∠PAB = ∠PQR (corresponding angles)
∠PBA = ∠PRQ (corresponding angles)
∠PAB = ∠PQR (AAA axiom)

Question 3.
In the figure, XY || BC. Find the length of XY. (C.B.S.E. 1994C)
Solution:
In the figure
In ∆ABC XY || BC
AX = 1 cm, BC = 6 cm
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 4

Question 4.
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on hypotenuse is x. Prove that ab = cx.
Solution:
Given : In right ∆ABC, ∠B is right angle BD ⊥ AC
Now AB = a, BC = b, AC = c and BD = x
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 6

Question 5.
In the figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.
Solution:
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 8

Question 6.
In the figure, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.
Solution:
In right ∆ABC, ∠B = 90°
BD ⊥ AC
AB = 5.7 cm, BD = 3.8 and CD = 5.4 cm
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 9

Question 7.
In the figure, DE || BC such that AE = \(\frac { 1 }{ 4 }\) AC. If AB = 6 cm, find AD.
Solution:
In the figure, in ∆ABC, DE || BC
AE = \(\frac { 1 }{ 4 }\) AC, AB = 6 cm
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 11

Question 8.
In the figure, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, prove that ∆CED ~ ∆ABC.
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 12
Solution:
Given : In the figure AB ⊥ BC, DC ⊥ BC and DE ⊥ AC
To prove : ∆CED ~ ∆ABC.
Proof: AB ⊥ BC
∠B = 90°
and ∠A + ∠ACB = 90° ….(i)
DC ⊥ BC
∠DCB = 90°
=> ∠ACB + ∠DCA = 90° ….(ii)
From (i) and (ii)
∠A = ∠DCA
Now in ∆CED and ∆ABC,
∠E = ∠B (each 90°)
∠DEA or ∠DCE = ∠A (proved)
∆CED ~ ∆ABC (AA axiom)
Hence proved.

Question 9.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion
for two triangles, show that \(\frac { OA }{ OC }\) = \(\frac { OB }{ OD }\)
Solution:
Given : ABCD is a trapezium in which AB || DC and diagonals AC and BD intersect each other at O
To Prove : \(\frac { OA }{ OC }\) = \(\frac { OB }{ OD }\)
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 13

Question 10.
In ∆ABC and ∆AMP are two right triangles, right angled at B and M respectively such that ∠MAP = ∠BAC. Prove that
(i) ∆ABC ~ ∆AMP
(ii) \(\frac { CA }{ PA }\) = \(\frac { BC }{ MP }\).
Solution:
Given : In ∆ABC and ∆AMP,
∠B = ∠M = 90°
∠MAP = ∠BAC
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 14

Question 11.
A vertical stick 10 cm long casts a shadow of 8 cm long. At the same time a tower casts a shadow 30 m long. Determine the height of the tower. (CB.S.E. 1991)
Solution:
The shadows are casted by a vertical stick and a tower at the same time
Their angles will be equal
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 16

Question 12.
In the figure, A = CED, prove that ∠CAB ~ ∠CED. Also find the value of x.
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 17
Solution:
Given : In ∆ABC,
∠CED = ∠A
AB = 9 cm, BE = 2 cm, EC = 10 cm, AD = 7 cm and DC = 8 cm
To prove :
(i) ∆CAB ~ ∆CED
(ii) Find the value of x
Proof: BC = BE + EC = 2 + 10 = 12 cm
AC = AD + DC = 7 + 8 = 15 cm
(i) Now in ∆CAB and ∆CED,
∠A = ∠CED (given)
∠C = ∠C (common)
∆CAB ~ ∆CED (AA axiom)
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 18

Question 13.
The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm, what is the corresponding side of the other triangle? (C.B.S.E. 2002C)
Solution:
Let perimeter of ∆ABC = 25 cm
and perimeter of ∆DEF = 15 cm
and side BC of ∆ABC = 9 cm
Now we have to find the side EF of ∆DEF
∆ABC ~ ∆DEF (given)
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 19

Question 14.
In ∆ABC and ∆DEF, it is being given that: AB = 5 cm, BC = 4 cm and CA = 4.2 cm; DE = 10 cm, EF = 8 cm and FD = 8.4 cm. If AL ⊥ BC and DM ⊥ EF, find AL : DM.
Solution:
In ∆ABC and ∆DEF,
AB = 5 cm, BC = 4 cm, CA = 4.2 cm, DE = 10 cm, EF = 8 cm and FD = 8.4 cm
AL ⊥ BC and DM ⊥ EF
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 20

Question 15.
D and E are the points on the sides AB and AC respectively of a ∆ABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = \(\frac { 5 }{ 2 }\) DE.
Solution:
Given : In ∆ABC, points D and E are on the sides AB and AC respectively
and AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 22

Hence proved

Question 16.
D is the mid-point of side BC of a ∆ABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1.
Solution:
Given : In ∆ABC, D is mid point of BC, and E is mid point of AD
BE is joined and produced to meet AC at X
To prove : BE : EX = 3 : 1
Construction : From D, draw DY || BX meeting AC at Y
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 24

Hence proved.

Question 17.
ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the rectangle contained AB and BC.
Solution:
Given : ABCD is a parallelogram.
APQ is a straight line which meets BC at P and DC on producing at Q
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 26

Question 18.
In ∆ABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that :
(i) ∆OMA ~ ∆OLC
(ii) \(\frac { OA }{ OC }\) = \(\frac { OM }{ OL }\)
Solution:
Given : In ∆ABC, AL ⊥ BC, CM ⊥ AB which intersect each other at O
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 28
(ii) \(\frac { OA }{ OC }\) = \(\frac { OM }{ OL }\)
Hence proved.

Question 19.
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
Solution:
Given : In quadrilateral ABCD, AD = BC
P, Q, R and S are the mid points of AB, AC, CD and AD respectively
PQ, QR, RS, SP are joined
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 29

Question 20.
In an isosceles ∆ABC, the base AB is produced both the ways to P and Q such that AP x BQ = AC². Prove that ∆APC ~ ∆BCQ.
Solution:
Given : In ∆ABC, AC = BC
Base AB is produced to both sides and points P and Q are taken in such a way that
AP x BQ = AC²
CP and CQ are joined
To prove : ∆APC ~ ∆BCQ
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 30

Question 21.
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/sec. If the lamp is 3.6 m above ground, find the length of her shadow after 4 seconds.
Solution:
Let AB be the lamp post and CD be the girl and AB = 3.6 m, CD = \(\frac { 90 }{ 100 }\) = 9 m
Distance covered in 4 seconds = 1.2 m x 4 = 4.8 m
BD = 4.8 m
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 31
x = 1.6
Length of her shadow = 1.6 m

Question 22.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:
Let AB be stick and DE be tower.
A stick 6 m long casts a shadow of 4 m i.e., AB = 6 m and BC = 4 m
Let DE casts shadow at the same time which is EF = 28 m
Let height of tower DE = x
Now in ∆ABC and ∆DEF,
∠B = ∠E (each 90°)
∠C = ∠F (shadows at the same time)
∆ABC ~ ∆DEF (AA criterion)
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 32

Question 23.
In the figure, ∆ABC is right angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE.
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 33
Solution:
Given: In the figure, ∆ABC is a right angled triangle right angle at C.
DE ⊥ AB
To prove:
(i) ∆ABC ~ ∆ADE
(ii) Find the length of AE and DE
Proof: In ∆ABC and ∆ADE,
∠ACB = ∠AED (each 90°)
∠BAC = ∠DAE (common)
∆ABC ~ ∆ADE (AA axiom)
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 34

Question 24.
In the figure, PA, QB and RC are each perpendicular to AC. Prove that
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 36
Solution:
Given : In the figure, PA, QB and RC are perpendicular on AC and PA = x, QB = z and RC = y

Hence proved.

Question 25.
In the figure, we have AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y.
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 40
Solution:
In the figure, AB || CD || EF
AB = 6 cm, EF = 10 cm, BD = 4 cm, CD = x cm and DE = y cm
In ∆ABE, CE || AB
∆CED ~ ∆AEB

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4

January 10, 2023

RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4

Other Exercises

Question 1.
(i) In figure, if AB || CD, find the value of x.
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4 1
(ii) In figure, if AB || CD, find the value of x.

(iii) In figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x. (C.B.S.E. 2000C)

Solution:
(i) In the figure, AB || CD
The diagonals of a trapezium divides each other proportionally
RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4 4

=> (x – 8)(x – 11) = 0
Either x – 8 = 0, then x = 8 or x – 11 =0, then x = 11
x = 8 or 11

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

CA Foundation Business Economics Study Material Chapter 2 Theory of Demand and Supply – MCQs

January 9, 2023

CA Foundation Business Economics Study Material Chapter 2 Theory of Demand and Supply – MCQs

MULTIPLE CHOICE QUESTIONS

Law of Demand and Elasticity of Demand

1. Demand in economic sense means-
(a) mere desire for a commodity
(b) mere ability to pay price of the commodity
(c) mere wiling to pay the price of the commodity
(d) desire backed by ability and willingness to pay for the commodity desired

2. In economics, demand refers to-
(a) quantity demanded at a particular time
(b) quantity demanded backed by ability to pay
(c) quantity demanded of all goods
(d) quantity demanded at a particular price in a given period of time

3. The concept of demand demonstrates that-
(a) demand is always with reference to price
(b) demand is referred to in a given period of time
(c) buyer’s ability and willingness to pay
(d) all the above

4. Demand is a
(a) flow concept Le. quantity per unit of time
(b) stock concept
(c) wealth concept
(d) none of the above

5. Demand concept explains the ________ behaviour in response to change in price of a good.
(a) producer’s
(b) seller’s
(c) consumer’s
(d) none of the above

6. Individual Demand is also called-
(a) industrial demand
(b) market demand
(c) household’s demand
(d) all the above

7. ________ means quantity demanded of a good by a single consumer at various prices per unit of time.
(a) Market Demand
(b) Individual Demand
(c) Industrial Demand
(d) None of the above

8. _______ means the aggregates of the quantities
demanded by all consumers in the market at different prices per unit of time.
(a) Market Demand
(b) Individual Demand
(c) Industrial Demand
(d) Household Demand

9. All but one are the factors which affect individual demand. Find the odd one out.
(a) Price of related good
(b) Income of the consumer
(c) Tastes and preferences of consumer
(d) Number of consumers in the market

10. _________ is a tabular presentation showing different quantities demanded by buyers at different levels of prices in a given period.
(a) Supply Schedule
(b) Demand Schedule
(c) Production Schedule
(d) Cost Schedule

11. A demand schedule is shown as-
(a) a result of increase in the size of the family
(b) a result of change in tastes and preferences
(c) a function of price
(d) all the above

12. Market Demand is the sum total of-
(a) all quantities that producer’s can produce
(b) all quantities actually sold in the market
(c) all quantities demanded by individual households and consumers
(d) all the above

13. Demand of a good of several consumers when added together is called _______ demand.
(a) individual
(b) market
(c) joint
(d) independent

14. When a good can be used to satisfy two or more wants, it is said to have _______ demand.
(a) composite
(b) competitive
(c) joint
(d) market

15. Indirect demand of a good is also known as _______ demand.
(a) direct
(b) derived
(c) joint
(d) competitive

16. Which of the following is a determinant of Individual Demand?
(a) Cost of production
(b) Nature of commodity
(c) Economic Policies of the Government
(d) Tastes and Preferences of consumers

17. Which of the following is NOT the determinant of demand?
(a) Price of the commodity
(b) Price of related commodities
(c) Income of consumer
(d) None of the above

18. How are APPLES and ORANGES related when as a result of rise in price of Apples, demand for Oranges increases?
(a) Substitute goods
(b) Complementary goods
(c) Normal goods
(d) Inferior goods

19. If two goods are complementary then rise in the price of one results in-
(a) rise in demand for the other
(b) fall in demand for the other
(c) rise in demand for both
(d) none of these

20. If the demand for CNG increases as price of petrol increases, the two goods are-
(a) Normal goods
(b) Complementary goods
(c) Substitute goods
(d) Superior goods

21. Comforts lies between-
(a) inferior goods and necessaries
(b) luxuries and inferior goods
(c) necessaries and luxuries
(d) none of the above

22. When price of commodity rises, the demand for it _______ .
(a) rises
(b) contracts
(c) remain constant
(d) becomes negative

23. When the price of petrol goes up, demand for two-wheelers will-
(a) rise
(b) fall
(c) remain same
(d) none of these

24. An increase in the income of a consumer has effect on demand in general.
(a) no
(b) negative
(c) opposite
(d) positive

25. The demand for Scooter and petrol is an example of _______ demand.
(a) joint
(b) composite
(c) competitive
(d) market

26. _______ goods are those goods which are used for the production of other goods.
(a) Durable
(b) Producer’s
(c) Non-Durable
(d) Consumer’s

27. _______ goods are those which are used for final consumption.
(a) Durable
(b) Producer’s
(c) Non-Durable
(d) Consumer’s

28. Bread, Milk, Readymade clothes, T.V., etc. are examples of _______ goods
(a) perishable
(b) producer’s
(c) consumer’s
(d) inferior

29. The goods which cannot be consumed more than once, like milk are known as _______ goods.
(a) non-durable consumer goods
(b) producer’s
(c) inferior
(d) durable consumer goods

30. _______ goods meets only our current demand.
(a) producers
(b) durable consumer goods
(c) non-durable consumer goods
(d) inferior

31. The goods which can be consumed more than once over a period of time are known as _______ goods.
(a) non-durable consumer goods
(b) producer’s
(c) durable consumer goods
(d) inferior

32. When demand of any good depends upon the demand of another good, it is said to have _______ demand.
(a) joint
(b) derived
(c) competitive
(d) direct

33. The total demand for steel in the country denotes _______ demand.
(a) industry
(b) company
(c) both ‘a’ and ‘b’
(d) autonomous

34. If the demand for a product is independent of the demand for other goods, it is called as _______ demand.
(a) company
(b) industry
(c) autonomous
(d) derived

35. If the construction activity in housing sector, infrastructure, etc. rises, the demand for cement will _______ as it has _______ demand.
(a) rise ; autonomous
(b) fall; autonomous
(c) rise ; derived
(d) none of these

36. Demand for steel produced by Tata Iron and Steel Company is an example of _______ demand.
(a) industry
(b) company
(c) autonomous
(d) joint

37. When demand of any good reacts immediately to price changes, income changes, etc. it is said to have _______ demand.
(a) short-run
(b) long-run
(c) very short run
(d) very long run

38. A relative price is-
(a) price expressed in terms of money
(b) what you get paid for babysitting your cousin
(c) the ratio of one price to another
(d) equal to a money price

39. The quantity demanded of a good or service is the amount that-
(a) consumer plan to buy during a given period at a given price.
(b) firms are willing to sell during a given time period at a given price.
(c) a consumer would like to buy but may not be able to afford.
(d) is actually bought during a given period at a given price.

40. Coca-Cola and Thumbs-Up are substitutes. A rise in the price of Coca-Cola will _______ the demand of Thumbs-Up and the quantity demanded of Thumbs-Up will _______ .
(a) increase ; increase
(b) increase;decrease
(c) decrease ; decrease
(d) decrease;increase

41. If the price of Orange Juice falls, the demand for Apple Juice will _______ .
(a) increase
(b) decrease
(c) remain the same
(d) become negative

42. The demand for consumer goods is a _______ demand.
(a) direct
(b) indirect
(c) constant
(d) company

43. If the price of inferior goods fall, the demand for them will _______.
(a) rise
(b) fall
(c) remain constant
(d) become zero

44. The Law of Demand states _______ relation between demand and price of a commodity.
(a) a direct
(b) positive
(c) an indirect
(d) no

45. When total demand for a commodity whose price has fallen increases, it is due to
(a) income effect
(b) substitution effect
(c) complementary effect
(d) price effect

46. With a fall in the price of a commodity
(a) Consumer’s real income increases
(b) Consumer’s money income increases
(c) Consumer’s real income falls
(d) Consumer’s money income falls

47. When we draw a market demand curve, we _______.
(a) do not consider tastes, incomes and all prices
(b) assume that tastes, incomes and all other prices change in the same way price changes
(c) assume that tastes, incomes and all other prices are irrelevant
(d) assume that tastes, incomes and all other prices remain the same

48. All but one of the following are assumed to remain the same while drawing individual’s demand curve for a commodity. Which are is it?
(a) The tastes and preferences of the consumer
(b) Income of consumer
(c) The price of the commodity
(d) The prices of related commodities

49. A fall in price of a commodity leads to _______.
(a) a shift in demand curve
(b) a rise in consumer’s real income
(c) a fall in demand
(d) none of the above

50. If a fall in price of ‘y’ results in a decrease in the sale of ‘x’, the two good appear to be-
(a) substitute goods
(b) complementary goods
(c) inferior goods
(d) neutral goods

51. Which of the following is not a complementary good for pen?
(a) refills
(b) paper
(c) notebook
(d) rice

52. _______ goods are the goods which can be used with equal case in place of each other.
(a) Neutral
(b) Normal
(c) Complementary
(d) Substitute

53. Which of the following pairs of goods are an example of substitutes?
(a) Tea and Sugar
(b) Tea and Coffee
(c) Pen and Ink
(d) Shirt and Trouser

54. When the price of a substitute of good ‘X’ falls, the demand for good ‘X’
(a) rises
(b) falls
(c) remains unchanged
(d) None of these

55. If the demand rises with the rise in consumer’s real income, such a good is called _______.
(a) Normal goods
(b) Neutral goods
(c) Inferior goods
(d) Luxury goods

56. Giffen goods are-
(a) Normal goods
(b) Inferior goods
(c) Luxury goods
(d) Neutral goods

57. As the consumer’s income increases, the demand for necessaries of life will increase _______ to the increase in income.
(a) Less than proportionate
(b) More than proportionate
(c) Proportionate
(d) Nothing can be said

58. As the consumer’s income increases, the demand for comforts and luxuries will increase _______ to the increase in income.
(a) Less than proportionate
(b) More than proportionate
(c) Proportionate
(d) Nothing can be said

59. During boom period in economy, the demand for goods in general _______.
(a) rises
(b) falls
(c) remains same
(d) none of these

60. Larger the size of population of a country _______ is the demand for goods and services in general.
(a) lower
(b) ineffective
(c) neutral
(d) higher

61. In case the consumer expects a steep rise in price of Potatoes in future, his current demand for it will _______.
(a) remain same
(b) fall
(c) rise
(d) none of the above

62. All but one of the good’s demand is not affected by changes in weather conditions-
(a) Ice-cream
(b) Woollen clothes
(c) Cold drinks
(d) Wheat

63. If the government increase the rate of indirect taxes on goods and services, the demand for then will _______ in general.
(a) rise
(b) fall
(c) remain neutral
(d) be ineffective

64. If the government reduces the tax on any pro-duct, the demand for the product _______ in the short run.
(a) rises
(b) falls
(c) remain unchanged
(d) tax has nothing to do with the demand of any product

65. If the demand for petrol remains unchanged with rise in its price, it means petrol is a _______
(a) Normal good
(b) Necessity
(c) Luxury good
(d) Inferior good

66. If quantity demanded of good ‘X’ is plotted against the price of its substitute good ‘Y’, the demand curve will be-
(a) Vertical Straight line
(b) Positively sloped
(c) Horizontal Straight line
(d) Negatively sloped

67. Consider the following figure:

In the above figure, RS part of the demand curve represents-
(a) Superior good
(b) Inferior good
(c) Normal good
(d) Giffen’s good

68. In case of normal goods the income effect is _______
(a) zero
(b) negative
(c) positive
(d) constant

69. Income effect on demand of a good is _______.
(a) positive for normal goods
(b) always positive
(c) negative for normal goods
(d) always negative

70. The Law of Demand is explained by-
(a) Cardinal approach
(b) Ordinal approach
(c) Both ‘a’ and ‘b’
(d) Neither ‘a’ nor ‘b’

71. The Law of Demand refers to functional relation between-
(a) Price & Supply
(b) Price & Cost
(c) Price & Income
(d) Price & Demand

72. The term “Ceteris Paribus” in the Law of Demand means-
(a) All factors except one remain constant
(b) All factors remain constant
(c) All factors are variable
(d) None of the above

73. Which of the following is a variable and influencing factor in the Law of Demand?
(a) Consumer’s Income
(b) Consumer’s Tastes and Preferences
(c) Price of related goods
(d) Price of the good

74. The phrase “Other things being equal” in the Law of Demand means-
(a) Income of the consumer remain unchanged
(b) Price of related goods remain unchanged
(c) Tastes and Preferences of consumer remain unchanged
(d) All the above

75. The total effect of price change of a good is-
(a) Substitution Effect + Income Effect
(b) Substitution Effect + Price Effect
(c) Substitution Effect + Demonstration Effect
(d) Demonstration Effect + Veblen Effect

76. Substitution Effect subscribe to the inverse relation between P_x and Q_x in case of-
(a) normal goods only
(b) inferior goods only
(c) normal and inferior goods both
(d) none of the above

77. Income Effect does not subscribe to the inverse relation between P_x and Q_x in case of-
(a) both normal and inferior goods
(b) inferior goods
(c) normal goods
(d) none of the above

78. The Law of Demand will fail in case of inferior goods only if-
(a) Substitution Effect is greater than Income Effect
(b) Income Effect is greater than’Substitution Effect
(c) Both ‘a’ and ‘b’
(d) Neither ‘a’ nor ‘b’

79. The Law of Demand is a _______ statement.
(a) Positive
(b) Normative
(c) Descriptive
(d) Both ‘a’ and ‘c’

80. _______ refers to the effect of change in the price of a product on the consumer’s purchasing power.
(a) Real Income Effect
(b) Substitution Effect
(c) Consumer’s Surplus
(d) None of the above

81. When the price of Thumbs-up falls, other things being constant, buyers substitute Thumbs-up for Coca-Cola. This is called-
(a) Price Effect
(b) Substitution Effect
(c) Income Effect
(d) Veblen Effect

82. _______ refers to the buyer’s reaction to a change in the relative prices of two products, keeping the total utility constant.
(a) Consumer’s Surplus
(b) Income Effect
(c) Substitution Effect
(d) None of the above

83. The Law of Demand can be explained by-
(a) The Law of Diminishing Marginal Utility
(b) Indifference Curves
(c) Both ‘a’ and ‘b’
(d) Neither ‘a’ nor ‘b’

84. Consumers buy a good till P_x = MU_x. If the price falls, the consumer will reach equilibrium-
(a) at a lower quantity
(b) at a higher quantity
(c) at zero quantity level
(d) all the above

85. “Petrol is becoming cheaper, yet the demand for cars is not rising”. This statement indicates that-
(a) The Law of Demand is not operative for cars
(b) The Law of Demand is operative for petrol
(c) The Demand Curve for cars will shift
(d) All the above

86. Downward slope of the demand curve shows-
(a) positive relationship between price and quantity demanded
(b) inverse relationship between price and quantity demanded
(c) no relationship between price and quantity demanded
(d) none of the above

87. In case of NORMAL GOODS, demand curve shows:
(a) a negative slope
(b) a positive slope
(c) zero slope
(d) none of these

88. Law of Demand fails in case of –
(a) normal goods
(b) Giffen goods
(c) inferior goods
(d) both ‘b’ and ‘c’

89. In case of Giffen’s Paradox, the slope of the demand curve is-
(a) parallel to X-axis
(b) positive
(c) negative
(d) parallel to Y-axis

90. A Giffen good is one for which a small change in price results in-
(a) zero income effect out weighted by a positive substitution effect
(b) zero income effect being equal to zero substitution effect
(c) negative income effect out weighed by a positive substitution effect
(d) none of these

91. The Law of Demand indicates the
(a) direction of change in demand of a commodity
(b) magnitude/amount of change in demand of a commodity
(c) both ‘a’ and ‘b’
(d) elasticity of demand

92. In case of Giffen goods, demand varies _______ with the price.
(a) inversely
(b) directly
(c) proportionately
(d) none of these

93. Analysis of the relationship between demand of a commodity and prices of related commodities is-
(a) Price Demand analysis
(b) Income Demand analysis
(c) Cross Demand analysis
(d) Market Demand analysis

94. _______ observed that when the price of inferior goods fall, the demand for such goods also fall.
(a) Adam Smith
(b) Dr. Alfred Marshall
(c) Ragnar Frisch
(d) Sir Robert Giffens

95. The Law of Demand was propounded by _______ in his book ‘Principles of Economics’.
(a) Lord Keyens
(b) Adam Smith
(c) Dr. Alfred Marshall
(d) Ragnar

96. The tendency of low income group to imitate the consumption pattern of high income group is known as _______ effect.
(a) Demonstration
(b) Copy
(c) Prestige
(d) Veblen

97. The Law of Demand is applicable for _______.
(a) Giffen’s Goods
(b) Prestige Goods
(c) Necessary Goods
(d) Normal Goods

98. When price changes and proportionate change in market demand is more than proportionate change in individual demand implies that the market demand curve is _______ than the individual demand curves.
(a) Steeper
(b) Flatter
(c) Vertical
(d) None of the above

99. A positively sloped demand curve implies
(a) Violation of the law of demand
(b) Giffen good
(c) Income effect is negative and greater than substitution effect
(d) All the above

100. An increase in consumer’s income will increase demand for a _______ but decrease demand for a _______.
(a) substitute good; inferior good
(b) normal good ; inferior good
(c) substitute good ; complementary good
(d) inferior good ; normal good

101. When the quantity of a good that a buyer demands rises when there is growth of purchases by other individuals, such an effect is called _______
(a) Bandwagon Effect
(b) Snob Effect
(c) Veblen Effect
(d) None of the above

102. When the quantity of a commodity that an individual buyer demand falls in response to the growth of purchases by other buyers, such an effect is called _______
(a) Bandwagon Effect
(b) Snob Effect
(c) Veblen Effect
(d) None of the above

103. Some buyer’s demand more of certain commodities at a higher price, such an effect is called _______.
(a) Bandwagon Effect
(b) Snob Effect
(c) Veblen Effect
(d) None of the above

104. The market demand curve in case of Veblen Effect is _______.
(a) steeper
(b) flatter
(c) vertical
(d) horizontal

105. The market demand curve in case of Bandwagon Effect is _______.
(a) less elastic
(b) steeper
(c) flatter
(d) horizontal

106. The market demand curve in case of Snob Effect is _______.
(a) flatter
(b) steeper
(c) less elastic
(d) both ‘b’ and ‘c’

107. A downward sloping Engel Curve shows –
(a) Normal goods
(b) Inferior goods
(c) Substitute goods
(d) Complementary goods

108. Assume that the market demand curve for Dinshaw Ice cream is known and given to us. With summer setting in, price remaining the same the consumers would –
(a) shift to a lower demand curve leftward
(b) move upward along the same demand curve
(c) shift to a higher demand curve rightward
(d) move downward along the same demand curve

109. An exceptional demand curve is one that slopes-
(a) upward to the right
(b) downward to the right
(c) upward to the left
(d) horizontal

110. What will be the impact on the demand curve of CARS when the price of petrol rises?
(a) There will be downward movement on demand curve
(b) Demand curve will shift to left
(c) There will be an upward movement on demand curve
(d) Demand curve will shift to right

111. What will be the impact on the demand curve of DESKTOP COMPUTERS when the price of LAPTOPS increase?
(a) There will be downward movement on demand curve
(b) Demand curve will shift to left
(c) There will be an upward movement on demand curve
(d) Demand curve will shift to right

112. What will be the impact on the demand curve of SUGAR with increase in its price?
(a) Downward movement along the demand curve
(b) Leftward shift of the demand curve
(c) An upward movement along the demand curve
(d) Rightward shift of the demand curve

113. The demand for TROUSERS will lead to _______ due to change in the preference in favour of JEANS.
(a) Extension in Demand of trousers
(b) Increase in Demand of trousers
(c) Contraction in Demand of trousers
(d) Decrease in Demand in trousers

114. The demand curve for BAJRA will when a poor person’s income rises.
(a) shift to the right
(b) shift to the left
(c) be downward sloping
(d) none of the above

115. Match the following—

116. If more is demanded at the same price or the same quantity is demanded at a higher price, it is known as-
(a) Extension of Demand
(b) Contraction of Demand
(c) Increase in Demand
(d) Decrease in Demand

117. A downward movement along the same demand curve means –
(a) more is demanded when the price of good falls
(b) more is demanded at the same price
(c) less is demanded at the same price
(d) less is demanded when the price of good rises

118. A leftward shift of the demand curve shows-
(a) more is demanded at the same price
(b) less is demanded when the price of good rises
(c) less is demanded at the same price
(d) more is demanded when the price of good falls

119. When same quantity of a good is demanded at a lower price, it is known as-
(a) Extension of Demand
(b) Increase in Demand
(c) Contraction of Demand
(d) Decrease in Demand

120. When less quantity is demanded as the price of good rises, there is ________.
(a) Downward movement along the demand curve
(b) Leftward shift of the demand curve
(c) An upward movement along the demand curve
(d) Rightward shift of the demand curve

For Q. Nos. 121 to 124 refer the following demand equation Q = 180 – 6p

121. At what price no one would be willing to buy the commodity?
(a) Rs. 20
(b) Rs. 30
(c) Rs. 40
(d) Rs. 15

122. If the commodity is given free Le. if the demand is autonomous, what is the quantity demanded?
(a) 180
(b) 160
(c) 140
(d) 120

123. If the price of the commodity falls down to Rs. 1, by how much will the quantity demanded change?
(a) 6
(b) 5
(c) 12
(d) 10

124. The total quantity demanded when the price is Rs. 1 p.u. is-
(a) 180
(b) 174
(c) 190
(d) 186

For Q. Nos. 125 to 127 refer the following demand equation
Q_x = 12 – 2 P_x

125. What would be the quantity demanded at a price of Rs. 3?
(a) 4 units
(b) 5 units
(c) 6 units
(d) 8 units

126. What would be the price when quantity demanded is zero?
(a) Rs. 8
(b) Rs. 4
(c) Rs. 5
(d) Rs. 6

127. What would be the quantity demanded when the price is zero?
(a) 12 units
(b) 10 units
(c) 22 units
(d) 20 units

128. The demand function of a commodity ‘X’ is given by Q_x = 20 – 3 P_x. What would be he value of P_x when the corresponding value of Q_x = 14.
(a) Rs. 5
(b) Rs. 4
(c) Rs. 3
(d) Rs. 2

129. At a price of Rs. 10 p.u. the market demand of a commodity is 58 units, out of which consumer ‘A’ has purchased 20 units and consumer ‘B’ has purchased 10 units. How much quantity consumer ‘C’ has purchased?
(a) 28 units
(b) 26 units
(c) 24 units
(d) 22 units

130. The linear demand function is given as- Q = 80 – 20 P. Derive the market demand function when there are 100 consumers in the market.
(a) Q = 8000 – 20 P
(b) Q = 80 – 2000 P
(c) Q = 8000 – 2000 P
(d) None of the above

131. All but one can be referred as Variations in Demand. Which one is not variation in demand?
(a) Movement along the same demand curve
(b) Shifting of demand curve
(c) Changes in the Quantity Demanded
(d) Expansion and Contraction of Demand

132. In case of Expansion and Contraction of Demand, the demand curve-
(a) shifts to the right
(b) shifts to the left
(c) remains the same
(d) none of the above

133. A movement along the demand curve means-
(a) expansion of demand
(b) contraction of demand
(c) changes in the quantity demanded
(d) all the above

134. Change in the demand of a commodity due to the factors other than price is known as-
(a) Increase and Decrease in Demand
(b) Changes in Demand
(c) Shift in Demand
(d) All the above

135. Increase in demand leads to-
(a) Leftward shift of the demand curve
(b) Rightward shift of the demand curve
(c) Upward movement on the same demand curve
(d) Downward movement on the same demand curve

136. Which of the following would result in the shifting of the demand curve?
(a) Increase in the tax on shoes
(b) Growth in the size of population
(c) Changes in weather conditions
(d) All the above

137. Shift in demand does not take place due to-
(a) Change in consumer’s tastes and preferences
(b) Advertisement
(c) Trade conditions
(d) Change in the price of the commodity

138. A rightward shift in the demand curve for Bread would be predicted from-
(a) A decrease in the number of breakfast eaters
(b) A change in tastes
(c) A fall in the price of Bread
(d) A rise in the price of Corn Flakes

139. Consider the following demand curve-

State whether-
(a) The two goods are complementary
(b) The two goods are substitutes
(c) The two goods are not related
(d) None of the above

140. Consider the following figure-

It shows-
(a) Inferior goods
(b) Giffen goods
(c) Normal or Superior goods
(d) All the above

141. Consider the following figure-

Demand
It shows demand curve for-
(a) Necessities
(b) Comforts and Luxuries
(c) Inferior Goods
(d) None of the above

142. Consider the following figure-

It shows demand curve for-
(a) Necessities
(b) Comforts and Luxuries
(c) Inferior Goods
(d) None of the above

143. Consider the following figure-

It shows demand curve for-
(a) Necessities
(b) Comforts and Luxuries
(c) Inferior Goods
(d) None of the above

144. Which of the following is shown in the figure?

(a) An increase in demand
(b) Indifference Curve
(c) Supply Curve
(d) None of the above

145. Other things being equal a decrease in demand can be caused by-
(a) A rise in the price of the commodity
(b) A rise in the income of the commodity
(c) A fall in the price of the commodity
(d) A fall in the income of the consumer

146. A rational consumer is a person who
(a) behaves judiciously all the time
(b) is not influenced by the advertisement
(c) knows the prices of goods in different markets and buy the cheapest
(d) has perfect knowledge of the market

147. A normal demand curve of a commodity-
(a) is vertical straight line curve
(b) has a negative slope
(c) is horizontal straight line curve
(d) has a positive slope

148. If the quantity demanded of a commodity is plotted against the price of a substitute goods ceteris paribus the curve is expected to be-
(a) Vertical
(b) Negatively sloped
(c) Horizontal
(d) Positively sloped

149. Income effect operates when there is an-
(a) increase in real income due to fall in price of the commodity
(b) increase in real income due to rise in price of the commodity
(c) increase in real income due to rise in demand of the commodity
(d) increase in money income due to fall in the price of the commodity

150. Who explained the abnormal shape of demand curve for diamonds through the doctrine of conspicuous consumption?
(a) Thorstein Veblen
(b) Robert Giffen
(c) David Ricardo
(d) Alfred Marshall

151. Conspicuous good are also known as-
(a) prestige goods
(b) snob goods
(c) Veblen goods
(d) all the above

152. Elasticity of demand is defined as the responsiveness of the quantity demanded of a good to changes in
(a) price of the commodity
(b) price of related goods
(c) income of the consumer
(d) all the above

153. ________ was the economist to formulate the concept of price elasticity of demand.
(a) Alfred Marshall
(b) Adam Smith
(c) Paul Samuelson
(d) Edwin Cannon

154. The concept of Elasticity of Demand whenever referred unless otherwise specified always means-
(a) Price Elasticity of Demand
(b) Income Elasticity of Demand
(c) Cross Elasticity of Demand
(d) All the above

155. The concept of price elasticity of demand analyses-
(a) direction of change in response to change in price of the commodity
(b) degree of change in response to change in price of the commodity
(c) absolute change in response to change in price of the commodity
(d) none of these

156. When there is no change in quantity demanded in response to any change in price, it is a situation of-
(a) infinite price elasticity
(b) unitary price elasticity
(c) zero price elasticity
(d) high price elasticity

157. Price Elasticity of Demand is defined as-
(a) Change in quantity demanded ÷ Change in Price
(b) % Change in quantity demanded ÷ % Change in Price
(c) Change in quantity demanded ÷ % Change in Price
(d) % Change in quantity demanded ÷ Change in Price

158. Price Elasticity of Demand is given by-

159. When percentage change demand is less than percentage change in price, demand is-
(a) perfectly elastic
(b) perfectly inelastic
(c) less than unitary elastic
(d) more than unitary elastic

160. When percentage change in demand is equal to percentage change in price, demand is-
(a) perfectly elastic
(b) unitary elastic
(c) perfectly inelastic
(d) more elastic

161. Price Elasticity of demand is always because of relationship between price and quantity demanded
(a) negative ; inverse
(b) positive ; direct
(c) negative ; positive
(d) positive ; inverse

162. Coefficient of price elasticity of demand ranges from to
(a) one ; infinity
(b) zero ; infinity
(c) zero ; one
(d) none of the above

163. When there is an infinite demand at a particular price and demand becomes zero with a slight rise in the price then
(a) demand by commodity is perfectly elastic
(b) E_d = ∞
(c) demand curve is horizontal straight line parallel to X-axis
(d) all the above

164. When percentage in quantity demanded is more than percentage change in price then
(a) demand of commodity is highly elastic
(b) E_d > 1 and demand curve is flatter
(c) E_d < 1 and demand curve is steeper
(d) Only ‘a’ and ‘b’ 1

165. When demand curve is parallel to X-axis, elasticity of demand is-
(a) unity
(b) zero
(c) greater than unity
(d) infinity

166. Which curve is called rectangular hyperbola?
(a) Highly Elastic Demand Curve
(b) Less Elastic Demand Curve
(c) Unitary Elastic Demand Curve
(d) None of the above

167. When demand curve is parallel to Y-axis, elasticity of demand is-
(a) unity
(b) zero
(c) less than unity
(d) more than unity

168. As the demand curve becomes flatter and flatter, the elasticity of demand becomes-
(a) higher
(b) lower
(c) equal to infinity
(d) equal to zero

169. When the demand for a commodity does not change with the increase in its price from Rs. 2 to Rs. 5, then elasticity of demand is
(a) E = ∞
(b) Ed = 0
(c) E_d < 1
(d) E_d > 1

170. Slope of perfectly elastic demand curve is equal to ________
(a) 0
(b) 1
(c) 2
(d) 3

171. On all points of a rectangular hyperbola demand curve, elasticity of demand is –
(a) equal to one
(b) zero
(c) more than one
(d) less than one

172. When slope of demand curve = 0, the elasticity of demand is-
(a) 0
(b) 1
(c) oo
(d) none of the above

173. To say that the demand for a commodity is elastic means-
(a) That the demand curve slopes downward to the right
(b) That more is sold at a lower price
(c) That a rise in price will increase total revenue
(d) That the change in quantity sold is proportionately greater than the change in price

174. A demand curve is perfectly inelastic if-
(a) a rise in price causes a fall in quantity demanded
(b) a fall in price causes rise in sellers total receipts
(c) the commodity in question is very perishable
(d) a change in price does not change quantity demanded

175. When the demand curve is vertical straight line, demapd is-
(a) perfectly elastic
(b) perfectly inelastic
(c) relatively elastic
(d) relatively inelastic

176. For goods with perfectly inelastic demand-
(a) ∆q = 0
(b) ∆q < ∆p
(c) ∆q = ∆p
(d) ∆p = 0

177. For goods with less elastic demand-
(a) ∆q > ∆p
( b) ∆q = ∆p
(c) ∆q < ∆p
(d) none of the above

178. If the demand of a commodity is less elastic the demand curve will be-
(a) Horizontal line
(b) Vertical line
(c) Downward sloping to the right, flatter
(d) Downward sloping to the right, steeper

179. Rectangular hyperbola is also called-
(a) Equilateral Hyperbola
(b) Vertical Line
(c) Square
(d) Horizontal Line

180. The factor which generally keeps the price elasticity of demand for a good low is-
(a) Variety of uses of that good
(b) Its low price
(c) Close – substitutes for that good
(d) High proportion of the consumer’s income spent on it

181. If you spend more on rent than on soap, your price elasticity of demand for housing is likely to be-
(a) greater than your price elasticity of demand for soap
(b) less than your price elasticity of demand for soap
(c) equal to your price elasticity of demand for soap
(d) none of the above

182. The demand for common salt has low price elasticity because-
(a) it has no close substitute
(b) it is necessity
(c) it constitutes only a small proportion of consumer’s expenditure
(d) all the above

183. The devaluation of currency would increase the export earnings only when demand for the nation’s exports in foreign market is-
(a) Elastic
(b) Inelastic
(c) Perfectly Inelastic
(d) Unitary Elastic

184. The demand for sugar and tea is usually:
(a) Elastic
(b) Inelastic
(c) Perfectly elastic
(d) Perfectly inelastic

185. Availability of close substitutes makes the demand-
(a) Less elastic
(b) More elastic
(c) Perfectly elastic
(d) Perfectly inelastic

186. Elasticity is greater than unity for-
(a) necessaries
(b) luxuries
(c) complementary goods
(d) inferior goods

187. Complementary goods exhibit ________ elasticity of demand.
(a) low
(b) high
(c) unitary
(d) none of the above

188. All but one of the following commodities has elastic demand. Which one has inelastic demand?
(a) Coca-Cola
(b) Butter for poor person
(c) Cigarettes
(d) Electricity

189. Demand is ________ in the long period than in the short period.
(a) less elastic
(b) perfectly elastic
(c) perfectly inelastic
(d) more elastic

190. The demand for necessities is ________
(a) Highly elastic
(b) Highly inelastic
(c) Slightly elastic
(d) Slightly inelastic

191. If the demand for a commodity is ________, the entire burden of indirect tax will fall on the consumer.
(a) Relatively inelastic
(b) Perfectly inelastic
(c) Relatively elastic
(d) Perfectly elastic

192. Which of the following helps the manager to estimate the demand of a commodity?
(a) Price of the commodity
(b) Price of the substitute commodities
(c) Elasticity of the commodity
(d) All the above

193. The price elasticity of demand for a face cream is estimated to be ONE, no matter what the price or quantity demanded. In this case-
(a) a 1096 increase in price will result in 1096 increase in quantity demanded
(b) a 1096 increase in price will result in 1096 fall in quantity demanded
(c) an increase in price will increase the seller’s revenue
(d) none of the above

194. If demand is ________ then price cuts will ________ spending.
(a) perfectly inelastic ; increase
(b) elastic; increase
(c) elastic; decrease
(d) none of the above

195. Suppose the demand for Dosa at Dosa Plaza is elastic. If the owner of the restaurant is consid¬ering raising the price, it can expect relatively-
(a) large fall in quantity demanded
(b) large fall in demand
(c) small fall in quantity demanded
(d) small fall in demand

196. If a 1096 rise in the price of a commodity causes the demand to fall by 2096
(a) demand was inelastic
(b) demand was infinitely elastic
(c) demand was elastic
(d) none of the above

197. On typical straight line demand curve, the elasticity of demand at a point where it meets the price axis is-
(a) 2
(b) 0.75
(c) 1
(d) infinite

198. On a straight line demand curve the elasticity of demand at the mid-point of the curve is-
(a) 1/2
(b) 2
(c) 0
(d) 1

199. To measure price elasticity over large changes in price we use ________
(a) point elasticity method
(b) arc elasticity method
(c) income elasticity method
(d) none of the above

200. If the demand for a good is elastic, an increase in its price will cause the total expenditure of the consumers of the good to
(a) Remain the same
(b) Increase
(c) Decrease
(d) None of these

201. When the price of Good ‘X’ goes up by 1096 its demand falls from 800 units to 600 units. What is the price elasticity of Good ‘X?
(a) – 2.5 with flatter demand curve
(b) 2.5 with flatter demand curve
(c) – 1.5 with steeper demand curve
(d) 1.5 with steeper demand curve

202. The demand by a consumer for a commodity falls by 1096 when its price increases from ₹ 5 to ₹ 6 per unit. What is the price elasticity of demand?
(a) unitary elastic
(b) 0.5
(c) .8
(d) 1.5

203. 30 units of a commodity is purchased by a consumer at the price of ₹ 46 per unit. When the price rises to ₹ 50 per unit, he buy 15 units only. The co-efficient of elasticity do demand is –
(a) 4.75
(b) 5
(c) 5.75
(d) 6

204. A consumer spends ₹ 40 on a good at a price of ₹ 1 per unit and ₹ 60 at a price of ₹ 2 per unit. The elasticity of demand is-
(a) 0.25
(b) 2.5
(c) .35
(d) 3.5

205. A consumer buy 20 units of a good at ? ₹ 10 p.u. The price elasticity of demand of this good is -1. How much quantity would be demanded by the consumer when the PRICE FALLS to ₹8 p.u.?
(a) 21 units
(b) 22 units
(c) 23 units
(d) 24 units

206. A consumer buy 40 units of a commodity at ₹ 5 per unit. Its Ed = -3. How much demand of quantity he will buy at ₹ 6 per unit?
(a) 15 units
(b) 16 units
(c) 17 units
(d) 18 units

207. The market demand of a commodity at ₹ 4 per unit is 100 units. The price RISES and as a result its market demand falls to 75 units. If E_d = -1, find out its new price.
(a) ₹ 5
(b) ₹ 6
(c) ₹ 7
(d) ₹ 8

208. A consumer buy 80 units of a commodity at ₹ 4 per unit. When the price FALLS, he buy 100 units. If E_d = -1, the new price will be-
(a) ₹ 3.5
(b) ₹ 3
(c) ₹ 2.5
(d) ₹ 2

209. Demand for good ‘X’ is perfectly inelastic. What will be the change in demand if price falls from ₹ 10 per unit to ₹ 5 per unit?
(a) No change in demand
(b) Large change in demand
(c) Medium change in demand
(d) None of the above

210. What happens to total expenditure on a commodity when its price falls and its demand is price elastic?
(a) Total expenditure will remain constant
(b) Total expenditure will fall
(c) Total expenditure will increase
(d) None of the above

211. As the price of a product falls by 7%, the total expenditure on it has gone up by 3.5%. The elasticity of demand of this product is-
(a) E_d = 0
(b) E_d > l
(c) E_d < 1
(d) E_d = 1

212. Let Q_x = 1400/p Find, total expenditure on good ‘X’ when P_x falls from ₹ 6 to ₹ 1 ; derive the value of E_d and what shape the demand curve will take?
(a) ₹ 1400 ; E_d = 1 and rectangular hyperbola
(b) ₹ 1400 ; E_d < 1 and steep demand curve
(c) ₹ 1400 ; E_d > 1 and flatter demand curve
(d) ₹ 2800 ; E_d = 1 and rectangular hyperbola

213. The demand of a commodity was 100 units initially. With the rise in price by ₹ 5, the quantity demanded falls by 5 units. Elasticity of demand is 1.2. Find out the price BEFORE the change in demand.
(a) ₹ 100
(b) ₹ 140
(c) ₹ 120
(d) ₹ 160

214. Regardless of changes in its price, if the quantity demanded of a good remains constant, then the demand curve for the good will be-
(a) horizontal
(b) vertical
(c) positively sloped
(d) negatively sloped

215. The total revenue of the seller will increase with a fall in price if-
(a) demand is unitary
(b) the percentage change in quantity demand¬ed is less than percentage in price
(c) demand is inelastic
(d) the percentage in quantity demanded is greater than the percentage change in price

216. Point elasticity is useful for which of the following situations?
(a) A restaurant is considering increasing the price of dosa from ₹ 100 to ₹ 200
(b) Lakme is considering lowering the price of its lipsticks by 50%
(c) Maruti Car Ltd. lower the price of Alto 800 by ₹ 1,000
(d) None of the above

217. If there are finite change in price and quantity demanded over a stretch on the demand curve, it is called-
(a) Arc elasticity
(b) Point elasticity
(c) Average elasticity
(d) Both ‘a’ and ‘c’

218. The formula used in the Arc Elasticity method is-

219. When price elasticity at a single point on a demand curve is measured, we use ____
(a) Proportionate Method
(b) Geometric Method
(c) Total Expenditure Method
(d) Arc Elasticity

220. The exact and precise co-efficient of elasticity cannot be found by _____ method.
(a) Proportionate Method
(b) Geometric Method
(c) Total Expenditure Method
(d) Arc Elasticity

221. ____ method only classifies elasticity into elastic, inelastic or unitary elastic.
(a) Proportionate Method
(b) Geometric Method
(c) Total Expenditure Method
(d) Arc Elasticity

222. Slope of a demand curve may remain constant but elasticity still can does change. This is-
(a) Absolutely correct as slope of a curve and its elasticity are not the same thing
(b) Absolutely incorrect as slope of a curve and its elasticity are same thing
(c) Partly correct and partly incorrect
(d) None of the above

223. Let slope of demand curve = -0.5. The elasticity of demand will be ____ if initial price is ₹ 20 per unit and initial quantity is 50 units of the commodity
(a) – 0.6
(b) – 0.7
(c) – 0.8
(d) – 0.9
CA Foundation Business Economics Study Material Chapter 2 Theory of Demand and Supply - MCQs 223

For Q. Nos. 224 to 226 refer the following information. Given –

224. What is the price of the commodity when Quantity Demanded is 20 units ?
(a) ₹ 4
(b) ₹ 5
(c) ₹ 6
(d) ₹ 7

225. What is the price of the commodity when the Quantity Demanded is 30 units?
(a) ₹ 4
(b) ₹ 5
(c) ₹ 6
(d) ₹ 7

226. Using percentage method, the price elasticity of demand is-
(a) 1.5
(b) 2.0
(c) 2.5
(d) 3.0

227. Life saving drugs has ____ demand.
(a) inelastic
(b) elastic
(c) perfectly elastic
(d) perfectly inelastic

228. The price elasticity of demand is 0.5. The percentage change in quantity is 4. What is the percentage in price?
(a) 6
(b) 8
(c) 10
(d) 12

229. When price of a commodity gets doubled, its quantity demanded is reduced to half. The coefficient of price elasticity of demand will be-
(a) – 1
(b) – 0.5
(c) – 1.5
(d) – 2

230. Calculate the price elasticity of demand-

(a) – 1
(b) – 2
(c) – 2.5
(d) – 1.5

231. The price elasticity of demand for good ‘X’ is twice that of good ‘Y’. Price of ‘X’ falls by 5% while that of good ‘Y’ rises by 5%. The percentage change in the quantities demanded of X and Y will be
(a) 10% and 5%
(b) 5% and 10%
(c) 10% and 15%
(d) 15% and 20%

232. A consumer buys a certain quantity of a good at a price of ₹ 10 per unit. When the price falls to ₹ 8 per unit, he buys 40% more quantity. The price elasticity of demand will be-
(a) 8
(b) 6
(c) 4
(d) 2
Consider the following diagram to answer questions from 233 to 234

233. At a price of OP the total expenditure of the consumer is-
(a) OC RP₁
(b) OBTP
(c) BCRT
(d) None of the above

234. At a price of OP₁ the total expenditure of the consumer is-
(d) OC RP₁
(b) OBTP
(c) BCRT
(d) None of the above

235. All demand curves but one indicate same elasticity of demand at all their points-
(a) Horizontal Straight Line Demand Curve
(b) Vertical Straight Line Demand Curve
(c) Relatively Elastic Demand Curve
(d) Rectangular Hyperbola

236. The point where the downward sloping straight line demand curve intercept the horizontal axis, price elasticity of demand is ____ because price at the point is ____
(a) zero ; zero
(b) = 1; zero
(c) > 1 ; zero
(d) < 1 ; zero

237. If the price elasticity of demand is ZERO, it means expenditure on the commodity may ____ with the change in price of the commodity.
(a) increase
(b) decrease
(c) increase or decrease
(d) remain constant

238. The price elasticity of demand is higher, when the price of the commodity is-
(a) higher
(b) lower
(c) constant
(d) zero

239. If 10% increase in price of good ‘X’ causes a 10% increase in expenditure on good ‘X’, elasticity of demand is equal to ____
(a) 2
(b) 3
(c) 1
(d) zero

240. Price of the commodity increases from ₹ 10 to ₹ 12 per unit and expenditure on the commodity increases by 20%, elasticity of demand would be-
(a) 3
(b) zero
(c) 2
(d) 1

241. The income elasticity of demand in case of an inferior good is-
(a) positive
(b) zero
(c) negative
(d) infinite

242. If a good is a luxury, its income elasticity of demand is-
(a) positive & less than one
(b) negative but greater than one
(c) positive and greater than one
(d) zero

243. When a given change in income does not lead to any change in the quantity demanded, it is called as-
(a) negative income elasticity of demand
(b) income elasticity of demand less than one
(c) zero income elasticity of demand
(d) income elasticity of demand is greater than one

244. The goods having zero income elasticity of demand are called goods.
(a) luxury
(b) comfort
(c) necessity
(d) neutral

245. Salt, Match Box, etc. are ____ goods as Σy = 0
(a) neutral
(b) necessary
(c) luxury
(d) none of the above

246. As income rises, the consumer will go in for superior goods and as a result the demand for inferior goods will fall. This implies-
(a) income elasticity of demand less than one
(b) negative income elasticity of demand
(c) zero income elasticity of demand
(d) unitary income elasticity of demand

247. Firms that supply products with higher income elasticity of demand can expect ____ as the economy grows.
(a) rise in sales
(b) fall in sales
(c) constant sales
(d) first rise then

248. Firms that supply products with relatively low income elasticity of demand experience in an economic downturn.
(a) rise in sales
(b) fall in sales
(c) stable sales
(d) none of the above

249. Which one of the following is income inelastic product/service?
(a) Air travel
(b) Visit to water park
(c) Life Saving Drugs
(d) Dinner at a five star hotel

250. The responsiveness of demand of a commodity to the change in income is known as-
(a) price elasticity of
(b) income elasticity demand of demand
(c) cross-elasticity
(d) none of the above of demand

251. The responsiveness of the change in quantity demanded of one commodity due to a change in the price of another commodity is known as-
(a) price elasticity of demand
(b) income elasticity of demand
(c) cross elasticity of demand
(d) none of the above

252. Cross elasticity of demand between two perfect substitutes will be-
(a) low
(b) very high
(c) infinity
(d) very low

253. Complementary goods like tea and sugar have a ____ cross elasticity of demand.
(a) Negative
(b) Positive
(c) Zero
(d) Infinite

Consider the following information to answer Q. Nos. 254 to 256
The following elasticities relating to demand for CORN are given-

Price Elasticity E_P = 1.50
Cross Elasticity between the demand for CORN and price of WHEAT = 0.75
Income Elasticity, E_y = 0.50

254. If the price of corn rises, other things being the same, the consumers will spend ____ on corn.
(a) more
(b) less
(c) same amount
(d) none of the above

255. The above information shows that wheat and corn are ____
(a) neutral goods
(b) necessity
(c) complementary goods
(d) substitute goods

256. If income rises, the share of income spent on corn will-
(a) remain same
(b) increase
(c) fall
(d) none of the above

257. Given – Q_x = 500 – 4 P_x
Find elasticity demand when price = ₹ 25
(a) .50
(b) .25
(c) 1
(d) .75

258. Give – Q_x = 20 – 2 P_x, what is the price elasticity of demand when price is ₹ 5?
(a) 0.50
(b) .25
(c) 1
(d) .75

259. If the amounts of two goods purchased increase or decrease simultaneously when the price of one changes, then the cross elasticity of demand between then is-
(a) one
(b) negative
(c) positive
(d) zero

260. Of the following commodities, which has the lowest elasticity of demand?
(a) Car
(b) Tea
(c) Houses
(d) Salt

261. Suppose your income increases by 20% and demand for a commodity increases by 10%, then the income elasticity of demand is-
(a) infinity
(b) negative
(c) zero
(d) positive

262. Which of the following does not have uniform elasticity of demand at all points?
(a) A downward sloping demand curve
(b) A vertical demand curve
(c) A rectangular hyperbola demand curve
(d) A horizontal demand curve

263. A negative income elasticity of demand for a commodity indicates that as income falls the amount of commodity purchased-
(a) remains unchanged
(b) falls
(c) rises
(d) none of these

264. In which case the elasticity shown by different points of a curve is the same?
(a) A rectangular hyperbola curve
(b) A straight line curve
(c) A downward sloping curve
(d) None of these

265. “The proportional change in quantity purchased divided by the proportional change in price”. The quotation is given by-
(a) Alfred Marshall
(b) Cobb – Douglas
(c) Joan Robionson
(d) Adam Smith

266. If the quantity demanded of a commodity is plotted against the price of a substitute goods, the curve is expected to be-
(a) Vertical
(b) Positively sloped
(c) Horizontal
(d) Negatively sloped

267. Cross elasticity of demand between petrol and automobiles is-
(a) infinite
(b) high
(c) zero
(d) low

268. There are two goods ‘X’ and ‘Y’. The cross elas¬ticity of demand for ‘X’ with respect to price of ‘Y’ is greater than zero, they are-
(a) complementary to each other
(b) complementary goods
(c) substitutes
(d) close substitutes

269. If two demand curves are shooting downward from the same point, then-
(a) flatter curve have greater elasticity of demand
(b) steeper curve have greater elasticity of demand
(c) both curves show same elasticity of demand since they shoot down from the same point
(d) none of the above

270. If income elasticity for the household for good A is 2, then the good is-
(a) necessity item
(b) inferior good
(c) luxury item
(d) neutral good
Consider the following figure to answer Q. Nos. 271 to 273

271. In the figure above elasticity of demand at point ‘D’ is-
(a) < elasticity of demand at point ‘C’
(b) > elasticity of demand at point ‘C’
(c) = elasticity of demand at point ‘C’
(d) None of the above

272. Price at point ‘B’ price is ____ and therefore elasticity of demand is ____
(a) high ; high
(b) low; low
(c) zero ; zero
(d) zero ; high/low

273. The elasticity of demand at point ‘A’ is-
(a) low
(b) infinite
(c) high
(d) zero
Consider the following figure to answer Q. Nos. 274 to 276

274. In the figure above, for a given fall in price to P₁ the change in quantity is highest in case of-
(a) d₁
(b) d₂
(c) d₃
(d) None of the above as all curves shoot from same point

275. Demand curve d₂ is-
(a) more elastic than d₁
(b) less elastic than d₁
(c) more elastic than d₂
(d) none of the above

276. Of the three demand curves highest elasticity is denoted by-
(a) d₁
(b) d₂
(c) d₃
(d) all show same elasticity

277. If the quantity demanded of a commodity is plotted against the price of a complementary good, the demand curve will be-
(a) Negatively sloped
(b) Positively sloped
(c) Vertical
(d) Horizontal

278. Income of a household rises by 10% and its demand for jawar falls by 4%. In this case jawar is ____ good.
(a) Normal
(b) Luxurious
(c) Inferior
(d) Neutral

279. If Cross Elasticity of Demand is equal to Zero, it means that the goods are-
(a) Perfect Substitute goods
(b) Complementary goods
(c) Unrelated goods
(d) Substitutes

280. If the quantity demanded of Tea rises by 5% when the price of Coffee increase by 20%, the Cross Elasticity of demand between Tea and Coffee is-
(a) – 0.25
(b) 0.25
(c) – 4
(d) 4

Theory of Consumer Behaviour

281. Want satisfying power of a commodity is called-
(a) consumption
(b) utility
(c) production
(d) value addition

282. Utility depends on the ____ of a want.
(a) intensity
(b) quality
(c) novelty
(d) uniformity

283. All but one are the commodities that have both utility and usefulness except-
(a) pencil
(b) notebook
(c) tobacco
(d) clothes

284. Utility is-
(a) a subjective and relative concept
(b) morally or ethically colourless
(c) different from pleasure
(d) all the above

285. Utility may be defined as-
(a) power of a commodity to satisfy wants
(b) usefulness of a commodity
(c) desire for a commodity
(d) none of the above

286. The utility of a commodity is ____
(a) its accepted social value
(b) the extent to which it is of practical use
(c) the fact that it is wanted by some people
(d) its relative scarcity

287. Utility is measured in terms of-
(a) Grams
(b) Seconds
(c) Centimeter
(d) Utils

288. Utility is-
(a) usefulness
(b) moral implications
(c) legal implications
(d) none of the above

289. The cardinal approach postulates that utility can be ____
(a) compared
(b) measured
(c) ranked
(d) all the above

290. Cardinal Utility Theory is associated with-
(a) W.S. Jevons
(b) Dr. A. Marshall
(c) H.H. Gossen and Walras
(d) All the above

291. Cardinal Utility approach is also known as-
(a) Indifference Curve Analysis
(b) Hicks and Allen Approach
(c) Marginal Utility Analysis
(d) All the above

292. Marginal Utility Approach is also called-
(a) Ordinal Utility Analysis
(b) Hicks and Allen Approach
(c) Cardinal Utility Analysis
(d) All the above

293. According to marginal utility analysis, utility can be measured as-
(a) 1^st, 2^nd, 3^rd ……
(b) 1,2,3, ……
(c) Nominal numbers
(d) All the above

294. Cardinal measure of utility is required in-
(a) Marginal Utility Theory
(b) Indifference Curve Theory
(c) Revealed Preference Theory
(d) None of the above

295. Which of the following approaches uses MONEY as a measuring rod of utility-
(a) Ordinal
(b) Cardinal
(c) Both ‘a’ and ‘b’
(d) Neither ‘a’ nor ‘b’

296. Which of the theories is applicable under Cardinal Approach to Utility?
(a) Law of Diminishing Marginal Utility
(b) Law of Equi-Marginal Utility
(c) Consumer Surplus Theory
(d) All the above

297. All but one are the assumptions of the Cardinal Utility Theory. Which one is not the assumption?
(a) Rational Consumer
(b) Constant Marginal Utility of money
(c) Perfectly Competitive Market
(d) Independent Utilities

298. Which of the following assumptions ignores the presence of complementary and substitute goods in Cardinal Utility Theory?
(a) Rational Consumer
(b) Constant Marginal Utility of money
(c) Independent Utilities
(d) None of the above

299. The price that a consumer is ready to pay for a commodity represents the utility he is expecting from the commodity means-
(a) Utility is measurable
(b) Utility is not measurable
(c) Money is the measuring rod of utility
(d) Both ‘a’ and ‘c’

300. Consumer makes all calculations carefully and then purchase the commodities in order to maximize his utility means consumer is-
(a) careless
(b) rational
(c) irrational
(d) unpredictable

301. Which of the following statements regarding ordinal utility is true?
(a) Utility can be measured, but cannot be ranked in order of preferences
(b) Utility can be measured only
(c) Utility can neither be measured nor be ranked in order or preferences
(d) Utility cannot be measured, but can be ranked in order of preferences

302. The cardinal approach to utility assumes marginal utility of money is-
(a) Zero
(b) Constant
(c) Increasing Trend
(d) Decreasing Trend

303. ____ is the sum total of the utility derived from additional units of a commodity
(a) Average utility
(b) Marginal utility
(c) Total utility
(d) Ordinal utility

304. _____ is the addition made to the total utility by the consumption of additional unit of a commodity
(a) Marginal Utility
(b) Total Utility
(c) Average Utility
(d) Ordinal Utility

305. Marginal Utility can be stated by-
(a)

(b) Additional utility derived from additional unit of a commodity
(c) TU_n – TU_n-1
(d) All the above

306. Utility of a good can be termed as the ____
(a) Monetary value a consumer gains from consuming a particular good
(b) The difference between what a consumer is willing to pay and actually pays
(c) The satisfaction a consumer derives from the consumption of a particular good
(d) The desire to consume a good

307. Marginal Utility-
(a) is always positive
(b) is always negative
(c) can be positive or negative but not zero
(d) can be positive or negative or zero

308. Total Utility can be calculated as-
(a) TU = Σ MU
(b) TU = MU₁ + MU₂ + MU₃ + MU_n(c) Both ‘a’ and ‘b’
(d) none of the above

309. When only ONE unit of the commodity is consumed-
(a) MU = TU
(b) MU > TU
(c) MU < TU
(d) none of these

310. When marginal utility is negative, total utility is-
(a) zero
(b) diminishing
(c) maximum
(d) minimum

311. When total utility is maximum, marginal utility becomes-
(a) zero
(b) unity
(c) positive
(d) negative

312. Total Utility is ____ when marginal utility is positive
(a) maximum
(b) diminishing
(c) increasing
(d) minimum

313. When TU is increasing at a diminishing rate, MU must be-
(a) increasing
(b) decreasing
(c) constant
(d) negative

314. MU of a particular commodity at the point of saturation is-
(a) zero
(b) unity
(c) greater than unity
(d) less than unity

315. Which of the following equation is incorrect?

CA Foundation Business Economics Study Material Chapter 2 Theory of Demand and Supply - MCQs 315

316. The rate of which TU changes is indicated by-
(a) MU
(b) TU
(c) both ‘a’ and ‘b’
(d) none of these

317. With the increase in consumption by ONE unit of the commodity, TU increases from 120 to 150, then marginal utility is-
(a) 50
(b) 1.25
(c) 0.88
(d) 30

318. The shape of MU curve is-
(a) upward sloping
(b) Concave to origin
(c) downward sloping
(d) straight line

319. TU starts diminishing when-
(a) MU is positive
(b) MU is increasing
(c) MU is negative
(d) MU is constant

320. TU curve-
(a) always rises
(b) always falls
(c) first falls and then rises
(d) first rises at a diminishing rate, reaches maximum point and then falls

321. MU curve will be below X-axis when-
(a) MU is positive
(b) MU is negative
(c) MU is zero
(d) MU is constant

322. What is called the point of satiety?
(a) The point where MU >0
(b) The point where MU < 0
(c) The point where MU = 0
(d) None of these

323. ____ states that marginal utility of a good diminishes as the consumer consumers additional units of a good.
(a) The Law of Equi-Marginal Utility
(b) The Law of Diminishing Marginal Utility
(c) Revealed Preference theory
(d) None of the above

324. MU curve of a consumer is also his ____
(a) indifference curve
(b) total utility curve
(c) supply curve
(d) demand curve

325. ____ curve is the slope of the TU curve.
(a) MU Curve
(b) Average Utility Curve
(b) Supply Curve
(d) Indifference Curve

326. At saturation point the slope of total utility curve is ____
(a) rising
(b) falling
(c) zero
(d) none of these

327. Constant Marginal Utility of Money means ___
(a) quantity
(b) importance
(c) composition
(d) Both ‘a’ and ‘c’

328. A curve which first move upwards then down wards is naturally ____
(a) Marginal Utility Curve
(b) Average Utility Curve
(c) Total Utility Curve
(d) Demand Curve

329. The peradox of value means that-
(a) people are irrational in consumption choices
(b) the total utilities yielded by commodities do not necessarily have relationship to their prices
(c) value has no relationship to utility schedule
(d) free goods are goods that are essential to life

330. The value paradox (diamond and water paradox) arises because-
(a) Water has too low price
(b) Value in use differs from utility
(c) Diamonds are too high priced
(d) Value-in-use differs from value-in-exchange

331. In ONE COMMODITY, case, the consumer is at equilibrium when-

332. The second samosa consumed gives lesser satisfaction to Mohan. This is a case of-
(a) Law of Demand
(b) Law of Diminishing Returns
(c) Law of Diminishing Marginal Utility
(d) Law of Supply

333. Marginal Utility of a commodity depends on its quantity and is –
(a) inversely proportional to its quantity
(b) not proportional to its quantity
(c) independent of its quantity
(d) none of the above

334. Which of the following is NOT an assumption of Law of Diminishing Marginal Utility?
(a) Homogenity
(b) Continuity
(c) Standard Unit
(d) None of the above

335. MU of one commodity has no relation with MU of another commodity implies-
(a) assumption of uniform quality
(b) assumption of rational consumer
(c) assumption of independent utilities
(d) assumption of reasonable quantity

336. Consumer in consumption of single commodity ‘X’ will be at equilibrium when-
(a) MUx = Px
(b) Mux >Px
(c) Mux < Px
(d) all the above

337. if Mux >Px then consumer-
(a) is not at equilibrium
(b) he will buy more of X good
(c) he will buy less of X good
(d) both ‘a’ and ‘b’

338. Suppose the price of good X is given as ₹ 8 and the MU in terms of money for 4 units is given as-

How many units should a consumer purchase to maximize satisfaction?
(a) 4 units
(b) 3 units
(c) 2 units
(d) 1 unit

339. Following is the utility schedule of a person-

If the commodity is sold for ₹ 4 and MU of one rupee is 5 utils, how many units will the consumer buy to maximize satisfaction?
(a) 1 unit
(b) 2 units
(c) 3 units
(d) 4 units
CA Foundation Business Economics Study Material Chapter 2 Theory of Demand and Supply - MCQs 339.1

340. Suppose that an ice-cream is sold for ₹ 30. Ritu has already eaten 3 ice-creams. Her MU from eating the 3rd ice-cream is 90 utils. MU of ₹ 1 is 3 utils. Should she eat more ice-creams or stop?
(a) Stop eating more ice-creams
(b) Continue eating more ice-creams
(c) Stop after eating one more ice-cream
(d) Eat 2 more ice-creams

341. If one burger give you satisfaction of 15 utils and two burgers give total satisfaction of 25 utils, then the marginal utility of second burger is-
(a) 10 utils
(b) 11 utils
(c) 12 utils
(d) 13 utils

342. ____ refers to a situation when a consumer maximizes his satisfaction with his limited income.
(a) Producer’s Equilibrium
(b) General Equilibrium
(c) Consumer’s Equilibrium
(d) None of these

343. The general condition of consumer’s equilibrium with respect to any particular product is-

344. The consumer is in equilibrium and is consuming good-X only. The MU from last unit of good X consumed is 50 utils and Mu_m =10. What is the price of good X?
(a) ₹ 5
(b) ₹ 40
(c) ₹ 10
(d) ₹ 4

345. The principal limitation of utility analysis re¬lates to the basic assumption that utility can be expressed in terms of-
(a) cardinal numbers
(b) ordinal numbers
(c) both ‘a’ and ‘b’
(d) none of these

346. Marginal Utility theory is based on ____ from a good.
(a) actual satisfaction
(b) anticipated satisfaction
(c) realised satisfaction
(d) none of these

347. Which one of the following is the ODD one?
(a) Law of Substitution
(b) Law of Diminishing Marginal Utility
(c) Indifference curve analysis
(d) Law of Variable Proportions

348. Which statement is correct in connection with utility?
1. It is same for all consumer
2. It is a subjective concept
3. It is different for all its consumers
4. It’s a want satisfying power
5. It decreases uniformly for all its consumers
(a) 1, 2 and 3 only
(b) 2, 3 and 4 only
(c) 3, 4 and 5 only
(d) 1, 3 and 5 only

349. The excess of the price which a person would be willing to pay rather than go without the thing over that he actually does pay is called-
(a) extra satisfaction
(b) surplus satisfaction
(c) consumer’s surplus
(d) all the above

350. The doctrine of consumer’s surplus is based on ____
(a) Elasticity of Demand
(b) Indifference Curve Analysis
(c) Law of Substitution
(d) Law of Diminishing Marginal Utility

351. The term optimum allocation of consumer’s expenditure on different goods and services is used in-
(a) Law of Demand
(b) Giffens Paradox
(c) Law of Equi-Marginal Utility
(d) Law of Diminishing Marginal Utility

352. Buyer’s surplus is highest in the case of _____
(a) Luxuries
(b) Comforts
(c) Necessaries
(d) All the above
For Q – Nos. 353 to 355, refer the following figure :

353. In the above figure, the total utility is represented by the area ____
(a) DPR
(b) OQRP
(e) OQRD
(d) none of these

354. In the above figure, the given price is _____ and the consumer for OQ amount of commodity spends a total amount of money equal to the area _____
(a) OP ; POOR
(b) OD ; POOR
(c) OP ; DPR
(d) OD ; DPR

355. In the above figure, the consumer’s surplus is shown by the area-
(a) POOR
(b) DPR
(c) OQRD
(d) none of these
For Q. Nos. 356 and 359 refer the following figure

356. In the above diagram, the consumer’s surplus at the price of P₁ is equal to the area-
(a) P₁CA
(b) P₁OQ₁
(c) Both ‘a’ and ‘b’
(d) none of these

357. In the above diagram when price of the commodity decreases from P₁ to P₂, the gain in consumer’s surplus is equal to ____
(a) AP₃C
(b) AP₂D
(c) P₁P₂DC
(d) AP₃B

358. In the above diagram, when price of the commodity rises from P1 to P3, the loss in consumer’s surplus is equal to ___
(a) AP3B
(b) AP1C
(c) AP2D
(d) P1P3 BC

359. The consumer’s surplus at the price P₁ is ____ than the consumer’s surplus at the price of P₃ but ____ at the price of P₂.
(a) greater; less
(b) less ; greater
(c) same at all the prices
(d) none of these

360. The area of consumer’s surplus is correctly shaded in ____

361. The concept of consumer’s surplus is useful in ____
(a) Distinguishing between value-in-use and value-in-exchange
(b) Comparing the advantages of different places
(c) Useful in cost benefit analysis of projects
(d) All the above

362. Amit divides his income entirely between Good X and Good Y. He allocates his income between these two goods is such a way that he maximizes his satisfaction. His MU from extra unit of Y is 4 Utils and the price of Y is ₹ 40. If the price of X is ₹ 80, how much of X good he consumes per day?
(a) 4
(b) 6
(c) 8
(d) 10

363. A free good is plentiful so as to have no price, will be used upto the point where its marginal utility is ____
(a) zero
(b) highest
(c) lowest
(d) none of these

364. The more rapidly the marginal utility of additional units of a good falls, the will be the elasticity of demand.
(a) more
(b) less
(c) zero
(d) infinite

365. According to utility theory, for a consumer who is maximizing total utility, Mu_a/ Mu_b

366. In which of the following fields the concept of consumer’s surplus is useful?
(a) Monetary policy
(b) Tax policy
(c) Investment policy
(d) Fixing remuneration on factors

367. An example of a commodity having consumers surplus is ____
(a) Salt
(b) Branded Shirt
(c) Machinery
(d) Pen

368. Consumer’s surplus means-
(a) difference between market price and individual price
(b) difference between actual and potential price
(c) low price is prevailing
(d) happiness of the consumer

369. Consumer’s surplus is measured with the help of ____
(a) market demand curve
(b) marginal productivity curve
(c) marginal utility curve
(d) none of these

Consider the following details to answer Q. Nos. 370 to 372
Given Px = ₹ 2 and Py = ₹ 1 and income = ₹ 12.
Also given is the utility schedule of good X & Y.

370. How many units of X and Y the consumer will buy in order to maximize utility?
(a) 2 units of X & 6 units of Y
(b) 3 units of X & 5 units of Y
(c) 4 units of X & 4 units of Y
(d) 3 units of X & 6 units of Y

371. What will be the total utility received by the Consumer from the two commoddities
(a) 90
(b) 92
(c) 93
(d) 95

372. How much of total income will the consumer spend on good X and good Y?
(a) ₹ 3 & ₹ 6
(b) ₹ 6 & ₹ 6
(c) ₹ 6 & ₹ 3
(d) ₹ 3 & ₹ 3

373. When the price of both the commodities is same, the consumer attains maximum satisfaction where

CA Foundation Business Economics Study Material Chapter 2 Theory of Demand and Supply - MCQs 373

374. A consumer will purchase more of Good-x than Good-Y, only when :

375. A locus of constant utility is called the ____
(a) expansion path
(b) utility function
(c) indifference curve
(d) demand function

376. An indifference curve is ____
(a) downward sloping and convex to origin
(b) downward sloping and concave to origin
(c) upward sloping and convex to origin
(d) vertical and parallel to y-axis

377. The slope of indifference curve show-
(a) marginal rate of substitution
(b) level of satisfaction to the consumer
(c) elasticity of indifference curve
(d) none of the above

378. At a point near the right hand below corner of a indifference curve, the MRS of commodity ‘X’ for commodity ‘Y’ is-
(a) very high
(b) very low
(c) zero
(d) neither high nor low

379. As one moves upward towards left along an indifference curve, the MRS of commodity ‘X’ for commodity ‘Y’-
(a) increases
(b) decreases
(c) is constant
(d) fluctuates

380. A higher IC denotes-
(a) a higher level of satisfaction
(b) a lower level of satisfaction
(c) same level of satisfaction
(d) none of the above

381. Which of the following is not a characteristics of the indifference curve-
(a) downward sloping to the right
(b) convex to the origin
(c) intersecting at one point
(d) none of the above

382. IC theory assumes that-
(a) buyers can measure satisfaction
(b) buyers can identify preferred combinations of goods
(c) the prices of the goods are equal
(d) none of the above

383. An IC shows all combinations of two commodities which-
(a) give the same level of satisfaction to the consumer
(b) represent the highest level of satisfaction to the consumer
(c) give the different level of satisfaction to the consumer
(d) none of the above

384. The slope of IC tends to diminish as we move down the curve means-
(a) MRS is constant
(b) MRS is increasing
(c) MRS is decreasing
(d) none of the above

385. Marginal rate of substitution of ‘X’ for ‘Y’ is calculated as-

386. In an indifference map, higher IC indicates :
(a) lower level of satisfaction
(b) same level of satisfaction
(c) higher level of satisfaction
(d) either same or higher level of satisfaction

387. MRS is determined by-
(a) satisfaction level of the consumer
(b) income of the consumer
(c) tastes of the consumer
(d) preferences of the consumer

388. A set of ICs drawn in a graph is called-
(a) indifference curve
(b) indifference map
(c) budget line
(d) budget set

389. An IC is convex to origin because of-
(a) diminishing marginal utility
(b) diminishing marginal productivity
(c) diminishing marginal cost
(d) diminishing marginal rate of substitution

390. Marginal Rate of Substitution indicates the slope of-
(a) budget line
(b) indifference curve
(c) total utility curve
(d) demand curve

391. The slope of IC is different at different points of the curve
(a) Correct
(b) Incorrect
(c) ∴ slope of IC is measured by MRS which falls
(d) Both ‘a’ & ‘c’

392. Only one IC will pass through a given point on an indifference map implies that-
(a) One combination can lie only on one IC
(b) One combination can lie on two ICs.
(c) One combination can lie on as many ICs.
(d) none of the above

393. Considering the map, the satisfaction derived from the combination is _____

(а) A > B, B > C but A > C
(b) A>B>C
(c) A < B > C
(d) C > B > A

394. A consumer may not be in equilibrium at point C or D because _____

(a) MRS_xy = Px / Py
(b) The whole income is not spent
(c) Point E gives higher level of Satisfaction with the same expenditure as on point C and D
(d) Of sufficiency of income

395. On an indifference curve, the MRS falls when-
(a) moving upwards
(b) moving downwards
(c) at the middle
(d) none of these

396. Should a consumer move upward along an IC, his total utility-
(a) First increases and then decreases
(b) First decreases and then increases
(c) Remains constant
(d) Increases

397. Which of the following is not an assumption of ordinal utility analysis?
(a) Consumers are consistent in their preference
(b) Consumers can measure the total utility
(c) Consumers are non-satiated with respect of two goods
(d) None of the above

398. All points on the same IC represent-
(a) Equal satisfaction
(b) Higher satisfaction
(c) Lower satisfaction
(d) All the above

399. IC approach deals with-
(a) One commodity only
(b) Two commodities
(c) Many commodities
(d) No commodities at all

400. If two goods were perfect substitutes of each other, the IC will be-
(a) Curvilinear
(b) linear
(c) right angled
(d) convex to origin

401. A downward sloping linear IC indicates that the rate of MRSxy is-
(a) diminishing
(b) increasing
(c) constant
(d) zero

402. In the case of two perfect substitute goods, the IC will be-
(a) L – shaped
(b) U – shaped
(c) S – shaped
(d) Straight line

403. If a consumer has monotonic preferences, which bundle will he choose?
(a) (10,8)
(b) (8,6)
(c) (10,7)
(d) (8,8)

404. If a consumer has monotonic preferences how would he rank his preference over the bundles (10,9); (9,9) (10,10)-
(a) (10,9) (10,10) ; (9,9)
(b) (10,10) (10,9) ; (9,9)
(c) (9,9) (10,10) ; (10,9)
(d) None of the above

405. When an IC is L shaped, then two goods will be-
(a) Perfect Substitute Goods
(b) Perfect Substitute
(c) Perfect Complementary Goods
(d) Complementary Goods

406. The Other name associated with ordinal approach apart from R.G.D. Allen and J.R. Hicks is-
(a) Edgeworth
(b) Vilfredo Pareto
(c) Slutsky
(d) All the above

407. _____ depicts complete scale of consumer’s tastes and preferences.
(a) Budget Line
(b) MU curve
(c) Indifference curve map
(d) One indifference curve

408. One combination can lie only on one IC means-
(a) Only one IC will pass through the point
(b) Two ICs will pass through the point
(c) As many ICs can pass through the point
(d) None of the above

409. When the quantity of one good is increased in the combination, the quantity of other is reduced to maintain same level of satisfaction. This means that IC is ____
(a) positively sloped
(b) vertical straight line
(c) horizontal straight line
(d) negatively sloped

410. When the combinations on a IC do not represent same level of satisfaction, it means IC is _____
(a) positively sloped
(b) horizontal straight line
(c) vertical straight line
(d) all the above

411. is a graphical representation of all possible combination of two goods which can be purchased given income and prices.
(a) Budget Line
(b) Price Opportunity Line
(c) Consumption Possibility Line
(d) All the above

412. If a combination is below the Budget Line, it indicates that there is-
(a) Underspending by a consumer
(b) Overspending by a consumer
(c) Full spending by a consumer
(d) None of the above

413. All combinations that lie on the budget line are _____
(a) unaffordable by consumer
(b) affordable by consumer
(c) attainable by consumer
(d) Both ‘b’ and ‘c’

414. Each point on the budget line shows-
(a) the ratio of change in MU
(b) the ratio of prices of two goods
(c) Marginal Rate of Substitution .
(d) Both ‘b’ and ‘c’

415. A shift of the budget line, when prices are constant, is due to-
(a) change in demand
(b) change in income
(c) change in preference
(d) change in utility

416. Slope of budget line is indicated by-

417. The budget line of a consumer in the analysis of IC is-
(a) Vertical straight line
(b) Horizontal straight line
(c) Straight line sloping down towards right
(d) Straight line sloping upwards towards right

418. The budget line is not known as-
(a) consumption possibility curve
(b) price line
(c) price opportunity line
(d) isoutility line

419. Refer the following figure-

Figure denotes-
(a) Change in income
(b) Change in price of Good-X
(c) Change in price of Good-Y
(d) Change in the prices of both Good X & Y

420. When the prices of both Good-X and Good-Y change by same percentage, a rise in price will-
(a) shift the budget line upwards
(b) shift the budget line downwards
(c) no shift in budget line
(d) all the above

421. If the budget line does not shift it means-
(a) prices of both goods X & Y has changed by same percentage
(b) there is no change in the prices of both goods X & Y
(c) money income of consumer has changed
(d) income of the consumer and prices of both goods X & Y change by same percentage

422. If price of Goods-X falls and price of Good-Y rises then budget line will-
(a) shift upward
(b) shift downward
(c) rotate
(d) remain same

423. Refer the following figure, what change budget line shows –

(a) Px fails and Py rises
(b) Px rise and Pv falls
(c) Px=Py
(d) none of the above

Refer the following to answer question nos. 424 to 426
A consumer wants to buy two good X and Y. The prices of the two goods are ₹ 4 and ₹ 5 respectively. The consumers income is ₹ 20.

424. If the consumer spends the entire money income to buy only Good-X, how much quantity he can buy of it?
(a) 5 units
(b) 6 units
(c) 4 units
(d) 3 units

425. If the consumer spends the full income only to buy Good-Y, how much quantity he would be able to buy of it-
(a) 5 units
(b) 6 units
(c) 4 units
(d) 3 units

426. The slope of the budget line is-
(a) 0.9
(b) 0.8
(c) 0.7
(d) 0.5

427. A consumer can buy 6 units Good-X and 8 units of Good-Y if he spends his entire income. The prices of the two goods are ₹ 6 and ₹ 8 respectively. What is the consumer’s income.
(a) ₹ 100
(b) ₹ 150
(c) ₹ 200
(d) ₹ 250

428. Ravi consumes Apples and Bananas whose price are ₹ 6 and ₹ 3 p.u. respectively. If he is in the state of equilibrium, the value of marginal rate of substitution is-
(a) 4
(b) 3
(c) 2
(d) 1

429. A budget constraint line is a result of
(a) market price of good X
(b) market price of good Y
(c) income of the consumer
(d) all the above

430. The budget line equation is-

431. The consumer will maximize his satisfaction and will be at equilibrium where-
(a) budget line is tangent to IC
(b) price line crosses on IC
(c) price line does not touch the IC
(d) none of the above

432. How many indifference curves can touch the price line-
(a) Two
(b) One
(c) As many as possible
(d) No IC will touch

433. MRSxy = p_x / p_y where-
(a) consumer is in equilibrium
(b) consumer is not at equilibrium
(c) producer is at equilibrium
(d) none of the above

434. The point where the budget line is tangent to an IC-
(a) equal amounts of goods give equal satisfaction
(b) the ratio of prices of the two goods equals MRS
(c) the prices of the goods are equal
(d) none of the above

435. Maximisation of total utility is an assumption of a consumer in an analysis that is-
(a) Indifference curve approach
(b) Demand analysis
(c) Utility analysis
(d) All the above

436. A consumer is in equilibrium at the point of tangency of his IC and the price line, because-
(a) He cannot go below
(b) He cannot go beyond
(c) He cannot go along
(d) None of the above

437. Which of the following conditions is necessary for utility to be maximum?

Consider the following figure and answer question Nos. 438 and 439

438. The consumer is not at equilibrium at point C, since-
(a) MRSxy > Px / Py
(b) MRSxy = Px / Py
(c) MRSxy < Px / Py (d) None of the above

439. The consumer is at equilibrium at point E, since-
(a) MRSxy > Px / Py
(b) MRSxy = Px / Py
(c) MRSxy < Px / Py
(d) MUx = MUy

440. In a situation where MRSxy > p_x / p_y , the consumer would react by-
(a) reducing the consumption of Good – X
(b) increasing the consumption of Good – Y
(c) increasing the consumption of Good – X
(d) none of these

441. When MRSxy < p_x / p_y , in order to reach equilibrium, the consumption of-
(a) Good-Y should increase
(b) Good-X should increase
(c) Good-Y should decrease
(d) None of these

442. The situation of a consumer is better when-
(a) MRSxy >Px / Py
(b) MRSxy < Px / Py
(c) MRSxy = Px / Py
(d) none of these

Read the following to answer question Nos. 443 and 444
A consumer wants to buy two goods X and Y. He has ₹ 24 to spend. The prices of two goods X and Y are ₹ 4 and ₹ 2 respectively.

443. Which of the following bundles a consumer would be able to buy-
(a) 4X and 5Y
(b) 2X and 7Y
(c) 3Xand6Y
(d) None of the above

444. What will be the MRSxy when the consumer is at equilibrium-
(a) 1:2
(b) 2:1
(c) 1:1
(d) 2:2

445. At the point of equilibrium on Indifference Curve-
(a) Slope of budget line = slope of IC
(b) Slope of budget line > slope of IC
(c) Slope of budget line < slope of IC
(d) None of the above

446. In case of IC approach, an income effect means-
(a) a movement towards X-axis
(b) a movement towards the right
(c) a movement towards another indifference curve
(d) a movement along the indifference curve

447. In the case of substitution effect in IC approach, the consumer moves-
(a) along the same IC from left to right
(b) up and down along the same IC
(c) from a point on IC to a point on budget line
(d) none of these

448. IC is downward sloping from left to right since more X and less Y gives-
(a) less satisfaction
(b) more satisfaction
(c) equal satisfaction
(d) maximum satisfaction

Supply

449. In economics, supply means-
(a) quantity of a commodity which is actually offered for sale at a given price in a given period of time
(b) quantity of a commodity which is offered for sale at a particular price
(c) stock of commodity which is sold at a give price
(d) none of the above

450. Which of the following is not true in case of supply?
(a) Supply is a flow concept
(b) Supply is a stock concept
(c) Supply is directly related to price
(d) Market supply is horizontal summation of the individual supply curves

451. When price rises, quantity supplied-
(a) expand
(b) falls
(c) increases
(d) is unchanged

452. Which of the following statement is correct?
(a) Supply does not depends on Govts, tax policy
(b) Stock is the quantity brought to market for sale
(c) There is difference between stock and supply
(d) Stock and supply are always equal

453. The supply of good refers to-
(a) actual production of a good
(b) total stock of the good
(c) stock available for sale
(d) amount of the good offered for sale at a particular price per unit of time

454. According to law of Supply-
(a) there is positive relation between supply and price
(b) there is negative relation between supply and price
(c) there is constant relation between supply and price
(d) there is no relation between supply and price

455. ______ shows the quantity of goods a producer or seller wishes to sell at a given price level
(a) Average Product Curve
(b) Marginal Product Curve
(c) Supply Curve
(d) Total Product Curve

456. The supply curve slopes-
(a) Slopes downward from left to right
(b) Slopes upwards from left to right
(c) Slopes upward from right to left
(d) None of the above

457. Graphical presentation of supply curve of an individual firm in the market is called-
(a) producer’s demand curve
(b) consumers demand curve
(c) individual supply curve
(d) market supply curve

458. When the state of technology improves, supply
(a) fall
(b) contract
(c) increase
(d) expand

459. When government imposes taxes, supply will
(a) expand
(b) increase
(c) contract
(d) decrease

460. Movement along the supply curve occurs due to-
(a) rise in price of the commodity
(b) fall in price of the commodity
(c) factors other than own price of the commodity
(d) both ‘a’ and ‘b’

461. Supply curve shifts rightward due to-
(a) increase in the number of firms
(b) fall in the price of factors of production
(c) new and better technology
(d) all the above

462. Expansion of supply takes place due to-
(a) change in goal of the firm
(b) rise in price of the commodity
(c) number of firms
(d) technique of production

463. If producer expects an increase in price of goods in the near future, then current supply will:
(a) fall
(b) rise
(c) remain constant
(d) become zero

464. When more units of the good are supplied at a higher price, it is called-
(a) Contraction of supply
(b) Change in supply
(c) Extension in supply
(d) Increase in supply

465. When supply price increases in the short run, the profit of the producer-
(a) Increases
(b) Decreases
(c) Remains constant
(d) Decreases a bit

466. The long-run supply curve of a diminishing cost industry is-
(a) downward sloping to right
(b) upward sloping to left
(c) horizontal
(d) vertical

467. The law of supply does not apply to-
(a) agriculture goods
(b) industrial goods
(c) perishable goods
(d) both ‘a’ and ‘c’

468. When supply falls due to factors other than own price of the commodity, it means-
(a) contraction of supply
(b) decrease in supply
(c) extension of supply
(d) none of these

469. In case of contraction of supply, there is-
(a) an upward movement on supply curve
(b) shift of supply curve to the right
(c) downward movement on supply curve
(d) shift to supply curve to the left

470. In case of increase in supply, there is –
(a) an upward movement on supply curve
(b) shift of supply curve to the right
(c) downward movement on supply curve
(d) shift to supply curve to the left

471. Imposition of a unit tax, shifts the supply curve-
(a) to the right
(b) to the left
(c) to the right as well
(d) none of these as to the left

472. Due to incentives like tax holiday, subsidies which reduces the cost of production, the supply quantity will-
(a) Increase
(b) Decrease
(c) Remain Constant
(d) Become zero

473. In case of failure of rains, floods, etc. the supply of agricultural goods will-
(a) Increase
(b) Decrease
(c) Remain constant
(d) Become zero

474. The percentage change in quantity supplied due to percentage in price is called-
(a) Expansion of supply
(b) inelastic supply
(c) elasticity of supply
(d) changes in supply

475. Elasticity of supply refers to the responsiveness of quantity supplied to changes in its-
(a) Demand
(b) Price
(c) Cost of production
(d) State of technology

476. When supply curve is a vertical straight line, it indicates _____ supply
(a) unitary elastic
(b) perfectly elastic
(c) perfectly inelastic
(d) relatively elastic

477. A straight line supply curve passing through origin forming 50° indicates-
(a) E =0
(b) E_s= 1
(c) E_s > 1
(d) E_s < 1

478. Elasticity of supply for a positively sloped supply cure that starts from price axis is –
(a) zero
(b) greater than one
(c) less than one
(d) equal to one

479. In case of perfectly elastic supply the supply curve is-
(a) rising
(b) vertical
(c) falling
(d) horizontal

480. Supply is relatively elastic in-
(a) very short period
(b) short period
(c) long period
(d) both ‘b’ and ‘c’

481. When supply curve is parallel to X-axis, elasticity of supply is-
(a) zero
(b) infinity
(c) unity
(d) negative

482. If the co-efficient of elasticity of supply is 0.6, the supply is-
(a) perfectly inelastic
(b) inelastic
(c) perfectly elastic
(d) elastic

483. When upward sloping straight line curve shoots up from quantity axis, it implies-
(a) E_s < 1
(b) E_s > 1
(c) E_s = 1
(d) E_s = 0

484. Which of the above curves unitary elastic demand?

(a) Curve A
(b) Curve B
(c) Curve C
(d) all the above

485. Elasticity of supply for a positively sloped supply that shoots from origin
(a) E_s < 1
(b) E_s > 1
(c) E_s = 1
(d) E_s = ∞

486. The supply of perishable goods is-
(a) relatively elastic
(b) relatively inelastic
(c) perfectly elastic
(d) none of the above

487. The supply function of a commodity is given by – Q = 20 + 3 Px. If the price is ₹ 6, the quantity supplied is-
(a) 35 units
(b) 38 units
(c) 40 units
(d) 42 units

Refer the following supply function to answer 0. Nos. 488 to 490
Q_s = -10 + 2p

488. How much quantity is supplied at a price of ₹ 10?
(a) 10 units
(b) 8 units
(c) 12 units
(d) 6 units

489. At which price, the supply would be zero?
(a) ₹ 1
(b) ₹ 3
(c) ₹ 4
(d) ₹ 5

490. Calculate the price at which, the firm is willing to supply 100 units
(a) ₹ 55
(b) ₹ 50
(c) ₹ 45
(d) ₹ 40

491. When price of a commodity falls by 20%, the quantity supplied falls by 25%, the price elasticity of supply is-
(a) 0.75
(b) 1.25
(c) 1.50
(d) 1.75

492. A vegetable vendor sells 80 quintals of potatoes at a price of ₹ 4 p. kg. The elasticity of supply of potatoes is known to be 2. How much quantity will he sell at ₹ 5 p. kg.?
(a) 100 quintals
(b) 110 quintals
(c) 120 quintals
(d) 130 quintals

493. When the price of a good rises from ₹ 15pu to ₹ 19pu, its quantity supplied increases from 75 units to 95 units. The price elasticity of supply is-
(a) 1
(b) 2
(c) 3
(d) 4

494. Total revenue of a firm rises from ₹ 50 to ₹ 100 when the price rises from ₹ 5 pu to ₹ 10 pu. The co-efficient of E_s =
(a) 0
(b) 0.8
(c) 1
(d) 1.2

495. The price of a commodity doubles, to its response the quantity supplied increases 4 times of orig¬inal quantity supplied. The co-efficient of price elasticity of supply is-
(a) 1
(b) 2
(c) 3
(d) 4

496. A price of ₹ 10 p.u. the quantity supplied is 500 units. If the price falls by 10% and quantity supplied falls to 400 units, the co-efficient of price elasticity of supply is-
(a) 1
(b) 2
(c) 3
(d) 4

497. Market forces refer to-
(a) Demand
(b) Supply
(c) Both ‘a’ and ‘b’
(d) Neither ‘a’ nor ‘b’

498. Supply is the-
(a) limited resources that are available with the seller
(b) cost of producing a good
(c) entire relationship between the quantity supplied and the price of good
(d) willingness to produce

499. In a very short period the supply-
(a) can be changed
(b) cannot be changed
(c) can be increased
(d) none of the above

500. If the demand is more than supply, then the pressure on price will be-
(a) upward
(b) downward
(c) constant
(d) none of the above

501. A perfectly inelastic supply curve shooting up from X-axis shows-
(a) constant supply at higher price
(b) constant supply at lower price
(c) constant supply at zero price
(d) all the above

502. What is incorrect about advertisement elasticity?
(a) It is the responsiveness of good’s demand to changes in firm’s expenditure on advertising
(b) It is also called promotional elasticity of demand
(c) Advertising elasticity of demand is typically positive
(d) all the above

503. All but one are correct about demand forecasting. Which one is not correct?
(a) Demand forecasting is the art and science of predicting probable demand of a product in future
(b) Demand forecasting is a simple guesses
(c) It considers past behaviour pattern and prevailing trends in the present
(d) Demand forecasting plays an important role in planning and decision making

504. The burden of forecasting is put on customers in _____ method of demand forecasting
(a) Survey of buyers intentions
(b) collective opinion
(c) Expert opinion
(d) Controlled experiments

505. Delphi technique was developed by-
(a) Schumpeter
(b) Nicholas Kaldor
(c) Olaf Helmer
(d) Hawtrey

506. Collective opinion method of demand forecasting is useful for _____ forecasting.
(a) short run
(b) long run
(c) secular period
(d) none of the above

507. _____ method of forecasting is useful in use of capital goods.
(a) Collective opinion
(b) Expert Opinion
(c) Barometric
(d) Survey of buyer’s intention

508. Which of the following affect the demand for non-durable consumer goods?
(a) Disposable Income
(b) Price
(c) Demography
(d) All the above

509. What would be the shape of the supply curve of T-shirts, if the seller offers to sell any number of T-shirts at ₹ 250?
(a) Vertical
(b) Horizontal
(c) Upward sloping
(d) Downward sloping

510. All the following factors affect the demand for durable consumer goods except-
(a) special facilities for use
(b) credit facilities
(c) disposable income
(d) social status

511. ____ is considered as a ‘naive’ approach to demand forecasting.
(a) Trend Projection Method
(b) Expert Opinion Method
(c) Collective Opinion Method
(d) Regression Analysis

512. Short-term demand forecasting is useful for-
(a) current production scheduling
(b) purchases of. raw materials
(c) inventory of stocks
(d) all the above

513. A firm planning capacity expansion and diversification will go in for-
(a) Short term demand forecasting
(b) Medium term demand forecasting
(c) Long term demand forecasting
(d) Current demand forecasting

Answers

CA Foundation Business Economics Study Material Chapter 2 Theory of Demand and Supply - MCQs answer

RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS

January 9, 2023

RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS

Other Exercises

Mark the correct alternative in each of the following :
Question 1.
The distance between the points (cosθ, sinθ) and (sinθ, -cosθ) is
(a) √3
(b) √2
(c) 2
(d) 1
Solution:
(b) Distance between (cosθ, sinθ) and (sinθ, -cosθ)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 1

Question 2.
The distance between the points (a cos 25°, 0) and (0, a cos 65°) is
(a) a
(b) 2a
(c) 3a
(d) None of these
Solution:
(a) Distance between (a cos 25°, 0) and (0, a cos 65°)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 3

Question 3.
If x is a positive integer such that the distance between points P (x, 2) and Q (3, -6) is 10 units, then x =
(a) 3
(b) -3
(c) 9
(d) -9
Solution:
(c) Distance between P (x, 2) and Q (3, -6) = 10 units
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 4
=> x (x – 9) + 3 (x – 9) = 0
(x – 9) (x + 3) = 0
Either x – 9 = 0, then x = 9 or x + 3 = 0, then x = -3
x is positive integer
Hence x = 9

Question 4.
The distance between the points (a cosθ + b sinθ, 0) and (0, a sinθ – b cosθ) is
(a) a² + b²
(b) a + b
(c) a² – b²
(d) √(a²+b²)
Solution:
(d) Distance between (a cosθ + b sinθ, 0) and (0, a sinθ – b cosθ)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 5

Question 5.
If the distance between the points (4, p) and (1, 0) is 5, then p =
(a) ±4
(b) 4
(c) -4
(d) 0
Solution:
(a) Distance between (4, p) and (1, 0) = 5
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 6

Question 6.
A line segment is of length 10 units. If the coordinates of its one end are (2, -3) and the abscissa of the other end is 10, then its ordinate is
(a) 9, 6
(b) 3, -9
(c) -3, 9
(d) 9, -6
Solution:
(b) Let the ordinate of other end = y
then distance between (2, -3) and (10, y) = 10 units
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 8

Question 7.
The perimeter of the triangle formed by the points (0, 0), (1, 0) and (0, 1) is
(a) 1 ± √2
(b) √2 + 1
(c) 3
(d) 2 + √2
Solution:
(d) Let the vertices of ∆ABC be A (0, 0), B(1, 0) and C (0, 1)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 9

Question 8.
If A (2, 2), B (-4, -4) and C (5, -8) are the vertices of a triangle, then the length of the median through vertices C is
(a) √65
(b) √117
(c) √85
(d) √113
Solution:
(c) Let mid point of A (2, 2), B (-4, -4) be D whose coordinates will be
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 11

Question 9.
If three points (0, 0), (3, √3) and (3, λ) form an equilateral triangle, then λ =
(a) 2
(b) -3
(c) -4
(d) None of these
Solution:
(d) Let the points (0, 0), (3, √3) and (3, λ) from an equilateral triangle
AB = BC = CA
=> AB² = BC² = CA²
Now, AB² = (x₂ – x₁)² + (y₂ – y₁)²
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 12

Question 10.
If the points (k, 2k), (3k, 3k) and (3, 1) are collinear, then k
(a) \(\frac { 1 }{ 3 }\)
(b) \(\frac { -1 }{ 3 }\)
(c) \(\frac { 2 }{ 3 }\)
(d) \(\frac { -2 }{ 3 }\)
Solution:
(b) Let the points A (k, 2k), B (3k, 3k) and C (3, 1) be the vertices of a ∆ABC
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 13

Question 11.
The coordinates of the point on x-axis which are equidistant from the points (-3, 4) and (2, 5) are
(a) (20, 0)
(b) (-23, 0)
(c) (\(\frac { 4 }{ 5 }\) , 0)
(d) None of these
Solution:
(d)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 15

Question 12.
If (-1, 2), (2, -1) and (3, 1) are any three vertices of a parallelogram, then
(a) a = 2, b = 0
(b) a = -2, b = 0
(c) a = -2, b = 6
(d) a = 0, b = 4
Solution:
(d) In ||gm ABCD, diagonals AC and AD bisect each other at O
O is mid-point of AC
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 16

Question 13.
If A (5, 3), B (11, -5) and P (12, y) are the vertices of a right triangle right angled at P, then y =
(a) -2, 4
(b) -2, 4
(c) 2, -4
(d) 2, 4
Solution:
(c) A (5, 3), B (11, -5) and P (12, y) are the vertices of a right triangle, right angle at P
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 17

Question 14.
The area of the triangle formed by (a, b + c), (b, c + a) and (c, a + b) is
(a) a + b + c
(b) abc
(c) (a + b + c)²
(d) 0
Solution:
(d) Vertices of a triangle are (a, b + c), (b, c + a) and (c, a + b)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 19

Question 15.
If (x, 2), (-3, -4) and (7, -5) are coliinear, then x =
(a) 60
(b) 63
(c) -63
(d) -60
Solution:
(c) Area of triangle whose vertices are (x, 2), (-3, -4) and (7, -5)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 20

Question 16.
If points (t, 2t), (-2, 6) and (3, 1) are collinear, then t =
(a) \(\frac { 3 }{ 4 }\)
(b) \(\frac { 4 }{ 3 }\)
(c) \(\frac { 5 }{ 3 }\)
(d) \(\frac { 3 }{ 5 }\)
Solution:
(b) The area of triangle whose vertices are (t, 2t), (-2, 6) and (3, 1)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 22

Question 17.
If the area of the triangle formed by the points (x, 2x), (-2, 6) and (3, 1) is 5 square units, then x =
(a) \(\frac { 2 }{ 3 }\)
(b) \(\frac { 3 }{ 5 }\)
(c) 2
(d) 5
Solution:
(c) Area of triangle whose vertices are (x, 2x), (-2, 6) and (3, 1)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 23

Question 18.
If points (a, 0), (0, b) and (1, 1) are collinear, then \(\frac { 1 }{ a }\) + \(\frac { 1 }{ b }\) =
(a) 1
(b) 2
(c) 0
(d) -1
Solution:
(a) The area of triangle whose vertices are (a, 0), (0, b) and (1, 1)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 24

Question 19.
If the centroid of a triangle is (1, 4) and two of its vertices are (4, -3) and (-9, 7), then the area of the triangle is
(a) 183 sq. units
(b) \(\frac { 183 }{ 2 }\) sq. units
(c) 366 sq. units
(d) \(\frac { 183 }{ 4 }\) sq. units
Solution:
(b) Centroid of a triangle = (1, 4)
and two vertices of the triangle are (4, -3) and (-9, 7)
Let the third vertex be (x, y), then
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 26
= \(\frac { 183 }{ 2 }\) sq. units

Question 20.
The line segment joining points (-3, -4) and (1, -2) is divided by y-axis in the ratio
(a) 1 : 3
(b) 2 : 3
(c) 3 : 1
(d) 2 : 3
Solution:
(c) The point lies on y-axis
Its abscissa will be zero
Let the point divides the line segment joining the points (-3, -4) and (1, -2) in the ratio m : n
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 27

Question 21.
The ratio in which (4, 5) divides the join of (2, 3) and (7, 8) is
(a) -2 : 3
(b) -3 : 2
(c) 3 : 2
(d) 2 : 3
Solution:
(d) Let the point (4, 5) divides the line segment joining the points (2, 3) and (7, 8) in the ratio m : n
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 28

Question 22.
The ratio in which the X-axis divides the segment joining (3, 6) and (12, -3) is
(a) 2 : 1
(b) 1 : 2
(c) -2 : 1
(d) 1 : -2
Solution:
(a) The point lies on x-axis
Its ordinate is zero
Let this point divides the line segment joining the points (3, 6) and (12, -3) in the ratio m : n
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 29

Question 23.
If the centroid of the triangle formed by the points (a, b), (b, c) and (c, a) is at the origin, then a³ + b³ + c³ =
(a) abc
(b) 0
(c) a + b + c
(d) 3 abc
Solution:
(d) Centroid of the triangle formed by the points (a, b), (b, c) and (c, a) is origin (0, 0)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 30

Question 24.
If points (1, 2), (-5, 6) and (a, -2) are collinear, then a =
(a) -3
(b) 7
(c) 2
(d) -2
Solution:
(b) The area of a triangle whose vertices are (1, 2), (-5, 6) and (a, -2)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 31

Question 25.
If the centroid of the triangle formed by (7, x), (y, -6) and (9, 10) is at (6, 3), then (x, y) =
(a) (4, 5)
(b) (5, 4)
(c) (-5, -2)
(d) (5, 2)
Solution:
(d) Centroid of (7, x), (y, -6) and (9, 10) is (6, 3)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 33

Question 26.
The distance of the point (4, 7) from the x-axis is
(a) 4
(b) 7
(c) 11
(d) √65
Solution:
(b) The distance of the point (4, 7) from x-axis = 7

Question 27.
The distance of the point (4, 7) from the y-axis is
(a) 4
(b) 7
(c) 11
(d) √65
Solution:
(a) The distance of the point (4, 7) from y-axis = 4

Question 28.
If P is a point on x-axis such that its distance from the origin is 3 units, then the coordinates of a point Q on OY such that OP = OQ, are
(a) (0, 3)
(b) (3, 0)
(c) (0, 0)
(d) (0, -3)
Solution:
(a) P is a point on x-axis and its distance from 0 is 3
Co-ordinates of P will be (3, 0)
Q is a point on OY such that OP = OQ
Co-ordinates of Q will be (0, 3)

Question 29.
If the point (x, 4) lies on a circle whose centre is at the origin and radius is 5, then x =
(a) ±5
(b) ±3
(c) 0
(d) ±4
Solution:
(b) Point A (x, 4) is on a circle with centre O (0, 0) and radius = 5
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 34

Question 30.
If the point P (x, y) is equidistant from A (5, 1) and B (-1, 5), then
(a) 5x = y
(b) x = 5y
(c) 3x = 2y
(d) 2x = 3y
Solution:
(c)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 35

Question 31.
If points A (5, p), B (1, 5), C (2, 1) and D (6, 2) form a square ABCD, then p =
(a) 7
(b) 3
(c) 6
(d) 8
Solution:
(c) Vertices of a square are A (5, p), B (1, 5), C (2, 1) and D (6, 2)
The diagonals bisect each other at O
O is the mid-point of AC and BD
O is mid-point of BD, then
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 36

Question 32.
The coordinates of the circumcentre of the triangle formed by the points O (0, 0), A (a, 0) and B (0, b) are
(a) (a, b)
(b) (\(\frac { a }{ 2 }\) , \(\frac { b }{ 2 }\))
(c) (\(\frac { b }{ 2 }\) , \(\frac { a }{ 2 }\))
(d) (b, a)
Solution:
(b) Let co-ordinates of C be (x, y) which is the centre of the circumcircle of ∆OAB
Radii of a circle are equal
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 37

Question 33.
The coordinates of a point on x-axis which lies on the perpendicular bisector of the line segment joining the points (7, 6) and (-3, 4) are
(a) (0, 2)
(b) (3, 0)
(b) (0, 3)
(d) (2, 0)
Solution:
(d) The given point P lies on x-axis
Let the co-ordinates of P be (x, 0)
The point P lies on the perpendicular bisector of of the line segment joining the points A (7, 6), B (-3, 4)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 39

Question 34.
If the centroid of the triangle formed by the points (3, -5), (-7, 4), (10, -k) is at the point (k, -1), then k =
(a) 3
(b) 1
(c) 2
(d) 4
Solution:
(c) O (k, -1) is the centroid of triangle whose vertices are
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 40

Question 35.
If (-2, 1) is the centroid of the triangle having its vertices at (x, 0), (5, -2), (-8, y), then x, y satisfy the relation
(a) 3x + 8y = 0
(b) 3x – 8y = 0
(c) 8x + 3y = 0
(d) 8x = 3y
Solution:
(-2, 1) is the centroid of triangle whose vertices are (x, 0), (5, -2), (-8, y)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 41

Question 36.
The coordinates of the fourth vertex of the rectangle formed by the points (0, 0), (2, 0), (0, 3) are
(a) (3, 0)
(b) (0, 2)
(c) (-2, 3)
(d) (3, 2)
Solution:
(c) Three vertices of a rectangle are A (0, 0), B (2, 0), C (0, 3)
Let fourth vertex be D (x, y)
The diagonals of a rectangle bisect eachother at O
O is the mid-point of AC, then
Coordinates of O will be (\(\frac { 0+0 }{ 2 }\) , \(\frac { 0+3 }{ 2 }\))
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 42

Question 37.
The length of a line segment joining A (2, -3) and B is 10 units. If the abscissa of B is 10 units, then its ordinates can be
(a) 3 or -9
(b) -3 or 9
(c) 6 or 27
(d) -6 or-27
Solution:
(a) Abscissa of B is 10 and co-ordinates of A are (2, -3)
Let ordinates of B be y, then
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 43

Question 38.
The ratio in which the line segment joining P(x₁, y₁) and Q (x₂, y₂) is divided by x-axis is
(a) y₁ : y₂
(b) -y₁ : y₂
(c) x₁ : x₂
(d) -x₁ : x₂
Solution:
(b) Let a point A on x-axis divides the line segment joining the points P (x₁, y₁), Q (x₂, y₂) in the ratio m₁ : m₂ and
let co-ordinates of A be (x, 0)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 44

Question 39.
The ratio in which the line segment joining points A (a₁, b₁) and B (a₂, b₂) is divided by y-axis is
(a) -a₁ : a₂
(b) a₁ : a₂
(c) b₁ : b₂
(d) -b₁ : b₂
Solution:
(a) Let the point P on y-axis, divides the line segment joining the point A (a₁, b₁) and B (a₂, b₂) is the ratio m₁ : m₂ and
let the co-ordinates of P be (0, y), then
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 45

Question 40.
If the line segment joining the points (3, -4) and (1, 2) is trisected at points P
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 46
Solution:
(b)

Question 41.
If the coordinates of one end of a diameter of a circle are (2, 3) and the coordinates of its centre are (-2, 5), then the coordinates of the other end of the diameter are [CBSE 2012]
(a) (-6, 7)
(b) (6, -7)
(c) (6, 7)
(d) (-6, -7)
Solution:
(a) Let AB be the diameter of a circle with centre O
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 49

Question 42.
The coordinates of the point P dividing the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1 are
(a) (2, 4)
(b) (3, 5)
(c) (4, 2)
(d) (5, 3) [CBSE 2012]
Solution:
(b) Point P divides the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1
Let coordinates of P be (x, y), then
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 50

Question 43.
In the figure, the area of ∆ABC (in square units) is [CBSE 2013]
(a) 15
(b) 10
(c) 7.5
(d) 2.5
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 51
Solution:
(c)

Question 44.
The point on the x-axis which is equidistant from points (-1, 0) and (5, 0) is
(a) (0, 2)
(b) (2, 0)
(c) (3, 0)
(d) (0, 3) [CBSE 2013]
Solution:
(c) Let the point P (x, 0) is equidistant from the points A (-1, 0), B (5, 0)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 53

Question 45.
If A (4, 9), B (2, 3) and C (6, 5) are the vertices of ∆ABC, then the length of median through C is
(a) 5 untis
(b) √10 units
(c) 25 units
(d) 10 units [CBSE 2014]
Solution:
(b) A (4, 9), B (2, 3) and C (6, 5) are the vertices of ∆ABC
Let median CD has been drawn C (6, 5)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 54

Question 46.
If P (2, 4), Q (0, 3), R (3, 6) and S (5, y) are the vertices of a paralelogram PQRS, then the value of y is
(a) 7
(b) 5
(c) -7
(d) -8 [CBSE 2014]
Solution:
(a) P (2, 4), Q (0, 3), R (3, 6) and S (5, y) are the vertices of a ||gm PQRS
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 55

Question 47.
If A (x, 2), B (-3, -4) and C (7, -5) are collinear, then the value of x is
(a) -63
(b) 63
(c) 60
(d) -60 [CBSE 2014]
Solution:
(a) A (x, 2), B (-3, -4) and C (7, -5) are collinear, then area ∆ABC = 0
Now area of ∆ABC
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 57

Question 48.
The perimeter of a triangle with vertices (0, 4) and (0, 0) and (3, 0) is
(a) 7 + √5
(b) 5
(c) 10
(d) 12 [CBSE 2014]
Solution:
(d) A (0, 4) and B (0, 0) and C (3, 0) are the vertices of ∆ABC
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 58

Question 49.
If the point P (2, 1) lies on the line segment joining points A (4, 2) and B (8, 4), then
(a) AP = \(\frac { 1 }{ 3 }\) AB
(b) AP = BP
(c) BP = \(\frac { 1 }{ 3 }\) AB
(d) AP = \(\frac { 1 }{ 2 }\) AB
Solution:
(d) Given that, the point P (2, 1) lies on the line segment joining the points (4, 2) and B (8, 4), which shows in the figure below:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 59

Question 50.
A line intersects the y-axis and x-axis at P and Q, respectively. If (2, -5) is the mid-point of PQ, then the coordinates of P and Q are, respectively
(a) (0, -5) and (2, 0)
(b) (0, 10) and (-4, 0)
(c) (0, 4) and (-10, 0)
(d) (0, -10) and (4, 0)
Solution:
(d) Let the coordinates of P and Q (0, y) and (x, 0), respectively.
So, the mid-point of P (0, y) and Q (x, 0) is
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS 61
2 = \(\frac { x + 0 }{ 2 }\) and -5 = \(\frac { y + 0 }{ 2 }\)
=> 4 = x and -10 = y
=> x = 4 and y = -10
So, the coordinates of P and Q are (0, -10) and (4, 0).

Hope given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS

January 9, 2023

RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS

Other Exercises

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
Write the distance between the points A (10 cosθ, 0) and B (0, 10 sinθ).
Solution:
Distance between the points A (10 cosθ, 0) and B (0, 10 sinθ)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 1

Question 2.
Write the perimeter of the triangle formed by the points O (0, 0), A (a, 0), and B (0, b).
Solution:
The vertices of a ∆OAB, O (0, 0), A (a, 0), and B (0, b)
Now length of OA
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 2

Question 3.
Write the ratio in which the line segment joining points (2, 3) and (3, -2) is divided by x-axis.
Solution:
The required point is on x-axis
Its ordinate will be 0
Let the point be (x, 0) and let this point divides the join of the points (2, 3) and (3, -2) in the ratio m : n
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 3

Question 4.
What is the distance between the points (5 sin 60°, 0) and (0, 5 sin 30°) ?
Solution:
Distance between the given points
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 4

Question 5.
If A (-1, 3), B (1, -1) and C (5, 1) are the vertices of a triangle ABC, what is the length of the median through vertex A ?
Solution:
The vertices of ∆ABC are A (-1, 3), B (1, -1) and C (5, 1)
Let AD be the median
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 5

Question 6.
If the distance between points (x, 0) and (0, 3) is 5, what are the value of x ?
Solution:
Distance between (x, 0) and (0, 3) = 5
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 7

Question 7.
What is the area of the triangle formed by the points O (0, 0), A (6, 0) and B (0, 4) ?
Solution:
The vertices of the triangle OAB are O (0, 0), A (6, 0) and B (0, 4)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 8

Question 8.
Write the coordinates of the point dividing line segment joining points (2, 3) and (3, 4) internally in the ratio 1 : 5.
Solution:
Let the coordinates of the required point be (x, y), then
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 10

Question 9.
If the centroid of the triangle formed by points P (a, b), Q (b, c) and R (c, a) is at the origin, what is the value of a + b + c ?
Solution:
Vertices of ∆PQR are P (a, b), Q (b, c) and R (c, a) and its centroid = O (0, 0)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 11

Question 10.
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 12
Solution:

Question 11.
Write the coordinates of a point on x- axis which is equidistant from the points (-3, 4) and (2, 5).
Solution:
The point is on x-axis
Its ordinates of the point P is (x, 0)
P is equidistant from A (-3, 4) and B (2, 5)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 15

Question 12.
If the mid-point of the segment joining A (x, y + 1) and B (x + 1, y + 2) is C (\(\frac { 3 }{ 2 }\) , \(\frac { 5 }{ 2 }\)) find x, y.
Solution:
C (\(\frac { 3 }{ 2 }\) , \(\frac { 5 }{ 2 }\)) is mid point of the line segment
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 16

Question 13.
Two vertices of a triangle have co-ordinates (-8, 7) and (9, 4). If the centroid of the triangle is at the origin, what are the co-ordinates of the third vertex ?
Solution:
Two vertices of a triangle are (-8, 7) and (9, 4)
Let the third vertex be (x, y)
Centroid of the triangle is (0, 0)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 17

Question 14.
Write the coordinates the reflections of points (3, 5) in x and y-axes.
Solution:
Reflection of P (3, 5) in x-axis is will be (3, -5)
and reflection of P in y-axis will be (-3, 5)

Question 15.
If points Q and R reflections of point P (-3, 4) in X and Y axes respectively, what is QR ?
Solution:
Reflection of point P (-3, 4) in X-axis will be Q with coordinates Q (-3, -4) and reflection in Y-axis will be R (3, 4)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 18

Question 16.
Write the formula for the area of the triangle having its vertices at (x₁, y₁), (x₂, y₂) and (x₃, y₃).
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 19

Question 17.
Write the condition of collinearity of points (x₁, y₁), (x₂, y₂) and (x₃, y₃).
Solution:
Three points (x₁, y₁), (x₂, y₂) and (x₃, y₃). are said to be collinear if the area of the triangle formed by these point = 0 i.e.,
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 20

Question 18.
Find the values of x for which the distance between the point P (2, -3) and Q (x, 5) is 10.
Solution:
Distance between P (2, -3) and Q (x, 5) = 10
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 21

Question 19.
Write the ratio in which the line segment joining the points A (3, -6) and B (5, 3) is divided by X-axis.
Solution:
The point lies on x-axis
Its ordinate will be = 0
Let the point P (x, 0) divides the line segment joining the points A (3, -6) and B (5, 3) in the ratio m : n.
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 23

Question 20.
Find the distance between the points (\(\frac { -8 }{ 5 }\) , 2) and (\(\frac { 2 }{ 5 }\) , 2). (C.B.S.E. 2009)
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 24

Question 21.
Find the value of a so that the point (3, a) lies on the line represented by 2x – 3y + 5 = 0. (C.B.S.E. 2009)
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 26

Question 22.
What is the distance between the points A (c, 0) and B (0, – c) ? [CBSE 2010]
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 27

Question 23.
If P (2, 6) is the mid-point of the line segment joining A (6, 5) and B (4, y), find y. [CBSE 2010]
Solution:
P (2, 6) is the mid-point of the line segment A (6, 5) and b (4, y)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 28

Question 24.
If the distance between the points (3, 0) and (0, y) is 5 units and y is positive, then what is the value of y ? [CBSE 2010]
Solution:
Distance between (3, 0) and (0, y) is 5 units
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 29

Question 25.
If P (x, 6) is the mid-point of the line segment joining A (6, 5) and B (4, y), find y. [CBSE 2010]
Solution:
P (x, 6) is the mid-point of the line segment joining the points A (6, 5), B (4, y)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 30

Question 26.
If P (2, p) is the mid-point of the line segment joining the points A (6, -5) and B (-2, 11), find the value of p. [CBSE 2010]
Solution:
P (2, p) is the mid-point of the line segment joining the points A (6, -5) and B (-2, 11)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 31

Question 27.
If A (1, 2), B (4, 3) and C (6, 6) are the three vertices of a parallelogram ABCD, find the coordinates of fourth vertex D. [CBSE 2010]
Solution:
vertices of a parallelogram Let co-ordinates of D be (x, y)
Diagonals AC and BD bisect each other at O
Co-ordinates of O will be
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 32

Question 28.
What is the distance between the points A (sinθ – cosθ, 0) and B (0, sinθ + cosθ)? [CBSE 2015]
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 34

Question 29.
What are the coordinates of the point where the perpendicular bisector of the line segment joining the points A (1, 5) and B (4, 6) cuts the y-axis?
Solution:
Firstly, we plot the points of the line segment on the paper and join them.
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 35

Now, we draw a straight line on paper passes through the mid-point P.
We see that the perpendicular bisector cuts the y-axis at the point (0, 13).
Hence, the required point is (0, 13).

Question 30.
Find the area of the triangle with vertices (a, b + c), (b, c + a) and (c, a + b).
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 37

Question 31.
If the points A (1, 2), O (0, 0) and C (a, b) are collinear, then find a : b.
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 38
=> 2a = b
Hence, the required relation is 2a = b

Question 32.
Find the coordinates of the point which is equidistant from the three vertices A (2x, 0), O (0, 0) and B (0, 2y) of ∆AOB.
Solution:
Let the coordinate of the point which is equidistant from the three vertices O (0, 0), A (0, 2y) and B (2x, 0) is P (h, k).
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 39

Question 33.
If the distance between the points (4, k), and (1, 0) is 5, then what can be the possible value of k? [CBSE 2017]
Solution:
Let the points x (4, k) and y (1, 0)
It is given that the distance xy is 5 units.
By using the distance formula,
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS 42

Hope given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS

January 9, 2023

RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS

Other Exercises

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
Solution:
Diameter of a circle and side of an equilateral triangle are same
Let the diameter of the circle = a
Then radius (r) = \(\frac { a }{ 2 }\)
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 1

Question 2.
If the circumference of two circles are in the ratio 2 : 3, what is the ratio of their areas ?
Solution:
Let R and r be the radii of two circles, then the ratio between their circumferences = 2πR : 2πr
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 2

Question 3.
Write the area of the sector of a circle whose radius is r and length of the arc is l.
Solution:
Let arc l subtends angle 9 at the centre of the circle
Now radius of a circle = r
and length of arc =l
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 4

Question 4.
What is the length (in terms of π) of the arc that subtends an angle of 36° at the centre of a circle of radius 5 cm?
Solution:
Radius of the circle = 5 cm
Angle at the center = 36°
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 5

Question 5.
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3π cm ?
Solution:
Let the arc subtends angle θ at the centre of a circle
Radius of circle (r) = 6 cm
Length of arc = 3π cm
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 6

Question 6.
What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm ?
Solution:
Radius of the circle (r) = 5 cm
Length of arc (l) = 3.5 cm
Let angle 9 be subtended by the arc at the centre
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 7

Question 7.
In a circle of radius 10 cm, an arc subtends an angle of 108° at the centre. What is the area of the sector in terms of π ?
Solution:
Radius of the circle = 10 cm
Angle at the centre = 108°
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 8

Question 8.
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square ?
Solution:
A square ABCD is inscribed in a circle with centre O
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 9
Let the radius of the circle = r
Then its area = πr²
Now diagonal of the square = diameter of the circle = 2r

Question 9.
Write the formula for the area of a sector of angle θ (in degrees) of a circle of radius r.
Solution:
Area of a sector of a circle whose radius = r
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 11

Question 10.
Write the formula for the area of a segment in a circle of radius r given that the sector angle is 0 (in degrees).
Solution:
Radius of the circle = r
and angle subtended by the sector at the centre = θ
Area of the segment
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 12

Question 11.
If the adjoining figure is a sector of a circle of radius 10.5 cm, what is the perimeter of the sector ? (Take π= 22/7)
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 13
Solution:
Radius of the circle = 10.5 cm
Angle at the centre of the circle = 60°

Question 12.
If the diameter of a semi-circular protractor is 14 cm then find its perimeter. (C.B.S.E. 2009)
Solution:
Diameter of semicircular protractor = 14 cm
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 15
∴ Radius (r) = \(\frac { 14 }{ 2 }\) = 7 cm
Now perimeter of protractor

Question 13.
An arc subtends an angle of 90° at the centre of the circle of radius 14 cm. Write the area of minor sector thus formed in terms of π.
Solution:
AB is an arc of the circle with centre O and radius 14 cm and subtends an angle of 90° at the centre O.
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 17

Question 14.
Find the area of the largest triangle that can be inscribed in a semi-circle of radius r units. [CBSE 2015]
Solution:
Radius of semicircle = r
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 18
In semicircle ΔABC is the largest triangle whose base is AC = 2 x r = 2r units
and height OB = r units

Question 15.
Find the area of a sector of circle of radius 21 cm and central angle 120°.
Solution:
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 20

Question 16.
What is the area of a square inscribed in a circle of diameter p cm?
Solution:
Diameter AC of the circle is p.
Also AC is diagonal of square ABCD.
Each angle of square is of 90°
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 21

Question 17.
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
Solution:
False.
It is true only in the case of minor segment. But in case of major segment, area is always greater than the area of sector.

Question 18.
If the numerical value of the area of a circle is equal to the numerical value of its circumference, find its radius.
Solution:
∵ Numerical value of area of circle = Numerical value of circumference
∴ πr² = 2πr
or r = 2 units

Question 19.
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
Solution:
Radius of circular of wheel (r) = r m
Circumference of a circular wheel = 2πr
Distance to be covered = Sm
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 22

Question 20.
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square.
Solution:
Let each side of of square = x
∴ Diameter of inner circle = x
Radius r = \(\frac { x }{ 2 }\)
Diameter of outer circle = AD
RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS 23

Hope given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5

January 9, 2023

RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5

Other Exercises

Question 1.
Find the area of a triangle whose vertices are :
(i) (6, 3), (-3, 5) and (4, -2)
(ii) (\({ at }_{ 1 }^{ 2 }\), 2at₁), (\({ at }_{ 2 }^{ 2 }\), 2at₂) and (\({ at }_{ 3 }^{ 2 }\), 2at₃)
(iii) (a, c + a), (a, c) and (-a, c – a)
Solution:
(i) Co-ordinates of ∆ABC are A (6, 3), B (-3, 5) and C (4, -2)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 1

Question 2.
Find the area of the quadrilaterals, the coordinates of whose vertices are
(i) (-3, 2), (5, 4), (7, -6) and (-5, -4)
(ii) (1, 2), (6, 2), (5, 3) and (3, 4)
(iii) (-4, -2), (-3, -5), (3, -2), (2, 3) (C.B.S.E. 2009)
Solution:
(i) Let vertices of quadrilateral ABCD be A (-3, 2), B (5, 4), C (7, -6) and D (-5, -4)
Join AC
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 4

Question 3.
The four vertices of a quadrilaterals are (1, 2), (-5, 6), (7, -4) and (k, -2) taken in order. If the area of the quadrilateral is zero, find the value of k ?
Solution:
Let the vertices of quadrilateral ABCD be
A (1, 2), B (-5, 6), C (7, -4) and D (k, -2)
Join AC
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 10

Question 4.
The vertices of ∆ABC are (-2, 1), (5, 4) and (2, -3) respectively. Find the area of the triangle and the length of the altitude through A.
Solution:
Vertices of ∆ABC are A (-2, 1), B (5, 4) and C (2, -3) and AD ⊥ BC, let AD = h
Now area of ∆ABC
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 13

Question 5.
Show that the following sets of points are collinear
(a) (2, 5), (4, 6) and (8, 8)
(b) (1, -1), (2, 1) and (4, 5)
Solution:
We know that points are collinear if the area of the triangle formed by them is zero
(a) Vertices of ∆ABC are (2, 5), (4, 6) and (8, 8)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 15

Question 6.
Find the area of a quadrilateral ABCD, the coordinates of whose varities are A (-3, 2), B (5, 4), C (7, -6) and D (-5, -4). [CBSE 2016]
Solution:
Area of quadrilateral ABCD
= area of ∆ABC + area of ∆ACD
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 17

Question 7.
In ∆ABC, the coordinates of vertex A are (0, -1) and D (1, 0) and E (0, 1) respectively the mid-points of the sides AB and AC. If F is the mid-point of side C, find the area of ∆DEF. [CBSE 2016]
Solution:
Let B (p, q), C (r, s) and F (x, y)
Mid-point of AB = Coordinates of D
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 18

Question 8.
Find the area of the triangle PQR with Q (3, 2) and the mid-points of the sides through Q being (2, -1) and (1, 2). [CBSE 2015]
Solution:
In ∆PQR, L and N are mid points of QR and QP respectively coordinates of Q are (3, 2) of L are (2, -1) and of N are (1, 2)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 21

Question 9.
If P (-5, -3), Q (-4, -6), R (2, -3) and S (1, 2) are the vertices of a quadrilateral PQRS, find its area. [CBSE 2015]
Solution:
P (-5, -3), Q (-4, -6), R (2, -3) and S (1,2) are the vertices of a quadrilateral PQRS
Join PR which forms two triangles PQR and PSR
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 23

Question 10.
If A (-3, 5), B (-2, -7), C (1, -8) and D (6, 3) are the vertices of a quadrilateral ABCD, find its area. [CBSE 2014]
Solution:
A (-3, 5), B (-2, -7), C (1,-8) and D (6, 3) are the vertices of a quadrilateral ABCD
Join AC
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 25

Question 11.
For what value of ‘a’ the points (a, 1), (1, -1) and (11, 4) are collinear?
Solution:
Let the vertices of ∆ABC are A (a, 1), B (1, -1) and C (11, 4)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 27

Question 12.
Prove that the points (a, b), (a₁, b₁) and (a – a₁, b – b₁) are collinear if ab₁ = a₁b.
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 28

Question 13.
If the vertices of a triangle are (1, -3), (4, p) and (-9, 7) and its area is 15 sq. units, find the value(s) of p. [CBSE 2012]
Solution:
The vertices of a triangle are (1, -3), (4, p) and (-9, 7) and area of triangle = 15 sq. units
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 29

Question 14.
If (x, y) be on the line joining the two points (1, -3) and (-4, 2), prove that x + y + 2 = 0.
Solution:
Point (x, y) be on the line joining the two points (1, -3) and (-4, 2)
Points (x, y), (1, -3) and (-4, 2) are collinear
Let the points (x, y) (1, -3) and (-4, 2) are the vertices of a triangle, then
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 31

Question 15.
Find the value of k if points (k, 3), (6, -2) and (-3, 4) are collinear. [CBSE 2008]
Solution:
Let the points (k, 3), (6, -2) and (-3, 4) be the vertices of a triangle, then
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 32

Question 16.
Find the value of k, if the points A (7, -2), B (5, 1) and C (3, 2k) are collinear. [CBSE 2010]
Solution:
Points A (7, -2), B (5, 1) and C (3, 2k) are collinear
area of ∆ABC = 0
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 34

Question 17.
If the point P (m, 3) lies on the line segment joining the points A (\(\frac { -2 }{ 5 }\) , 6) and B (2, 8), find the value of m.
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 35

Question 18.
If R (x, y) is a point on the line segment joining the points P (a, b) and Q (b, a), then prove that x + y = a + b. [CBSE 2010]
Solution:
Point R (x, y) lies on the line segment joining the points P (a, b) and Q (b, a)
Area of ∆PRQ = 0
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 36

Question 19.
Find the value of k, if the points A (8, 1), B (3, -4) and C (2, k) are collinear. [CBSE 2010]
Solution:
The points A (8, 1), B (3, -4) and C (2, k) are collinear
Area of ∆ABC = 0
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 38

Question 20.
Find the value of a for which the area of the triangle formed by the points A (a, 2a), B (-2, 6) and C (3, 1) is 10 square units.
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 39

Question 21.
If a ≠ b ≠ 0, prove that the points (a, a²), (b, b²), (0, 0) are never collinear. [CBSE 2017]
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 40

Question 22.
The area of a triangle is 5 sq. units. Two of its vertices are at (2, 1) and (3, -2). If the third vertex is (\(\frac { 7 }{ 2 }\) , y), find y. [CBSE 2017]
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 42

Question 23.
Prove that the points (a, 0), (0, b) and (1, 1) are collinear if, \(\frac { 1 }{ a }\) + \(\frac { 1 }{ b }\) = 1.
Solution:
Let the points are A (a, 0), B (0, b) and C (1, 1) which form a triangle
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 43

Question 24.
The point A divides the join of P (-5, 1) and Q (3, 5) in the ratio k : 1. Find the two values of k for which the area of ∆ABC where B is (1, 5) and C (7, -2) is equal to 2 units.
Solution:
Let the coordinates of A be (x, y) which divides the join of P (-5, 1) and Q (3, 5) in the ratio. Then
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 44

Question 25.
The area of a triangle is 5. Two of its vertices are (2, 1) and (3, -2). The third vertex lies on y = x + 3. Find the third vertex.
Solution:
Let the coordinates of third vertex of the triangle be (x, y) and other two vertices are (2, 1) and (3, 2)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 47

Question 26.
If a ≠ b ≠ c, prove that the points (a, a²), (b, b²), (c, c²) can never be collinear.
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 49

Question 27.
Four points A (6, 3), B (-3, 5), C (4, -2) and D (x, 3x) are given in such a way that \(\frac { \triangle DBC }{ \triangle ABC } =\frac { 1 }{ 2 }\) , find x?
Solution:
Let A (6, 3), B (-3, 5), C (4, -2) and D (x, 3x) are the vertices of quadrilateral ABCD
AC and BD are joined
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 51

Question 28.
If three points (x₁, y₁), (x₂, y₂), (x₃, y₃) lie on the same line, prove that
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 54
Solution:
Let the points (x₁, y₁), (x₂, y₂), (x₃, y₃) are the vertices of a triangle

Question 29.
Find the area of a parallelogram ABCD if three of its vertices are A (2, 4), B (2 + √3, 5) and C (2, 6). [CBSE 2013]
Solution:
Three vertices of a ||gm ABCD are A (2, 4), B (2 + √3 , 5) and C (2, 6).
Draw one diagonal AC of ||gm ABCD
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 56

Question 30.
Find the value (s) of k for which the points (3k – 1, k – 2), (k, k – 7) and (k – 1, -k – 2) are collinear. [CBSE 2014]
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 58

Question 31.
If the points A (-1, -4), B (b, c) and C (5, -1) are collinear and 2b + c = 4, find the values of b and c. [CBSE 2014]
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 59

Question 32.
If the points A (-2, 1), B (a, b) and C (4, -1) are collinear and a – b = 1, find the values of a and 6. [CBSE 2014]
Solution:
Points A (-2, 1), B (a, b) and C (4, -1) are
collinear if area ∆ABC = 0
Now area of ∆ABC
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 61

Question 33.
If the points A (1, -2), B (2, 3), C (a, 2) and D (-4, -3) form a parallelogram, find the value of a and height of the parallelogram taking AB as base. [NCERT Exemplar]
Solution:
In parallelogram, we know that, diagonals bisects each other
i.e., mid-point of AC = mid-point of BD
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 63

Question 34.
A (6, 1), B (8, 2) and C (9, 4) are three vertices of a parallelogram ABCD. If E is the mid-point of DC, find the area of ∆ADE. [NCERT Exemplar]
Solution:
Given that, A (6,1), B (8,2) and C (9,4) are three vertices of a parallelogram ABCD.
Let the fourth vertex of parallelogram be (x, y).
We know that, the diagonal of a parallelogram bisect each other.
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 68

Question 35.
If D (\(\frac { -1 }{ 2 }\), \(\frac { 5 }{ 2 }\)) E (7, 3) and F (\(\frac { 7 }{ 2 }\), \(\frac { 7 }{ 2 }\)) are the mid-points of sides of ∆ABC, find the area of ∆ABC. [NCERT Exemplar]
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 70

Hope given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4

January 9, 2023

RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4

Other Exercises

Question 1.
Find the centroid of the triangle whose vertices are :
(i) (1, 4), (-1, -1), (3, -2)
(ii) (-2, 3), (2, -1), (4, 0)
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4 1

Question 2.
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the Co-ordinates of the third vertex.
Solution:
Centroid of a triangle is O(0, 0) ….(i)
Co-ordinates of two vertices of a ∆ABC are A (1, 2) and B (3, 5)
Let the third vertex be (x, y)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4 2

Question 3.
Find the third vertex of a triangle, if two of its vertices are at (-3, 1) and (0, -2) and the centroid is at the origin.
Solution:
Let two vertices of a ∆ABC be A (-3, 1) and B (0, -2) and third vertex C be (x, y)
Centroid of the ∆ABC is O (0, 0)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4 3

Question 4.
A (3, 2) and B (-2, 1) are two vertices of a triangle ABC whose centroid G has the coordinates (\(\frac { 5 }{ 3 }\) , \(\frac { -1 }{ 3 }\)) . Find the coordinates of the third vertex C of the triangle. [CBSE 2004]
Solution:
A (3, 2) and B (-2, 1) are the two vertices of ∆ABC whose centroid is G (\(\frac { 5 }{ 3 }\) , \(\frac { -1 }{ 3 }\))
Let third vertex C be (x, y)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4 4

Question 5.
If (-2, 3), (4, -3) and (4, 5) are the mid-points of the sides of a triangle, find the co-ordinates of its centroid.
Solution:
In ∆ABC, D, E and F are the mid-points of the sides BC, CA and AB respectively.
The co-ordinates of D are (-2, 3), of E are (4,-3) and of F are (4, 5)
Let the co-ordinates of A, B and C be (x₁, y₁), (x₂, y₂), (x₃, y₃) respectively
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4 5

Question 6.
Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
Solution:
In ∆ABC,
D and E are the mid points of the sides AB and AC respectively
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4 9

Question 7.
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another.
Solution:
Let A (x₁, y₁), B (x₂, y₂), C (x₃, y₃) and D (x₄, y₄) be the vertices of quadrilateral ABCD
E and F are the mid points of side BC and AD respectively and EF is joined G and H are the mid points of diagonal AC and BD.
GH are joined
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4 11

Question 8.
If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA² + PB² + PC² = GA² + GB² + GC² + 3GP².
Solution:
In AABC, G is the centroid of it Let P (h, x) is any point in the plane
Let co-ordinates of A are (x₁, y₁) of B are (x₂, y₂) and of C are (x₃, y₃)
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4 14

Hence proved.

Question 9.
If G be the centroid of a triangle ABC, prove that AB² + BC² + CA² = 3 (GA² + GB² + GC²)
Solution:
Let the co-ordinates of the vertices of ∆ABC be A (x₁, y₁), B (x₂, y₂), C (x₃, y₃) and let G be the centroid of the triangle
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4 16

Hence proved.

Question 10.
In the figure, a right triangle BOA is given. C is the mid-point of the hypotenuse AB. Show that it is equidistant from the vertices O, A and B.
Solution:
RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4 19
In right ∆OAB, co-ordinates of O are (0, 0) of A are (2a, 0) and of B are (0, 2b)
C is the mid-point of AB
Co-ordinates of C will be

We see that CO = CA = CB
Hence C is equidistant from the vertices O, A and B.
Hence proved.

Hope given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.