Prasanna

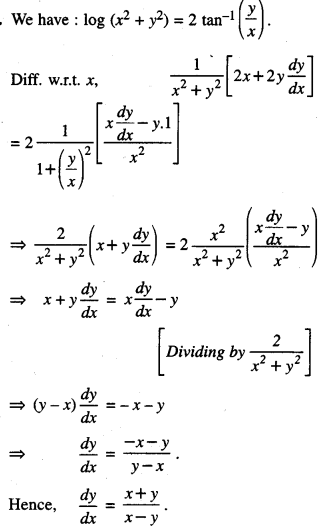
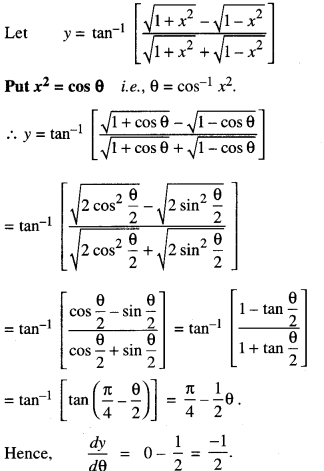
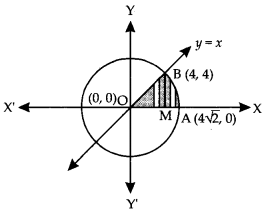
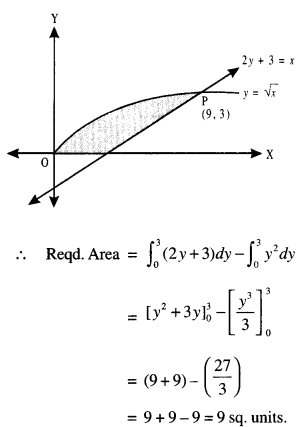
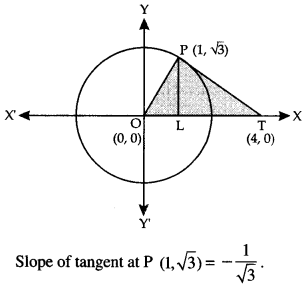
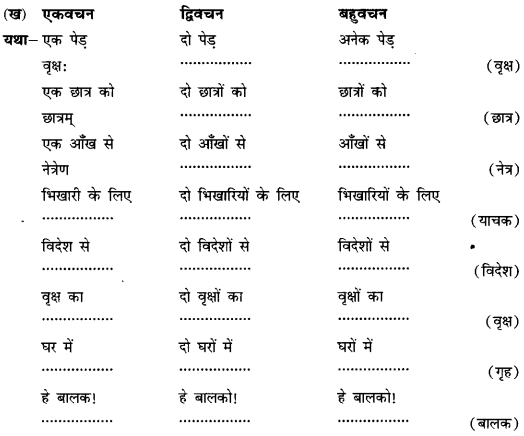
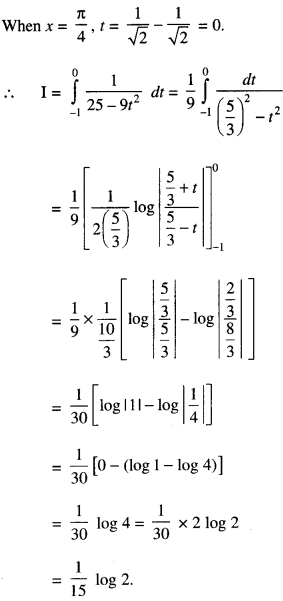
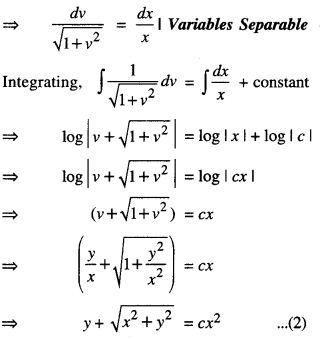
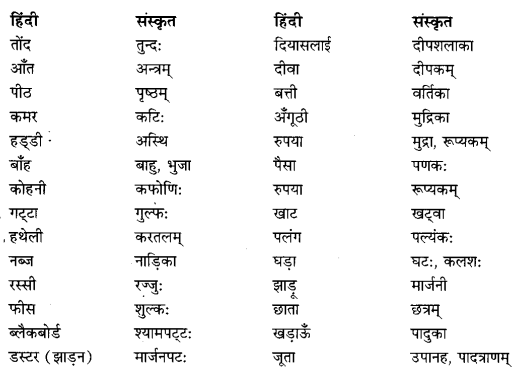
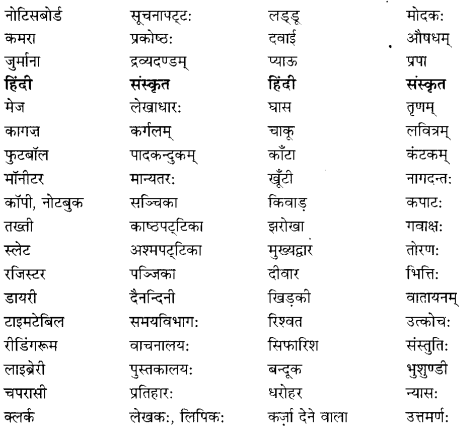
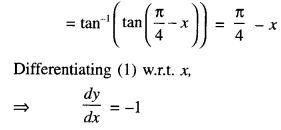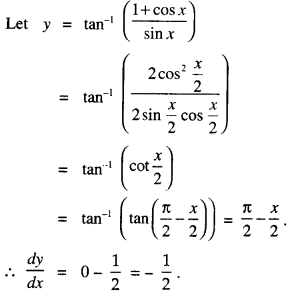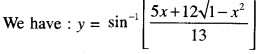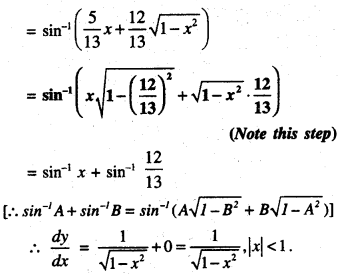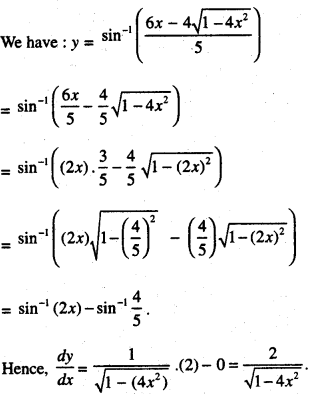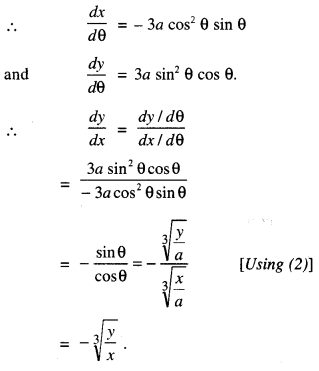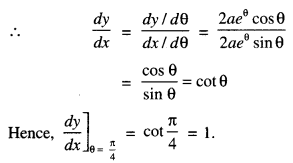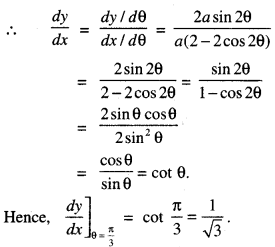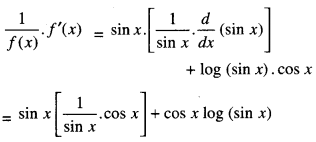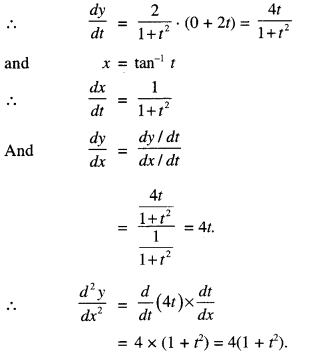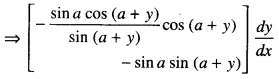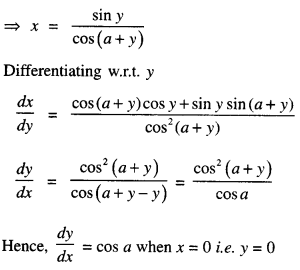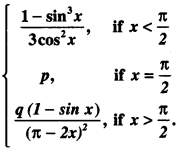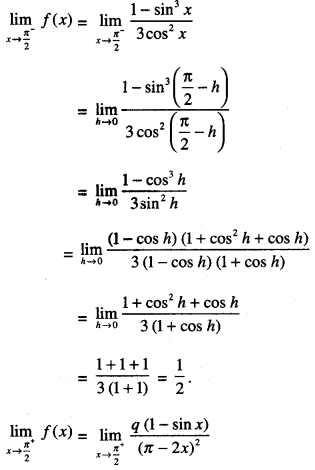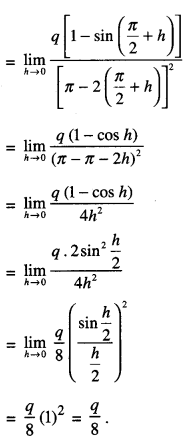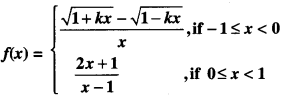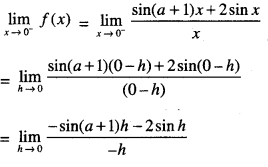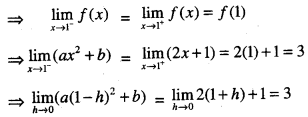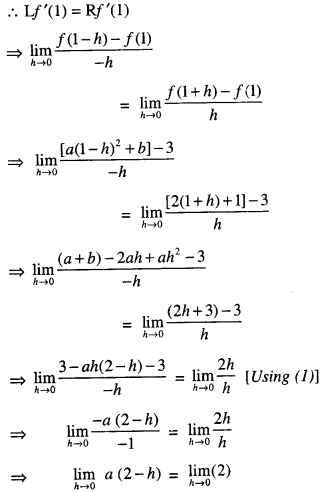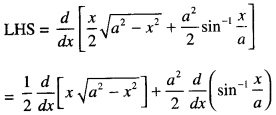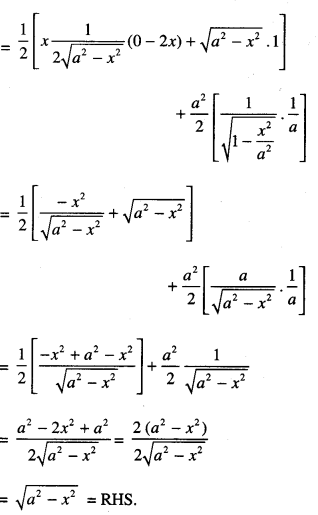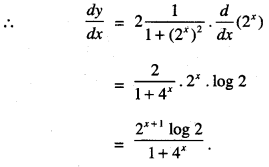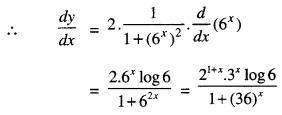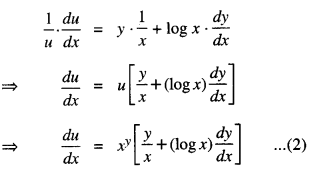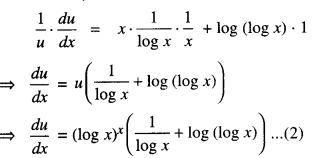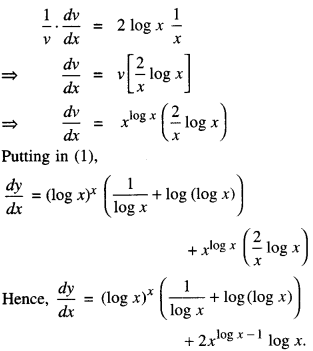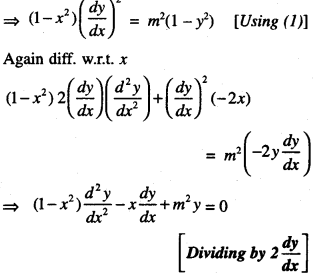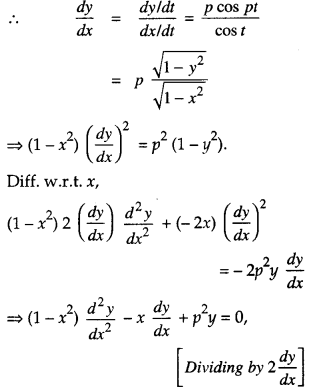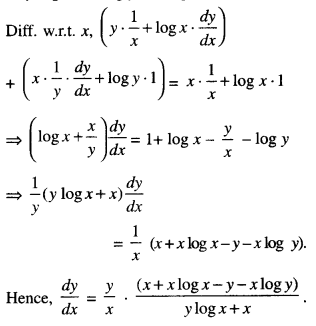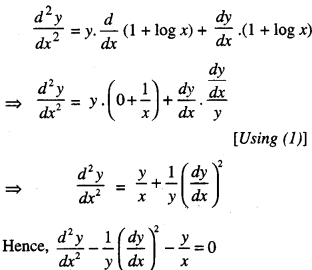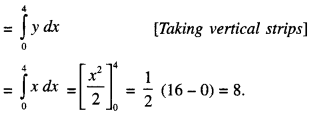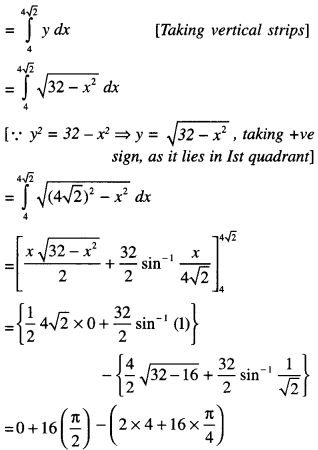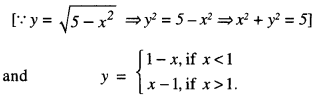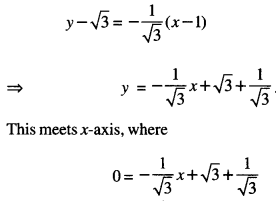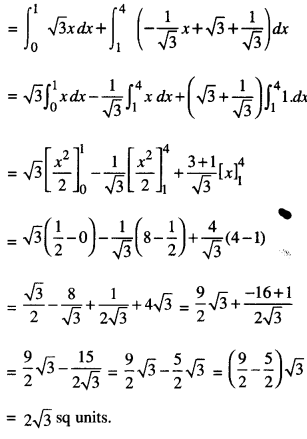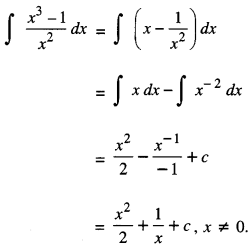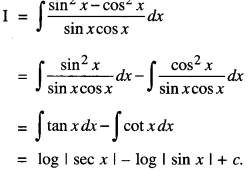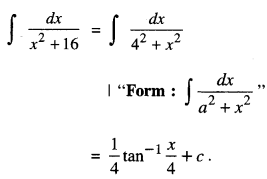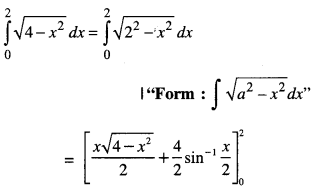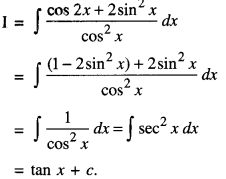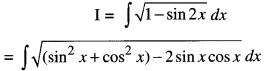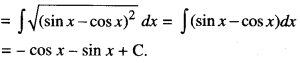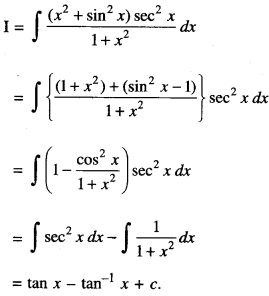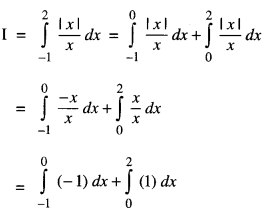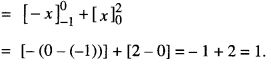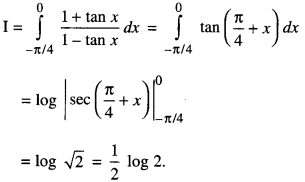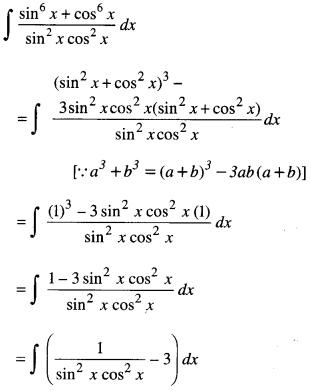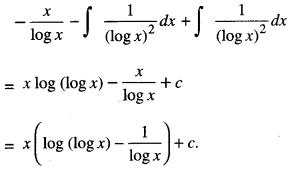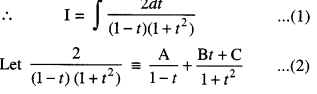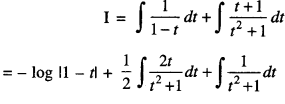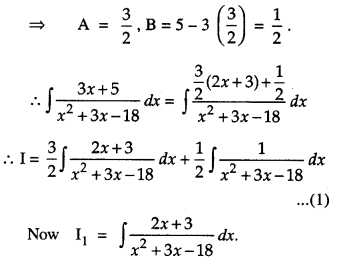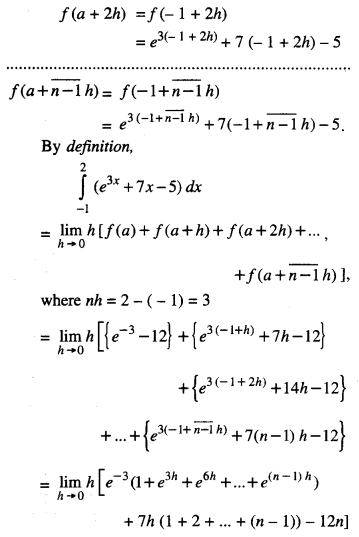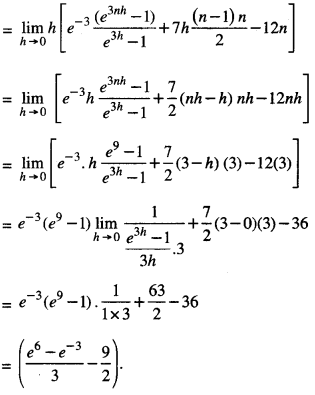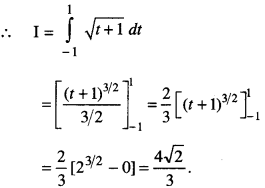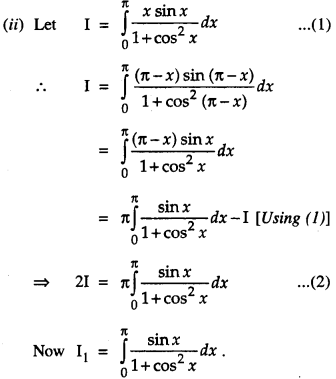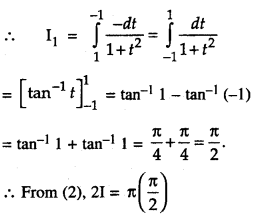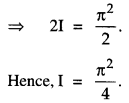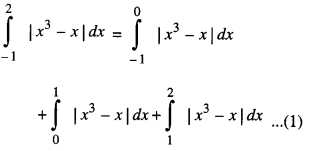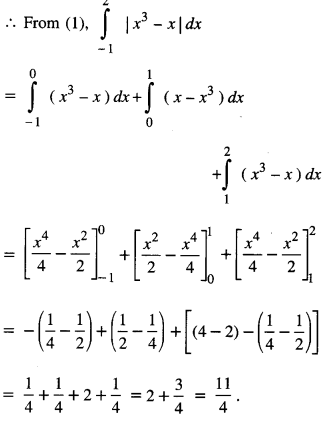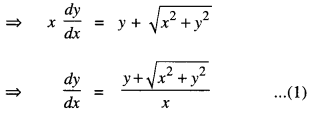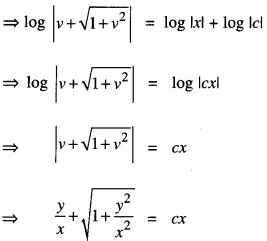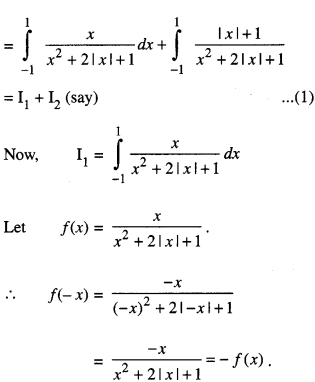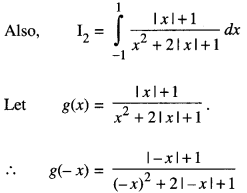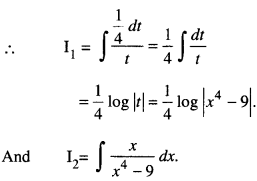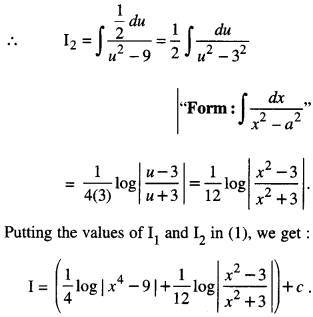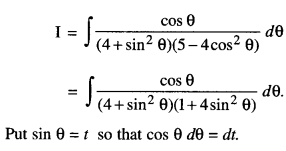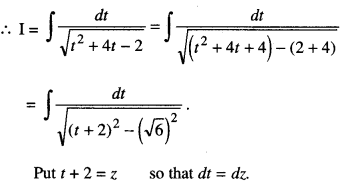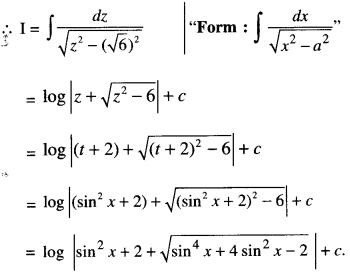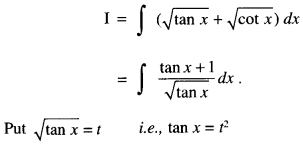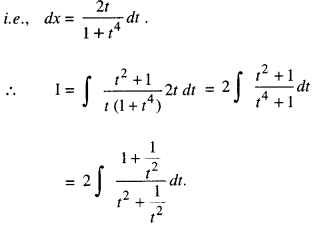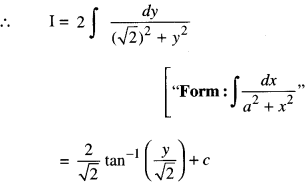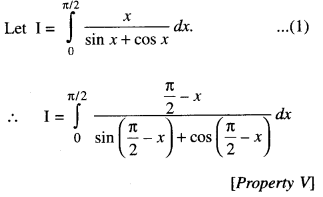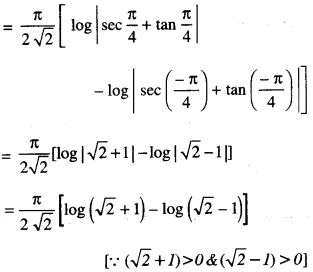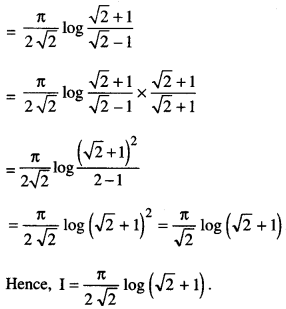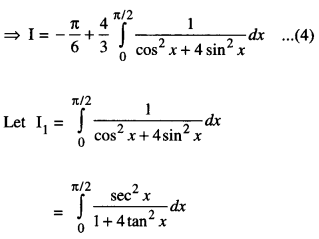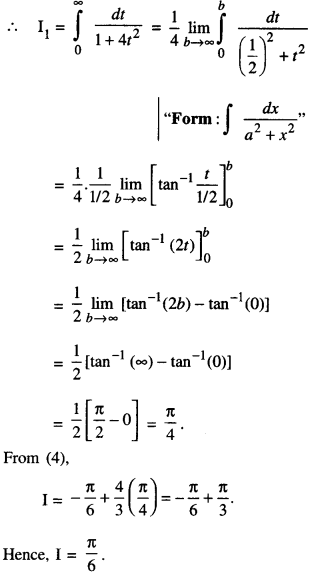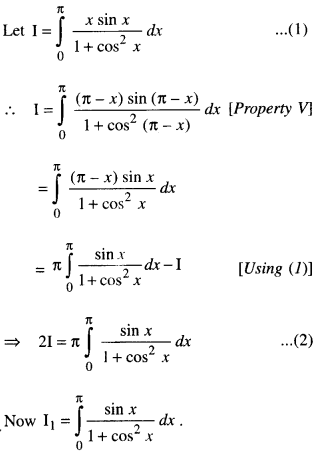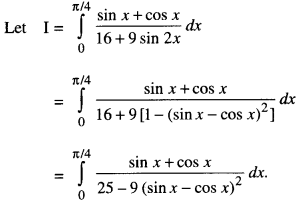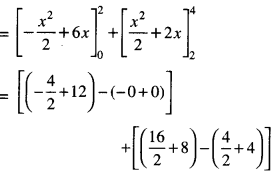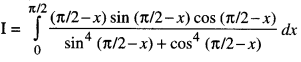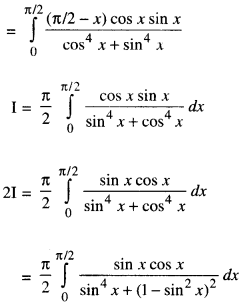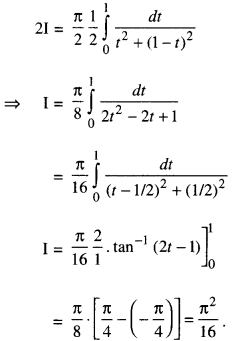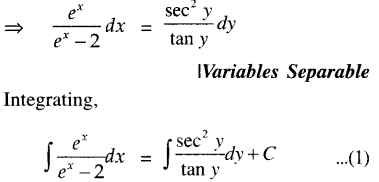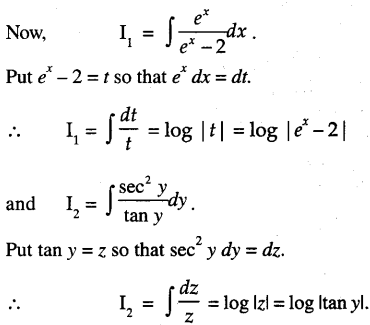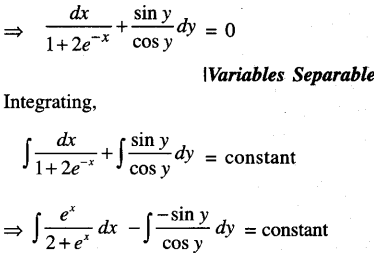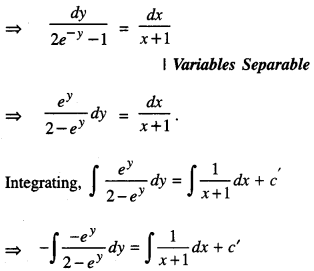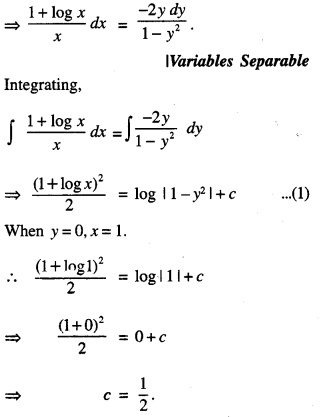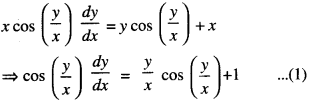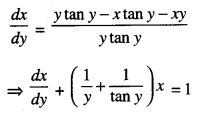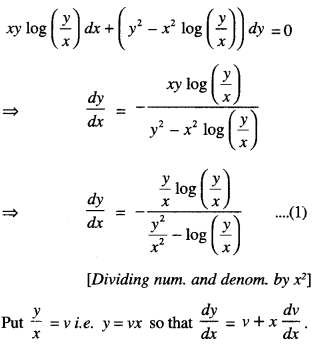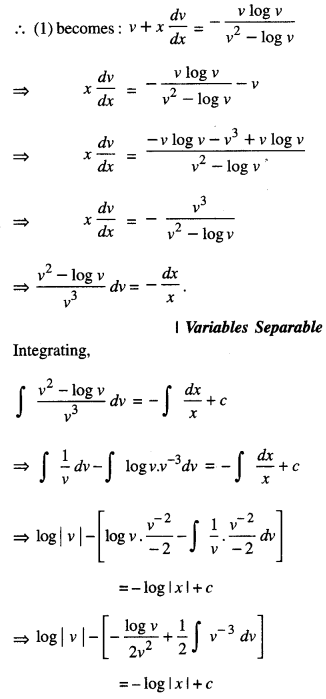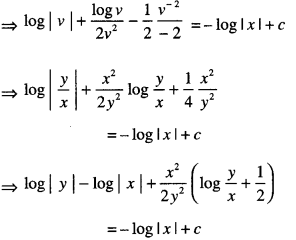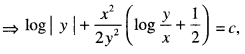We have given detailed NCERT Solutions for Class 10 Sanskrit Abhyasvan Bhav Sanskrit Class 10 Solutions Chapter 7 समासा: Questions and Answers come in handy for quickly completing your homework.

Abhyasvan Bhav Sanskrit Class 10 Solutions Chapter 7 समासा:

श्रुतिः – अहं दिनम् दिनम् विद्यायाः आलयम् समयम् अनतिक्रम्य गच्छामि।
अनुकृतिः – अहम् अपि प्रतिदिनं विद्यालयं यथासमयं गच्छामि।
श्रुतिः – किं त्वं जानासि यद् वसुदेवस्य सुतः कः आसीत्?
अनुकृतिः – जानामि। वसुदेवसुतः श्रीकृष्णः आसीत्।
श्रुतिः – मां पीतः वर्णः रोचते। सः अपि पीतम् अम्बरं धारयति स्म।
अनुकृतिः – सत्यं वदसि। सः पीताम्बरं धारयति स्म अतः सः ‘पीताम्बरः’ इति नाम्ना अपि प्रसिद्धः। मया पठितं यत् कृष्णः च बलरामः च यमुनायाः तटे क्रीडतः स्म।
श्रुतिः – मयापि पठितं यत् कृष्णबलरामौ यमुनातटे क्रीडतः स्म।

उपरिलिखितेषु संवादवाक्येषु श्रुतिः यानि वाक्यानि वदति तेषु रेखाङ्कित-पदानि पृथक् पृथक् सन्ति परन्तु अनुकृतिः यानि वाक्यानि वदति तेषु वाक्येषु तानि एव रेखाङ्कित-पदानि समस्तरूपेण (संक्षिप्तरूपेण) योजयित्वा प्रदर्शितानि सन्ति। यथा शब्दानां पृथक्-पृथक् लेखनं ‘विग्रहः’ कथ्यते तथैव समस्तरूपेण (संक्षिप्तरूपेण) वा लेखनं ‘समासः’ इति कथयते।
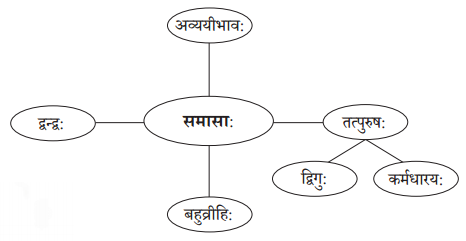
समासानां विभाजनं मुख्यतः चतुर्धा भवति-
1. अव्ययीभावः
2. तत्पुरुषः
3. द्वन्द्वः
4. बहुव्रीहिः
(कर्मधारयः द्विगुः चेति तत्पुरुष-समासस्य एव द्वौ भेदी स्तः।)

1. अव्ययीभावः

(क) प्रायः जनाः प्रत्यक्षम् एव सत्यं स्वीकुर्वन्ति।
(ख) तस्मिन् विद्यालये प्रतिमासं परीक्षाः भवन्ति।
(ग) छात्राः यथामति अध्ययनं कुर्वन्ति।
(घ) हरिद्वारे उपङ्गम् अनेके देवालयाः सन्ति।
उल्लिखितवाक्येषु रेखाङ्कितपदेषु चतस्रः विशेषताः सन्ति-
(i) सर्वेषु पदेषु प्रथम/पूर्व-पदम् अव्ययम् उपसर्गो वा अस्ति।
(ii) सर्वाणि पदानि नपुसंकलिङ्गे सन्ति।
(iii) सर्वेषां पदानां प्रयोगः अव्ययवत् भवति।
(iv) एतेषु समस्तपदेषु पूर्वपदम् प्रधानम् अस्ति यतो हि वाक्येषु क्रियापदानि प्रथम/पूर्व पदस्य अनुसारम् अर्थ बोधयन्ति।

इत्थं वयं जानीमः यत् अव्ययीभाव समासः पूर्वपदप्रधानः भवति। अयं समासः सर्वदा नपुसंकलिने तिष्ठति।
एवम् अव्ययीभावसमासं स्पष्टरूपेण विज्ञाय अस्त इतिराणि उदाहरणानि द्रष्टव्यानि-

क्रमः	समस्तपदम्	विग्रहः
1.	यथामति	मतिम् अनतिक्रम्य
2.	अनुगुणम्	गुणानाम् अनुरूपम्
3.	निर्बाधम्	बाधानाम् अभाव:
4.	अनुरथम्	रथस्य पश्चात्
5.	निर्विघ्नम्	विघ्नानाम् अभाव:
6.	प्रतिमासम्	मासं मासम् इति
7.	उपगुरु	गुरोः समीपम्
8.	अधिहरि	हरौ इति
9.	सपरिवारम्	परिवारेण सह
10.	प्रतिदिनम्	दिन दिने इति

अभ्यासः

प्रदत्त-तालिकायां समस्तपदं विग्रहं वा लिखत-

क्रमः	समस्तपदम्	विग्रहः
1.	निर्मलम्	____________
2.	____________	एकम् एकम् इति
3.	____________	दोषाणाम् अभाव:
4.	सव्यवधानम्	____________
5.	निरर्थकम्	____________
6.	____________	चिन्तायाः अभाव:
7.	स्नेहेन सहितम्	____________
8.	____________	समयम् अनतिक्रम्य
9.	____________	गङ्गायाः समीपम्
10.	सहर्षम्	____________

उत्तरम्:

1. मलस्य/मलानाम् अभावः
2. प्रत्येकम्
3. निर्दोषम्
4. व्यवधानेन सह
5. अर्थस्य अभावः
6. निश्चितम्
7. सस्नेहम्
8. यथासमयम्
9. उपगङ्गगम्
10. हर्षेण सह

2. तत्पुरुषः

(क) वानराः वृक्षोपरि क्रीडन्ति। (वृक्षस्य उपरि)
(ख) वनराजः उच्चैः गर्जति। (वनस्य राजा)
(ग) संन्यासी पदनिर्लिप्तः भवति। (पदाय निर्लिप्तः)
(घ) रामः शरणागतं विभीषणम् अरक्षत्। (शरणम् आगतम्)
(ङ) चिकित्सकः अग्निदग्धस्य उपचारम् अकरोत्। (अग्निना दग्धस्य)

उल्लिखितेषु उदाहरणेषु वयं पश्यामः यत्-
(i) प्रथम/पूर्वपदेषु द्वितीया, तृतीया, चतुर्थी, षष्ठी चेति भिन्न-भिन्न विभक्तीनां प्रयोगः वर्तते।
(ii) क्रियायाः प्रयोगः द्वितीय/उत्तरपदाय भवति।

अतः यस्मिन् समासे प्रथम/पूर्वपदेषु द्वितीया विभक्तितः सप्तमी विभक्ति-पर्यन्तं विभिन्नविभक्तीनां प्रयोगः भवति सः समासः तत्पुरुषसमासः भवति।

तत्पुरुषसमासस्य इतराणि उदाहरणानि-

क्रमः	समासः	विग्रहः	उपभेदः
1.	ग्रामगतः	ग्रामं गतः	द्वितीया-तत्पुरुषः
2.	पर्वतारूढः	पर्वतम् आरूढः	द्वितीया-तत्पुरुषः
3.	कालिदासलिखितम्	कालिदासेन लिखितम्	तृतीया-तत्पुरुषः
4.	चक्रहतः	चक्रेण हतः	तृतीया-तत्पुरुषः
5.	यज्ञसामग्री	यज्ञाय सामग्री	चतुर्थी-तत्पुरुषः
6.	निद्राकुलः	निद्रया आकुलः	चतुर्थी-तत्पुरुषः
7.	सिंहभीत:	सिंहात् भीतः	पञ्चमी-तत्पुरुषः
8.	आकाशपतितम्	आकाशात् पतितम्	पञ्चमी-तत्पुरुषः
9.	गृहपतिः	गृहस्य पतिः	षष्ठी-तत्पुरुषः
10.	गौरीशः	गौर्याः ईशः	षष्ठी-तत्पुरुषः
11.	सङ्गीतपटुः	सङ्गीते पटुः	सप्तमी-तत्पुरुषः
12.	चिन्तामग्नः	चिन्तायां मग्नः	सप्तमी-तत्पुरुषः
13.	असत्यम्	न सत्यम्	नञ्-तत्पुरुषः
14.	अनुपकार:	न उपकार:	नञ्-तत्पुरुषः

आकाशात् पतितं तोयं यथा गच्छति सारगम्। सर्वदेव नमस्कार: केशवं प्रति गच्छति।

अभ्यासः

अधोलिखितेषु समासं विग्रहं वा कृत्वा लिख्यताम्-

क्रमः	समासः	विग्रहः
1.	___________	न्यायस्य अधीश:
2.	देहविनाश:	___________
3.		न मन्त्रः
4.	अयोग्यः	___________
5.	वृक्षोपरि	___________
6.	___________	निद्रायाः भङ्गस्य दुःखम्
7.	वनराज:	___________राजा
8.	___________	नराणां पतिः
9.	पक्षिकुलम्	___________
10.	___________	प्रीते: लक्षणम्
11.	निशान्धकारे	___________
12.	___________	न पक्वम्
13.	मृत्तिकाक्रीडनकम्	___________
14.	___________	वृद्धेः लाभाः
15.	अधर्मः	___________

उत्तरम्:

1. न्यायाधीशः
2. देहस्य विनाशः
3. अमन्त्रः
4. न योग्यः
5. वृक्षस्य उपरि
6. निद्राभङ्गदुःखम्,
7. वनस्य
8. नरपतिः
9. पक्षिणाम् कुलम् / पक्षीणाम् कुलम्
10. प्रीतिलक्षणम्
11. निशाया: अन्धकारः, तस्मिन्
12. अपक्वम्
13. मृत्तिकायाः क्रीडनकम्
14. वृद्धिलाभः
15. न धर्मः

कर्मधारयः

(विशेषण – विशेष्यौ)
(i) कृष्णसर्पः बिलम् प्राविशत्। (कृष्णः च एषः सर्प: / कृष्णः सर्पः)
(ii) महादेवी करुणां करोतु। (महति च इयं देवी / महती देवी)
(ii) महावृक्षः फलानि ददाति। (महान् च अयं वृक्ष: / महान् वक्षः) (उपमानोपमेयौ (उपमान + उपमेयौ)
(iv) सिंहपुरुष:/पुरुषसिंहः श्री रामः रावणं हतवान्। (सिंह इव पुरुष: / पुरुषः सिंह: इव)
(v) देव्याः कमलनेत्रे दृष्ट्वा भक्तः प्रसन्नः अभवत्। (कमलम् इव नेत्रे)
(vi) तस्याः चन्द्रमुखं दृष्ट्वा सः मोहितः अभवत्। (चन्द्रः इव मुखम्)

उल्लिखितेषु वाक्येषु रेखाङ्कितपदेषु विशेषणविशेष्ययोः अथवा उपमानोपमेययोः प्रयोगः अस्ति। एतेषु विशेष्यपदम् अथवा उपमेयपदम् एव प्रधानं भवति। उपमानपदस्य पश्चात् ‘इव’ इति अव्ययस्य प्रयोगेण उपमानोपमेय-कर्मधारयसमासस्य विग्रहः भवति। किन्तु विशेषण-विशेष्ययोः प्रथमा-विभक्त्या: प्रयोगेण समासविग्रहः भवति।

अभ्यासः

समस्तपदं विग्रह वा लिखत-

क्रमः	समस्तपदम्	विग्रहः
1.	_________	महान् वृक्षः
2.	पुरुषव्याघ्रः	_________
3.	_________	महत् कम्पनम्
4.	महाविनाशः	_________
5.	_________	रक्तम् उत्पलम्
6.	पीतपुष्पाणि	_________
7.	_________	घन इव श्यामः
8.	महोत्सवः	_________
9.	_________	विशालः पर्वतः
10.	महागौरी	_________

उत्तरम्:

1. महावृक्षः
2. पुरुषः व्याघ्रः द्व
3. महाकम्पनम्
4. महान् विनाशः
5. रक्तोत्पलम्
6. पीतानि पुष्पाणि
7. घनश्यामः
8. महान् उत्सवः
9. विशालपर्वतः
10. महती गौरी

द्विगु-समासः

(i) जगत्पालकः त्रिलोकं रक्षति।
(ii) नवरात्रे सः सप्तशतीं पठति।
(ii) दानस्य महत्त्वं चतुर्युगं यावद् भवति।
(iv) दण्डकारण्ये ‘पञ्चवटी‘ इति स्थाने श्रीरामः सीतया लक्ष्मणेन च सह अवसत्।
(v) इयं शताब्दी विज्ञानस्य अस्ति।

उल्लिखितेषु वाक्येषु रेखाङ्कितपदेषु चतस्रः विशेषताः सन्ति-
(क) एतानि पदानि सङ्ख्याशब्दैः प्रारभन्ते।
(ख) बहुवचनसङ्ख्या प्रयोगे अपि सर्वेषु पदेषु एकवचनस्य प्रयोगः विद्यते।
(ग) समस्तपदानि नपुंसकलिङ्गे अथवा स्त्रीलिङ्गे भवन्ति।
(घ) समस्तपदानि/समूहस्य/समाहारस्य बोधं कारयन्ति।

एतादृशाः समासाः/एतादृशानि समस्तपदानि द्विगुसमासाः कथ्यन्ते।
इत्थं वयं जानीमः यत् द्विगुसमासेषु प्रथमशब्दः सङ्ख्यावाचको भवति। एते समासाः नपुंसकलिङ्गे स्त्रीलिलिङ्गे वा भवन्ति।

समाहार / समूहकारणात् एतेषां समासानां विग्रहः एवं भवति-

क्रमः	समस्तपदम्	विग्रहः
1.	नवरात्रम्	नवाना रात्रीणां समाहारः
2.	पञ्चवटी	पञ्चानां वटानां समाहारः
3.	चतुर्युगम् / चतुर्युगी	चतुर्णा युगानां समाहार:
4.	त्रिलोकम् / त्रिलोकी	त्रयाणां लोकानां समाहारः
5.	शताब्दम् / शताब्दी	शतस्य अब्दानां समाहार:

अधोलिखित-तालिकायाम् समस्तपदं विग्रह वा लिख्यन्ताम्-

क्रमः	समस्तपदानि	विग्रहः
1.	__________	सप्तानाम् अह्रां समाहारः
2.	पञ्चानां पात्राणां समाहारः	__________
3.	__________	त्रयाणां भुवनानां समाहारः
4.	पञ्चरात्रम्	__________
5.	अष्टाध्यायी	__________

उत्तरम्:

1. सप्ताहम्
2. पञ्चपात्रम्
3. त्रिभुवनम्
4. पञ्चानां रात्रीणाम् समाहारः
5. अष्टाणाम् अध्यायाम् समाहार:

3. द्वन्द्व-समासः

(i) इतरेतरद्वन्द्वः
(क) दशरथस्य चत्वारः पुत्राः रामलक्ष्मणभरतशत्रुघ्नाः आसन्। (रामः च लक्ष्मणः च भरतः च शत्रुघ्नः च)
(ख) रामलक्ष्मी मिथिलाम् अगच्छताम्। (रामः च लक्ष्मणः च)
(ग) मयूरीकुक्कुटौ संवदत:/कुक्कुटमयूयौं संवदतः। (मयूरी च कुक्कुटः च/कुक्कुटः च मयूरी च)

उल्लिखितवाक्येषु चतस्रः विशेषताः सन्ति-
(i) समासेषु शब्दानां सङ्ख्यायाः अनुसार द्विवचन बहुवचन वा प्रयुक्तम्।
(ii) वाक्येषु सर्वेषां पदानां सङ्ख्यायाः अनुसार क्रियापदस्य वचनं निर्धारितम् भवति अतः सर्वाणि पदानि प्रधानानि सन्ति।
(iii) समासस्य अन्तिमपदानुसारं समासस्य लिङ्ग निर्धार्यते।

(ii) समाहार द्वन्द्वः
(i) योगिनं शीतोष्णं न बाधते। (शीतं च उष्णं च, तयोः समाहारः)
(ii) सः पुत्रपौत्रं दृष्ट्वा प्रसीदति। (पुत्रः च पौत्रः च, तयोः समाहारः)
(iii) सः दिवारानं प्रसन्नः तिष्ठति (दिवा च रात्रिः च, तयोः समाहारः)

उल्लिखितवाक्येषु रेखाङ्कितपदेषु यद्यपि द्वे एव पदे प्रधाने परन्तु तयोः समाहार / समूहकरणात् एकवचनस्य प्रयोगः अभवत् एवम् एतेषु उदाहरणेषु अधोलिखित-विशेषताः सन्ति-
(i) समस्तपदानि नपुंसकलिङ्गे एकवचने सन्ति।
(ii) द्वयोः पदयोः एकः समहारः भवति।

(iii) एकशेषद्वन्द्वः
पितरौ- माता च पिता च अत्र एकस्य पितृशब्दस्य द्विवचने प्रयोगेण एकशेषद्वन्द्वः समासः कथ्यते। इतरेतरद्वन्द्व समासे ‘मातापितरौ’ इत्यस्य अपि प्रयोगः भवति।

अभ्यासः

अधोलिखिततालिकायां समस्तपदेभ्यः विग्रह विग्रहेभ्यः च समस्तपदानि लिख्यन्ताम्-

क्रमः	समस्तपदम्	विग्रहः
1.	अग्निसोमो	___________
2.	पाणिपादम्	___________
3.	___________	साता च रामः च
4.	इन्द्रः च वरुणः च	___________
5.	___________	रमा च शारदा च
6.	___________	धर्मः च अर्थः च कामः च मोक्षः च
7.	लतापुष्पम्	___________
8.	___________	मूषकः च मार्जारः च
9.	अहोरात्रम्	___________
10.	___________	सुखं च दुःखम् च

उत्तरम्:
1. अग्निः च सोमः च
2. पाणी च पादौ च तेषां समाहारः
3. सीतारामौ
4. इन्द्रवरुणौ
5. रसाशारदे,
6. धर्मार्थकाममोक्षाः
7. लताः च पुष्पाणि च तेषां समाहारः
8. मूषकमार्जारौ
9. आहश्च रात्रिः च तयोः समाहारः
10. सुखदुःखम्

4. बहुव्रीहिः

(क) चतुर्मुखः ब्रह्मा सृष्टिरचनां करोति। (चत्वारि मुखानि यस्य सः)
(ख) चतुर्भुजः विष्णुः सृष्टेः पालनं करोति। (चतस्रः भुजाः यस्य सः)
(ग) त्रिनेत्रः शिवः जगत् सहरति। (त्रीणि नेत्राणि यस्य सः)
(घ) क्रूरकर्मा जनः आतङ्कवादी भवति। (क्रूरं कर्म यस्य सः)
(ङ) सिंहवाहना दुर्गा महिषासुरस्य वधम् अकरोत्। (सिंहः वाहनं यस्याः सा)

उल्लिखितवाक्येषु रेखाङ्कितपदेषु किमपि पदं प्रधानं नास्ति। अपि तैः पदैः सङ्केतितं किमपि अन्यद् एव पदं प्रधानम् अस्ति। एतेषु समासेषु अधोलिखिताः विशेषताः सन्ति।
(i) द्वे पदे मिलित्वा अन्यपदं सङ्केतयन्ति।
(ii) द्वे पदे यदा परस्परं विशेषणम् विशेष्यं च भवतः तदा ते प्रथमाविभक्तौ समानलिङ्गे च तिष्ठतः।
(iii) विग्रहाय अन्ते यस्य सः/यस्याः सा इत्यादीनां प्रयोगः भवति।

इत्थं वयं जानीमः यद् बहुव्रीहिसमासः अन्यपदप्रधानः भवति। यदा बहुव्रीहिसमासे द्वे पदे एकस्मिन् एव विभक्तौ भवतः तदा समानाधिकरण बहुव्रीहिः भवति। बहुव्रीहिसमासे यदा द्वे पदे पृथक्-पृथक् विभक्तौ भिन्न-लिङ्गे वा तदा व्यधिकरण-बहुव्रीहिः समासः भवति।

अभ्यासः

अधोलिखितसमस्तपदेभ्यः विग्रहाः, विग्रहेभ्यः च समस्तपदानि लिख्यन्ताम्-

क्रमः	समस्तपदानि	विग्रहः
1.	___________	लम्बम् उदरं यस्य सः
2.	पीताम्बरः	___________
3.	___________	कृतः उपकारः येन सः
4.	प्रत्युपन्नमतिः	___________
5.	___________	गज इव आननं यस्य सः
6.	चन्द्रमुखी	___________
7.	___________	चक्रं पाणौ यस्य सः
8.	चन्द्रमौलि:	___________
9.	___________	बहूनि कमलानि यस्मिन् तत्
10.	___________	जितानि इन्द्रियाणि येन सः

उत्तरम्:
1. लम्बोदरः
2. पीतम् अम्बरं यस्य सः
3. कृतोपकारः
4. प्रत्युत्पन्ना मतिः यस्य सः
5. गजाननः
6. चन्द्रम् इव मुखं यस्याः सा
7. चक्रपाणिः
8. चन्द्रः मौलौ यस्य सः
9. बहुकमलम्
10. जितेन्द्रियः

मिश्रिताभ्यास:
अधोलिखितसमस्तपदेभ्यः विग्रहान् विग्रहेभ्यः च समस्तपदानि निर्माय तेषां नामानि अपि लिख्यन्ताम्-

क्रमः	समस्तपदम्	विग्रहः	समासनाम
1.	मेघश्यामः	_____________	_____________
2.	_____________	न युक्तम्	_____________
3.	देहाविनाशाय	_____________	_____________
4.	_____________	नीलं च तत् कमलम्	_____________
5.	_____________	हर्षेण मिश्रितम्	_____________
6.	_____________	कर्कश: ध्वनिः	_____________
7.	_____________	पञ्चानां वटानां समाहारः	_____________
8.	वनराज	_____________	_____________
9.	_____________	स्थिता प्रज्ञा यस्यः सः	_____________
10.	_____________	माता च पिता च	_____________

उत्तरम्:
1. मेघः इव श्यामः, कर्मधारयः
2. अयुक्तम्, नञ् तत्पुरुषः
3. देहस्य विनाशाय, षष्ठी तत्पुरुषः
4. नीलकमलम्, कर्मधारयः
5. हर्षमिश्रितम्, तृतीया तत्पुरुषः
6. कर्कशध्वनिः, कर्मधारयः
7. पञ्चवटम् / पञ्चवटी, द्विगुः
8. वनस्य राजा, षष्ठी तत्पुरुषः
9. स्थितप्रज्ञः, बहुव्रीहिः
10. मातापितरौ, इतरेतर द्वन्द्वः

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 5 Continuity and Differentiability. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 5 Important Extra Questions Continuity and Differentiability

Continuity and Differentiability Important Extra Questions Very Short Answer Type

Question 1.
If y = log (cos e^x), then find \(\frac{d y}{d x}\) (Delhi 2019)
Solution:
We have :y = log (cos e^x)
∴ \(\frac{d y}{d x}=\frac{1}{\cos e^{x}}\left(-\sin e^{x}\right) \cdot e^{x}\)
= – e^x tan e^x

Question 2.
Differentiate cos {sin (x)²} w.r.t. x. (Outside Delhi 2019)
Solution:
Let y = cos {sin (x)²}.
∴ \(\frac{d y}{d x}\)= – sin {sin (x)²}. \(\frac{d y}{d x}\){sin (x)²}
= – sin {sin (x)²}. cos(x)² \(\frac{d y}{d x}\) (x²)
= – sin {sin (x)²}. cos(x)²2x
= -2x cos(x)² sin {sin(x)²}.

Question 3.
Differentiate sin²(x²) w.r.t. x².   (C.B.S.E. Sample Paper 2018-19)
Solution:
Let y = sin²(x²).
∴ \(\frac{d y}{d x}\) = 2 sin (x²) cos (x²) = sin (2x²).

Question 4.
Find \(\frac{d y}{d x}\), if y + siny = cos or.
Solution:
We have: y + sin y = cos x.
Differentiating w.r,t. x, we get:
\(\frac{d y}{d x}\) + cos y. \(\frac{d y}{d x}\) = – sin x
(1 + cos y)\(\frac{d y}{d x}\) = -sin x
Hence, \(\frac{d y}{d x}\) = \(-\frac{\sin x}{1+\cos y}\)
where y ≠ (2n + 1)π, n ∈ Z.

Question 5.
If y = \(\sin ^{-1}\left(6 x \sqrt{1-9 x^{2}}\right),-\frac{1}{3 \sqrt{2}}<x<\frac{1}{3 \sqrt{2}}\) then find \(\frac{d y}{d x}\). (C.B.S.E. 2017)
Solution:
Here y = sin^-1\(\left(6 x \sqrt{1-9 x^{2}}\right)\)
Put 3x = sin θ.
y = sin^-1 (2 sin θ cos θ)
= sin^-1 (sin 2θ) = 2θ
= 2 sin^-1 3x
\(\frac{d y}{d x}=\frac{6}{\sqrt{1-9 x^{2}}}\)

Question 6.
Is it true that x = e^logx for all real x? (N.C.E.R.T.)
Solution:
The given equation is x = e^logx
This is not true for non-positive real numbers.
[ ∵ Domain of log function is R+]
Now, let y = e^logx
If y > 0, taking logs.,
log y = log (e^logx) = log x.log e
= log x . 1 = log x
⇒ y = x.
Hence, x = e^logx is true only for positive values of x.

Question 7.
Differentiate the following w.r.t. x : 3^{x + 2}. (N.C.E.R.T.)
Solution:
Let y = 3^{x + 2}.
\(\frac{d y}{d x}\) = 3^{x + 2}.log3. \(\frac{d}{d x}\)(x + 2)
= 3^{x + 2} .log3.(1 + 0)
= 3^{x + 2}. log 3 = log 3 (3^{x + 2}).

Question 8.
Differentiate log (1 + θ) w.r.t. sin^-1θ.
Solution:
Let y = log (1 + θ) and u = sin^-1θ.

Question 9.
If y = x^x , find \(\frac{d y}{d x}\).
Solution:
Here y = x^x …(1)
Taking logs., log y = log x^x
⇒ log y = x log x.
Differentiating w.r.t. x, we get:
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x \(\frac{1}{x}\) + logx.(1)
= 1 + log x.
Hence, \(\frac{d y}{d x}\) = y (1 + log x) dx
= x^x (1 + log x). [Using (1)]

Question 10.
If y = \(\sqrt{2^{x}+\sqrt{2^{x}+\sqrt{2^{x}+\ldots \ldots+0 \infty}}}\) then prove that: (2y – 1)\(\frac{d y}{d x}\) = 2^x log 2.
Solution:
The given series can be written as :
y = \(\sqrt{2^{x}+y}\)
Squaring, y² = 2^x + y
⇒ y² – y = 2^x.
Diff. w.r.t. x, (2y -1)\(\frac{d y}{d x}\) = 2^x log 2.

Question 11.
Discuss the applicability of Rolle’s Theorem for the function f(x) = (x- 1)^2/5 in the interval [0, 3].
Solution:
Since f(x) is a polynomial in x,
∴ it is continuous in [0, 3].
And f'(x) = \(\frac { 2 }{ 5 }\)(x-1) ^-3/5 = \(\frac{2}{5} \cdot \frac{1}{(x-1)^{3 / 5}}\)
which does not exist at x = 1
⇒ f(x) is not derivable in (0, 3).
Hence, Rolle’s theorem is not applicable.

Continuity and Differentiability Important Extra Questions Short Answer Type

Question 1.
Discuss the continuity of the function : f(x) = |x| at x = 0. (N.C.E.R.T.)
Solution:

Hence ‘f’ is continuous at x = 0.

Question 2.
If f(x) = x + 1, find \(\frac{d}{d x}\)(fof)(x). (C.B.S.E. 2019)
Solution:
We have : f(x) = x + 1 …(1)
∴ fof(x) = f (f(x)) =f(x)+ 1
= (x + 1) + 1 = x + 2.
∴ \(\frac{d}{d x}\)(fof)(x).) = \(\frac{d}{d x}\)(x + 2) = 1 + 0 = 1.

Question 3.
Differentiate \(\tan ^{-1}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)\) with respect to x. (C.B.S.E. 2018 C)
Solution:

Question 4.
Differentiate: tan^-1 \(\left(\frac{1+\cos x}{\sin x}\right)\) with respect to x. (C.B.S.E. 2018)
Solution:

Question 5.
Write the integrating factor of the differential equation :
(tan^-1 y – x) dy = (1 + y²) dx. (C.B.S.E. 2019 (Outside Delhi))
Solution:
The given differential equation is :
(tan^-1 y – x) dy = (1 + y²) dx
⇒ \(\frac{d x}{d y}+\frac{x}{1+y^{2}}=\frac{\tan ^{-1} y}{1+y^{2}}\) Linear Equation
∴ I.F = \(e^{\int \frac{1}{1+y^{2}} d x}=e^{\tan ^{-1} y}\)

Question 6.
Find \(\frac{d y}{d x}\) if y = sin^-1\(\left[\frac{5 x+12 \sqrt{1-x^{2}}}{13}\right]\) (A.I.C.B.S.E. 2016)
Solution:

Question 7.
Find \(\frac{d y}{d x}\) if y = \(\sin ^{-1}\left[\frac{6 x-4 \sqrt{1-4 x^{2}}}{5}\right]\) (A.I.C.B.S.E. 2016)
Solution:

Question 8.
If y = {x + \(\sqrt{x^{2}+a^{2}}\)}ⁿ , prove that \(\frac{d y}{d x}=\frac{n y}{\sqrt{x^{2}+a^{2}}}\)
Solution:
y = {x + \(\sqrt{x^{2}+a^{2}}\)}ⁿ ……… (1)

Question 9.
The total cost C(x) associated with the production of ‘x’ units of an item is given by C(x) = 0.005x³ – 0.02x² + 30x + 5000.
Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of the total cost at any level of output. (C.B.S.E. 2018)
Solution:
We have: 0.005x³ – 0.02x² + 30x + 5000
∴ Marginal cost,
C'(x) = (0.005)(3x²) – 0.02(2x) + 30.
Hence,C'(3) = (0.005) (3×9)- (0.02) (6) + 30
= 0.135-0.12 + 30
= 30.135 – 0.12
= 30.02 units nearly

Question 10.
If (x² + y²)² = xy, find \(\frac{d y}{d x}\). (C.B.S.E. 2018)
Solution:
We have : (x² + y²)² = xy
Diff. w.r.t. x,
2(x² + y²)\(\frac{d}{d x}\)(x²+ y²) = x\(\frac{d y}{d x}\) + y(1)
2(x² + y²) [2x +2y\(\frac{d y}{d x}\) ] = x\(\frac{d y}{d x}\) + y
4x(x² + y²) – y = \(\frac{d y}{d x}\) [x – 4y(x² + y²)]
Hence \(\frac{d y}{d x}=\frac{4 x^{3}+4 x y^{2}-y}{x-4 y x^{2}-4 y^{3}}\)

Question 11.
Fing \(\frac{d y}{d x}\) if x^2/3 + y^2/3 = a^2/3 (N.C.E.R.T)
Solution:
The given equation is
if x^2/3 + y^2/3 = a^2/3
Its parametric equations are :
x = a cos³ θ,
y = a sin³ θ
[x^2/3 + y^2/3 = a^2/3 (cos²θ + sin²θ) = a^2/3(I) = a^2/3]

Question 12.
Find the value of \(\frac{d y}{d x}\) at θ = \(\frac{\pi}{4}\), if:
x = ae^θ (sin θ – cos θ)
and y = ae^θ (sin θ + cos θ). (A.I.C.B.S.E. 2014)
Solution:
We have : x= ae^θ (sin θ – cos θ)
and y= ae^θ(sin θ + cos θ).
\(\frac{d x}{d \theta}\) = ae^θ (cos θ + sin θ) + ae^θ(sin θ – cos θ)
= 2ae^θsin θ
and \(\frac{d y}{d \theta}\) = ae^θ (cos θ – sin θ) + ae^θ(sinθ + cosθ)
= 2ae^θ cos θ

Question 13.
If x = a(2θ – sin 2θ) and y = a(1 – cos 2θ), find \(\frac{d y}{d x}\) where θ = \(\frac{\pi}{3}\) (C.B.S.E 2018)
Solution:
We have :
x = a(2θ – sin 2θ)
and y = a(1 – cos 2θ).
∴ \(\frac{d x}{d \theta}\) = a(2 – 2 cos 2θ)
and \(\frac{d y}{d \theta}\) = a(0 + 2 sin 2θ) = 2a sin 2θ.

Question 14.
Find f’ (x), if f(x) = (sin x)^{sin x} for all 0 < x < π. (N.C.E.R.T.)
Solution:
We have :
f(x) = (sin x)^{sin x} …(1)
Taking logs., log f(x) = log (sin x)^{sin x}
⇒ log f(x) = sin x log (sin x).
Diff. w.r.t. x,

= cos x (1 + log sin x)
⇒ f’ (x) = f(x) cos x (1 + log sin x).
Hence ,f'(x) = (sin x)^{sin x}cos x (1 + log sin x).
[Using (i)]

Question 15.
If x¹⁶ y⁹ = (x² + y)¹⁷, prove that \(\frac{d y}{d x}=\frac{2 y}{x}\) (C.B.S.E. (F) 2012)
Solution:
We have :
x¹⁶ y⁹ = (x² + y)¹⁷.
Taking logs.,
log (x¹⁶ y⁹) = log (x² + y)¹⁷
⇒ 16 log x + 9 log y = 17 log (x² + y).
Diff. w.r.t. x,

Question 16.
If y = ae^2x + be^-x, then show that \(\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}-2 y=0\)   (C.B.S.E. Sample Paper 2019-20)
Solution:
Here,
y = ae^2x + be^-x ……… (1)
∴ \(\frac{d y}{d x}\) = 2ae^2x – be^-x …….. (2)
And \(\frac{d^{2} y}{d x^{2}}\) = 4ae^2x + be^-x ……….. (3)
Now, \(\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}-2 y\)
= [4ae^2x + be^-x] – [2ae^2x – be^-x] – 2[ae^2x + be^-x] [Using (1), (2) & (3)]
= 4ae^2x + be^-x – 2ae^2x + be^-x – 2ae^2x – 2be^2x = 0.

Question 17.
If y = log(1 + 2t² + t⁴), x = tan^-1t, find \(\frac{d^{2} y}{d x^{2}}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
We have : y = log(1 + 2t² + t⁴)
⇒ y = log (1 + t²)²
⇒ y = 21og (1 + t²).

Question 18.
If x sin (a + y) + sin a cos (a + y) = 0, then prove that: \(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\) (A.I.C.B.S.E. 2013)
Solution:
We have :
x sin (a + y) + sin a cos (a + y) = 0 …(1)
⇒ x = \(-\frac{\sin a \cos (a+y)}{\sin (a+y)}\) …..(2)
Diff (1) w.r.t x,
x cos (a + y)(0+\(\frac{d y}{d x}\) ) + sin (a + y). 1 + sina(-sin(a+y))(0+\(\frac{d y}{d x}\)) = 0
(xcos(a + y) – sin a sin (a + y)] \(\frac{d y}{d x}\) = – sin (a + y)

⇒ – sin (a + y) [Using (2)]
⇒ -sin a[cos²(a+y)+sin²(a+y)] \(\frac{d y}{d x}\) = -sin² (a+y)
⇒ -sin a(1) \(\frac{d y}{d x}\) = = -sin² (a+y)
Hence \(\frac{d y}{d x}\) = \(\frac{\sin ^{2}(a+y)}{\sin a}\)
Which is true.

Question 19.
If sin y = x cos (a + y), then show that \(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\cos a}\) Also, show that \(\frac{d y}{d x}\) = cos a, when x = 0. (C.B.S.E. 2018C)
Solution:
Given, sin y = x cos (a + y)

Question 20.
Find the value of ‘c’ in Rolle’s Theorem for the function f (x) = x³ – 3x in [-√3, 0]. (A.1.C.B.S.E. 2017)
Solution:
We have : f(x) = x³ – 3x.
(i) f(x) is continuous in [-√3, 0].
[∵ f(x) is a polynomial in x]

(ii) f'(x) = 3x² – 3 …(1)
∴ f'(x) exists for each x in (-√3,0)

(iii) f(-√3) = (-√3)3 – 3(-√3)
= -3√3 + 3√3 = 0
f(0) = 0 – 0 = 0.
∴ f(-√3) =f(0).
Thus all the conditions of Rolle’s Theorem are satisified.
∴ There exists at least one number ‘c’ between – √3 and 0 such that f'(c) = 0.

But f'(c) = 3c² – 3. [Putting x – c in (1)
∴ f'(c) = 0
3c² – 3 = 0
c² = 1
c = ± 1.
c = – 1 ∈ (-√3,0).
Hence, Rolle’s Theorem is verified and c = – 1.

Question 21.
Find a point on the parabola y = (x – 3)², where the tangent is parallel to the chord joining (3, 0) and (4,1).
Solution:
We have : y = f(x) = (x – 3)².
We discuss the applicability of L.M.V. Theorem in [3, 4],
(i) fix) is continuous in [3, 4],
[ ∵ f(x) is a polynomial]

(ii) f'(x) = 2(x – 3), which exists for all x ∈ (3,4).
∴ f(x) is derivable in (3, 4).
Thus both the conditions of Lagrange’s Mean Value Theorem are satisfied.
∴ There exists at least one number c ∈ (3, 4) such that

⇒ 2(c – 3) = 1
⇒ 2c = 1
⇒ c = \(\frac{7}{2}\) ∈ (3, 4).
When x = \(\frac{7}{2}\), then y = (\(\frac{7}{2}\) – 3)² = 1/4
Hence, the required point is ( \(\frac{7}{2}, \frac{1}{4}\) )

Continuity and Differentiability Important Extra Questions Long Answer Type 1

Question 1.
Find the value of ‘a’ for which the function ‘f’ defined as :

is continuous at x =0 (CBSE 2011)
Solution:


Also f(0) = a sin π/2 (0+1)
= a sin π/2 = a(1) = a
For continuity,
\(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ a = 1/2 = a
Hence, a = 1/2

Question 2.
Find the values of ‘p’ and ‘q’ for which :

is continuous at x = 2 (CBSE 2016)
Solution:


Also f(\(\frac{\pi}{2},\)) = p
For continuity \(\lim _{x \rightarrow \frac{\pi^{-}}{2}} f(x)=\lim _{x \rightarrow \frac{\pi^{*}}{2}} f(x)\)
= f(\(\frac{\pi}{2},\))
⇒ \(\frac{1}{2}=\frac{q}{8}\) = p
Hence p = 1/2 and q = 4

Question 3.
Find the value of ‘k’ for which

is continuous at x = 0 (A.I.C.B.S.E. 2013)
Solution:


For continuity \(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ k = -1 = -1
Hence k = -1

Question 4.
For what values of ‘a’ and ‘b\ the function ‘f’ defined as :

is continuous at x = 1. (CBSE 2011)
Solution:
\(\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{-}}\) (3ax +b)
= \(\lim _{h \rightarrow 0}\) (3a (1-h) + b]
= 3a(1 – 0) + b
= 3a + b
\(\lim _{x \rightarrow 1^{+}} f(x)=\lim _{x \rightarrow 1^{+}}(5 a x-2 b)\)
= \(\lim _{h \rightarrow 0}\) [5a (1+h) – 2b]
= 5a (1+0) – 2b
= 5a – 2b
Also f(1) = 11
Since ‘f’ is continuous at x = 1,
∴ \(\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{+}} f(x)\)= f(1)
⇒ 3a + b = 5a – 2b = 11.
From first and third,
3a + b = 11 …………… (1)
From last two,
5a – 2b = 11 …………… (2)
Multiplying (1) by 2,
6a + 2b = 22 ………….. (3)
Adding (2) and (3),
11a = 33
⇒ a = 3.
Putting in (1),
3(3) + b = 11
⇒ b = 11 – 9 = 2.
Hence, a = 3 and b = 2.

Question 5.
If f(x) , defined by the following is continuous at x = 0, find the values of a, b, and c.

(A.I.C.B.S.E 2011)
Solution:


Also f(0) = 2
Since f(x) is continuous at x = 0,
∴ \(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{+}} f(x)=f(0)\)
⇒ a + 3 = b/2 = 2
Hence,a = -1 and b = 4.

Question 6.
Find ‘a’ and ‘b’, if the function given by :
f(x) = \(\left\{\begin{array}{ll}
a x^{2}+b, & \text { if } x<1 \\ 2 x+1, & \text { if } x \geq 1 \end{array}\right.\) is differentiable at x = 1. (C.B.S.E. Sample Paper 2018)
Solution:
Since ‘f’ is derivable at x = 1, ∴ ‘f’ is continuous at x = 1 im 33 => a + b = 2 + 1 = 3
⇒ a + b = 3 …………. (1)
Again since ‘f is differentiable at x = 1


2a = 2
Putting in (1),
1 + b = 3
⇒ b = 3 – 1
⇒ b = 2.
Hence, a = 1 and b = 2.

Question 7.
Prove that: \(\frac{d}{d x}\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1} \frac{x}{a}\right]\) = \(\sqrt{a^{2}-x^{2}}\)
(C.B.S.E. (F) 2011)
Solution:

Question 8.
Differentiate \(\sin ^{-1}\left(\frac{2^{x+1}}{1+4^{x}}\right)\) w.r.t x (N.C.E.R.T)
Solution:
Let y = \(\sin ^{-1}\left(\frac{2^{x+1}}{1+4^{x}}\right)\)
= \(\sin ^{-1}\left(\frac{2.2^{x}}{1+\left(2^{x}\right)^{2}}\right)\)
Put 2^x = tan θ
so that θ = tan^-1(2^x) ………… (1)
Then y = \(\sin ^{-1}\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\)
= sin^-1 (sin 2θ)
= 2θ = 2tan^-1(2^x).
[Using (1)]

Question 9.
If log (x² + y²) = 2 tan^-1 [ y/x] show that : \(\frac{d y}{d x}=\frac{x+y}{x-y}\) (C.B.S.E. 2019)
Solution:

Question 10.
If y = tan^-1\(\left(\frac{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}\right)\), x² ≤ 1, then find \(\frac{d y}{d x}\)
We have : log (x2 + y2) = 2 tan-1 (A.I.C.B.S.E. 2015)
Solution:

Question 11.
Differentiate the following with respect to x = sin^-1\(\left(\frac{2^{x+1} \cdot 3^{x}}{1+(36)^{x}}\right)\) (A.I.C.B.S.E. 2013)
Solution:
= sin^-1\(\left(\frac{2^{x+1} \cdot 3^{x}}{1+(36)^{x}}\right)\)
= sin^-1\(\left(\frac{2.2^{x} \cdot 3^{x}}{1+(6)^{2 x}}\right)\)
= sin^-1\(\left(\frac{2.6^{x}}{1+(6)^{2 x}}\right)\)
Put 6^x = tan θ
So that θ = tan^-1(6^x) …………(1)
Then y = sin^-1( \(\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\) )
= sin^-1(sin 2θ)
= 2θ = 2tan^-1(6^x) [Using (1)]

Question 12.
Differentiate : tan^-1\(\left[\frac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}\right]\) w.r.t cos^-1 x² (C.B.S.E. Outside Delhi 2019)
Solution:

Question 13.
If x^y – y^x = a^b, find \(\frac{d y}{d x}\). (Delhi 2019)
Solution:
We have : x^y – y^x = a^b
Putting x^y = u and y^x = v, we get:
u – v = a^b
so that, \(\frac{d u}{d x}-\frac{d v}{d x}\) =0 ………….(1)
Now, u = x^y
Taking logs.,
log u = log x^y
⇒ log u = y log x.
Diff. w.r.t. x,

And, v = y^x
Taking logs., log v = log y^x
⇒ log v = x log y.

Question 14.
If y = (log x)^x + x^logx, find \(\frac{d y}{d x}\) (C.B.S.E. 2019)
Solution:
Let y = (log x)^x + x^logx = u + v,
where u = (log x)^x and v = x^logx
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ……….(1)
Now, u = (log x)^x
so that log u = x log (log x).
Diff. w.r.t. x,

Again, v = x^logx
so that log v = log x. log x = (logx)²
Diff w.r.t x,

Question 15.
If \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}=a(x-y)\) then prove that \(\frac{d y}{d x}=\frac{\sqrt{1-y^{2}}}{\sqrt{1-x^{2}}}\) (C.B.S.E. Sample Paper 2019-20)
Solution:
We have: \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}=a(x-y)\)
Putting x = sin A and y = sin B, we get:
\(\sqrt{1-\sin ^{2} \mathrm{~A}}+\sqrt{1-\sin ^{2} \mathbf{B}}=a\)= a (sin A – sin B) ⇒ cos A + cos B = a (sin A – sin B)

Question 16.
If x = a sec³ θ and y = a tan³θ, find \(\frac{d^{2} y}{d x^{2}}\)
Solution:
Given : x = a sec³ θ
y = a tan³θ

Question 17.
Find \(\frac{d y}{d x}\), if x^y. y^x = x^x. (C.B.S.E 2018C)
Solution:
We have: x^y y^x = x^x.
Taking logs.,log x^y y^x = log x^x
⇒ y log x + x log y=x log x

Question 18.
Find \(\frac{d y}{d x}\) if y^x + x^y + x^x = a^b (N.C.E.R.T. A.I.C.B.S.E.2015)
Solution:
We have: y^x + x^y + x^x
Putting y^x = u. x^y = v and x^x = w, we get:
u + y + w = a^b
Diff. w.r.t. x, \(\frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}\) = 0 …………… (1)
Now u = y^x ………….(2)
Taking logs., log u = log y^x
log u = x log y.
Diff. w.r.t. x,

And v = x^y
Taking logs., log v = log x^y
log v = y log x.
Diff. w.r.t. x,

[using (4)]
Lastly w = x^x
Taking logs.,
log w = xlog x
∴ \(\frac{d w}{d x}\) = x (1+log x) …………. (7)
From (1) , using (3), (5) and (7), we get:

Question 19.
If y = e^{tan-1 x}, prove that:\(\left(1+x^{2}\right) \frac{d^{2} y}{d x^{2}}+(2 x-1) \frac{d y}{d x}=0\)
(C.B.S.E. 2018C)
Solution:
Given: y = e^tan-1x,
Differentiating w.r.t. x
\(\frac{d y}{d x}=e^{\ln ^{-1} x}\left(\frac{1}{1+x^{2}}\right)=\frac{y}{1+x^{2}}\)
Agian differentiating w.r.t. x
(1 + x²)\(\frac{d y}{d x}\) = y
(1 + x²)\(\frac{d^{2} y}{d x^{2}}\) + 2x \(\frac{d y}{d x}\) = \(\frac{d y}{d x}\)
(1 + x²)\(\frac{d^{2} y}{d x^{2}}\) + (2x – 1) \(\frac{d y}{d x}\) = 0

Question 20.
If x cos (a + y) = cos y, then prove that:
\(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\sin a}\)
Hence show that :
sin a \(\frac{d^{2} y}{d x^{2}}\) + sin 2(a + y)\(\frac{d y}{d x}\) = 0
Solution:
We have : x cos (a + y) = cos y …………(1)
x = \(\frac{\cos y}{\cos (a+y)}\) …………..(2)
Diff. (I) w.r.t. x,
-x sin (a + y) (0 + \(\frac{d y}{d x}\) ) + cos (a + y) .1
⇒ -sin y.\(\frac{d y}{d x}\)
⇒ (xsin(a+y) – siny)\(\frac{d y}{d x}\) = cos(a +y)
⇒ (\(\frac{\cos y}{\cos (a+y)}\) sin (a+y) – sin y)\(\frac{d y}{d x}\)
⇒ cos (a + y) [Using (2)]
(sin (a + y) cos y – cos (a + y) sin y)\(\frac{d y}{d x}\)
⇒ cos² (a + y)
⇒ sin (a + y – y) \(\frac{d y}{d x}\) = cos²(a+y)
\(\frac{d y}{d x}\) = \(\frac{\cos ^{2}(a+y)}{\sin a}\)
which is true.

Question 21.
If y = (sin^-1 x)², prove that:
\(\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-2=0\) (C.B.S.E. 2019)
Solution:
We have y = (sin^-1 x)²
∴ y₁ = 2(sin^-1 x). \(\frac{1}{\sqrt{1-x^{2}}}\)
⇒ \(\sqrt{1-x^{2}} \cdot y_{1}\) = 2(sin^-1 x).
Squaring, (1 – x²) y₁² = 4(sin^-1 x)²
⇒ (1 – x²) y₁² = 4y [Using (1)]
Diff. w.r.t x,
(1 – x²) 2y₁y₂ + (-2x) y₁² = 4y₁
⇒ (1 – x²) y₂ – xy₁ = 2 [Dividing by 2y₁ ]
Hence, (1-x²)\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) – 2 = 0.

Question 22.
If y = cos (m cos^-1 x), show that
(a – x²)\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) + m²y = 0 (C.B.S.E. Sample Paper 2018-2019)
Solution:
We have :

Question 23.
If y = sin (sin x), prove that
\(\frac{d^{2} y}{d x^{2}}\) + tanx \(\frac{d y}{d x}\) + y cos²x = 0. (C.B.S.E. 2018)
Solution:
We have :
y = sin (sin x)
∴ \(\frac{d y}{d x}\) = cos (sin x) . cos x ……(2)
and \(\frac{d^{2} y}{d x^{2}}\) = cos (sin x) (- sin x) + cos x [- sin (sin x). cos x]
= – sin x cos (sin x) – cos²x sin (sin x) …(3)
:. LHS = \(\frac{d^{2} y}{d x^{2}}\) + tan x \(\frac{d y}{d x}\) + y cos² x
⇒ – sin x cos (sin x) – cos² x sin (sin x) + tan x cos (sin x).cos x + sin (sin x) cos² x
[Using (1). (2) and (3)]
⇒ – sin x cos (sin x) – cos² x sin (sin x) + sin x cos (sin x) + cos² x sin (sin x)
⇒ – sin x cos (sin x) + sin x cos (sin x)
= 0 = RHS.

Question 24.
If x = sin t, y = sin pt, prove that:
(1 – x²)\(\frac{d^{2} y}{d x^{2}}\) – x \(\frac{d y}{d x}\) + p²y = 0
(Outside Delhi 2019)
Solution:
We have : x = sin t
and y = sin pt.
\(\frac{d y}{d x}\) = cos t
and \(\frac{d y}{d x}\) = p cos pt

which is true.

Question 25.
Find \(\frac{d y}{d x}\), if x^y.y^x = x^x. (C.B.S.E. 2019 C)
Solution:
We have: x^y.y^x = x^x
Taking logs., logx^y y^x = log x^x
⇒ y log x + x log y = x log x

Question 26.
If y = x^x, prove that
\(\frac{d^{2} y}{d x^{2}}-\frac{1}{y}\left(\frac{d y}{d x}\right)^{2}-\frac{y}{x}=0\) (C.B.S.E. 2016,14)
Solution:
We have : y = x^x.
Taking logs.,
log y = x log x.
Duff. w.r.t. x,
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x. \(\frac{1}{y}\) + log x.1
\(\frac{d y}{d x}\) = y(1+1ogx) ………….(1)
Again duff. w.r.t. x,

Question 27.
If x = a (cos 2θ + 2θ sin 2θ) andy = a (sin 2θ – 2θ cos 2θ), find \(\frac{d^{2} y}{d x^{2}}\) at θ = \(\frac{\pi}{8}\)
(C.B.S.E. Sample Paper 2019-20)
Solution:
We have: x – a (cos 2θ + 2θ sin 2θ)
∴ \(\frac{d x}{d \theta}\) = a (- 2 sin 2θ + 2 sin 2θ + 4θ cos 2θ).
⇒ \(\frac{d x}{d \theta}\) = 4aθ cos 2θ ………..(1)
And y = a (sin 2θ – 2θ cos 2θ).
∴ \(\frac{d y}{d \theta}\) = a (2 cos 2θ + 4θ sin 2θ – 2 cos 2θ)
\(\frac{d y}{d \theta}\) = 4aθsin 2θ ………….. (2)

Question 28.
If x = cos t + log tan (t/2) y = sin t , then find the values of \(\frac{d^{2} y}{d t^{2}}\) and \(\frac{d^{2} y}{d x^{2}}\) at t = \(\frac{\pi}{4}\)
(C.B.S.E. 2019 Delhi Set-II)
Solution:
We have x = cos t log tan (t/2) and
y = sin t

Question 29.
If y = a cos (log x) + b sin (log x), show that:
\(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+y=0\) (C.B.S.E. 2019C)
Solution:
We have:
y = a cos (log x) + b sin (log x) …..(1)
\(\frac{d y}{d x}\) = – a sin (log x) \(\frac{1}{x}\) + b cos (log x) \(\frac{1}{x}\)
x\(\frac{d y}{d x}\) = -asin (log x) + b cos (log x).
Again diff. w.r.t.x., \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \cdot 1\)
= – a cos (log x) . \(\frac{1}{x}\) – b sin (log x) . \(\frac{1}{x}\)
\(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}\)
= – [a cos (log x) + b sin (log x)]
= -y. [Using (1)]
Hence, \(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+y=0\)

Question 30.
Use Lagrange’s Theorem to determine a point P on the curve f(x) = \(\sqrt{x-2}\), defined in the interval [2, 3], where the tangent is parallel to the chord joining the end points on the curve.
Solution:
We have y = f(x) = \(\sqrt{x-2}\) …….(1)
∴ f'(x) = \(\frac{1}{2 \sqrt{x-2}}\)
now f(a) = f(2) = \(\sqrt{2-2}=\sqrt{0}\) = 0
and f(b) = f(3) = \(\sqrt{3-2}=\sqrt{1}\) = 1.
By Lagrange’s Theorem, we have :

⇒ \(\frac{1}{4(x-2)}\) = 1 [Squaring both
⇒ 1 = 4x – 8
⇒ 4x = 9
⇒ x = \(\frac{9}{4}\) ∈ (2, 3).
Putting in (1), y = \(\sqrt{\frac{9}{4}-2}=\sqrt{\frac{1}{4}}=\frac{1}{2}\)
Hence, ( \(\frac{9}{4}, \frac{1}{2}\) ) is the reqd. point.

We have given detailed NCERT Solutions for Class 6 Sanskrit Ruchira Chapter 15 मातुलचन्द्र Textbook Questions and Answers come in handy for quickly completing your homework.

NCERT Solutions for Class 6 Sanskrit Ruchira Chapter 15 मातुलचन्द्र

Class 6th Sanskrit Chapter 15 मातुलचन्द्र Textbook Questions and Answers

अभ्यासः

प्रश्न 1.
बालगीतं साभिनयं सस्वरं गायत। (बालगीत अभिनय के साथ गाइए- Sing the nursery rhyme with gestures.)
उत्तर:
छात्र बालगीत स्वयं गाएँ।

प्रश्न 2.
रिक्तस्थानानि पूरथत पद्यांशान् योजयत- (पद्यांशों का मिलान कीजिए- Match the verses.)

मातुल! किरसि — सितपरिधानम्
तारकखचितं — श्रावय गीतिम्
त्वरितमेहि मां — चन्द्रिकावितानम्
अतिशयविस्तृत — कथं न स्नेहम्
धवलं तव — नीलाकाशः
उत्तर:
मातुल किरसि — कथं न स्नेहम्।
तारकखचितम् — सितपरिधानम्।
त्वरितमेहि मां — श्रावय गीतिम्।
अतिशयविस्तृत — नीलाकाशः।
धवलं तव — चन्द्रिकावितानम्।

प्रश्न 3.
पद्यांशों  (पद्यांशों में रिक्त स्थान भरिए- Fill in the blanks in the verses.)

(क) प्रिय मातुल! …………….. प्रीतिम्।
(ख) …………….. कथं प्रयास्यसि
(ग) …………….. क्वचिदवकाशः।
(घ) …………….. दास्यसि मातुलचन्द्र!!
(ङ) कथमायासि न …………….. गेहम्।
उत्तर:
(क) वर्धय मे
(ख) मातुलचन्द्र
(ग) नैव दृश्यते
(घ) मह्यम्
(ङ) भो! मम।

प्रश्न 4.
प्रश्नानाम् उत्तराणि लिखत- (प्रश्नों के उत्तर लिखिए- Answer the questions.)

(क) अस्मिन् पाठे क: मातुल:?
(ख) नीलाकाशः कीदृशः अस्ति?
(ग) मातुलचन्द्रः किं न किरति?
(घ) किं श्रावयितुं शिशुः चन्द्रम् कथयति?
(ङ) चन्द्रस्य सितपरिधानम् कथम् अस्ति?
उत्तर:
(क) अस्मिन् पाठे चन्द्रः मातुलः।
(ख) नीलाकाशः विस्तृतः अस्ति।
(ग) मातुलचन्द्रः स्नेहं न किरति।
(घ) गीतिं श्रावयितुं शिशुः चन्द्र कथयति।
(ङ) चन्द्रस्य सितपरिधानम् तारकखचितम् अस्ति।

प्रश्न 5.
उदाहरणानुसारं निम्नलिखित पदानि सम्बोधने परिवर्तयत- (उदाहरणानुसार निम्नलिखित पदों को सम्बोधन में बदलिए- Change the words given below into vocative case as per example.)

यथा – चन्द्रः – चन्द्र!
(क) शिष्यः – …………..
(ख) गोपाल: – …………..
उत्तर:
(क) शिष्य!
(ख) गोपाल!

ग्रथा – बालिका – बालिके!
(क) प्रियंवदा – …………..
(ख) लता – …………..
उत्तर:
(क) प्रियंवदे!
(ख) लते!

यथा – फलम् – फल!
(क) मित्रम् – …………..
(ख) पुस्तकम् – …………..
उत्तर:
(क) मित्र!
(ख) पुस्तक!

यथा – रविः – रवे!
(क) मुनिः – …………..
(ख) कविः – …………..
उत्तर:
(क) मुने!
(ख) कवे!

यथा – साधुः – साधो!

(क) भानुः – …………..
(ख) पशुः – …………..
उत्तर:
(क) भानो!
(ख) पशो!

यथा – नदी – नदि!

(ख) देवी – …………..
(ख) मानिनी – …………..
उत्तर:
(क) देवि!
(ख) मानिनि!

प्रश्नः 6.
मञ्जूषातः उपयुक्तानाम् अव्ययपदानां प्रयोगेण रिक्तस्थानानि पूरयत- (मञ्जूषा से उपयुक्त अव्ययपदों का प्रयोग करके रिक्त स्थान भरिए- Fill in the blanks by using appropriate indeclinables from the box.)

कुतः , कदा , कुत्र , कथं , किम् |

(क) जगन्नाथपुरी …………… अस्ति?
(ख) त्वं …………… पुरीं गमिष्यसि?
(ग) गङ्गानदी प्रवहति?
(घ) तव स्वास्थ्यं ……… अस्ति ?
(ङ) वर्षाकाले मयूराः ………… कुर्वन्ति?
उत्तर:
(क) कुत्र
(ख) कदा
(ग) कुतः
(घ) कथम्
(ङ) किम्।

प्रश्नः 7.
तत्समशब्दान् लिखत- (तत्सम शब्द लिखिए- write these words as they are in Sanskrit.)

मामा ……………
मोर ……………
तारा ……………
कोयल ……………
कबूतर ……………
उत्तर:
(क) मातुलः
(ख) मयूरः
(ग) तारकम्
(घ) कोकिलः
(ङ) कपोतः।

Class 6th Sanskrit Chapter 15 मातुलचन्द्र Additional Important Questions and Answers

प्रश्न 1.
मञ्जूषायाः सहायतया रिक्तस्थानानि पूरयत। (मञ्जूषा की सहायता से रिक्त स्थान भरिए। Fill in the blanks with help from the box.)

दास्यसि , कुत्र , मातुल , गीतिम् , कुतः

(क) त्वरितमेहि मां श्रावय ……. ।
(ख) ……… आगच्छसि मातुलचन्द्र?
(ग) ……….. गमिष्यसि मातुलचन्द्र?
(घ) ……….. किरसि कथं न स्नेहम्?
(ङ) मह्यम् ……….. मातुलचन्द्र?
उत्तर:
(क) गीतिम्
(ख) कुतः
(ग) कुत्र
(घ) मातुल
(ङ) दास्यसि।

प्रश्न 2.
मञ्जूषात् समानार्थकं पदं चित्वा रिक्तस्थाने लिखत। (मञ्जूषा से समानार्थक शब्द चुनकर सामने रिक्त स्थान में लिखिए। Pick out the word having similar meanings and write down in the blank space.)

त्वरितम् , आयासि , एहि , आकाशः , प्रीतिम् , गेहम् |

(क) आगच्छसि ………..
(ख) आगच्छ ……………
(ग) गगनम् ……………
(घ) शीघ्रम् ……………
(ङ) गृहम् ……………
(च) स्नेहम् ……………
उत्तर:
(क) आयासि
(ख) एहि
(ग) आकाशः
(घ) त्वरितम्
(ङ) गेहम्
(च) प्रीतिम्।

प्रश्न 3.
भिन्नप्रकृतिकम् पदं चिनुत। (भिन्न प्रकृति वाला पद चुनिए। Pick out the word that is different from the rest.)

(क) बालिका, बालकः, बालकौ, गृहम्।
(ख) आगमिष्यति, आनयति, आगच्छति, आगच्छ।
(ग) कदा, कः, कुत्र, कुतः।।
(घ) छात्रान्, छात्रेभ्यः, छात्राणाम्, छात्रस्य।
उत्तर:
(क) बालकौ
(ख) आगच्छ
(ग) कः
(घ) छात्रस्य।

प्रश्न 4.
मञ्जूषात् उचितम् अव्ययपदं चित्वा अधोदत्तान् प्रश्नान् पूरयत- (मञ्जूषा से उचित अव्ययपद चुनकर निम्नलिखित प्रश्न पूरे कीजिए-Fick out the appropriate indeclinable from the box and complete the questions given below.)

किम् , कदा , कुतः , कथम् , कुत्र |

(क) बालक! त्वम् इदानीं ………. गच्छसि?
(ख) बालिके! त्वम् इदानीं ………. आगच्छसि?
(ग) ………. त्वम् इदानीं आपणम् गच्छसि?
(घ) ………. प्रयास्यसि मातुलचन्द्र?
(ङ) छात्राः विद्यालयात् ………. आगच्छन्ति?
उत्तर:
(क) कुत्र
(ख) कुतः
(ग) किम्
(घ) कथम्
(ङ) कदा।

बहुविकल्पीयप्रश्नाः

प्रश्न 1.
उचितेन विकल्पस्य प्रयोगे वाक्यपूर्तिं कुरुत। (उचित विकल्प चुनकर वाक्य पूर्ति कीजिए। Complete the sentences by using the correct option.)

(क)
(i) कथमायासि न भो! मम (स्नेहम्, गेहम्, मातुलम्)
(ii) त्वरितमेहि मां श्रावय ………. । (नीतिम्, प्रीतिम्, गीतिम्)
(iii) नैव दृश्यते क्वचिद् ………. । (अवकाशः, नीलाकाशः, चन्द्रः)
(iv) ………. तव चन्द्रिकावितानम्। (तारकखचितम्, धवलम्, सितपरिधानम्)
(v) मातुल! किरसि ………. न स्नेहम्? (किम्, मम, कथम्)
उत्तर:
(i) गेहम्
(ii) गीतिम्
(iii) अवकाशः
(iv) धवलम्
(v) कथम्।

(ख)
(i) कुत्र …………… मातुलचन्द्र? (गमिष्यति, गमिष्यन्ति, गमिष्यसि)
(ii) किं त्वं उपहारं दास्यसि …………… ? (माम्, मम्, मह्यम्)
(iii) कुतः आगच्छसि …………… ? (मातुलचन्द्रः, मातुलः, मातुलचन्द्र)
(iv) …………… वर्धय मे प्रीतिम्। (प्रिय मातुलः, प्रिय मातुल, प्रियः मातुलः)
(v) मातुलचन्द्रः कुत्र …………… ? (गमिष्यसि, गमिष्यति, गमिष्यामि)
उत्तर:
(i) गमिष्यसि
(ii) मह्यम्
(iii) मातुलचन्द्र
(iv) प्रिय मातुल
(v) गमिष्यसि।

प्रश्न 2.
उचितं विकल्पं चित्वा प्रश्नान् उत्तरत- (उचित विकल्प चुनकर प्रश्नों के उत्तर दीजिए Pick out the correct option and answer the questions.)

(क) अस्मिन् बालगीते मातुलः कः अस्ति? (सूर्यः, चन्द्रः, बालकः)
(ख) बालकः कं सम्बोधयति? (आकाशम्, चन्द्रिकावितानम्, मातुलचन्द्रम्)
(ग) नीलाकाशः कीदृशः वर्तते? (विस्तृतः, धवलः, प्रियः)
(घ) सितपरिधानम् कथं खचितम्? (स्नेहेन, चन्द्रिकया, तारकैः)
(ङ) मातुलचन्द्रः कुत्र न आयाति/आगच्छति। (गेहम्, आकाशम्, स्नेहम्)
उत्तर:
(क) अस्मिन् बालगीते चन्द्रः मातुलः वर्तते।
(ख) बालक: मातुलचन्द्रम् सम्बोधयति।
(ग) नीलाकाशः विस्तृतः वर्तते।
(घ) सितपरिधानम् तारकैः खचितम्।
(ङ) मातुलचन्द्रः गेहम् न आयाति।

We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book वाक्य रचना एवं अशुद्धि-शोधनम् Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions वाक्य रचना एवं अशुद्धि-शोधनम्

प्रश्न 1.
अधोदत्तेषु वाक्येषु रेखांकितानि पदानि संशोध्य समक्षं रिक्तस्थाने लिखत। (निम्नलिखित वाक्यों में रेखांकित पद शुद्ध करके सामने रिक्त स्थान में लिखिए। Correct the underlined words in the following sentences and write them in the blank spaces given below.)

(क) कर्ता-क्रियापद-समन्वयः — उत्तरम्
(i) त्वं किम् पठति? — …………
(ii) अहं संस्कृतं पठति। — …………
(iii) ते भ्रमणाय गच्छति। — …………
(iv) यूयम् कुत्र गच्छति? — …………
(v) वयम् क्रीडाक्षेत्रम् गच्छन्ति। — …………
(vi) युवाम् किम् कुरुथ? — …………
(vii) आवाम् खेलामः। — …………
उत्तर:
(i) पठसि
(ii) पठामि
(iii) गच्छन्ति
(iv) गच्छथ
(v) गच्छामः
(vi) कुरुथः
(vii) खेलावः

(ख) संज्ञा-सर्वनाम-समन्वयः — उत्तरम्
(i) उद्याने लताः सन्ति। ते फलन्ति। — ……………
(ii) पर्यटकाः आगच्छन्ति। ताः इस्ततः भ्रमन्ति। — ……………
(iii) सरोवरे कमले स्तः। तौ विकसतः।। — ……………
(iv) आम्रम् पक्वम् अस्ति। एषः मधुरं भवेत्। — ……………
(v) बालिके खेलतः। तौ हसतः अपि। — ……………
(vi) यः समाचार-पत्रं पठति, तत् मम पितामहः। — ……………
(vii) वस्त्राणि अत्र सन्ति। एते मालिनानि सन्ति। — ……………
उत्तर:
(i) ताः
(ii) ते
(iii) ते
(iv) एतत्
(v) ते
(vi) सः
(vii) एतानि

(ग) शुद्ध-लिंग प्रयोगः — उत्तरम्
(i) सरोवरे कमला: विकसन्ति। — ………….
(ii) सः फलान् खादति स्वस्थः च भवति। — ………….
(iii) वृक्षात् पत्रः पतति। — ………….
(iv) अत्र पुस्तकालयम् अपि सन्ति। — ………….
(v) यदा चक्राः भ्रमन्ति, वाहनम् चलति। — ………….
(vi) किम् एतत् तव गृहः ? — ………….
(vii) दुग्धम्: स्वास्थ्याय भवति। — ………….
उत्तर:
(i) कमलानि
(ii) फलानि
(iii) पत्रम्
(iv) पुस्तकालयाः
(v) चक्राणि,
(vi) गृहम्,
(vii) दुग्धम्

(घ) शुद्ध विभक्ति प्रयोगः
उत्तरम्
(अ)
(i) जनाः प्रातः व्यायामः कुर्वन्ति। — ………….
(ii) अहम् लेख लेखिष्यामि। — ………….
(iii) कृषकाः अन्न उत्पादयन्ति। — ………….
(iv) शिक्षक: छात्रम् प्रश्नः पृच्छति। — ………….
(v) आवाम् विदेश गमिष्यावः। — ………….
उत्तर:
(i) व्यायामम्
(ii) लेखम्
(iii) अन्नम्
(iv) प्रश्नम्
(v) विदेशम्

(आ)
(i) छात्राः बसयानं विद्यालयं गच्छन्ति। — ………….
(ii) वयम् मुखात् वदामः। — ………….
(iii) जनाः पादैः चलन्ति। — ………….
(iv) बालकः कन्दुकं खेलति। — ………….
(v) अहं ध्यानं पाठं पठिष्यामि। — ………….
उत्तर:
(i) बसयानेन
(ii) मुखेन
(iii) पादाभ्याम्
(iv) कन्दुकेन
(v) ध्यानेन

(इ)
(i) सज्जनाः परोपकारेण जीवन्ति। — ………….
(ii) पितामही पूजनम् देवालयम् अगच्छत्। — ………….
(iii) बालकाः खेलने क्रीडाक्षेत्रे गच्छन्ति। — ………….
(iv) दीपकः प्रकाशः भवति। — ………….
(v) जनाः पर्यटनम् अत्र आगच्छन्ति। — ………….
उत्तर:
(i) परोपकाराय
(ii) पूजनाय
(iii) खेलनाय
(iv) प्रकाशाय
(v) पर्यटनाय

(ई)
(i) कृषकाः सायं क्षेत्रैः आगच्छन्ति। — ………….
(ii) छात्रः विद्यालयेन गृहम् आगच्छत्। — ………….
(iii) पुस्तकं हस्तम् पतति। — ………….
(iv) महिला कूपम् जलम् आनयति। — ………….
(v) गङ्गा हिमालये निर्गच्छति। — ………….
उत्तर:
(i) क्षेत्रेभ्यः
(ii) विद्यालयात्
(iii) हस्तात्
(iv) कूपात्
(v) हिमालयात्

(उ)
(i) रविवासरं विद्यालये अवकाशः भवति।
(ii) सायंकालम् अहं भ्रमणाय गमिष्यामि।
(iii) पितामही. पञ्चावदनम् शयनात् उत्तिष्ठति।
(iv) घटम् अल्पम् जलम् आसीत्।
(v) हस्तः पञ्च अंगुलयः सन्ति।
उत्तर:
(i) रविवासरे
(ii) सायंकाले
(iii) पञ्चवादने
(iv) घटे
(v) हस्ते

प्रश्न 2.
उचितं विकल्पं चित्वा वाक्यपूर्तिं कुरुत। (उचित विकल्प चुनकर वाक्यों की पूर्ति कीजिए। Pick out the correct option and fill in the blanks.)

(क) (i) किं त्वं वृक्षान् ……… ? (पश्यसि, पश्यथः, पश्यथ)
(ii) अहं मित्रैः सह ………….. (खेलामि, खेलामः, खेलन्ति)
(iii) अध्यापिका कक्षायाम् ……… (आगमिष्यन्ति, आगच्छति, आगच्छन्ति)
(iv) श्वः जनकः मुम्बई नगरं ………. (गच्छति, गमिष्यन्ति, गमिष्यति)
(v) ……… मम संस्कृत परीक्षा आसीत्। (श्वः, ह्यः, अद्यः)
(vi) किम् ……… तव पुस्तकम्? (एषः, एषा, एतत्)
(vii) अधुना वयम् किम् ………? (करोमि, करिष्यामि, करिष्यामः)
उत्तर:
(i) पश्यसि
(ii) खेलामि
(iii) आगच्छति
(iv) गमिष्यति
(vi) एतत्
(vii) करिष्यामः

(ख)
(i) …………….. नमः। (सूर्यः, सूर्यम्, सूर्याय)
(ii) पिता ……… शतरुप्यकाणि यच्छति। (पुत्रः, पुत्राय, पुत्रम्)
(iii) वयम् ……………… संस्कृतं पठामः। (अध्यापकम्, अध्यापकेन, अध्यापकात्)
(iv) …………….. उभयतः वृक्षाः सन्ति। (मार्गम्, मार्गस्य, मार्गः)
(v) राजा दुष्यन्तः ……………… प्रति अगच्छत्। (आश्रमस्य, आश्रमः, आश्रमम्)
(vi) गुरुः …………….. प्रश्नम् अपृच्छत्। (शिष्यम्, शिष्येन, शिष्यात्)
(vii) मृगाः …………….. सह चरन्ति। (मृगाः, मृगाणाम्, मृगैः)
उत्तर:
(i) सूर्याय
(ii) पुत्राय
(ii) अध्यापकात्
(iv) मार्गम्
(v) आश्रमम्
(vi) शिष्यम्
(vii) मृगैः

(ग)
(i) मम विद्यालयः …………….. अस्ति। (विशालम्, विशालः, विशाल)
(ii) एषा वाटिका …………….. अस्ति। (रमणीयम्, रमणीया, रमणीयः)
(iii) जलम् …………….. अस्ति । (शीतलः, शीतलम्, शीतल)
(iv) आम्रणि …………….. सन्ति। (मधुर, मधुरम्, मधुराणि)
(v) मोहितः …………….. छात्रः अस्ति। (योग्य, योग्यम्, योग्यः)
उत्तर:
(i) विशालः
(ii) रमणीया
(iii) शीतलम्
(iv) मधुराणि
(v) योग्यः

We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book अनुवाद विधिः Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions अनुवाद विधिः

प्रश्न 1.
संस्कृत-पर्यायम् लिखत- (संस्कृत पर्याय लिखिए- write the Sanskrit equivalent.)

यथा-घर = गृहम्

(क)
(i) भवन = ………….
(ii) बाग़ = ………….
(iii) मोर = ………….
(iv) कबूतर = ……………..
(v) केले = ……………..
(vi) मंदिर = ……………..
(vii) दुकान = ……………..
(viii) गेंद = ……………..
(ix) फूलमालाएँ = ……………..
(x) नारियल = ……………..
उत्तर:
(i) भवनम्
(ii) उद्यानम्
(iii) मयूरः
(iv) कपोतः
(v) कदलीफलानि
(vi) मंदिरम्
(vii) आपणः
(viii) कंदुकम्
(ix) पुष्पमालाः
(x) नारिकेलम्

उत्तर:

(ग)
(i) पेड़ों को – …………..
(ii) बालक के लिए – …………..
(iii) पुत्र का – …………..
(iv) दो पैरों से – …………..
(v) फूलों का – …………..
(vi) बादल में – …………..
(vii) दो घोंसलों में – …………..
(viii) गाँव से (अलग) – …………..
उत्तर:
(i) वृक्षान्
(ii) बालकाय
(iii) पुत्रस्य
(iv) पादाभ्याम्
(v) पुष्पाणाम्
(vi) मेघेषु
(vii) नीड़योः
(viii) ग्रामात्

(घ)
(i) हँसता है = ……………
(ii) नमस्कार करती है = ………..
(iii) गिरते हैं (दो) = ……………
(iv) जाएँगे (हम) = …………
(v) दौड़ता है (वह) = …………
(vi) चरते हैं (वे) = …………….
(vii) खेलोगे (तुम) = ………………..
(viii) तैरता है (वह) = ………………..
उत्तर:
(i) हसति
(ii) नमति
(iii) पततः
(iv) गामष्यामः
(v) धावति
(vi) चरन्ति
(vii) खेलिष्यसि
(viii) तरति

प्रश्न 2.
अधोदत्तानि वाक्यानि संस्कृतेन लिखत- (निम्नलिखित वाक्यों को संस्कृत में लिखिए– Write the following sentences in Sanskrit.)

उत्तर:
(क) वानरः कदलीफलम् खादति।
(ख) यूयम् कुत्र गच्छथ?
(ग) वयम् पादाभ्याम् चलामः।
(घ) छात्रा: पठनाय विद्यालयम् गच्छन्ति।
(ङ) सर्पः बिलात् निस्सरति।।
(च) उद्याने शोभनानि पुष्पाणि सन्ति।
(छ) पर्णानाम् वर्णः हरितः भवति।
(ज) भो मित्र! त्वम् कदा आगमिष्यसि?

प्रश्न 3.
परस्परं मेलयत। (परस्पर मेल कीजिए। Match the following.)

(क) वाहनेषु – दो घोंसलों में
(ख) नीडे – मुख से (अलग)
(ग) मुखेन – हिरणों का
(घ) मुखात् – वाहन द्वारा
(ङ) नीड़योः – घोंसले में
(च) मृगैः – गाड़ियों/वाहनों में
(छ) मृगाणाम् – मुख द्वारा/ से
(ज) वाहनेन – हिरणों द्वारा
उत्तर:
(क) वाहनेषु – गाड़ियों/वाहनों में
(ख) नीडे – घोंसले में
(ग) मुखेन – मुख द्वारा/से
(घ) मुखात् – मुख से (अलग)
(ङ) नीडयोः – दो घोंसलों में
(च) मृगैः – हिरणों द्वारा
(छ) मृगाणाम् – हिरणों का
(ज) वाहनेन – वाहन द्वारा

अधोदत्तानि वाक्यानि अवलोकयत अनुवाद विधिं च अवगच्छत। (निम्नलिखित वाक्यों को देखिए और अनुवाद-विधि को समझिए। Look at the sentences given below and understand the rules of translation.)

संज्ञा-सर्वनाम का समन्वय (तालमेल) संज्ञा के लिंग व वचन के अनुसार सर्वनाम का रूप प्रयोग में आता है

कर्ता-क्रियापद का समन्वय

कर्ता के पुरुष व वचन के अनुसार क्रियापद का रूप निर्धारित होता है

अवधेयम्हिं

दी भाषा में ‘को’, ‘द्वारा’, ‘से’, ‘के लिए’, ‘का’/’की’ आदि परसर्ग शब्द से पृथक रहते हैं, किंतु संस्कृत में शब्द के साथ जुड़ जाते हैं और शब्द में रूपांतर आ जाता है। यथा- बालक का = बालकस्य, बालक को = बालकम् इत्यादि।

विशेष्यपद (संज्ञा) के लिंग व वचन के अनुसार विशेषण शब्द का रूप प्रयोग में लाया जाता है

धातुरूप का प्रयोग

वाक्य में आई हुई क्रिया के कालानुसार धातुरूप (लकार) का प्रयोग किया जाता है

इस प्रकार-वर्तमान काल की क्रिया दर्शाने के लिए लट्, भविष्यत् के लिए लृट् तथा भूतकाल के लिए ललकार के धातुरूप का प्रयोग होता है।

अव्ययपद का प्रयोग

संस्कृत भाषा में अव्ययपद ही ऐसे पद हैं जिनमें लिंग, पुरुष, वचन, काल आदि के प्रभाव से कोई रूपांतर नहीं आता

अनुवाद करते समय

सर्वप्रथम वाक्य के कर्ता को पहचानें। तदनुसार क्रियापद का रूप निर्धारित कर लें। वाक्य के शेष शब्दों में प्रयोगानुसार विभक्ति लगाएँ। शब्दरूप निर्धारित करते समय शब्द के
अंतिम अक्षर/स्वर तथा लिंग के अनुसार शब्द रूप चलाएँ। यथा

(क) विद्यालय में – विद्यालये – (विद्यालय शब्द अकारांत पुल्लिग)
पाठशाला में – पाठशालायाम् – (पाठशाला शब्द आकारांत स्त्रीलिंग)

(ख) पौधे – पादपाः – (पादप शब्द पुल्लिग)
पुस्तकें – पुस्तकानि – (पुस्तक शब्द नपुंसकलिंग) इत्यादि।

प्रारंभिक अवस्था में छात्र पाठ्यपुस्तक के व्याकरण भाग में शब्द रूप देख सकते हैं, ठीक वैसे ही जैसे आंग्ल (अंग्रेजी) भाषा का प्रयोग करते समय वर्तनी आदि के लिए शब्द कोष की सहायता ली जाती है। अभ्यास होने पर सहज ही शुद्ध प्रयोग करने लगेंगे।

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 7 Integrals. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 7 Important Extra Questions Integrals

Integrals Important Extra Questions Very Short Answer Type

Question 1.
Find \(\int \frac{3+3 \cos x}{x+\sin x} d x\)   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = \(\int \frac{3+3 \cos x}{x+\sin x} d x\) = 3 log lx + sin xl + c.
[∵ Num. = \(\frac{d}{d x}\) denom.]

Question 2.
Find : ∫(cos² 2x – sin² 2x)dx.   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = ∫cos 4x dx = \(\frac{\sin 4 x}{4}\)+ c.

Question 3.
Find : ∫ \(\frac{d x}{\sqrt{5-4 x-2 x^{2}}}\)   (C.B.S.E. Outside Delhi 2019)
Solution:

Question 4.
Evaluate ∫ \(\frac{x^{3}-1}{x^{2}}\) dx (N.C.E.R.T. C.B.S.E. 2010C)
Solution:

Question 5.
Find : \(\int \frac{\sin ^{2} x-\cos ^{2} x}{\sin x \cos x} d x\) (A.I.C.B.S.E. 2017)
Solution:

Question 6.
Write the value of \(\int \frac{d x}{x^{2}+16}\)
Solution:

Question 7.
Evaluate: ∫ (x³ + 1)dx.   (C.B.S.E. Sample Paper 2019-20)
Solution:
I = \(\int_{-2}^{2} x^{3} d x+\int_{-2}^{2} 1 \cdot d x\) = I₁
⇒ 0 + \([x]_{-2}^{2}\) [∵ I₁ is an odd function] = 2 – (-2) = 4.
⇒ 2 – (-2) = 4.

Question 8.
Evaluate: \(\int_{0}^{\pi / 2}\) e^x (sin x -cosx)dx. (C.B.S.E. 2014)
Solution:
\(\int_{0}^{\pi / 2}\) e^x (sin x -cosx)dx
\(\int_{0}^{\pi / 2}\)e^x (-cos x + sinx)dx
|“Form: ∫e^x (f(x) + f'(x) dx”
= \(\left[e^{x}(-\cos x)\right]_{0}^{\pi / 2}\)
= -e ^π/2cos\(\frac{\pi}{2}\) + e⁰ cos 0
= -e ^π/2 (0) + (1) (1)
= -0 + 1 = 1

Question 9.
Evaluate: \(\int_{0}^{2} \sqrt{4-x^{2}} d x\). (A.I.C.B.S.E. 2014)
Solution:

= [0 + 2 sin^-1(1)] – [0 + 0]
= 2sin^-1(1)= 2(π/2) = π

Question 10.
Evaluate : If f(x) = \(\int_{0}^{x}\) t sin t dt, then write the value of f’ (x). (A.I. C.B.S.E. 2014)
Solution:
We have : f(x) = \(\int_{0}^{x}\) t sin t dt.
f'(x) = x sin x. \(\frac{d }{d x}\) (x) – 0
[Property XII ; Leibnitz’s Rule]
= x sin x . (1)
= x sin x.

Question 11.
Prove that: \(\int_{0}^{2a}\) f(x)dx = \(\int_{0}^{2a}\) f(2a-x)dx. o o
Solution:
Put x = 2a – t so that dx = – dt.
When x = 0, t – 2a. When x = 2a, t – 0.
\(\int_{0}^{2a}\) f(x)dx = \(\int_{2a}^{0}\) f(2a-t)(-dt)
=\(\int_{2a}^{0}\) f{2a-t)dt = \(\int_{0}^{2a}\) f(2a-t)dt o
[Property II]
= \(\int_{0}^{2a}\) (2a – x) dx, [Property I]
which is true.

Integrals Important Extra Questions Short Answer Type

Question 1.
Evaluate :
\(\int \frac{\cos 2 x+2 \sin ^{2} x}{\cos ^{2} x} d x\) (C.B.S.E)
Solution:

Question 2.
Find : \(\int \frac{\sec ^{2} x}{\sqrt{\tan ^{2} x+4}} d x\)
Solution:
I = \(\int \frac{\sec ^{2} x}{\sqrt{\tan ^{2} x+4}} d x\)
Put tan x = t so that sec² x dx = dt.
∴ I = \(\int \frac{d t}{\sqrt{t^{2}+2^{2}}}\)
= log |t + \(\sqrt{t^{2}+4}\)| + C
= log |tan x + \(\sqrt{tan^{2}+4}\)| + C

Question 3.
Find : \(\int \sqrt{1-\sin 2 x} d x, \frac{\pi}{4}<x<\frac{\pi}{2}\)
Solution:

Question 4.
Find ∫sinx . log cos x dx (C.B.S.E 2019 C)
Solution:
∫sinx . log cos x dx
Put cox x = t
so that – sin x dx = dt
i.e., sin x dx = – dt.
∴ I = -∫log t.1dt
= -[ log t.t – ∫ 1/t. t dt ]
[Integrating by parts]
= – [t log t – t] + C = f(1 – log t) + C
= cos x (1 – log (cos x)) + C.

Question 5.
Find : \(\int \frac{\left(x^{2}+\sin ^{2} x\right) \sec ^{2} x}{1+x^{2}} d x\) (CBSE Sample Paper 2018-19)
Solution:

Question 6.
Evaluate \(\int \frac{e^{x}(x-3)}{(x-1)^{3}} d x\) (CBSE Sample Paper 2018-19)
Solution:
I = \(\int \frac{e^{x}(x-3)}{(x-1)^{3}} d x\)

Question 7.
Find ∫sin^-1 (2x)dx
Solution:

Question 8.
Evaluate : \(\int_{-\pi}^{\pi}\) (1 – x²) sin x cos² x dx.
Solution:
Here, f(x)=( 1-x²) sin x cos² x.
f(x) = (1 – x²) sin (-x) cos² (-x)
= – (1 – x²) sin x cos² x
= -f(x)
⇒ f is an odd function.
Hence, I = 0.

Question 9.
Evaluate : \(\int_{-1}^{2} \frac{|x|}{x} d x\) dx.
Solution:

Question 10.
Find \(\int \frac{3-5 \sin x}{\cos ^{2} x} d x\)   (C.B.S.E. 2018 C)
Solution:
\(\int \frac{3-5 \sin x}{\cos ^{2} x} d x\)
= 3∫sce² x dx – 5∫sec x tan x dx
= 3tan x – 5sec x + C

Question 11.
Find :
\(\int \frac{\tan ^{2} x \sec ^{2} x}{1-\tan ^{6} x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:
Let I = \(\int \frac{\tan ^{2} x \sec ^{2} x}{1-\tan ^{6} x} d x\)
Put tan³ x = t
so that 3 tan² x sec² x dx = dt
i.e tan² x sec²x dx = \(\frac{d t}{3}\)

Question 12.
Find : ∫ sin x .log cos x dx.   (CBSE 2019C)
Solution:
I = ∫ sin x .log cos x dx.
Put cos x = t
i.e. sinx dx = -dt
∴ I = – ∫log t.1 dt
= -[logt.t – ∫1/t . t. dt]
[Integrating by parts]
= – [t log t – t] + C
= t(1 – log t) + C
= cos x (1 – log (cos JC)) + C.

Question 13.
Evaluate : \(\int_{-\pi}^{\pi}\) (1 – x²) sin x cos² x dx   (C.B.S.E. 2019 (Delhi))
Solution:
Here, f(x) = (1 – x²) sin x cos² x
∴ f(-x) – (1 – x²) sin (-x) cos² (-x)
= – (1 – x²) sin x cos² x
= -f(x)
⇒ f is an odd function.
Hence, I = 0.

Question 14.
Evaluate \(\int_{-1}^{2} \frac{|x|}{x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:

Question 15.
Find : \(\int_{-\pi / 4}^{0} \frac{1+\tan x}{1-\tan x} d x\)
Solution:

Integrals Important Extra Questions Long Answer Type 1

Question 1.
Evaluate : \(\int \frac{\sin ^{6} x+\cos ^{6} x}{\sin ^{2} x \cos ^{2} x} d x\)   (C.B.S.E. 2019 (Delhi))
Solution:

Question 2.
Integrate the function \(\frac{\cos (x+a)}{\sin (x+b)}\) w.r.t. x. (C.B.S.E. 2019 (Delhi))
Solution:

Question 3.
Evaluate : ∫ x² tan^-1 x dx. (C.B.S.E. (F) 2012)
Solution:

Question 4.
Find : ∫[log (log x) + \(\frac{1}{(\log x)^{2}}\) ] dx (N.C.E.R.T.; A.I.C.B.S.E. 2010 C)
Solution:
Let ∫[log (log x) + \(\frac{1}{(\log x)^{2}}\) ] dx
= ∫ log(log x)dx + ∫\(\frac{1}{(\log x)^{2}}\) dx …… (1)
Let I = I₁ + I₂
Now I₁ = ∫ log (log x) dx
=∫ log (log x) 1 dx
= log (log x).x – ∫ \(\frac{1}{\log x \cdot x}\)x.dx
(Integrating by parts)
= xlog(logx) – ∫ \(\frac{1}{\log x}\)dx ……….. (2)
Let I₁ = I₃ + I₄

Putting in (2),
I₁ = x log (x) – \(\frac{x}{\log x}-\int \frac{1}{(\log x)^{2}}\) dx
Putting in (1),
I = x log (log x)

Question 5.
Integrate : ∫ e^x ( tan^-1 x + \(\frac{1}{1+x^{2}}\) ) dx   (N.C.E.R.T.)
Solution:
∫ e^x ( tan^-1 x + \(\frac{1}{1+x^{2}}\) ) dx
[From ∫ e^xf(x) + f'(x) ]dx”]
= ∫ e^x tan^-1 x dx +∫ e^x \(\frac{1}{1+x^{2}}\) ) dx
= ∫ tan^-1 x. e^x dx +∫ \(\frac{1}{1+x^{2}}\) ) e^x dx
= tan^-1 x. e^x – ∫ \(\frac{1}{1+x^{2}}\) ) e^x dx
+∫ \(\frac{1}{1+x^{2}}\) ) e^xdx
(integrating first integral by parts)
= e^x tan^-1x + c.

Question 6.
Integrate : \(\int e^{x}\left(\frac{x^{2}+1}{(x+1)^{2}}\right) d x\) (N.C.E.R.T)
Solution:

Question 7.
Find \(\int \frac{2 \cos x}{(1-\sin x)\left(1+\sin ^{2} x\right)} d x\) (C.B.S.E. 2018)
Solution:
Let i = \(\int \frac{2 \cos x}{(1-\sin x)\left(1+\sin ^{2} x\right)} d x\)
Put sin x = t so that cos x dx = dt.

⇒ 2 ≡ A(1 + t²) + (Bt + C) (1 – t)
2 ≡ (A – B)t² + (B – C)t + (A + C).
Comparing coeffs. of t²,
A-B = 0
⇒ A = B
Comparing coeffs. of t,
0 = B – C
⇒ B = C.
Comparing constant terms,
2 = A + C.
Thus, A = B = C = 1.
∴ From (2),
\(\frac{2}{(1-t)\left(1+t^{2}\right)}=\frac{1}{1-t}+\frac{t+1}{t^{2}+1}\)
∴ From (1)

= – log |1 — t| + \(\frac { 1 }{ 2 }\) log |t² + 1| + tan^-1 t + c
= – log |1 — t| + \(\frac { 1 }{ 2 }\) log (t² + 1) + tan^-1t + c
[∵ t² ≥ 0 ⇒ t² + 1 > 0 ∴ |t² + |1 = t² + 1]
= – log |1 – sin x| + \(\frac { 1 }{ 2 }\) log (sin² x + 1) + tan^-1 (sin x) + c
= – log (1 – sin x) + \(\frac { 1 }{ 2 }\) log (1 + sin²x)
+ tan^-1 |sin x| + c.
[∵’ 1 – sin x ≥ 0 |1 – sin x| = 1 – sin x]

Question 8.
Find : \(\int \frac{3 x+5}{x^{2}+3 x-18} d x\) (C.B.S.E. 2019)
Solution:
Let 3x + 5 = A(2x + 3) + B.
Comparing,
2A = 3, 3A + B = 5

Put x2 + 3x – 18 – t
so that (2x + 3 )dx = dt.
∴ I₁ = \(\int \frac{d t}{t}\) = log |t|
= log + | x² + 3x – 18 |

Question 9.
Find: \(\int \frac{\cos x}{(1+\sin x)(2+\sin x)} d x\) 2019C)
Solution:

Question 10.
Find: \(\int \frac{x^{4}+1}{2\left(x^{2}+1\right)^{2}} d x\) (C.B.S.E. Sample Paper 2018-19)
Solution:

⇒ t² + 1 ≡ A(t + 1)² + Bdt + 1) + Ct …(2)
Comparing coeffs. of like terms, we get :
A = 1, B = 0 and C = – 2.
Putting in (1),

Question 11.
Evaluate : \(\int \frac{x+2}{\sqrt{x^{2}+5 x+6}} d x\) (A.I.C.B.S.E. 2014)
Solution:

Question 12.
Evaluate : \(\int \frac{2 x+5}{\sqrt{7-6 x-x^{2}}} d x\)
Solution:

Question 13.
Evaluate : \(\int \frac{d x}{5+4 \cos x}\)
Solution:
I = \(\int \frac{d x}{5+4 \cos x}\)
Put cos x = \(\frac{1-t^{2}}{1+t^{2}}\)
where t = tan \(\frac { x }{ 2 }\) so that dt = \(\frac { 1 }{ 2 }\) sec² \(\frac { x }{ 2 }\) dx
i.e dt = \(\frac { 1 }{ 2 }\)( 1+ tan²\(\frac { x }{ 2 }\))dx
i.e. dt = \(\frac { 1 }{ 2 }\) (1 + t2) dx i.e. dx = \(\frac{2 d t}{1+t^{2}}\)

Question 14.
Evaluate : \(\int \frac{d x}{x\left(x^{3}+1\right)}\) (A.I. C.B.S.E 2013)
Solution:
I = \(\int \frac{d x}{x\left(x^{3}+1\right)}=\int \frac{x^{2} d x}{x^{3}\left(x^{3}+1\right)}\)
[Multiplying numerator and denominator by x²]
Put x³ = t so that 3x² dx = dt
i.e , x² dx = \(\frac { 1 }{ 3 }\) dt

Question 15.
Evaluate : \(\int_{0}^{2} e^{x} d x\) as the limit of a sum. (N.C.E.R.T.)
Solution:
Here f(x) = e^x ; a = 0, b = 2.
∴ f(a) -f(0) = e° = 1
f(a + h) =f(0 + h) = e^h
f(a + 2h) =f(0 + 2h) = e^2h, …….,

where nh = b – a = 2 – 0 = 2
= \(\lim _{h \rightarrow 0}\) h[1 + e^h +e^2h +… + e^(n-1)hh]
= \(\lim _{h \rightarrow 0} h \frac{1 \cdot\left(e^{n h}-1\right)}{e^{h}-1}\)

Question 16.
Evaluate: \(\int_{-1}^{2}\) (e^3x + 7x – 5)dx as a limit of sums. (A.I.C.B.S.E. 2015)
Solution:
Here f(x) = e^3x + 7x – 5 ; a = – 1, b = 2.
f (a) = f(- 1) = e^-3 – 7 – 5 = e^-3 – 12
f (a + h) = f(-1 + h)
= e^-3(-1 + h) + 1 (-1 + h)-5

Question 17.
Evaluate: \(\int_{-1}^{1} 5 x^{4} \sqrt{x^{5}+1} d x\). (N.C.E.R.T.)
Solution:
Let I = \(\int_{-1}^{1} 5 x^{4} \sqrt{x^{5}+1} d x\)
Put x⁵ = t so that 5x⁴ dx = dt.
When x = – 1, t = – 1. When x = 1, t= 1.

Question 18.
Prove that:
\(\int_{0}^{a} f(x)=\int_{0}^{a} f(a-x) d x\) , hence evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E 2019C)
Solution:
(i) Put x = a – y so that dx = -dy.
When x = 0, y = a. When x = a, y = 0.
∴ \(\int_{0}^{a}\) f(x) dx = \(\int_{0}^{a}\) f(a – y)(-dy)
= \(\int_{0}^{a}\) f(a-y)dy
= \(\int_{0}^{a}\) f(a-y)dy
= \(\int_{0}^{a}\) f{a-x)dx.

Put cos x = t
so that – sin x dx = dt
i.e. sin x dx = -dt.
When x = 0, t – cos 0=1.
When x = π, t – cos π = -1.

Question 19.
Evaluate : \(\int_{-1}^{2}\) |x³ – x | dx   (N.C.E.R.T.; C.B.S.E. 2016; A.I.C.B.S.E. 2012)
Solution:

On [- 1, 0], x³ – x ≥ 0
⇒ | x³ – x | = x³ – x;
On [0, 1], x³ – x ≤ 0
⇒ | x³ – x | = -(x³ – x) = x – x³
On [1, 2], x³ – x > 0
⇒ | x³ – x | = x³ – x

Question 20.
Solve the differential equation:
x dy -y dx = \(\sqrt{x^{2}+y^{2}}\) dx.
Solution:
The given differential equation is:
x dy -y dx = \(\sqrt{x^{2}+y^{2}}\) dx

Put y = vx, so that \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
∴(1) becomes:



Which is the reqd. solution.

Question 21.
Evaluate : \(\int_{-1}^{1} \frac{x+|x|+1}{x^{2}+2|x|+1} d x\) (CB.S.E. Sample Paper 2018 – 19)
Solution:

Thus f(-x) = -f(x)
⇒ f(x) is an odd function
∴ I₁ = 0 …… (2)


= 2 [log |x + 1|]\(\text { ] }_{0}^{1}\)
= 2 [log 2 – log 1]
= 2 [log 2-0]
= 2 log 2 …(3)
∴ From (1), (2) and (3), we get:
I = 2 log 2.

Question 22.
Find : \(\int \frac{4}{(x-2)\left(x^{2}+4\right)} d x\) (C.B.S.E. 2018 C)
Solution:
\(\frac{4}{(x-2)\left(x^{2}+4\right)} \equiv \frac{\mathrm{A}}{x-2}+\frac{\mathrm{B} x+\mathrm{C}}{x^{2}+4}\)
4 ≡ A(x² + 4) + (Bx + C)(x-2)
By comparison,
A = \(\frac { 1 }{ 2 }\), B = –\(\frac { 1 }{ 2 }\)
and C = 1.

Integrals Important Extra Questions Long Answer Type 2

Question 1.
Evaluate : \(\int \frac{e^{\tan ^{-1} x}}{\left(1+x^{2}\right)^{2}} d x\)
Solution:
Let I = \(\int \frac{e^{\tan ^{-1} x}}{\left(1+x^{2}\right)^{2}} d x\)
Put tan^-1 x = t i.e, x = tan t
So that \(\frac{1}{1+x^{2}} d x\) = dt

Question 2.
Integrate : \(\int \frac{x^{3}+x}{x^{4}-9} d x\)
Solution:

Now I₁ = \(\int \frac{x^{3}}{x^{4}-9} d x\)
Put x⁴ – 9 = t so that 4x³ dx – dt
i.e x³dx = \(\frac{d t}{4}\)

Put x² = u so that 2x dx = du
i.e, xdx = \(\frac{1}{2}\) du
Putting the values of Ij and I2 in (1), we get:

Question 3.
Find : \(\int \frac{\cos \theta}{\left(4+\sin ^{2} \theta\right)\left(5-4 \cos ^{2} \theta\right)} d \theta\) (A.I.C.B.S.E. 2017)
Solution:

Question 4.
Evaluate : \(\int \frac{\sin 2 x}{\sqrt{\sin ^{4} x+4 \sin ^{2} x-2}} d x\)
Solution:
I = \(\int \frac{\sin 2 x}{\sqrt{\sin ^{4} x+4 \sin ^{2} x-2}} d x\)
Put sin² x = t so that 2 sin x cos x dx = dt
i.e. sin 2x dx = dt.

Question 5.
Evaluate : \(\int \frac{x^{2}-1}{x^{4}+1} d x\)
Solution:

Question 6.
Evaluate: \(\int(\sqrt{\tan x}+\sqrt{\cot x}) d x\) (N.C.E.R.T.; A.I.C.B.S.E. 2014; C.B.S.E. 2010S)
Solution:

so that sec2 x dx = 2t dt
i.e., (1 + tan² x) dx = 2t dt
⇒ (1 + f) dx = 21 dt

[Dividing Num.. & Denom. by t²]
Put t – \(\frac { 1 }{ t }\)= y so that (1 + \(\frac{1}{t^{2}}\) )dt = dy
Also t² – 2 + \(\frac{1}{t^{2}}\) = y²
t² + \(\frac{1}{t^{2}}\) = y² + 2

Question 7.
Evaluate \(\int_{0}^{\pi / 2} \frac{x+\sin x}{1+\cos x} d x\) (A.I.C.B.S.E. 2011)
Solution:


= – [log|1+0|] – [log|1+1|]
= – [0-log2] = log 2
[log|1| = log I = 0]
From (1), I = (\(\frac{\pi}{2}\)– log 2) + log 2 = \(\frac{\pi}{2}\)

Question 8.
Evaluate :
\(\int_{0}^{\pi} e^{2 x} \cdot \sin \left(\frac{\pi}{4}+x\right) d x\) (C.B.S.E. 2016)
Solution:
Let I = \(\int_{0}^{\pi} e^{2 x} \cdot \sin \left(\frac{\pi}{4}+x\right) d x\)
Put \(\frac{\pi}{4}\) + x = t
x = t – \(\frac{\pi}{4}\) so that dx = dt
when x = 0, t = \(\frac{\pi}{4}\)
when x = π, t = \(\frac{5\pi}{4}\)

Question 9.
Evaluate : \(\int_{1}^{3}\) (x² + 3x + e^x )dx, as the limit of the sum. (C.B.S.E. 2018)
Solution:
Let f (x) = x² + 3x + e^x
f(x) = f(1)
= 1² + 3(1) + e¹ = 4 + e
f(a + h) = f(1 + h.)
= (1+h)² + 3(1+h) + e^1+h
= 4 + 5 h + h² + e^1+h
f(a + 2h) = f(1 + 2h)
= (1 +2h)² + 3(1 +2h) + e^1+2h
= 4 + 10h+ 4h² + e^1+2h

Question 10.
Evaluate : \(\int_{0}^{\pi / 2} \frac{x}{\sin x+\cos x} d x\)
Solution:

Question 11.
Evaluate : \(\int_{0}^{\pi / 2} \frac{\cos ^{2} x}{\cos ^{2} x+4 \sin ^{2} x} d x\)
Solution:


[Dividing Num. and Denom. by cos² x]
Put tan x = t so that sec² x dx = dt.
When x = \(\frac{\pi}{2}\), t = tan \(\frac{\pi}{2}\) → ∞

Question 12.
Evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E. 2017; A.I.C.B.S.E. 2013, 12)
Solution:

Put cos x = t so that – sin x dx = dt
i.e. sin x dx = – dt.
When x = 0, t = cos 0 = 1.
When x = π, t = cos π = – 1.

Question 13.
Evaluate \(\int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x\) (C.B.S.E. 2018)
Solution:

Put sin x – cos x = t
so that (cos x + sin x) dx = dt.
When x = 0, t = 0 – 1 = -1.

Question 14.
Evaluate \(\int_{0}^{3 / 2}|x \sin \pi x| d x\) (C.B.S.E. 2017)
Solution:

In (0, 1), x sin πx is +ve
⇒ | x sin πx | = x sin πx.
In (0, 3/2), x sin πx is +ve
⇒ | x sin πx | = -x sin πx.

Question 15.
\(\int_{0}^{4}\) |x| + |x-2| + |x-4|)dx (C.B.S.E. 2013)
Solution:
By definition,

Now, \(\int_{0}^{4}\) (| x | + | x – 2| + | x – 4|) dx
= \(\int_{0}^{4}\) (|x| + |x-2| + |x-4|)dx
\(\int_{0}^{4}\) (| x | + | x – 2| + |x – 4| ) dx
= \(\int_{0}^{4}\) [x + (x-2)}-(x-4)]dx
= \(\int_{0}^{4}\) [(-x +6) dx + = \(\int_{0}^{4}\) (x+2)dx

= 10 +(16-6)= 10+10 = 20.

Question 16.
Evaluate : \(\int_{0}^{\pi / 2} \frac{x \sin x \cos x}{\sin ^{4} x+\cos ^{4} x} d x\) (C.B.S.E. 2018 C)
Solution:


Let sin² x = t
⇒ sin x cos x dx = 1/2 dt
For x-0,t = sin² 0 = 0
and for x = π/2, t = sin² π/2 = 1

Question 17.
Evaluate : \(\int_{1}^{3}\)(3x² + 2x + 1)dx as the limit ofa sum. (C.B.S.E. 2018 C)
Solution:
a = 1, b = 3
and h = 2/n
nh = 2
\(\int_{1}^{3}\)(3x² + 2x + 1)dx
\(\lim _{h \rightarrow 0}\)
= lim h\f(l) +/(1 + h) +/(1 + 2h) + …
= \(\lim _{h \rightarrow 0}\) h[f(1) +f(1 + h) +f(1 + 2h) + …+ f(1 + (n — 1)h)]
= \(\lim _{h \rightarrow 0}\) h[(6+ {3(1 +h)² + 2(1 + h)+ 1} + (3(1 + 2h)² + 2(1 + 2h) + 1) + … + {3(1 +(n – 1)h)² + 2(1 +(n – 1)h)+ 1)]
= \(\lim _{h \rightarrow 0}\) h[6+ {3(1 + h² + 2h) + 2(1 +h) + 1) + {3(1 +4h² + 4h) } + 2(1 +2h)+ 1}+… + {3(1 + (n – 1)² h² + 2(n – 1)h) + 2(1 +(n—1)h)+(l +(n – 1)h}

= \(\lim _{h \rightarrow 0}\) h[(6) + (6 + 8h + 3h²) + (6 + 16h + 12h²) + … + [(6 + 3(n – 1)² h² + 8 (n —1)h}]

= \(\lim _{h \rightarrow 0}\)[6n+8h(1 + 2 +…+(n – 1))
+3h² {(1² + 2² + …+(n – 1)²}]

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 9 Differential Equations. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 9 Important Extra Questions Differential Equations

Differential Equations Important Extra Questions Very Short Answer Type

Question 1.
Find the order and the degree of the differential equation: \(x^{2} \frac{d^{2} y}{d x^{2}}=\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{4}\)
(Delhi 2019)
Solution:
Here, order = 2 and degree = 1.

Question 2
Determine the order and the degree of the differential equation:\(\left(\frac{d y}{d x}\right)^{3}+2 y \frac{d^{2} y}{d x^{2}}=0\) (C.B.S.E. 2019 C)
Solution:
Order = 2 and Degree = 1.

Question 3.
Form the differential equation representing the family of curves: y = b (x + a), where « and b are arbitrary constants. (C.B.S.E. 2019 C)
Solution:
Wehave:y= b(x + a) …(1)
Diff. w.r.t. x, b.
Again diff. w.r.t. x, \(\frac{d^{2} y}{d x^{2}}\) = 0,
which is the reqd. differential equation.

Question 4.
Write the general solution of differential equation:
\(\frac{d y}{d x}\) = e^x+y (C.B.S.E. Sample Paper 2019-20)
Solution:
We have: \(\frac{d y}{d x}\) = e^x+y
⇒ e^-y dy = e^x dx [Variables Separable
Integrating, \(\int e^{-y} d y+c=\int e^{x} d x\)
⇒ – e^-y + c = e^x
⇒ e^x + e^-y = c.

Question 5.
Find the integrating factor of the differential equation:
y\(\frac{d y}{d x}\) – 2x = y³e^-y
Solution:
The given equation can be written as.

Question 6.
Form the differential equation representing the family of curves y = a sin (3x – b), where a and b are arbitrary constants. (C.B.S.E. 2019C)
Solution:
We have: y – a sin (3x – b) …(1)
Diff. W.r.t y \(\frac{d y}{d x}\) = a cos (3x – b) .3
= 3a cos (3x – b)
\(\frac{d^{2} y}{d x^{2}}\) = -3a sin (3x – b) 3
= -9a sin (3x – b)
= -9y [Using (1)]
\(\frac{d^{2} y}{d x^{2}}\) + 9y = 0,m
which in the reqd. differential equation.

Differential Equations Important Extra Questions Short Answer Type

Question 1.
Determine the order and the degree of the differential equation:
\(\left(\frac{d y}{d x}\right)^{3}+2 y \frac{d^{2} y}{d x^{2}}=0\) (Outside Delhi 2019C)
Solution:
Order = 2 and Degree = 1.

Question 2.
Form the differential equation representing the family of curves: y = e^2x (a + bx), where ‘a’ and ‘h’ are arbitray constants. (Delhi 2019)
Solution:
We have : y = e^2x (a + bx) …(1)
Diff. w.r.t. x, \(\frac{d y}{d x}\) = e^2x (b) + 2e2x (a + bx)
⇒ \(\frac{d y}{d x}\) = be^2x + 2y ………….. (2)
Again diff. w.r.t. x,
\(\frac{d^{2} y}{d x^{2}}\) = 2be^2x + 2^2x
\(\frac{d^{2} y}{d x^{2}}\) = 2(\(\frac{d y}{d x}\) – 2y) + \(\frac{d y}{d x}\)
[Using (2)]
Hence, \(\frac{d^{2} y}{d x^{2}}\) -4 \(\frac{d y}{d x}\) + 4y = 0, which is the reqd. differential equation.

Question 3.
Solve the following differentia equation:
\(\frac{d y}{d x}\) + y = cos x – sin x (Outside Delhi 2019)
Solution:
The given differential equation is :
\(\frac{d y}{d x}\) + y = cos x – sin x dx Linear Equation
∴ I.F. = e^∫1dx = e^x
The solution is :
y.e^x = ∫ (cos x — sin x) e^x dx + C
⇒ y.e^x = e^x cos x + C
or y = cos x + C e^-x

Question 4.
Solve the following differential equation :
\(\frac{d x}{d y}\) + x = (tan y + sec²y). (Outside Delhi 2019 C)
Solution:
The given differential equation is :
\(\frac{d x}{d y}\) + x = (tany + sec²y).
Linear Equation
∵ I.F. = Jldy = ey
∴ The solution is :
x. ey = ∫ ey (tan y + sec² y)dy + c
⇒ x. ey = ey tan y + c
= x = tan y + c e-y, which is the reqd. solution.

Differential Equations Important Extra Questions Long Answer Type 1

Question 1.
Solve the differential equation
(x² – y²)dx + 2xydy = 0 (C.B.S.E. 2018)
Solution:

log x = -log (1 + v²) + log C
x(1 + v²) = C
x(1 + \(\frac{y^{2}}{x^{2}}\)) = C
x² + y² = C.

Question 2.
Find the particular solution of the differential equation (1 + x²)\(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^{2}}\), given that y = 0 when x = 1(C.B.S.E. 2018 C)
Solution:

Solution is y( 1 + x²) = \(\int \frac{1}{1+x^{2}} d x\)
= tan^-1 x + C
When y = 0,x = 1,
then 0 = \(\frac{\pi}{4}\) + C
C = \(\frac{\pi}{4}\)
∴ y(1 + x²) = tan ^-1 x – \(\frac{\pi}{4}\)
i.e, y = \(\frac{\tan ^{-1} x}{1+x^{2}}-\frac{\pi}{4\left(1+x^{2}\right)}\)

Question 3.
Find the differential equation representing the family of curves y = ae^{bx + 5}, where ‘a’and ‘A’are arbitrary constants. {C.B.S.E. 2018)
Solution:
We have: y = ae^{bx + 5} + 5 …(1)
Diff. w.r.t. x, \(\frac{d y}{d x}\) = ae^{bx + 5}. (b)
\(\frac{d y}{d x}\) = dy ……(2) [Using (1)]]
Again diff. w.r.t x.,
\(\frac{d^{2} y}{d x^{2}}=b \frac{d y}{d x}\) ………(3)

Dividing (3) by (2),

which is the required differential equation.

Question 4.
Find the particular solution of the differential equation x dx – ye^y \(\sqrt{1+x^{2}}\) dy = 0, given that y = 1 when x = 0. (C.B.S.E. 2019 C)
Solution:
The given differential equation is:

When x = 0,y = 1, ∴ 1 = c + c(0) ⇒ c = 1.
Putting in (2), \(\sqrt{1+x^{2}}\) = 1 + e^y(y -1),
which is the reqd. particular solution.

Question 5.
Obtain the differential equation of the family of circles, which touch the x-axis at the origin.   (N.C.E.R.T.; C.B.S.E. Sample Paper 2018)
Solution:
Let (0, α) be the centre of any member of the family of circles.

Then the equation of the family of circles is : x² + (y-α)² = α²
⇒ x² + y² – 2αy = 0 …(1)
Diff. w.r.t. x, 2x + 2y \(\frac{d y}{d x}\) 2α \(\frac{d y}{d x}\) = 0

which is the required differential equation.

Question 6.
Obtain the differential equation representing the family of parabolas having vertex at the origin and axis along the positive direction of x-axis. (N.C.E.R.T.)
Solution:
Let S (a, 0) be the focus of any member of the family of parabolas.
Then the equation of the family of curves is y² = 4 ax …………. (1)
Diff. w.r.t. x, 2y\(\frac{d y}{d x}\) = 4a ……………. (2)
Using (2) in (1), we get:
y² = (2y\(\frac{d y}{d x}\))x

y² – 2xy\(\frac{d y}{d x}\) = 0
which is the required differential equation.

Question 7.
Find the general solution of the differential equation:
(tan²x + 2 tanx + 5) \(\frac{d y}{d x}\) = 2 (1 + tanx) sec² x
Solution:
We have : (tan² x + 2 tan x + 5)\(\frac{d y}{d x}\)
= 2 (1 + tanx) sec²x
Integrating

Put t² + 2t + 5 = z
so that (2t+ 2) dt = dz.
∴ From (2),
1 = \(\int \frac{d z}{z}\) = log| z | = log |t² + 2t + 5|
= log |tan² x| + 2 tan x + 5|
From (1), y = log |tan² x| + 2 tan x + 5| + c,
which is the required general solution.

Question 8.
Solve the differential equation:
(x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1 ; y(0) = 0. (C.B.S.E. 2019)
Solution:
The given equation can be written as :
\(\frac{d y}{2 e^{-y}-1}=\frac{d x}{x+1}\)
| Variables Separable

Integrating, \(\int \frac{e^{y} d y}{2-e^{y}}=\int \frac{d x}{x+1}\)
⇒ – log |2 – e^y| + log |C| = log |x + 1|
⇒ (2 – e^y) (x + 1) = C.
When x = 0, y = 0, then C = 1.
Hence, the solution is (2 – e^y) (x + 1) = 1.

Question 9.
Solve: (a) (i) \(\frac{d y}{d x}\) = 1 + x + y + xy
(ii) xyy’ = 1 + x + y + xy. (N.C.E.R.T.)
(b) Find the particular solution of the differential dy
equation \(\frac{d y}{d x}\) = 1 + x + y + xy, given that y = 0 when x = 1. (A.I.C.B.S.E. 2014)
Solution:
(a), (i) The given equation is :
\(\frac{d y}{d x}\) = 1 + x + y + xy
\(\frac{d y}{d x}\) = (1 +x) (1 +y)
\(\frac{d}{1+y}\) = (1 + x)dx.
|Variables Separable

Integrating,
\(\int \frac{d y}{1+y}\) = ∫(1 + x)dx + c
⇒ log |1 + y | = x + \(\frac { 1 }{ 2 }\) x² + c,
which is the required solution.

(ii) The given equation is xyy’ = 1 + x + y + xy
⇒ xy\(\int \frac{d y}{1+y}\) = (1 + x)(1 + y)

= y – log|1 + y| = log|x|+ x + c
= x + log |x (1 + y)|+ c,
which is the required solution.

(b) From part (a) (i),
Iog|1+y| = x + \(\frac { 1 }{ 2 }\)x² + c …(1)
When x = 1, y = 0, then:
log |1+0|= 1 + \(\frac { 1 }{ 2 }\)(1)² + c
log 1 = 1 + \(\frac { 1 }{ 2 }\) + c
0 = \(\frac { 3 }{ 2 }\) + c
c = \(-\frac { 3 }{ 2 }\)
Putting in (1), log |1 + y| = x + \(\frac { 1 }{ 2 }\)x² – \(\frac { 3 }{ 2 }\)
which is the required particular solution.

Question 10.
Solve the differential equation:
\(\frac{d y}{d x}\) = 1 + x² + y² + x²y²
given thaty = 1 when x = 0. (Outside Delhi 2019)
Solution:
The given equation is \(\frac{d y}{d x}\) = 1 + x² + y² + x²y²
⇒ \(\frac{d y}{d x}\) = (1+x²)(1 +y²)
⇒ \(\frac{d y}{1+y^{2}}\) (x² + 1) dx
|Variables Separable

Integrating, ∫\(\frac{d y}{1+y^{2}}\) = ∫(x² + 1) dx + C
tan^-1y = \(\frac{x^{3}}{3}\) + x + C ………. (1)
Where x = 0,y = 1,
∴ tan^-1 (1) = C
C = \(\frac{\pi}{4}\)
Putting in (1),
tan^-1 y = \(\frac{x^{3}}{3}+x+\frac{\pi}{4}\)
which is the reqd. particular solution.

Question 11.
Find the particular solution of the differential equation: e^x tan y dx + (2 – e^x) sec² y dy = 0, given thaty = \(\frac{\pi}{4}\) where x = 0.
Solution:
The given differential equation is:

∴ From (1),
log C + log |e^x – 2| = log |tan y|
⇒ tany = C(e^x – 2) …(2)
When x = 0, y = y = \(\frac{\pi}{4}\)
∴ 1 = C(1 – 2)
C = -1
Putting in (2),
tan y = 2 – e^x
which is the required particular solution.

Question 12.
Find the particular solution of the following differential equation:
cosy dx + (1 + 2e^-x) siny dy = 0; y(0) = \(\frac{\pi}{4}\) .
(CBSE Sample Paper 2018 – 19)
Solution:
The given differential equation is:
cos y dx + (1 + 2e^-x) sin ydy = 0

log |e^x| – log |cos y| = log|C|
e^x + 2 = C cos y ….. (1)

Substituting, x = 0, y = \(=\frac{\pi}{4}\) in(1),we get:
1 + 2 = C cos \(=\frac{\pi}{4}\)
C = \(\frac{3}{1 / \sqrt{2}}\)
C = 3√2
Putting in (1),
e^x + 2 = 3√2 cos y
which is the required particular solution.

Question 13.
Find the particular solution of the following differential equation:
(x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1 ; y = 0 when x = 0. (C.B.S.E. 2012)
Solution:
The given equation is (x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1

-log|2 – e^y| = log|x + 1| + log|c|,
where c’ = log |c|
⇒ log \(\left|\frac{1}{2-e^{y}}\right|\) = log |c(x + 1)|
⇒ \(\frac{1}{2-e^{y}}\) = c(x + 1)
When x = 0, y = 0;
\(\frac{1}{2-e^{0}}\) = c(0 + 1)
⇒ c = \(\frac{1}{2-1}=\frac{1}{1}\) = 1

Putting (1)
\(\frac{1}{2-e^{y}}\) = 1.(x + 1)
⇒ (x + 1)(2 – e^y) = 1
which is the required particular solution.

Question 14.
Solve the differential equation:
(1 – y²) (1 + log x)dx + 2xy dy = 0, given that when x = 1 ,y = 0.
(C.B.S.E. 2016)
Solution:
The given equation is :
(1 – y²) (1 + log x)dx + 2xy dy = 0

Putting in (1),
\(\frac{(1+\log x)^{2}}{2}\) = log|1 – y²| + 1/2
(1 + log x)² = 2 log|1 – y²| + 1
which is the required solution.

Question 15.
Solve the differential equation:
x cos x (\(\frac { y }{ x }\)) \(\frac{d y}{d x}\) = y cos(\(\frac { y }{ x }\)) = x (C.B.S.E. 2019 C)
Solution:
The given equation is:

Put \(\frac { y }{ x }\) = v i.e, y = vx so that \(\frac { dy }{ dx }\) = v + x \(\frac { dv }{ dx }\)
∴ (1) becomes:
cos v (v + x\(\frac { dv }{ dx }\)) = vcosv + 1
= v + x \(\frac { dv }{ dx }\) = v + \(\frac { 1 }{ cos v }\)
x \(\frac { dv }{ dx }\) = \(\frac { 1 }{ cos v }\)
cos v dv = \(\frac { dx }{ x }\)
[Variables Seperable]

Integrating, ∫ cos v dv = ∫ \(\frac{d x}{ x}\) + c
sin = log|x| + c
sin \(\frac{y}{ x}\) = log|x| + c,
which is the reqd. solution.

Question 16.
Find the general solution of the differential equation: \(\frac{d x}{d y}=\frac{y \tan y-x \tan y-x y}{y \tan y}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
The given differential equation is :

|Linear Equation
Comparing with \(\frac{d x}{d y}\) + Py = Q, we have :
‘P’ = \(\frac{1}{y}+\frac{1}{\tan y}\) and ‘Q’ = 1

∴ I.F = \(e^{\int\left(\frac{1}{y}+\frac{1}{\tan y}\right) d y}=e^{\log y+\log \sin y}\)
e^log(ysiny) = ysiny.
∴ The solution is
x x I.F. = ∫ (Q x I.F.)dy + C
⇒ x(y sin y) = ∫(1 x y sin y)dy + C
⇒ xy sin y = ∫ y sin y dy + C
⇒ xy sin y = y (- cos y) – ∫(1) -cos y)dy + C

(Integrating by Parts)
⇒ xy sin y = – y cos y + ∫ cos ydy + C
⇒ xy sin y = – y cos y + sin y + C
⇒ x = \(\frac{\sin y-y \cos y+C}{y \sin y}\)
which is the required general solution.

Question 17.
Solve the differential equation :
xdy – ydx = \(\sqrt{x^{2}+y^{2}}\) dx , given that y = 0 when x = 1. (C.B.S.E. 2019)
Solution:
The given equation can be written as :


where x = 1, y = 0
∴ 0 + \(\sqrt{1+0} \) = c(1)
⇒ c = 1
Putting in (2), y + \(\sqrt{x^{2}+y^{2}}\) = x²,
which is the reqd. solutions.

Question 18.
Solve the following differential equation:
\(x y \log \left(\frac{y}{x}\right) d x+\left(y^{2}-x^{2} \log \left(\frac{y}{x}\right)\right) d y=0\) (C.B.S.E. 2010 C)
Solution:
The given equation can be written as:

Question 19.
Solve the differential equation:
xdy-y dx= \(\sqrt{x^{2}+y^{2}}\) dx.
(iC.B.S.E. Sample Paper 2019)
Solution:
The given differential equation is:

Put y = vx, so that \(\frac{d y}{d x}\) = dv + x \(\frac{d v}{d x}\)
(1) becomes:

⇒ y+ \(\sqrt{x^{2}+y^{2}}\) = cx²,
which is the reqd. solution.

Question 20.
Prove that x² – y² = c(x² + y²)² is the general solution of the differential equation: (x³ – 3xy²)dx = (y³ – 3x²y)dy, where c is a parameter. (C.B.S.E. 2017)
Solution:
We have :(x³ – 3xy²) dx = (y³ – 3x²y)dy

∴ v³ – 3v = A(1 + v)(1 + v²) + B(1 – v) (1 + v²) + (Cv + D) (1 – v²).
Putting v= 1,
1-3 = A(2) (2)
⇒ A = -1/2

Putiing v = -1, -1 + 3 = B(2)(1 + 1)
⇒ B = 1/2

Putting v = 0
⇒ 0 = A(1)(1) + B(1)(1) + D(1)
⇒ 0 = \(-\frac{1}{2}+\frac{1}{2}\) + D
D = 0
Comparing coeff. of v³, 1 = A – B – C
⇒ C = A – B – 1 = \(-\frac{1}{2}-\frac{1}{2}\) – 1 = -2
∴ From (2),

Squaring , x² – y² = c’²(x²+ y²)²
⇒ x² – y² = c’² (x² + y² )²
where c’² = c,
which is the required solution.

Question 21.
Show that the differential equation:
2ye^x/y dx + (y – 2x e^x/y) dy = 0 is homogeneous and find the particular solution, given that x = 0 when y = 1. (C.B.S.E. 2013)
Solution:
(i) The given equation is :
2ye^x/y dx + (y – 2x e^x/y) dy = 0

Thus f(x, y) is homogeneous function of degree zero.

⇒ 2e^v = – log |y| + c
⇒ e^x/y = -log|y| + c …………….(2)

Now x = 0 when y = 1,
∴ 2(1) = -log |1| + c
⇒ 2 = – log 1 + c
⇒ 2 = —0 + c
⇒ c = 2.

Putting in (2),
2e^x/y = – log |y|+ 2,
which is the required solution.

Question 22.
Solve the differential equation:
(1 + x²)\(\frac{d y}{d x}\) + 2xy – 4x² =0, subject to the initial condition y (0) = 0. (C.B.S.E. 2019)
Solution:
The given equation can be written as :

Multiplying (1) by (1 + x²), we get:
(1 + x²)\(\frac{d y}{d x}\) + 2xy = 4x² dx
⇒ \(\frac{d}{d x}\) y.(1 + x²) = 4x²

Integrating, y.(1 + x²) = ∫ 4x² dx = \(\frac{4 x^{3}}{3}\) + C
⇒ y(1 + x²) = \(\frac{4}{3}\) x² + C …(2)
When x = 0, y = 0,
∴ C = 0 + C
⇒ C = 0.
ry 4 T
Putting in (2), y(1 + x²) = \(\frac{4}{3}\) x³ , which is the required solution.

Question 23.
Solve the differential equation :
\(\frac{d y}{d x}-\frac{2 x}{1+x^{2}} y\) = x² + 2 (C.B.S.E. 2019)
Solution:
The given equation is :

Hence, y = (1 + x²) (x + tan^-1 x + C).

Question 24.
Find the general solution of the following differential equation:
(1 + y²) + (x – e^tan-1y)\(\frac{d y}{d x}\) (C.B.S.E. 2016)
Solution:
The given equation is:


Putting xee^tan-1y = \(\frac{1}{2}\)e^2tan-1y + c
x = \(\frac{1}{2}\)e^tan-1y + c
which is the required solution.

Question 25.
(i) Solve the differential equation:
(tan^-1 y – x)dy = (1 + y²) dx. (N.C.E.R.T.; C.B.S.E. 2015)
(ii) Find the particular solution when x = 0, y = 0. (A.I.C.B.S.E. 2013)
Solution:
(i) The given equation can be written as :
\(\frac{d x}{d y}+\frac{x}{1+y^{2}}=\frac{\tan ^{-1} y}{1+y^{2}}\) …… (1)
Comparing with \(\frac{d x}{d y}\)+ Px = Q , we have:


which is the required solution.

(ii) When
x – 0, y = 0.
0 = (tan^-10 – 1) + ce-tan^-10,
⇒ 0 – (0 – 1) + ce^-0
⇒ 0 = – 1 + c
⇒ c = 1.
Putting in (3),
x = (tan^-1 y – 1) + e^-tan-1y,
which is the required particular solution.

We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book व्यावहारिक शब्दकोश Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions व्यावहारिक शब्दकोश

पशुओं के नाम (Name of Animals)|

पक्षियों के नाम (Name of Birds)

खाद्य पदार्थ (Name of Edibles)

व्यवसाय और संबंधवाचक शब्द (Words related to Business and Relation)

शरीर के अंग (Parts of Body)

फलों के नाम (Name of Fruits)

फलों के नाम (Name of Fruits)

कुछ अन्य उपयोगी शब्द (Roots of Verbs in Practice)

कुछ अन्य उपयोगी शब्द (Some other Useful Words)

 

We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book अपठित गद्यांश Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions अपठित गद्यांश

अधोलिखितम् अनुच्छेदान् पठित्वा प्रदत्त-प्रश्नानाम् उत्तराणि लिखत- (नीचे दिए गए अनुच्छेदों को पढ़कर दिए गए प्रश्नों के उत्तर लिखिए- Read the following paragraphs and answer the questions.)

1. पितामही शयन-कक्षे गच्छति। सा ईश्वरं स्मरति। तत्पश्चात् सा शयनं करोति। प्रातः सा पञ्चवादने उत्तिष्ठति। सा स्नानं करोति। स्नानस्य पश्चात् सा देवस्य पूजनं करोति। सा भक्ति-गानं गायति। सा सूर्यम् नमति। सा वदति-‘सूर्याय नमः।’ सूर्यः संसाराय जीवनं ददाति, अतः सः पूज्यः अस्ति।

I. एकपदेन उत्तरत। (एक पद में उत्तर दीजिए। Answer in one word.)

(क) पितामही कुत्र गच्छति?
(ख) सा कदा उत्तिष्ठति?
(ग) सा कम् नमति?
(घ) कः संसाराय जीवनं ददाति?
उत्तर:
(क) शयन कक्षे
(ख) पञ्चवादने
(ग) सूर्यम्
(घ) सूर्यः

II. पूर्णवाक्येन उत्तरत। (संपूर्ण वाक्य में उत्तर दीजिए। Answer in sentences.)

(क) पितामही कदा पूजनम् करोति?
(ख) सूर्यः किमर्थं पूज्यः अस्ति? ।
उत्तर:
(क) पितामही प्रातः स्नानस्य पश्चात् देवस्य पूजनं करोति।
(ख) सूर्यः संसाराय जीवनं ददाति, अतः सः पूज्यः अस्ति।

III. भाषाकार्यम्-निर्देशानुसार उत्तरत। (भाषाकार्य-निर्देशानुसार उत्तर दीजिए। Answer as per directions.)

(क) ‘स्नानम्’ इति अस्य समविभक्तिपदम् (कर्मकारकम्) लिखत। यथा
ईश्वरम् (i) ………….. (ii) ………….. (ii) ………….. (iv) …………..
उत्तर:
(i) शयनम्
(ii) स्नानम्
(iii) पूजनम्
(iv) सूर्यम् अथवा जीवनम्।

(ख) ‘गच्छति’ इति सम-पुरुष-वचन-क्रियापदं लिखत। यथा
भजति (i) ………. (ii) ………….. (iii) …………….(iv) …………..
उत्तर:
(i) करोति
(ii) नमति
(iii) वदति
(iv) ददाति अथवा अस्ति।

(ग) ‘सूर्याय नमः’ इति प्रयोगम् अनुसृत्य रिक्तस्थानानि पूरयत। यथा
गणेशाय (गणेश) नमः (i) ………….. (अध्यापक) (ii) ……….. (पितामह) नमः।
उत्तर:
(i) अध्यापकाय
(ii) पितामहाय

2. राहुल: जंतुशालाम् गच्छति। सः जनकेन सह गच्छति। तत्र सः सिंहम् पश्यति। सिंहः उच्चैः गर्जति। ततः सः मयूरं पश्यति। मयूरः उपवने शोभनं नृत्यति। सः वृक्षे वानरं दृष्ट्वां भयभीतः अस्ति। वानरः कदलीफलं खादति। एकः अन्यः वानरः अपि तत्र कूर्दति। जंतुशालायाम् अनेके मृगाः सन्ति। राहुलः सर्वान् मृगान् पश्यति प्रसन्नः च भवति। ततः सः गृहम् आगच्छति।

I. एकपदेन उत्तरत। (एक पद में उत्तर दीजिए। Answer in one word.)

(क) राहुलः कुत्र गच्छति?
(ख) स: केन सह गच्छति?
(ग) क: उच्चैः गर्जति?
(घ) वानरः किम् खादति?
उत्तर:
(क) जंतुशालाम्
(ख) जनकेन
(ग) सिंहः
(घ) कदलीफलम्

II. पूर्णवाक्येन उत्तरत। (संपूर्ण वाक्य में उत्तर दीजिए। Answer in sentences.)

(क) मयूरः किं करोति?
(ख) राहुलः कदा भयभीतः अस्ति?
उत्तर:
(क) मयूरः उपवने शोभनं नृत्यति।
(ख) राहुलः वृक्षे वानरं दृष्ट्वा भयभीतः अस्ति।

III. भाषाकार्यम् निर्देशानुसार उत्तरत। (भाषाकार्य-निर्देशानुसार उत्तर दीजिए। Answer as per directions.)

उत्तर:

2. कर्तृपदम् बहुवचने परिवर्तय वाक्यं पुनः लिखत।
यथा- सः सिंहम् पश्यति – ते सिंहम् पश्यन्ति।

(i) सिंहः उच्चैः गर्जति।
(ii) वानरः अपि तत्र कूर्दति।
उत्तरम्-
(i) सिंहाः उच्चैः गर्जन्ति।
(ii) वानराः अपि तत्र कूर्दन्ति।

3. यथानिर्देशनम् रिक्तस्थानपूर्ति कुरुत।

(i) उपवने ………… (द्विवचन) ………… (बहुवचन)
(ii) कदलीफलम् ………… (द्विवचन) ………… (बहुवचन)
(iii) भवति ………… (द्विवचन) ………… (बहुवचन)
(iv) अस्ति …………. (द्विवचन) ………… (बहुवचन)
उत्तर:
(i) उपवनयोः, उपवनेषु
(ii) कदलीफले, कदलीफलानि
(iii) भवतः, भवन्ति
(iv) स्तः, सन्ति।

3. ऋषि: वाल्मीकिः महाकविः आसीत्। सः रामायणम् अरचयत्। वाल्मीकिः आदिकविः मन्यते। रामायणम् आदिकाव्यम् अस्ति। रामायणे श्रीरामस्य कथा अस्ति। श्रीरामः स्वजनकस्य दशरथस्य आज्ञाम् अपालयत्। सः सीतालक्ष्मणभ्यां सह वने अवसत्। सः रावणम् अमारयत्। रामराज्ये सर्वे धर्मस्य मार्गेण चलन्ति स्म। श्रीरामः आदर्शः पुत्रः आदर्शः राजा च आसीत्। तस्य राज्ये जनाः सुखिनः आसन्।

I. एकपदेन उत्तरत। (एक पद में उत्तर दीजिए। Answer in one word.)

(क) कः ऋषि महाकविः आसीत्?
(ख) किम् आदिकाव्यम् अस्ति?
(ग) रामायणे कस्य कथा अस्ति?
(घ) रामः सीतालक्ष्मणांभ्याम् सह कुत्र अवसत्?
उत्तर:
(क) वाल्मीकिः
(ख) रामायणम्
(ग) श्रीरामस्य
(घ) वने

II. पूर्णवाक्येन उत्तरत। (संपूर्ण वाक्य में उत्तर दीजिए। Answer in sentences.)

(क) रामराज्ये सर्वे कथं चलन्ति स्म? ।
(ख) श्रीरामः काम् अपालयत्?
उत्तर:
(क) रामराज्ये सर्वे धर्मस्य मार्गेण चलन्ति स्म।
(ख) श्रीरामः स्वजनकस्य दशरथस्य आज्ञा अपालयत्।

III. भाषाकार्यम्-यथानिर्देशम् उत्तरत। (भाषाकार्य-निर्देशानुसार उत्तर दीजिए। Answer as per directions.)

(क)
(i) अस्ति – धातुः – …………. लकार: – …………. पुरुषः वचनम्
(ii) मार्गेण – …………. विभक्ति – …………. वचनम्
(iii) कथा – …………. (द्विवचन) – …………. (बहुवचन)
(iv) मार्गेण – …………. (द्विवचन) – …………. (बहुवचन)
उत्तर:
(i) अस्, लट्, प्रथमः, एक
(ii) तृतीया एक
(iii) कथे, कथाः
(iv) मार्गाभ्याम्, मार्ग:

(ख) यथा- आसीत् – अस्ति
(i) अरचयत् – ………….
(ii) अपालयत् – ………….
उत्तर:
(i) रचयति
(ii) पालयति

(ग) यथा- आसीत् – अस् धातुः
(i) अवसत् – धातुः ………….
(ii) अपालयत् – धातुः ………….
उत्तर:
(i) वस्
(ii) पाल्

(घ) कर्तृपदं बहुवचने परिवर्त्य वाक्यं पुनः लिखत।
स: रावणम् मारयति स्म। ………………..
उत्तर:
ते रावणं मारयन्ति स्म।

प्रश्न 4. अद्य विद्यालये अवकाशः अस्ति। राघवः पाठं न पठति। सः दूरदर्शनेन क्रिकेट प्रतियोगितां पश्यति। राघवस्य मित्रं रोहणः अपि विद्यालय-कार्यम् न करोति। रोहणः पुत्तलिका खेलं द्रष्टुम् गच्छति। सः मित्रैः सह खेलम् पश्यति। पुत्तलिका खेल: अतीव रोचकः अस्ति। पुत्तलिकाः नृत्यन्ति। सूत्रधारः खेलं करोति। खेलं दृष्ट्वा सर्वे प्रमुदिताः सन्ति।

I. एकपदेन उत्तरत। (एक पद में उत्तर दीजिए। Answer in one word.)

(क) अवकाशः कुत्र अस्ति?
(ख) क: पाठं न पठति?
(ग) रोहणः कस्य मित्रम्?
(घ) रोहणः किं न करोति?
उत्तर:
(क) विद्यालये
(ख) राघवः
(ग) राघवस्य
(घ) विद्यालय-कार्यम्

II. पूर्णवाक्येन उत्तरत। (संपूर्ण वाक्य में उत्तर दीजिए। Answer in sentences.)

(क) रोहण: किमर्थं गच्छति?
(ख) सूत्रधारः किं करोति, पुत्तलिकाः च किं कुर्वन्ति?
उत्तर:
(क) रोहणः पुत्तलिका खेलं द्रष्टुम् गच्छति।
(ख) सूत्रधारः खेलं करोति, पुत्तालिकाः च नृत्यन्ति।

III. भाषाकार्यम्-निर्देशानुसार उत्तरत। (भाषाकार्य-निर्देशानुसार उत्तर दीजिए। Answer as per Directions.)

1.’पुत्तलिकाखेलः’ इति पदस्य किं विशेषणम् अत्र प्रयुक्तम्?
(i) अतीव
(ii) रोचकः
(iii) अस्ति
उत्तर:
(i) रोचकः

2.’रोहण: पुत्तलिकाखेलं द्रष्टुम् गच्छति’ इति वाक्ये ‘गच्छति’ इति क्रियापदस्य
(क) कः कर्ता?
(i) रोहणः
(ii) पुत्तलिकाखेलम्
(iii) दुष्टुम्

(ख) किम्-कर्मपदम्?
(i) पुत्तलिका खेलम्
(i) द्रष्टुम्
उत्तर:
(i) रोहणः
(ii) पुत्तलिकाखेलम्

3.(क) सः ‘मित्रैः सह खेलम् पश्यति’। इति वाक्यं बहुवचने परिवर्तय पुनः लिखत।
उत्तर:
ते मित्रैः सह खेलान् पश्यन्ति।

(ख) “पुत्तलिकाः नृत्यन्ति’ इति वाक्यम् एकवचने परिवर्त्य लिखत।
उत्तर:
पुत्तलिका नृत्यति।

We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book रचनात्मक-कार्यम् Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions रचनात्मक-कार्यम्

अनुच्छेद-पूर्तिः

प्रश्न 1.
मञ्जूषायाः सहायतया अधोदत्तम् प्रत्येकम् अनुच्छेदम् पूरयत।(मञ्जूषा की सहायता से नीचे दिए गए प्रत्येक अनुच्छेद को पूरा कीजिए। Complete each para given below with the help of the words in the box.)

(क) प्रातःकाल:

भ्रमणाय, समाचार-पत्रम्, विद्यालयम्, प्रात:कालः, कूजन्ति। यदा ………………….. भवति तदा प्रकाशः भवति। खगाः ……… “”””। जनाः गच्छन्ति। जनकः …………………. पठति। अहम् । ………………….. गच्छामि।
उत्तर:
प्रात:कालः, कूजन्ति, भ्रमणाय, समाचारपत्रं, विद्यालयम्।

(ख) सायंकाल:

प्रसन्नाः, मिष्टान्नम्, दूरदर्शनम्, भोजनम्, सायंकालः।

यदा ……………………… भवति, जनकः आगच्छति। सः ……………………….. आनयति। वयम् ………………….. खादामः ………… पश्यामः । वयम ………………….. भवामः।
उत्तर:
सायंकालः, मिष्टान्नम्, भोजनम्, दूरदर्शनम्, प्रसन्नाः।

(ग) विद्यालयः क्रीडाकालांशः

छात्राः, विद्यालयः, अल्पाहारम्, मध्यावकाशः।। एषः …………. । विद्यालये अनेके …………. भवति ते क्रीडाक्षेत्रे क्रीडन्ति। यदा ………………….. पठन्ति। यदा …………… भवति ते ………………. खादन्ति।
उत्तर:
विद्यालयः, छात्राः, क्रीडाकालांश, मध्यावकाशः, अल्पाहारम्।

(घ) एतत् गृहम्

उद्यानम्, शयनकक्षः, गृहम्, पाकशालायाम्, दूरदर्शनम्।।

एतत् रोहितस्य ……….. अस्ति । सः आवास-कक्षे ………….. पश्यति। ……….. अम्बा पचति । एषः रोहितस्य …………….. । अत्र सः शयनम् करोति । एतत् गृहस्य ………………….।
उत्तर:
गृहम्, दूरदर्शनम्, पाकशालायाम्, शयनकक्षः, उद्यानम्।

(ङ) पितामही भक्तिगीतम्

देवस्य, सूर्यम्, नमः, पितामही। …………. प्रातः उत्तिष्ठति। सा …………. पूजनम् करोति। सा वदति ‘सूर्याय …………….’। सा …………………… नमति। सा …………. गायति।
उत्तर:
पितामही, देवस्य नमः, सूर्यम्, भक्तिगीतम्।

(च) आम्रवृक्षः

कोकिलः, आम्रवृक्षे, आम्राणि, जलेन, आम्रवृक्षः, फलम्।। उद्याने एकः …………… अस्ति। अहम् ……………. वृक्षं सिञ्चामि। ग्रीष्मकाले ……… आम्रणि भवन्ति। …………….. मधुराणि सन्ति। आम्रम् मम प्रियं …………. अस्ति। वृक्षे ……………… कूजति।
उत्तर:
आम्रवृक्षः, जलेन, आम्रवृक्षे, आम्रणि, फलम्, कोकिलः।

संवाद-पूर्तिः

मञ्जूषायाः सहायतया अधोदत्तं प्रत्येकम् संवादं पूरयत। (मञ्जूषा की सहायता से नीचे दिए गए प्रत्येकसंवाद को पूरा कीजिए। Complete each dialogue given below with the help of words in the box.)

उदाहरणम्- उच्चैः, सिंहः, वने, गर्जामि।

प्रथमः – त्वम् कः असि?
द्वितीयः – ‘अहम् ……….. अस्मि ।
प्रथमः – त्वम् किम् करोषि?
द्वितीयः अहम् ………… |
पथमः , – त्वम् कथम् गर्जसि?
द्वितीयः – अहम् ………… गर्जामि।
प्रथमः – त्वम् कुत्र वससि?
द्वितीयः – अहम् ………. वसामि।
उत्तर:
सिंहः, गर्जामि, उच्चैः, वने

(क) मधुरम्, नीडे, खगः, कूजामि।

प्रथमः – त्वम् कः असि?
द्वितीयः – अहम् …………… अस्मि
प्रथमः – त्वम् किम् करोषि?
द्वितीयः – अहम् ……………
प्रथमः – त्वम् कथम् कूजसि?
द्वितीयः – अहम् …………… कूजसि
प्रथमः – त्वम् कुत्र वससि?
द्वितीयः – अहम् …………… वससि
उत्तर:
खगः, कूजामि, मधुरम्, नीडे।

(ख) सेवम्, मित्रैः सह, फलरसम्, क्रीडाक्षेत्रम्।

प्रथमः – त्वम् किं करोषि?
द्वितीयः – अहम् …………… खादामि। त्वम् किम् करोषि?
प्रथमः – अहम् ………………. पिबामि।
द्वितीयः – किं त्वम् ……………. आगच्छसि?
प्रथमः – तत्र त्वम् किं करोषि?
द्वितीयः – तत्र अहम् ……………. क्रीडामि।
उत्तर:
सेवम्, फलरसम्, क्रीडाक्षेत्रम्, मित्रैः सह।

(ग) फलानि, छायाम्, परोपकाराय, परोपकारम्, वृक्षः।।

प्रथमः – त्वम् कः असि?
द्वितीयः – अहम् ……….. अस्मि ।
प्रथमः – त्वम् किं करोषि?
द्वितीयः – अहम् ……….. यच्छामि।
प्रथमः – त्वम् किमर्थं फलसि?
द्वितीयः – अहम् ……………………….. फलामि।
प्रथमः – अहं सर्वेभ्यः ……………….. यच्छामि। अहं छायावृक्षः अस्मि।
द्वितीयः – शोभनम् ! त्वम् अपि ………………………. करोषि।
उत्तर:
वृक्षः, फलानि, परोपकाराय, छायाम्, परोपकारम्।

(घ) जनाः, उद्यानम्, प्रतिदिनम्, गच्छति, व्यायामम्, भ्रमणाय।

पौत्रः – पितामहः प्रातः कुत्र ………………..?
पितामही – तव पितामहः प्रातः …………………………. गच्छति?
पौत्रः – किं सः ………………………….. गच्छति?
पितामही – आम् सः
प्रतिदिनम् ……………….. गच्छति।
पौत्रः – किं सः एकाकी गच्छति?
पितामही – नहि, अन्ये …………… अपि आगच्छन्ति।
पौत्रः – तत्र ते किं कुर्वन्ति?
पितामही – ते ” ………….. कुर्वन्ति।
उत्तर:
गच्छति, उद्यानम्, प्रतिदिनम्, भ्रमणाय, जनाः, व्यायामम्

(ङ)

• तत्र अहम् क्रिकेटखेल खेलिष्यामि। त्वं कुत्र गच्छसि?
• आम् मम गृहकार्य संपन्नम्।
• अहम् क्रीडाक्षेत्रं गच्छामि।
• किं त्वम् अद्य खेलनाय न आगमिष्यसि?

रविः – मित्र! कुत्र गच्छसि?
भानुः – ……………..
रविः – तत्र त्वं कं खेलं खेलिष्यसि?
भानुः ……………..
रविः – अहम् कलमाय आपणं गच्छामि।
भानुः ……………..
रविः – नहि, मम विद्यालय कार्य न पूर्णम्।
किं तव गृहकार्य सम्पन्नम्?
भानुः – ……………..
उत्तर:
अहम् क्रीडाक्षेत्रं गच्छामि।
तत्र अहम् क्रिकेटखेल खेलिष्यामि। त्वं कुत्र गच्छसि?
किं त्वम् अद्य खेलनाय न आगमिष्यसि?
आम् मम गृहकार्य संपन्नम्।