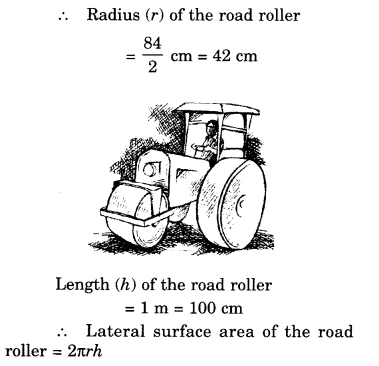
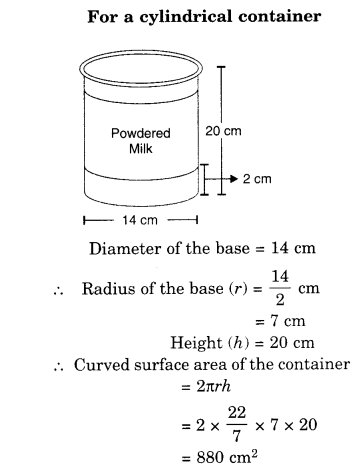
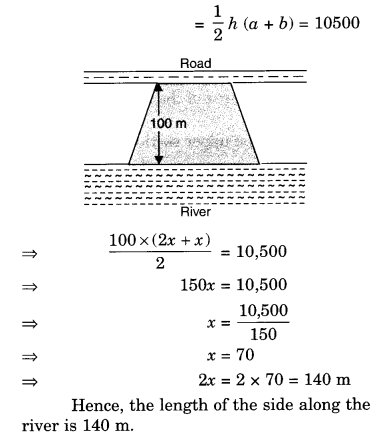
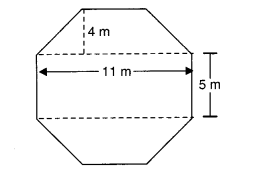
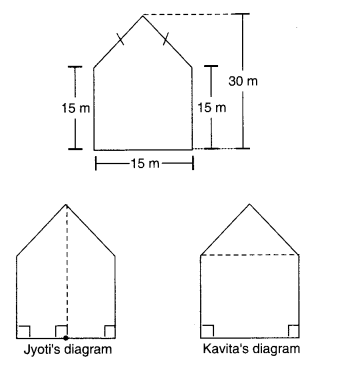
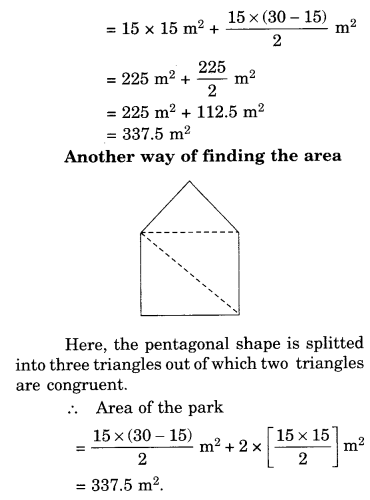
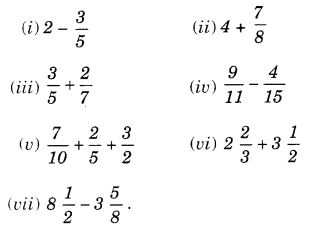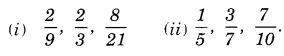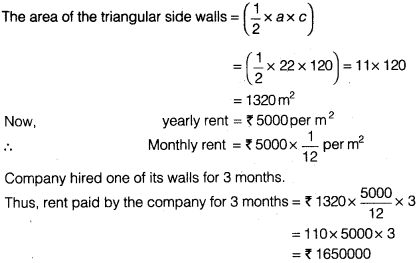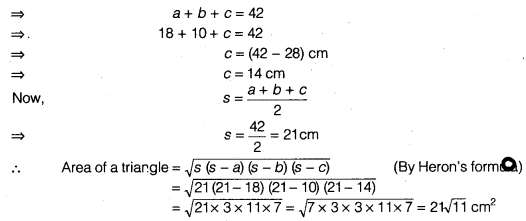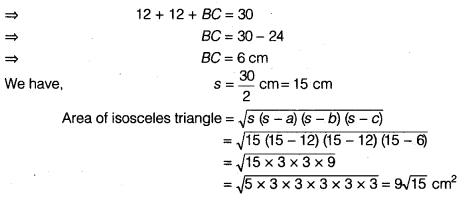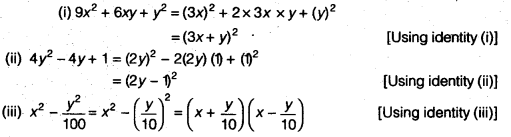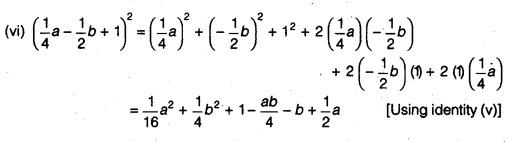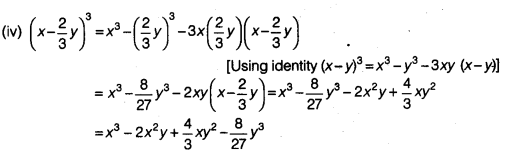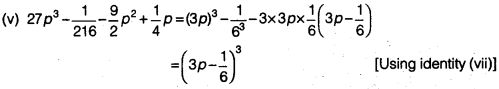Dattu – Page 34 – NCERT MCQ

NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1

February 28, 2023

NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1.

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 5
Chapter Name	Data Handling
Exercise	Ex 5.1
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1

Question 1.
For which of these would you use a histogram to show the data?
(a) The number of letters for different areas in a postman’s bag.
(b) The height of competitors in an athletics meet.
(c) The number of cassettes produced by 5 companies.
(d) The number of passengers boarding trains from 7:00 a.m. to 7:00 p.m at a station.
Give reasons for each.
Solution.
For (b) and (d) because in these two cases data can be grouped into class intervals.

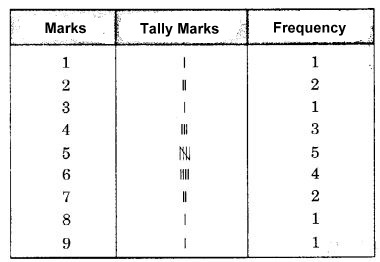
Question 2.
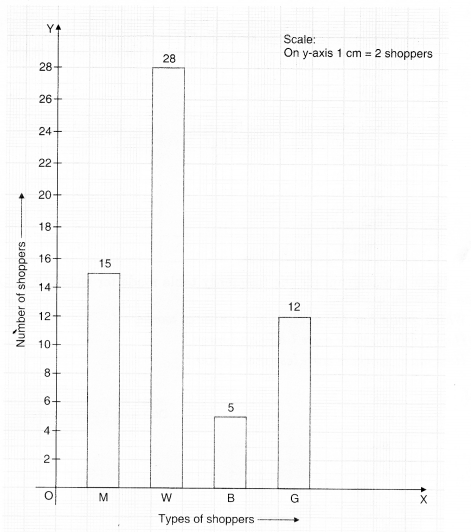
The shoppers who come to a departmental store are marked as man (M), woman (W), boy (B) or girl (G). The following list gives the shoppers who came during the first hour in the morning.
WWWGBWWMGGMMWWWWG
BMWBGGMWWMMWW
WMWBWGMWWWWGWMMWW
MWGWMGWMMBGGW
Make a frequency distribution table using tally marks. Draw a bar graph to illustrate it.
Solution.
NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1 1

Question 3.
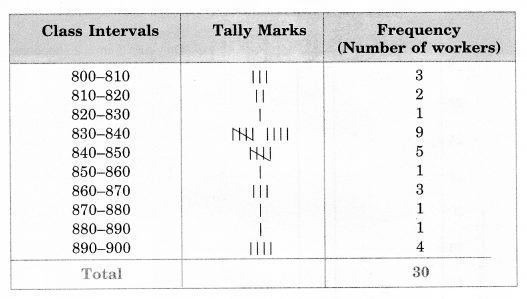
The weekly wages (in of 30 workers in a factory are:
830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860,
832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 835, 836,
878, 840, 868, 890, 806, 840.
Solution.
NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1 3

Question 4.
Draw a histogram for the frequency table made for the data in Question 3, and answer the following questions:
(i) Which group has the maximum number of workers?
(ii) How many workers earnt 850 and more?
(iii) How many workers earn less than? 850?
Solution.
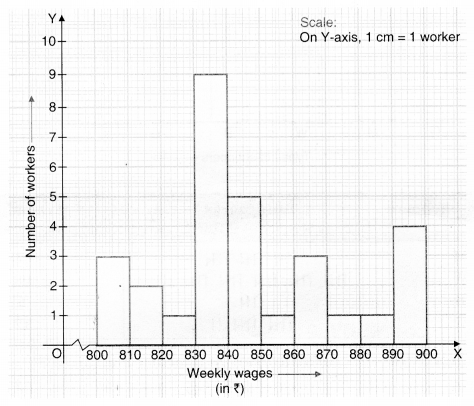
NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1 4
(i) Group 830—840, has the maximum number of workers.
(ii) 1 + 3 + 1 + 1 + 4 = 10, workers earn ? 850 and more.
(iii) 3 + 2 + l + 9 + 5 = 20, workers earn less than ? 850.

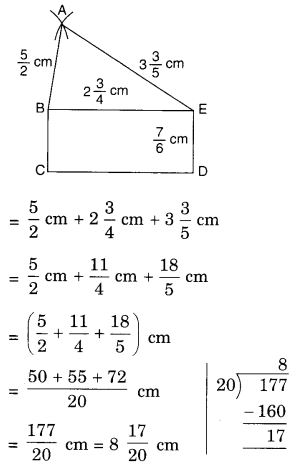
Question 5.
The number of hours for which students of a particular class watched television during holidays is shown through the given graph:
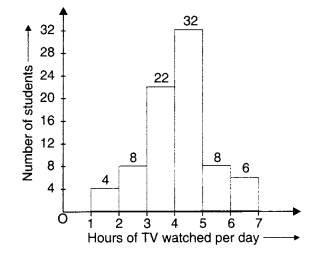
NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1 5
Answer the following:
(i) For how many hours did the maximum number of students watch TV?
(ii) How many students watched TV for less than 4 hours?
(iii) How many students spent more than 5 hours watching TV?
Solution.
(i) The maximum number of students watch TV for 4 to 5 hours.
(ii) 4 + 8 + 22 = 34 students watch TV for less than 4 hours.
(iii) 8 + 6 = 14 students spend more than 5 hours in watching TV.

We hope the NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1

February 28, 2023

NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1.

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 12
Chapter Name	Algebraic Expressions
Exercise	Ex 12.1
Number of Questions Solved	7
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1

Question 1.
Get the algebraic expressions in the following cases using variables, constants, and arithmetic operations.
(i) Subtraction of z from y.
Solution:
y – z

(ii) One-half of the sum of numbers x and y.
Solution:
\(\frac{1}{2}\) (x -y)

(iii) The number z multiplied by itself.
Solution:
z × z i.e., z²

(iv) One-fourth of the product of numbers p and q.
Solution:
\(\frac{1}{4}\) pq

(v) Numbers x and y both squared and added.
Solution:
x² + y²

(vi) Number 5 added to three times the product of numbers m and n.
Solution:
3mn + 5

(vii) Product of numbers y and z subtracted from 10.
Solution:
10 – yz

(viii) Sum of numbers a and 6 subtracted from their product.
Solution:
ab – (a + b)

Question 2.
(i) Identify the terms and their factors in the following expressions. Show the terms and factors by tree diagrams :

(a) x – 3
(b) 1 + x + x²
(c) y – y³
(d) 5xy² + 7x²y
(e) -ab + 2b² -3a²

(ii) Identify terms and factors in the expressions given below :

(a) – 4x + 5
(b) – 4x + 5y
(c) 5y + 3y²
(d) xy + 2x²y²
(e) pq + q
(f) 1.2 ab -2.4 b + 3.6 a
(g) \(\frac { 3 }{ 4 } \) x + \(\frac { 1 }{ 4 } \)
(h) 0.1 p² + 0.2 q²

Solution:

Question 3.
Identify the numerical coefficients of terms (other than constants) in the following expressions :

5 – 3t²
1 + t + t² + t³
x + 2xy + 3y
100m + 1000n
-p²q² + 7pq
1.2 a + 0.8 b
3.14 r²
2 (l + b)
0.1 y + 0.01 y².

Solution:

Question 4.
(a) Identify terms which contain x and give the coefficient of x.

y²x + y
13y² – 8yx
x + y + 2
5 + z + zx
1 + x + xy
12xy² + 25
7x + xy².

(b) Identify terms which contain y² and give the coefficient of y².

8 – xy²
5y² + 7x
2x²y – 15xy² + 7y²

Solution:

Question 5.
Classify into monomials, binomials and trinomials.

4y – 7z
y²
x + y – xy
100
ab – a – b
5 – 3t
4p²q – 4pq²
7mn
z² – 3z + 8 a² + b²
z² + z
1 + x+ x²

Solution:
We know that an algebraic expression containing only one term is called a monomial. So, the monomials are : (ii), (iv), and (viii).

We know that an algebraic expression containing two terms is called a binomial. So, the binomials are : (i), (vi), (vii), (x) and (xi).

We know that an algebraic expression containing three terms is called a trinomial. So, the trinomial are : (iii), (v), (ix) and (xii).

Question 6.
State whether a given pair of terms is of like or unlike terms :
(i) 1, 100
Solution:
Like

(ii) -7x, \(\frac{5}{2}\)x
Solution:
Like

(iii) – 29x, – 29y
Solution:
Unlike

(iv)14xy, 42yx
Solution:
Like

(v) 4m²p, 4mp²
Answer:
Unlike

(vi) 12xz, 12x²z²
Solution:
Unlike

(i) 4y – 7z.
This expression is a binomial because it contains two terms: 4y and – Iz.
(ii) y².
This expression is a monomial because it contains only one term: y²
(iii) x + y – xy.
This expression is a trinomial because it contains three terms: x, y, and – xy.
(iv) 100.
This expression is a monomial because it contains only one term: 100
(v) ab – a – b.
This expression is a trinomial because it contains three terms: ab, -a, and -b
(vi) 5 – 3t.
This expression is a binomial because it contains two terms : 5 and – 31.
(vii) 4p²q – 4pq².
This expression is a binomial because it contains two terms: 4p²q and – 4pq².
(viii) 7mn.
This expression is a monomial because it contains only one term : 7mn.
(ix) z² – 3z + 8.
This expression is a trinomial because it contains three terms : z², – 3z and 8.
(x) a² + b².
This expression is a binomial because it contains two terms: a² and b².
(xi) z² + z.
This expression is a binomial because it contains two terms : z² and z.
(xii) 1 + x + x².
This expression is a trinomial because it contains three terms: 1, x, and x².

Question 6.
State whether a given pair of terms is of like or unlike terms :
(i) 1, 100
Solution:
Like

(ii) -7x, \(\frac{5}{2}\)x
Solution:
Like

(iii) – 29x, – 29y
Solution:
Unlike

(iv)14xy, 42yx
Solution:
Like

(v) 4m²p, 4mp²
Answer:
Unlike

(vi) 12xz, 12x²z²
Solution:
Unlike

Question 7.
Identify like terms in the following :
NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1 10
Solution:

We hope the NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1, drop a comment below and we will get back to you at the earliest.

RD Sharma Class 11 Solutions Chapter 23 The Straight Lines Ex 23.8

February 28, 2023

RD Sharma Class 11 Solutions Chapter 23 The Straight Lines Ex 23.8

These Solutions are part of RD Sharma Class 11 Solutions. Here we have given RD Sharma Class 11 Solutions 23 The Straight Lines Ex 23.8.

RD Sharma Class 11 Solutions Chapter 23 The Straight Lines Ex 23.8 1.1

We hope the RD Sharma Class 11 Solutions Chapter 23 The Straight Lines Ex 23.8, help you. If you have any query regarding RD Sharma Class 11 Solutions Chapter 23 The Straight Lines Ex 23.8, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1

February 27, 2023

NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1.

Board	CBSE
Textbook	NCERT
Class	Class 9
Subject	Maths
Chapter	Chapter 5
Chapter Name	Triangles
Exercise	Ex 5.1
Number of Questions Solved	8
Category	NCERT Solutions

NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1

Exercise 5.1

Question 1.
In quadrilateral ACBD, AC = AD and AB bisects ∠ A (see figure). Show that ∆ABC ≅ ∆ABD. What can you say about BC and BD?
NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 img 1
Solution:
In ∆ABC and ∆ABD, we have
AC = AD (Given)
∠ CAB = ∠ DAB (∵ AB bisects ∠A)
and AB = AB (Common)
∴ ∆ ABC ≅ ∆ABD (By SAS congruence axiom)
∴ BC = BD (By CPCT)

Question 2.
ABCD is a quadrilateral in which AD = BC and ∠ DAB = ∠ CBA (see figure). Prove that
NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 img 2
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠ BAC
Solution:
In ∆ ABC and ∆ BAC, we have
AD = BC (Given)
∠DAB = ∠CBA (Given)
and AB = AB (Common)
∴ ∆ ABD ≅ ∆BAC (By SAS congruence axiom)
Hence, BD = AC (By CPCT)
and ∠ABD= ∠BAC (By CPCT)

Question 3.
AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.
NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 img 3
Solution:
In ∆AOD and ∆BOC, we have
∠AOD = ∠BOC
∵ AB and CD intersects at O.
∴ Which are vertically opposite angle
∵ ∠DAO = ∠CBO = 90°
and AD = BC (Given)
∴ ∆AOD ≅ ∆BOC (By SAS congruence axiom)
⇒ O is the mid-point of AB.
Hence, CD bisects AB.

Question 4.
l and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC = ∆CDA.
NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 img 4
Solution:
From figure, we have
∠ 1 = ∠ 2 (Vertically opposite angles).. .(i)
∠ 1 = ∠ 6 (Corresponding angles)…(ii)
∠ 6 = ∠ 4 (Corresponding angles) …(iii)
From Eqs. (i) (ii) and (iii), we have
∠ 1 = ∠ 4
and ∠ 2 = ∠ 4 …..(iv)
NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 img 5
In ∆ABC and ∆CDA, we have
∠ 4 = ∠ 2 [From Eq. (iv]
∠5 = ∠ 3 (Alternate interior angles)
and AC = AC (Common)
∴ ∆ABC ≅ ∆ CDA (By AAS congruence axiom)

Question 5.
Line l is the bisector of an ∠ A and ∠ B is any point on l. BP and BQ are perpendiculars from B to the arms of LA (see figure). Show that
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms ot ∠A.
NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 img 6
Solution:
In ∆ APB and ∆AQB, we have
∠ APB = ∠ AQB = 90°
∠ PAB = ∠ QAB (∵ AB bisects ∠ PAQ)
and AB = AB (Common)
∴ ∆ APB ≅ ∆ AQB (By AAS congruence axiom)
⇒ BP = BQ (By CPCT)
⇒ B is equidistant from the arms of ∠ A.

Question 6.
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 img 7
Solution:
In ∆ABC and ∆ADE, we have
AB = AD (Given)
∠ BAD = ∠ EAC (Given)…(i)
On adding ∠ DAC on both sides in Eq. (i)
⇒ ∠ BAD + ∠ DAC = ∠ EAC + ∠ DAC
⇒ ∠ BAC = ∠ DAE
and AC = AE (Given)
∴ ∆ABC ≅ ∆ADE (By AAS congruence axiom)
⇒ BC = DE (ByCPCT)

Question 7.
AS is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠ BAD = ∠ ABE and ∠ EPA = ∠ DPB. (see figure). Show that
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE
NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 img 8
Solution:
We have,
AP = BP [∵ P is the mid-point of AB (Given)]… (i)
∠ EPA = ∠ DPB (Given)…(ii)
∠ BAD = ∠ ABE (Given).. .(iii)
On adding ∠ EPD on both sides in Eq. (ii); we have
⇒ ∠ EPA + ∠ EPD = ∠DPB + ∠ EPD
⇒ ∠ DP A = ∠ EPB …..(iv)
Now, In ∆DAP and ∆EBP, we have
∠ DPA = ∠ EPB [ From Eq(4)]
∠ DAP = ∠ EBP (Given)
and AP = BP [From Eq. (i)]
∴ ∆ DAP ≅ ∆ EBP (By ASA congruence axiom)
Hence, AD = BE (By CPCT)

Question 8.
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB
NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 img 9
(iv) CM = \(\frac { 1 }{ 2 }\) AB
Solution:
Given ∆ACB in which ∠C = 90° and M is the mid- point of AB.

NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 img 10
To prove (i) ∆ AMC = ∆ BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB
(iv) CM = \(\frac { 1 }{ 2 }\) AB
Construction Produce CM to D, such that CM = MD. Join DB.
Proof In ∆ AMC and ∆ BMD, we have
AM = BM (M is the mid-point of AB)
CM = DM (Given)
and ∠AMC=∠BMD (Vertically opposite angles)
∴ ∆ AMC ≅ ∆ BMD (By SAS congruence axiom)
⇒ AC = DB (By CPCT) …(i)
and ∠1 = ∠2 (By CPCT)
Which are alternate angles
∴ BD || CA
Now, BD || CA and BC is transversal
∴ ∠ ACB + ∠CBD =180°
⇒ 90°+ ∠CBD = 180°
⇒∠CBD =90°
⇒ ∠ DBC = 90° [Which is part (ii)]
In ∆ DBC and ∆ ACB, we have
CB = BC (Common)
DB = AC [Using part (i)]
and ∠ CBD = ∠ BCA (Each 90°)
∴ ∆ DBC ≅ ∆ACB (By SSA congruence axiom) [Which is part (iii)]
⇒ DC=AB (by CPCT)
⇒ \(\frac { 1 }{ 2 }\) DC = \(\frac { 1 }{ 2 }\) AB
⇒ CM = \(\frac { 1 }{ 2 }\) AB (∵ CM = \(\frac { 1 }{ 2 }\) DC) [ Which is part(iv)]

We hope the NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 5 Triangles Ex 5.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1

February 27, 2023

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1.

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 2
Chapter Name	Fractions and Decimals
Exercise	Ex 2.1
Number of Questions Solved	8
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1

Question 1.
Solve :
NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1 1
Solution:

Question 2.
Arrange the following in descending order
NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1 4
Solution:
(i) Converting the given fractions into like fractions, we have

(ii) Converting the given fractions into like fractions, we have

Question 3.
In a “magic square”, the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?
NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1 8
Solution:
Yes ! this is a magic square.

Question 4.
A rectangular sheet of paper is 12 \(\frac { 1 }{ 2 } \) cm long 10 \(\frac { 2 }{ 3 } \) cm wide. find its perimeter
Solution:
Perimeter of the rectangular sheet of paper
NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1 9

Question 5.
Find the perimeters of (i) A ABE (ii) the rectangle BCDE in this figure. Whose perimeter is greater?
Solution:
(i) Perimeter of ∆ ABE = AB + BE + EA
NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1 10
(ii) Perimeter of the rectangle BCDE = BC + CD + DE + EB

So, the perimeter of A ABE is greater than the perimeter of the rectangle BCDE.

Question 6.
Salil wants to put a picture in a frame. The picture is 7 \(\frac { 3 }{ 5 } \) cm wide. To fit in the frame the picture cannot be more than 7 \(\frac { 3 }{ 10 } \) cm wide. How much should the picture be trimmed?
Solution:
The picture should be trimmed by
NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1 12

Question 7.
Ritu are \(\frac { 3 }{ 5 } \) part of an apple and the remaining apple was eaten by her brother Somu. How much part of the apple did Somu eat? Who had the larger share? By how much?
Solution:
Part of the apple ate by Somu
NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1 13

Question 8.
Michael finished colouring a picture in \(\frac { 7 }{ 12 } \) hour. Vaibhav finished colouring the same picture in \(\frac { 3 }{ 4 } \) hour. Who worked longer? By what fraction was it longer?
Solution:

We hope the NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.1

February 27, 2023

NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.1 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.1

Board	CBSE
Textbook	NCERT
Class	Class 9
Subject	Maths
Chapter	Chapter 7
Chapter Name	Heron’s Formula
Exercise	Ex 7.1
Number of Questions Solved	6
Category	NCERT Solutions

NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.1

Question 1.
A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side a. Find the area of the signal board, using Heron’s formula.If its perimeter is 180 cm, what will be the area of the signal board?
Solution:
We know that, an equilateral triangle has equal sides. So, all sides are equal to a.
NCERT Solutions for Class 9 Maths Chapter 7 Heron's Formula Ex 7.1 img 1

Question 2.
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see figure). The advertisements yield an earning of ₹5000 per m² per year. A company hired one of its walls for 3 months. How much rent did it pay?
NCERT Solutions for Class 9 Maths Chapter 7 Heron's Formula Ex 7.1 img 2
Solution:
Leta = 122m,
b = 22m
c = 120m
We have, b² + c² = (22)² + (120)² = 484 + 14400 = 14884= (122)² = a²
Hence, the side walls are in right triangled shape.

Question 3.
There is a slide in a park. One of its side Company hired one of its walls for 3 months.walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see figure). If the sides of the wall are 15 m, 11 m and 6m, find the area painted in colour.
NCERT Solutions for Class 9 Maths Chapter 7 Heron's Formula Ex 7.1 img 4
Solution:
The given figure formed a triangle whose sides are
a = 15m
b = 11m,
c = 6m

Question 4.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:
Solution Let the sides of a triangle, a = 18cm b = 10 cm and c
We have, perimeter = 42 cm
NCERT Solutions for Class 9 Maths Chapter 7 Heron's Formula Ex 7.1 img 6

Question 5.
Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
Solution:
Suppose that the sides in cm, are 12x, 17x and 25x.
Then, we know that 12x + 17x + 25x = 540 (Perimeter of triangle)
⇒ 54x = 540
⇒ x=10
So, the sides of the triangle are 12 x 10 cm, 17 x 10 cm 25 x 10 cm
i.e., 120 cm, 170 cm, 250 cm
NCERT Solutions for Class 9 Maths Chapter 7 Heron's Formula Ex 7.1 img 7

Question 6.
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution:
NCERT Solutions for Class 9 Maths Chapter 7 Heron's Formula Ex 7.1 img 8
Let in isosceles ∆ ABC,
AB = AC = 12 cm (Given)

We hope the NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.1 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex 8.1

February 27, 2023

NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex 8.1 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex 8.1.

Board	CBSE
Textbook	NCERT
Class	Class 9
Subject	Maths
Chapter	Chapter 8
Chapter Name	Linear Equations in Two Variables
Exercise	Ex 8.1
Number of Questions Solved	2
Category	NCERT Solutions

NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex 8.1

Question 1.
The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.
(Take the cost of a notebook to be ₹ x and that of a pen to be ₹ y)
Solution:
Let the cost of a notebook = ₹ x
and the cost of a pen = ₹ y
According to question,
Cost of a notebook = 2(cost of a pen)
∴ x = 2y
⇒ x- 2y = 0

Question 2.
Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case.
(i) 2x + 3y = 9.\(\overline { 35 }\)
(ii) x – \(\frac { y }{ 5 }\) – 10 = 0
(iii) – 2x + 3y = 6
(iv) x = 3y
(v) 2x = – 5y
(vi) 3x + 2 = 0
(vii) y – 2 = 0
(viii) 5 = 2x
Solution:
(i) 2x + 3y = 9.\(\overline { 35 }\)
⇒ 2x + 3y – 9..\(\overline { 35 }\) = 0
On comparing with ax+by+c = 0.
Then, the values of a = 2, b = 3 and c = 9..\(\overline { 35 }\)

(ii) x- \(\frac { y }{ 5 }\) -10= 0
On comparing with ax + by + c = 0, then the values of
a = 1, b = \(\frac { -1 }{ 5 }\) andc = – 10

(iii) – 2x+ 3y = 6
⇒ -2x + 3y – 6=0
On comparing with ax + by + c = 0, then the values of a = – 2, b = 3 and c = – 6

(iv) x = 3y ⇒ x-3y+0=0
On comparing with ax + by + c = 0, then the values of a = 1, b = – 3 and c = 0.

(v) 2x = -5y
⇒ 2x + 5y + 0=0
On comparing with ax + by + c = 0, then the values of a = 2, b = 5 and c = 0.

(vi) 3x + 2 = 0
⇒ 3x + 0y + 2 = 0
On comparing with ax + by + c = 0, then the values of a = 3, b = 0 and , c= 2.

(vii) y – 2 = 0
⇒0x+y-2 = 0
On comparing with ax + by + c = 0, then the values of a = 0, b = 1 and c = – 2.

(viii) 5 = 2x ⇒ 2x + 0y – 5 = 0
On comparing with ax + by + c = 0, then the values of a = 2, b = 0 and c = – 5.

We hope the NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex 8.1 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex 8.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1

February 27, 2023

NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1.

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 3
Chapter Name	Data Handling
Exercise	Ex 3.1
Number of Questions Solved	9
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1

Question 1.
Find the range of heights of any ten students of your class.
Solution:
Let the heights (in cm) of 10 students in the class be 150, 152, 151, 148, 149, 149, 150, 152, 153, 146.
Arranging the heights in ascending order, we have 146, 148, 149, 149, 150, 150, 151, 152, 152, 153.
Range of height of students = 153 – 146 = 7

Question 2.
Organize the following marks in a class assessment, in a tabular form.
4, 6, 7, 5, 3, 5, 4, 5, 2, 6, 2, 5, 1, 9, 6, 5, 8, 4, 6, 7
(i) Which number is the highest?
(ii) Which number is the lowest?
(iii) What is the range of the data?
(iv) Find the arithmetic mean.
Solution:
NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1
(i) Highest number is 9.
(ii) Lowest number is 1.
(iii) Range of the data = Highest observation – Lowest observation
= 9 – 1
= 8

Question 3.
Find the mean of the first five whole numbers.
Solution:
The first 5 whole numbers are 0, 1, 2, 3, and 4.
Their arithmetic mean
NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.3

Question 4.
A cricketer scores the following runs in eight innings:
58, 76, 40, 35, 46, 45, 0, 100.
Find the mean score.
Solution:

Question 5.
Following table shows the points of each player scored in four games:
NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.5
Now answer the following questions:

Find the mean to determine A’s average number of points scored per game.
To find the mean number of points per game for C, would you divide the total points by 3 or by 4? Why?
B played in all four games. How would you find the mean?
Who is the best performer?

Solution:
NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.6
So, A’s average number of points scored per game is 12.5.
(ii) To find the mean number of points per game for C, we shall divide the total points by 3 because the number of games under consideration is 4 but ‘C’ did not play game 3.
NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.7

Question 6.
The marks (out of 100) obtained by a group of students in a science test are 85, 76, 90, 85, 39, 48, 56, 95, 81 and 75. Find the:

Highest and the lowest marks obtained by the students.
Range of the marks obtained.
Mean marks obtained by the group.

Solution:

Highest marks obtained by the students = 95
Lowest marks obtained by the students = 39
Range of the marks obtained = Highest marks – Lowest marks = 95 – 39 = 56
Mean marks obtained by the group

Question 7.
The enrolment of a school during six consecutive years was as follows:
1555, 1670, 1750, 2013, 2540, 2820.
Find the mean enrolment of the school for this period.
Solution:
Mean enrolment of the school for this period.
NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.10

Question 8.
The rainfall (in mm) in a city on 7 days of a certain week was recorded as follows:
NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.11
(i) Find the range of the rainfall in the above data.
(ii) Find the mean rainfall for the week.
(iii) On how many days was the rainfall less than the mean rainfall?
Solution:
(i) Range of the rainfall = Highest rainfall – Lowest rainfall = 20.5 mm – 0.0 mm = 20.5 mm
(ii) Mean rainfall for the week
NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.12
(iii) The rainfall was less than the mean rainfall on 5 days.

Question 9.
The heights of 10 girls were measured in cm and the results are as follows:
135, 150, 139, 128, 151, 132, 146, 149, 143, 141.
(i) What is the height of the tallest girl?
(i) What is the height of the shortest girl?
(iii) What is the range of the data?
(iv) What is the mean height of the girls?
(v) How many girls have heights more than the mean height?

Solution:
(i) Height of the tallest girl = 151 cm
(ii) Height of the shortest girl = 128 cm
(iii) Range of the data
NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.13
(v) 5 girls have heights more than the mean height.

We hope the NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1 helps you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5

February 27, 2023

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5.

Board	CBSE
Textbook	NCERT
Class	Class 9
Subject	Maths
Chapter	Chapter 2
Chapter Name	Polynomials
Exercise	Ex 2.5
Number of Questions Solved	16
Category	NCERT Solutions

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5

Question 1.
Use suitable identities to find the following products
(i) (x + 4)(x + 10)
(ii) (x+8) (x -10)
(iii) (3x + 4) (3x – 5)
(iv) (y²+ \(\frac { 3 }{ 2 }\)) (y²– \(\frac { 3 }{ 2 }\))
(v) (3 – 2x) (3 + 2x)
Solution:
(i) (x+ 4) (x + 10)
Using identity (iv), i.e., (x+ a) (x+ b) = x² + (a + b) x+ ab.
We have, (x+4) (x + 10) = x²+(4 + 10) x + (4x 10) (∵ a = 4, b = 10)
= x² + 14x+40

(ii) (x+ 8) (x -10)
Using identity (iv), i.e., (x + a) (x + b) = x² + (a + b) x + ab
We have, (x + 8) (x – 10) = x² + [8 + (-10)] x + (8) (- 10)(∵a = 8, b = -10)
= x² – 2x – 80

(iii) (3x + 4) (3x – 5)
Using identity Eq. (iv), i.e.,
(x + a) (x + b) = x² + (a + b) x + ab
We have, (3x + 4) (3x – 5) = (3x)² + (4 – 5) x + (4) (- 5) (∵a = 4, b = -5)
= 9x² – x – 20

Question 2.
Evaluate the following products without multiplying directly
(i) 103 x 107
(ii) 95 x 96
(iii) 104 x 96
Solution:
(i) 103 x 107 = (100 + 3) (100 + 7)
= 100 x 100+ (3 + 7) (100)+ (3 x 7) [Using identity (iv)]
= 10000+ 1000+21 = 11021
(ii) 95 x 96 = (100-5) (100-4)
= 100 x 100 + [(- 5) + (- 4)] 100 + (- 5 x – 4) [Using identity (iv)]
= 10000 – 900 + 20 = 9120
(iii) 104 x 96 = (100 + 4) (100 – 4)
= (100)²-4² [Using identity (iii)]
= 10000-16 = 9984

Question 3.
Factorise the following using appropriate identities
(i) 9x²+6xy+ y²
(ii) 4y²-4y + 1
(iii) x² –\(\frac { { y }^{ 2 } }{ 100 }\)
Solution:
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5 img 1

Question 4.
Expand each of the following, using suitable identity
(i) (x+2y+ 4z)²
(ii) (2x – y + z)²(iii) (- 2x + 3y + 2z)²
(iv) (3a -7b – c)^z(v) (- 2x + 5y – 3z)²
(vi) ( \(\frac { 1 }{ 4 }\)a –\(\frac { 1 }{ 4 }\)b + 1) ²Solution:
(i) (x + 2y + 4z)² = x² + (2y)² + (4z)² + 2 (x) (2y) + 2 (2y) (4z) + 2(4z) (x) [Using identity (v)]
= x² + 4y² + 16z² + 4xy + 16yz + 8 zx
(ii) (2x – y + z)² = (2x)² + (- y)² + z² + 2 (2x) (- y)+ 2 (- y) (z) + 2 (z) (2x) [Using identity (v)]
= 4x² + y² + z² – 4xy – 2yz + 4zx
(iii) (- 2x + 3y + 2z)² = (- 2x)² + (3y)² + (2z)² + 2 (- 2x) (3y)+ 2 (3y) (2z) + 2 (2z) (- 2x) [Using identity (v)]
= 4x² + 9y² + 4z² – 12xy + 12yz – 8zx
(iv) (3a -7b- c)²= (3a)² + (- 7b)² + (- c)² + 2 (3a) (- 7b) + 2 (- 7b) (- c) + 2 (- c) (3a) [Using identity (v)]
= 9a² + 49b² + c² – 42ab + 14bc – 6ac
(v) (- 2x + 5y- 3z)² = (- 2x)² + (5y)² + (- 3z)² + 2 (- 2x) (5y) + 2 (5y) (- 3z) + 2 (- 3z) (- 2x) [Using identity (v)]
= 4x² + 25y² + 9z² – 20xy – 30yz + 12zx
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5 img 2

Question 5.
Factorise
(i) 4 x² + 9y² + 16z² + 12xy – 24yz – 16xz
(ii) 2x² + y² + 8z² – 2√2xy + 4√2yz – 8xz
Solution:
(i) 4x² + 9y² + 16z² +12xy-24yz-16xz
= (2x)² + (3y)² + (- 4z)² + 2 (2x) (3y) + 2 (3y) (- 4z) + 2 (- 4z) (2x)
= (2x + 3y – 4z)²(ii) 2x² + y² + 8z² – 2√2xy + 4√2yz – 8xz
= (- √2x)² + (y)² + (2 √2z)² + 2(- √2x) (y)+ 2 (y) (2√2z) + 2 (2√2z) (- √2x)
= (- √2x + y + 2 √2z)²

Question 6.
Write the following cubes in expanded form
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5 img 3
Solution:
(i) (2x + 1)³ = (2x)³ + 1³ + 3 (2x) (1) (2x + 1) [Using identity (x + y)³ = x³ + y³ + 3xy (x + y)]
= 8x³ + 1 + 6x (2x + 1)
= 8x³ + 1 + 12x² + 6x= 8x³ + 12x² + 6x + 1
(ii) (2a – 3b)³ = (2a)³ – (3b)³ -3(2a)(3b)(2a-3b) [Using identity (x-y)³=x³-y³ -3xy(x-y)]
= 8a³-27b³-18ab(2a-3b)
= 8a³ – 27 b³ – 36a²b + 54ab²=8a³ – 36a²b + 54ab² – 27 b³
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5 img 4

Question 7.
Evaluate the following using suitable identities
(i) (99)³
(ii) (102)³
(iii) (998)³Solution:
(i) (99)³ =(100-1)³ = 100³ -(1)³ – 3x 100x 1(100-1) [Using identity (x-y)³ =x³-y³-3xy (x-y)]
=1000000-1-300(100-1)
=1000000-1-30000+300
=970299
(ii) (102)³ = (100+ 2)³ = 100³ + 2³ + 3x 100x 2 (100+ 2 [Using identity (x + y)³ = x³ + y³ + 3xy (x + y)]
=1000000 + 8 + 600(100+ 2)
=1000000 + 8 + 60000+ 1200=1061208
(iii) (998)³ = (1000-2)³ =1000³ – 2³ – 3x 1000x 2(1000-2) [Using identity (x-y)³=x³-y³-3xy (x-y)]
=1000000000-8-6000(1000-2)
= 1000000000- 8 – 6000000+12000
=994011992

Question 8.
Factorise each of the following
(i) 8a³ +b³ + 12a²b+6ab²
(ii) 8a³ -b³-12a²b+6ab²(iii) 27-125a³ -135a+225a² (iv) 64a³ -27b³ -144a²b + 108ab²

Solution:
(i) 8a³ +b³ +12a²b+6ab² = (2a)³ + b³ + 3x 2axb (2a+ b)
=(2a+b)³ [Using identity (vi)]
(ii) 8a³ -b³ -12a²b+ 6ab² = (2a)³ + (-b)³ + 3x2ax (-b)[(2a)+ (-b)]
= (2a)³ – (b)³ – 3 x 2ax b (2a-b) [Using identity (vii)]
=(2 a-b)³(iii) 27-125a³-135a + 225a² =(3)³ + (-5a)³ + 3x3x(-5a)[(3)+(-5a)]
= (3)³ -(5a)³– 3x3x5a(3-5a) [Using identity (vii)]
= (3=5 a)³(iv) 64a³ – 27b³ -144a²b +108ab²=(4a)³ + (-3b)³ + 3x4ax(-3b)[4a+ (-3b)]
=(4a)³-(3b)³-3x4ax3b(4a-3b)
=(4a-3b)³ [Using identity (vii)]
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5 img 7

Question 9.
Verify
(i) x³ + y³ = (x + y)-(x² – xy + y²)
(ii) x³ – y³ = (x – y) (x² + xy + y²)
Solution:
(i) We know that,
(x + y)³ = x³ + y³ + 3xy (x + y)
⇒ x3 + y3 = (x + y)3 – 3xy (x + y)
= (x + y) [(x + y)² – 3xy]
= (x + y) [x² + y² + 2xy – 3xy]
= (x + y) [x² + y² – xy]
= RHS
Hence proved,
(ii) We .know that,
(x – y)³ = x³ – y³ – 3xy (x – y) x³ – y³
= (x – y)³ + 3xy (x – y)
= (x – y) [(x – y)² + 3xy]
= (x – y) [x² + y² + 2xy + 3xy]
= (x – y) [x² + y² + xy]
= RHS
Hence proved.

Question 10.
Factorise each of the following
(i) 27y³ + 125z
(ii) 64rh³ – 343n [Hint See question 9]
Solution:
(i) 27y³ + 125z³ = (3y)³ + (5z)³= (3y + 5z) [(3y)² – (3y) (5z) + (5z)²]
= (3y + 5z) (9y² – 15yz + 25z²)
(ii) 64 m³ – 343 n³ = (4m)³ – (7n)³= (4m – 7n) [(4m)² + (4m) (7n) + (7n)²]
= (4m – 7 n) [16m² + 28mn + 49n²]

Question 11.
Factorise 27x³ +y³ +z³ -9xyz.
Solution:
27x³ + y³ + z³-9xyz=(3x)³ + y³ + z³ -3x 3xx yx z
=(3x+y+z)[(3x)² + y² + z²– 3xy – yz -z(3x)][Using identity (viii)]
=(3x+ y + z) (9x² + y² + z² -3xy -yz -3zx)

Question 12.
Verify that
x³ +y³ +z³ -3xyz = \(\frac { 1 }{ 2 }\) (x + y+z)[(x-y)² +(y-z)² +(z-x)²]
Solution:
x³ + y³ + z³-3xyz = (x+y+z)[x² + y² + z²-xy-yz-zx]
= \(\frac { 1 }{ 2 }\)(x+ y+ z)[2x² + 2y² + 2z² – 2xy- 2yz – 2zx]
= \(\frac { 1 }{ 2 }\)(x+y+z)[x² + x² + y² + y² + z² + z²– 2xy – 2yz – 2zx]
= \(\frac { 1 }{ 2 }\)(x+y+ z)[x² + y² – 2xy+ y² + z² – 2yz+ z² + x² -2zx]
= \(\frac { 1 }{ 2 }\)(x+y+z)[(x-y)² + (y-z)² + (z-x)²]

Question 13.
If x + y + z = 0, show that x³ + y³ + z³ = 3 xyz.
Solution:
We know that,
x³ + y³ + z³ – 3 xyz = (x + y + z) (x² + y² + z² – xy – yz – zx [Using identity (viii)]
= 0(x² + y² + z² – xy – yz – zx) (∵ x + y + z = 0 given)
= 0
⇒ x³ + y³ + z³ = 3 xyz
Hence proved.

Question 14.
Without actually calculating the cubes, find the value of each of the following
(i) (- 12)³ + (7)³ + (5)³ (ii) (28)³ + (- 15)³ + (- 13)³
Solution:
We know that, x³ + y³ + z³ -3xyz
=(x+y+z)(x² + y² + z²– xy – yz – zx)
If x+y+z=0, then x³ + y³ + z³-3xyz=0
or x³ + y³ + z³ = 3xyz
(i) We have to find the value of (-12)³ + (7)³ + (5)³Here, -12+7+5=0
So, (-12)³ + (7)³ + (5)³= 3x(-12)(7)(5)
=-1260
(ii) We have to find the value of (28)³ + (-15)³ + (-13)³.
Here, 28+(-15)+(-13)=28-15-13 =0
So, (28)³ + (-15)³ + (-13)³
= 3x (28) (-15) (-13)
= 16380

Question 15.
Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given
(i) Area 25a² – 35a + 12
(ii) Area 35y² + 13y – 12
Solution:
(i) We have, area of rectangle
= 25a²– 35a+12
= 25a²– 20a – 15a+12
= 5a(5a – 4)-3(5a – 4)=(a-4)(5a – 3)
Possible expression for length =5a-3
and breadth =5a-4
(ii) We have, Area of rectangle = 35y²+13y – 12=35y² -15y + 28y – 12
=5y(7y – 3)+4(7y – 3) = (7y – 3)(5y+4)
Possible expression on for length =7y-3
and breadth =5y+4

Question 16.
What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
(i) Volume 3x² – 12x
(ii) Volume 12ky² + 8ky – 20k
Solution:
(i) We have, volume of cuboid =3x²-12x=3x(x – 4)
One possible expressions for the dimensions of the cuboid is 3, x and x-4.
(ii) We have, volume of cuboid =12ky² + 8ky-20k
=12ky² + 20ky-12ky-20k
=4ky (3y+5) – 4k(3y+5)
=(3y+5)(4ky – 4k)
=(3y+5)4k(y – 1)
One possible expressions for the dimensions of the cuboid is 4k, 3y+5 and y – 1.

We hope the NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5, help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5, drop a comment below and we will get back to you at the earliest.

Online Education NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3

February 27, 2023

In Online Education NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3.

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 11
Chapter Name	Mensuration
Exercise	Ex 11.3
Number of Questions Solved	10
Category	NCERT Solutions

Online Education NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3

Question 1.
There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 1
Solution.

Question 2.
A suitcase with measures 80 cm x 48 cm x 24 cm is to be covered with a tarpau¬lin cloth. How many meters of tarpaulin of width 96 cm is required to cover 100 such suitcases?
Solution.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 3

Question 3.
Find the side of a cube whose surface area is 600 \({ cm }^{ 2 }\).
Solution.
Let the side of the cube be a cm.
Then, Total surface area of the cube = 6\({ a }^{ 2 }\)
According to the question,
6\({ a }^{ 2 }\)= 600
⇒ \({ a }^{ 2 }\) = \(\frac { 600 }{ 6 } \)
⇒ \({ a }^{ 2 }\) = 100
⇒ a = \(\sqrt { 100 } \)
⇒ a = 10 cm
Hence, the side of the cube is 10 cm.

Question 4.
Rukhsar painted the outside of the cabinet of measure 1 m x 2 m x 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet?
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 4
Solution.

Question 5.
Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth, and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 \({ m }^{ 2 }\) of area is painted.
How many cans of paint will she need to paint the room?
Solution.
l = 15 m
b = 10 m
h = 7 m
Surface area to be painted
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 6
Hence, she will need 5 cans of paint to paint the room.

Question 6.
Describe how the two figures at the right are alike and how they are different. Which box has a larger lateral surface area?
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 7
Solution.
Similarity → Both have the same heights.
Difference → One is a cylinder, the other is a cube;
The cylinder is a solid obtained by revolving a rectangular area about its one side whereas a cube is a solid enclosed by six square faces; a cylinder has two circular faces whereas a cube has six square faces.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 8

Question 7.
A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How many sheets of metal is required?
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 9
Solution.

Question 8.
The lateral surface area of a hollow cylinder is 4224 \({ cm }^{ 2 }\). It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of rectangular sheet?
Solution.
Lateral surface area of the hollow cylinder = 4224 \({ cm }^{ 2 }\)
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 11

Question 9.
A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m.
Solution.
Diameter of the road roller = 84 cm
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 12

Question 10.
A company packages its milk powder in the cylindrical container whose base has a diameter of 14 cm and height 20 cm. The company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label?
Solution.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 14

We hope the NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3, drop a comment below and we will get back to you at the earliest.

Online Education NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2

February 27, 2023

In Online Education NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2.

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 11
Chapter Name	Mensuration
Exercise	Ex 11.2
Number of Questions Solved	11
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2

Question 1.
The shape of the top surface of a table is a trapezium. Find its area, if its parallel sides are 1 m and 1.2 man the d perpendicular distance between them is 0.8 m.
Solution.
Area of the top surface of the table
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 1
= \(\frac { 1 }{ 2 } h(a+b)\)
= \(\frac { 1 }{ 2 } \times 0.8\times (1.2+1)\)
= \(0.88{ m }^{ 2 }\)

Question 2.
The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the another parallel side.
Solution.
Area of trapezium
= \(\frac { 1 }{ 2 } h(a+b)\)
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 2
⇒ \(34=\frac { 1 }{ 2 } \times 4(10+b)\)
⇒ \(34=2\times (10+b)\)
⇒ \(10+b=\frac { 34 }{ 2 } \)
⇒ 10 + b=17
⇒ b = 17 – 10
⇒ b = 7 cm
Hence, the length of another parallel side is 7 cm.

Question 3.
Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 3
Solution.
Fence of the trapezium shaped field ABCD = 120 m
⇒ AB + BC + CD + DA = 120
⇒ AB + 48 + 17 + 40 = 120
⇒ AB + 105 = 120
⇒ AB = 120 – 105
⇒ AB = 15 m
∴ Area of the field
= \(\frac { (BC+AD)\times AB }{ 2 } \)
= \(\frac { (48+40)\times 16 }{ 2 } \) = 660 \({ m }^{ 2 }\)

Question 4.
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 4
Solution.
Area of the field
= \(\frac { 1 }{ 2 } d({ h }_{ 1 }+{ h }_{ 2 })\)
= \(\frac { 24\times (8+13) }{ 2 } \) = \(\frac { 24\times 21 }{ 2 } \)
= 12 x 21 = 252\({ m }^{ 2 }\)

Question 5.
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Solution.
Area of the rhombus
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 5
= \(\frac { 1 }{ 2 } \times { d }_{ 1 }\times { d }_{ 2 }\)
= \(\frac { 1 }{ 2 } \times 7.5\times 12\)
= 45 \({ m }^{ 2 }\)

Question 6.
Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Solution.
Area of the rhombus
= base (b) x altitude (h) = 5
= 5 x 4.8 = 24 \({ cm }^{ 2 }\)
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 6

Question 7.
The floor of a building consists of 3,000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per \({ m }^{ 2 }\) is ₹ 4.
Solution.
Area of a tile
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 7

Question 8.
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10,500 \({ m }^{ 2 }\) and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
Solution.
Let the length of the side along the road be x m. Then, the length of the side along the river is 2x m.
Area of the field = 10,500 square metres
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 8

Question 9.
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
Solution.
Area of the octagonal surface
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 9

Question 10.
There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 11
Find the area of this park using both ways. Can you suggest some other way of finding its area ?
Solution.

Question 11.
Diagram of the adjacent picture frame has outer dimensions = 24 cm x 28 cm and inner dimensions 16 cm x 20 cm. Find the area of each section of the frame, if the width of each section the same.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 14
Solution.

We hope the NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2, drop a comment below and we will get back to you at the earliest.