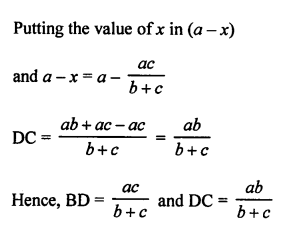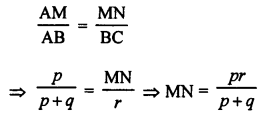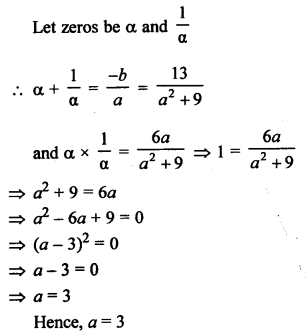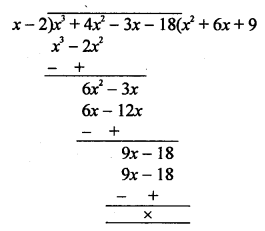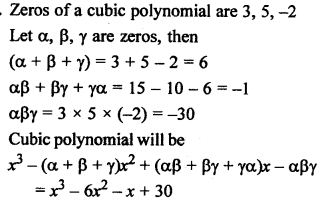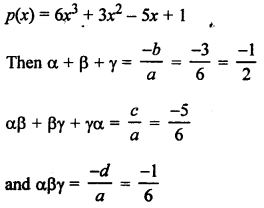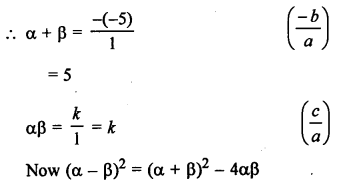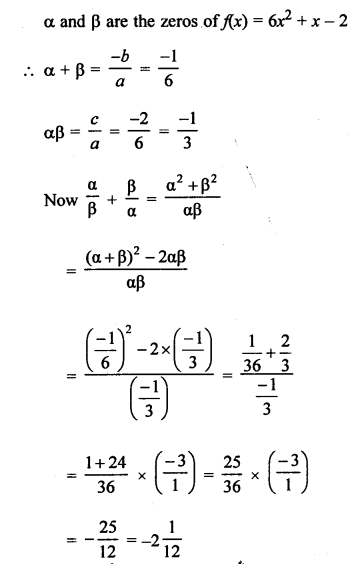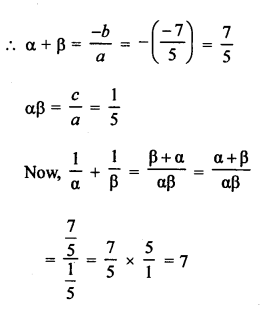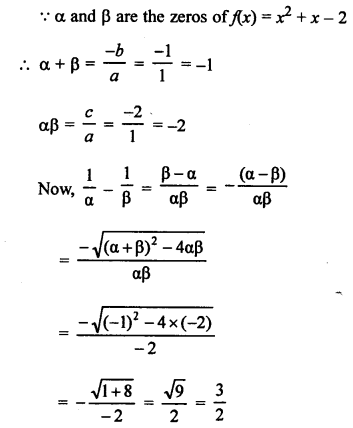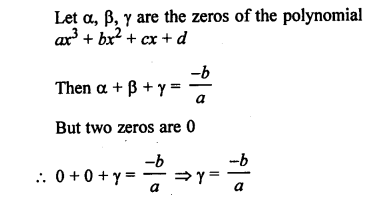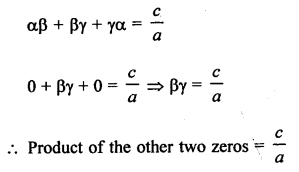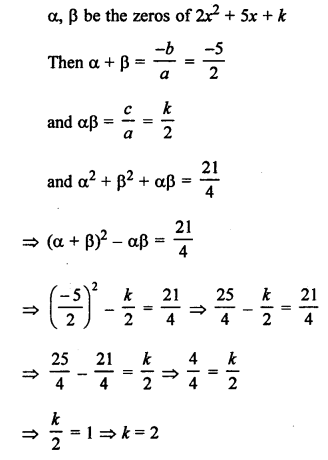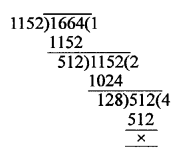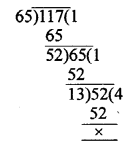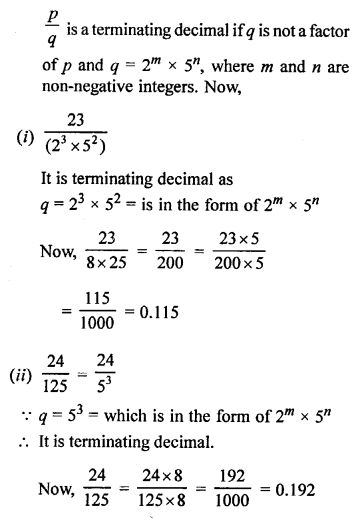Category: CBSE Class 10

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

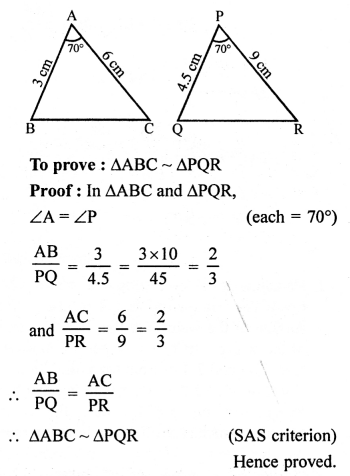
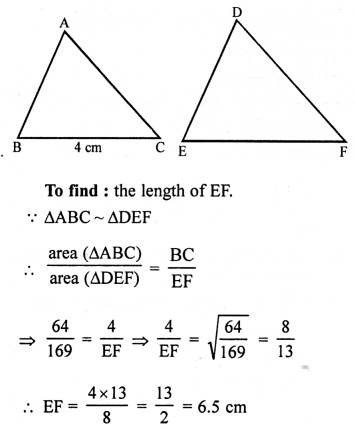
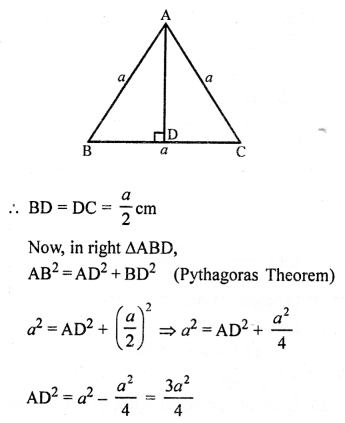
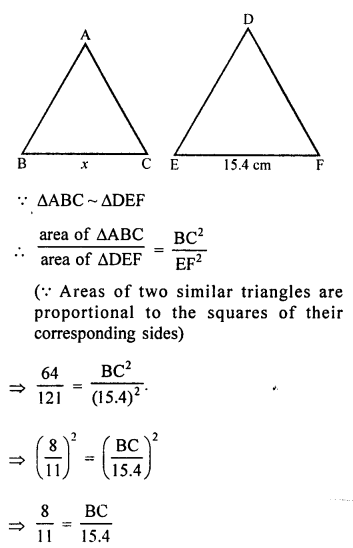
Question 1.
Solution:
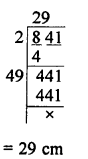
Given : Area of ∆ABC = 64 cm²
and area of ∆DEF =121 cm²
EF = 15.4 cm

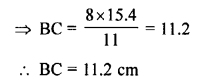
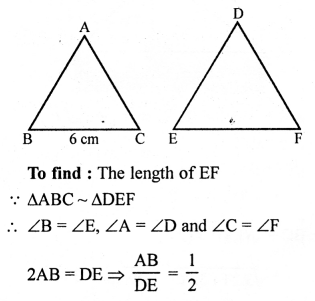
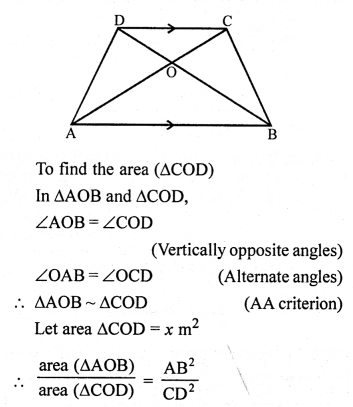
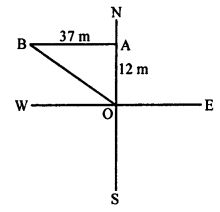
Question 2.
Solution:

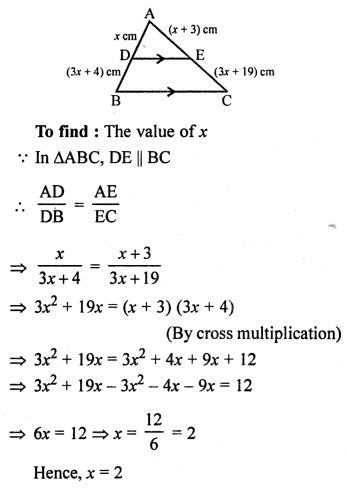
Question 3.
Solution:
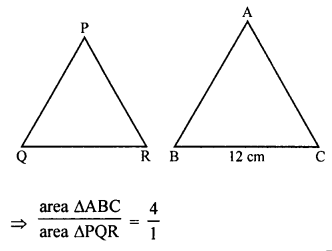
∆ABC ~ ∆PQR
ar (∆ABC) = 4ar (∆PQR),

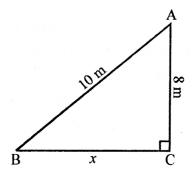
Question 4.
Solution:
Areas of two similar triangles are 169 cm² and 121 cm²
Longest side of largest triangle = 26 cm
Let longest side of smallest triangle = x
∆s are similar

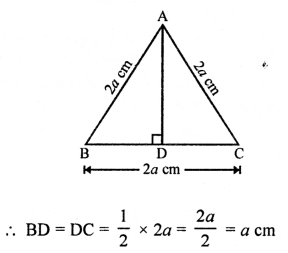
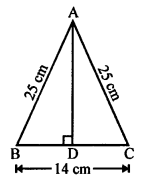
Question 5.
Solution:
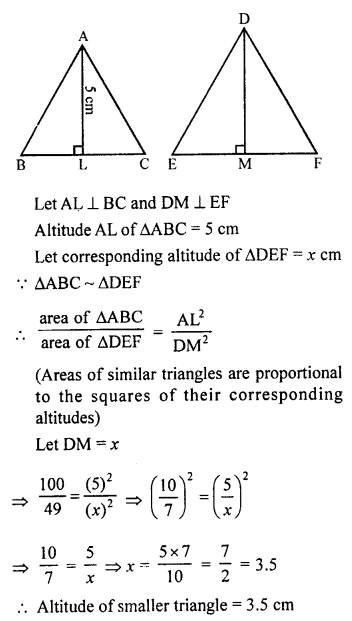
Area of ∆ABC = 100 cm²
and area of ∆DEF = 49 cm²

Question 6.
Solution:
Given : Corresponding altitudes of two similar triangles are 6 cm and 9 cm
We know that the areas of two similar triangles are in the ratio of the squares of their corresponding altitudes.
Ratio in the areas of two similar triangles = (6)² : (9)² = 36 : 81 = 4 : 9 (Dividing by 9)

Question 7.
Solution:
The areas of two similar triangles are 81 cm² and 49 cm²
Altitude of the first triangle = 6.3 cm
Let altitude of second triangle = x cm
The areas of two similar triangles are in the ratio of the squares on their corresponding altitude,
Let area of ∆ABC = 81 cm²
and area of ∆DEF = 49cm²
Altitude AL = 6 – 3 cm
Let altitude DM = x cm

Question 8.
Solution:
Areas of two similar triangles are 100 cm² and 64 cm²
Let area of ∆ABC = 100 cm²
and area of ∆DEF = 64 cm²
Median DM of ∆DEF = 5.6 cm
Let median AL of ∆ABC = x
The areas of two similar triangles is proportional to the squares of their corresponding median.

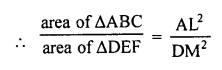
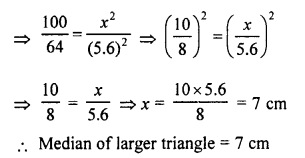
Question 9.
Solution:
Given : In ∆ABC, PQ is a line which meets AB in P and AC in Q.
AP = 1 cm, PB = 3 cm, AQ = 1.5 cm QC = 4.5 cm

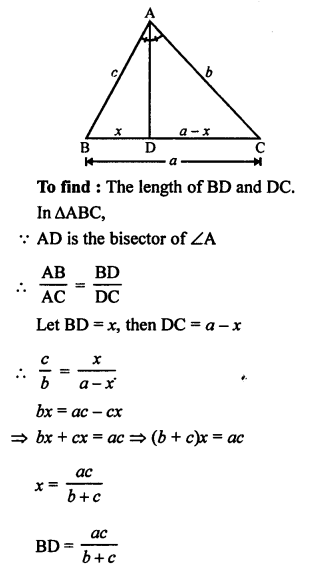
Question 10.
Solution:
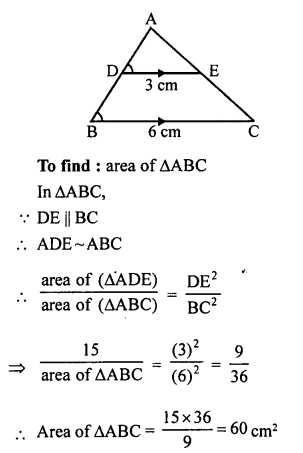
In ∆ABC,
DE || BC
DE = 3 cm, BC = 6 cm
area (∆ADE) = 15 cm²

Question 11.
Solution:
Given : In right ∆ABC, ∠A = 90°
AD ⊥ BC
BC = 13 cm, AC = 5 cm
To find : Ratio in area of ∆ABC and ∆ADC
In ∆ABC and ∆ADC
∠C = ∠C (common)
∠BAC = ∠ADC (each 90°)
∆ABC ~ ∆ADC (AA axiom)

Question 12.
Solution:
In the given figure ∆ABC,
DE || BC and DE : BC = 3 : 5.
In ∆ABC and ∆ADE,
DE || BC
∆ABC ~ ∆ADE

Question 13.
Solution:
In ∆ABC, D and E are the midpoints of sides AB and AC respectively.
DE || BC and DE = \(\frac { 1 }{ 2 }\) BC
∆ADE ~ ∆ABC

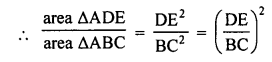
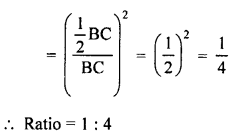
Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Very-Short-Answer and Short-Answer Questions
Question 1.
Solution:
Two properties for similarity of two triangles are:
(i) Angle-Angle-Angle (AAA) property.
(ii) Angle-Side-Angle (ASA) property.

Question 2.
Solution:
In a triangle, if a line parallel to one side is drawn, it will divide the other two sides proportionally.

Question 3.
Solution:
If a line divides any two sides of a triangle in the same ratio. Then, the line must be parallel to the third side.

Question 4.
Solution:
The line joining the midpoints of two sides of a triangle, is parallel to the third side.

Question 5.
Solution:
In two triangles, if three angles of the one triangle are equal to the three angles of the other, the triangles are similar.

Question 6.
Solution:
In two triangles, if two angles of the one triangle are equal to the corresponding angles of the other triangle, then the triangles are similar.

Question 7.
Solution:
In two triangles, if three sides of the one are proportional to the corresponding sides of the other, the triangles are similar.

Question 8.
Solution:
In two triangles, if two sides of the one are proportional to the corresponding sides of the other and their included angles are equal, the two triangles are similar.

Question 9.
Solution:
In a right angled triangle, the square on the hypotenuse is equal to the sum of squares on the other two sides.

Question 10.
Solution:
In a triangle, if the square on the longest side is equal to the sum of the squares on the other two sides, then the angle opposite to the hypotenuse is a right angle.

Question 11.
Solution:
The ratio of their areas will be 1 : 4.

Question 12.
Solution:
In two triangles ∆ABC and ∆PQR,
AB = 3 cm, AC = 6 cm, ∠A = 70°
PR = 9 cm, ∠P = 70° and PQ= 4.5 cm

Question 13.
Solution:
∆ABC ~ ∆DEF
2AB = DE, BC = 6 cm

Question 14.
Solution:
In the given figure,
DE || BC
AD = x cm, DB = (3x + 4) cm
AE = (x + 3) cm and EC = (3x + 19) cm

Question 15.
Solution:
AB is the ladder and A is window.
AB =10 m, AC = 8 m

We have to find the distance of BC
Let BC = x m
In right ∆ABC,
AB² = AC² + BC² (Pythagoras Theorem)
(10)² = 8² + x²
⇒ 100 = 64 + x²
⇒ x² = 100 – 64 = 36 = (6)²
x = 6
Distance between foot of ladder and base of the wall = 6 m.

Question 16.
Solution:
∆ABC is an equilateral triangle with side = 2a cm
AD ⊥ BC
and AD bisects BC at D

Now, in right ∆ABD,
AB² = AD² + BD² (Pythagoras Theorem)
⇒ (2a)² = AD² + (a)²
⇒ 4a² = AD² + a²
⇒ AD² = 4a² – a² = 3a²
AD = √3 a² = √3 a cm

Question 17.
Solution:
Given : ∆ABC ~ ∆DEF
and ar (∆ABC) = 64 cm²
and ar (∆DEF) = 169 cm², BC = 4 cm.

Question 18.
Solution:
In trape∠ium ABCD,
AB || CD
AB = 2CD
Diagonals AC and BD intersect each other at O
and area(∆AOB) = 84 cm².

Question 19.
Solution:
Let ∆ABC ~ ∆DEF

Question 20.
Solution:
In an equiangular ∆ABC,
AB = BC = CA = a cm.
Draw AD ⊥ BC which bisects BC at D.

Question 21.
Solution:
ABCD is a rhombus whose sides are equal and diagonals AC and BD bisect each other at right angles.

∠AOB = 90° and AO = OC, BO = OD
AO = \(\frac { 24 }{ 2 }\) = 12 cm
and BO = \(\frac { 10 }{ 2 }\) = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² (Pythagoras Theorem)
= (12)² + (5)² = 144 + 25 = 169 = (13)²
AB = 13
Each side of rhombus = 13 cm

Question 22.
Solution:
∆DEF ~ ∆GHK
∠D = ∠G = 48°
∠E = ∠H = 57°
∠F = ∠K

Now, in ∆DEF,
∠D + ∠E + ∠F = 180° (Angles of a triangle)
⇒ 48° + 57° + ∠F = 180°
⇒ 105° + ∠F= 180°
⇒ ∠F= 180°- 105° = 75°

Question 23.
Solution:
In the given figure,
In ∆ABC,
MN || BC
AM : MB = 1 : 2

Question 24.
Solution:
In ∆BMP,
PB = 5 cm, MP = 6 cm and BM = 9 cm
and in ∆CNR, NR = 9 cm

Question 25.
Solution:
In ∆ABC,
AB = AC = 25 cm
BC = 14 cm

AD ⊥ BC which bisects the base BC at D.
BD = DC = \(\frac { 14 }{ 2 }\) = 7 cm
Now, in right ∆ABD,
AB² = AD² + BD² (Pythagoras Theorem)
(25)² = AD² + 7²
625 = AD² + 49
⇒ AD² = 625 – 49 = 576
⇒ AD² = 576 = (24)²
AD = 24 cm
Length of altitude = 24 cm

Question 26.
Solution:
A man goes 12 m due north of point O reaching A and then 37 m due west reaching B.

Join OB,
In right ∆OAB,
OB² = OA² + AB² (Pythagoras Theorem)
= (12)² + (35)² = 144 + 1225 = 1369 = (37)²
OB = 37 m
The man is 37 m away from his starting point.

Question 27.
Solution:
In ∆ABC, AD is the bisector of ∠A which meets BC at D.
AB = c, BC = a, AC = b

Question 28.
Solution:
In the given figure, ∠AMN = ∠MBC = 76°
p, q and r are the lengths of AM, MB and BC Express the length of MN in terms of p, q and r.
In ∆ABC,
∠AMN = ∠MBC = 76°
But there are corresponding angles
MN || BC
∆AMN ~ ∆ABC

Question 29.
Solution:
In rhombus ABCD,
Diagonals AC and BD bisect each other at O at right angles.

AO = OC = \(\frac { 40 }{ 2 }\) = 20 cm
BO = OD = \(\frac { 42 }{ 2 }\) = 21 cm
Now, in right ∆AOB,
AB2 = AO2 + BO2 = (20)2 + (21)2 = 400 + 441 = 841
AB = √841 cm = 29 cm

Each side of rhombus = 29 cm

For each of the following statements state whether true (T) or false (F):
Question 30.
Solution:
(i) True.
(ii) False, as sides will not be proportion in each case.
(iii) False, as corresponding sides are proportional, not necessarily equal.
(iv) True.
(v) False, in ∆ABC,
AB = 6 cm, ∠A = 45° and AC = 8 cm

(vi) False, the polygon joining the midpoints of a quadrilateral is not a rhombus but it is a parallelogram.
(vii) True.
(viii) True.
(ix) True, O is any point in rectangle ABCD then
OA² + OC² = OB² + OD² is true.

(x) True.

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Test Yourself

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Test Yourself

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2A
• RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2B
• RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2C
• RS Aggarwal Solutions Class 10 Chapter 2 Polynomials MCQS
• RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Test Yourself

MCQ
Question 1.
Solution:
(b) Polynomial is x² – 2x – 3
=> x² – 3x + x – 3
= x(x – 3) + 1(x – 3)
= (x – 3) (x + 1)
Either x – 3 = 0, then x = 3
or x + 1 = 0, then x = -1
Zeros are 3, -1

Question 2.
Solution:
(a) α, β, γ are the zeros of Polynomial is x³ – 6x² – x + 30
Here, a = 1, b = -6, c = -1, d = 30
αβ + βγ + γα = \(\frac { c }{ a }\) = \(\frac { -1 }{ 1 }\) = -1

Question 3.
Solution:
(c)

Question 4.
Solution:
(c) Let α and β be the zeros of the polynomial 4x² – 8kx + 9

Short-Answer Questions
Question 5.
Solution:

Either x + 15 = 0, then x = -15
or x – 13 = 0, then x = 13
Zeros are 13, -15

Question 6.
Solution:
The polynomial is (a² + 9) x² + 13x + 6a

Question 7.
Solution:
Zeros are 2 and -5
Sum of zeros = 2 + (-5) = 2 – 5 = -3
and product of zeros = 2 x (-5) = -10
Now polynomial will be
x² – (Sum of zeros) x + Product of zeros
= x² – (-3)x + (-10)
= x² + 3x – 10

Question 8.
Solution:
(a – b), a, (a + b) are the zeros of the polynomial x³ – 3x² + x + 1
Here, a = 1, b = -3, c = 1, d = 1
Now, sum of zeros = \(\frac { -b }{ a }\) = \(\frac { -(-3) }{ 1 }\) = 3
a – b + a + a + b = 3

Question 9.
Solution:
Let f(x) = x³ + 4x² – 3x – 18
If 2 is its zero, then it will satisfy it
Now, (x – 2) is a factor Dividing by (x – 2)
Hence, x = 2 is a zero of f(x)

Question 10.
Solution:
Sum of zeros = -5
and product of zeros = 6
Quadratic polynomial will be
x² – (Sum of zeros) x + Product of zeros
= x² – (-5) x + 6
= x² + 5x + 6

Question 11.
Solution:

Question 12.
Solution:
p(x) = x³ + 3x² – 5x + 4
g(x) = x – 2
Let x – 2 = 0, then x = 2
Remainder = p(2) = (2)³ + 3(2)² – 5(2) + 4 = 8 + 12 – 10 + 4 = 14

Question 13.
Solution:
f(x) = x³ + 4x² + x – 6
and g(x) = x + 2
Let x + 2 = 0, then x = -2
f(-2) = (-2)³ + 4(-2)² + (-2) – 6 = -8 + 16 – 2 – 6 = 0
Remainder is zero, x + 2 is a factor of f(x)

Question 14.
Solution:

Question 15.
Solution:

Question 16.
Solution:
f(x) = x⁴ + 4x² + 6
=> (x²)² + 4(x²) + 6 = y² + 4y + 6 (Let x² = y)
Let α, β be the zeros of y² + 4y + 6
Sum of zeros = -4
and product of zeros = 6
But there are no factors of 6 whose sum is -4 {Factors of 6 = 1 x 6 and 2 x 3}
Hence, f(x) Has no zero (real).

Long-Answer Questions
Question 17.
Solution:
3 is one zero of p(x) = x³ – 6x² + 11x – 6
(x – 3) is a factor of p(x)
Dividing, we get

Question 18.
Solution:

Question 19.
Solution:
p(x) = 3x⁴ + 5x³ – 7x² + 2x + 2
Dividing by x² + 3x + 1,
we get,
Quotient = 3x² – 4x + 2

Question 20.
Solution:
Let p(x) = x³ + 2x² + kx + 3
g(x) = x – 3
and r(x) = 21
Dividing p(x) by g(x), we get

But remainder = 21
3 + 3k + 45 = 21
3k = 21 – 45 – 3
=> 3k = 21 – 48 = -27
k = -9
Second method:
x – 3 is a factor of p(x) : x = 3
Substituting the value of x in p(x)
p(3) = 3³ + 2 x 3² + k x 3 + 3
= 27 + 18 + 3k + 3
48 + 3k = 21
=> 3k = -48 + 21 = -27
k = -9
Hence, k = -9

Hope given RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Test Yourself are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2C. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Very-Short-Answer Questions
Question 1.
Solution:
Let other zero of x² – 4x + 1 be a, then
Sum of zeros = \(\frac { -b }{ a }\) = \(\frac { -(-4) }{ 1 }\) = 4
But one zero is 2 + √3
Second zero = 4 – (2 + √3) =4 – 2 – √3 = 2 – √3

Question 2.
Solution:
Let f(x) = x² + x – p(p + 1)
= x² + (p + 1) x – px – p(p + 1)
= x(x + p + 1) – p(x + p + 1)
= (x + p + 1) (x – p)
Either x + p + 1 = 0, then x = -(p + 1)
or x – p = 0, then x = p
Hence, zeros are p and -(p + 1)

Question 3.
Solution:
p(x) = x² – 3x – m(m + 3)
= x² – (m + 3)x + mx – m(m + 3)
= x(x – m – 3) + m(x – m – 3)
= (x – m – 3)(x + m)
Either x – m – 3 = 0, then x = m + 3
or x + m = 0, then x = -m
Zeros are (m + 3), -m

Question 4.
Solution:
a and p are the zeros of a polynomial
and α + β = 6, αβ = 4
Polynomial = x² – (α + β)x + αβ = x² – (6)x + 4 = x² – 6x + 4

Question 5.
Solution:
One zero of kx² + 3x + k is 2
x = 2 will satisfy it
⇒ k(2)² + 3 x 2 + k = 0
⇒ 4k + 6 + k= 0
⇒5k + 6 = 0
⇒ 5k = -6
⇒ k = \(\frac { -6 }{ 5 }\)
Hence, k = \(\frac { -6 }{ 5 }\)

Question 6.
Solution:
3 is a zero of the polynomial 2x² + x + k
Then 3 will satisfy it
2x² + x + k = 0
⇒ 2(3)² + 3 + k = 0
⇒ 18 + 3+ k = 0
⇒ 21 + k = 0
⇒ k = -21
Hence, k = -21

Question 7.
Solution:
-4 is a zero of polynomial x² – x – (2k + 2)
Then it will satisfy the equation
x² – x – (2k + 2) = 0
⇒ (-4)2 – (-4) – 2k – 2 = 0
⇒ 16 + 4 – 2k – 2 = 0
⇒ -2k + 18 = 0
⇒ 2k = 18
k = 9

Question 8.
Solution:
1 is a zero of the polynomial ax² – 3(a – 1)x – 1
Then 1 will satisfy the equation ax² – 3(a – 1) x – 1 = 0
a(1)² – 3(a – 1) x 1 – 1 = 0
⇒ a x 1 – 3a + 3 – 1 = 0
⇒ a – 3a + 2 = 0
⇒ -2a + 2 = 0
⇒ 2a = 2
⇒ a = 1

Question 9.
Solution:
-2 is a zero of 3x² + 4x + 2k
It will satisfy the equation 3x² + 4x + 2k = 5
3(-2)² + 4(-2) + 2k = 0
⇒ 3 x 4 + 4(-2) + 2k = 0
⇒ 12 – 8 + 2k = 0
⇒ 4 + 2k=0
⇒ 2k = -4
⇒ k = -2
k = -2

Question 10.
Solution:
Let f(x) = x² – x – 6
= x² – 3x + 2x – 6
= x(x – 3) + 2(x – 3)
= (x – 3)(x + 2)
(x – 3)(x + 2) = 0
Either x – 3 = 0, then x = 3
or x + 2 = 0, then x = -2
Zeros are 3, -2

Question 11.
Solution:
Sum of zeros = 1
and polynomial is kx² – 3x + 5
Sum of zeros = \(\frac { -b }{ a }\) = \(\frac { -(-3) }{ k }\) = \(\frac { 3 }{ k }\)
\(\frac { 3 }{ k }\) = 1
⇒ k = 3
Hence, k = 3

Question 12.
Solution:
Product of zeros of polynomial x² – 4x + k is 3
Product of zeros = \(\frac { c }{ a }\)
⇒ \(\frac { k }{ 1 }\) = 3
⇒ k = 3

Question 13.
Solution:
x + a is a factor of
f(x) = 2x² + (2a + 5) x + 10
Let x + a = 0, then
Zero of f(x) = -a
Now f(-a) = 2 (-a)² + (2a + 5)(-a) + 10 = 0
2a² – 2a² – 5a + 10 = 0
⇒ 5a = 10
⇒ a = 2

Question 14.
Solution:
(a – b), a, (a + b) are the zeros of 2x³ – 6x² + 5x – 7
Sum of zeros = \(\frac { -b }{ a }\)
⇒ a – b + a + a + b = \(\frac { -(-6) }{ 2 }\)
⇒ 3a = \(\frac { 6 }{ 2 }\)
⇒ 3a = 3
⇒ a = 1

Question 15.
Solution:
f(x) = x³ + x² – ax + 6 is divisible by x² – x
Remainder will be zero
Now dividing f(x) by x² – x
Remainder = (2 – a) x + b

(2 – a) x + b = 0
2 – a = 0
⇒ a = 2 and b = 0
Hence, a = 2, b = 0

Question 16.
Solution:
α and β are the zeros of polynomial f(x) = 2x² + 7x + 5

Question 17.
Solution:
Division algorithm for polynomials:
If f(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomial q(x) and r(x).
f(x) = q(x) x g(x) + r(x)
where r (x) = 0
or [degree of r(x) < degree of g(x)]
or Dividend=Quotient x Division + Remainder

Question 18.
Solution:
Sum of zeros = \(\frac { -1 }{ 2 }\)
Product of zeros = -3
Polynomial: x² – (Sum of zeros) x + product of zeros

Short-Answer Questions
Question 19.
Solution:

Question 20.
Solution:

Question 21.
Solution:
α and β are the zeros of polynomial f(x) = x² – 5x + k

(1)² = (5)² – 4 k
1 ⇒ 25 – 4k
⇒ 4k = 25 – 1 = 24
Hence, k = 6

Question 22.
Solution:

Question 23.
Solution:
α and β are the zeros of polynomial
f(x) = 5x² – 7x + 1

Question 24.
Solution:

Question 25.
Solution:
(a – b), a and (a + b) are the zeros of the polynomial
f(x) = x³ – 3x² + x + 1

Hope given RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

NCERT Maths Solutions for Ex 2.2 class 10 Polynomials is the perfect guide to boost up your preparation during CBSE 10th Class Maths Examination.

RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2B. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Question 1.
Solution:
Zeros are 3, -2, 1 of
p(x) = x³ – 2x² – 5x + 6
Here, a = 1, b = -2, c = -5, d = 6
We know that if α, β and γ are the roots of
f(x) = ax³ + bx² + cx + d, then

Question 2.
Solution:
Zeros are 5, -2 and \(\frac { 1 }{ 3 }\) of

Question 3.
Solution:

Question 4.
Solution:

Question 5.
Solution:

Find the quotient and the remainder when:
Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Question 9.
Solution:
f(x) = 2x⁴ + 3x³ – 2x² – 9x – 12
g(x) = x² – 3
Quotient [q(x)] = 2x² + 3x + 4
Remainder [r(x)] = 0
Remainder is zero.
x² – 3 is a factor of f(x)

Question 10.
Solution:

Question 11.
Solution:

Question 12.
Solution:

= (x + 1) (x + 4) (x – 3)
If x + 4 = 0, then x = -4
If x – 3 = 0, then x = 3
Zeros are -1, -4, 3

Question 13.
Solution:

Question 14.
Solution:

=> (x – 3) (x + 3) [x (x + 2) – 1 (x + 2)]
=> (x – 3) (x + 3) (x + 2) (x – 1)
Other zeros will be
If x + 2 = 0 then x = -2
and if x – 1 =0, then x = 1
Zeros are 3, -3, -2, 1

Question 15.
Solution:
2 and -2 are the two zeros of the polynomial
f(x) = x⁴ + x³ – 34x² – 4x + 120,
Then (x – 2) (x + 2) or x² – 4 will its the factor of f(x)
Now dividing f(x) by x² – 4, we get

f(x) = (x – 2) (x + 2) (x² + x – 30)
= (x – 2)(x + 2)[x² + 6x – 5x – 30]
= (x – 2) (x + 2)[x(x + 6) – 5(x + 6)]
= (x – 2) (x + 2) (x + 6) (x – 5)
Other two zeros are
If x + 6 = 0, then x = -6 and
if x – 5 = 0, then x = 5
Roots of f(x) are 2, -2, -6, 5

Question 16.
Solution:

Other two zeros are :
if x + 5 = 0, then x = -5
and if x – 4 = 0, then x = 4
Hence, all the zeros of f(x) are : √3, – √3, 4, -5

Question 17.
Solution:
√3 and – √3 are the zeros of the polynomial
f(x) = 2x⁴ – 3x³ – 5x² + 9x – 3
=> (x – √3) (x + √3) or (x² – 3) is a factor of f(x)
Now, dividing f(x) by x² – 3, we get

Question 18.
Solution:

Question 19.
Solution:

Hope given RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 2 Polynomials MCQS

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Class 10 Solutions Chapter 2 Polynomials MCQS

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2A
• RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2B
• RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2C
• RS Aggarwal Solutions Class 10 Chapter 2 Polynomials MCQS
• RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Test Yourself

Choose the correct answer in each of the following questions.
Question 1.
Solution:
(d) √2 x² – 3√3 x + √6 is polynomial, others are not polynomial.

Question 2.
Solution:
(d) x + \(\frac { 3 }{ x }\) is not a polynomial, other are polynomial.

Question 3.
Solution:
(c) Let f(x) = x² – 2x – 3
= x² – 3x + x – 3
= x(x – 3) + 1(x – 3)
= (x – 3)(x + 1)
If x – 3 = 0, then x – 3
and if x + 1 = 0, then x = -1
Zeros are 3, -1

Question 4.
Solution:
(b)

Question 5.
Solution:
(c)

Question 6.
Solution:
(b) Polynomial is x² + \(\frac { 1 }{ 6 }\) x – 2

Question 7.
Solution:
(a)

Question 8.
Solution:
(c) Sum of zeros = 3
Product of zeros = -10
Polynomial : x² – (Sum of zeros) x + Product of zeros
= x² – 3x – 10

Question 9.
Solution:
(c) Zeros are 5 and -3
Sum of zeros = 5 – 3 = 2
Product of zeros = 5 x (-3) = -15
Polynomial: x² – (Sum of zeros) x + Product of zeros
= x² – 2x – 15

Question 10.
Solution:
(d)

Question 11.
Solution:
(b) Let f(x) = x² + 88x +125
Here, sum of roots = \(\frac { -b }{ a }\) = -88
and product = \(\frac { c }{ a }\) = 125
Product is positive,
Both zeros can be both positive or both negative.
Sum is negative.
Both zeros are negative.

Question 12.
Solution:
(b) α and β are the zeros of x² + 5x + 8
Then sum of zeros (α + β) = \(\frac { -b }{ a }\) = \(\frac { -5 }{ 1 }\) = -5

Question 13.
Solution:
(c) α and β are the zeros of 2x² + 5x – 9
Product of zeros (αβ) = \(\frac { c }{ a }\) = \(\frac { -9 }{ 2 }\)

Question 14.
Solution:
(d) 2 is a zero of kx² + 3x + k
It will satisfy the quadratic equation kx² + 3x + k = 0
k(2)² + 3x² + 1 = 0
4k + 6 + k = 0
=> 5k = -6
k = \(\frac { -6 }{ 5 }\)

Question 15.
Solution:
(b) -4 is a zero of (k – 1) x² + 4x + 1
-4 will satisfy the equation (k – 1) x² + kx + 1 = 0
=> (k – 1)(-4)² + k(-4) + 1 =0
=> 16k – 16 – 4k + 1 = 0
=> 12k – 15 = 0
=> 12k = 15
=> k = \(\frac { 15 }{ 12 }\) = \(\frac { 5 }{ 4 }\)

Question 16.
Solution:
(c)

Question 17.
Solution:
(a)

Question 18.
Solution:
(d) Polynomial: kx² + 2x + 3k

Question 19.
Solution:
(b) α, β are the zeros of the polynomial x² + 6x + 2

Question 20.
Solution:
(a) α, β, γ are the zeros of x³ – 6x² – x + 30
Then αβ + βγ + γα = \(\frac { c }{ a }\) = \(\frac { -1 }{ 1 }\) = -1

Question 21.
Solution:
(a) α, β, γ are the zeros of 2x³ + x² – 13x + 6, then
αβγ = \(\frac { -d }{ a }\) = \(\frac { -6 }{ 2 }\) = -3

Question 22.
Solution:
(c) α, β, γ are the zeros of p(x) such that

Question 23.
Solution:
(a)

Question 24.
Solution:
(b) If one zero of cubic polynomial ax³ + bx² + cx + d = 0
Let a be zero, then

Question 25.
Solution:
(c)

Question 26.
Solution:
(d)

Question 27.
Solution:
(c) p(x) is divided by q(x), then
p(x) = q(x) x g(x) + r(x)
Either r(x) = 0
Degree of r(x) < deg of g(x)

Question 28.
Solution:
(d) (a) is not a linear polynomial.
(b) is trinomial not binomial.
(c) is not a monomial.
(d) 5x² is monomial is true.

Hope given RS Aggarwal Solutions Class 10 Chapter 2 Polynomials MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers MCQS

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQS.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1B
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQs
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself

Choose the correct answer in each of the following questions.
Question 1.
Solution:
(b) We know that HCF of two co-prime number is 1
HCF of 14, 35 is 7
HCF of 18, 25 is 1
HCF of 31, 93 is 31
HCF of 32, 60 is 4
Required co-prime number is (18, 25)

Question 2.
Solution:
(b) a = (2² x 3³ x 5⁴), b = (2³ x 3² x 5)
HCF = 2² x 3² x 5 = 2 x 2 x 3 x 3 x 5 = 180

Question 3.
Solution:
(c) HCF of 2³ x 3² x 5, 2² x 3³ x 5², 2⁴ x 3 x 5³ x 7
HCF = 2² x 3 x 5 = 2 x 2 x 3 x 5 = 60

Question 4.
Solution:
(d) LCM of 2³ x 3 x 5, 2⁴ x 5 x 7 = 2⁴ x 3 x 5 x 7
=2 x 2 x 2 x 2 x 3 x 5 x 7
= 1680

Question 5.
Solution:
(d) HCF of two numbers = 27
LCM = 162
One number = 54

Question 6.
Solution:
(c) Product of two numbers = 1600
HCF = 5

Question 7.
Solution:
(c) Largest number that divides each one of 1152 and 1664
HCF of 1152 and 1664 =128

Question 8.
Solution:
(a) Largest number that divides 70 and 125 leaving remainders as 5 and 8 respectively.
Required number = 70 – 5 = 65
and 125 – 8= 117
HCF of 65, 117 = 13

Question 9.
Solution:
(b) Largest number that divides 245 and 1029 leaving remainder as 5 in each case. .
Required number = 245 – 5 = 240 and 1029 – 5 = 1024
Now, HCF of 240 and 1020 = 16

Question 10.
Solution:
(d)

Question 11.
Solution:
(c) In a = bq + r
r must satisfy i.e. 0 ≤ r < b

Question 12.
Solution:
(d) Let the given number when divided by 143 gives q as quotient and 31 as remainder.
Number = 143q + 31
= (13 x 11) q + 31
= 13 x 11 q+ 13 x 2 + 5
= 13 (110 + 2) + 5
The number where divided by 73, gives 5 as remainder.

Question 13.
Solution:
(d) 3.141141114… is irrational because it is non terminating non-repeating.

Question 14.
Solution:
(c) π is an irrational number.

Question 15.
Solution:
(b) \(2.\bar { 35 }\) is a rational number as it is non-terminating repeating decimal.

Question 16.
Solution:
(c) 2.13113111311113… is an irrational number.
It is non-terminating non-repeating decimal.

Question 17.
Solution:
(b) 3.24636363…
= \(3.24\bar { 63 }\)
It is non-terminating repeating decimal.
It is a rational number.

Question 18.
Solution:
(c) \(\frac { 2027 }{ 625 }\) = \(\frac { 2027 }{ { 5 }^{ 4 } }\) is a rational because it has terminating decimal as q = 5⁴ which is in form of 2^m x 5ⁿ.

Question 19.
Solution:
(b)

Question 20.
Solution:
(d)

Question 21.
Solution:
(b) 1.732 is a rational number.
As it is terminating decimal.

Question 22.
Solution:
(a) Least prime factor of a positive integer a is 3 and b is 5
2 is neither a factor of a nor of b
a and b are odd
Then (a + b) = even
(Sum of two odd numbers is even)
(a + b) is divisible by 2
Which is the least prime factor.

Question 23.
Solution:
(b) √2 is an irrational number.

Question 24.
Solution:
(c)

Question 25.
Solution:
(c) 2 + √2 is an irrational number as sum of a rational and an irrational is an irrational

Question 26.
Solution:
(c) LCM of 1 to 10 = 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520

Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers Test Yourself

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1B
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQs
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself

Question 1.
Solution:
(b)

Its decimal will be nonterminating repeating decimal.

Question 2.
Solution:
(b) \(\frac { p }{ q }\) is terminating decimal if q = 2^m x 5ⁿ
Now, 91 = 7 x 13, 45 = 3² x 5
80 = 2⁴ x 5, 42 = 2 x 3 x 7
80 is of the form 2^m x 5ⁿ
\(\frac { 19 }{ 80 }\) is terminating decimal expansion,

Question 3.
Solution:
(b) Divisor = 9 and remainder = 7
Let b be the divisor, then
n = 9b + 7
Multiplying both sides by 3 and subtracting 1.
3n – 1 = 3(9b + 7) – 1
3n – 1 = 27b + 21 – 1
3n – 1 = 9(3b) + 9 x 2 + 2
3n – 1 = 9(3b + 2) + 2
Remainder = 2

Question 4.
Solution:
(b) \(0.\bar { 68 }\) + \(0.\bar { 73 }\)
0.686868 ……… + 0.737373……
= 1.424241 = \(1.\bar { 42 }\)

Short-Answer Questions (2 marks)
Question 5.
Solution:
4ⁿ, n ∈ N
4¹ = 4
4² = 4 x 4 = 16
4³ = 4 x 4 x 4 = 64
4⁴ = 4 x 4 x 4 x 4 = 256
4⁵ = 4 x 4 x 4 x 4 x 4 = 1024
We see that value of 4ⁿ, ends with 4 or 6 only.
Hence, the value of 4ⁿ, n ∈ N, never ends with 0.

Question 6.
Solution:
HCF of two numbers = 27 and LCM =162
One number = 81

Question 7.
Solution:
\(\frac { 17 }{ 30 }\) = \(\frac { 17 }{ 2 x 3 x 5 }\)
Here, q is in the form of 2^m x 5ⁿ
It is not terminating decimal.

Question 8.
Solution:

Question 9.
Solution:

Question 10.
Solution:
Let (2 + √3) is rational and 2 is rational.
Difference of them is also rational.
=> (2 + √3) – 2 = 2 + √3 – 2
= √3 is rational
But it contradicts the fact.
(2 + √3) is irrational.

Short-Answer Questions (3 marks)
Question 11.
Solution:
HCF of 12, 15, 18, 27
12 = 2 x 2 x 3 = 2² x 3
15 = 3 x 5
18 = 2 x 3 x 3 = 2 x 3²
27 = 3 x 3 x 3 = 3³
Now, HCF = 3
and LCM = 2² x 3³ x 5 =2 x 2 x 3 x 3 x 3 x 5
= 4 x 27 x 5 = 540

Question 12.
Solution:
Let 2 + √3 and 2 – √3 are two irrational number.
Sum = 2 + √3 + 2 – √3 = 4 which is a rational.

Question 13.
Solution:
4620

Question 14.
Solution:
1008

Question 15.
Solution:

Question 16.
Solution:
Give numbers are 546 and 764 and remainders are 6 and 8 respectively.
Remaining number 546 – 6 = 540
and 764 – 8 = 756
Now, required largest number = HCF of 540 and 756 = 108

Long-Answer Questions (4 marks)
Question 17.
Solution:
Let √3 is a rational number.
Let √3 = \(\frac { p }{ q }\) where p and q are integers and have no common factor, other than 1 and q ≠ 0
Squaring both sides.
3 = \(\frac { { p }^{ 2 } }{ { q }^{ 2 } }\) => 3q² – p²
=> 3 divides p²
=> 3 divides p
Let p = 3c for some integer c
3q² = 9c² => q² – 3c²
=> 3 divides q² (3 divides 3c²)
=> 3 divides q
3 is common factors of p and q
But it contradicts the fact that p and q have
no common factors and also contradicts that √3 is a rational number.
Hence, √3 is irrational number.

Question 18.
Solution:
Let n be an arbitrary odd positive integer on dividing n by 4, let m be the quotient and r be the remainder.
By Euclid’s division lemma,
n = 4q + r where 0 ≤ r < 4
n = 4q or (4q + 1) or (4q + 2) or (4q + 3)
Clearly, 4q and (4q + 2) are even number
since n is odd.
n ≠ 4q and n ≠ (4q + 2)
n = (4 q + 1) or (4q + 3) for same integer n
Hence, any positive odd integer of the form 4q + 1 or 4q + 3 for some integer q.

Question 19.
Solution:
On dividing n by 3, let q be the quotient and r be the remainder, then
n = 3q + r where 0 ≤ r < 3 => n = 3q + r where r = 0, 1 or 2
n = 3q or n = 3q + 1 or n = 3q + 2
(i) Case (I)
If n = 3q then n is divisible by 3
(ii) Case (II)
If n = (3q + 1) then n + 2 = 3q + 3 = 3q (q + 1) which is divisible by 3
In this case, n + 2 is divisible by 3
(iii) Case (III)
If n = (3q + 2) then n + 1 (n + 1) = 3q + 3 = 3(q + 1) which also divisible by 3
In this case, (n + 1) is divisible by 3
Hence, one and only one out of n, (n + 1) and (n + 2) is divisible by 3.

Question 20.
Solution:
Let (4 + 3√2) is rational number and 4 is also a rational number.
Difference of two rational numbers is also a rational number.
4 + 3√2 – 4 = 3√2 is a rational number
Product of two rational numbers is rational
3 is rational and √2 is rational
But it contradicts the fact
√2 is irrational
Hence, (4 + 3√2 ) is irrational.

Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself  are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers Ex 1E

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1B
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQs
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself

Very-Short Answer Questions
Question 1.
Solution:
For any two given positive integers a and b there exist unique whole numbers q and r such that
a = bq + r, where 0 ≤ r < b.
Here, we call ‘a’ as dividend, b as divisor, q is quotient and r as remainder.
Dividend = (Divisor x Quotient) + Remainder

Question 2.
Solution:
Every composite number can be uniquely expressed as a product of two primes, except for the order in which these prime factors occurs.

Question 3.
Solution:
360 = 2 x 2 x 2 x 3 x 3 x 5 = 2³ x 3² x 5

Question 4.
Solution:
We know that HCF of two primes is
HCF (a, b) = 1

Question 5.
Solution:
a and b are two prime numbers then their
LCM = Product of these two numbers
LCM(a, b) = a x b = ab.

Question 6.
Solution:
We know that product of two numbers is equal to their HCF x LCM
LCM = \(\frac { Product of two numbers }{ HCF }\)
= \(\frac { 1050 }{ 25 }\) = 42
LCM of two numbers = 42

Question 7.
Solution:
A composite number is a number which is not a prime. In other words, a composite number has more than two factors.

Question 8.
Solution:
a and b are two primes, then their
HCF will be 1
HCF of a and b = 1

Question 9.
Solution:
\(\frac { a }{ b }\) is a rational number and it has terminating decimal
b will in the form 2^m x 5ⁿ where m and n are some non-negative integers.

Question 10.
Solution:

Question 11.
Solution:

Question 12.
Solution:
2ⁿ x 5ⁿ = (2 x 5)ⁿ = (10)ⁿ
Which always ends in a zero
There is no value of n for which (2ⁿ x 5ⁿ) ends in 5

Question 13.
Solution:
We know that HCF is always a factor is its LCM
But 25 is not a factor of 520
It is not possible to have two numbers having HCF = 25 and LCM = 520

Question 14.
Solution:
Let two irrational number be (5 + √3) and (5 – √3).
Now their sum = (5 + √3) + (5 – √3) = 5 + √3 + 5 – √3 = 10
Which is a rational number.

Question 15.
Solution:
Let the two irrational number be (3 + √2) and (3 – √2)
Now, their product = (3 + √2) (3 – √2)
= (3)² – (√2)² {(a + b) (a – b) = a² – b²}
= 9 – 2 = 7
Which is a rational number.

Question 16.
Solution:
a and b are relative primes
their HCF = 1

Question 17.
Solution:
LCM of two numbers = 1200
and HCF = 500
But we know that HCF of two numbers divides their LCM.
But 500 does not divide 1200 exactly
Hence, 500 is not their HCF whose LCM is 1200.

Short-Answer Questions
Question 18.
Solution:
Let x = 0.4 = 0.444
Then 10x = 4.444….
Subtracting, we get
9x = 4 => x = \(\frac { 4 }{ 9 }\)
\(\bar { 0.4 }\) = \(\frac { 1 }{ 2 }\) which is in the simplest form.

Question 19.
Solution:
\(\bar { 0.23 }\)
Let x = \(\bar { 0.23 }\) = 0.232323…….
and 100x = 23.232323……
Subtracting, we get
99x = 23 => x = \(\frac { 23 }{ 99 }\)
\(\bar { 0.23 }\) = \(\frac { 23 }{ 99 }\) which is in the simplest form.

Question 20.
Solution:
0.15015001500015
It is non-terminating non-repeating decimal.
It is an irrational number.

Question 21.
Solution:
\(\frac { \surd 2 }{ 3 }\) = \(\frac { 1 }{ 3 }\) √2
Let \(\frac { 1 }{ 3 }\) √2 is a rational number
Product of two rational numbers is a rational
\(\frac { 1 }{ 3 }\) is rational and √2 is rational contradicts
But it contradicts the fact
\(\frac { \surd 2 }{ 3 }\) or \(\frac { 1 }{ 3 }\) √2 is irrational.

Question 22.
Solution:
√3 and 2.
√3 = 1.732 and 2.000
A rational number between 1.732 and 2.000 can be 1.8 or 1.9
Hence, 1.8 or 1.9 is a required rational.

Question 23.
Solution:
\(\bar { 3.1416 }\)
It is non-terminating repeating decimal.
It is a rational number.

Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers Ex 1D

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Question 1.
Solution:
(i) Rational numbers: Numbers in the form of \(\frac { p }{ q }\) where p and q are integers and q ≠ 0, are called rational numbers.
(ii) Irrational numbers : The numbers which are not rationals, are called irrational numbers. Irrational numbers can be expressed in decimal form as non terminating non-repeating decimal.
(iii) Real numbers : The numbers which are rational or irrational, are called real numbers.

Question 2.
Solution:
(i) \(\frac { 22 }{ 7 }\)
It is a rational number as it is in the form of \(\frac { p }{ q }\)
(ii) 3.1416
It is a rational number as it is a terminating decimal.
(iii) π
It is an irrational number as it is nonterminating non-repeating decimal.
(iv) \(3.\bar { 142857 }\)
It is a rational number as it is nonterminating repeating decimal.
(v) 5.636363… = 5.63
It is a rational number as it is nonterminating repeating decimal.
(vi) 2.040040004…
It is an irrational number as it is nonterminating non-repeating decimal.
(vii) 1.535335333…
It is an irrational number as it is non terminating non-repeating decimal.
(viii) 3.121221222…
It is an irrational number as it is nonterminating non-repeating decimal.
(ix) √21
It is an irrational number aS it is not in the form of \(\frac { p }{ q }\)
(x) \(\sqrt [ 3 ]{ 3 }\)
It is an irrational number as it is not in the form of \(\frac { p }{ q }\)

Question 3.
Solution:
(i) √6 is irrational.
Let √6 is not an irrational number, but it is a rational number in the simplest form of \(\frac { p }{ q }\)
√6 = \(\frac { p }{ q }\) (p and q have no common factors)
Squaring both sides,
6 = \(\frac { { p }^{ 2 } }{ { q }^{ 2 } }\)
p² = 6q²
p² is divisible by 6
=> p is divisible by 6
Let p = 6a for some integer a
6q² = 36a²
=> q² = 6a²
q² is also divisible by 6
=> q is divisible by 6
6 is common factors of p and q
But this contradicts the fact that p and q have no common factor
√6 is irrational
(ii) (2 – √3) is irrational
Let (2 – √3) is a rational and 2 is also rational, then
2 – (2 – √3 ) is rational (Difference two rationals is rational)
=> 2 – 2 + √3 is rational
=> √3 is rational
But it contradicts the fact
(2 – √3) is irrational
(iii) (3 + √2 ) is irrational
Let (3 + √2 ) is rational and 3 is also rational
(3 + √2 ) – 3 is rational (Difference of two rationals is rational)
=> 3 + √2 – 3 is rational
=> √2 is rational
But it contradicts the fact (3 + √2 ) is irrational
(iv) (2 + √5 ) is irrational
Let (2 + √5 ) is rational and 2 is also rational
(2 + √5) – 2 is rational (Difference of two rationals is rational)
=> 2 + √5 – 2 is rational
=> √5 is rational
But it contradicts the fact (2 + √5) is irrational
(v) (5 + 3√2 ) is irrational
Let (5 + 3√2 ) is rational and 5 is also rational
(5 + 3√2 ) – 5 is rational (Difference of two rationals is rational)
=>5 + 3√2 – 5 is rational
=> 3√2 is rational
Product of two rationals is rational
3 is rational and √2 is rational
√2 is rational
But it contradicts the fact
(5 + 3√2 ) is irrational
(vi) 3√7 is irrational
Let 3√7 is rational
3 is rational and √7 is rational (Product of two rationals is rational)
But √7 is rational, it contradicts the fact
3√7 is irrational
(vii) \(\frac { 3 }{ \surd 5 }\) is irrational
Let \(\frac { 3 }{ \surd 5 }\) is rational
\(\frac { 3\times \surd 5 }{ \surd 5\times \surd 5 } =\frac { 3\surd 5 }{ 5 }\) is rational
\(\frac { 3 }{ 5 }\) is rational and √5 is rational
But √5 is a rational, it contradicts the fact
\(\frac { 3 }{ \surd 5 }\) is irrational
(viii)(2 – 3√5) is irrational
Let 2 – 3√5 is rational, 2 is also rational
2 – (2 – 3√5) is rational (Difference of two rationals is rational)
2 – 2 + 3√5 is rational
=> 3√5 is rational
3 is rational and √5 is rational (Product of two rationals is rational)
√5 is rational
But it contradicts the fact
(2 – 3√5) is irrational
(ix) (√3 + √5) is irrational
Let √3 + √5 is rational
Squaring,
(√3 + √5)² is rational
=> 3 x 5 + 2√3 x √5 is rational
=> 8 + 2√15 is rational
=> 8 + 2√15 – 8 is rational (Difference of two rationals is rational)
=> 2√15 is rational
2 is rational and √15 is rational (Product of two rationals is rational)
√15 is rational
But it contradicts the fact
(√3 + √5) is irrational

Question 4.
Solution:
Let \(\frac { 1 }{ \surd 3 }\) is rational
= \(\frac { 1 }{ \surd 3 } \times \frac { \surd 3 }{ \surd 3 } =\frac { \surd 3 }{ 3 } = \frac { 1 }{ 3 } \surd 3\) is rational
\(\frac { 1 }{ 3 }\) is rational and √3 is rationals (Product of two rationals is rational)
√3 is rational But it contradicts the fact
\(\frac { 1 }{ \surd 3 }\) is irrational

Question 5.
Solution:
(i) We can take two numbers 3 + √2 and 3 – √2 which are irrationals
Sum = 3 + √2 + 3 – √2 = 6 Which is rational
3 + √2 and 3 – √2 are required numbers
(ii) We take two. numbers
5 + √3 and 5 – √3 which are irrationals
Now product = (5 + √3) (5 – √3)
= (5)² – (√3 )² = 25 – 3 = 22 which is rational
5 + √3 and 5 – √3 are the required numbers

Question 6.
Solution:
(i) True.
(ii) True.
(iii) False, as sum of two irrational can be rational number also such as
(3 + √2) + (3 – √2) = 3 + √2 + 3 – √2 = 6 which is rational.
(iv) False, as product of two irrational numbers can be rational also such as
(3 + √2)(3 – √2 ) = (3)2 – (√2 )2 = 9 – 2 = 7
which is rational
(v) True.
(vi) True.

Question 7.
Solution:
Let (2√3 – 1) is a rational number and 1 is a rational number also.
Then sum = 2√3 – 1 + 1 = 2√3
In 2√3, 2 is rational and √3 is rational (Product of two rational numbers is rational)
But √3 is rational number which contradicts the fact
(2√3 – 1) is an irrational.

Question 8.
Solution:
Let 4 – 5√2 is a rational number and 4 is also a rational number
Difference of two rational number is a rational numbers
4 – (4 – 5√2 ) is rational
=> 4 – 4 + 5√2 is rational
=> 5√2 is rational
Product of two rational number is rational
5 is rational and √2 is rational
But it contradicts the fact that √2 is rational √2 is irrational
Hence, 4 – 5√2 is irrational

Question 9.
Solution:
Let (5 – 2√3) is a rational number and 5 is also a rational number
Difference of two rational number is rational
=> 5 – (5 – 2√3) is rational
=> 5 – 5 + 2√3 or 2√3 is rational
Product of two rational number is rational
2 is rational and √3 is rational
But it contradicts the fact
(5 – 2√3) is an irrational number.

Question 10.
Solution:
Let 5√2 is a rational
Product of two rationals is a rational
5 is rational and √2 is rational
But it contradicts the fact
5√2 is an irrational.

Question 11.
Solution:
\(\frac { 2 }{ \surd 7 } =\frac { 2\surd 7 }{ \surd 7\times \surd 7 } =\frac { 2\surd 7 }{ 7 } =\frac { 2 }{ 7 } \surd 7\)
Let \(\frac { 2 }{ 7 } \surd 7\) is a rational number, then
\(\frac { 2 }{ 7 }\) is rational and √7 is rational
But it contradicts the fact \(\frac { 2 }{ \surd 7 }\) is an irrational number.

 

Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers Ex 1C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1B
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQs
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself

Question 1.
Solution:

Question 2.
Solution:

Question 3.
Solution:

Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.