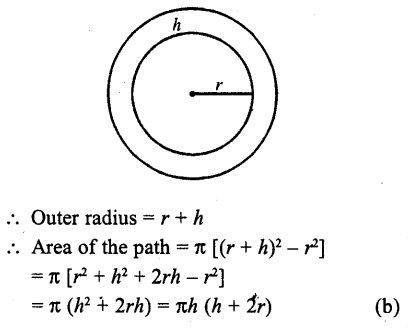
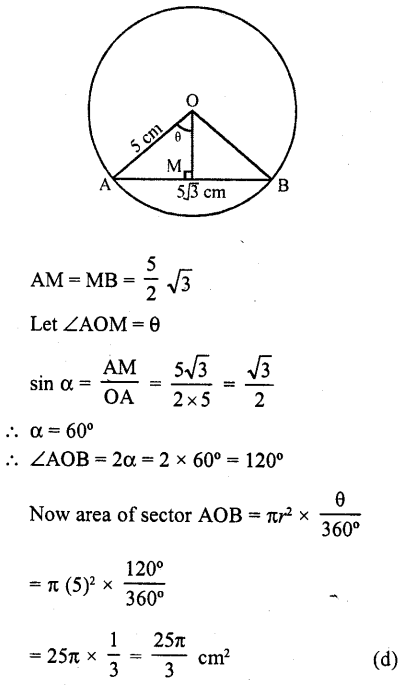
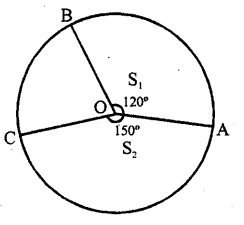
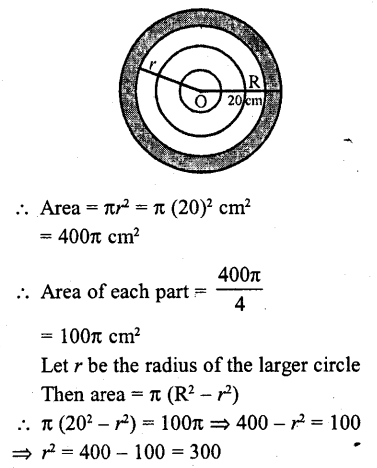
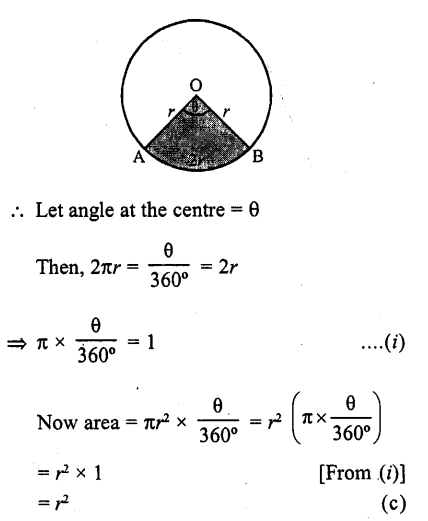
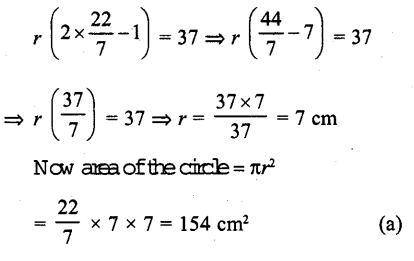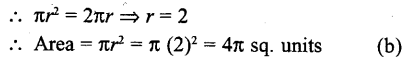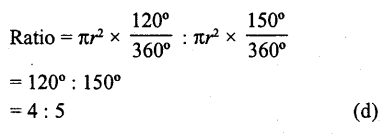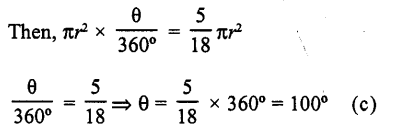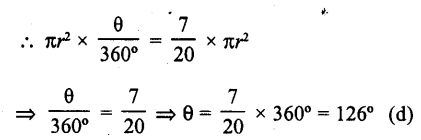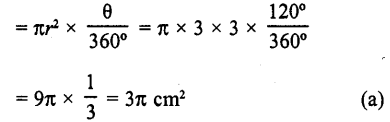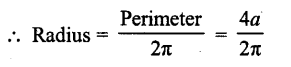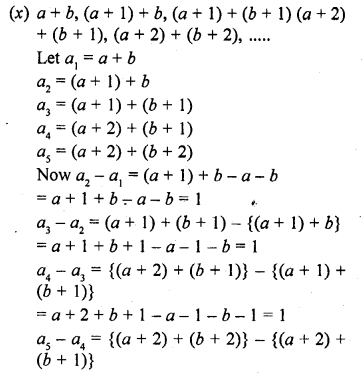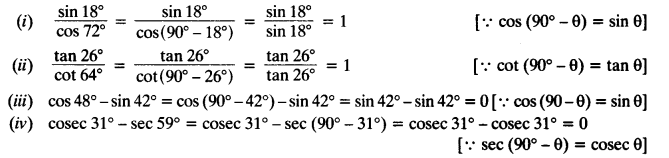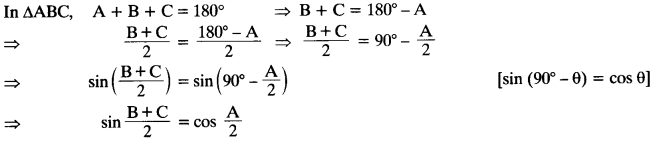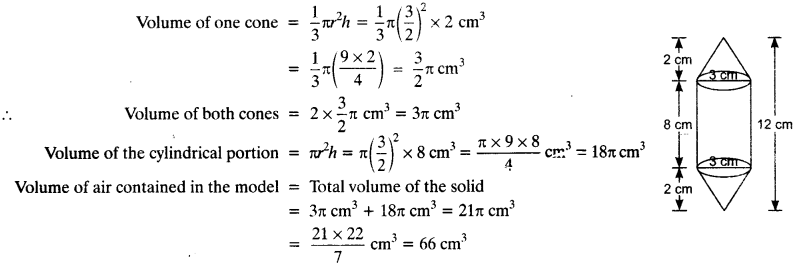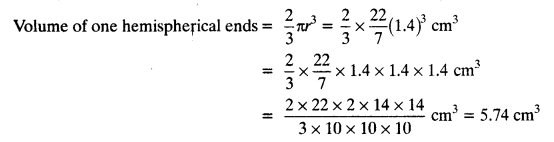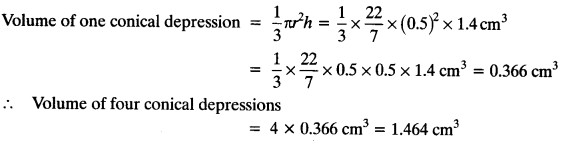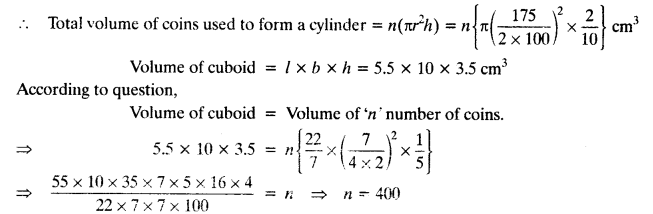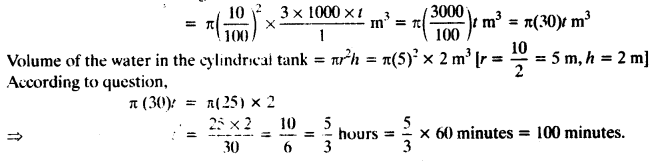RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
Other Exercises
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.1
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6
- RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7
- RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise
- RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS
- RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS
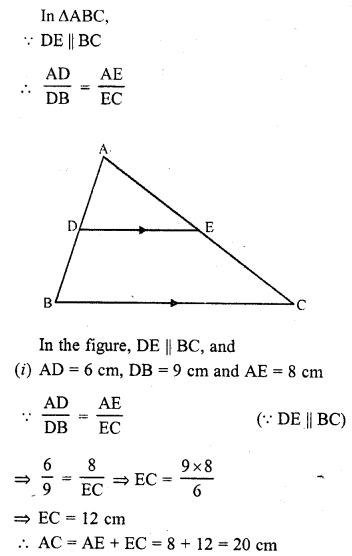
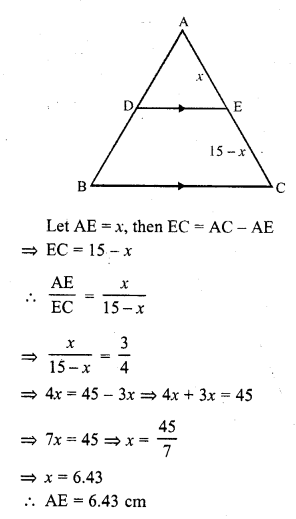
Question 1.
In a ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC.
(i) If AD = 6 cm, DB = 9 cm and AE = 8 cm, find AC. (C.B.S.E. 1995)
(ii) If \(\frac { AD }{ DB }\) = \(\frac { 3 }{ 4 }\) and AC = 15 cm, find AE. (C.B.S.E. 1994)
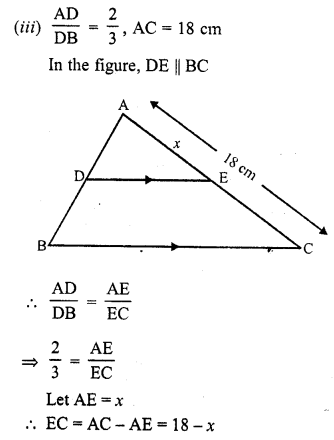
(iii) If \(\frac { AD }{ DB }\) = \(\frac { 2 }{ 3 }\) and AC = 18 cm, find AE. (C.B.S.E. 1994C)
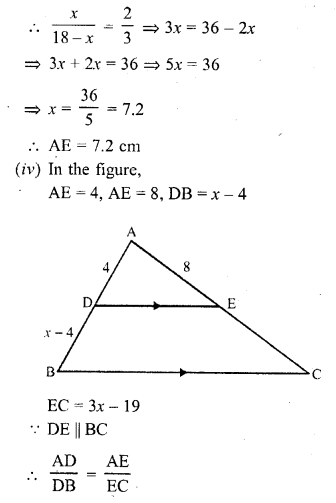
(iv) If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x. (C.B.S.E. 1992C)
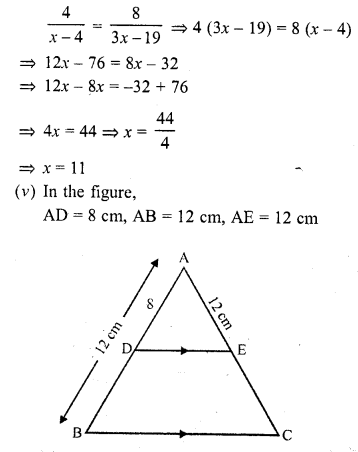
(v) If AD = 8 cm, AB = 12 cm and AE = 12 cm, find CE. (C.B.S.E. 1992C)
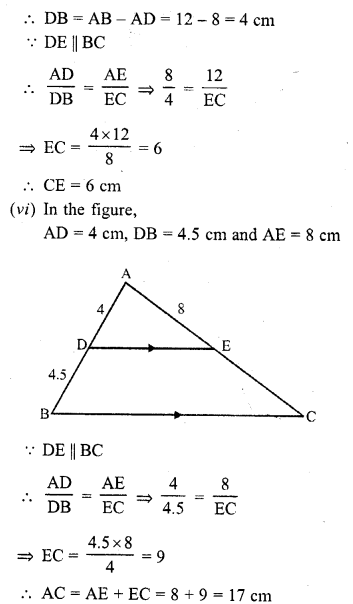
(vi) If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC. (C.B.S.E. 1992C)
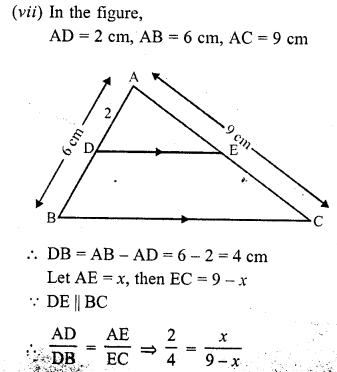
(vii) If AD = 1 cm, AB = 6 cm and AC = 9 cm, findAE. (C.B.S.E. 1992C)
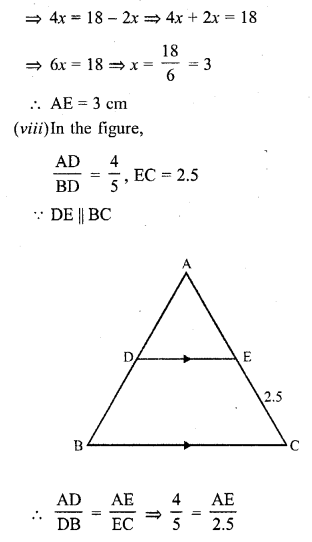
(viii) If \(\frac { AD }{ DB }\) = \(\frac { 4 }{ 5 }\) and EC = 2.5 cm, find AE.
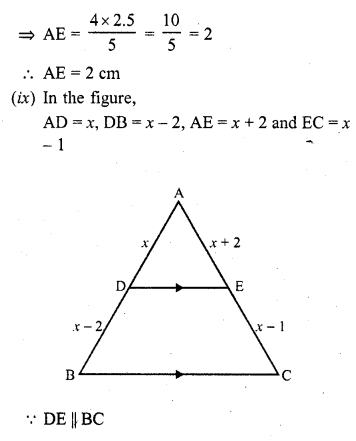
(ix) If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, find the value of x. (C.B.S.E. 1993C)
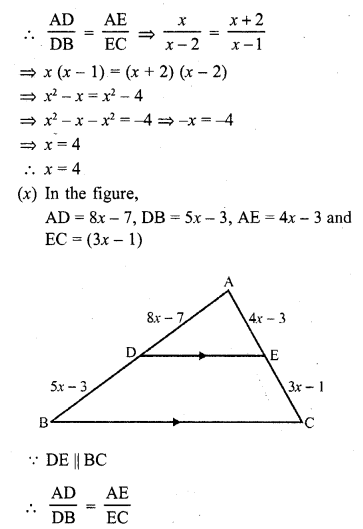
(x) If AD = 8x – 7, DB = 5x – 3, AE = 4x – 3 and EC = (3x – 1), find the value of x.
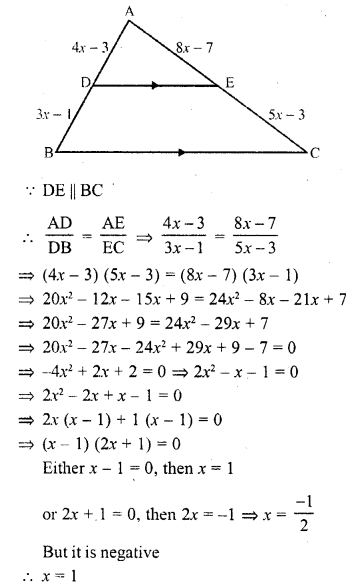
(xi) If AD = 4x – 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x – 3, find the value of x. (C.B.S.E. 2002)
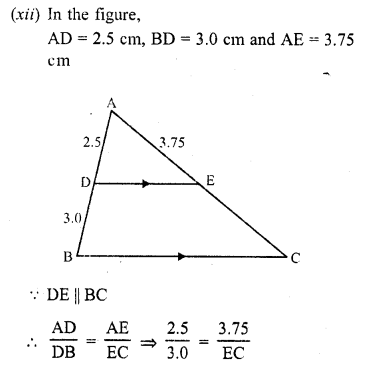
(xii) If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm, find the length of AC. (C.B.S.E. 2006C)
Solution:

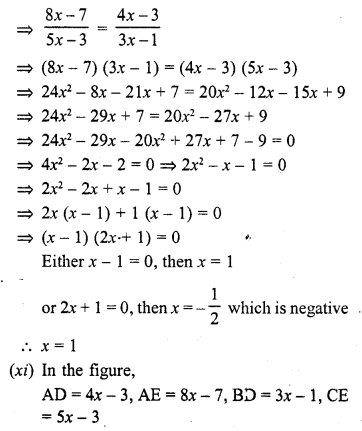
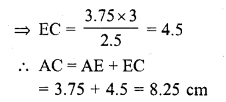
Question 2.
In a ∆ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DE || BC:
(i) AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm. (C.B.S.E. 1991)
(ii) AB = 5.6 cm, AD = 1.4 cm, AC = 7.2 cm and AE = 1.8 cm. (C.B.S.E. 1990)
(ii) AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
(iv) AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
Solution:
In ∆ABC, D and E are points on the sides AB and AC respectively
(i) AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm
DB = AB – AD = 12 – 8 = 4 cm and EC = AC – AE = 18 – 12 = 6 cm


Question 3.
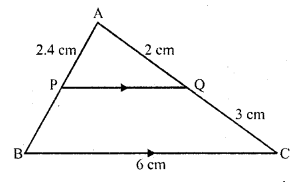
In a ∆ABC, P and Q are points on sides AB and AC respectively, such that PQ || BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, find AB and PQ.
Solution:
In ∆ABC,
P and Q are points on AB and AC respectively such that PQ || BC
AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm

Question 4.
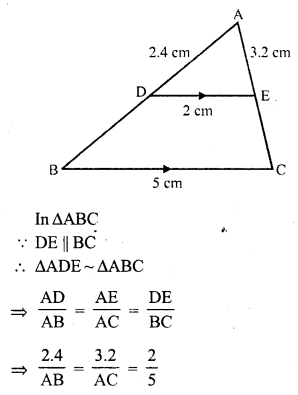
In a ∆ABC, D and E are points on AB and AC respectively such that DE || BC. If AD = 2.4 cm, AE = 3.2 cm, DE = 2 cm and BC = 5 cm, find BD and CE. (C.B.S.E. 2001C)
Solution:
In the ∆ABC, DE || BC
AD = 2.4 cm, AE = 3.2 cm, DE = 2 cm and BC = 5 cm
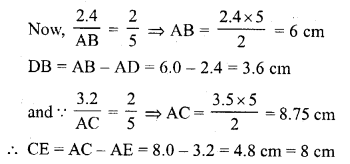
Question 5.
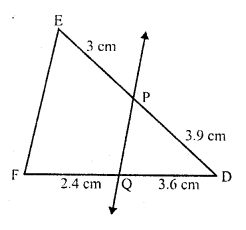
In the figure, state if PQ || EF.
Solution:
In ∆DEF
PQ intersects DE and DF at P and Q respectively
Such that DP = 3.9 cm, PE = 3 cm DQ = 3.6 cm, QF = 2.4 cm

Question 6.
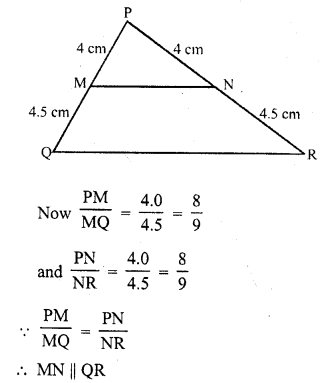
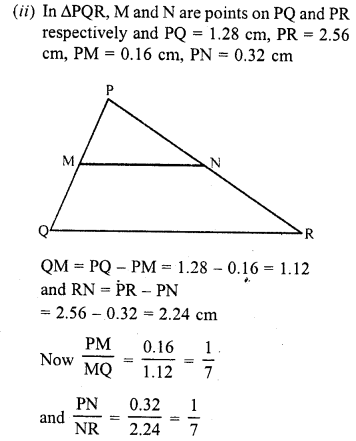
M and N are points on the sides PQ and PR respectively of a ∆PQR. For each of the following cases, state whether MN || QR.
(i) PM = 4 cm, QM = 4.5 cm, PN = 4 cm, NR = 4.5 cm
(ii) PQ = 1.28 cm, PR = 2.56 cm, PM = 0.16 cm, PN = 0.32 cm
Solution:
(i) In the ∆PQR
M and N are points on PQ and PR respectively
PM = 4 cm, QM = 4.5 cm, PN = 4 cm, RN = 4.5 cm
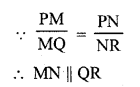
Question 7.
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN || AC.
Solution:
Given : On OA, OB and OC, points are L, M, and N respectively
Such that LM || AB, MN || BC
Question 8.
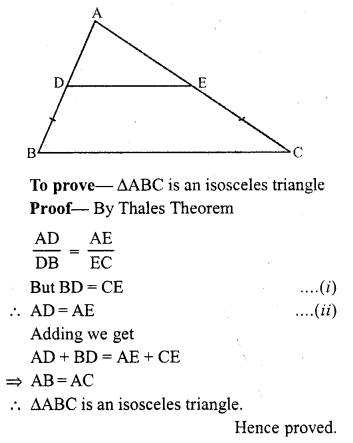
If D and E are points on sides AB and AC respectively of a ∆ABC such that DE || BC and BD = CE. Prove that ∆ABC is isosceles. (C.B.S.E. 2007)
Solution:
Given : In ∆ABC, D and E are points on the sides AB and AC such that BD = CD
Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.