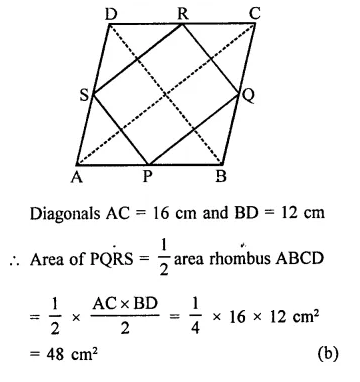
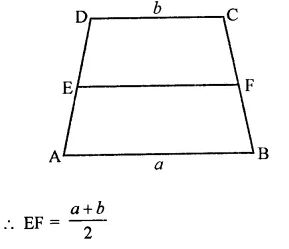
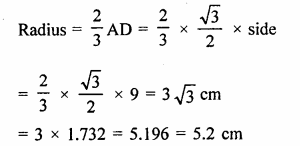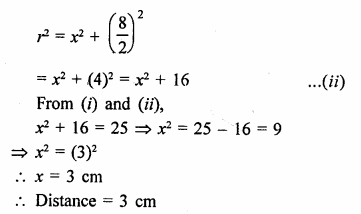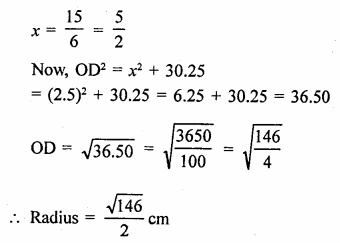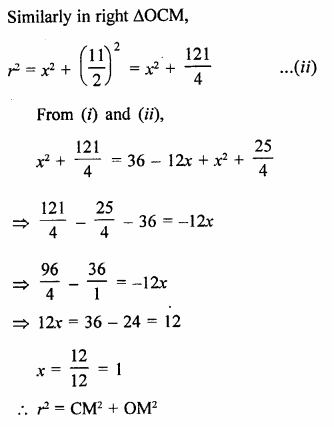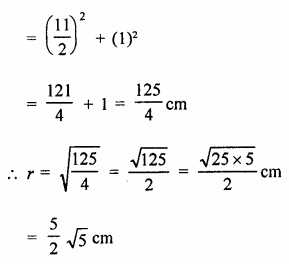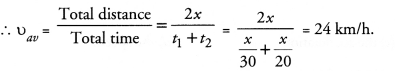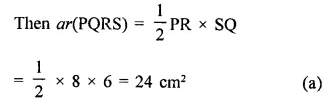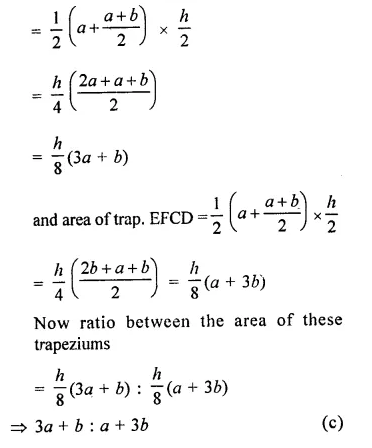RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3

Other Exercises

Question 1.
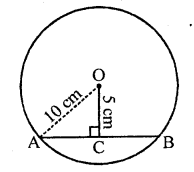
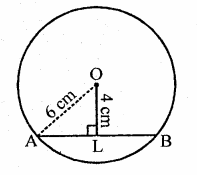
Three girls Ishita, Isha and Nisha are playing a game by standing on a circle of radius 20 m drawn in a park. Ishita throws a ball to Isha, Isha to Nisha and Nisha to Ishita. If the distance between Ishita and Isha and between Isha and Nisha is 24 m each, what is the distance between Ishita and Nisha. [NCERT]
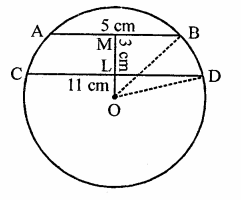
Solution:
∵ Distance between Isha and Ishita and Ishita and Nisha is same
∴ RS = SM = 24 m
∴They are equidistant from the centre
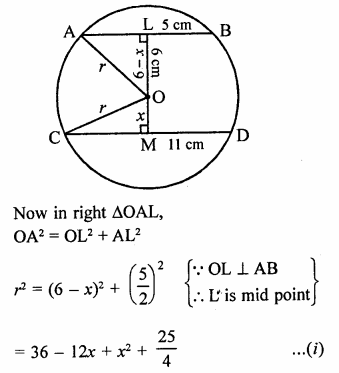
In right ∆ORL,
OL² = OR² – RL²
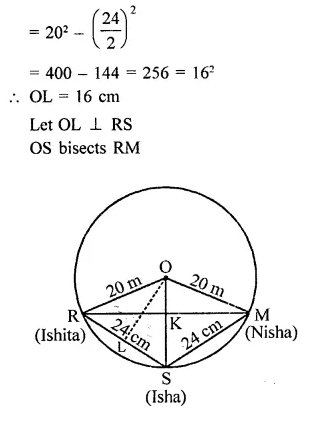
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3 Q1.1
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3 Q1.2
Hence distance between Ishita and Nisha = 38.4 m

Question 2.
A circular park of radius 40 m is situated in a colony. Three beys Ankur, Amit and Anand are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other. Find thelength of the string of each phone. [NCERT]
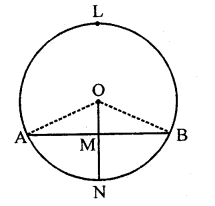
Solution:
Radius of circular park = 40 m
Ankur, Amit and Anand are sitting at equal distance to each other By joining them, an equilateral triangle ABC is formed produce BO to L which is perpendicular bisector of AC
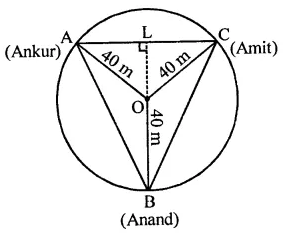
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3 Q2.1
∴ BL = 40 + 20 = 60 m (∵ O is centroid of ∆ABC also)
Let a be the side of ∆ABC
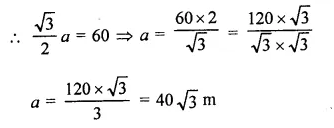
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3 Q2.2
Hence the distance between each other = 40\(\sqrt { 3 } \) m

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2

Other Exercises

Question 1.
The radius of a circle is 8 cm and the length of one of its chords is 12 cm. Find the distance of the chord from the centre.
Solution:
Radius of circle with centre O is OA = 8 cm
Length of chord AB = 12 cm
OC ⊥ AB which bisects AB at C
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q1.1
∴ AC = CB = 12 x \(\frac { 1 }{ 2 }\) = 6 cm
In ∆OAC,
OA2 = OC2 + AC2 (Pythagoras Theorem)
⇒ (8)2 = OC2 + (6)2
⇒ 64 = OC2 + 36
OC2 = 64 – 36 = 28
∴ OC = \(\sqrt { 28 } \) = \(\sqrt { 4×7 } \) cm
= 2 x 2.6457 = 5.291 cm

Question 2.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 10 cm.
Solution:
Let AB be a chord of a circle with radius 10 cm. OC ⊥ AB
∴ OA = 10 cm
OC = 5 cm
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q2.1
∵ OC divides AB into two equal parts
i.e. AC = CB
Now in right AOAC,
OA2 = OC2 + AC2 (Pythagoras Theorem)
⇒ (10)2 = (5)2 + AC2
⇒ 100 = 25 + AC2
⇒ AC2 = 100 – 25 = 75
∴ AC = \(\sqrt { 75 } \)= \(\sqrt { 25×3 } \) = 5 x 1.732
∴ AB = 2 x AC = 2 x 5 x 1.732 = 10 x 1.732 = 17.32 cm

Question 3.
Find the length of a chord which is at a distance of 4 cm from the centre of the circle of radius 6 cm.
Solution:
In a circle with centre O and radius 6 cm and a chord AB at a distance of 4 cm from the centre of the circle
i.e. OA = 6 cm and OL ⊥ AB, OL = 4 cm
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q3.1
∵ Perpendicular OL bisects the chord AB at L 1
∴ AL = LB=\(\frac { 1 }{ 2 }\) AB
Now in right ∆OAL,
OA2 = OL2 + AL2 (Pythagoras Theorem)
(6)2 = (4)2 + AL2
⇒ 36=16+AL2
⇒ AL2 = 36 – 16 = 20
∴ AL = \(\sqrt { 20 } \) = \(\sqrt { 4×5 } \) = 2 x 2.236 = 4.472 cm
∴ Chord AB = 4.472 x 2 = 8.944 = 8.94 cm

Question 4.
Give a method to find the centre of a given circle.
Solution:
Steps of construction :
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q4.1
(i) Take three distinct points on the circle say A, B and C.
(ii) Join AB and AC.
(iii) Draw the perpendicular bisectors of AB and AC which intersect each other at O.
O is the required centre of the given circle

Question 5.
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Solution:
Given : In circle with centre O
CD is the diameter and AB is the chord
which is bisected by diameter at E
OA and OB are joined
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q5.1
To prove : ∠AOB = ∠BOA
Proof : In ∆OAE and ∆OBE
OA = OB (Radii of the circle)
OE = OE (Common)
AE = EB (Given)
∴ ∆OAE = ∆OBE (SSS criterian)
∴ ∠AOE = ∠BOE (c.p.c.t.)
Hence diameter bisect the angle subtended by the chord AB.

Question 6.
A line segment AB is of length 5 cm. Draw a circle of radius 4 cm passing through A and B. Can you draw a circle of radius 2 cm passing through A and B? Give reason in support of your answer.
Solution:
Steps of construction :
(i) Draw a line segment AB = 5 cm.
(ii) Draw a perpendicular bisector of AB.
(iii) With centre A and radius 4 cm, draw an arc which intersects the perpendicular bisector at O.
(iv) With centre O and radius 4 cm, draw a circle which passes through A and B.
With radius 2 cm, we cannot draw the circle passing through A and B as diameter
i. e. 2 + 2 = 4 cm is shorder than 5 cm.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q6.1

Question 7.
An equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
Solution:
Steps of construction :
(i) Draw a line segment BC = 9 cm.
(ii) With centres B and C, draw arcs of 9 cm radius which intersect each other at A.
(iii) Join AB and AC.
∆ABC is the required triangle.
(iv) Draw perpendicular bisectors of sides AB and BC which intersect each other at O.
(v) With centre O and radius OB, draw a circle which passes through A, B and C.
This is the require circle in which ∆ABC is inscribed.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q7.1
On measuring its radius, it is 5.2 cm
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q7.2

Question 8.
Given an arc of a circle, complete the circle.
Solution:
Steps of construction :
(i) Take three points A, B and C on the arc and join AB and BC.
(ii) Draw the perpendicular bisector of AB and BC which intersect each other at O.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q8.1
(iii) With centre O and radius OA or OB, complete the circle.
This is the required circle.

Question 9.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
Below, three different pairs of circles are drawn:
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q9.1
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q9.2
(i) In the first pair, two circles do not intersect each other. Therefore they have no point in common. .
(ii) In the second pair, two circles intersect (touch) each other at one point P. Therefore they have one point in common.
(iii) In the third pair, two circles intersect each other at two points. Therefore they have two points in common.
There is no other possibility of two circles intersecting each other.
Therefore, two circles have at the most two points in common.

Question 10.
Suppose you are given a circle. Give a construction to find its centre.
Solution:
See Q. No. 4 of this exercise.

Question 11.
The length of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre? [NCERT]
Solution:
A circle with centre O and two parallel chords
AB and CD are AB = 6 cm, CD = 8 cm
Let OL ⊥ AB and OM ⊥ CD
∴ OL = 4 cm
Let OM = x cm
Let r be the radius of the circle
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q11.1
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q11.2

Question 12.
Two chords AB, CD of lengths 5 cm and 11 cm respectively of a circle are parallel. If the distance between AB and CD is 3 cm, find the radius of the circle.
Solution:
Let two chords AB and CD of length 5 cm and 11 cm are parallel to each other AB = 5 cm, CD = 11 cm
Distance between AB and LM = 3 cm
Join OB and OD
OL and OM are the perpendicular on CD and AB respectively. Which bisects AB and CD.
Let OL = x, then OM = (x + 3)
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q12.1
Now in right ∆OLD,
OD2 = OL2 + LD2
= x2 + (5.5)2
Similarly in right ∆OMB,
OB2 = OM2 + MB2 = (x + 3)2 + (2.5)2
But OD = OB (Radii of the circle)
∴ (x + 3)2 + (2.5)2 = x2 + (5.5)2
x2 + 6x + 9 + 6.25 = x2 + 30.25
6x = 30.25 – 6.25 – 9 = 15
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q12.2

Question 13.
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
Solution:
Given : A circle with centre O and a chord AB
Let M be the mid point of AB and OM is joined and produced to meet the minor arc AB at N
To prove : M is the mid point of arc AB
Construction : Join OA, OB
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q13.1
Proof: ∵ M is mid point of AB
∴ OM ⊥ AB
In AOAM and OBM,
OA = OB (Radii of the circle)
OM = OM (common)
AM = BM (M is mid point of AB)
∴ ∆OAM = ∆OBM (SSS criterian)
∴ ∠AOM = ∠BOM (c.p.c.t.)
⇒ ∠AOM = ∠BOM
But these are centre angles at the centre made by arcs AN and BN
∴ Arc AN = Arc BN
Hence N divides the arc in two equal parts

Question 14.
Prove that two different circles cannot intersect each other at more than two points.
Solution:
Given : Two circles
To prove : They cannot intersect each other more than two points
Construction : Let two circles intersect each other at three points A, B and C
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q14.1
Proof : Since two circles with centres O and O’ intersect at A, B and C
∴ A, B and C are non-collinear points
∴ Circle with centre O passes through three points A, B and C
and circle with centre O’ also passes through three points A, B and C
But one and only one circle can be drawn through three points
∴Our supposition is wrong
∴ Two circle cannot intersect each other not more than two points.

Question 15.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle. [NCERT]
Solution:
Let r be the radius of the circle with centre O.
Two parallel chords AB = 5 cm, CD = 11 cm
Let OL ⊥ AB and OM ⊥CD
∴ LM = 6 cm
Let OM = x, then
OL = 6 – x
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q15.1
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q15.2
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 Q15.3

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1

Other Exercises

Question 1.
Fill in the blanks: [NCERT]
(i) All points lying inside / outside a circle are called …….. points / ………. points.
(ii) Circles having the same centre and different radii are called …….. circles.
(iii) A point whose distance from the centre of a circle is greater than its radius lies in …….. of the circle.
(iv) A continuous piece of a circle is …….. of the circle.
(v) The longest chord of a circle is a ……… of the circle.
(vi) An arc is a …….. when its ends are the ends of a diameter.
(vii) Segment of a circle is the region between an are and ……..of the circle.
(viii)A circle divides the plane, on which it lies, in …….. parts.
Solution:
(i) All points lying inside / outside a circle are called interior points / exterior points.
(ii) Circles having the same centre and different radii are called concentric circles.
(iii) A point whose distance from the centre of a circle is greater than its radius lies in exterior of the circle.
(iv) A continuous piece of a circle is arc of the circle.
(v) The longest chord of a circle is a diameter of the circle.
(vi) An arc is a semi-circle when its ends are the ends of a diameter.
(vii) Segment of a circle is the region between an arc and centre of the circle.
(viii) A circle divides the plane, on which it lies, in three parts.

Question 2.
Write the truth value (T/F) of the following with suitable reasons: [NCERT]
(i) A circle is a plane figure.
(ii) Line segment joining the centre to any point on the circle is a radius of the circle.
(iii) If a circle is divided into three equal arcs each is a major arc.
(iv) A circle has only finite number of equal chords.
(v) A chord of a cirlce, which is twice as long is its radius is a diameter of the circle.
(vi) Sector is the region between the chord and its corresponding arc.
(vii) The degree measure of an arc is the complement of the central angle containing the arc.
(viii)The degree measure of a semi-circle is 180°.
Solution:
(i) True.
(ii) True.
(iii) True.
(iv) False. As it has infinite number of equal chords.
(v) True.
(vi) False. It is a segment not sector.
(vii) False. As total degree measure of a circle is 360°.
(viii) True.

 

 

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion

NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion

These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion

MULTIPLE CHOICE QUESTIONS

Question 1.
A particle is moving in a circular path of radius r. The displacement after half a circle would be :
(a) Zero       (b) πr            (c) 2r                  (d) 2πr.
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 1
Answer:
(c) Explanation : Particle is just opposite to the initial position on the circle.

More Resources

Question 2.
A body is thrown vertically upward with velocity u, the greatest height h to which it will rise is,
(a) u/g             (b) u2/2g                (c) u2/g                (d) u/2g.
Answer:
(b) Explanation : u2 – v2 = – 2gh or 0 – u2 = – 2gh (∴ u = 0 at highest point).
∴ h = u2/2g.

Question 3.
The numerical ratio of displacement to distance for a moving object is
(a) always less than 1
(b) always equal to 1
(c) always more than 1
(d) equal or less than 1
Answer:
(d) Explanation : Displacement ≤ distance.

Question 4.
If the displacement of an object is proportional to square of time, then the object moves with
(a) uniform velocity
(b) uniform acceleration
(c) increasing acceleration
(d) decreasing acceleration.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 2

Question 5.
From the given u -t graph (Fig. 1), it can be inferred that the object is
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 3
(a) in uniform motion
(b) at rest
(c) in non-uniform motion
(d) moving with uniform acceleration.
Answer:
(a) Explanation : Velocity of object is constant.

Question 6.
Suppose a boy is enjoying a ride on a merry-go-round which is moving with a constant speed of 10 m s-1. It implies that the boy is
(a) at rest
(b) moving with no acceleration
(c) in accelerated motion
(d) moving with uniform velocity.
Answer:
(c) Explanation : Velocity of the boy changes continuously due to the change in direction of motion in circular path.

Question 7.
Area under a v — t graph represents a physical quantity which has the unit
(a) m2          (b) m                (c) m3              (d) m s-1.
Answer:
(b) Explanation : Area = v x t = (m/s) x s = m.

Question 8.
Four cars A, B, C and D are moving on a levelled road. Their distance versus time graphs are shown in Fig. 2 Choose the correct statement Q
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 4
(a) Car A is faster than car D
(b) Car B is the slowest
(c) Car D is faster than car C
(d) Car C is the slowest.
Answer:
(b) Explanation : Slope of distance – time graph = speed of object.

Question 9.
Which of the following figures represents uniform motion of a moving object correctly ?
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 5
Answer:
(a) Explanation : For uniform motion, distance ∞ time.

Question 10.
Slope of a velocity – time graph gives
(a) the distance
(b) the displacement
(c) the acceleration
(d) the speed.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 6

Question 11.
In which of the following cases of motions, the distance moved and the magnitude of displacement are equal ?
(a) If the car is moving on straight road
(b) If the car is moving in circular path
(c) The pendulum is moving to and fro
(d) The earth is revolving around the Sun.
Answer:
(a)

SHORT ANSWER QUESTIONS

Question 12.
The displacement of a moving object in a given interval of time is zero. Would the distance travelled by the object also be zero ? Justify your answer.
Answer:
No. When object moves in a circular path of radius r, then displacement of object .after completing a circle is zero but distance travelled = 2πr.

Question 13.
How will the equations of motion for an object moving with a uniform velocity change ?
Answer:
Equations of motion of a uniformly accelerated motion of an object are

  1. V = u + at,
  2. S = ut + ½ at2,
  3. v2 – u2 = 2aS.

When object moves with a uniform velocity, its acceleration, a = 0. Hence equations of motion become

  1. V = u,
  2. S = ut,
  3. v2 = u2.

Question 14.
A girl walks along a straight path to drop a letter in the letterbox and comes back to her initial position. Her displacement-time graph is shown in Fig. 4. Plot a velocity-time graph for the same.
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 7
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 8

Question 15.
A car starts from rest and moves along the x-axis with constant acceleration 5 m s-2 for 8 seconds. If it then continues with constant velocity, what distance will the car cover in 12 seconds since it started from the rest ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 9
Velocity after 8 s,V = u + at = 0 + 5 x 8 = 40 ms-1.
Distance travelled in last 4 s moving with constant velocity, x2 = v t = 40 x 4 = 160 m
∴Total distance = x1 + x2 = 320 m.

Question 16.
A motorcyclist drives from A to B with a uniform speed of 30 km h-1 and returns back with a speed of 20 km h-1. Find its average speed.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 10
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 11

Question 17.
The velocity-time graph (Fig. 6) shows the motion of a cyclist. Find
(i) its acceleration
(ii) its velocity and
(iii) the distance covered by the cyclist in 15 seconds.
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 12
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 13

Question 18.
Draw a velocity versus time graph of a stone thrown vertically upwards and then coming downwards after attaining the maximum height
Answer:
When stone is thrown vertically upwards, it has some initial velocity (u). The velocity of the stone goes on decreasing as it goes upwards and becomes zero at the maximum height. There after, stone begins to fall and its velocity goes on increasing but in opposite direction and becomes equal to the initial velocity (u) when it reaches the point of projection. v – t graph of a stone is shown in figure 7 A. The speed-time graph of the stone is shown in figure 7 B.
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 14

Question 19.
An object is dropped from rest at the height of 150m and simultaneously another object is dropped from rest at the height of 100m.
What is the difference in their heights after 2 s if both the objects drop with same accelerations ? How does the difference in heights vary with time ?
Answer:
Distance moved by the object dropped from height of 150m in 2 seconds can be calculated using
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 15
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 16
Height of the object from ground after 2 seconds = 150 – 20 = 130 m Similarly, distance moved by the other object in 2 seconds = 20 m
Height of the second object from ground after 2 seconds = 100 – 20 = 80 m
∴ Difference in their heights after 2 seconds = 130 m – 80 m = 50 m
Difference in height of both objects remains the same with time.

Question 20.
An object starting from rest travels 20 m in first 2 s and 160 m in next 4 s. What will be the velocity after 7 s from the start ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 17

Question 21.
Using following data, draw time-displacement graph for a moving object :

Time (s)     0      2 4 6 8 10 12 14 16
Displacement (m) 0 2 4 4 4 6 4 2 0

Use this graph to find average velocity for first 4 s, for next 4 s and for last 6 s.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 18
Displacement-time graph is shown in figure 8.
Average velocity for first 4s = Slope of displacement-time graph
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 19

Question 22.
An electron moving with a velocity of 5 x 104 ms-1 enters into a uniform electric field and acquires a uniform acceleration of 104 ms-2 in the direction of its initial motion.
(i) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(ii) How much distance the electron would cover in this time ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 20

Question 23.
Obtain a relation for the distance travelled by an object moving with a uniform acceleration in the interval between 4th and 5th seconds.
Answer:
We know, distance travelled by a uniformly accelerated object in time t is given by
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 21

Question 24.
Two stones are thrown vertically upwards simultaneously with their initial velocities u1 and u2 respectively. Prove that the heights reached by them would be in the ratio of u12 : u22 (Assume upward acceleration is -g and downward acceleration to be +g).
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion image - 22

Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

Value Based Questions in Science for Class 9 Chapter 14 Natural Resources

Value Based Questions in Science for Class 9 Chapter 14 Natural Resources

These Solutions are part of Value Based Questions in Science for Class 9. Here we have given Value Based Questions in Science for Class 9 Chapter 14 Natural Resources

Question 1.
It has been made mandatory to install rain water harvesting system and solar water heater in all buildings in urban areas,

  1. What is the rationale when rain water already passes into drains ?
  2. Why are solar water heaters being installed when electric geijers are available ?

Answer:

  1. Rain water passed into drain does not enter the ground but is taken out of the urban area and poured into a water body at quite a distance with or without treatment. However, ground water is being withdrawn everywhere for drinking, industrial and irrigation purposes. As a result, the level of ground water is going down and arid conditions are being faced in many areas. In rain water harvesting, rain water from a building is passed directly into ground, dug wells or water pumps. This recharges ground water.
  2. Installation of solar water heaters is a method of saving electricity which is always in short supply due to rapid urbanisation, Industrialisation and intensive agriculture. Coal/gas based power plants are adding CO2 to the atmosphere causing global warming. Saving electricity is now an important social responsibility.

More Resources

Question 2.

  1. Sheela saw blue-green algae forming bloom in the village pond,
  2. Fish, which was previously abundant was no-where to be seen.
  3. The pond is giving a stink. Water of the pond is not even fit for cattle. Some of the cattle who were taken to the pond for drinking and bathing have fallen sick,
  4. What explanation will Sheela give for this to the villagers.

Answer:

  1. Bloom forming algae occur in a pond only when the quality of pond water has deteriorated due to pollution. Blue-green algae secrete toxins that are harmful to animals and humans,
  2. Fish must have died due to deficiency of oxygen in pond water. Oxygen deficiency occurs when there is excess of organic matter (organic loading). The aerobic decomposers consume the dissolved oxygen. This is followed by anaerobic decomposition of organic matter. It produces sulphides and other sludge producing substances. Blue-green algae can grow under such circumstances.
  3. Stink comes from anaerobic breakdown products of organic matter. The toxins released by blue-green algae further deteriorate the quality of water causing sickness and skin rashes in animals and humans.
  4. Sheela could explain to the villagers that deterioration of pond has been due to excess fertilizers used by them in their fields. Rain wash brought these fertilizers into the pond. There was initial spurt in the growth of plants due to this. The phenomenon is called eutrophication. Excess plant matter slowly caused organic loading of water that reduced its oxygen content, killing the fish and other aquatic animals. So fertilizers should be used very judiciously in the fields.

Question 3.

  1. Carbon dioxide concentration in the atmosphere has reached more than 390 ppm
  2. The antarctic and arctic waters are becoming acidic causing thinning of animal shells.
  3. Polar ice is melting,
  4. Some low lying islands have submerged in sea.

(a) What are the reasons behind all these changes occurring on earth ?
(b) Suggest a mechanism to control the same and if possible to reverse the trend.

Answer:

(a) The reason for these global changes is faulty recycling of carbon dioxide. More of carbon dioxide is being produced than its consumption in photosynthesis due to

  1. Excess combustion of fossil fuels in industries, power houses, automobiles, homes and other places,
  2. Reduced intake of CO2 by plants due to deforestation,
  3. Higher amounts of CO2 entering the atmosphere not only increases its atmospheric concentration but also the concentration of dissolved CO2 in water, especially in colder seas. This is making colder waters acidic. The acidity is thinning the shells of many marine animals.
  4. CO2 is a green house gas which is causting global warming. Rise in global temperature is melting snow over poles. This is raising the level of sea water slowly. It was already submerged some low lying islands.

(b) Suggestions :

  1. Large scale tree plantation in all vacant areas,
  2. Reduced felling of forest trees.
  3. Reducing consumption of fossil fuel by reducing dependence on thermal power plants, increasing efficiency of automobiles and switching over to alternate technologies that do not consume fossil fuels.

Question 4.
On a school trip to an industrial estate, students found that the marble used in the office buildings of most factories has lost its shine and become pitted.

  1. What is the reason of marble pitting
  2. Can this factor cause harm to vegetation as well ?
  3. Suggest way to prevent this.

Answer:

  1. Pitting and discolouring of marble is due to corrosive action of dry or wet acid rain, comprising sulphur dioxide and nitrogen oxides, emitted during combustion of fossil fuels in industries. The acid reacts with insoluble calcium carbonate of marble and converts it into soluble calcium sulphate and calcium nitrate.
  2. Yes, Acid rain can also cause harm to vegetation by
    1. Direct action of acid over plants causing death of leaves,
    2. Solubilisation of essential minerals and their leaching leaving only toxic minerals in the soil.
  3. Use of wet scrubbers to remove acidic gases from the industrial emissions.

Hope given Value Based Questions in Science for Class 9 Chapter 14 Natural Resources are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

NCERT Exemplar Solutions for Class 9 Science Chapter 14 Natural Resources

NCERT Exemplar Solutions for Class 9 Science Chapter 14 Natural Resources

These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 14 Natural Resources

Question 1.
Rivers from land, add minerals to sea water. Discuss how.
Answer:
Rivers are formed from springs, melting snow and rain water flowing over land as run off. While, passing through and over the rocks, the flowing water picks up minerals. These dissolved minerals are taken by rivers to sea and make them available to marine organisms.

More Resources

Question 2.
How can we prevent loss of top soil ?
Answer:
Control of Soil Erosion: Soil erosion can be prevented by providing plant cover to soil. Roots of plants hold the soil firmly around them. They increase water percolation during rains and decrease runoff. Vegetation cover also reduces direct pounding of soil by rain drops. The various methods to control soil erosion are as follows :

  1. Vegetation Cover: Soil should not be left uncovered. Tree plantation should be undertaken where vegetation cover is poor or absent.
  2. Controlled Grazing: Grazing should be limited to certain seasons and for limited number of animals.
  3. Slope is divided into a number of flat fields for slowing down the flow of water.
  4. Contour Bunding: Small bunds are raised on the edges of fields to prevent loss of top soil through wind or water.
  5. Conservation Tillage: Instead of conventional tillage, reduced or no tillage can be practised. It prevents erosion.
  6. Wind Breaks: Wind erosion is reduced if rows of trees and shrubs are planted at right angles to the prevailing direction of wind.

Question 3.
How is the life of organisms living in water affected when water gets polluted ? (CCE 2012)
Answer:
Water gets polluted from domestic wastes, fertilizers, pesticides (from fields) and industrial wastes.

  1. Fertilizers and domestic wastes cause eutrophication or excessive growth and increased organic loading. This, reduces oxygen available to aquatic animals,
  2. Domestic waste carries pathogens of a number of diseases. Some of them can cause diseases in aquatic animals as well,
  3. Pesticides and industrial wastes carry toxins that directly harm the aquatic organisms.

Question 4.
During summer, if you go near the lake, you feel relief from heat. Why ?
Answer:
During day time, air over the land becomes heated up, rises upward and creates an area of low pressure. Lake water is not heated up so quickly. Evaporation of water from its surface also cools it up. Therefore, air over the surface of lake is cooler. It moves towards the land where low pressure exists. Therefore, during day dme a cool breeze flows from lake to the land nearby.

Question 5.
In coastal area, wind current moves from sea towards the land during day but during night it moves from land to the sea. Discuss the reason.
Answer:
Air Movement in Coastal Areas: In coastal areas, there is a regular flow of cooler air from sea towards the land during the daytime. It is because during the daytime land gets heated faster than water. Reradiation from land heats the air above it. The hot air rises and creates an area of low pressure. Sea water is not heated so rapidly. Air above sea remains comparatively cool. It has a higher pressure as compared to air over land. Therefore, cooler air present over sea moves towards land where low pressure exists.

Question 6.
Following are a few organisms :
(a) Lichens
(b) Mosses
(c) Mango tree
(d) Cactus.
Which among the above can grow on stones and also help in formation of soil ? Write the mode of their action for making soil.
Answer:
Lichens and Mosses.
Weathering by Living Organisms:
Living Organisms are cause biological weathering. Lichens growing on rock surface are able to extract minerals from the same. This produces small crevices where a thin layer of soil builds up. Mosses grow over these crevices. They cause deepening of crevices and building up of more soil in them. Deeper crevices form cracks.
The cracks become bigger when the roots of short lived herbs pass into them. With the passage of time roots of bigger plants pass into cracks. Cracks widen and cause slow fragmentation and later pulverisation of rocks.

Question 7.
Soil formation is done by both abiotic and biotic factors. List the name of these factors by classifying them as abiotic and biotic.
(CCE 2012)
Answer:
Abiotic Factors : Sun, water, wind.
Biotic Factors : Lichens, mosses, herbs, shrubs and trees.

Question 8.
All the living organisms are basically made up of C, N, S, P, H and O. How do they enter the living forms ? Discuss.
Answer:
Most of them first enter plants and become components of organic materials during the process of photosynthesis. They enter plants from air (CO2), water and ions (from soil). From plants the chemicals pass on to other organisms.

Question 9.
Why does the percentage of gases like oxygen, nitrogen and carbon dioxide remain almost the same in the atmosphere ?
Answer:
Through biogeochemical cycling where there is repeated circulation of biogenetic nutrients between abiotic and biotic components of the environment.

Question 10.
Why has moon very cold and very high temperature variations, e.g., from -190°C to 110°C even though it is at the same distance from the sun as the earth is ? (CCE 2012)
Answer:
Moon does not possess atomosphere. Atmosphere being a bad conductor acts as a temperature buffer on earth. This is not so on the moon. Therefore, moon gets heated up as the sun rays fall on its surface. It cools down drastically when there is no sunlight.

Question 11.
Why do people love to fly kites near the sea shore ? (CCE2012)
Answer:

  1. There is a regular unidirectional wind from sea to land.
  2. It helps in flying the kite high.
  3. The wind is cooler and provides comfort even in bright sun.

Question 12.
Wliy does Mathura refinery pose problems to the Taj Mahal ? (CCE 2014)
Answer:
Mathura refinery emits hydrocarbons and sulphur oxides. Hydrocarbons induce the formation of ozone which is highly oxidising. Sulphur dioxide produces acid rain which has a corroding effect on marble. Therefore, Mathura refinery does pose problems to Taj Mahal.

Question 13.
Why do not lichens occur in Delhi/Mumbai whereas they commonly grow in Manali/Ooty or Darjeeling ? (CCE 2011, 2012)
Answer:
Lichens are sensitive to sulphur dioxide which occurs in sufficient quantity in the atmosphere of Delhi due to large number of
vehicles, homes and factories using fossil fuels. Moreover, Delhi occurs in semi-arid area where, atmospheric moisture is low. In Manali and Darjeeling, the atmosphere is humid and sulphur dioxide pollution is comparatively low.

Question 14.
Wliy does water need conservation even though large oceans surround the land masses ? (CCE 2012)
Answer:
Marine water is unfit for consumption by humans, industries or land plants and animals. Therefore, terrestrial biota and human beings have to depend upon fresh water resources available on land (only about 0.5% of the total). The same has to be conserved.

Question 15.
There is a mass mortality of fish in a pond. What may be the reasons ?
Answer:

  1. Passage of pesticide rich water from crop fields. ,
  2. Pouring of industrial waste. .
  3. Pouring of hot water from an industry or thermal power plant.
  4. Release of waste rich in heavy metal and mercury.
  5. Blockage of fish gills by some suspended pollutant.
  6. Excessive eutrophication.

Question 16.
Lichens are called pioneer colonisers of bare rock. How can they help in formation of soil ?
Answer:
Ans. Lichens release small quantity of acids which corrode the surface of rocks creating small pores and releasing minerals. With the passage of time the porous surface changes into thin layer of soil.

Question 17.
“Soil is formed by water”. If you agree with this statement, then give reasons.
Answer:
Yes,  “action of water in weathering” (wetting and drying, frost action, abrasion).

  1. Wetting and Drying. Certain rock components can pick up and lose moisture. They undergo swelling and contraction resulting in fragmentation of rocks.
  2. Frost Action. Water seeping in cracks would swell up and exert a great pressure if it freezes due to low temperature. The rock would undergo fragmentation.
  3. Running water carrying rock fragments would break and grind rocks occurring in the pathway. Rain and hail also cause rock breaking.

Question 18.
Fertile soil has lots of hurpus. Why ? (CCE 2012)
Answer:
Fertile soils possess lots of humus because

  1. Humus is required for binding soil particles into crumbs. Crumb formation is needed for both hydration and aeration of soil,
  2. Humus makes the soil porous for easy passage of roots,
  3. It is source of minerals.
  4. Humus contains chemicals that promote growth of plants.

Question 19.
Why step farming is common in hills ?
Answer:
Step farming or terracing is carried out in the hills because it slows down the speed of rain water currents, checks soil erosion and increases water absorption by soil.

Question 20.
Why are root nodules useful for the plants ? (CCE 2012)
Answer:
Root nodules mostly occur in legume plants. These nodules contain nitrogen fixing bacteria named Rhizabium. The bacteria pick up nitrogen from soil atmosphere and convert it into organic compounds. The same pass into plant so that legumes become rich in proteins and other nitrogen compounds.

Question 21.
How do fossil fuels cause air pollution ? (CCE 2012)
Answer:
Fossil fuels (coal, petroleum) are burnt to obtain energy.
Combustion produces

  1. Suspended particles
  2. Sulphur oxides
  3. Nitrogen oxides
  4. Carbon monoxide
  5. Vapours of hydrocarbons.

All these are air pollutants. Hydrocarbons are a source of cancer. They also damage internal organs. Alongwith nitrogen oxides, they produce ozone and smog. Sulphur and nitrogen oxides give rise to acid rain. They are also irritants and damage eyes and nasal tract.

Question 22.
What are the causes of water pollution ? Discuss how you can contribute in reducing water pollution ?
Answer:
Causes of Water Pollution:

  1. 21% of all infectious diseases and 66% of all deaths of children below 5 years are caused by contamination of drinking and bathing water by pathogens present in sewage, e.g., cholera, typhoid, diarrhoea, dysentery, jaundice, etc.
  2. Toxic Chemicals: Industrial effluents pass down a number of toxic chemicals, g., mercury by paper industry (minamata disease), cadmium (itai-itai disease), lead (plumbism), nitrate (met-haemoglobinaemia).

Reduction in Water Pollution :

  1. Sewage: The authorities can be prevailed upon not to pass untreated sewage into water bodies.
  2. Garbage: Domestic waste or garbage should not be thrown on the banks of water body.
  3. Industrial Effluents. Asking the industrial houses not to pass the untreated effluents into water body.
  4. Washing Clothes: Washing clothes should be discouraged on the banks of water bodies as detergents are a source of eutrophication.
  5. Vegetation: Plant trees, shrubs and herbs on the banks. This checks soil erosion and siltation of water bodies. It also reduces run off from fields.

Question 23.
A motor car, with its glass totally closed, is parked directly under the sun. The inside temperature of the car rises very high. Explain why? (CCE 2012)
Answer:
Glass is transparent to sunlight, allowing it to pass into the interior of the car. It heats up the interior. But heat waves do not escape from the car due to glass being opaque to the same. As a result, the interior of the car placed in the sun will become very hot. It is similar to glass house effect.

Question 24.
Justify “Dust is a pollutant.” (CCE 2012)
Answer:

  1. Dust consists of suspended particles. The latter pass into nasal tract and cause a lot of discomfort including allergic asthma, bronchitis, cough and cold,
  2. Dust reduces light intensity,
  3. Its particles are eye irritants,
  4. Dust settles over plant foliage and reduces photosynthetic activity,
  5. Dust particles block stomata reducing gaseous exchange,
  6. Dust particles can pick up toxic metals and chemicals being emitted by industries.

Question 25.
Explain the role of the sun in the formation of soil.
Answer:

Paedogenesis: It is the process of formation of soil from rocky crust of earth. Paedogenesis occurs in two stages, weathering and humification.

  1. Weathering
    It is the process of breaking down of rock present on the surface of earth into fine particles. Weathering is caused by three types of processes — physical, chemical and biological. Physical weathering is pulverisation of rocky matter caused by physical phenomena like atmospheric changes (heating, cooling, wetting-drying, frost action) and mechanical forces (abrasion by rain and hail, rolling stones carried by water, wave action, sand blast by wind). Chemical weathering is pulverisation of rocks by chemical action in wet weather like hydration, oxidation, reduction, carbonation and solubilisation. Biological weathering is the breaking down of rocks by the action of living organisms.
    Sun: It heats up the rocks during the day. Heating causes the rocks to expand. During night, the rocks cool and contract. Different parts of a rock expand and contract at different rates resulting in its cracking and breaking up into smaller pieces or fragments.
  2. Humification
    It is the addition of partially decomposed organic matter or humus to the weathered rock particles to form soil. Humus binds the finely ground rock particles into aggregates called crumbs. Crumb formation is needed for both hydration and aeration of soil.

Question 26.
Carbon dioxide is necessary for plants. Why do we consider it as a pollutant ? (CCE 2014)
Answer:
Besides being essential for photosynthesis, carbon dioxide is a green house gas. Upto 350 ppm, it is both a good raw material as well as essential for keeping the earth warm. However, when its concentration rises (as presently it is 400 ppm), it becomes pollutant because it results in global warming. The latter is quite dangerous because it will melt polar ice, raise the water level of oceans and submerge several coastal areas and islands.

Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 14 Natural Resources are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

HOTS Questions for Class 9 Science Chapter 8 Motion

HOTS Questions for Class 9 Science Chapter 8 Motion

These Solutions are part of HOTS Questions for Class 9 Science. Here we have given HOTS Questions for Class 9 Science Chapter 8 Motion

Question 1.
Under what condition, the average speed is equal to the magnitude of the average velocity. Justify your answer.
(CBSE 2010, 2012)
Answer:
HOTS Questions for Class 9 Science Chapter 8 Motion image - 1
Now, the average speed = magnitude of average velocity if the total distance travelled by an object in a given time interval is equal to the magnitude of the displacement of the object in the same time interval. This is possible, when an object moves in one direction along a straight line. Thus, average speed is equal to the magnitude of the average velocity if an object moves in one direction along a straight line.

More Resources

Question 2.
A body can have zero average velocity but not zero average speed. Explain. (CBSE 2013)

Or

Give an example of a motion in which average velocity is zero, but the average speed is not zero. (CBSE 2015)
Answer:
HOTS Questions for Class 9 Science Chapter 8 Motion 2
Since, the total distance travelled by a moving body increases with the time, so average speed of a moving body can not be zero.
HOTS Questions for Class 9 Science Chapter 8 Motion image - 2
Since total displacement of a moving body can be zero, so the average velocity of a moving body can be zero.
Example. When an athlete completes one round in a circular track in the given time interval, then his total displacement is zero but total distance travelled is equal to the length of the circular track. Hence, his average velocity is zero but his average speed is not zero.

Question 3.
An object P is moving with a constant velocity for 5 minutes. Another object Q is moving with changing velocity for 5 minutes. Out of these two objects, which one has acceleration. Explain. (CBSE 2012)
Change in velocity
Answer:
HOTS Questions for Class 9 Science Chapter 8 Motion image - 4
Since, the velocity of object P is not changing or change in velocity of the object is zero, therefore, object P has no acceleration. On the other hand, there is change in velocity of the object Q, so it has acceleration.

Question 4.
Can an object be accelerated if it is moving with constant speed ? Justify your answer with an example.

Or

Can a body have constant speed and still be accelerating ? Give an example. (CBSE 2010)

Or

Explain how is it possible for an object to move with a constant speed but with uniform acceleration.
(CBSE 2012)
Answer:
An object moving with constant speed can be accelerated if its direction of motion changes. For example, an object moving with a constant speed in a circular path has an acceleration because its direction of motion changes continuously.

Question 5.
Two trains A and B start moving at the same time. The distances travelled by them in given intervals of time are given below. State which train has uniform motion and which train has non-uniform motion.

Time Distance travelled by train A (in km) Distance travelled by train B (in km)
6.00 pm 0 0
6.15 pm 10 15
6.30 pm 20 24
6.45 pm 30 32
7.00 pm 40 38
7.15 pm 50 42
7.30 pm 60 47

Answer:
Since train A travels equal distances in equal intervals of time (i.e. in every 15 minutes), so the motion of train A is uniform motion. On the other hand, train B travels unequal distances in equal intervals of time (i.e. in every 15 minutes), so the motion of train B is non-uniform motion.

Hope given HOTS Questions for Class 9 Science Chapter 8 Motion are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

Value Based Questions in Science for Class 9 Chapter 8 Motion

Value Based Questions in Science for Class 9 Chapter 8 Motion

These Solutions are part of Value Based Questions in Science for Class 9. Here we have given Value Based Questions in Science for Class 9 Class 9 Chapter 8 Motion

VALUE BASED QUESTIONS

Question 1.
Ram hired a three wheeler from bus stand to his house. The driver A’ of three wheeler followed the shortest path and reached the destination in half an hour. He charged Rs. 50 from Ram. On the same day, Ram’s sister also came to her house after attending a function in other city. She also hired a three wheeler. The driver ‘B’ of the three wheeler took an hour to reach her house and charged Rs. 150 from her.

  1. Is the displacement of both the three wheelers from bus stand to Ram’s house same or different ?
  2. What values are shown by driver A ?

Answer:

  1. Displacement of both the three wheelers is same.
  2. Driver A is honest. He is concerned for others.

More Resources

Question 2.
Two boys A and B were driving cars on a road. There was a sign board on the side of road reading “speed limit” : 50 km/h. Boy A applied brakes and started driving at 45 km/h. On the other hand boy B did not bother about the speed limit. He continued to drive his car at 70 km/h. A police man stopped the car of boy B and fined him If Rs. 500.00. What values are shown by boy A ?
Answer:
boy A is good observer and being a good citizen, he follows the traffic rules.

Hope given Value Based Questions in Science for Class 9 Chapter 8 Motion are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

NCERT Solutions for Class 9 Science Chapter 8 Motion

NCERT Solutions for Class 9 Science Chapter 8 Motion

These Solutions are part of NCERT Solutions for Class 9 Science. Here we have given NCERT Solutions for Class 9 Science Chapter 8 Motion. LearnInsta.com provides you the Free PDF download of NCERT Solutions for Class 9 Science (Biology) Chapter 8 – Motion solved by Expert Teachers as per NCERT (CBSE) Book guidelines. All Chapter 8 – Motion Exercise Questions with Solutions to help you to revise complete Syllabus and Score More marks.

More Resources

NCERT TEXT BOOK QUESTIONS

IN TEXT QUESTIONS

Question 1.
An object has moved through a distance. Can it have zero displacement ? If yes, support your answer with an example. (CBSE 2015)
Answer:
Yes, The displacement of the object can be zero. Let a boy completes one round of a circular track in 5 minutes. The distance travelled by the boy = circumference of the circular track. However, displacement of the boy is zero because his initial and final positions are same.

Question 2.
A farmer moves along the boundary of a square field of side 10 m in 40 s.
What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds ? (CBSE 2010, 2015)
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 1
Answer:
ABCD is a square field of side 10 m.
The farmer moves along the boundary of the field from the corner A via the corners B, C and D.
After every 40 s, the farmer is again at the corner A, so his displacement after every 40 s is zero.
At the end of 2 minutes 20 seconds = (2 x 60 + 20) = 140 s, the farmer will be at the corner C.
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 2

Question 3.
Distinguish between speed and velocity. (CBSE 2010, 2012, 2013, 2015)
Answer:

Speed

Velocity
1. Distance travelled by an object per unit time is known as its speed. The distance travelled by an object in a particular direction (i.e. displacement) per unit time is known as its velocity.
2. Average speed of a moving object cannot be zero. Average velocity of a moving object can be zero.
3. tells how fast an object moves. Velocity tells how fast an object moves and in which direction it moves.
4. Speed is a scalar quantity. Velocity is a vector quantity.
5. Speed of an object is always positive. Velocity of an object can be positive or negative.

Question 4.
Under what conditions) is the magnitude of the average velocity of an object equal to its average speed ? (CBSE 2012, 2013)
Answer:
When an object moves in one direction along a straight line.

Question 5.
What does the odometer of an automobile measure ? (CBSE 2010, 2011, 2014, 2015)
Answer:
Odometer of an automobile measures distance travelled by the automobile.

Question 6.
What does the path of an object look like when it is in uniform motion ? (CBSE 2012)
Answer:
Straight path.

Question 7.
During an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station ? The signal travels at the speed of light, that is, 3 x 108 m s-1
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 3

Question 8.
When will you say a body is in

  1. uniform acceleration ?
  2. non-uniform acceleration (CBSE 2012, 2013)

Answer:

  1. A body has uniform acceleration if its velocity changes by an equal amount in equal intervals of time. .
  2. A body has non-uniform acceleration if its velocity changes by unequal amount in equal intervals of time.

Question 9.
A bus decreases its speed from 80 kmh-1 to 60 kmh-1 in 5 s. Find the acceleration of the bus.
(CBSE 2010, 2011, 2012, 2015)
Answer:
Here,
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 4
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 5

Question 10.
A train starting from a railway station and moving with a uniform acceleration attains a speed of 40 km h-1 n 10 minutes. Find its acceleration.
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 6

Question 11.
What is the nature of the distance-time graphs for uniform and non-uniform motion of an object ?
(CBSE 2012)
Answer:

  1. For uniform motion, distance-time graph is a straight line having constant gradient or slope as shown in figure.
  2. For non-uniform motion, distance-time graph is a curve having increasing gradient or slope or decreasing gradient as shown in figures.
    NCERT Solutions for Class 9 Science Chapter 8 Motion image - 7

Question 12.
What can you say about the motion of an object whose distance-time graph is a straight line parallel to
the time axis ? (CBSE 2010, 2012)
Answer:
When distance-time graph is a straight line parallel to the time axis, it means, the distance of the object is not changing with time. Thus, the object is stationary.

Question 13.
What can you say about the motion of an object if its speed-time graph is a straight line parallel to the time-axis ?
Answer:
In this case, speed of the object is constant. That is, the object travels equal distances in equal intervals of time along a straight line. Hence, motion of the object is uniform motion.

Question 14.
What is the quantity which is measured by the area occupied below the velocity-time graph ?
(CBSE 2010, 2012)
Answer:
Magnitude of the displacement of a body is measured by the area under the velocify-time graph.

Question 15.
A bus starting from rest moves with a uniform acceleration of 0.1 m s-2 for 2 minutes. Find
(a) the speed acquired,
(b) the distance travelled. (CBSE 2012)
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 8

Question 16.
A train is travelling at a speed of 90 km h-1. Brakes are applied so as to produce a uniform acceleration of – 0.5 m s-2 . Find how far the train will go before it is brought to rest ?
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 9

Question 17.
A trolley, while going down an inclined plane has an acceleration of 2 cm s-2. What will be its velocity 3 s after the start ?
Answer:
Here, u = 0,v = ?, a = 2 cm s-2, t = 3 s
Using, v = u + at, we get
v = 0 + 2 x 3 = 6 cm s-2.

Question 18.
A racing car has a uniform acceleration of 4 m s-2. What distance will it cover in 10 s after start ?
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 10

Question 19.
A stone is thrown in a vertically upward direction with a velocity of 5 m s-1 If the acceleration of the stone during its motion is 10 m s-2 in the downward direction, what will be the height attained by the stone and how much time will it take to reach there ?
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 11

NCERT CHAPTER END EXERCISE

Question 1.
An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes and 20 s ?
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 12
(ii) After every 40 s, athlete reaches his starting point, so after 40 s, his displacement is zero. It means, the athlete completes the circular track 3 times in 120 s and in the next 20 s, he is just opposite to his starting point. Therefore, the magnitude of the displacement of the athlete at the end of the 140 s (or 2 minutes 20 s) = Diameter of the circular track = 200 m.

Question 2.
Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 50 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging
(a) from A to B and
(b) from A to C ? (CBSE 2010, Term I)
Answer:
Distance from A to B – 300 m
Displacement from A to B = 300 m
Time taken to go from A to B =2 minutes 50 s = 170 s
T Solutions for Class 9 Science Chapter 8 Motion image - 13

Question 3.
Abdul, while driving to school, computes the average speed for his trip to be 20 km h-1. On his return trip along the same route, there is less traffic and the average speed is 40 km h-1. What is the average speed for Abdul’s trip ? (CBSE 2011)
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 14

Question 4.
A motor boat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0 m s-2 for 8.0 s. How far does the boat travel during this time ? (CBSE 2011, 2013)
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 15

Question 5.
A driver of a car travelling at 52 km h-1 applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at 3 km h-1 in another car applies his breaks slowly and stops in 10 s. On the same graph paper plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied ?
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 16

Question 6.
Figure shows the distance-time graph of three objects A, B and C. Study the graph and answer the following questions :
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 17
(a) Which of the three is travelling the fastest ?
(b) Are all three ever at the same point on the road ?
(c) How far has C travelled when B passes A ?
(d) How far has B travelled by the time it passes C ?
Answer:
(a) Speed = Slope of distance-time graph.
Since slope of distance-time graph for object B is the greatest, so object B is travelling the fastest.
(b) All the three objects will be at the same point on the road if all the three distance-time graphs intersect each other at a time. Since, all the three distance-time graphs do not intersect each other at a time, so they are never at the same point on the road.
(c) When B passes A, distance travelled by C = 9.6 – 2 = 7.6 km.
(d) Distance travelled by B by the time it passes C = 6 km.

Question 7.
A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s-2, with what velocity will it strike the ground ? After what time will it strike the ground ?
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 18

Question 8.
The speed time graph for a car as shown in figure
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 19
(a) Find how far does the car travel in the firdt four seconds.
Shade the area on the graph that represents the distance travelled by the car during the period.
(b) Which part of the graph represents uniform motion of the car?
Answer:
(a)
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 20
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 21
(b) The straight part of the curve parallel to time axis represents the uniform motion of the car.

Question 9.
State which of the following situations are possible and give an example for each of these :
(a) an object with a constant acceleration but zero velocity.
(b) an object moving with an acceleration but with uniform speed.
(c) an object moving in a certain direction with an acceleration in the perpendicular direction.
(CBSE 2012)
Answer:
(a) When an object is thrown vertically upward, its velocity at the highest point is zero but it has constant acceleration = 9.8 m s-2
(b) Uniform circular motion.
(c) An object moving in a circular path with uniform speed, its acceleration is always perpendicular to the direction of the motion of the object.

Question 10.
An artificial satellite is moving in a circular orbit of radius 42250 km. Calculate its speed if it takes 24 . hours to revolve around the earth. (CBSE 2011)
Answer:
NCERT Solutions for Class 9 Science Chapter 8 Motion image - 22

NCERT Solutions for Class 9 Science Chapter 8 Motion

Hope given NCERT Solutions for Class 9 Science Chapter 8 are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

HOTS Questions for Class 9 Science Chapter 14 Natural Resources

HOTS Questions for Class 9 Science Chapter 14 Natural Resources

These Solutions are part of HOTS Questions for Class 9 Science. Here we have given HOTS Questions for Class 9 Science Chapter 14 Natural Resources

Question 1.
(a) Fill in the blanks : A, B and C.
HOTS Questions for Class 9 Science Chapter 14 Natural Resources image - 1
(b) Identify the biogeochemical cycle.
Answer:
(a) Fill in the blanks :
A- Organic molecules (C6H12O6).
B- Photosynthesis.
C- Respiration.
(b) Identification: Oxygen cycle.

More Resources

Question 2.
(a) Fill in the blanks: A to F.
HOTS Questions for Class 9 Science Chapter 14 Natural Resources image - 2
(b) What will happen if the step A does not take place ?
(c) What will happen if the step F does not take place ?
Answer:
(a) Fill in the blanks :
A- Ammonification.
B- Ammonia.
C- Nitrites.
D- Nitrates.
E- Nitrification.
F- Denitrification.
(b) Absence of step A: No breakdown of proteins to release ammonia.
(c) Absence of step F: There will be no replenishment of atmospheric nitrogen.

Hope given HOTS Questions for Class 9 Science Chapter 14 Natural Resources are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS

RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS

Other Exercises

Mark the correct alternative in each of the following:
Question 1.
Two parallelograms are on the same base and between the same parallels. The ratio of their areas is
(a) 1 : 2
(b) 2 : 1
(c) 1 : 1
(d) 3 : 1
Solution:
Two parallelograms which are on the same base and between the same parallels are equal in area
∴ Ratio in their areas =1 : 1 (c)

Question 2.
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
(a) 1 : 1
(b) 1 : 2
(c) 2 : 1
(d) 1 : 3
Solution:
A triangle and a parallelogram which are on the same base and between the same parallels, then area of triangle is half the area of the parallelogram
∴ Their ratio =1:2 (c)

Question 3.
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of sides of ∆ABC. Then the area of ∆PQR is
(a) 12 sq. units
(b) 6 sq. units
(c) 4 sq. units
(d) 3 sq. units
Solution:
Area of ∆ABC = 24 sq. units
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q4.1
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q4.2

Question 4.
The median of a triangle divides it into two
(a) congruent triangle
(b) isosceles triangles
(c) right triangles
(d) triangles of equal areas
Solution:
The median of a triangle divides it into two triangles equal in area (d)

Question 5.
In a ∆ABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If
ar(∆ABC) = 16 cm2, then ar(trapezium FBCE) =
(a) 4 cm²
(b) 8 cm²
(c) 12 cm²
(d) 10 cm²
Solution:
In ∆ABC, D, E and F are the mid points of sides BC, CA and AB respectively
ar(∆ABC) = 16 cm²
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q5.1

Question 6.
ABCD is a parallelogram. P is any point on CD. If ar(∆DPA) = 15 cm² and ar(∆APC) = 20 cm², then ar(∆APB) =
(a) 15 cm²
(b) 20 cm²
(c) 35 cm²
(d) 30 cm²
Solution:
In ||gm ABCD, P is any point on CD
AP, AC and PB are joined
ar(∆DPA) =15 cm²
ar(∆APC) = 20 cm²
Adding, ar(∆ADC) = 15 + 20 = 35 cm²
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q6.1
∵ AC divides it into two triangles equal in area
∴ ar(∆ACB) = ar(∆ADC) = 35 cm²
∵ ∆APB and ∆ACB are on the same base
AB and between the same parallels
∴ ar(∆APB) = ar(∆ACB) = 35 cm²(c)

Question 7.
The area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 16 cm and 12 cm is
(a) 28 cm²
(b) 48 cm²
(c) 96 cm²
(d) 24 cm²
Solution:
In rhombus ABCD,
P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively and are joined in order to get a quad. PQRS
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q7.1

Question 8.
A, B, C, D are mid points of sides of parallelogram PQRS. If ar(PQRS) = 36 cm²,then ar(ABCD) =
(a) 24 cm²
(b) 18 cm²
(c) 30 cm²
(d) 36 cm²
Solution:
A, B, C and D are the mid points of a ||gm PQRS
Area of PQRS = 36 cm²
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q8.1
The area of ||gm formed by joining AB, BC, CD and DA
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q8.2

Question 9.
The figure obtained by joining the mid-points of the adjacent sides of a rectangle of sides 8 cm and 6 cm is
(a) a rhombus of area 24 cm²
(b) a rectangle of area 24 cm²
(c) a square of area 26 cm²
(d) a trapezium of area 14 cm²
Solution:
Let P, Q, R, S be the mid points of sides of a rectangle ABCD. Whose sides 8 cm and 6 cm
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q9.1
Their PQRS is a rhombus
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q9.2

Question 10.
If AD is median of ∆ABC and P is a point on AC such that ar(∆ADP) : ar(∆ABD) = 2:3, then ar(∆PDC) : ar(∆ABC) is
(a) 1 : 5
(b) 1 : 5
(c) 1 : 6
(d) 3 : 5
Solution:
AD is the median of ∆ABC,
P is a point on AC such that
ar(∆ADP) : ar(∆ABD) = 2:3
Let area of ∆ADP = 2×2
Then area of ∆ABD = 3×2
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q10.1
But area of AABD = \(\frac { 1 }{ 2 }\) area AABC
∴ Area ∆ABC = 2 x area of ∆ABD
= 2 x 3x² = 6x²
and area of ∆PDC = area ∆ADC – (ar∆ADP) = area ∆ABD – ar ∆ADP
= 3x² – 2x² = x²
∴ Ratio = x² : 6x²
= 1 : 6 (c)

Question 11.
Medians of AABC, intersect at G. If ar(∆ABC) = 27 cm2, then ar(∆BGC) =
(a) 6 cm2
(b) 9 cm2
(c) 12 cm2
(d) 18 cm2
Solution:
In ∆ABC, AD, BE and CF are the medians which intersect each other at G
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q11.1

Question 12.
In a ∆ABC if D and E are mid-points of BC and AD respectively such that ar(∆AEC) = 4 cm², then ar(∆BEC) =
(a) 4 cm²
(b) 6 cm²
(c) 8 cm²
(d) 12 cm²
Solution:
In ∆ABC, D and E are the mid points of BC and AD
Join BE and CE ar(∆AEC) = 4 cm²
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q12.1
In ∆ABC,
∵ AD is the median of BC
∴ ar(∆ABD) = ar(∆ACD)
Similarly in ∆EBC,
ED is the median
∴ ar(∆EBD) = ar(∆ECD)
and in ∆ADC, CE is the median
∴ ar(∆FDC) = ar(∆AEC)
= 4 cm
∴ar∆EBC = 2 x ar(∆EDC)
= 2 x 4 = 8 cm (c)

Question 13.
In the figure, ABCD is a parallelogram. If AB = 12 cm, AE = 7.5 cm, CF = 15 cm, then AD =
(a) 3 cm
(b) 6 cm
(c) 8 cm
(d) 10.5 cm
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q13.1
Solution:
In ||gm ABCD, AB = 12 cm AE = 7.5 cm
∴ Area of ||gm ABCD = base x height = AB x AE = 12 x 7.5 cm² = 90 cm²
Now area ||gm ABCD = 90 cm²
and altitude CF = 15 cm
∴ Base AD = \(\frac { Area }{ Altitude }\) = \(\frac { 90 }{ 15 }\) = 6 cm (b)

Question 14.
In the figure, PQRS is a parallelogram. If X and Y are mid-points of PQ and SR respectively and diagonal SQ is joined. The ratio ar(||gm XQRY) : ar(∆QSR) =
(a) 1 : 4
(b) 2 : 1
(c) 1 : 2
(d) 1 : 1
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q14.1
Solution:
In ||gm PQRS, X and Y are the mid points of PQ and SR respectively XY and SQ are joined.
∵ XY bisects PQ and SR
∴ PXYS and XQRY are also ||gms and ar(∆PXYS) = nr(∆XQRY)
∵ ||gm PQRS and AQSR are on the same base and between the same parallel lines
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q14.2

Question 15.
Diagonal AC and BD of trapezium ABCD, in which AB || DC, intersect each other at O. The triangle which is equal in area of ∆AOD is
(a) ∆AOB
(b) ∆BOC
(c) ∆DOC
(d) ∆ADC
Solution:
In trapezium ABCD, diagonals AC and BD intersect each other at O. AB || DC
∆ABC and ∆ABD are on the same base and between the same parallels
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q15.1
∴ ar(∆ABC) = or(∆ABD)
Subtracting ar(∆AOB)
ar(∆ABC) – ar(∆AOB) = ar(∆ADB) – ar(∆AOB)
⇒ ar(∆BOC) = ar(∆AOD)
ar(∆AOD) = ar(∆BOC) (c)

Question 16.
ABCD is a trapezium in which AB || DC. If ar(∆ABD) = 24 cm² and AB = 8 cm, then height of ∆ABC is
(a) 3 cm
(b) 4 cm
(c) 6 cm
(d) 8 cm
Solution:
In trapezium ABCD, AB || DC
AC and BD are joined
ar(∆ABD) = 24 cm2
AB = 8 cm,
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q16.1

Question 17.
ABCD is a trapezium with parallel sides AB = a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFE and EFCD is
(a) a : b
(b) (a + 3b) : (3a + b)
(c) (3a + b) : (a + 3b)
(d) (2a + b) : (3a + b)
Solution:
In quadrilateral ABCD, E and F are the mid points of AD and BC
AB = a, CD = b
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q17.1
Let h be the height of trapezium ABCD then height of each quadrilateral
ABFE = altitude of quadrilateral EFCD = \(\frac { h }{ 2 }\)
Now area of trap. ABFE = \(\frac { 1 }{ 2 }\) (sum of parallel sides) x altitude
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q17.2

Question 18.
ABCD is a rectangle with O as any point in its interior. If or(∆AOD) = 3 cm2 and ar(∆BOC) = 6 cm2, then area of rectangle ABCD is
(a) 9 cm2
(b) 12 cm2
(c) 15 cm2
(d) 18 cm2
Solution:
In rectangle ABCD, O is any point
ar(∆AOD) = 3 cm2
and ar(∆BOC) = 6 cm2
Join OA, OB, OC and OD
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q18.1
We know that if O is any point in ABCD Then ar(AOB) + ar(COD) = ar(AOB) + ar(BOC)
= 3 + 6 = 9 cm
∴ ar(rect. ABCD) = 2 x 9 = 18 cm (d)

Question 19.
The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q19.1
Solution:
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q19.2
P,Q and R the mid points of the sides of a ∆ABC then area of any parallelogram formed by the mid points and one vertex of the given triangle has area = \(\frac { 1 }{ 2 }\) area ∆ABC (b)

Question 20.
In the figure, ABCD and FECG are parallelograms equal in area. If ar(∆AQE) = 12 cm2, then ar(||gm FGBQ) =
(a) 12 cm2
(b) 20 cm2
(c) 24 cm2
(d) 36 cm2
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS Q20.1
Solution:
In the figure, ABCD and EFCG are parallelograms equal in area and ar(∆AQE) = 12 cm2
In ||gm AQED, AE is the diagonal
∴ ar(∆AQE) = \(\frac { 1 }{ 2 }\) ar(||gm AQED)
⇒ 12 cm2 = \(\frac { 1 }{ 2 }\) ar(||gm AQED)
∴ ar(||gm AQED) = 24 cm2
∵ ar ||gm ABCD = ar ||gm FECG
⇒ ar(||gm ∆QED) + ar(|| gm QBCE)
= ar(||gm QBCE) + ar(||gm FGBQ)
⇒ ar(||gm ∆QED) = ar(||gm FGBQ)
= 24 cm2 (c)

Hope given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.