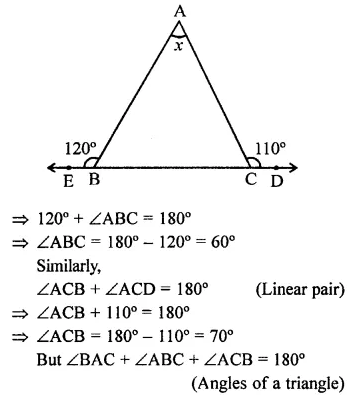
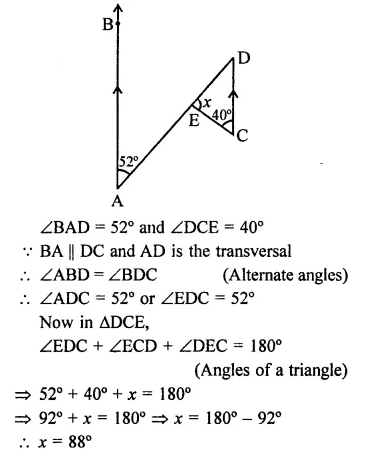
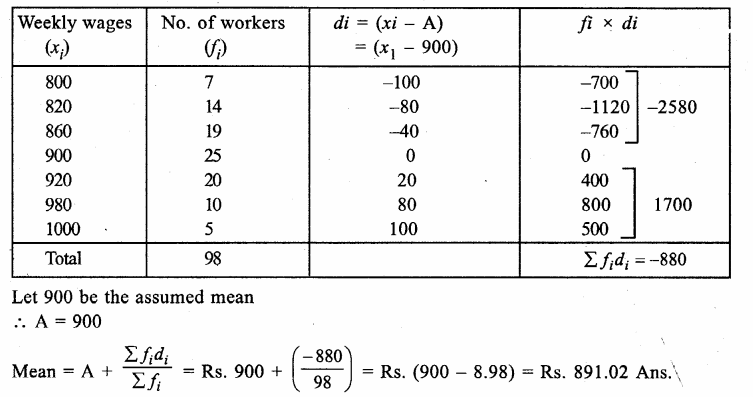
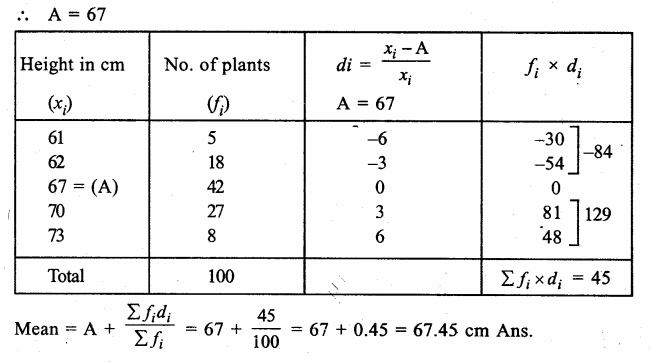
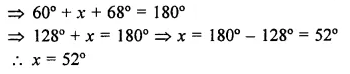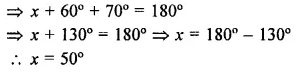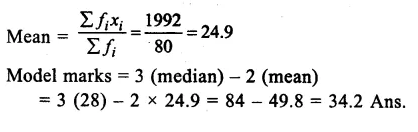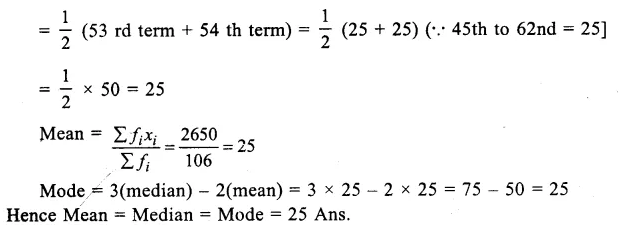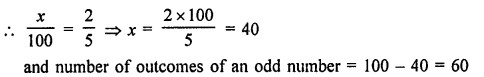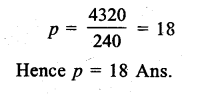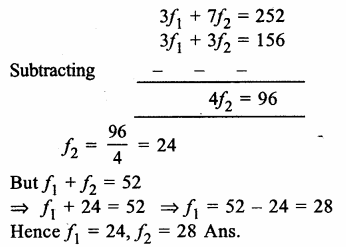Value Based Questions in Science for Class 9 Chapter 5 The Fundamental Unit of Life
These Solutions are part of Value Based Questions in Science for Class 9. Here we have given Value Based Questions in Science for Class 9 Chapter 5 The Fundamental Unit of Life
Question 1.
- A fruit is green when unripe but become beautifully coloured when ripe. How does this change occur ?
- What is the importance of this change ?
- What is mutualism involved ?
- Give an example of such a mutualism in our society.
Answer:
- An unripe fruit is green because it contains chloroplasts in its skin. Towards ripening of the fruit, the chloroplasts are changed into chromoplasts which give the fruit an attractive non-green (reddish, pink, purple, brownish) colour.
- The colour of ripe fruits attracts animals. The coloured fruits are often sweet and fleshy. Animals, like birds, come to feed over the fruits.
- While eating the flesh of fruits, the animals pick up the seeds and take them to different places visited by them. This helps in the dispersal of seeds. Therefore, both the animals and the plants are benefitted. It is mutualism.
- Mutualism or mutual dependence is the law of human society. No body can live and work alone. Every body is dependent on somebody else for most of one’s activities. For example, household helper, municipal worker, transport staff etc. work for you for which you pay so that the worker is able to run his/her family.
More Resources
- Value Based Questions in Science for Class 9
- HOTS Questions for Class 9 Science
- NCERT Solutions for Class 9 Science
- NCERT Exemplar Solutions for Class 9 Science
- Previous Year Question Papers for CBSE Class 9 Science
Question 2.
How does a cell show division of labour ? Is there any parallelism between the working of the cell and our society ?
Answer:
A cell has a number of organelles, viz., chloroplasts, mitochondria, Golgi apparatus, lysosomes, ribosomes, endoplasmic reticulum, nucleus, etc. Every organelle performs its specific function like food manufacture by chloroplasts, energy liberation by mitochondria, protein synthesis by ribosomes, transport by endoplasmic reticulum, control by nucleus. All the organelles coordinate their activities for the smooth functioning of the cell.
Human society has also a number of specialised activities being performed by different groups of persons, e.g., electricians, carpenters, plumbers, masons, transporters, scavengers, traffic controllers, teachers, doctors, agriculturists, engineers, manufactures, shopkeepers, managers, security persons, etc. All of them are however, coordinating with one another towards the smooth running of the society.
Question 3.
What are the functions of cell membrane ? How is the cell membrane able to perform diverse functions ? Give an example of diversity in functioning in any segment of human society.
Answer:
Cell membrane has a number of functions like providing shape to cell, acting as mechanical barrier between cell contents and environment, selective permeability, endocytosis, recognition, flow of information, passage of water, flow of external fluids by cilia or absorption of nutrients by its microvilli.
The diverse functions of cell membrane are possible due to adaptation of proteins to form channels, enzymes, carriers, receptors, etc. and their attachment to small carbohydrates.
Every human being is performing diverse functions. Seema is daughter of her parents, sister of her brother, student of her school, a badminton player, a friend to several classfellows, a companion of her pet, a gardener in home garden, a helper to her mother, a caretaker of her grand parents, an active social worker, etc.
Question 4.
What is the basis of long life of pickles and jams ? What lesson one gets from this fact ?
Answer:
Pickles and jams possess high concentration of osmotically active substances (salt in pickles, sugar in jams). They do not allow the microbial spores to germinate over them. Even on contamination, a microbe cannot survive in them as it will undergo exosmosis and die. Because of being microbe/germ free, pickles and jams do not get easily spoiled.
An active and long life can also occur in humans if they live in hygienic environment, avoid coming in contact with contaminated articles and visiting crowded places.
Hope given Value Based Questions in Science for Class 9 Chapter 5 The Fundamental Unit of Life are helpful to complete your science homework.
If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.