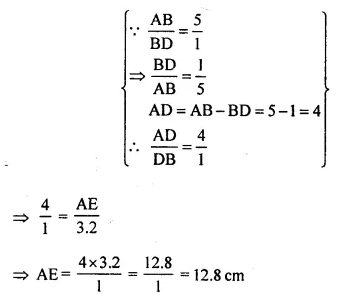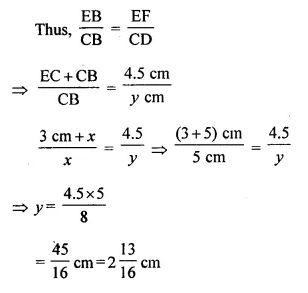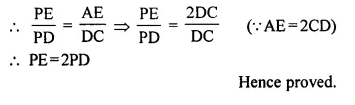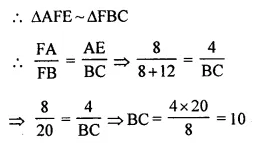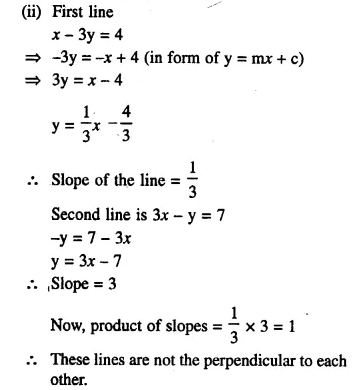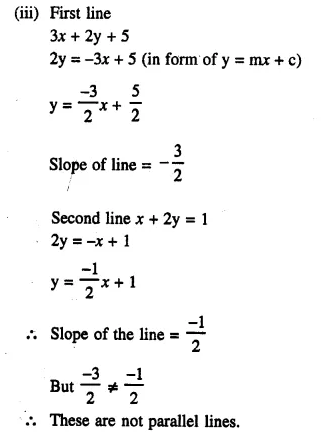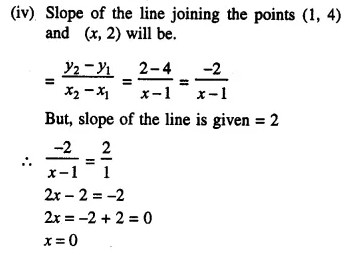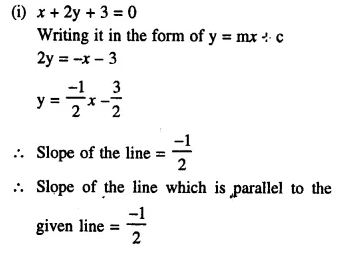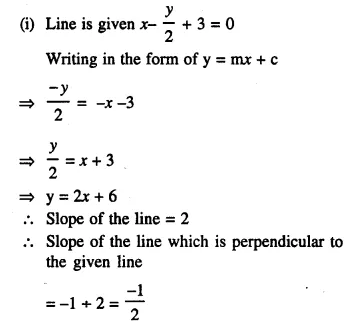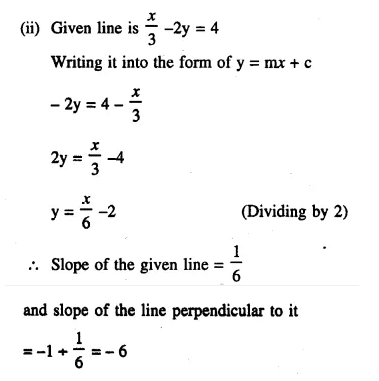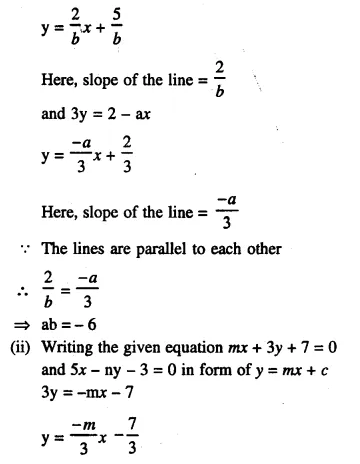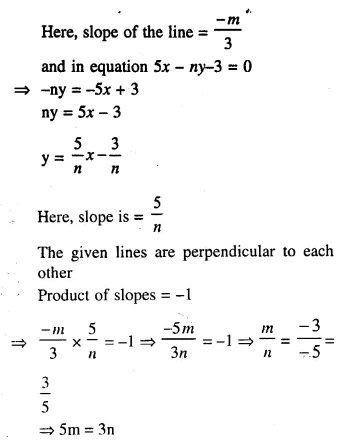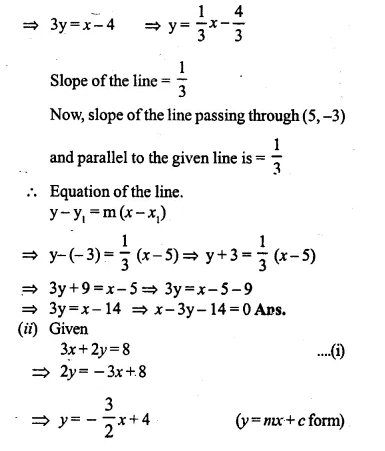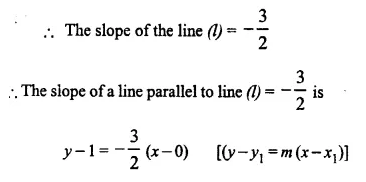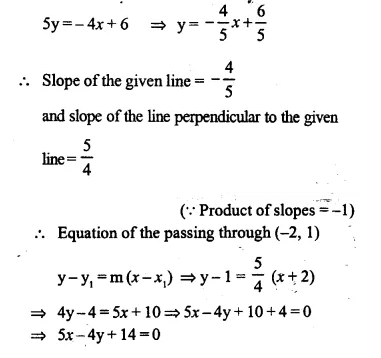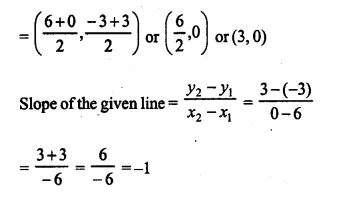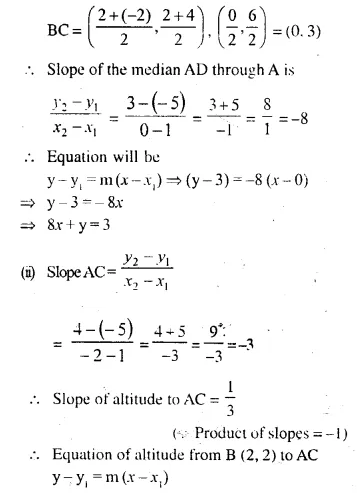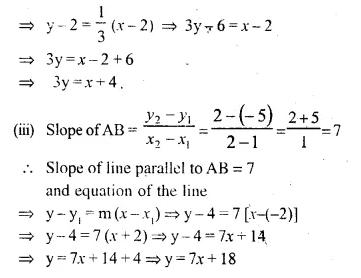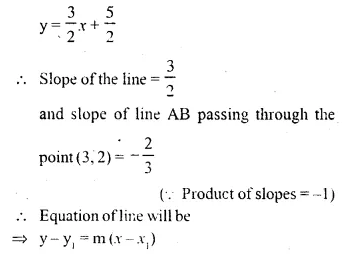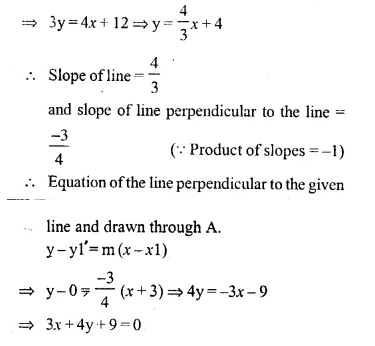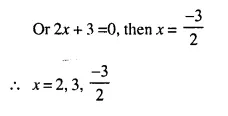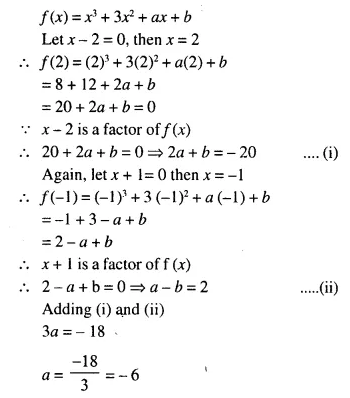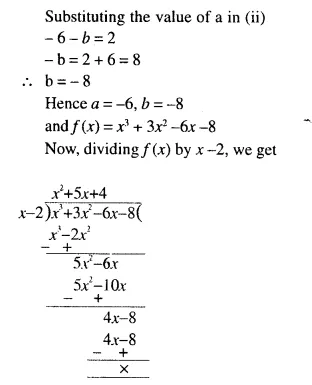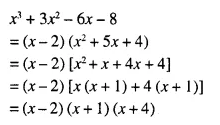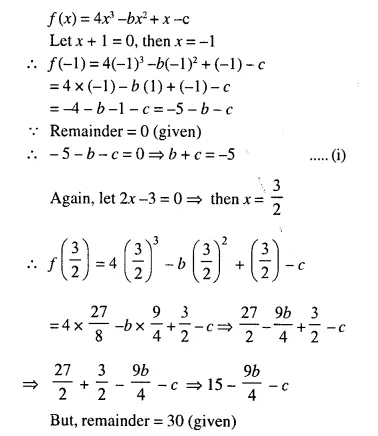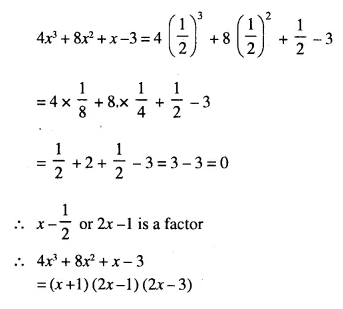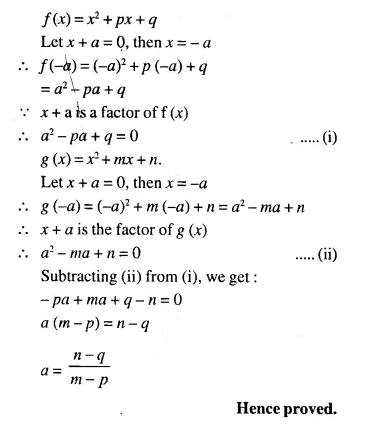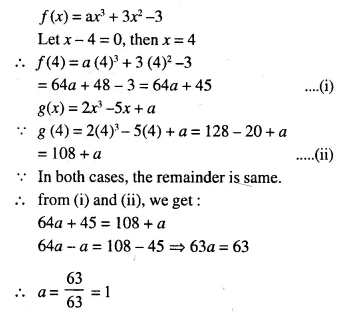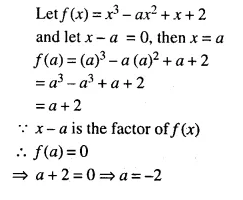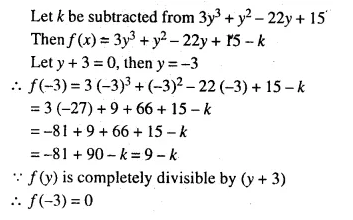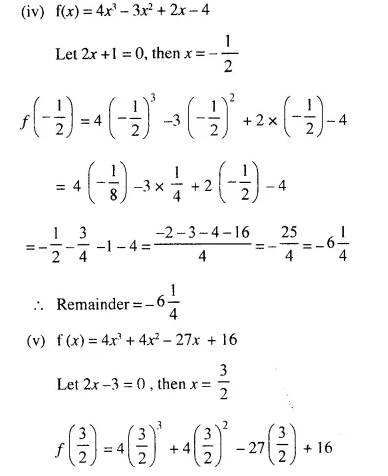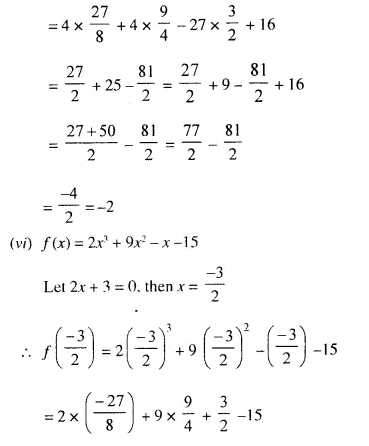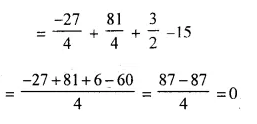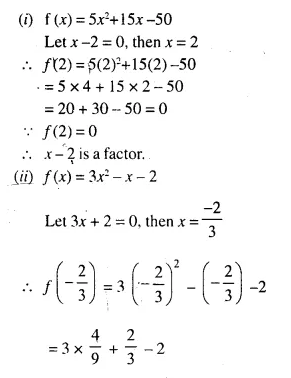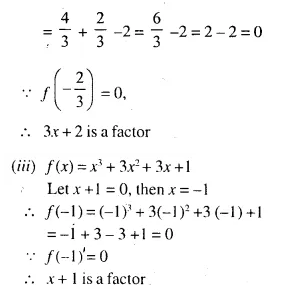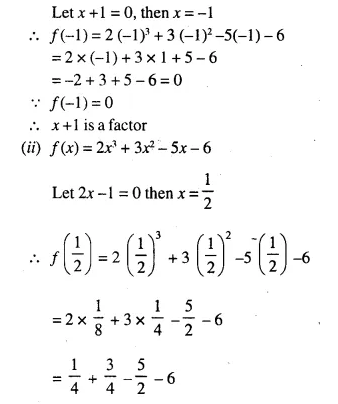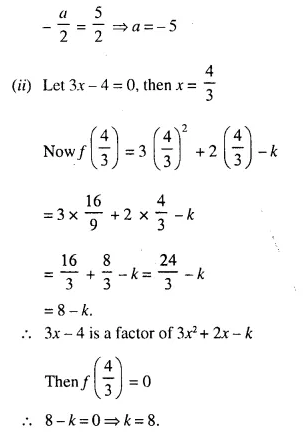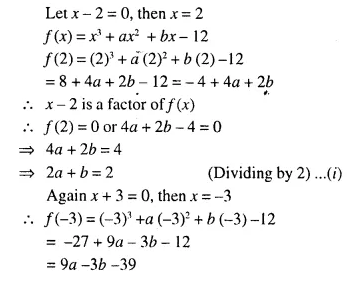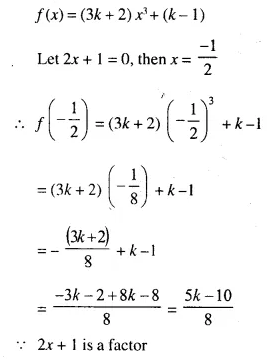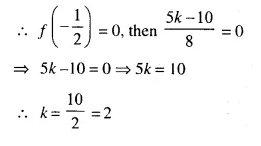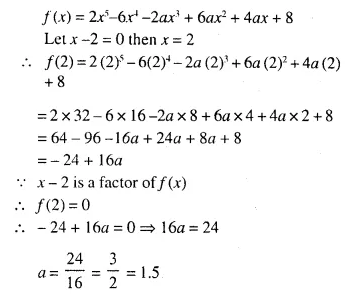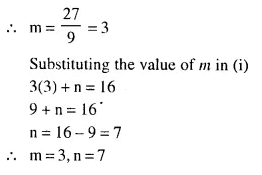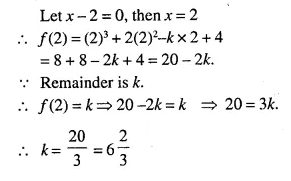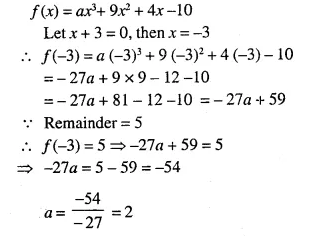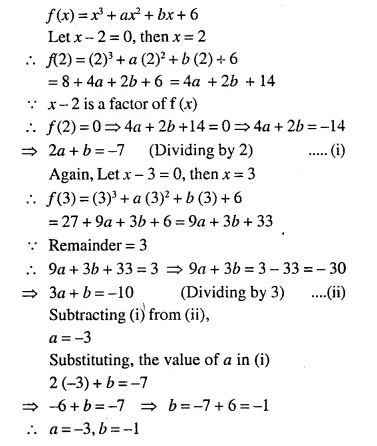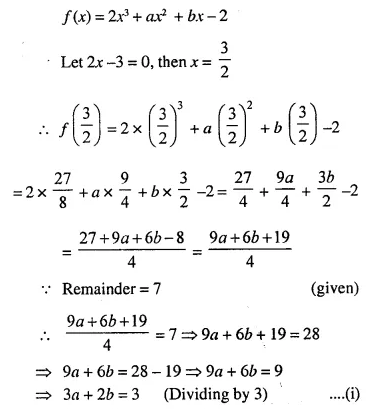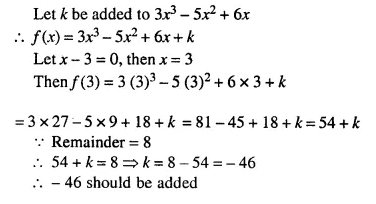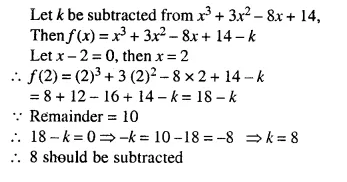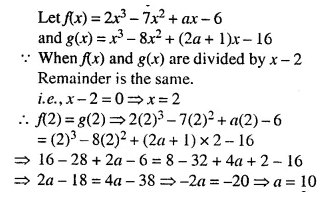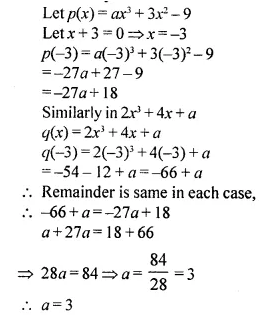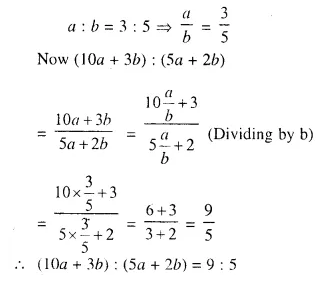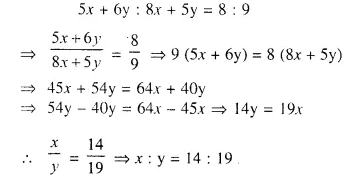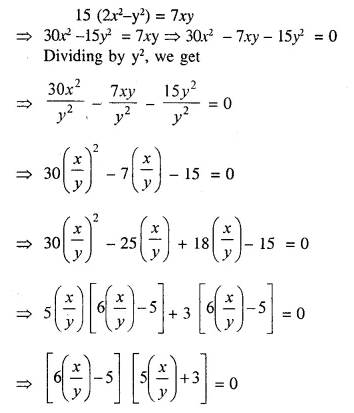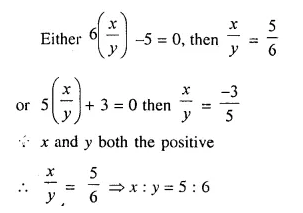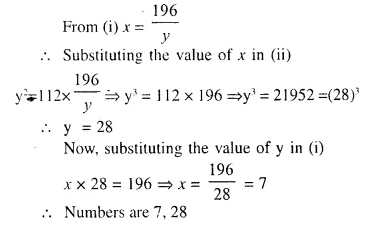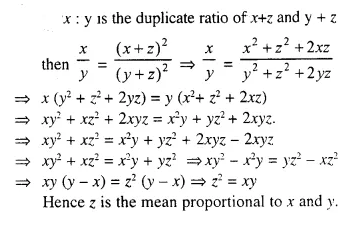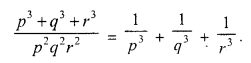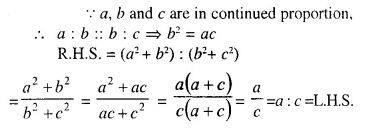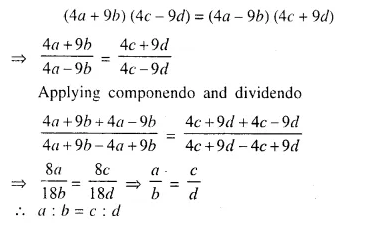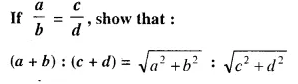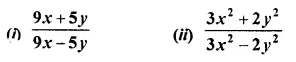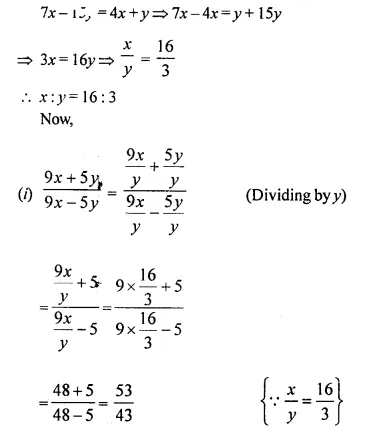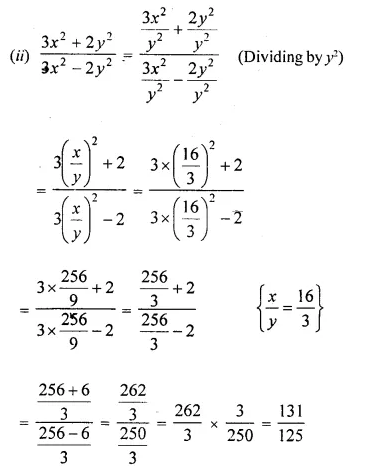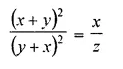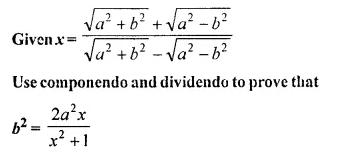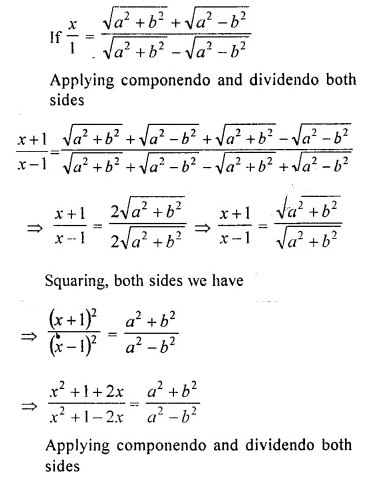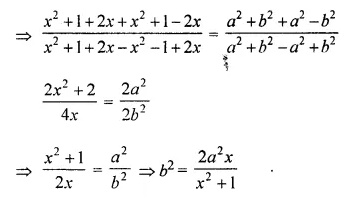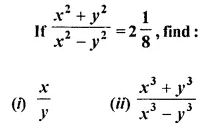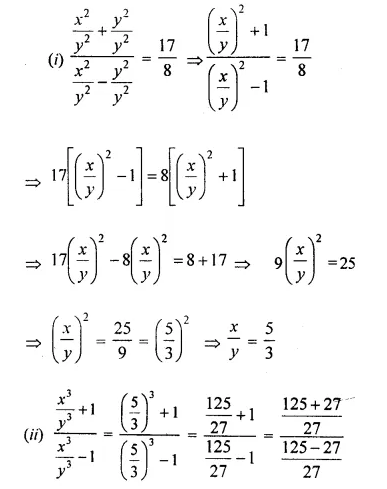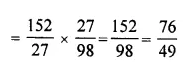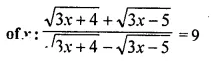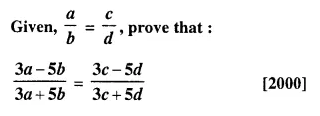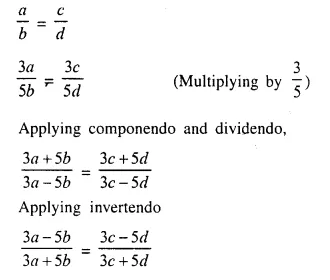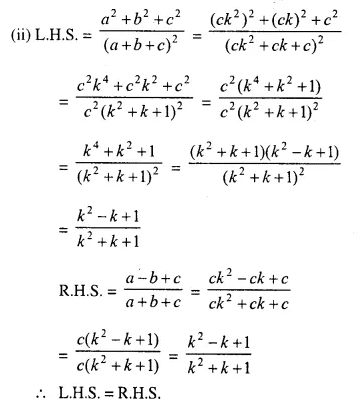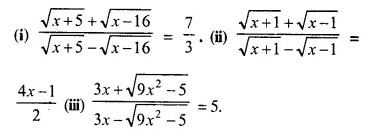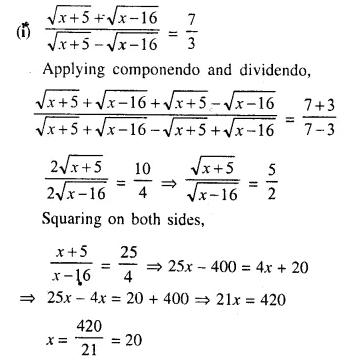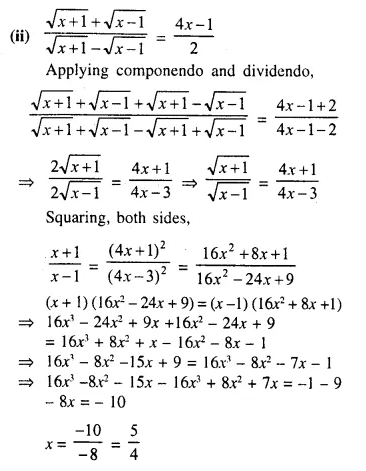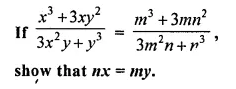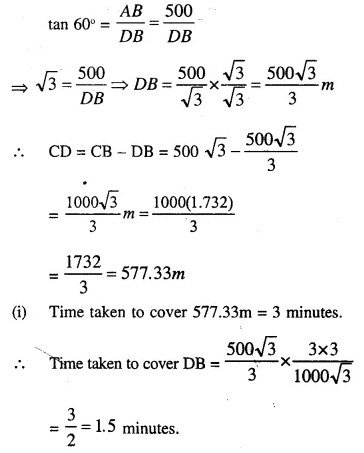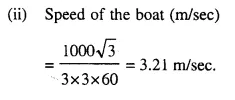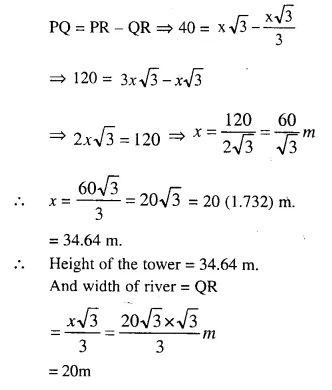Category: ICSE Class 10

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity (With Applications to Maps and Models) Ex 15C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15E

Question 1.
(i) The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
(ii) Areas of two similar triangles are 98 sq.cm and 128 sq.cm. Find the ratio between the lengths of their corresponding sides.
Solution:

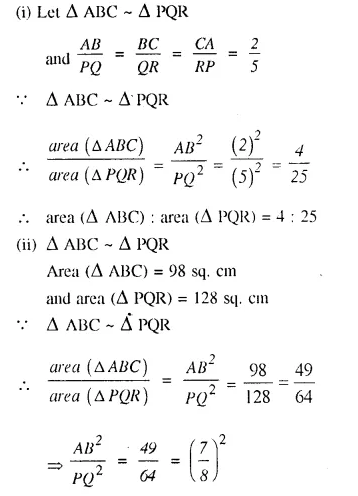
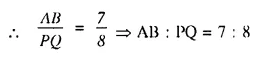
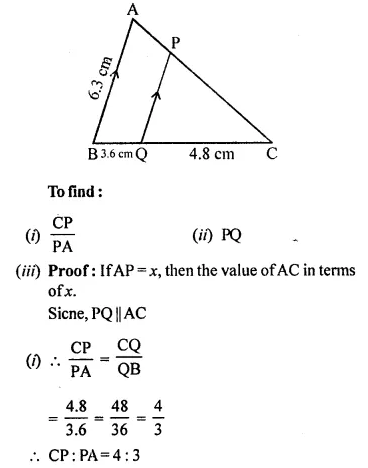
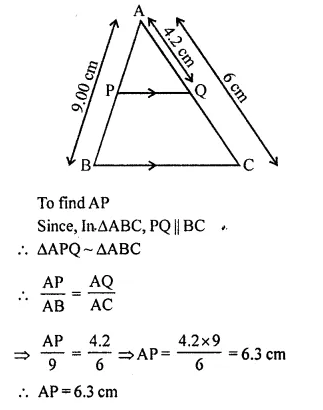
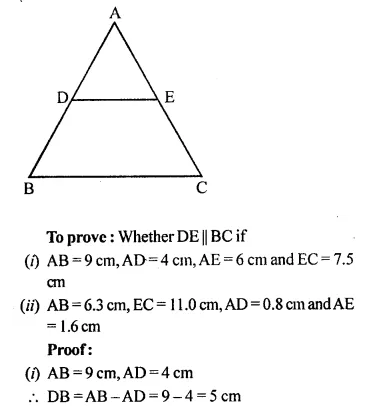
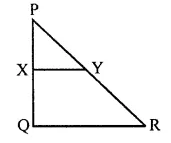
Question 2.
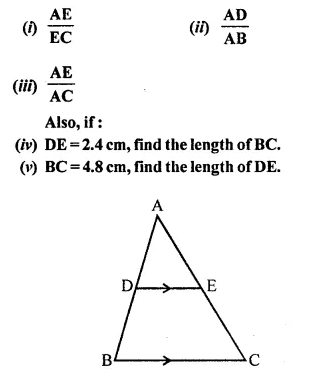
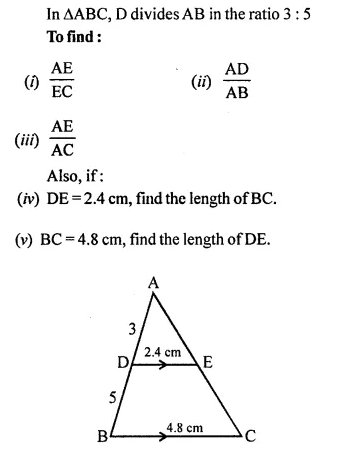
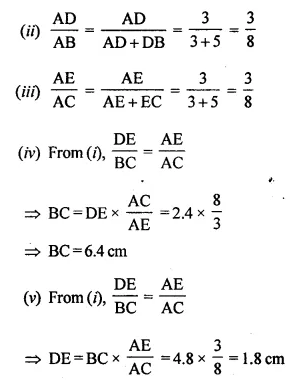
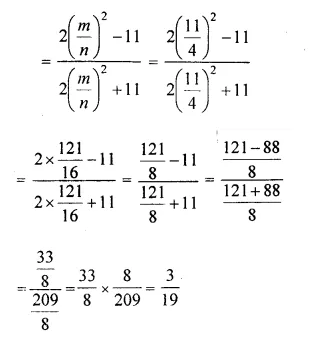
A line PQ is drawn parallel to the base BC, of ΔABC which meets sides AB and AC at points P and Q respectively. If AP = \(\frac { 1 }{ 3 }\) PB; find the value of:

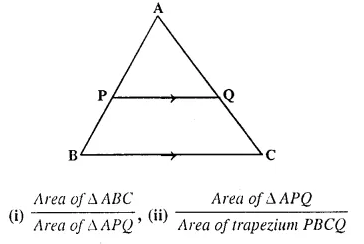
Solution:

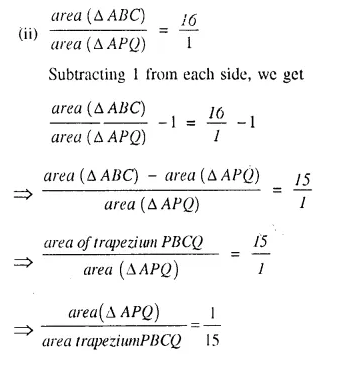
Question 3.
The perimeters of two similar triangles are 30 cm and 24 cm. If one side of first triangle is 12 cm, determine the corresponding side of the second triangle.
Solution:
Let we are given ΔABC and ΔPQR are similar.
Perimeter of ΔABC = 30 cm.
and perimeter of ΔPQR = 24 cm.
and side BC = 12 cm.
Now we have to find the length of QR, the corresponding side of ΔPQR
ΔABC ~ ΔPQR

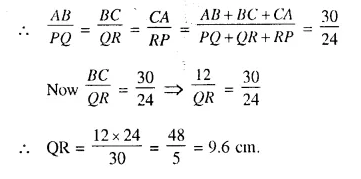
Question 4.
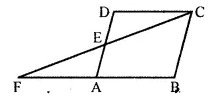
In the given figure AX : XB = 3 : 5

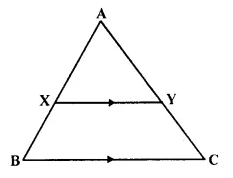
Find :
(i) the length of BC, if length of XY is 18 cm.
(ii) ratio between the areas of trapezium XBCY and triangle ABC.
Solution:
We are given in the ΔABC, AX : XB = 3 : 5
XY || BC.
Let AX = 3x and XB = 5x
AB = 3x + 5x = 8x.
Now in ΔAXY and ΔABC,
∠AXY = ∠ABC (corresponding angles)
∠A = ∠A (common)
ΔAXY ~ ΔABC (AA Postulate)

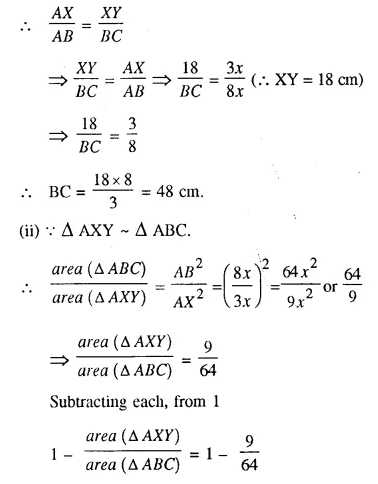
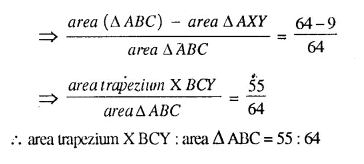
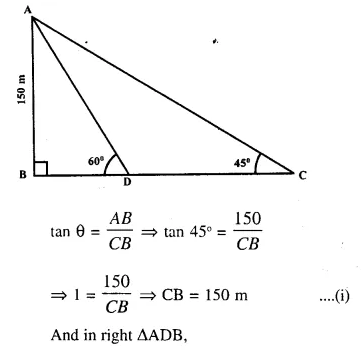
Question 5.
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
Given- In ΔABC, PQ || BC in such away that area APQ = area PQCB
To Find- The ratio of BP : AB

Solution:
In ΔABC, PQ || BC.
Z APQ = Z ABC (corresponding angles)
Now in ΔAPQ and ΔABC,
∠APQ = ∠ABC (proved)
∠A = ∠A (common)
ΔAPQ ~ ΔABC (AA postulate)

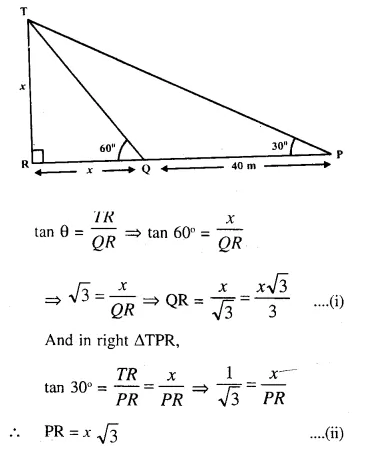
Question 6.
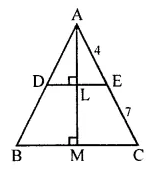
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4

Solution:
In ΔPQR, LM || QR in such away that PM : MR = 3 : 4
(i) In ΔPQR, LM || QR

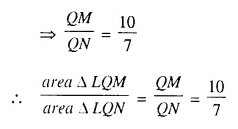
Question 7.
The given diagram shows two isosceles triangles which are similar also. In the given diagram, PQ and BC are not parallel: PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.

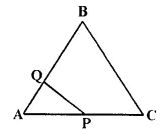
Calculate-
(i) the length of AP
(ii) the ratio of the areas of triangle APQ and triangle ABC.
Solution:

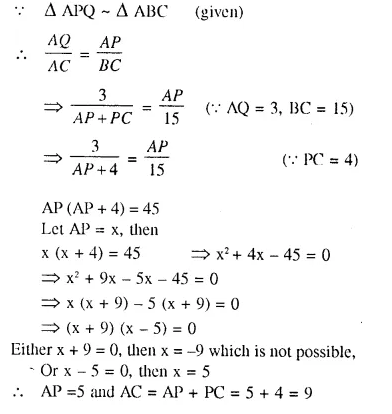
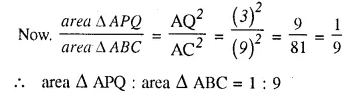
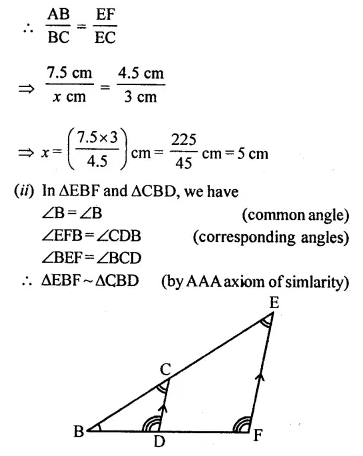
Question 8.
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20 cm². Calculate
(i) area of triangle CDP
(ii) area of parallelogram ABCD [1996]

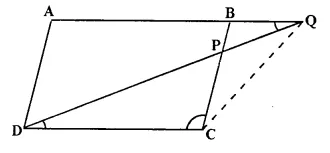
Solution:
(i) Join QC.
In ΔBPQ and ΔCPD,
∠DPC = ∠BPQ (vertically opposite angles.)
∠PDC = ∠BQP (Alternate angles.)
ΔBPQ ~ ΔCDP (AA postulate)

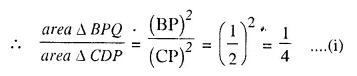
⇒ area ΔCDP = 4 (area ΔBPQ)
⇒ 2 (2 area ΔBPQ) = 2 x 20 = 40 cm² (2 area A BPQ = 20 cm²)
(ii) Area || gm ABCD = area ΔCPD + area ΔADQ – area ΔBPQ
= 40 + 9 (area BPQ) – area BPQ [(AD = CB = 3 BP)]
= 40 + 8 (area ΔBPQ)
= 40 + 8 (10) cm²
= 40 + 80
= 120 cm²

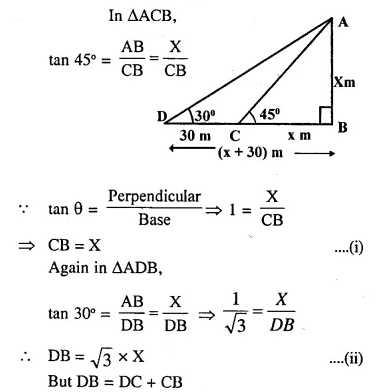
Question 9.
In the given figure. BC is parallel to DE. Area of triangle ABC = 25 cm². Area of trapezium BCED = 24 cm² and DE = 14 cm. Calculate the length of BC. Also. Find the area of triangle BCD.

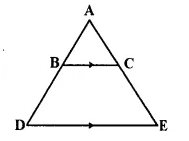
Solution:
In ΔADE, BC || DE
Area of ΔABC = 25 cm²
and area of trapezium BCED = 24 cm²
Area of ΔADE = 25 + 24 = 49 cm²
DE = 14 cm,
Let BC = x cm.
Now in ΔABC and ΔADE,
∠ABC = ∠ADE (corresponding angles)
∠A = ∠A (common)
ΔABC ~ ΔADE (AA postulate)

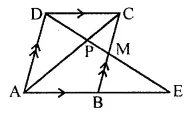
Question 10.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5.

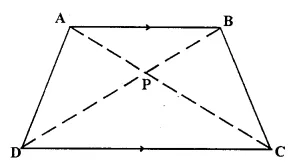
Find-
(i) ΔAPB : ΔCPB
(ii) ΔDPC : ΔAPB
(iii) ΔADP : ΔAPB
(iv) ΔAPB : ΔADB
Solution:
AP : CP = 3 : 5 ⇒ \(\frac { AP }{ CP }\) = \(\frac { 3 }{ 5 }\)
(i) Now in ΔAPB and ΔCPB,
These triangles have same vertex and their bases are in the same straight line
area ΔAPB : area ΔCPB = AP : PC = 3 : 5 or ΔAPB : ΔCPB = 3 : 5
(ii) In ΔAPB and ΔDPC,
∠APB = ∠DPC (vertically opposite angles)
∠PAB = ∠PCD (alternate angles)
ΔAPB ~ ΔDPC (AA postulate)

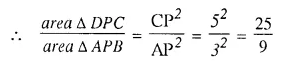
⇒ area ΔDPC : area ΔAPB = 25 : 9 or ΔDPC : ΔAPB = 25 : 9
(iii) In ΔADP and ΔAPB,
There have the same vertex and their bases arc in the same straight line.
area ΔADP : area ΔAPB = DP : PB
But PC : AP = 5 : 3
ΔADP : ΔAPB = 5 : 3
(iv) Similarly area ΔAPB : area ΔADB = PB : DB = 3 : (3 + 5) = 3 : 8

Question 11.
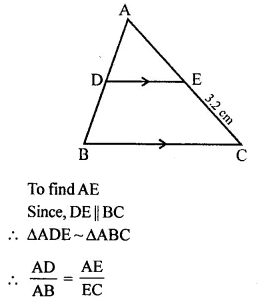
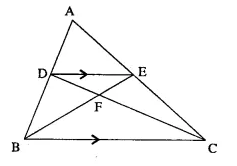
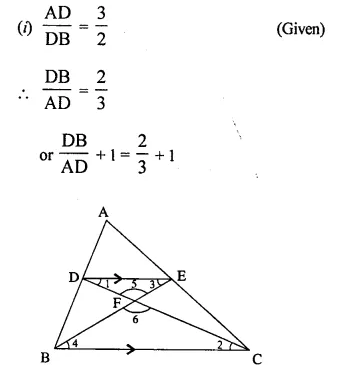
In the given figure, ARC is a triangle. DE is parallel to BC and \(\frac { AD }{ DB }\) = \(\frac { 3 }{ 2 }\).
(i) Determine the ratios \(\frac { AD }{ AB }\) , \(\frac { DE }{ BC }\)
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find \(\frac { EF }{ FB }\)
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?

Solution:

Question 12.
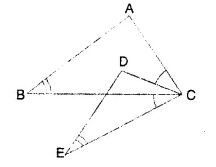
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ΔABC and ΔDEC.

Solution:
In the figure DE = 7.8 cm, AB = 10.4 cm
∠ACD = ∠BCE (given)
Adding ∠DCB both sides,
∠ACD + ∠DCB = ∠DCB + ∠BCE
∠ACB = ∠DCE
Now in ΔABC and ΔDCE
∠B = ∠E (given)
∠ACB = ∠DCE (proved)
ΔABC ~ ΔDCE (AA axiom)

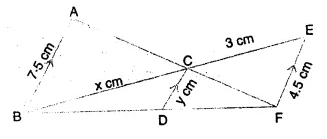
Question 13.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:

Solution:
In the figure, ΔABC is an isosceles triangle in which
AB = AC = 13 cm, BC = 10 cm,
AD ⊥ BC, CE = 8 cm and EF ⊥ AB
(i) Now in ΔADC and ΔFEB
∠C = ∠B (AB = AC)
∠ADC = ∠EFB (each = 90°)
ΔADC ~ ΔFEB (AA axiom)

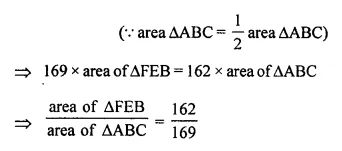
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Chapter 21 Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Ex 21D

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

Question 1.
Use tables to find sine of:
(i) 21°
(ii) 34°42′
(iii) 47° 32′                    
(iv) 62°57′
(v) 10°20′ + 20° 45′
Solution:
From tables of sine of angles, we find that:
(i) sin 21°= 0.3584,
(ii) sin 34°42’= .5693
(iii) sin 47° 32′ = 0.7377
(iv) sin 62° 57′ = 0.8906
(v) sin 10° 20′ + 20°45′ = sin 31°5′
= 0.5162

Question 2.
Use tables to find cosine of:
(i) 2°4′
(ii) 8°12′
(iii) 26°32’                     
(iv) 65°41′
(v) 9°23′ +15°54′
Solution:
From tables of cosine of angle, we find that:
(i) cos 2°4′ = 0.9993
(ii) cos 8° 12’ = 0.9898
(iii) cos 26°32′ = 0.8946
(iv) cos 65°41′ = 0.4118
(v) cos 9°23′ + 15°54′ = cos 25° 17′
= 0.9042

Question 3.
Use trigonometrical tables to find tangent of:
(i) 37°
(ii) 42°18′
(iii) 17°27′
Solution:
From the tables of tangents, we find that
(i) tan 35° = 0.7536
(ii) tan 42°18’= 0.9099
(iii) tan 17°27’= 0.3144

Question 4.
Use tables to find the acute angle θ, if the value of sin θ
(i) 4848
(ii) 0.3827
(iii) 0.6525
Solution:
From the tables of series, we find that of :
(i) sinθ = 0.4848, then θ = 29°
(ii) sinθ = 0.3827, then θ = 20° 30′
(iii) sin θ = 0.6525, then θ = 40° 42’ + 2′ = 40°44′

Question 5.
Use tables to find the acute angle θ, if the value of cos θ is :
(i) 0.9848
(ii) 0.9574
(iii) 0.6885
Solution:
From the tables of cosines, we find that if :
(i) cos θ = 0.9848, then θ = 10°
(ii) cos θ = 0.9574, then θ = 16°48′- 1’=16°47’
(iii) cos θ = 0.6885, then θ = 46° 30′ or 46°30′
= 46° 29’

Question 6.
Use tables to find the acute angle θ, if the value of tan θ is :
(i) 2419
(ii) 0.4741
(iii) 0.7391                     
(iv) 1.06
Solution:
From the table of tangents, we find that if:
(i) tan θ = 0.2419, then θ=13° 36’
(ii) tan θ = 0.4741, then θ = 25° 18’ + 4’ = 25°22′
(iii) tan θ = 0.7391, then θ= 36°24’+ 4′ = 36°28′
(iv) tan θ = 1.06, then θ = 46°36′ + 4′ = 46°40′

Question 7.
If sin θ=0.857; find:
(i) θ                              
(ii) tan θ
Solution:
From the tables of T. Ratio’s we find this :
(i) If sin θ = 0.857, then θ = 58°54′ + 4.5′ = 58° 58′ or 58°59’
(ii) tan 58°58’= 1.6577 +43 = 1.662 or tan 58° 59′ = 1.6577 + 53 = 1.663

Question 8.
If θ is the acute angle and cos θ = 0.7258; find:
(i) θ
(ii) 2 tan θ – sin θ
Solution:
From the tables of T-ratio’s, we find that:
(i) If cos θ = 0.7258, then θ= 43° 30′ -2′ = 43°28’
(ii) Now 2 tan θ – sin θ= 2 tan 43°28′ – sin 43°28′
2 tan 43°28’ = 2 x (0.9457 + 0.0022)
= 0:9479 x 2 = 1.8958
and sin 43°28′ = 0.6871 + 0.0008 = 0.6879
∴ 2 tan 43°28′ – sin 43° 28′ = 1.8958 – 0.6879 = 1.2079

Question 9.
Let θ be an acute angle and tan θ = 0.9490 find:
(i) θ
(ii) cos θ
(iii) sin θ – cos θ
Solution:
From the tables of T-raios, we find that:
(i) if tan θ = 0.9490 , then θ = 43°30′
(ii) cos θ = cos 43°30′ = 0.7254
(iii) sin θ = sin 43°50′ = 0.6884
∴ sin θ – cos θ = 0.6884 – 0.7254 = -0.0370 = -0.037

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14E

Question 1.
Find the slope and y-intercept of the line :
(i) y = 4
(ii) ax – by = 0
(iii) 3x – 4y = 5
Solution:
(i) y = 4 ⇒ y = 0x + 4
Here slope = 0 and y-intercept = 4
(ii) ax – by = 0
⇒ by = ax
⇒ y = \(\frac { a }{ b }\) x + 0
Here, slope = \(\frac { a }{ b }\) and y-intercept = 0
(iii) 3x – 4y = 5
⇒ – 4y = 5 – 3x
⇒ 4y = 3x – 5
⇒ y = \(\frac { 3 }{ 4 }\) x + \(\frac { -5 }{ 4 }\)
Here, slope = \(\frac { 3 }{ 4 }\) and y- intercept = \(\frac { -5 }{ 4 }\)

Question 2.
The equation of a line is x – y = 4. Find its – slope and y-intercept. Also, find its inclination.
Solution:
x – y = 4
writing the equation in form of y = mx + c
x = 4 + y
⇒ y = x – 4
Slope = 1 and y-intercept = – 4
Slope = 1
⇒ tanθ = 1
⇒ θ = 45°

Question 3.
(i) Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0 ?
(ii) Is the line x – 3y = 4 perpendicular to the line 3x – y = 7 ?
(iii) Is the line 3x + 2y = 5 parallel to the line x + 2y = 1 ?
(iv) Determine x so that the slope of the line through (1, 4) and (x, 2) is 2.
Solution:
(i) 3x + 4y + 7 = 0
Writing the equation in form of y = mx + c
4y = -3x – 7

Question 4.
Find the slope of the line which is parallel to:
(i) x + 2y + 3 = 0
(ii) \(\frac { x }{ 2 }\) – \(\frac { y }{ 3 }\) – 1 = 0
Solution:

Question 5.
Find the slope of the line which is perpendicular to:
(i) x – \(\frac { y }{ 2 }\) + 3 = 0
(ii) \(\frac { x }{ 3 }\) – 2y = 4
Solution:

Question 6.
(i) Lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel to each other. Find the relation connecting a and b.
(ii) Lines mx + 3y + 7 = 0 and 5x- ny – 3 = 0 are perpendicular to each other. Find the relation connecting m and n.
Solution:
(i) Writing the given equations in the form of y = mx + c, we get:
-by = -2x -5
by = 2x + 5

Question 7.
Find the value of p if the lines, whose equations are 2x – y + 5 = 0 and px + 3y = 4 are perpendicular to each other.
Solution:
Writing the given equations 2x – y + 5 = 0 and px + 3y = 4 in form of y = mx + c
2x – y + 5 = 0
-y = -2x -5
y = 2x + 5
Here, slope of the line = 2
Again, px + 3y = 4
3y = – px + 4

Question 8.
The equation of a line AB is 2x – 2y + 3 = 0.
(i) Find the slope of the line AB.
(ii) Calculate the angle that the line AB makes with the positive direction of the x-axis.
Solution:
The line AB is given.2* – 2y + 3 = 0
Writing it in the form of y = mx + c
-2y = -2x – 3
⇒ 2y = 2x + 3
⇒ y = x + \(\frac { 3 }{ 2 }\)
Here, slope of the line = 1
Angle of inclination = tanθ
tanθ = 1
θ = 45°

Question 9.
The lines represented by 4x + 3y = 9 and px – 6y + 3 = 0 are parallel. Find the value of p.
Solution:
Writing the given lines 4x + 3y = 9 and px – 6y + 3 = 0 in the form of y = mx + c
4x + 3y = 9
⇒ 3y = – 4x + 9

Question 10.
If the lines y = 3x + 7 and 2y +px = 3 are perpendicular to each other, find the value of p. (2006)
Solution:

Question 11.
The line through A (-2, 3) and B (4, 6) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Solution:
Gradient (mx) of the line passing through the points A (-2, 3) and B (4, b)

Question 12.
Find the equation of the line passing through (-5, 7) and parallel to
(i) x-axis
(ii) y-axis.
Solution:
(i) Slope of the line parallel to x-axis = 0
Equation of line passing through (-5, 7) whose slope is 0.
y – 7 = 0 [x – (-5)]
⇒ y – 7 = 0
⇒ y = 7
(ii) Slope of the line parallel to y-axis = 0
y – y1 = m (x – x1)
⇒ 0 = x – x1
⇒ x + 5 = 0

Question 13.
(i) Find the equation of the line passing through (5, -3) and parallel to x – 3y = 4.
(ii) Find the equation of the line parallel to the line 3x + 2y = 8 and passing through the point (0, 1). (2007)
Solution:
(i) Writing the equation x – 3y = 4 in form of y = mx + c
-3y = -x + 4


⇒ 2y – 2 = -3x
⇒ 3x + 2y – 2 = 0
Which is the required equation.

Question 14.
Find the equation of the line passing through (-2, 1) and perpendicular to 4x + 5y = 6.
Solution:
Writing the equation 4x + 5y = 6 in form of y = mx + c

Question 15.
Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, -3) and (0, 3).
Solution:
The perpendicular of the line segment bisects it.
Co-ordinates of mid-point of the line segment which is obtained by joining the points (6, -3) and (0, 3)

Slope of the line perpendicular to it = 1 (Product of slopes = -1)
Equation of the perpendicular bisector is y – y1 = m (x – x1)
y – 0 = 1 (x – 3)
y = x – 3

Question 16.
In the following diagram, write down:
(i) the co-ordinates of the points A, Band C.
(ii) the equation of the line through A and parallel to BC.

Solution:
(i) From the figure, the see that co-ordinates of A are (2, 3), B are (-1, 2) and C are (3, 0)

Question 17.
B (-5, 6) and D (1, 4) are the vertices of rhombus ABCD. Find the equation of diagonal BD and of diagonal AC.
Solution:

Question 18.
A = (7, -2) and C = (-1, – 6) are the vertices of a square ABCD. Find the equation of the diagonals AC and BD.
Solution:

Question 19.
A (1, -5), B (2, 2) and C (-2, 4) are the vertices of the ∆ABC, find the equation of:
(i) the median of the triangle through A.
(ii) the altitude of the triangle through B.
(iii) the line through C and parallel to AB.
Solution:
(i) Let D be the mid-point of BC
co-ordinates mid-point of

Question 20.
(i) Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
(ii) AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin. [1995]
Solution:
(i) Write the equation 2y = 3x + 5 in the form of y = mx + c. We get:

y – 2 = \(\frac { -2 }{ 3 }\) (x – 3)
⇒ 3y – 6 = -2x + 6
⇒ 2x + 3y = 6 + 6
⇒ 2x + 3y = 12 …… (i)
(ii) AB meets the x-axis at A
ordinate (y) of A = 0 i.e. y = 0
Substituting, the value of y in (i)
2x + 3 x 0 = 12
⇒ 2x = 12
⇒ x = 6
Co-ordinates of A are (6, 0)
Again. AB meets y-axis at B
Abscissa of B = 0 i.e. x = 0
Substituting the value of x in (i)
2 x 0 + 3y = 12
⇒ y = 4
Co-ordinates of B are (0, 4)
Area of ∆OAB = \(\frac { 1 }{ 2 }\) x Base x altitude
= \(\frac { 1 }{ 2 }\) x 4 x 6 = 12 square units

Question 21.
The line 4x – 3y + 12 = 0 meets the x-axis at A. Write the co-ordinates of A.
Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
Solution:
The line 4x – 3y + 12 = 0 meets x-axis at A.
Ordinates of A = 0. i.e. y = 0
Substituting, the value of y in the equation
4x – 3 x 0 + 12 = 0
⇒ 4x + 12 = 0
⇒ 4x = -12
⇒ x = -3
Co-ordinates of A are (-3, 0)
Writing the equation 4x – 3y + 12 = 0 in form of y = mx + c
⇒ -3y = -4x – 12

Question 22.
The point P is the foot of perpendicular from A (-5, 7) to the line is 2x – 3y + 18 = 0. Determine:
(i) the equation of the line AP.
(ii) the co-ordinates of P.
Solution:
Write the equation in form of y = mx + c
2x – 3y + 18 = 0
⇒ -3y = -2x – 18
⇒ y = \(\frac { 2 }{ 3 }\) x + 6 (Dividing by 3)
Slope of the line = \(\frac { 2 }{ 3 }\)
and slope of the line perpendicular to it = \(\frac { -3 }{ 2 }\) (Product of slopes = -1)
(i) Equation of line AP perpendicular to the given line and drawn through A (-5, 7)

y – y1 = m (x – x1)
⇒ y – 7 = \(\frac { -3 }{ 2 }\) (x + 5)
⇒ 2y – 14 = -3x – 15
⇒ 3x + 2y – 14 + 15 = 0
⇒ 3x + 2y + 1 = 0
(ii) P is the point of intersection of these lines
we will solve their equations
2x – 3y + 18 = 0 ….(i)
3x + 2y + 1 = 0 ….(ii)
Multiplying (i) by 2 and (ii) by 3, we get
4x – 6y + 36 = 0
9x + 6y + 3 = 0
Adding, we get:
13x + 39 = 0
⇒ 13x = -39
⇒ x = -3
Now, substituting the value of x in (i)
2(-3) – 3y + 18 = 0
⇒ -6 – 3y + 18 = 0
⇒ -3y + 18 – 6 = 0
⇒ -3y + 12 = 0
⇒ -3y = -12
⇒ 3y = 12
⇒ y = 4
Co-ordinates of P are (-3, 4)

Question 23.
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
Solution:

AB meets y- axis at P
abscissa of P = 0 i. e. x = 0
Substituting the value of y in (i)
0 + y = 4
⇒ y = 4
Co-ordinates of P are (0, 4)
BC meets x-axis at Q
ordinate of Q = 0 i.e. y = 0
Substituting, the value of y in (ii),
2x + 0 = 6
⇒ 2x = 6
⇒ x = 3
Co-ordinates of Q are (3, 0)

Question 24.
Match the equations A, B, C, and D with the lines L1, L2, L3 and L4, whose graphs are roughly drawn in the given diagram.
A = y = 2x;
B = y – 2x + 2 = 0;
C = 3x + 2y = 6;
D = y = 2 [1996]

Solution:
A → L3,
B → L4,
C → L2,
D → L1

Question 25.
Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line. (2014)
Solution:
A (a, 3), B (2,1) and C (5, a) are collinear.
Slope of AB = Slope of BC

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13C

Question 1.
Calculate the co-ordinates-of the point P which divides the line segment joining:
(i) A (1, 3) and B (5, 9) in the ratio 1 : 2
(ii) A (-4, 6) and B (3, -5) in the ratio 3 : 2
Solution:
(i) Let co-ordinates of P be (x,y)

Question 2.
In what ratio is the line joining (2, -3) and (5, 6) divided by the x-axis ?
Solution:
Let the point P (x, 0) divides in the ratio of m₁ : m₂ line joining the points A (2, -3) and B (5, 6)

Question 3.
In what ratio is the line joining (2, -4) and (-3, 6) divided by the y-axis ?
Solution:
Let the point P (0, y) divides the line joining the points A (2, -4) and (-3, 6) in the ratio of m₁ : m₂

Question 4.
In what ratio does the point (1, a) divide the join of (-1, 4) and (4, -1)? Also, find the value of ‘a’.
Solution:
Let the point P (1, a) divides the line joining the points (-1, 4) and (4, -1) in the ratio of m₁ : m₂

Question 5.
In what ratio does the point (a, 6) divide the join of (-4, 3) and (2, 8) ? Also, find the value of ‘a’.
Solution:
Let the point P (a, 6) divides the line joining the points A (-4, 3), B (2, 8) in the ratio of m₁ : m₂

Question 6.
In what ratio is the join of (4, 3) and (2, -6) divided by the x-axis. Also, find the co-ordinates of the point of intersection.
Solution:

Question 7.
Find the ratio in which the join of (-4, 7) and (3, 0) is divided by the y-axis. Also, find the co-ordinates of the point of intersection.
Solution:
Let, the points (0, y) be the point of intersection which divides the line joining the points A (-4, 7) and B (3, 0)

Question 8.
Points A, B, C and D divide the line segment joining the point (5, -10) and the origin in five equal parts. Find the co-ordinates of A, B, C and D.
Solution:
Points A, B, C and D divide the line segment joining the points (5, -10) and origin (0, 0) in five equal parts
Let co-ordinates of A be (x, y) which divides PO in the ratio of 1 : 4

Question 9.
The line joining the points A (-3, -10) and B (-2, 6) is divided by the point P such that = \(\frac { PA }{ PB }\) = \(\frac { 1 }{ 5 }\), find the co-ordinates of P.
Solution:
Let the co-ordinates of P be (x, y) which divides the line joining the points A (-3,-10) and B (-2,6) in the ratio of AP : PB i.e. (5 – 1) : 1 or 4 : 1

Question 10.
P is a point on the line joining A (4, 3) and B (-2, 6) such that 5AP = 2BP. Find the co-ordinates of P.
Solution:

Question 11.
Calculate the ratio in which the line joining the points (-3, -1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.
Solution:
Let the point P (2, y) divides the line joining the points A (-3, -1) and B (5, 7) in the ratio of m₁ : m₂

Question 12.
Calculate the ratio in which the line joining A (6, 5) and B (4, -3) is divided by the line y = 2.
Solution:
Let the point P (x, 2) divides the line joining the points A (6, 5) and B (4, -3) in the ratio of m₁ : m₂

Question 13.
The point P(5, -4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B.

Solution:
From the figure, the line AB intersects x-axis at A and y-axis at B.
Let the co-ordinates of A (x, 0) and B (0, y) and P (5, -4) divides it in the ratio of 2 : 5

Question 14.
Find the co-ordinates of the points of trisection of the line joining the points (-3, 0) and (6, 6).
Solution:

Question 15.
Show that the line segment joining the points (-5, 8) and (10, -4) is trisected by the co-ordinate axes.
Solution:

Let the points A (-5, 8) and B (10, -4).
Let P and Q be the two points on the axis which trisect the line joining the points A and B.
AP = PQ = QB
AP : PB = 1 : 2 and AQ : QB = 2 : 1

Question 16.
Show that A (3, -2) is a point of trisection of the line-segment joining the points (2, 1) and (5, -8). Also, find the co-ordinates of the other point of trisection.
Solution:

Let A and B are the points of trisection of the line segment joining the points P (2, 1) and Q (5, -8), then
PA = AB = BQ.
PA : AQ = 1 : 2 and PB : BQ = 2 : 1

Question 17.
If A = (-4, 3) and B = (8, -6)
(i) find the length of AB
(ii) In what ratio is the line joining A and B, divided by the x-axis ?
Solution:

Question 18.
The line segment joining the points M (5, 7) and N (-3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.
Solution:

Question 19.
A (2, 5), B (-1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that:
AP : PB = AQ : QC = 1 : 2.
(i) Calculate the co-ordinates of P and Q.
(ii) Show that PQ = \(\frac { 1 }{ 3 }\) BC.
Solution:

Question 20.
A (-3, 4), B ( 3, -1) and C (-2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP: PC = 2 : 3.
Solution:

Question 21.
ThelinesegmentjoiningA(2, 3)andB(6, -5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the pointK. [1990, 2006]
Solution:
Let the line segment Intersect the x-axis at the point P
Co-ordinates of P are (x, 0)
Let P divide the line segment in the ratio K : 1 then

Question 22.
The line segment joining A (4, 7) and B (-6, -2) is intercepted by the y-axis at the point K. Write down the abscissa of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
Solution:
Points A (4, -7), B (-6, -2) are joined which intersects y-axis at K. abscissa of K will be 0

Let the coordinates of K be (0, y) and K divides AB line segment in the ratio m₁ : m₂

Question 23.
The line joining P (-4, 5) and Q (3, 2), intersects they axis at point R. PM and QN are perpendiculars from P and Q on the x-axis. Find:
(i) The ratio PR: RQ.
(ii) The co-ordinates of R.
(iii) The areas of the quadrilateral PMNQ. [2004]
Solution:
(i) Let divides the line joining the points P (-4, 5) and Q (3, 2) in the ratio k : 1

Question 24.
In the given figure, line APB meets the x- axis at point A and y-axis at point B. P is the point (-4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.

Solution:
Let the co-ordinates of A be (x1, 0) (as it lies on x-axis)
and co-ordinates of B be (0, y2)
and co-ordinates of P are (-4, 2)
AP : PB = 1 : 2 i.e. m1 = 1, m2 = 2
Now, P divides AB in the ratio m₁ : m₂ or 1 : 2

Question 25.
Given a line segment AB joining the points A (-4, 6) and B (8, -3). Find:
(i) the ratio in which AB is divided by the y-axis.
(ii) find the coordinates of the point of intersection.
(iii) the length of AB.
Solution:
(i) Let the y-axis divide AB in the ratio m : 1

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 23 Graphical Representation (Histograms, Frequency Polygon and Ogives) Ex 23

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Chapter 23 Graphical Representation (Histograms, Frequency Polygon and Ogives) Ex 23.

Question 1.
Draw histograms for the following distributions :

Solution:

Question 2.
Draw a cumulative frequency curve (ogive) for each of the following distributions

Solution:

Question 3.
Draw an ogive for each of the following distributions :

Solution:

Now plotting the points (10, 8), (20, 25), (30, 38), (40, 50) and (50, 67) on the graph and join them with free hand to obtain an ogive as shown in the graph.

Now plot the points (10, 0), (20, 17), (30, 32), (40, 37), (50, 53), (60, 58) and (70, 65) on the graph and join them with free hand to get an ogive as shown in the graph.

Question 4.
Construct a frequency distribution table for the numbers given below, using the class intervals 21-30,31-40…. etc.
75, 67, 57, 50, 26, 33, 44, 58, 67,75, 78, 43, 41, 31, 21, 32, 40, 62, 54, 69, 48, 47,51,38, 39,43,61, 63, 68, 53, 56, 49, 59, 37, 40, 68, 23, 28, 36 and 47.
Use the table obtained to draw:
(i) a histogram
(ii) an ogive
Solution:



(ii) Ogive :
We plot the points (30, 4), (40, 13), (50, 22), (60, 29); (70, 37) and (80, 40) on the graph and join them in free hand to obtain an ogive.

Question 5.
(a) Use the information given in the adjoining histogram to c construct a f frequency table.
(b)Use this table to construct an ogive.

Solution:
From the histogram given, the required frequency table will be as given below.

Plot the points (12, 9), (16, 25), (20, 47), (24, 65), (28, 77), (32, 81) on the graph and join them with free hand to get an ogive as shown.

Question 6.

(a) From the distribution given above, construct a frequency table, (b) Use the table obtained in part (a) to draw :
(i) a histogram
(ii) an ogive.
Solution:
Difference in consecutive class marks. = 17.5 – 12.5 = 5
∴ first class interval will be : 10-15 and so on

(ii) We plot the point (15. 12), (20. 29), (25. 51), (30, 78). (35, 108), (40. 129) and (45, 145) on the graph and join them in free hand to obtain the ogive.

Question 7.
Use graph paper for this question.
The table given beiow shows the monthly wages of some factory workers.
(i) Using the table calculate the cumulative frequencies of workers.
(ii) Draw the cumulative frequency curve.
Use 2 cm = Rs. 500, starting the origin at Rs. 6500 on x-axis, and 2 cm = 10 workers on the y-axis

Solution:


(ii) We plot the points (7000, 10), (7500, 28), (8000, 50), (8500, 75), (9000, 92) (9500, 102) and (10000, 110) on the graph and join them in free hand to obtain an ogive.

Question 8.
The following table shows the distribution of the heights of a group of factory workers :

(i) Determine the cumulative frequencies.
(ii) Draw the ‘less than’ cumulative frequency curve on a graph paper. Use 2 cm = 5cm height on one axis and 2 cm = 10 workers on the other.
Solution:


We plot points (155, 6), (160, 18), (165, 36),
(170, 56), (175, 69), (180, 77) and (185, 83) on the graph and join them in free hand to obtain an ogive.

Question 9.
Construct a frequency distribution table for each of the following distributions :

Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 23 Graphical Representation Ex 23  are helpful to you.

If you have any doubts, please comment below. We try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8C

Question 1.
Using the Factor Theorem, show that:
(i) (x – 2) is a factor of x³ – 2x² – 9x +18. Hence, factorise the expression x³ – 2x² – 9x + 18 completely.
(ii) (x + 5) is a factor of 2x³ + 5x² – 28x – 15. Hence, factorise the expression 2x³ + 5x² – 28x – 15 completely.
(iii) (3x + 2) is a factor of 3x³ + 2x² – 3x – 2. Hence, factorise the expression 3x³ + 2x² – 3x – 2. completely.
(iv) 2x + 7 is a factor of 2x³ + 5x² – 11x – 14. Hence, factorise the given expression completely.
Solution:

Question 2.
Using the Remainder Theorem, factorise each of the following completely:
(i) 3x³ + 2x² – 19x + 6
(ii) 2x³ + x² – 13x + 6
(iii) 3x³ + 2x² – 23x – 30
(iv) 4x³ + 7x² – 36x – 63
(v) x³ + x² – 4x – 4. (2004)
Solution:

Question 3.
Using the Remainder Theorem factorise the expression 3x³ + 10x² + x – 6. Hence, solve the equation. 3x³ + 10x² + x – 6 = 0
Solution:

Question 4.
Factorise the expression f(x) = 2x³ – 7x² – 3x + 18. Hence, find all possible values of x for which f(x) = o.
Solution:

Question 5.
Given that x – 2 and x +1 are factors of f(x) = x³ + 3x² + ax + b; calculate the values of a and b. Hence, find all the factors of f(x).
Solution:

Question 6.
The expression 4x³ – bx² + x – c leaves remainders 0 and 30 when divided by x + 1 and 2x – 3 respectively. Calculate the values of b and c. Hence, factorise the expression completely.
Solution:

Question 7.
If x + a is a common factor of expressions f(x) = x² + px + q and g (x) = x² + mx + n show that a = \(\frac { n – q }{ m – p }\)
Solution:

Question 8.
The polynomials ax³ + 3x² – 3 and 2x³ – 5x + a, when divided by x – 4, leave the same remainder in each case. Find the value of a.
Solution:

Question 9.
Find the value of ‘a’ if (x – a) is a factor of x³ – ax² + x + 2.
Solution:

Question 10.
Find the number that must be subtracted from the polynomial 3y³ + y² – 22y + 15, so that the resulting polynomial is completely divisible by y + 3.
Solution:

⇒ 9 – k = 0 ⇒ k = 9
Hence 9 should be subtracted.

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8C

Question 1.
Find in each case, the remainder when :
(i) x⁴ – 3x² + 2x + 1 is divided by x – 1.
(ii) x³ + 3x² – 12x + 4 is divided by x – 2.
(iii) x⁴ + 1 is divided by x + 1.
(iv) 4x³ – 3x² + 2x – 4 is divided by 2x + 1.
(v) 4x³ + 4x² – 21x + 16 is divided by 2x – 3.
(vi) 2x³ + 9x² – x – 15 is divided by 2x + 3.
Solution:

Question 2.
Show that:
(i) x – 2 is a factor of 5x² + 15x – 50.
(ii) 3x + 2 is a factor of 3x² – x – 2.
(iii) x + 1 is a factor of x³ + 3x² + 3x + 1.
Solution:

Question 3.
Use the Remainder Theorem to find which of the following is a factor of 2x³ + 3x² – 5x – 6.
(i) x + 1
(ii) 2x – 1
(iii) x + 2
(iv) 3x – 2
(v) 2x – 3.
Solution:
(i) f(x) = 2×3 + 3×2 – 5x – 6

Question 4.
(i) If 2x + 1 is a factor of 2x² + ax – 3, find the value of a.
(ii) Find the value of k, if 3x – 4 is a factor of expression 3x² + 2x – k.
Solution:

Question 5.
Find the values of constants a and b when x – 2 and x + 3 both are the factors of expression, x³ + ax² + bx – 12.
Solution:

(x + 3) is a factor of f(x)
f(-3) = 0
9a – 3b – 39 – 0
⇒ 3a – b – 13 = 0
⇒ 3a – b = 13
Adding (i) and (ii) we get:
5a = 15 ⇒ a = 3
Substituting the value of a in (i)
2(3) + b = 2
⇒ 6 + b = 2
⇒ b = 2 – 6 = – 4
Hence a = 3, b = – 4

Question 6.
Find the value of k, if 2x + 1 is a factor of (3k + 2) x³ + (k – 1).
Solution:

Question 7.
Find the value of a, if x – 2 is a factor of 2x⁵ – 6x⁴ – 2ax³ + 6ax² + 4ax + 8.
Solution:

Question 8.
Find the values of m and n so that x – 1 and x + 2 both are factors of x³ + (3m + 1) x² + nx – 18.
Solution:

Question 9.
When x³ + 2x² – kx + 4 is divided by x – 2, the remainder is k. Find the value of constants.
Solution:
f(x) = x³ + 2x² – kx + 4

Question 10.
Find the value of a, if the division of ax³ + 9x² + 4x – 10 by x + 3 leaves a remainder 5.
Solution:

Question 11.
If x³ + ax² + bx + 6 has x – 2 as a factor and leaves a remainder 3 when divided by x – 3, find the values of a and b. [2005]
Solution:

Question 12.
The expression 2x³ + ax² + bx – 2 leaves remainder 7 and 0 when divided by 2x – 3 and x + 2 respectively. Calculate the values of a and b.
Solution:

Question 13.
What number should be added to 3x³ – 5x² + 6x so that when resulting polynomial is divided by x – 3, the remainder is 8 ?
Solution:

Question 14.
What number should be subtracted from x³ + 3x² – 8x + 14 so that on dividing it by x – 2, the remainder is 10.
Solution:

Question 15.
The polynomials 2x³ – 7x² + ax – 6 and x³ – 8x² + (2a + 1) x – 16 leave the same remainder when divided by x – 2. Find the value of ‘a’.
Solution:

Question 16.
If (x – 2) is a factor of the expression 7x³ + ax² + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b.
Solution:

Question 17.
Find ‘a’ if the two polynomials ax³ + 3x² – 9 and 2x³ + 4x + a, leave the same remainder when divided by x + 3. (2015)
Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion (Including Properties and Uses) Ex 7D

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7D.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7D

Question 1.
If a : b = 3 : 5, find : (10a + 3b) : (5a + 2b)
Solution:

Question 2.
If 5x + 6y : 8x + 5y = 8 : 9, find x : y
Solution:

Question 3.
If k (3x – 4y) : (2x – 3y) = (5x – 6y) : (4x – 5y), find x : y.
Solution:

Question 4.
Find the :
(i) duplicate ratio of 2√2 : 3√5
(ii) triplicate ratio of 2a : 3b,
(iii) sub-duplicate ratio of 9x² a⁴ : 25y⁶ b²
(iv) sub-triplicate ratio of 216 : 343
(v) reciprocal ratio of 3 : 5
(vi) ratio compounded of the duplicate ratio of 5 : 6, the reciprocal ratio of 25 : 42 and the sub-duplicate ratio of 36 : 49.
Solution:

Question 5.
Find the value of x, if :
(i) (2x + 3) : (5x – 38) is the duplicate ratio of √5 : √6
(ii) (2x + 1) : (3x + 13) is the sub-duplicate ratio of 9 : 25.
(iii) (3x -7): (4x + 3) is the sub-triplicate ratio of 8 : 27.
Solution:

Question 6.
What quantity must be added to each term of the ratio x : y so that it may become equal to c : d ?
Solution:

Question 7.
A woman reduces her weight in the ratio 7 : 5. What does her weight become if originally it was 84 kg?
Solution:
Ratio in reduction of weight = 7 : 5
Originally weight of the woman = 84 kg
Reduced weight = \(\frac { 84 x 5 }{ 7 }\) = 60 kg

Question 8.
If 15 (2x² – y²) = 7xy, find x : y, if x and y both are positive.
Solution:

Question 9.
Find the :
(i) fourth proportional to 2xy, x² and y².
(ii) third proportional to a² – b² and a + b.
(iii) mean proportion to (x – y) and (x³ – x²y)
Solution:
(i) Let a be the fourth proportional
Then 2xy : x² :: y² : a

Question 10.
Find two numbers such that the mean proportional between them is 14 and third proportional to them is 112.
Solution:
Let x and y be the two numbers.
Then 14 is the mean proportional between x and y
xy = 14² => xy = 196 ….(i)
and 112 is the third proportional to x, y
y² = 112 x ….(ii)

Question 11.
If x and y be unequal and x : y is the duplicate ratio of x + z and y + z, prove that z is mean proportional between x and y.
Solution:

Question 12.
If q is the mean proportional between p and r, prove that:

Solution:

Question 13.
If a, b and c are in continued proportion, prove that: a : c = (a² + b²) : (b² + c²).
Solution:

Question 14.

Solution:

Question 15.
If (4a + 9b) (4c – 9d) = (4a – 9b) (4c + 9d), prove that a : b = c : d.
Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.
There are 36 members in a student council in a school and the ratio of the number of boys to the number of girls is 3 : 1. How many more girls should be added to the council so that the ratio of number of boys to the number of girls may be 9 : 5 ?
Solution:
Total number of members = 36
Ratio in boys and girls = 3 : 1

Question 19.
If 7x – 15y = 4x + y, find the value of x : y. Hence, use componendo and dividendo to find the values of:

Solution:

Question 20.

Solution:

Question 21.
If x, y, z arc in continued proportion, prove that

Solution:

Question 22.

Solution:

Question 23.

Solution:

Question 24.
Using componendo and dividendo, find the value

Solution:

Question 25.

Solution:

Question 26.

Solution:

Question 27.

Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion (Including Properties and Uses) Ex 7C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7D

Question 1.
If a : b = c : d, prove that:
(i) 5a + 7b : 5a – 7b = 5c + 7d : 5c – 7d.
(ii) (9a + 13b) (9c – 13d) = (9c + 13d) (9a – 13b).
(iii) xa + yb : xc + yd = b : d.
Solution:

Question 2.
If a : b = c : d, prove that: (6a + 7b) (3c – 4d) = (6c + 7d) (3a – 4b).
Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.
If (7a + 8b) (7c – 8d) = (7a – 8b) (7c + 8d), prove that a : b = c : d.
Solution:

Question 6.

Solution:

Question 7.
If (a + b + c + d) (a – b – c + d) = (a + b – c – d) (a – b + c – d), prove that a : b = c : d.
Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.
If a, b and c are in continued proportion, prove that

Solution:

Question 11.
Using properties of proportion, solve for x:

Solution:



But x = – 1 does not satisfy it
x = 1

Question 12.

Solution:

Question 13.
Using the properties of proportion, solve for x, given

Solution:

Question 14.

Solution:

Question 15.

Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22B

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22C

Question 1.
In the figure given below, it is given that AB is perpendicular to BD and is of length X metres. DC = 30 m. ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
Solution:

Question 2.
Find the height of a tree when it is found that on walking away from it 20m, in a horizontal line through its base, the elevation of its top Changes from 60° to 30°.
Solution:
Let AB be the tree and its height be x DC = 20 m.
Now in right ∆ADB

Question 3.
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
Solution:
Let AB be the building and its
height be x and DC =40m
Now in right ∆ADB

Question 4.
From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if :
(i) the ships are on the same side of the light house,
(ii) the ships are on the opposite sides of the light house.
Solution:
AD = 100 m
In right angled ∆ABD

Question 5.
Two pillars of equal heights stand 011 either side of a roadway, which is 150m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30”; find the height of the pillars and the position of the point.
Solution:
Let AB and CD be the two pillars which stand on either side of a road BD, then BD = 150m
Let AB = CD = h
Let P be the point on the road such that the angles of elevation from P to the top of the pillars are 60° and 30° respectively.
Let BP = x then PD = 150 – x

Question 6.
From the figure given below, calculate the length of CD.

Solution:

Question 7.
The angle of elevation of the top of a tower is observed to be 60°. At a point 30 m vertically above the first point of observation, the elevation is found to be 45°. Find :
(i) the height of the tower,
(ii) its horizontal distance from the points of observation.
Solution:
Let height of tower = x i.e. AB = x
In the right ∆ADB,

Question 8.
From the top of a cliff. 60 metre high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
Solution:
Height of the cliff AB = 60m
Let the height of tower = x
Draw TR \(\parallel\) SB. meeting AB in R

Question 9.
A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later the angle of depression of the boat is found to be 60°. Assuming that the boat sails at a uniform speed, determine :
(i) how much more time it will take to reach the shore.
(ii) the speed of the boat in metre per second, if the height of the cliff is 500 m.
Solution:
Height of cliff = 500 m.
In right ∆ACD,

Question 10.
A man in a boat rowing away from a light house 150m high, takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 45°. Find the speed of the boat.
Solution:
Height of the lighthouse AB = 150m
Now is right ∆ACB,

Question 11.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find :
(i) the height of the tree, correct to 2 decimal places,
(ii) the width of the river.
Solution:
TR is the height of tree and RQ is the width of the river.
Let TR = x
Now in right ∆TQR

Question 12.
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160m high, is 45°. Find the height of the first tower.
Solution:

Let the height of first tower CD = x
and height of second tower AB = 160 m
Distance between them DB = 75 m.
In right ∆ACE,

Question 13.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30″ than when it was
45°. Prove that the height of the tower is y (\(\sqrt { 3 }\) +1) metres.
Solution:
Let AB be the tower and AB = x
Distance CD = 2y
In right ∆ADB,

Question 14.
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°, find the uniform speed of the aeroplane in km per hour.
Solution:
Height of aeroplane = 1 km = 1000 m.
In right ∆ACB,

Question 15.
From the top of a hill, the angles of depression of two consecutive kilometre stones, due east, are found to be 30° and 45° respectively. Find the distance of the two stones from the foot of the hill. (2007)
Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.