RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS

Question 1.
In the figure, the sides BA and CA have been produced such that BA = AD and CA = AE. Prove the segment DE || BC.

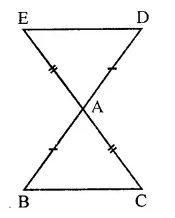
Solution:
Given : Sides BA and CA of ∆ABC are produced such that BA = AD are CA = AE. ED is joined.
To prove : DE || BC
Proof: In ∆ABC and ∆DAE AB=AD (Given)
AC = AE (Given)
∠BAC = ∠DAE (Vertically opposite angles)
∴ ∆ABC ≅ ∆DAE (SAS axiom)
∴ ∠ABC = ∠ADE (c.p.c.t.)
But there are alternate angles
∴ DE || BC

Question 2.
In a ∆PQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN = MN.
Solution:
Given : In ∆PQR, PQ = QR
L, M and N are the mid points of the sides PQ, QR and PR respectively

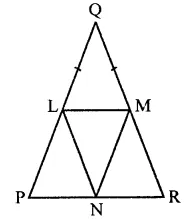
To prove : LM = MN
Proof : In ∆LPN and ∆MRH
PN = RN (∵ M is mid point of PR)
LP = MR (Half of equal sides)
∠P = ∠R (Angles opposite to equal sides)
∴ ALPN ≅ AMRH (SAS axiom)
∴ LN = MN (c.p.c.t.)

Question 3.
Prove that the medians of an equilateral triangle are equal.
Solution:
Given : In ∆ABC, AD, BE and CF are the medians of triangle and AB = BC = CA

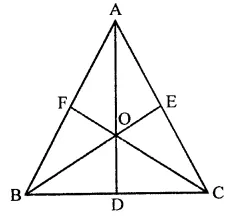
To prove : AD = BE = CF
Proof : In ∆BCE and ∆BCF,
BC = BC (Common side)
CE = BF (Half of equal sides)
∠C = ∠B (Angles opposite to equal sides)
∴ ABCE ≅ ABCF (SAS axiom)
∴ BE = CF (c.p.c.t.) …(i)
Similarly, we can prove that
∴ ∆CAD ≅ ∆CAF
∴ AD = CF …(ii)
From (i) and (ii)
BE = CF = AD
⇒ AD = BE = CF

Question 4.
In a ∆ABC, if ∠A = 120° and AB = AC. Find ∠B and ∠C.
Solution:
In ∆ABC, ∠A = 120° and AB = AC
∴ ∠B = ∠C (Angles opposite to equal sides)
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)

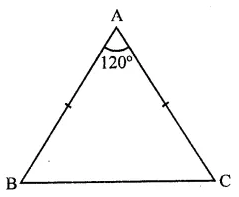
⇒ 120° + ∠B + ∠B = 180°
⇒ 2∠B = 180° – 120° = 60°
∴ ∠B = \(\frac { { 60 }^{ \circ } }{ 2 }\) = 30°
and ∠C = ∠B = 30°
Hence ∠B = 30° and ∠C = 30°

Question 5.
In a ∆ABC, if AB = AC and ∠B = 70°, find ∠A.
Solution:
In ∆ABC, ∠B = 70°
AB =AC
∴ ∠B = ∠C (Angles opposite to equal sides)

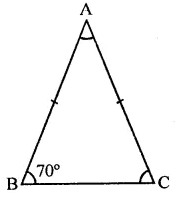
But ∠B = 70°
∴ ∠C = 70°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ ∠A + 70° + 70° = 180°
⇒ ∠A + 140°= 180°
∴∠A = 180°- 140° = 40°

Question 6.
The vertical angle of an isosceles triangle is 100°. Find its base angles.
Solution:
In ∆ABC, AB = AC and ∠A = 100°
But AB = AC (In isosceles triangle)

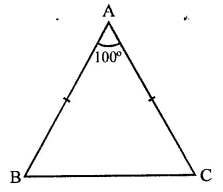
∴ ∠C = ∠B (Angles opposite to equal sides)
∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ 100° + ∠B + ∠B = 180° (∵ ∠C = ∠B)
⇒ 2∠B = 180° – 100° = 80°
∴ ∠C = ∠B = 40°
Hence ∠B = 40°, ∠C = 40°

Question 7.
In the figure, AB = AC and ∠ACD = 105°, find ∠BAC.
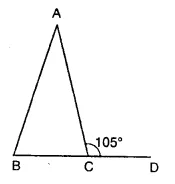Solution:
In ∆ABC, AB = AC
∴ ∠B = ∠C (Angles opposite to equal sides)
But ∠ACB + ∠ACD = 180° (Linear pair)
⇒ ∠ACB + 105°= 180°
⇒ ∠ACB = 180°-105° = 75°
∴ ∠ABC = ∠ACB = 75°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ ∠A + 75° + 75° = 180°
⇒ ∠A + 150°= 180°
⇒ ∠A= 180°- 150° = 30°
∴ ∠BAC = 30°

Question 8.
Find the measure of each exterior angle of an equilateral triangle.
Solution:
In an equilateral triangle, each interior angle is 60°

But interior angle + exterior angle at each vertex = 180°
∴ Each exterior angle = 180° – 60° = 120°

Question 9.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Solution:
Given : In an isosceles ∆ABC, AB = AC
and base BC is produced both ways

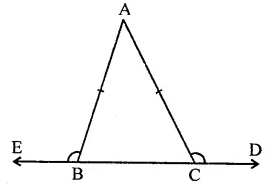
To prove : ∠ACD = ∠ABE
Proof: In ∆ABC,
∵ AB = AC
∴∠C = ∠B (Angles opposite to equal sides)
⇒ ∠ACB = ∠ABC
But ∠ACD + ∠ACB = 180° (Linear pair)
and ∠ABE + ∠ABC = 180°
∴ ∠ACD + ∠ACB = ∠ABE + ∠ABC
But ∠ACB = ∠ABC (Proved)
∴ ∠ACD = ∠ABE
Hence proved.

Question 10.
In the figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD.

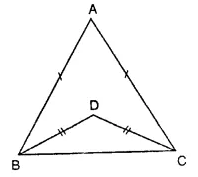
Solution:
In the given figure,
In ∆ABC,
AB = AC and DB = DC
In ∆ABC,
∵ AB = AC
∴ ∠ACD = ∠ABE …(i) (Angles opposite to equal sides)
Similarly, in ∆DBC,
DB = DC
∴ ∠DCB = ∠DBC .. (ii)
Subtracting (ii) from (i)
∠ACB – ∠DCB = ∠ABC – ∠DBC
⇒ ∠ACD = ∠ABD
∴ Ratio ∠ABD : ∠ACD = 1 : 1

Question 11.
Determine the measure of each of the equal angles of a rightangled isosceles triangle.
OR
ABC is a rightangled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Solution:
Given : In a right angled isosceles ∆ABC, ∠A = 90° and AB = AC
To determine, each equal angle of the triangle

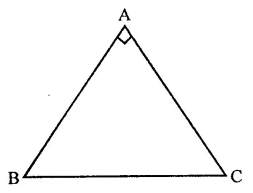
∵ ∠A = 90°
∴ ∠B + ∠C = 90°
But ∠B = ∠C
∴ ∠B + ∠B = 90°
⇒ 2∠B = 90°
90°
⇒ ∠B = \(\frac { { 90 }^{ \circ } }{ 2 }\)  = 45°
and ∠C = ∠B = 45°
Hence ∠B = ∠C = 45°

Question 12.
In the figure, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT
(ii) ∠TQR = 15°

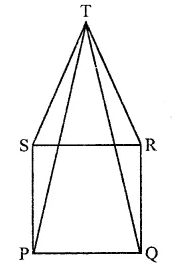
Solution:
Given : PQRS is a square and SRT is an equilateral triangle. PT and QT are joined.

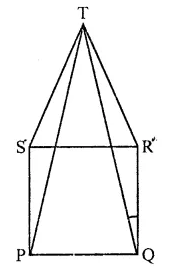
To prove : (i) PT = QT; (ii) ∠TQR = 15°
Proof : In ∆TSP and ∆TQR
ST = RT (Sides of equilateral triangle)
SP = PQ (Sides of square)
and ∠TSP = ∠TRQ (Each = 60° + 90°)
∴ ∆TSP ≅ ∆TQR (SAS axiom)
∴ PT = QT (c.p.c.t.)
In ∆TQR,
∵ RT = RQ (Square sides)
∠RTQ = ∠RQT
But ∠TRQ = 60° + 90° = 150°
∴ ∠RTQ + ∠RQT = 180° – 150° = 30°
∵ ∠PTQ = ∠RQT (Proved)
∠RQT = \(\frac { { 30 }^{ \circ } }{ 2 }\)  = 15°
⇒ ∠TQR = 15°

Question 13.
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the ponits A and B (see figure). Show that the line PQ is perpendicular bisector of AB.

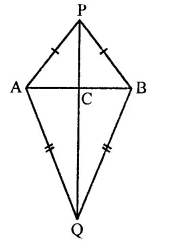
Solution:
Given : AB is a line segment.
P and Q are points such that they are equidistant from A and B
i.e. PA = PB and QA = QB AP, PB, QA, QB, PQ are joined
To prove : PQ is perpendicular bisector of AB

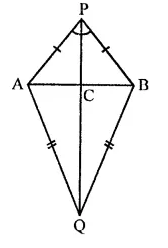
Proof : In ∆PAQ and ∆PBQ,
PA = PB (Given)
QA = QB (Given)
PQ = PQ (Common)
∴ ∆PAQ ≅ ∆PBQ (SSS axiom)
∴ ∠APQ = ∠BPQ (c.p.c.t.)
Now in ∆APC = ∆BPC
PA = PB (Given)
∆APC ≅ ∆BPC (Proved)
PC = PC (Common)
∴ ∆APC = ∆BPC (SAS axiom)
∴ AC = BC (c.p.c.t.)
and ∠PCA = ∠PCB (c.p.c.t.)
But ∠PCA + ∠PCB = 180° (Linear pair)
∴ ∠PCA = ∠PCB = 90°
∴ PC or PQ is perpendicular bisector of AB

 

Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.