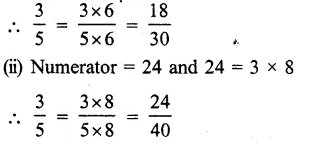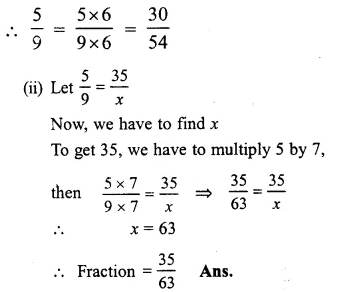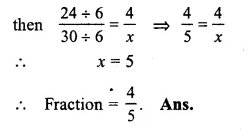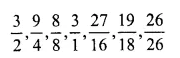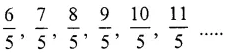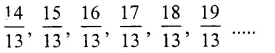RS Aggarwal Class 6 Solutions Chapter 22 Data Handling Ex 22
These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 22 Data Handling Ex 22
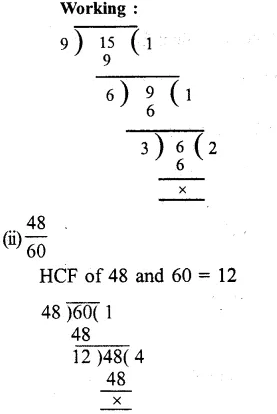
Question 1.
Solution:
(i) Data. The word data means information in the form of numerical figures.
(ii) Raw data. Data obtained in the original form is called raw data.
(iii) Array. Arranging the numerical figures (data) in an order i.e. ascending or descending order is called an array.
(iv) Tabulation of data. Arranging the given data in a systematic form in the form of a table is called tabulation of the data.
(v) Observations. Each numerical figure in a data is called an observation.
(vi) Frequency of an observation. The number of times a particular observation occurs is called its frequency.
(vii) Statistics. Statistics is a science which deals with the collection, presentation, analysis and interpretation of numerical data.
Question 2.
Solution:
Arranging the given data in ascending order, we get :
0, 0, 1, 1, 1, 1, 1, 1,2, 2, 2, 2,2, 2,2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4

Question 3.
Solution:
Below is given the frequency distribution table of the given data :

Question 4.
Solution:
Below is given the frequency distribution table of the given data :
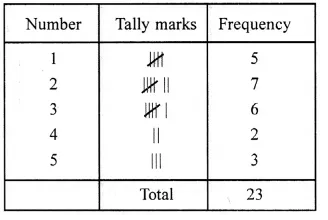
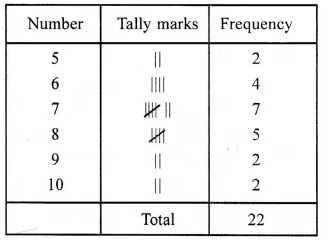
Question 5.
Solution:
Below is given the frequency distribution table of the given data
Question 6.
Solution:
(i) numerical figures
(ii) original
(iii) array
(iv) frequency
(v) tabulation
Hope given RS Aggarwal Solutions Class 6 Chapter 22 Data Handling Ex 22 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.