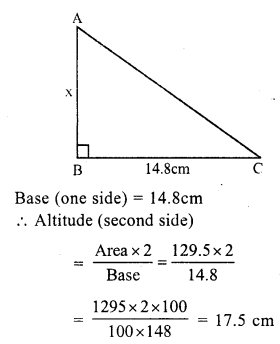
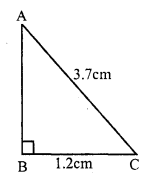
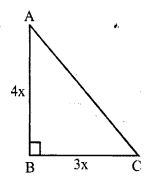
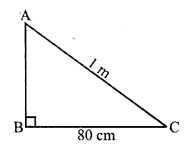
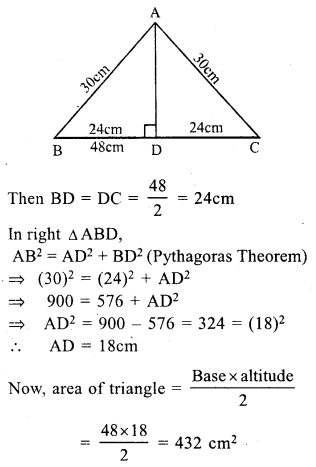
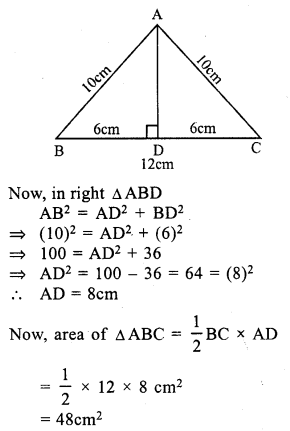
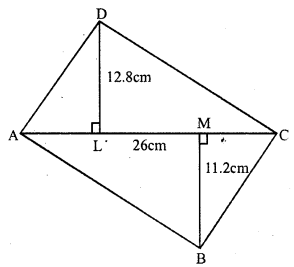
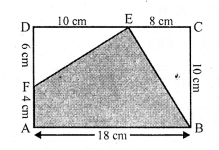
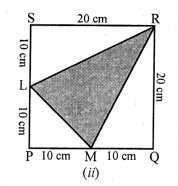
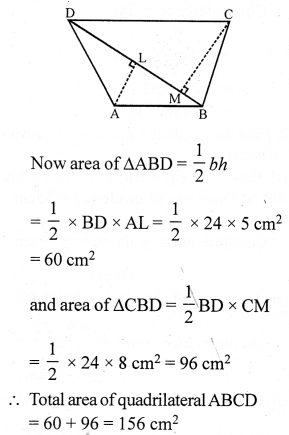
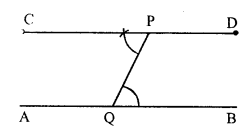
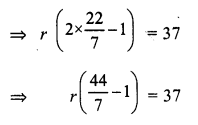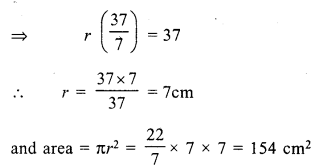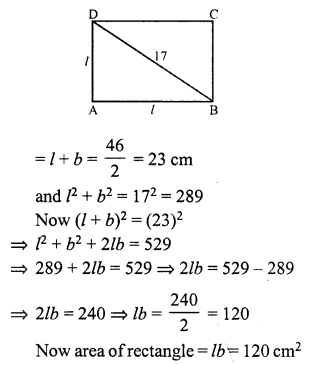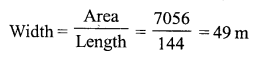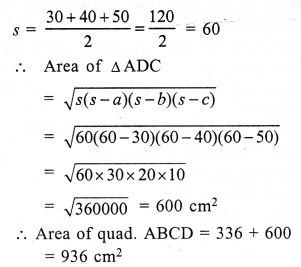RS Aggarwal Class 7 Solutions Chapter 18 Reflection and Rotational Symmetry Ex 18B
These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18B.
Other Exercises
- RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18A
- RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18B
Question 1.
Solution:
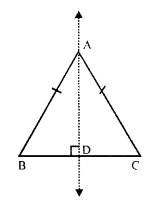
(a) An equilateral triangle has three lines of symmetry which are the angle bisectors.
(b) It has three order of rotational symmetry.
Question 2.
Solution:
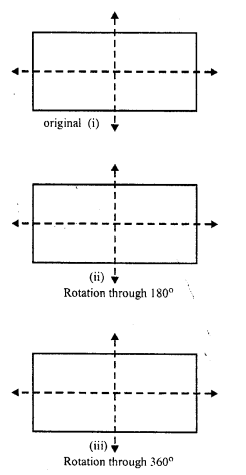
The rectangle should be rotated through 180° and 360° to be in symmetrical position with the original position as given below :
Question 3.
Solution:
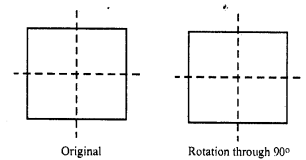
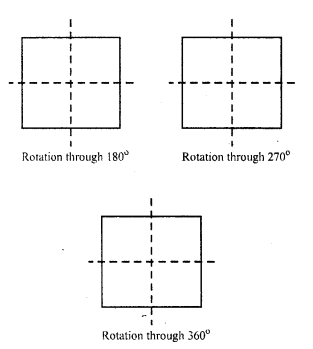
A square has four orders of rotational symmetry and angles through which the rotational symmetry are 90°, 180°, 270° and 360° as given below:
Question 4.
Solution:
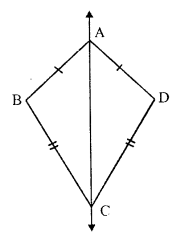
(i) A rhombus has two lines of symmetry which are its diagonal.
(ii) Order of rotational symmetry of a rhombus is not possible. Therefore it has no rotational symmetry.
Question 5.
Solution:
Three letters of the English Alphabet which have two lines of symmetry and rotational symmetry of order 2 are H, I and N.
Question 6.
Solution:
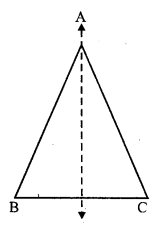
The figure which has only on line of symmetry but no rotational symmetry order is an isosceles triangle.
Question 7.
Solution:
No, only isosceles trapezium has a line of symmetry but not every trapezium.
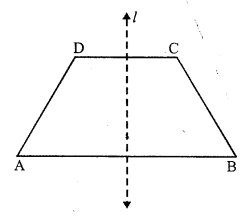
Question 8.
Solution:
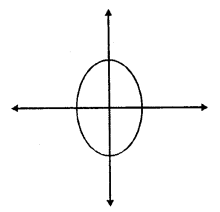
The line of symmetry of a semicircle is the perpendicular bisector of the diameter No, it has not any rotational symmetry.
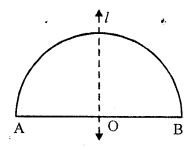
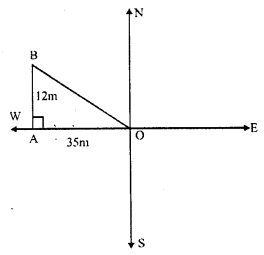
Question 9.
Solution:
A scalene triangle has neither any line of symmetry nor a rotational symmetry.
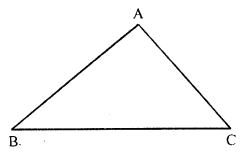
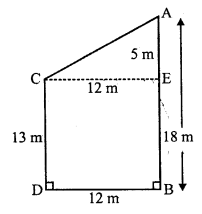
Question 10.
Solution:
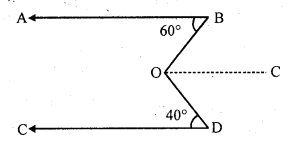
In the given figure, the line of symmetry has been drawn which is one. There is no rotational symmetry of this figure.
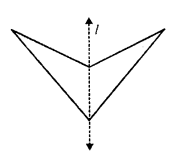
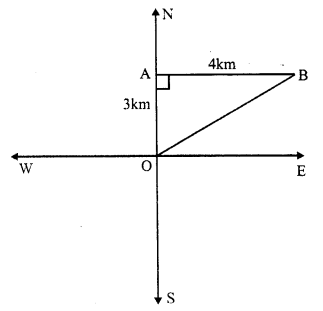
Question 11.
Solution:
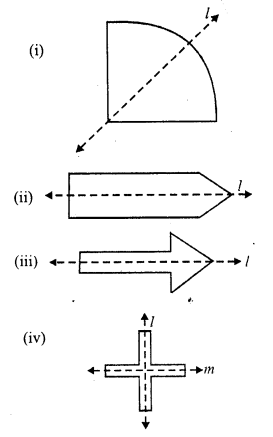
(i) The given figure has two lines of symmetry which has been drawn.
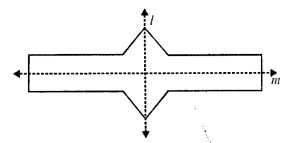
(ii) It has three orders of the rotational symmetry which are 90°, 270° and 360°.
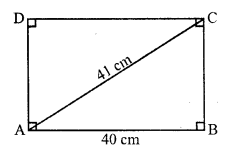
Question 12.
Solution:
There is one letter of the English Alphabet Z which has no line of symmetry but it has order two of rotational symmetry of 180° and 360°.

Hope given RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.