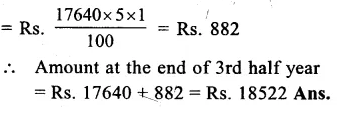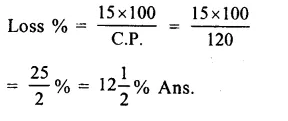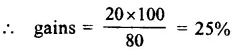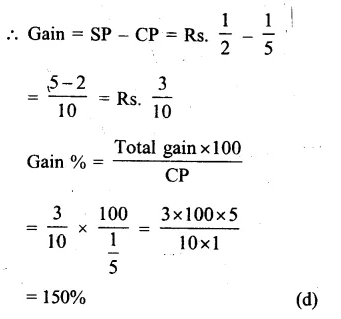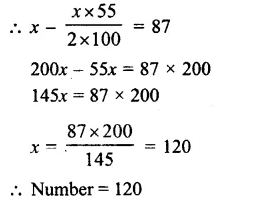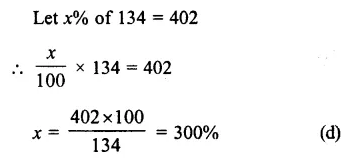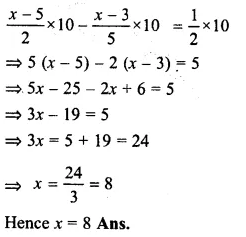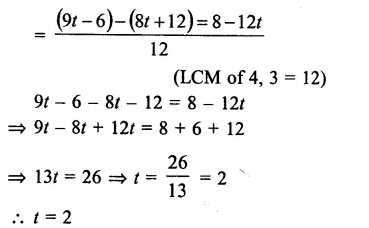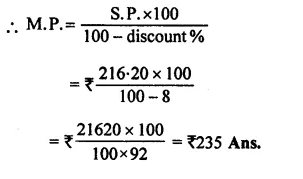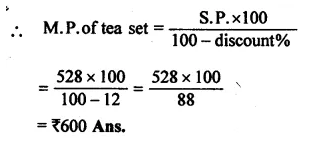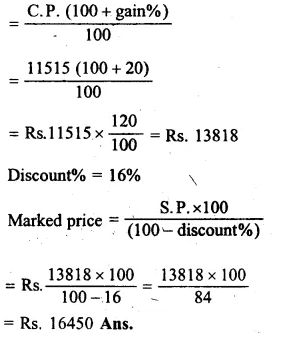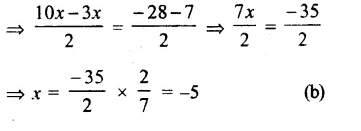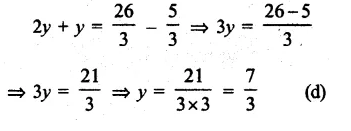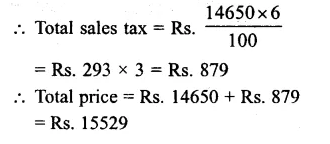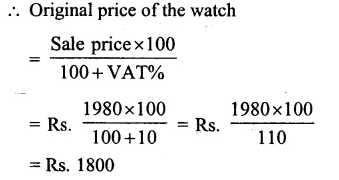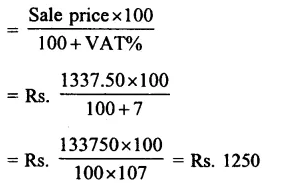RS Aggarwal Class 8 Solutions Chapter 11 Compound Interest Ex 11B
These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11B.
Other Exercises
- RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11A
- RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11B
- RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11C
- RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11D
By using the formula, find the amount and compound interest on :
Question 1.
Solution:
Principal (P) = Rs. 6000
Rate (R) = 9% p.a.
Period (n) = 2 years

Question 2.
Solution:
Principal (P) = Rs. 10000
Rate (R) = 11% p.a.
Period (n) = 2 years

You can also Download NCERT Solutions for Class 8 Maths to help you to revise complete Syllabus and score more marks in your examinations.
Question 3.
Solution:
Principal (P) = Rs. 31250
Rate (R) = 8% p.a.
Period (n) = 3 years
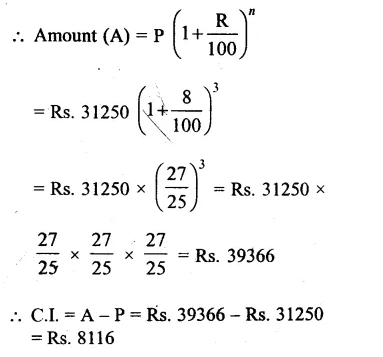
Question 4.
Solution:
Principal (P) = Rs. 10240
Rate (R) = \(12\frac { 1 }{ 2 } \)% = \(\\ \frac { 25 }{ 2 } \)% p.a.
Period (n) = 3 years

Question 5.
Solution:
Principal (P) = Rs. 62500
Rate (R) = 12% p.a.
Period (n) = 2 years 6 months

Question 6.
Solution:
Principal (P) = Rs. 9000
Rate (R) = 10% p.a.
Period (n) = 2 years 4 months
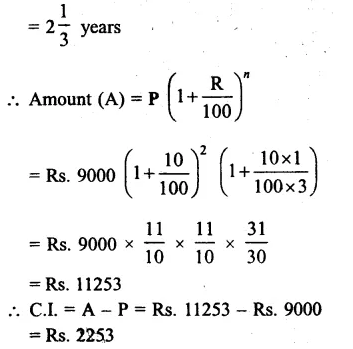
Question 7.
Solution:
Principal (P) = Rs. 8000
Period (n) = 2 years

Question 8.
Solution:
Principal (p) = Rs. 1, 25,000
Rate of interest (r) = 8% p.a.
Period (n) = 3 years
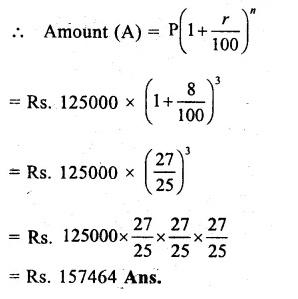
Question 9.
Solution:
Price of a buffalo (P) = Rs. 11000
Rate of interest (R) = 10% p.a.
Period (n) = 3 years
Price of buffalo at present
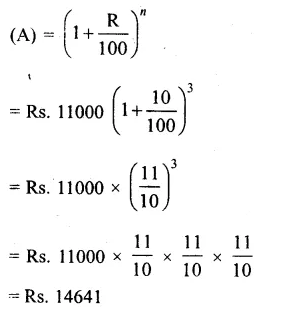
Question 10.
Solution:
Amount of loan taken (P)
= Rs. 18000

Question 11.
Solution:
Amount borrowed from Bank (P) = Rs. 24000
Rate (R) = 10% p.a.
Period (n) = 2 years 3 months

Question 12.
Solution:
In case of Abhay,
Principal (p) = Rs. 16000


Question 13.
Solution:
Simple interest (S.I.) = Rs. 2400
Rate (R) = 8% p.a.
Period (T) = 2 years

Question 14.
Solution:
Difference between C.I. and S.I.
= Rs. 90
Rate (R) = 6% p.a.
Period (n) = 2 years
Let principal (P) = Rs. 100


Question 15.
Solution:
Let sum (p) = Rs. 100
Rate (r) 10% p.a.
Period (t) = 3 years.


Question 16.
Solution:
Amount (A) = Rs. 10240
Rate (r) = \(6\frac { 2 }{ 3 } \)% = \(\\ \frac { 20 }{ 3 } \)% p.a.
Period (n) = 2 years
Let sum = P, then
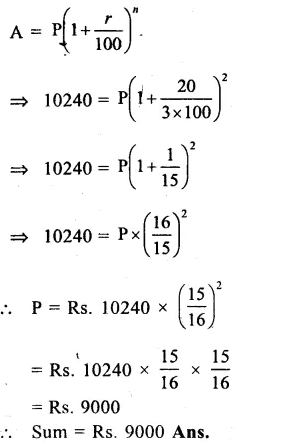
Question 17.
Solution:
Amount (A) = Rs. 21296
Rate (r) = 10% p.a.
Period (n) = 3 years.
Let P be the sum, Then
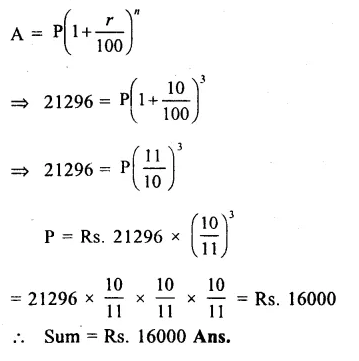
Question 18.
Solution:
Principal (P) = 4000
Amount (A) = Rs. 4410
Period (n) = 2 years
Let r be the rate per cent per annum
We know that,
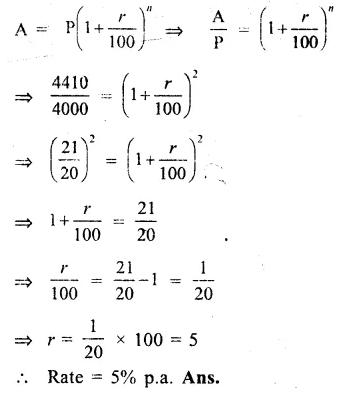
Question 19.
Solution:
Principal (P) = Rs. 640
Amount (A) = Rs. 774.40
Period (n) = 2 years
Let r be the rate per cent per annum.
We know that
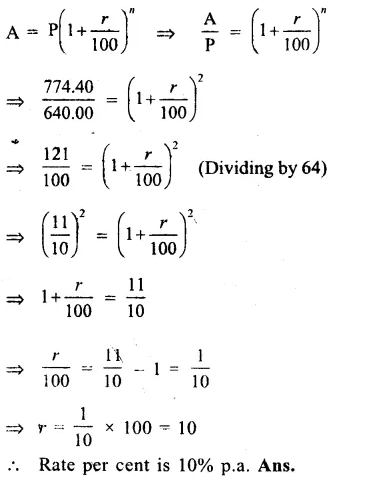
Question 20.
Solution:
Principal (P) = Rs. 1800
Amount (A) = Rs. 2178
Rate (r) = 10% p.a.
Let n be the number of years,
We know that
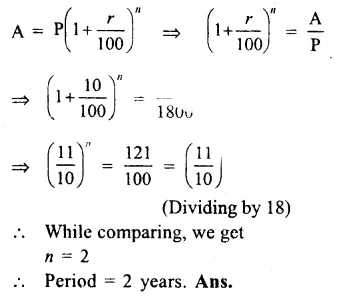
Question 21.
Solution:
Principal (P) = Rs. 6250
Amount (A) = Rs. 7290
Rate (R) = 8% p.a.
Let n be the time, then
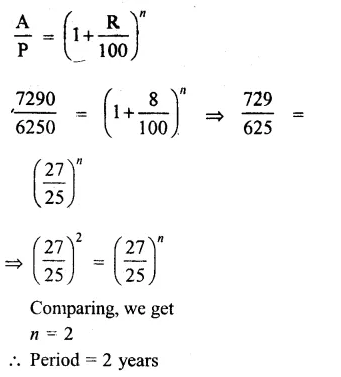
Question 22.
Solution:
Present population (P) = 125000
Rate of increasing (R) = 2% p.a.
Period (n) = 3 years
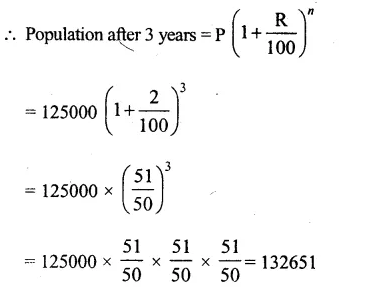
Question 23.
Solution:
3 years ago, the population was = 50000
Rate of increase successively (r1, r2, r3) = 4%, 5% and 3% p.a.
Period (n) = 3 years
Present Population
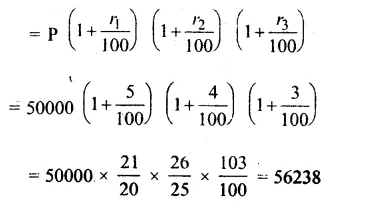
Question 24.
Solution:
Population of a city in 2013 = 120000
Increase in next year = 6%
and decrease in the following year = 5%
Population in 2015
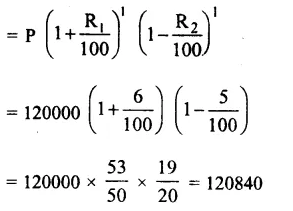
Question 25.
Solution:
Initially bacteria = 500000
Increase in bacteria = 2% per hour
Period (n) = 2 hours

Question 26.
Solution:
Growth of bacteria in a culture (R1) = 10% in first hour
Decrease in next hour (R2) = 10%
Increase in the third hour (R3) = 10%
Bacteria in the beginning = 20000
Bacteria after 3 hours
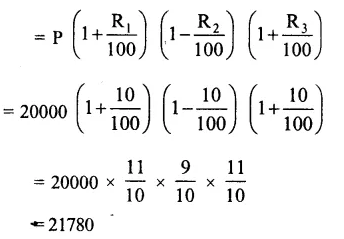
Question 27.
Solution:
Value of machine (P) = Rs. 625000
Rate of depreciation (R) = 8% p.a.
Period (n) = 2 years
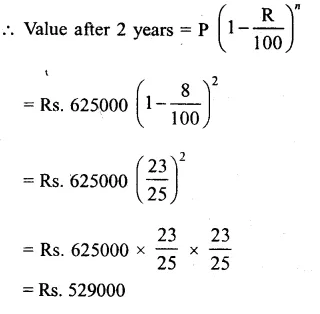
Question 28.
Solution:
Value of scooter (P) = Rs. 56000
Rate of depreciation (R) = 10% p.a.
Period = 3 years
Value of scooter after 3 years

Question 29.
Solution:
Cost of car = Rs. 34800
Rate of depreciation (R1) = 10% p.a. for first year
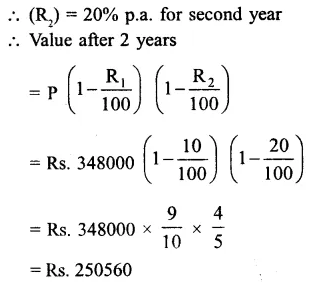
Question 30.
Solution:
Rate of depreciation (R) = 10% p.a.
Period (n) = 3 years
Present value (A) = Rs. 291600
Value of machine 3 years ago
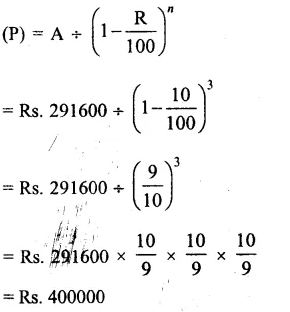
Hope given RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.