Tag: ML Aggarwal Maths for Class 10 ICSE Solutions Pdf Download

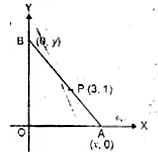
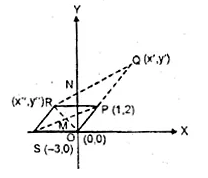
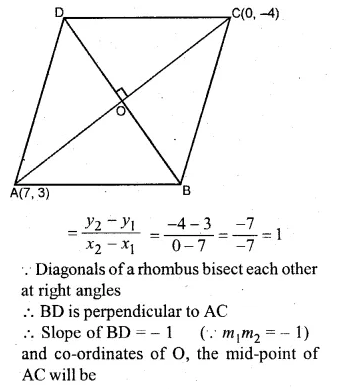
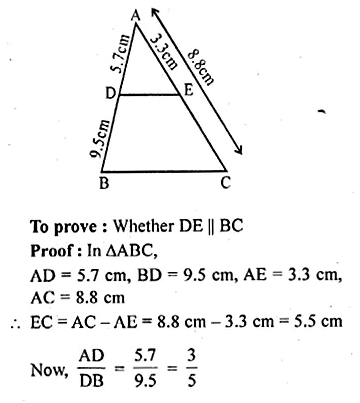
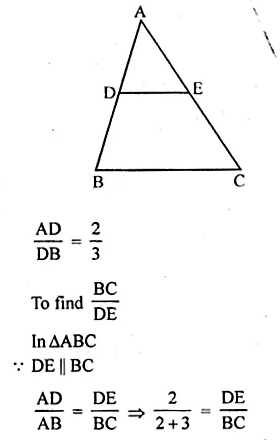
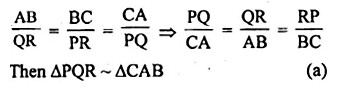
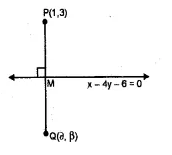
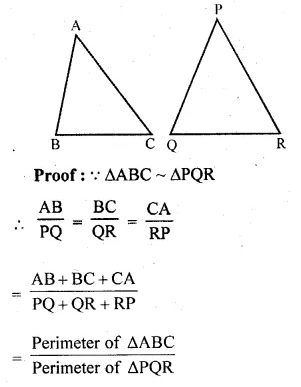
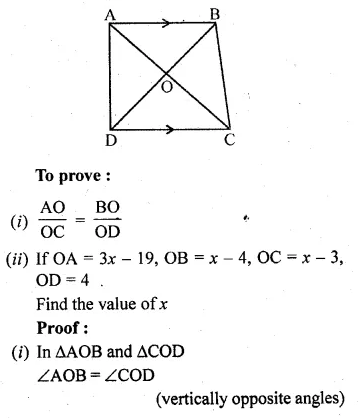
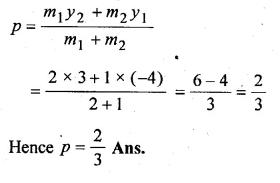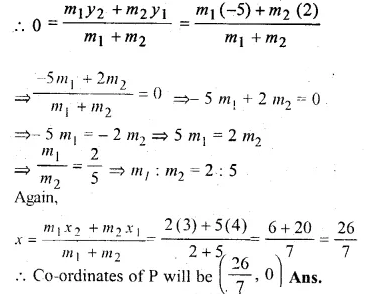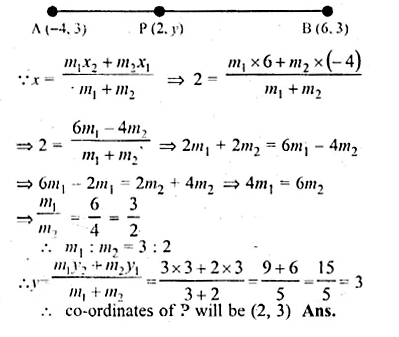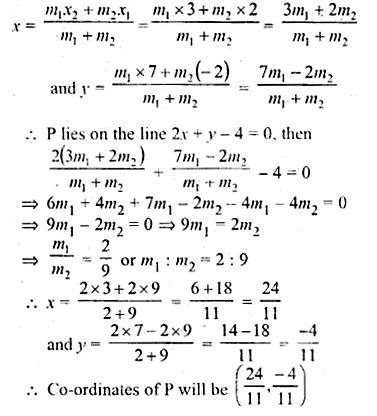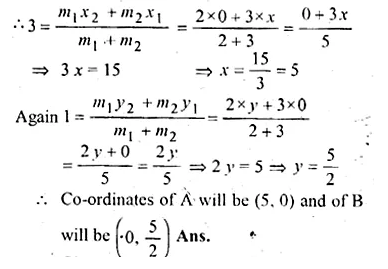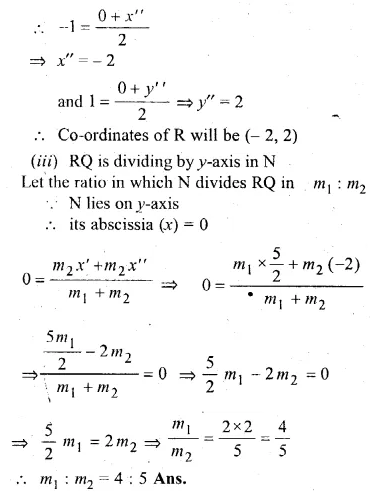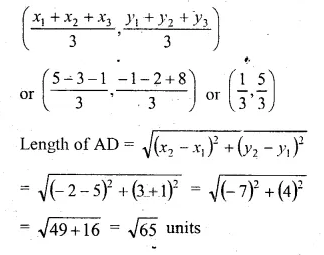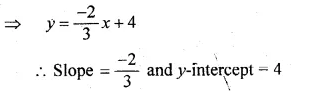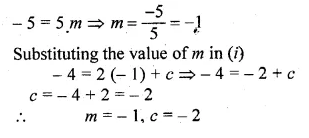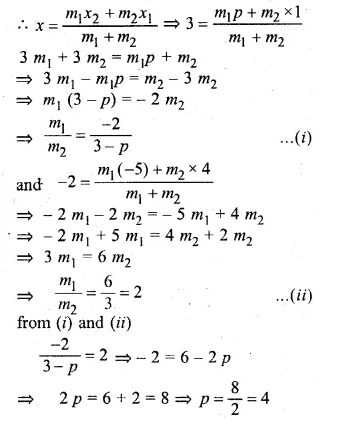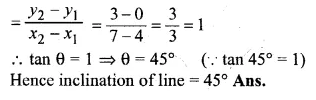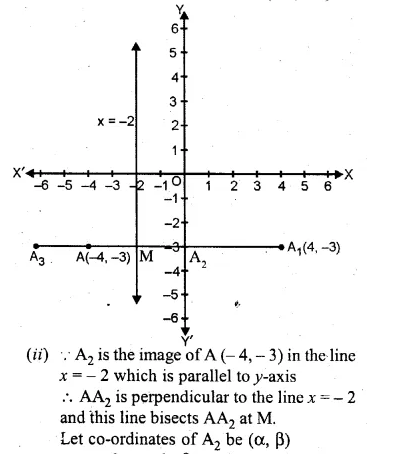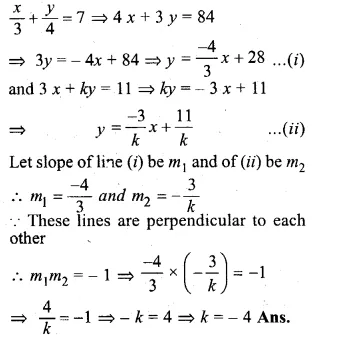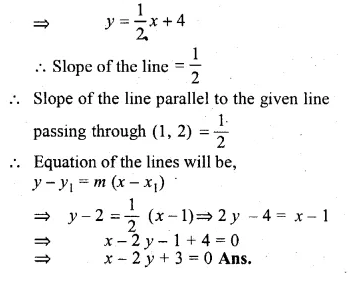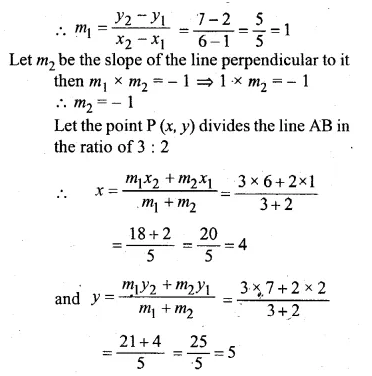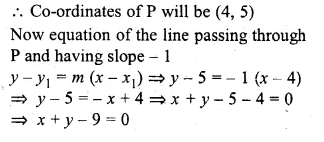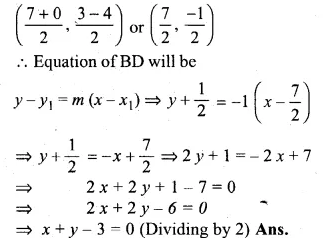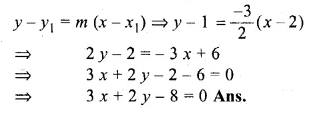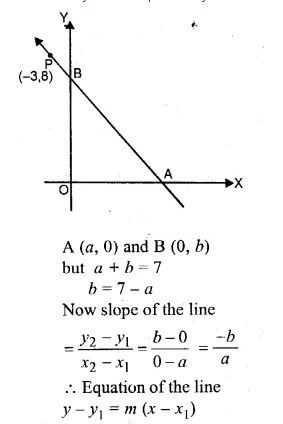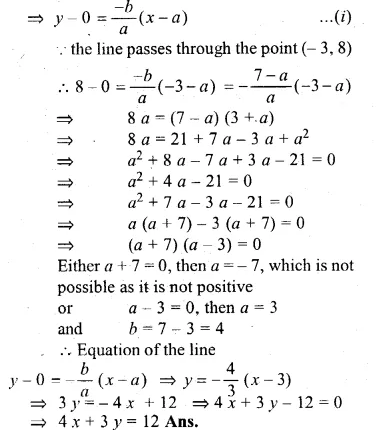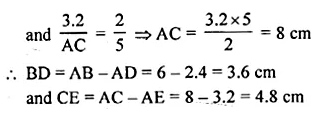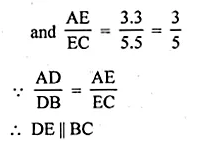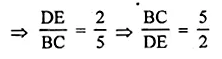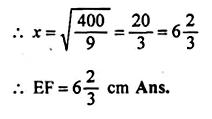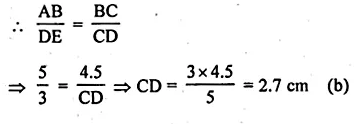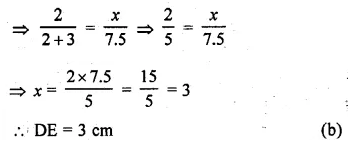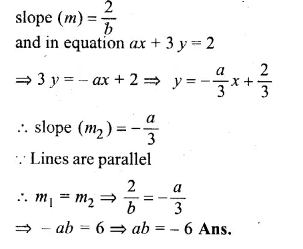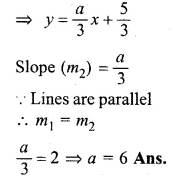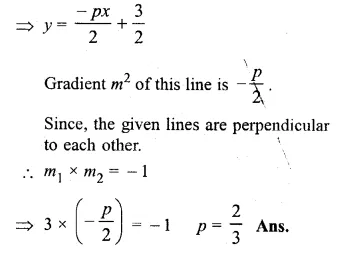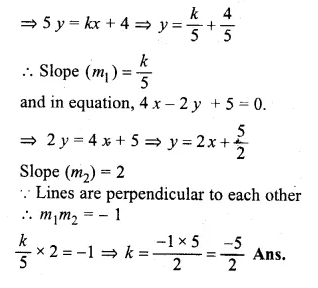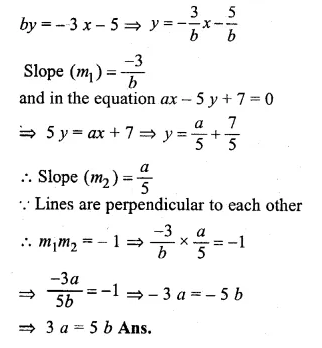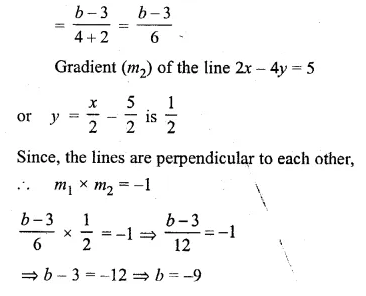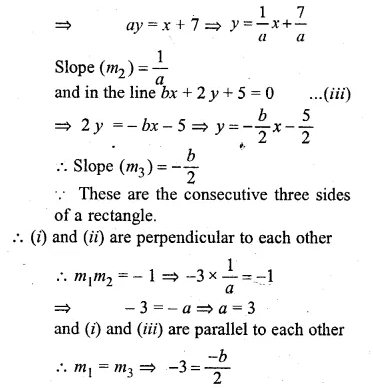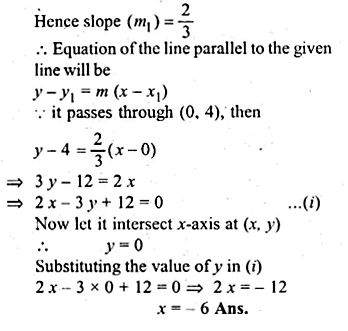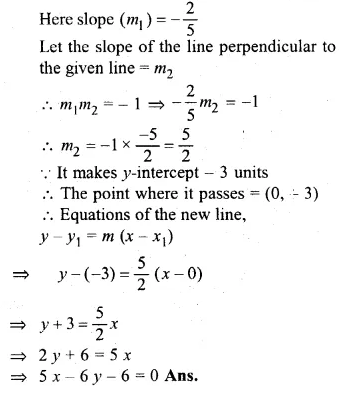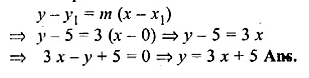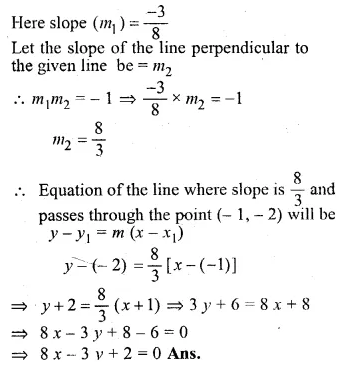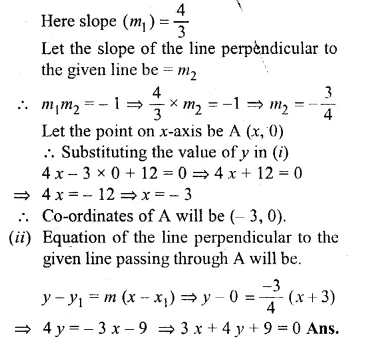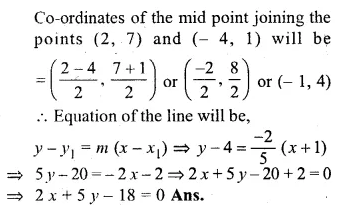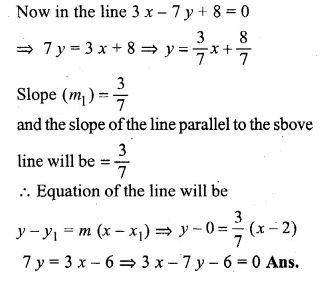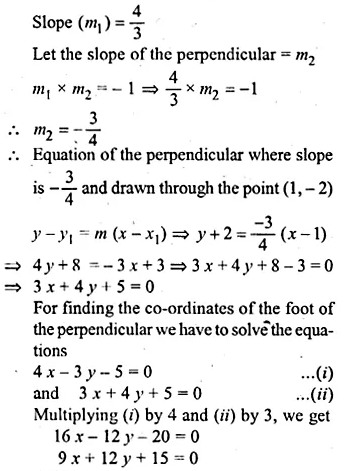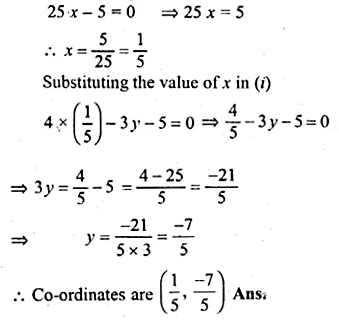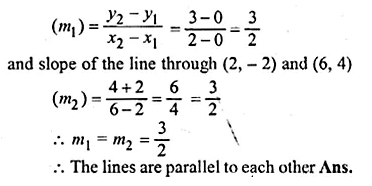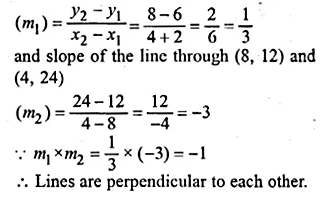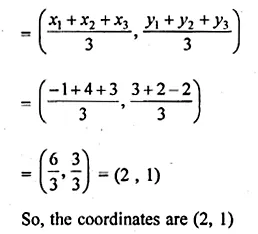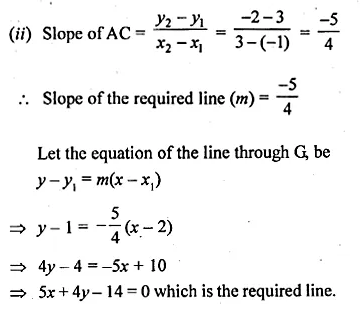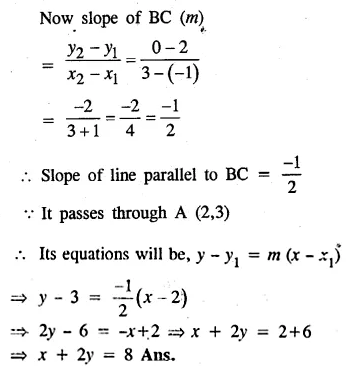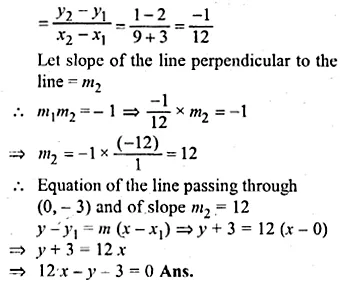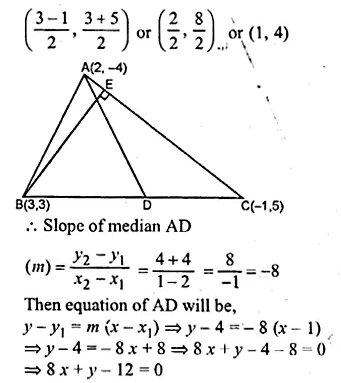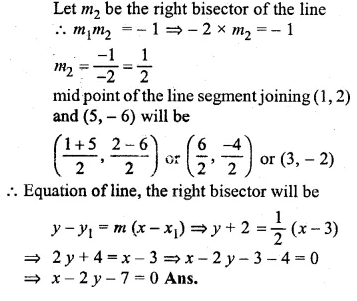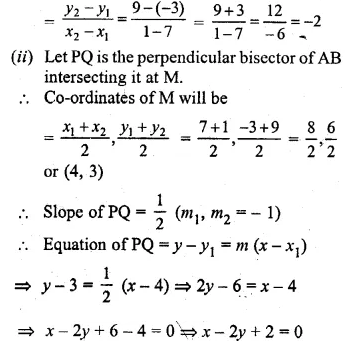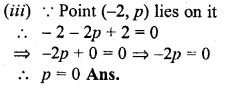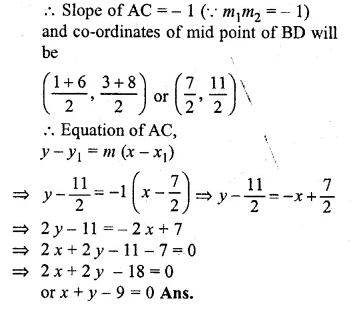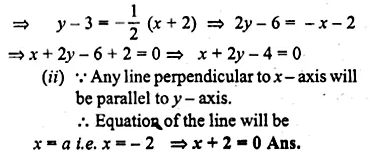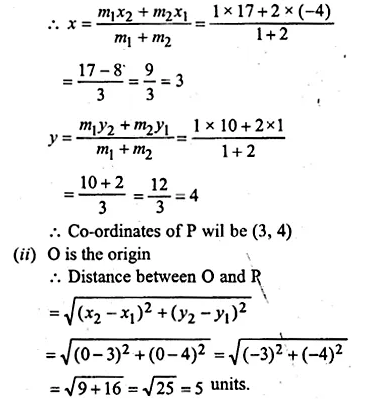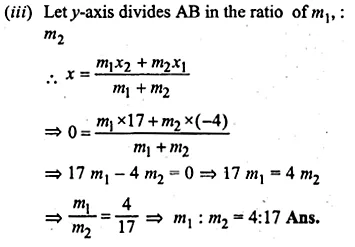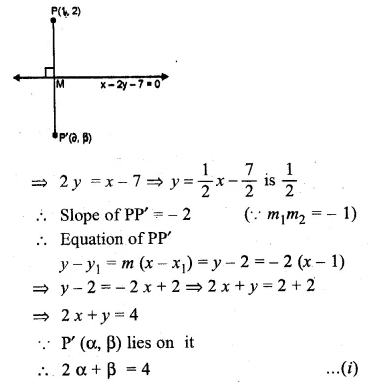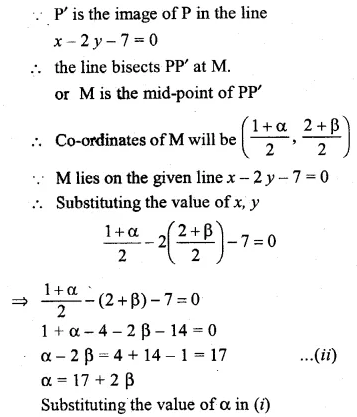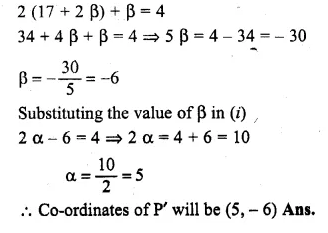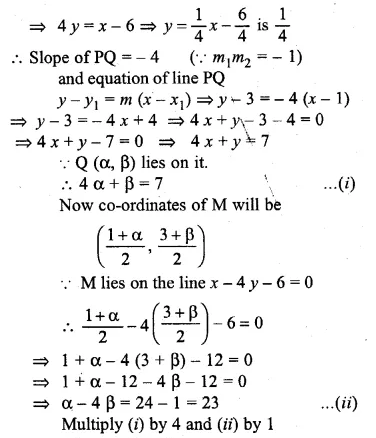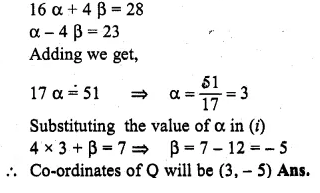ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Chapter Test

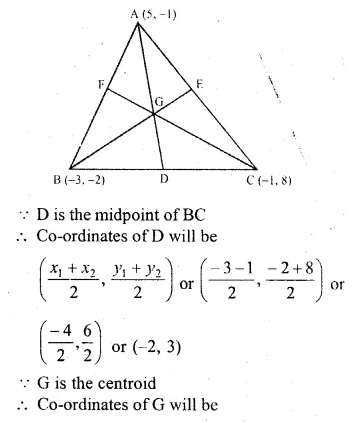
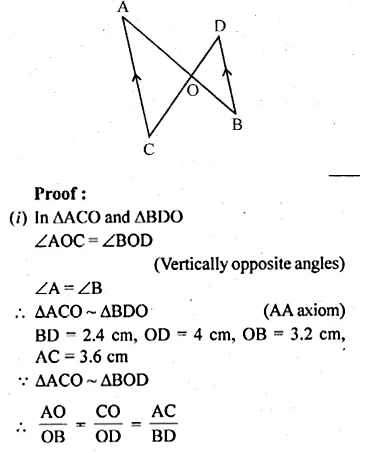
Question 1.
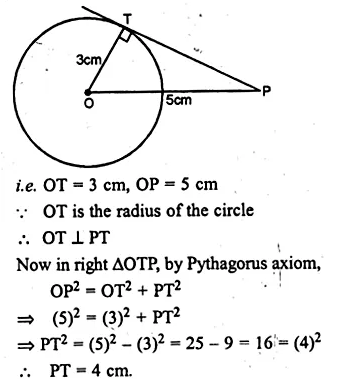
Find the length of the tangent drawn to a circle of radius 3 cm, from a point distant 5 cm from the centre.
Solution:
In a circle with centre O and radius 3 cm
and P is at a distance of 5 cm.

Question 2.
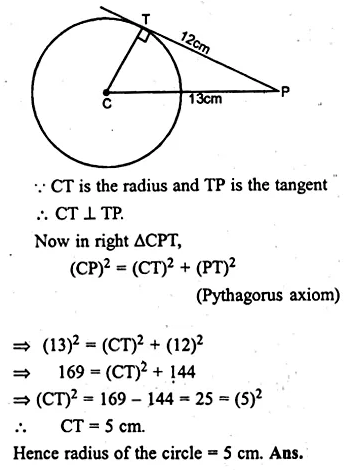
A point P is at a distance 13 cm from the centre C of a circle and PT is a tangent to the given circle. If PT = 12 cm, find the radius of the circle.
Solution:
CT is the radius
CP = 13 cm and tangent PT = 12 cm

Question 3.
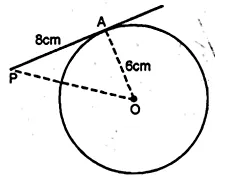
The tangent to a circle of radius 6 cm from an external point P, is of length 8 cm. Calculate the distance of P from the nearest point of the circle.

Solution:
Radius of the circle = 6 cm
and length of tangent = 8 cm
Let OP be the distance
i.e. OA = 6 cm, AP = 8 cm .
OA is the radius

Question 4.
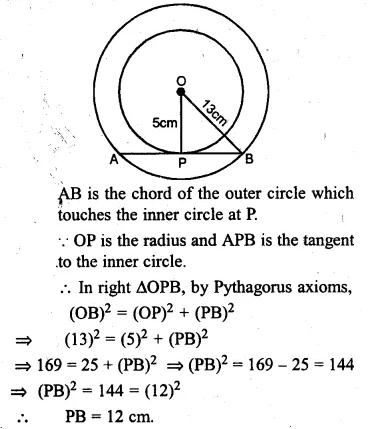
Two concentric circles are of the radii 13 cm and 5 cm. Find the length of the chord of the outer circle which touches the inner circle.
Solution:
Two concentric circles with centre O
OP and OB are the radii of the circles respectively, then
OP = 5 cm, OB = 13 cm.

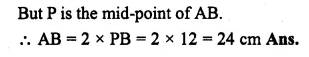
Question 5.
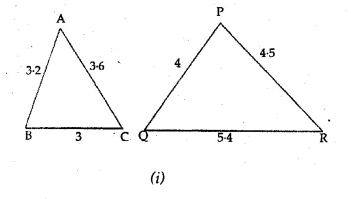
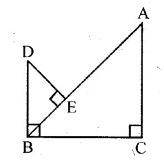
Two circles of radii 5 cm and 2-8 cm touch each other. Find the distance between their centres if they touch :
(i) externally
(ii) internally.
Solution:
Radii of the circles are 5 cm and 2.8 cm.
i.e. OP = 5 cm and CP = 2.8 cm.

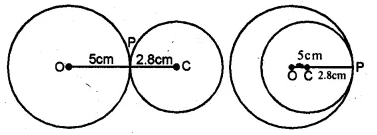
(i) When the circles touch externally,
then the distance between their centres = OC = 5 + 2.8 = 7.8 cm.
(ii) When the circles touch internally,
then the distance between their centres = OC = 5.0 – 2.8 = 2.2 cm

Question 6.
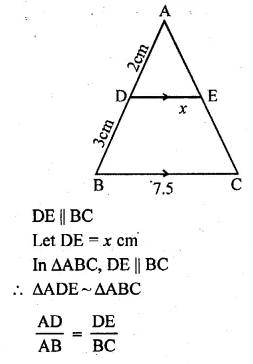
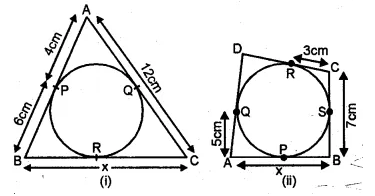
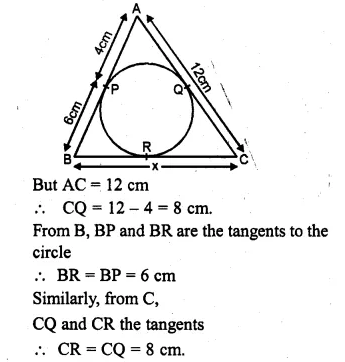
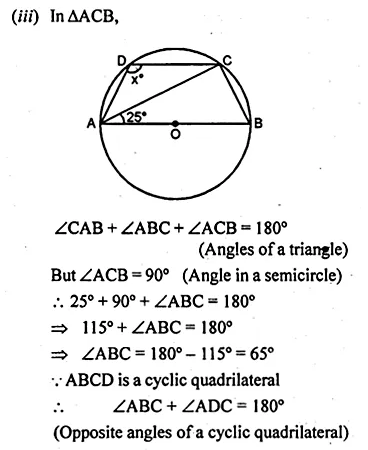
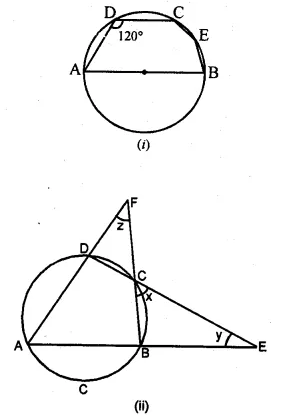
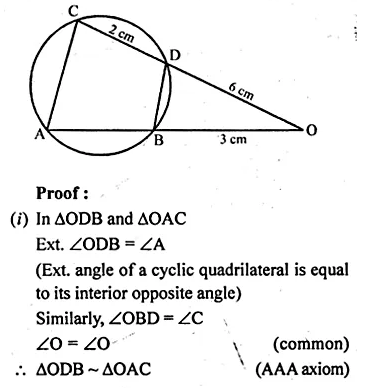
(a) In figure (i) given below, triangle ABC is circumscribed, find x.
(b) In figure (ii) given below, quadrilateral ABCD is circumscribed, find x.

Solution:
(a) From A, AP and AQ are the tangents to the circle
∴ AQ = AP = 4cm

Question 7.
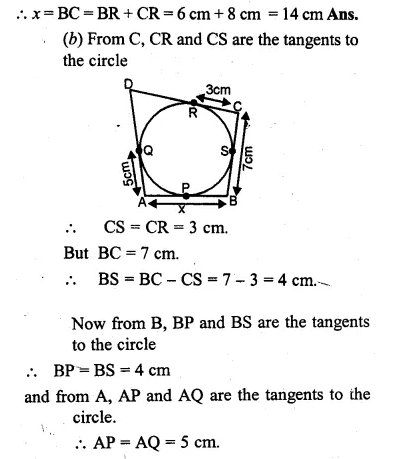
(a) In figure (i) given below, quadrilateral ABCD is circumscribed; find the perimeter of quadrilateral ABCD.
(b) In figure (ii) given below, quadrilateral ABCD is circumscribed and AD ⊥ DC ; find x if radius of incircle is 10 cm.

Solution:
(a) From A, AP and AS are the tangents to the circle
∴AS = AP = 6
From B, BP and BQ are the tangents
∴BQ = BP = 5
From C, CQ and CR are the tangents

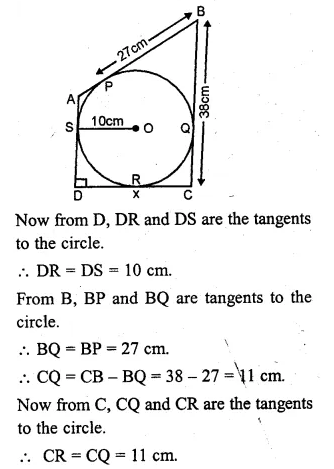
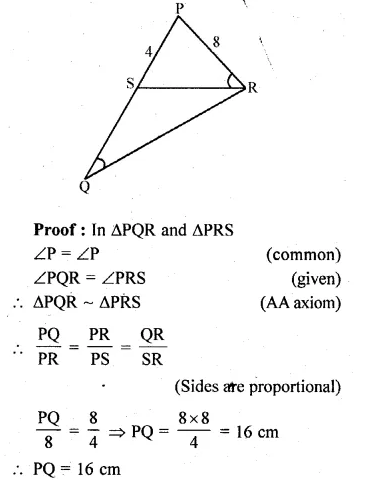
Question 8.
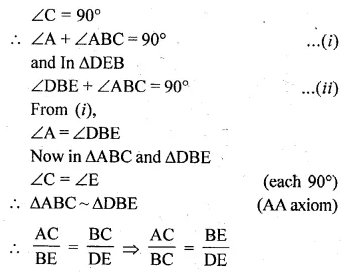
(a) In the figure (i) given below, O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, find the radius of the circle.
(b) In the figure (ii) given below, from an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D. If AP = 15 cm, find the perimeter of the triangle PEC.

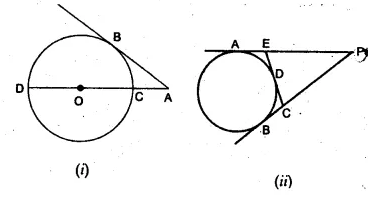
Solution:
(i) Join OB
∠OBA = 90°
(Radius through the point of contact is
perpendicular to the tangent)

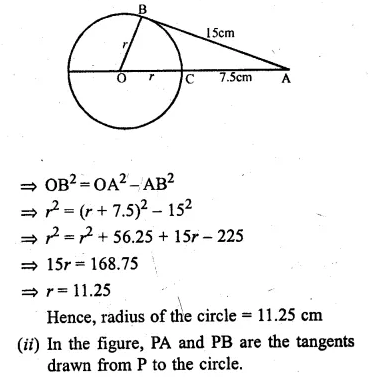
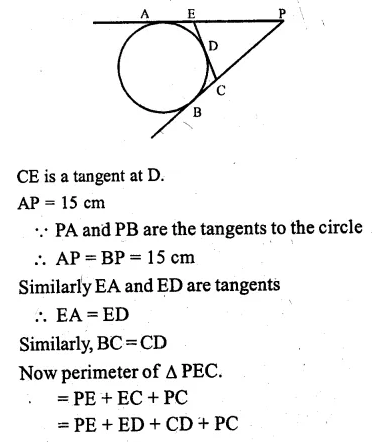
Question 9.
(a) If a, b, c are the sides of a right triangle where c is the hypotenuse, prove that the radius r of the circle which touches the sides of the triangle is given by
\(r= \frac { a+b-c }{ 2 } \)
(b) In the given figure, PB is a tangent to a circle with centre O at B. AB is a chord of length 24 cm at a distance of 5 cm from the centre. If the length of the tangent is 20 cm, find the length of OP.

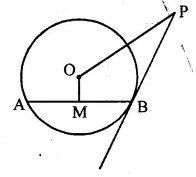
Solution:
(a) Let the circle touch the sides BC, CA and AB
of the right triangle ABC at points D, E and F respectively,
where BC = a, CA = b
and AB = c (as showing in the given figure).

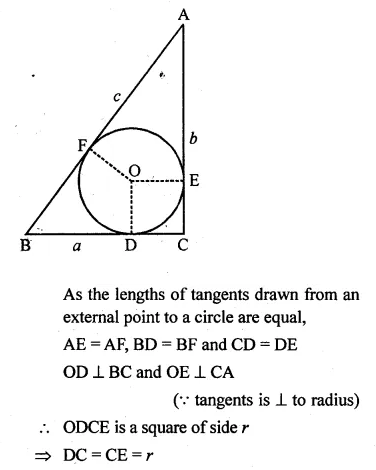
Question 10.
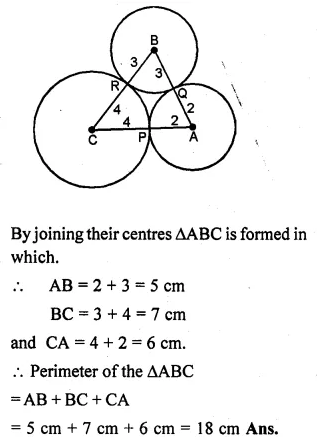
Three circles of radii 2 cm, 3 cm and 4 cm touch each other externally. Find the perimeter of the triangle obtained on joining the centres of these circles.
Solution:
Three circles with centres A, B and C touch each other externally
at P, Q and R respectively and the radii of these circles are
2 cm, 3 cm and 4 cm.

Question 11.
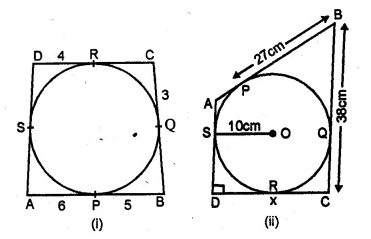
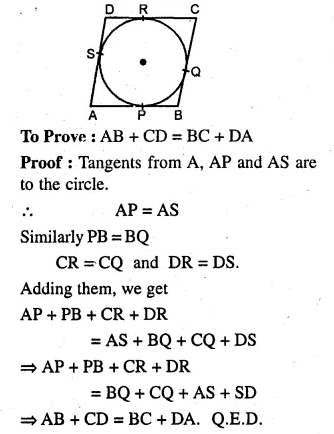
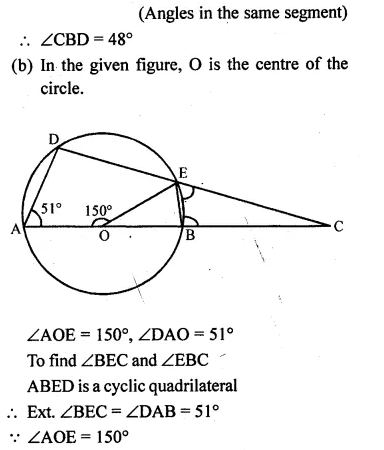
(a) In the figure (i) given below, the sides of the quadrilateral touch the circle. Prove that AB + CD = BC + DA.
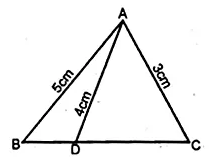
(b) In the figure (ii) given below, ABC is triangle with AB = 10cm, BC = 8cm and AC = 6cm (not drawn to scale). Three circles are drawn touching each other with vertices A, B and C as their centres. Find the radii of the three circles

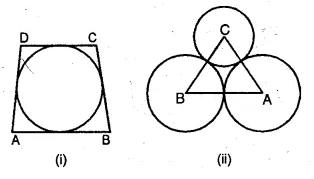
Solution:
(a) Given: Sides of quadrilateral ABCD touch the circle at
P, Q, R and S respectively.

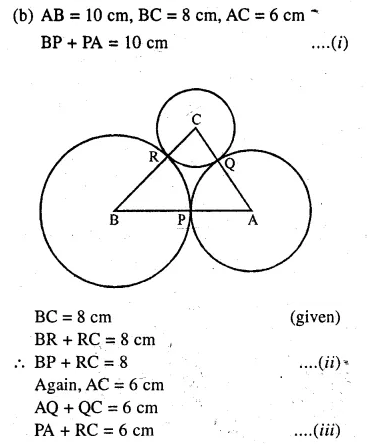
Question 12.
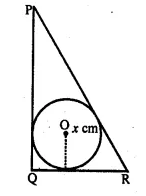
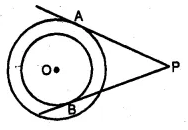
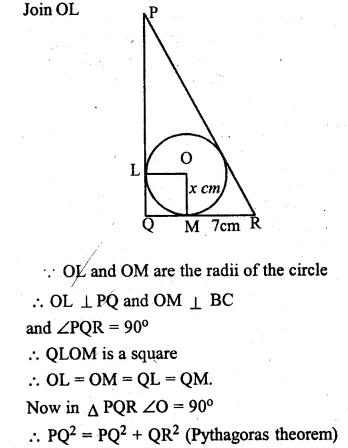
(a) ln the figure (i) PQ = 24 cm, QR = 7 cm and ∠PQR = 90°. Find the radius of the inscribed circle ∆PQR

(b) In the figure (ii) given below, two concentric circles with centre O are of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.

Solution:
(a) In the figure, a circle is inscribed in the triangle PQR
which touches the sides. O is centre of the circle.
PQ = 24cm, QR = 7 cm ∠PQR = 90°
OM is joined.

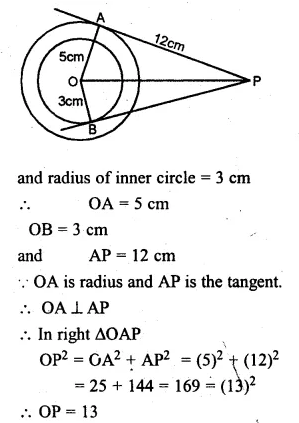
Question 13.
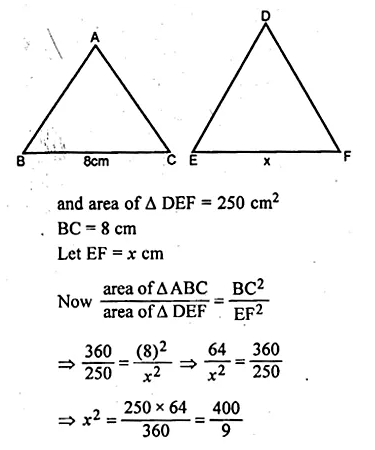
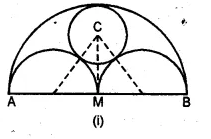
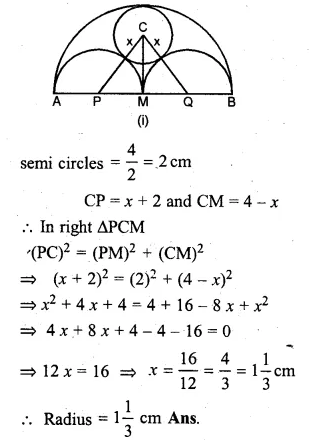
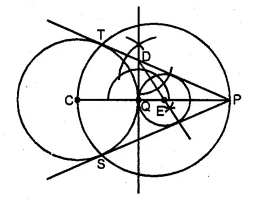
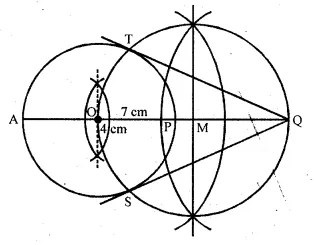
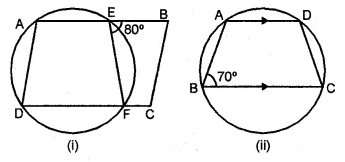
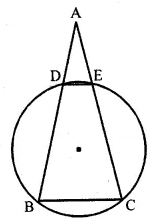
(a) In the figure (i) given below, AB = 8 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all three semi-circles as shown, find its radius.

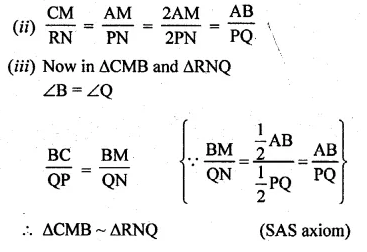
(b) In the figure (ii) given below, equal circles with centres O and O’ touch each other at X. OO’ is produced to meet a circle O’ at A. AC is tangent to the circle whose centre is O. O’D is perpendicular to AC. Find the value of :
(i) \(\\ \frac { AO’ }{ AO } \)
(ii) \(\frac { area\quad of\quad \Delta ADO’ }{ area\quad of\quad \Delta ACO } \)

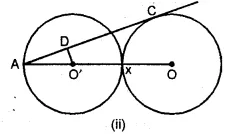
Solution:
(a) Let x be the radius of the circle
with centre C and radii of each equal

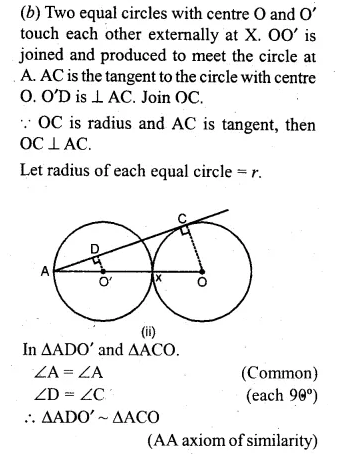
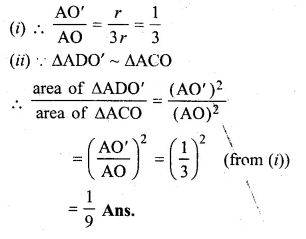
Question 14.
The length of the direct common tangent to two circles of radii 12 cm and 4 cm is 15 cm. Calculate the distance between their centres.
Solution:
Let R and r be the radii of the circles
with centre A and B respectively
Let TT’ be their common tangent.

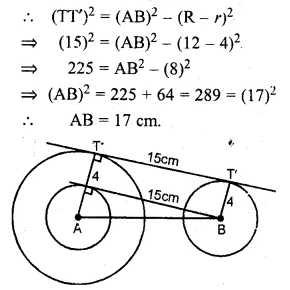
Hence distance between their centres = 17 cm Ans.

Question 15.
Calculate the length of a direct common tangent to two circles of radii 3 cm and 8 cm with their centres 13 cm apart.
Solution:
Let A and B be the centres of the circles
whose radii are 8 cm and 3 cm and
let TT’ length of their common tangent and AB = 13 cm.

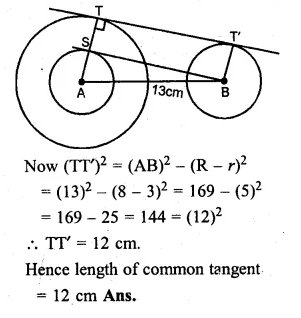
Question 16.
In the given figure, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.

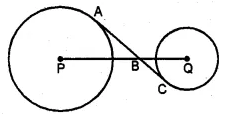
Solution:
AC is a transverse common tangent to the two circles
with centre P and Q and of radii 6 cm and 3 cm respectively
AB = 8 cm. Join AP and CQ.

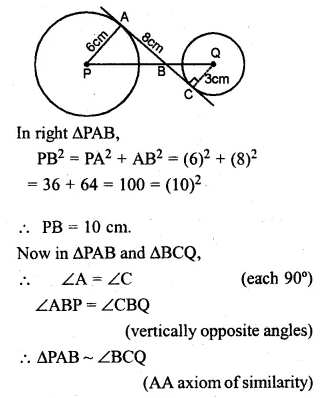
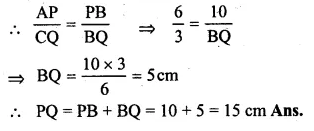
Question 17.
Two circles with centres A, B are of radii 6 cm and 3 cm respectively. If AB = 15 cm, find the length of a transverse common tangent to these circles.
Solution:
AB = 15 cm.
Radius of the circle with centre A = 6 cm
and radius of second circle with radius B = 3 cm.

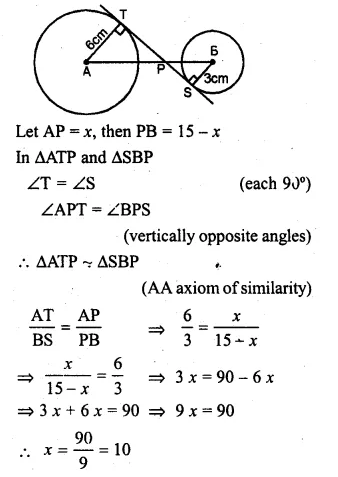
Question 18.
(a) In the figure (i) given below, PA and PB are tangents at a points A and B respectively of a circle with centre O. Q and R are points on the circle. If ∠APB = 70°, find (i) ∠AOB (ii) ∠AQB (iii) ∠ARB
(b) In the figure (ii) given below, two circles touch internally at P from an external point Q on the common tangent at P, two tangents QA and QB are drawn to the two circles. Prove that QA = QB.

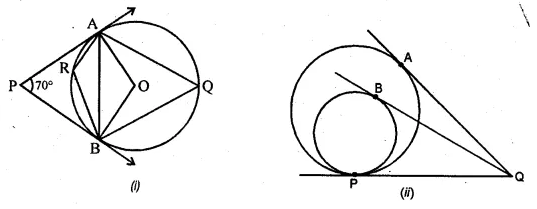
Solution:
(a) To find : (i) ∠AOB, (ii) ∠AQB, (iii) ∠ARB
Given: PA and PB are tangents at the points A and B respectively
of a circle with centre O and OA and OB are radii on it.
∠APB = 70°
Construction: Join AB

Question 19.
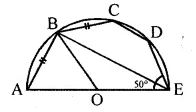
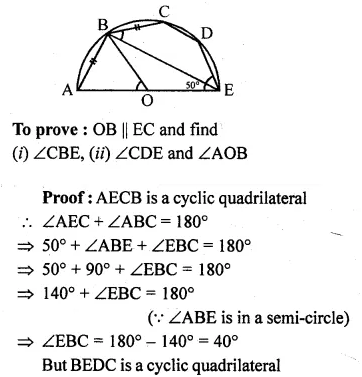
In the given figure, AD is a diameter of a circle with centre O and AB is tangent at A. C is a point on the circle such that DC produced intersects the tangent of B. If ∠ABC = 50°, find ∠AOC.

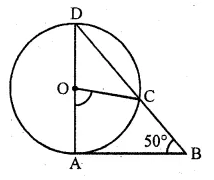
Solution:
Given AB is tangent to the circle at A and OA is radius, OA ⊥ AB
In ∆ABD

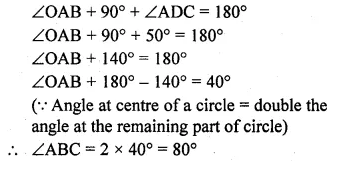
Question 20.
In the given figure, tangents PQ and PR are drawn from an external point P to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, Find ∠RQS

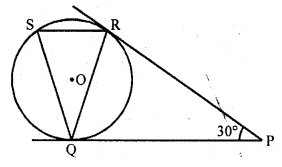
Solution:
In the given figure,
PQ and PR are tangents to the circle with centre O drawn from P
∠RPQ = 30°
Chord RS || PQ is drawn
To find ∠RQS
∴ PQ = PR (tangents to the circle)

Question 21.
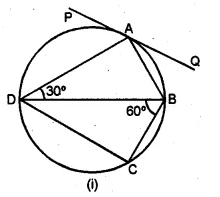
(a) In the figure (i) given below, PQ is a tangent to the circle at A, DB is a diameter, ∠ADB = 30° and ∠CBD = 60°, calculate (i) ∠QAB (ii) ∠PAD (iii) ∠CDB.

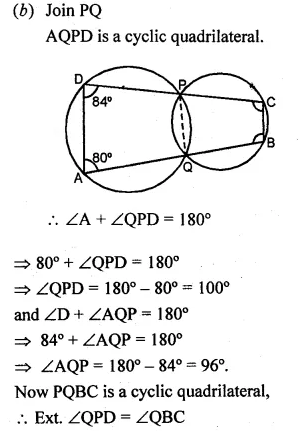
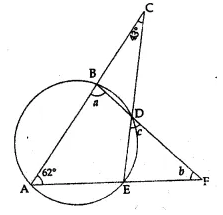
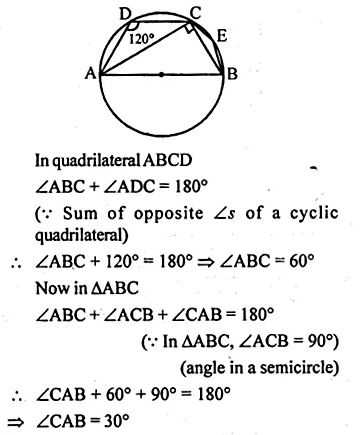
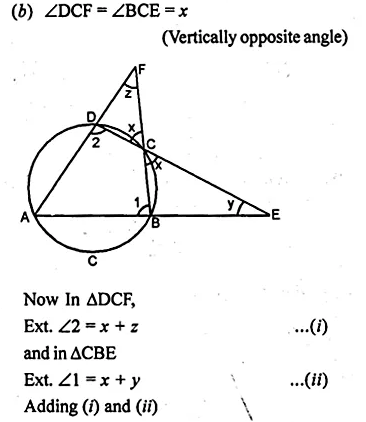
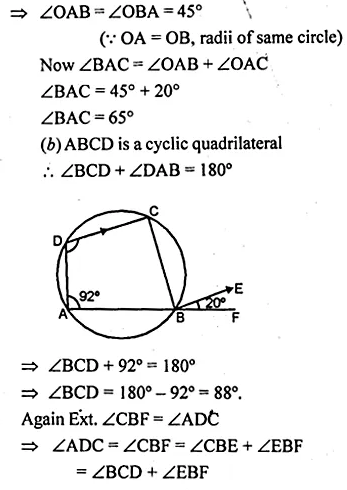
(b) In the figure (ii) given below, ABCD is a cyclic quadrilateral. The tangent to the circle at B meets DC produced at F. If ∠EAB = 85° and ∠BFC = 50°, find ∠CAB.

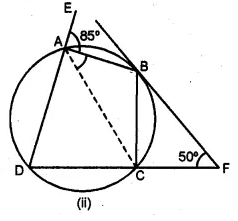
Solution:
(a) PQ is tangent and AD is chord
(i) ∴ ∠QAB = ∠BDA = 30°
(Angles in the alternate segment)
(ii) In ∆ADB,
∠DAB = 90° (Angle in a semi-circle)



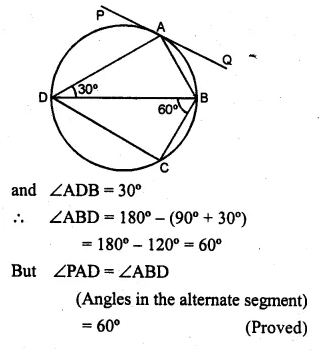
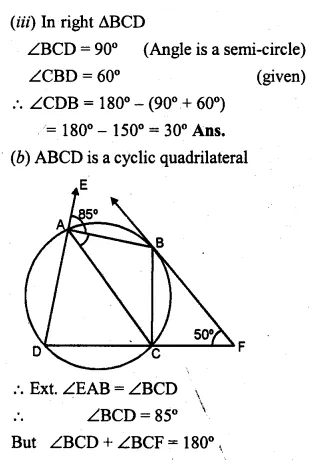
⇒ ∠CAB = 35°

Question 22.
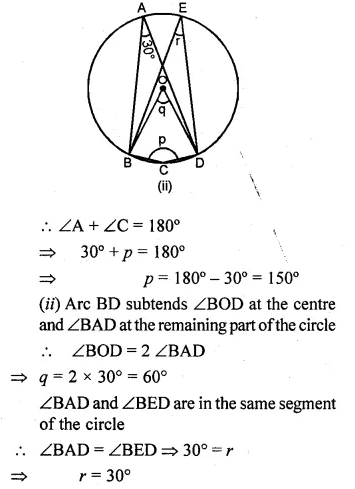
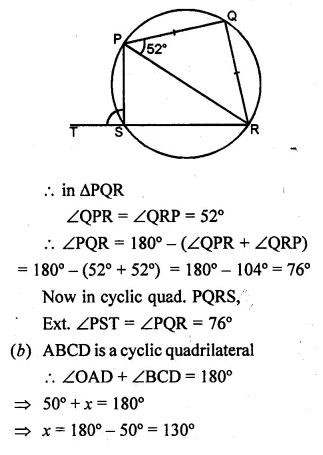
(a) In the figure (i) given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and z. (2015)
(b) In the figure (ii) given below, O is the centre of the circle. PS and PT are tangents and ∠SPT = 84°. Calculate the sizes of the angles TOS and TQS.

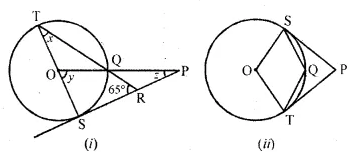
Solution:
Consider the following figure:
TS ⊥ SP,
∠TSR = ∠OSP = 90°
In ∆TSR,
∠TSR + ∠TRS + ∠RTS = 180°

Question 23.
In the given figure, O is the centre of the circle. Tangents to the circle at A and B meet at C. If ∠ACO = 30°, find
(i) ∠BCO (ii) ∠AOR (iii) ∠APB

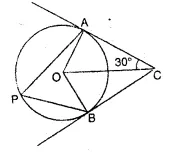
Solution:
(i) ∠BCO = ∠ACO = 30°
(∵ C is the intersecting point of tangent AC and BC)
(ii) ∠OAC = ∠OBC = 90°
∵∠AOC = ∠BOC = 180° – (90° + 30°) = 60°
(∵ sum of the three angles a ∆ is 180°)

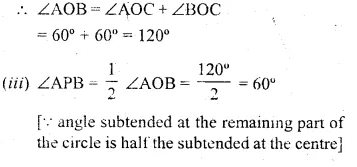
Question 24.
(a) In the figure (i) given below, O is the centre of the circle. The tangent at B and D meet at P. If AB is parallel to CD and ∠ ABC = 55°. find: (i)∠BOD (ii) ∠BPD
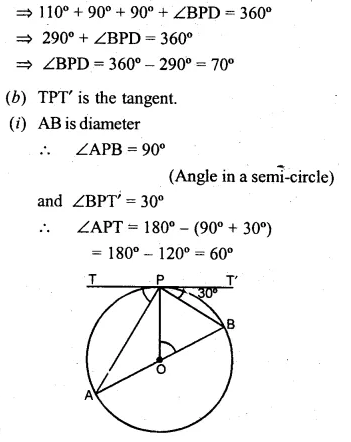
(b) In the figure (ii) given below. O is the centre of the circle. AB is a diameter, TPT’ is a tangent to the circle at P. If ∠BPT’ = 30°, calculate : (i)∠APT (ii) ∠B OP.

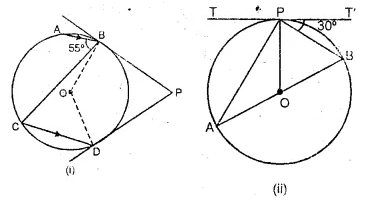
Solution:
(a) AB || CD
(i) ∠ABC = ∠BCD (Alternate angles)
⇒ ∠BCD = 55°

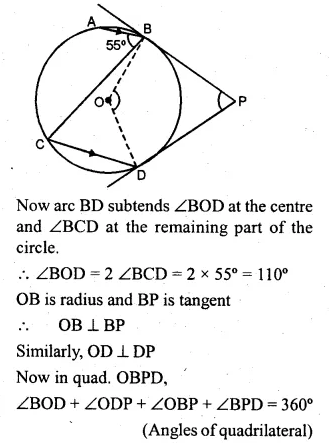
Question 25.
In the adjoining figure, ABCD is a cyclic quadrilateral.

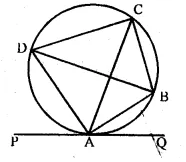
The line PQ is the tangent to the circle at A. If ∠CAQ : ∠CAP = 1 : 2, AB bisects ∠CAQ and AD bisects ∠CAP, then find the measure of the angles of the cyclic quadrilateral. Also prove that BD is a diameter of the circle.
Solution:
ABCD is a cyclic quadrilateral.
PAQ is the tangent to the circle at A.
∠CAD : ∠CAP = 1 : 2.
AB and AD are the bisectors of ∠CAQ and ∠CAP respectively

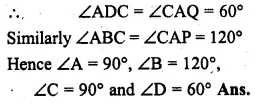
Question 26.
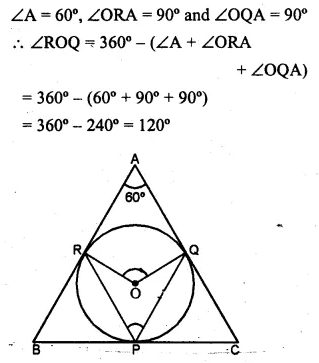
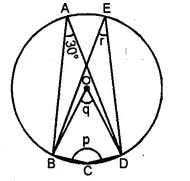
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at P, Q and R respectively. Calculate (i) ∠QOR (ii) ∠QPR given that ∠A = 60°.
Solution:
OQ and OR are the radii and AC and AB are tangents.
OQ ⊥ AC and OR ⊥ AB
Now in the quad. AROQ

Question 27.
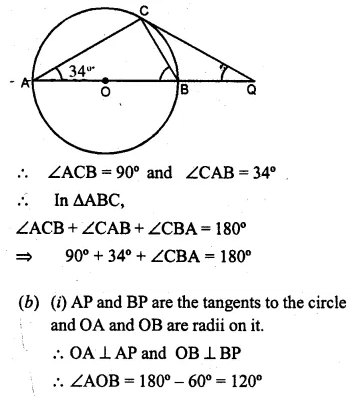
(a) In the figure (0 given below, AB is a diameter. The tangent at C meets AB produced at Q, ∠CAB = 34°. Find
(i) ∠CBA (ii) ∠CQA (2006)

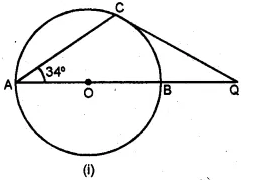
(b) In the figure (ii) given below, AP and BP are tangents to the circle with centre O. Given ∠APB = 60°, calculate.
(i) ∠AOB (ii) ∠OAB (iii) ∠ACB.

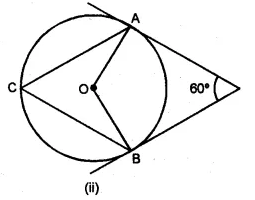
Solution:
(a) AB is the diameter.

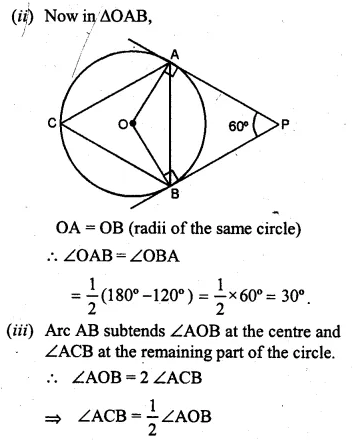
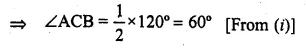
Question 28.
(a) In the figure (i) given below, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY. (1994)
(b) In the figure (ii) given below, O is the centre of the circle and PT is the tangent to the circle at P. Given ∠QPT = 30°, calculate (i) ∠PRQ (ii) ∠POQ.

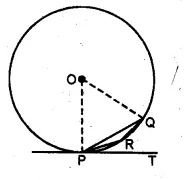
Solution:
(a) Join OY, OX and OY are the radii of the circle
and XT and YT are the tangents to the circle.

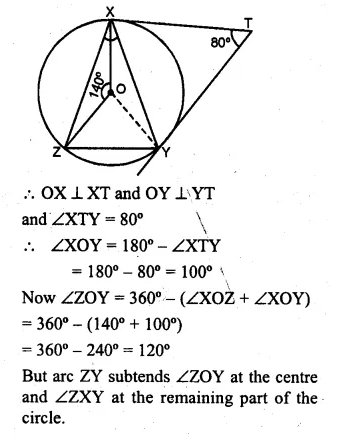
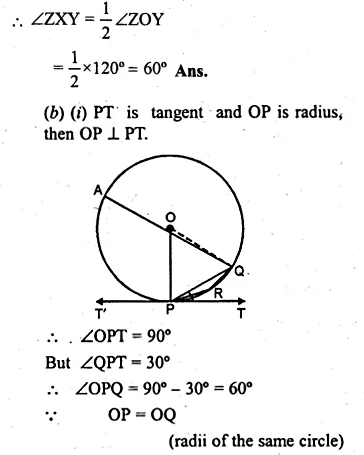
Question 29.
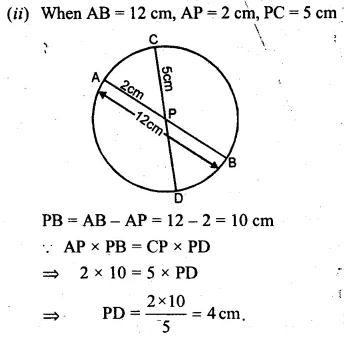
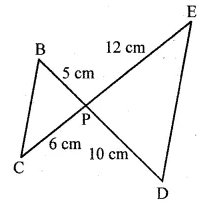
Two chords AB, CD of a circle intersect internally at a point P. If
(i) AP = cm, PB = 4 cm and PD = 3 cm, find PC.
(ii) AB = 12 cm, AP = 2 cm, PC = 5 cm, find PD.
(iii) AP = 5 cm, PB = 6 cm and CD = 13 cm, find CP.
Solution:
In a circle, two chords AB and CD intersect
each other at P internally.

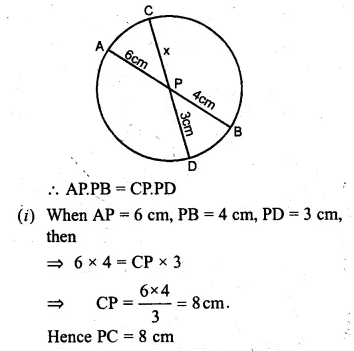
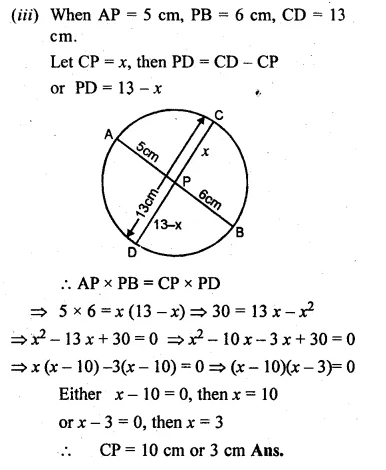
Question 30.
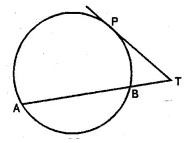
(a) In the figure (i) given below, PT is a tangent to the circle. Find TP if AT = 16 cm and AB = 12 cm.

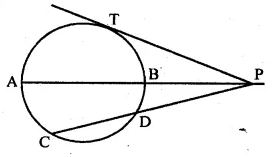
(b) In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find (i) AB. (ii)the length of tangent PT.

Solution:
(a) PT is the tangent to the circle and AT is a secant.
PT² = TA × TB
Now TA = 16 cm, AB = 12 cm
TB = AT – AB = 16 – 12 = 4 cm
∴ PT² = 16 + 4 = 64 = (8)²
⇒ PT = 8 cm or TP = 8 cm
(b) PT is tangent and PDC is secant out to the circle
∴ PT² = PC × PD

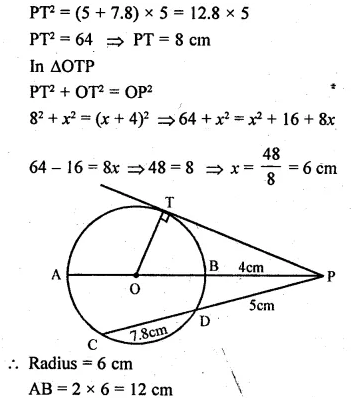
Question 31.
PAB is secant and PT is tangent to a circle
(i) PT = 8 cm and PA = 5 cm, find the length of AB.
(ii) PA = 4.5 cm and AB = 13.5 cm, find the length of PT.
Solution:
∵ PT is the tangent and PAB is the secant of the circle.

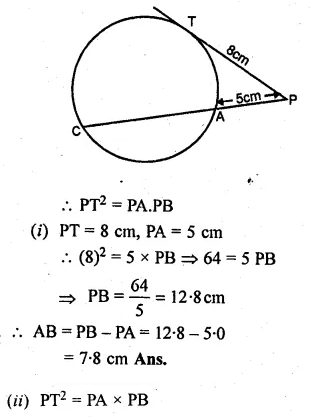
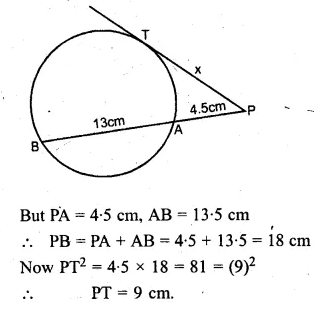
Question 32.
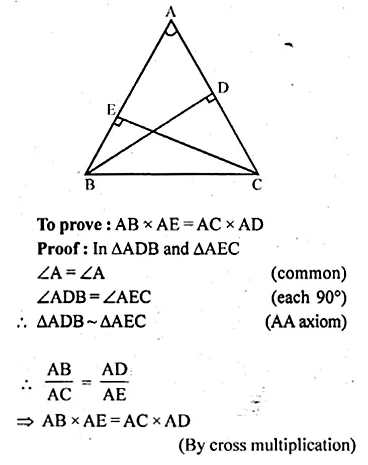
In the adjoining figure, CBA is a secant and CD is tangent to the circle. If AB = 7 cm and BC = 9 cm, then
(i) Prove that ∆ACD ~ ∆DCB.
(ii) Find the length of CD.

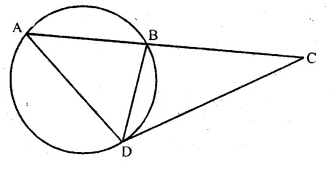
Solution:
In ∆ACD and ∆DCB
∠C = ∠C (common)
∠CAD = ∠CDB

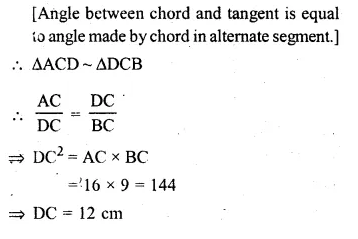
Question 33.
(a) In the figure (i) given below, PAB is secant and PT is tangent to a circle. If PA : AB = 1:3 and PT = 6 cm, find the length of PB.
(b) In the figure (ii) given below, ABC is an isosceles triangle in which AB = AC and Q is mid-point of AC. If APB is a secant, and AC is tangent to the circle at Q, prove that AB = 4 AP.

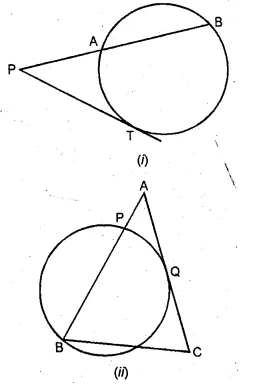
Solution:
(a) In the figure (i),
PAB is secant and PT is the tangent to the circle.
PT² = PA × PB

Question 34.
Two chords AB, CD of a circle intersect externally at a point P. If PA = PC, Prove that AB = CD.
Solution:
Given: Two chords AB and CD intersect
each other at P outside the circle. PA = PC.

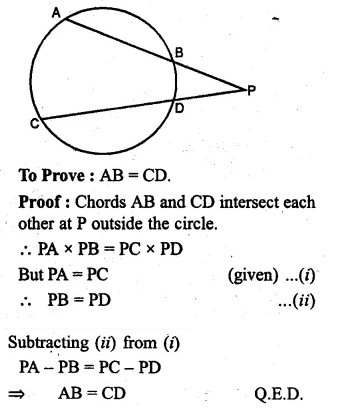
Question 35.
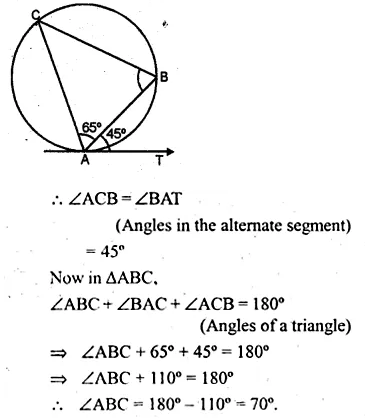
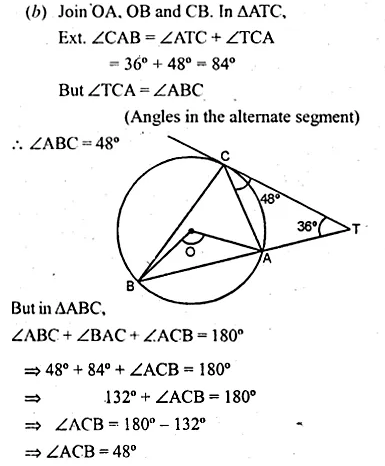
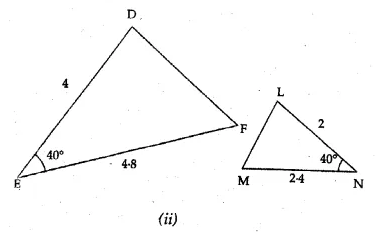
(a) In the figure (i) given below, AT is tangent to a circle at A. If ∠BAT = 45° and ∠BAC = 65°, find ∠ABC.

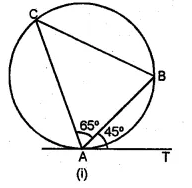
(b) In the figure (ii) given below, A, B and C are three points on a circle. The tangent at C meets BA produced at T. Given that ∠ATC = 36° and ∠ACT = 48°, calculate the angle subtended by AB at the centre of the circle. (2001)

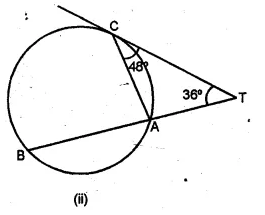
Solution:
(a) AT is the tangent to the circle at A
and AB is the chord of the circle.

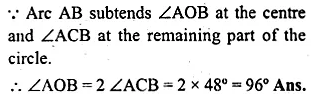
Question 36.
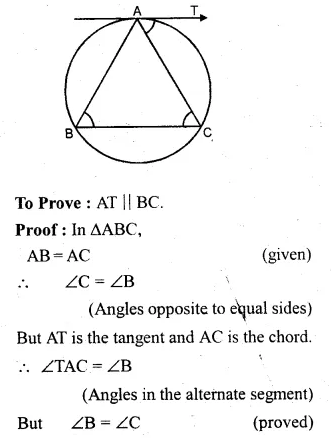
In the adjoining figure ∆ABC is isosceles with AB = AC. Prove that the tangent at A to the circumcircle of ∆ABC is parallel to BC.

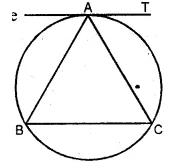
Solution:
Given: ∆ABC is an isosceles triangle with AB = AC.
AT is the tangent to the circumcircle at A.

Question 37.
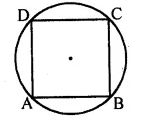
If the sides of a rectangle touch a circle, prove that the rectangle is a square.
Solution:
Given: A circle touches the sides AB, BC, CD and DA
of a rectangle ABCD at P, Q, R and S respectively.

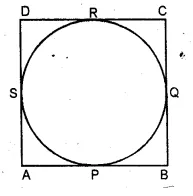
To Prove : ABCD is a square.

Question 38.
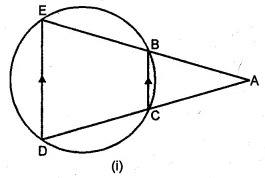
(a) In the figure (i) given below, two circles intersect at A, B. From a point P on one of these circles, two line segments PAC and PBD are drawn, intersecting the other circle at C and D respectively. Prove that CD is parallel to the tangent at P.

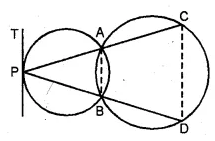
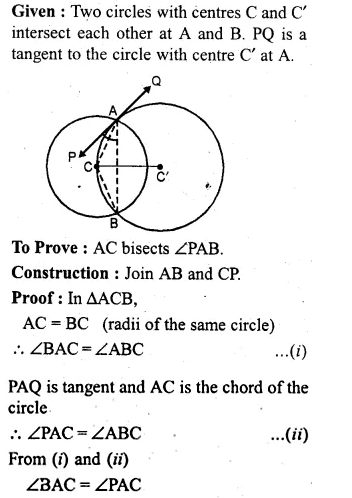
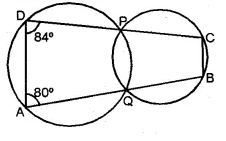
(b) In the figure (ii) given below, two circles with centres C, C’ intersect at A, B and the point C lies on the circle with centre C’. PQ is a tangent to the circle with centre C’ at A. Prove that AC bisects ∠PAB.

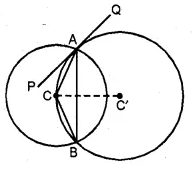
Solution:
Given: Two circles intersect each other at A and B.
From a point P on one circle, PAC and PBD are drawn.
From P, PT is a tangent drawn. CD is joined.

Question 39.
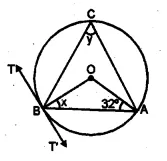
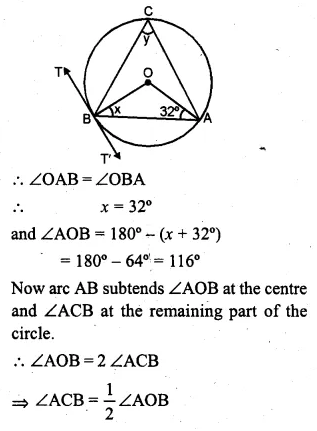
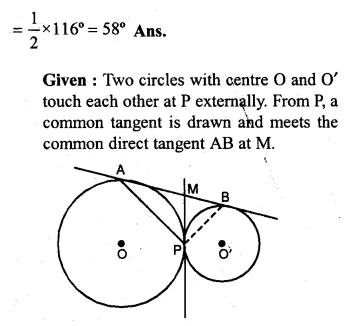
(a) In the figure (i) given below, AB is a chord of the circle with centre O, BT is tangent to the circle. If ∠OAB = 32°, find the values of x and y.

(b) In the figure (ii) given below, O and O’ are centres of two circles touching each other externally at the point P. The common tangent at P meets a direct common tangent AB at M. Prove that:
(i) M bisects AB (ii) ∠APB = 90°.

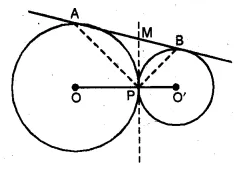
Solution:
AB is a chord of a circle with centre O.
BT is a tangent to the circle and ∠OAB = 32°.
∴ In ∆OAB,
OA = OB (radii of the same circle)

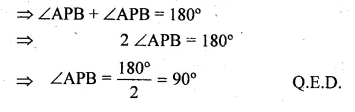
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Chapter Test

Question 1.
Draw a circle of radius 3 cm. Mark its centre as C and mark a point P such that CP = 7 cm. Using ruler and compasses only, Construct two tangents from P to the circle.
Solution:
Steps of Construction :

1. Draw a circle with centre C and radius 3 cm.
2. Mark a point P such that CP = 7 cm.
3. With CP as diameter, draw a circle intersecting the given circle at T and S.
4. Join PT and PS.
5. Draw a tangent at Q to the circle given. Which intersects PT at D.
6. Draw the angle bisector of ∠PDQ intersecting CP at E.
7. With centre E and radius EQ, draw a circle.
   It will touch the tangent T and PS and the given circle at Q.
   This is the required circle.
   

Question 2.
Draw a line AQ = 7 cm. Mark a point P on AQ such that AP = 4 cm. Using ruler and compasses only, construct :
(i) a circle with AP as diameter.
(ii) two tangents to the above circle from the point Q.
Solution:
Steps of construction :

1. Draw a line segment AQ = 7 cm.
2. From AQ,cut off AP = 4cm
3. With AP as diameter draw a circle with centre O.
4. Draw bisector of OQ which intersect OQ at M.
5. With centre M and draw a circle with radius MQ
   which intersects the first circle at T and S.
6. Join QT and QS.
   QT and QS are the tangents to the first circle.
   

Question 3.
Using ruler and compasses only, construct a triangle ABC having given c = 6 cm, b = 1 cm and ∠A = 30°. Measure side a. Draw carefully the circumcircle of the triangle.
Solution:
Steps of Construction :

1. Draw a line segment AC = 7 cm.
2. At C, draw a ray CX making an angle of 30°
3. With centre A and radius 6 cm draw an arc
   which intersects the ray CX at B.
4. Join BA.
5. Draw perpendicular bisectors of AB and AC intersecting each other at O.
6. With centre O and radius OA or OB or OC,
   draw a circle which will pass through A, B and C.
   This is the required circumcircle of ∆ABC
   

Question 4.
Using ruler and compasses only, construct an equilateral triangle of height 4 cm and draw its circumcircle.
Solution:
Steps of Construction :

1. Draw a line XY and take a point D on it.
2. At D, draw perpendicular and cut off DA = 4 cm.
3. From A, draw rays making an angle of 30°
   on each side of AD meeting the line XY at B and C.
4. Now draw perpendicular bisector of AC intersecting AD at O.
5. With centre O and radius OA or OB or OC
   draw a circle which will pass through A, B and C.
   This is the required circumcircle of ∆ABC.
   

Question 5.
Using ruler and compasses only :
(i) Construct a triangle ABC with the following data: BC = 7 cm, AB = 5 cm and ∠ABC = 45°.
(ii) Draw the inscribed circle to ∆ABC drawn in part (i).
Solution:
Steps of construction :

1. Draw a line segment BC = 7 cm.
2. At B, draw a ray BX making an angle of 45° and cut off BA = 5 cm.
3. Join AC.
4. Draw the angle bisectors of ∠B and ∠C intersecting each other at I.
5. From I, draw a perpendicular ID on BC.
6. With centre, I and radius ID, draw a circle
   which touches the sides of ∆ABC at D, E and F respectively.
   This is the required inscribed circle.
   

Question 6.
Draw a triangle ABC, given that BC = 4cm, ∠C = 75° and that radius of the circumcircle of ∆ABC is 3 cm.
Solution:
Steps of Construction:

1. Draw a line segment BC = 4 cm
2. Draw the perpendicular bisector of BC.
3. From B draw an arc of 3 cm radius which intersects the perpendicular bisector at O.
4. Draw a ray CX making art angle of 75°
5. With centre O and radius 3 cm draw a circle which intersects the ray CX at A.
6. Join AB.
   ∆ABC is the required triangle
   

Question 7.
Draw a regular hexagon of side 3.5 cm construct its circumcircle and measure its radius.
Solution:
Steps of construction:

1. Draw a regular hexagon ABCDEF whose each side is 3.5 cm.
2. Draw the perpendicular bisector of AB and BC
   which intersect each other at O.
3. Join OA and OB.
4. With centre O and radius OA or OB, draw a circle
   which passes through A, B, C, D, E and P.
   Then this is the required circumcircle.
   

Question 8.
Construct a triangle ABC with the following data: AB = 5 cm, BC = 6 cm and ∠ABC = 90°.
(i) Find a point P which is equidistant from B and C and is 5 cm from A. How many such points are there ?
(ii) Construct a circle touching the sides AB and BC, and whose centre is equidistant from B and C.
Solution:
Steps of Construction :

1. Draw a line segment BC = 6 cm.
2. At B, draw a ray BX making an angle of 90° and cut off BA = 5 cm.
3. Join AC.
4. Draw the perpendicular bisector of BC.
5. From A with 5 cm radius draw arc which intersects the perpendicular bisector of BC at P and P’.
   There are two points.
6. Draw the angle bisectors of ∠B and ∠C intersecting at 0.
7. From O, draw OD ⊥ BC.
8. With centre O and radius OD, draw a circle which will touch the sides AB and BC.
   This is the required circle.
   

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5

More Exercise

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test

Question 1.
The diameter of a metallic sphere is 6 cm. The sphere is melted and drawn into a wire of uniform cross-section. If the length of the wire is 36 m, find its radius.
Solution:
Diameter of metallic sphere = 6 cm
Radius(r) = \(\\ \frac { 6 }{ 2 } \) = 3cm

Question 2.
The radius of a sphere is 9 cm. It is melted and drawn into a wire of diameter 2 mm. Find the length of the wire in metres.
Solution:
Radius of sphere = 9 cm
Volume = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }=\frac { 4 }{ 3 } \pi \times { \left( 9 \right) }^{ 3 }{ cm }^{ 3 }\)

h = 97200 cm = 972 m
Length of wire = 972 m

Question 3.
A solid metallic hemisphere of radius 8 cm is melted and recasted into right circular cone of base radius 6 cm. Determine the height of the cone.
Solution:
Radius of a solid hemisphere (r) = 8 cm
Volume = \(\frac { 2 }{ 3 } \pi { r }^{ 3 }=\frac { 2 }{ 3 } \pi \times { \left( 8 \right) }^{ 3 }{ cm }^{ 3 }\)

Question 4.
A rectangular water tank of base 11 m x 6 m contains water upto a height of 5 m. if the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
Solution:
Base of a water tank = 11 m × 6 m
Height of water level in it (h) = 5 m
Volume of water =11 × 6 × 5 = 330 m³
Volume of water in the cylindrical tank

Question 5.
The rain water from a roof of dimensions 22 m x 20 m drains into a cylindrical vessel having diameter of base 2 m and height; 3.5 m. If the rain water collected from the roof just fill the cylindrical vessel, then find the rainfall in cm.
Solution:
Dimensions of roof = 22 m × 20 m
Let rainfall = x m
.’. Volume of water = 22 × 20 × x m³
Volume of water in cylinder = 22 × 20 × x m³
Diameter of its base = 2 m

Question 6.
The volume of a cone is the same as that of the cylinder whose height is 9 cm and diameter 40 cm. Find the radius of the base of the cone if its height is 108 cm.
Solution:
Diameter of a cylinder = 40 cm
Radius (r) = \(\\ \frac { 40 }{ 2 } \) = 20 cm
Height(h) = 9 cm

Question 7.
Eight metallic spheres, each of radius 2 cm, are melted and cast into a single sphere. Calculate the radius of the new (single) sphere.
Solution:
Radius of each metallic sphere (r) = 2 cm
Volume of one sphere = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)

Question 8.
A metallic disc, in the shape of a right circular cylinder, is of height 2.5 mm and base radius 12 cm. Metallic disc is melted and made into a sphere. Calculate the radius of the sphere.
Solution:
Height of disc cylindrical shaped = 2.5 mm
and base radius = 12 cm
Volume of the disc = πr²h

Question 9.
Two spheres of the same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the big sphere.
Solution:
Weight of first sphere = 1 kg
and weight of second sphere = 7 kg
Radius of smaller sphere = 3 cm
Let r be the radius of a larger sphere

R = 3 x 2 = 6 cm
Diameter of big sphere = 2 x 6 = 12 cm

Question 10.
A hollow copper pipe of inner diameter 6 cm and outer diameter 10 cm is melted and changed into a solid circular cylinder of the same height as that of the pipe. Find the diameter of the solid cylinder.
Solution:
Inner diameter of a hollow pipe = 6 cm
and outer diameter = 10 cm
Inner radius (r) = \(\\ \frac { 6 }{ 2 } \) = 3cm

Question 11.
A solid sphere of radius 6 cm is melted into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm and height is 72 cm, find the uniform thickness of the cylinder.
Solution:
Radius of a solid sphere (r) = 6 cm
Volume = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }=\frac { 4 }{ 3 } \pi \times { \left( 6 \right) }^{ 3 }{ cm }^{ 3 }\)

Question 12.
A hollow metallic cylindrical tube has an internal radius of 3 cm and height 21 cm. The thickness of the metal of the tube is \(\\ \frac { 1 }{ 2 } \) cm. The tube is melted and cast into a right circular cone of height 7 cm. Find the radius of the cone correct to one decimal place.
Solution:
Internal radius of a hollow metallic cylindrical tube (r) = 3 cm
and height (h) = 21 cm

Question 13.
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively, is melted into a cone of base diameter 8 cm. Find the height of the cone. (2002)
Solution:
Internal diameter of a hollow sphere = 4 cm
and external diameter = 8 cm
Internal radius (r) = 2 cm
and external radius (R) = 4 cm
Volume of hollow sphere

Question 14.
A well with inner diameter 6 m is dug 22 m deep. Soil taken out of it has been spread evenly all round it to a width of 5 m to form an embankment. Find the height of the embankment.
Solution:
Inner diameter of a well = 6 m
Depth (h) = 22 m

Question 15.
A cylindrical can of internal diameter 21 cm contains water. A solid sphere whose diameter is 10.5 cm is lowered into the cylindrical can. The sphere is completely immersed in water. Calculate the rise in water level, assuming that no water overflows.
Solution:
Internal diameter of cylindrical can = 21 cm
Radius (R) = \(\\ \frac { 21 }{ 2 } \) cm

Question 16.
There is water to a height of 14 cm in a cylindrical glass jar of radius 8 cm. Inside the water there is a sphere of diameter 12 cm completely immersed. By what height will the water go down when the sphere is removed?
Solution:
Radius of the cylindrical jar (R) = 8 cm
Height of water level (h) = 14 cm
Volume of water = πR²h

Question 17.
A vessel in the form of an inverted cone is filled with water to the brim. Its height is 20 cm and diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cone submerged? (2002)
Solution:
Height of conical vessel (h) = 20 cm
and diameter = 16.8 cm

Question 18.
A solid metallic circular cylinder of radius 14 cm and height 12 cm is melted and recast into small cubes of edge 2 cm. How many such cubes can be made from the solid cylinder?
Solution:
Radius of a solid metallic cylindrical (r) = 14 cm
and height (h) = 12 cm

Question 19.
How many shots each having diameter 3 cm can be made from a cuboidal lead solid of dimensions 9 cm x 11 cm x 12 cm?
Solution:
Diameter of a shot = 3 cm
Radius (r) = \(\\ \frac { 3 }{ 2 } \) cm
Volume of one shot = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)

Question 20.
How many spherical lead shots of diameter 4 cm can be made out of a solid cube of lead whose edge measures 44 cm?
Solution:
Diameter of lead shot = 4 cm
Radius (r) = \(\\ \frac { 4 }{ 2 } \) = 2 cm and
volume =\(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)

Question 21.
Find the number of metallic circular discs with 1.5 cm base diameter and height 0.2 cm to be melted to form a circular cylinder of height 10 cm and diameter 4.5 cm.
Solution:
Radius of the circular disc (r) = 0.75 cm
Height of circular disc (h) = 0.2 cm
Radius of cylinder (R) = 2.25 cm
Height of cylinder (H) = 10 cm
Now,

Question 22.
A solid metal cylinder of radius 14 cm and height 21 cm is melted down and recast into spheres of radius 3.5 cm. Calculate the number of spheres that can be made.
Solution:
Radius of a solid metallic cylinder (r) = 14 cm
and height (h) = 21 cm
Volume of cylinder = πr²h

Question 23.
A metallic sphere of radius 10.5 cm is melted and then recast into small cenes, each of radius 3.5 cm and height 3 cm. Find the number of cones thus obtained. (2005)
Solution:
Radius of a metallic sphere (r) = 10.5 cm
Volume = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)
= \(\\ \frac { 4 }{ 3 } \) × π × 10.5 × 10.5 × 10.5 = 1543.5π cm³

Question 24.
A certain number of metallic cones each of radius 2 cm and height 3 cm are melted and recast in a solid sphere of radius 6 cm. Find the number of cones. (2016)
Solution:
Radius of each cone (r) = 2 cm
and height (h) = 3 cm

Question 25.
A vessel is in the form of an inverted cone. Its height is 11 cm and the radius of its top, which is open, is 2.5 cm. It is filled with water upto the rim. When some lead shots, each of which is a sphere of radius 0.25 cm, are dropped into the vessel, \(\\ \frac { 2 }{ 5 } \) of the water flows out. Find the number of lead shots dropped into the vessel. (2003)
Solution:
Radius of the top of the inverted conical vessel (R) = 2.5 cm
and height (h)= 11 cm

Question 26.
The surface area of a solid metallic sphere is 616 cm². It is melted and recast into smaller spheres of diameter 3.5 cm. How many such spheres can be obtained? (2007)
Solution:
Surface area of a metallic sphere = 616 cm²

Question 27.
The surface area of a solid metallic sphere is 1256 cm². It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate
(i) the radius of the solid sphere.
(ii) the number of cones recast. (Use π = 3.14).
Solution:
Surface area of a solid metallic sphere = 1256 cm²

Question 28.
Water is flowing at the rate of 15 km/h through a pipe of diameter 14 cm into a cuboid pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
Solution:
Speed of water flow = 15 km/h
Diameter of pipe = 14 cm

Question 29.
A cylindrical can whose base is horizontal and of radius 3.5 cm contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate :
(i) the total surface area of the can in contact with water when the sphere is in it.
(ii) the depth of the water in the can before the sphere was put into the can. Given your answer as proper fractions.
Solution:
Radius of a cylindrical can = 3.5 cm
Radius of the sphere = 3.5 cm
and height of water level in the can = 3.5 × 2 = 7 cm

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Chapter Test

Question 1.
If O is the centre of the circle, find the value of x in each of the following figures (using the given information):

Solution:
From the figure
(i) ABCD is a cyclic quadrilateral

Question 2.
(a) In the figure (i) given below, O is the centre of the circle. If ∠AOC = 150°, find (i) ∠ABC (ii) ∠ADC.

(b) In the figure (i) given below, AC is a diameter of the given circle and ∠BCD = 75°. Calculate the size of (i) ∠ABC (ii) ∠EAF.

Solution:
(a) Given, ∠AOC = 150° and AD = CD
We know that an angle subtends by an arc of a circle
at the centre is twice the angle subtended by the same arc
at any point on the remaining part of the circle.

Question 3.
(a) In the figure, (i) given below, if ∠DBC = 58° and BD is a diameter of the circle, calculate:
(i) ∠BDC (ii) ∠BEC (iii) ∠BAC

(b) In the figure (if) given below, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°. Find:
(i) ∠CAD (ii) ∠CBD (iii) ∠ADC (2008)

Solution:
(a) ∠DBC = 58°
BD is diameter
∠DCB = 90° (Angle in semi circle)
(i) In ∆BDC
∠BDC + ∠DCB + ∠CBD = 180°
∠BDC = 180°- 90° – 58° = 32°

Question 4.
(a) In the figure given below, ABCD is a cyclic quadrilateral. If ∠ADC = 80° and ∠ACD = 52°, find the values of ∠ABC and ∠CBD.

(b) In the figure given below, O is the centre of the circle. ∠AOE =150°, ∠DAO = 51°. Calculate the sizes of ∠BEC and ∠EBC.

Solution:
(a) In the given figure, ABCD is a cyclic quadrilateral
∠ADC = 80° and ∠ACD = 52°
To find the measure of ∠ABC and ∠CBD

Question 5.
(a) In the figure (i) given below, ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. Given that ∠BEF = 80°, find ∠ABC.
(b) In the figure (ii) given below, ABCD is a cyclic trapezium in which AD is parallel to BC and ∠B = 70°, find:
(i)∠BAD (ii) DBCD.

Solution:
(a) ADFE is a cyclic quadrilateral
Ext. ∠FEB = ∠ADF
⇒ ∠ADF = 80°
ABCD is a parallelogram
∠B = ∠D = ∠ADF = 80°
or ∠ABC = 80°
(b)In trapezium ABCD, AD || BC
(i) ∠B + ∠A = 180°
⇒ 70° + ∠A = 180°
⇒ ∠A = 180° – 70° = 110°
∠BAD = 110°
(ii) ABCD is a cyclic quadrilateral
∠A + ∠C = 180°
⇒ 110° + ∠C = 180°
⇒ ∠C = 180° – 110° = 70°
∠BCD = 70°

Question 6.
(a) In the figure given below, O is the centre of the circle. If ∠BAD = 30°, find the values of p, q and r.

(b) In the figure given below, two circles intersect at points P and Q. If ∠A = 80° and ∠D = 84°, calculate
(i) ∠QBC (ii) ∠BCP

Solution:
(a) (i) ABCD is a cyclic quadrilateral

Question 7.
(a) In the figure given below, PQ is a diameter. Chord SR is parallel to PQ.Given ∠PQR = 58°, calculate (i) ∠RPQ (ii) ∠STP
(T is a point on the minor arc SP)

(b) In the figure given below, if ∠ACE = 43° and ∠CAF = 62°, find the values of a, b and c (2007)

Solution:
(a) In ∆PQR,
∠PRQ = 90° (Angle in a semi circle) and ∠PQR = 58°
∠RPQ = 90° – ∠PQR = 90° – 58° = 32°
SR || PQ (given)

Question 8.
(a) In the figure (i) given below, AB is a diameter of the circle. If ∠ADC = 120°, find ∠CAB.
(b) In the figure (ii) given below, sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E, the sides AD and BC are produced to meet at F. If x : y : z = 3 : 4 : 5, find the values of x, y and z.

Solution:
(a) Construction: Join BC, and AC then
ABCD is a cyclic quadrilateral.

Question 9.
(a) In the figure (i) given below, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E. If ∠ADE = 70° and ∠OBA = 45°, calculate
(i) ∠OCA (ii) ∠BAC
(b) In figure (ii) given below, ABF is a straight line and BE || DC. If ∠DAB = 92° and ∠EBF = 20°, find :
(i) ∠BCD (ii) ∠ADC.

Solution:
(a) ABCD is a cyclic quadrilateral

Question 10.
(a) In the figure (ii) given below, PQRS is a cyclic quadrilateral in which PQ = QR and RS is produced to T. If ∠QPR = 52°, calculate ∠PST.

(b) In the figure (ii) given below, O is the centre of the circle. If ∠OAD = 50°, find the values of x and y.

Solution:
(a) PQRS is a cyclic quadrilateral in which
PQ = QR

Question 11.
(a) In the figure (i) given below, O is the centre of the circle. If ∠COD = 40° and ∠CBE = 100°, then find :
(i) ∠ADC
(ii) ∠DAC
(iii) ∠ODA
(iv) ∠OCA.
(b) In the figure (ii) given below, O is the centre of the circle. If ∠BAD = 75° and BC = CD, find :
(i) ∠BOD
(ii) ∠BCD
(iii) ∠BOC
(iv) ∠OBD (2009)

Solution:
(a) (i) ∴ ABCD is a cyclic quadrilateral.
∴ Ext. ∠CBE = ∠ADC
⇒ ∠ADC = 100°
(ii) Arc CD subtends ∠COD at the centre
and ∠CAD at the remaining part of the circle
∴ ∠COD = 2 ∠CAD

Question 12.
In the given figure, O is the centre and AOE is the diameter of the semicircle ABCDE. If AB = BC and ∠AEC = 50°, find :
(i) ∠CBE
(ii) ∠CDE
(iii) ∠AOB.
Prove that OB is parallel to EC.

Solution:
In the given figure,
O is the centre of the semi-circle ABCDE
and AOE is the diameter. AB = BC, ∠AEC = 50°

Question 13.
(a) In the figure (i) given below, ED and BC are two parallel chords of the circle and ABE, ACD are two st. lines. Prove that AED is an isosceles triangle.

(b) In the figure (ii) given below, SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that SQ = RS.

Solution:
(a) Given: Chord BC || ED,
ABE and ACD are straight lines.
To Prove: ∆AED is an isosceles triangle.
Proof: BCDE is a cyclic quadrilateral.
Ext. ∠ABC = ∠D …(i)
But BC || ED (given)

Question 14.
In the given figure, ABC is an isosceles triangle in which AB = AC and circle passing through B and C intersects sides AB and AC at points D and E. Prove that DE || BC.

Solution:
In the given figure,
∆ABC is an isosceles triangle in which AB = AC.
A circle passing through B and C intersects
sides AB and AC at D and E.
To prove: DE || BC
Construction : Join DE.
∵ AB = AC
∠B = ∠C (angles opposite to equal sides)
But BCED is a cyclic quadrilateral
Ext. ∠ADE = ∠C
= ∠B (∵ ∠C = ∠B)
But these are corresponding angles
DE || BC
Hence proved.

Question 15.
(a) Prove that a cyclic parallelogram is a rectangle.
(b) Prove that a cyclic rhombus is a square.
Solution:
(a) ABCD is a cyclic parallelogram.

To prove: ABCD is a rectangle
Proof: ABCD is a parallelogram
∠A = ∠C and ∠B = ∠D

Question 16.
In the given figure, chords AB and CD of the circle are produced to meet at O. Prove that triangles ODB and OAC are similar. Given that CD = 2 cm, DO = 6 cm and BO = 3 cm, area of quad. CABD

Solution:
In the given figure, AB and CD are chords of a circle.
They are produced to meet at O.
To prove : (i) ∆ODB ~ ∆OAC
If CD = 2 cm, DO = 6 cm, and BO = 3 cm
To find : AB and also area of the
\(\frac { Quad.ABCD }{ area\quad of\quad \Delta OAC } \)
Construction : Join AC and BD

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test

Question 1.
State which pairs of triangles in the figure given below are similar. Write the similarity rule used and also write the pairs of similar triangles in symbolic form (all lengths of sides are in cm):


Solution:
Given
(i) In ∆ABC and PQR

Question 2.
It is given that ∆DEF ~ ∆RPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P ? Why?
Solution:
∆DEF ~ ∆RPQ
∠D = ∠R and ∠F = ∠Q not ∠P
No, ∠F ≠ ∠P

Question 3.
If in two right triangles, one of the acute angle of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles are similar? Why?
Solution:
In two right triangles,
one of the acute angles of the one triangle is
equal to an acute angle of the other triangle.
The triangles are similar. (AAA axiom)

Question 4.
In the given figure, BD and CE intersect each other at the point P. Is ∆PBC ~ ∆PDE? Give reasons for your answer.

Solution:
In the given figure, two line segments intersect each other at P.
In ∆BCP and ∆DEP
∠BPC = ∠DPE

Question 5.
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm.
Find the lengths of the remaining sides of the triangles.
Solution:
∆ABC ~ ∆EDF
AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm

Question 6.
(a) If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, then find the perimeter of ∆ABC.
(b) If ∆ABC ~ ∆PQR, Perimeter of ∆ABC = 32 cm, perimeter of ∆PQR = 48 cm and PR = 6 cm, then find the length of AC.
Solution:
(a) ∆ABC ~ ∆DEF
AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm

Question 7.
Calculate the other sides of a triangle whose shortest side is 6 cm and which is similar to a triangle whose sides are 4 cm, 7 cm and 8 cm.
Solution:
Let ∆ABG ~ ∆DEF in which shortest side of
∆ABC is BC = 6 cm.
In ∆DEF, DE = 8 cm, EF = 4 cm and DF = 7 cm

Question 8.
(a) In the figure given below, AB || DE, AC = , 3 cm, CE = 7.5 cm and BD = 14 cm. Calculate CB and DC.

(b) In the figure (2) given below, CA || BD, the lines AB and CD meet at G.
(i) Prove that ∆ACO ~ ∆BDO.
(ii) If BD = 2.4 cm, OD = 4 cm, OB = 3.2 cm and AC = 3.6 cm, calculate OA and OC.

Solution:
(a) In the given figure,
AB||DE, AC = 3 cm, CE = 7.5 cm, BD = 14 cm

Question 9.
(a) In the figure
(i) given below, ∠P = ∠RTS.
Prove that ∆RPQ ~ ∆RTS.
(b) In the figure (ii) given below,
∠ADC = ∠BAC. Prove that CA² = DC x BC.

Solution:
(a) In the given figure, ∠P = ∠RTS
To prove : ∆RPQ ~ ∆RTS
Proof : In ∆RPQ and ∆RTS
∠R = ∠R (common)
∠P = ∠RTS (given)
∆RPQ ~ ∆RTS (AA axiom)

Question 10.
(a) In the figure (1) given below, AP = 2PB and CP = 2PD.
(i) Prove that ∆ACP is similar to ∆BDP and AC || BD.
(ii) If AC = 4.5 cm, calculate the length of BD.

(b) In the figure (2) given below,
∠ADE = ∠ACB.
(i) Prove that ∆s ABC and AED are similar.
(ii) If AE = 3 cm, BD = 1 cm and AB = 6 cm, calculate AC.

(c) In the figure (3) given below, ∠PQR = ∠PRS. Prove that triangles PQR and PRS are similar. If PR = 8 cm, PS = 4 cm, calculate PQ.

Solution:
In the given figure,
AP = 2PB, CP = 2PD
To prove:

Question 11.
In the given figure, ABC is a triangle in which AB = AC. P is a point on the side BC such that PM ⊥ AB and PN ⊥ AC. Prpve that BM x NP = CN x MP.

Solution:
In the given figure, ABC in which AB = AC.
P is a point on BC such that PM ⊥ AB and PN ⊥ AC
To prove : BM x NP = CN x MP

Question 12.
Prove that the ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides.
Solution:
Given : ∆ABC ~ ∆PQR .
To prove : Ratio in their perimeters k
the same as the ratio in their corresponding sides.

Question 13.
In the given figure, ABCD is a trapezium in which AB || DC. The diagonals AC and BD intersect at O. Prove that \(\frac { AO }{ OC } =\frac { BO }{ OD } \)

Using the above result, find the value(s) of x if OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4.
Solution:
ABCD is a trapezium in which AB || DC
Diagonals AC and BD intersect each other at O.

Question 14.
In ∆ABC, ∠A is acute. BD and CE are perpendicular on AC and AB respectively. Prove that AB x AE = AC x AD.
Solution:
In ∆ABC, ∠A is acute
BD and CE are perpendiculars on AC and AB respectively

Question 15.
In the given figure, DB ⊥ BC, DE ⊥ AB and AC ⊥ BC. Prove that \(\frac { BE }{ DE } =\frac { AC }{ BC } \)

Solution:
In the given figure, DB ⊥ BC, DE ⊥ AB and AC ⊥ BC
To prove : \(\frac { BE }{ DE } =\frac { AC }{ BC } \)
Proof: In ∆ABC and ∆DEB

Question 16.
(a) In the figure (1) given below, E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. show that ∆ABE ~ ∆CFB.
(b) In the figure (2) given below, PQRS is a parallelogram; PQ = 16 cm, QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.
(i) Prove that triangle RLQ is similar to triangle PLN. Hence, find PN.
(ii) Name a triangle similar to triangle RLM. Evaluate RM.

Solution:
(a) In the given figure, ABCD is a ||gm
E is a point on AD and produced
and BE intersects CD at F.
To prove : ∆ABE ~ ∆CFB
Proof : In ∆ABE and ∆CFB
∠A = ∠C (opposite angles of a ||gm)
∠ABE = ∠BFC (alternate angles)
∆ABE ~ ∆CFB (AA axiom)
(b) In the given figure, PQRS is a ||gm PQ = 16 cm,
QR = 10 cm
L is a point on PR such that

Question 17.
The altitude BN and CM of ∆ABC meet at H. Prove that
(i) CN . HM = BM . HN .
(ii) \(\frac { HC }{ HB } =\sqrt { \frac { CN.HN }{ BM.HM } } \)
(iii) ∆MHN ~ ∆BHC.
Solution:
In the given figure, BN ⊥ AC and CM ⊥ AB of ∆ABC
which intersect each other at H.
To prove:
(i) CN.HM = BM.HN
(ii) \(\frac { HC }{ HB } =\sqrt { \frac { CN.HN }{ BM.HM } } \)
(iii) ∆MHN ~ ∆BHC.
Construction: Join MN

Question 18.
In the given figure, CM and RN are respectively the medians of ∆ABC and ∆PQR. If ∆ABC ~ ∆PQR, prove that:
(i) ∆AMC ~ ∆PNR
(ii) \(\frac { CM }{ RN } =\frac { AB }{ PQ } \)
(iii) ∆CMB ~ ∆RNQ.

Solution:
In the given figure, CM and RN are medians of ∆ABC and ∆PQR
respectively and ∆ABC ~ ∆PQR
To prove:
(i) ∆AMC ~ ∆PNR

>

Question 19.
In the given figure, medians AD and BE of ∆ABC meet at the point G, and DF is drawn parallel to BE. Prove that
(i) EF = FC
(ii) AG : GD = 2 : 1

Solution:
In the given figure,
AD and BE are the medians of ∆ABC
intersecting each other at G
DF || BE is drawn
To prove :

Question 20.
(a) In the figure given below, AB, EF and CD are parallel lines. Given that AB =15 cm, EG = 5 cm, GC = 10 cm and DC = 18 cm. Calculate
(i) EF
(ii) AC.

(b) In the figure given below, AF, BE and CD are parallel lines. Given that AF = 7.5 cm, CD = 4.5 cm, ED = 3 cm, BE = x and AE = y. Find the values of x and y.

Solution:
In the given figure,
AB || EF || CD
AB = 15 cm, EG = 5 cm, GC = 10 cm and DC = 18 cm
Calculate :

Question 21.
In the given figure, ∠A = 90° and AD ⊥ BC If BD = 2 cm and CD = 8 cm, find AD.

Solution:
In ∆ABC, we have ∠A = 90°
Also, AD ⊥ BC
Now,
In ∆ABC, we have,
∠BAC = 90°
⇒ ∠BAD + ∠DAC = 90°…..(i)

Question 22.
A 15 metres high tower casts a shadow of 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
Solution:
Height of a tower AB = 15 m
and its shadow BC = 24 m
At the same time and position
Let the height of a telephone pole DE = x m
and its shadow EF = 16 m

Question 23.
A street light bulb is fixed on a pole 6 m above the level of street. If a woman of height casts a shadow of 3 m, find how far she is away from the base of the pole?
Solution:
Height of height pole(AB) = 6m
and height of a woman (DE) = 1.5 m
Here shadow EF = 3 m .

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Ex 11
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Chapter Test

Question 1.
The base BC of an equilateral triangle ABC lies on y-axis. The coordinates of the point C are (0, – 3). If origin is the mid-point of the base BC, find the coordinates of the points A and B
Solution:
Base BC of an equilateral ∆ABC lies on y-axis
co-ordinates of point C are (0, – 3),
origin (0, 0) is the mid-point of BC.

Question 2.
A and B have co-ordinates (4, 3) and (0, 1), Find
(i) the image A’ of A under reflection in the y – axis.
(ii) the image of B’ of B under reflection in the lineAA’.
(iii) the length of A’B’.
Solution:

(i) Co-ordinates of A’, the image of A (4, 3)
reflected in y-axis will be ( – 4, 3).
(ii) Co-ordinates of B’ the image of B (0, 1)
reflected in the line AA’ will be (0, 5).
(iii) Length A’B’

Question 3.
Find the co-ordinates of the point that divides the line segment joining the points P (5, – 2) and Q (9, 6) internally in the ratio of 3 : 1.
Solution:
Let R be the point whose co-ordinates are (x, y)
which divides PQ in the ratio of 3:1.

Question 4.
Find the coordinates of the point P which is three-fourth of the way from A (3, 1) to B ( – 2, 5).
Solution:
Co-ordinates of A (3, 1) and B ( – 2, 5)
P lies on AB such that

Question 5.
P and Q are the points on the line segment joining the points A (3, – 1) and B ( – 6, 5) such that AP = PQ = QB. Find the co-ordinates of P and Q.
Solution:
Given
AP = PQ = QB

Question 6.
The centre of a circle is (α + 2, α – 5). Find the value of a given that the circle passes through the points (2, – 2) and (8, – 2).
Solution:
Let A (2, -2), B (8, -2) and centre of the circle be
O (α + 2, α – 5)

Question 7.
The mid-point of the line joining A (2, p) and B (q, 4) is (3, 5). Calculate the numerical values of p and q.
Solution:
Given
(3, 5) is the mid-point of A (2, p) and B (q, 4)

Question 8.
The ends of a diameter of a circle have the co-ordinates (3, 0) and ( – 5, 6). PQ is another diameter where Q has the coordinates ( – 1, – 2). Find the co-ordinates of P and the radius of the circle.
Solution:
Let AB be the diameter where co-ordinates of
A are (3, 0) and of B are (-5, 6).
Co-ordinates of its origin O will be

Question 9.
In what ratio does the point ( – 4, 6) divide the line segment joining the points A( – 6, 10) and B (3, – 8) ?
Solution:
Let the point (-4, 6) divides the line segment joining the points
A (-6, 10) and B (3, -8), in the ratio m : n

Question 10.
Find the ratio in which the point P ( – 3, p) divides the line segment joining the points ( – 5, – 4) and ( – 2, 3). Hence find the value of p.
Solution:
Let P (-3, p) divides AB in the ratio of m₁ : m₂ coordinates of
A (-5, -4) and B (-2, 3)

Question 11.
In what ratio is the line joining the points (4, 2) and (3, – 5) divided by the x-axis? Also find the co-ordinates of the point of division.
Solution:
Let the point P which is on the x-axis, divides the line segment
joining the points A (4, 2) and B (3, -5) in the ratio of m₁ : m₂.
and let co-ordinates of P be (x, 0)

Question 12.
If the abscissa of a point P is 2, find the ratio in which it divides the line segment joining the points ( – 4 – 3) and (6, 3). Hence, find the co-ordinates of P.
Solution:
Let co-ordinates of A be (-4, 3) and of B (6, 3) and of P be (2, y)
Let the ratio in which the P divides AB be m₁ : m₂

Question 13.
Determine the ratio in which the line 2x + y – 4 = 0 divide the line segment joining the points A (2, – 2) and B (3, 7). Also find the co-ordinates of the point of division.
Solution:
Points are given A (2, -2), B (3, 7)
and let the line 2x + y – 4 = 0 divides AB in the ratio m₁ : m₂
at P and let co-ordinates of

Question 14.
The point A(2, – 3) is reflected in the v-axis onto the point A’. Then the point A’ is reflected in the line x = 4 onto the:point A”.
(i) Write the coordinates of A’ and A”.
(ii) Find the ratio in which the line segment AA” is divided by the x-axis. Also find the coordinates of the point of division.
Solution:
A’ is the reflection of A(2, -3) in the x-axis
(i) ∴ Co-ordinates of A’ will be (2, 3)
Draw a line x = 4 which is parallel to y-axis
A” is the reflection of A’ (2, 3)
∴Co-ordinates OA” will be (6, 3)
(ii) Join AA” which intersects x-axis at P whose
co-ordinate are (4, 0)
Let P divide AA” in the ratio in m₁ : m₂

Hence P(4, 0) divides AA” in the ratio 1 : 1

Question 15.
ABCD is a parallelogram. If the coordinates of A, B and D are (10, – 6), (2, – 6) and (4, – 2) respectively, find the co-ordinates of C.
Solution:
Let the co-ordinates of C be (x, y) and other three vertices
of the given parallelogram are A (10, – 6), B, (2, – 6) and D (4, – 2)
∴ ABCD is a parallelogram
Its diagonals bisect each other.
Let AC and BD intersect each other at O.
∴O is mid-points of BD
∴ Co-ordinates of O will be

Question 16.
ABCD is a parallelogram whose vertices A and B have co-ordinates (2, – 3) and ( – 1, – 1) respectively. If the diagonals of the parallelogram meet at the point M(1, – 4), find the co-ordinates of C and D. Hence, find the perimeter of the parallelogram. find the perimeter of the parallelogram.
Solution:
ABCD is a || gm , m which co-ordinates of A are (2, -3) and B (-1, -1)
Its diagonals AC and BD bisect each other at M (1, -4)
∴ M is the midpoint of AC and BD
Let co-ordinates of C be (x₁, y₁) and of D be (x₂, y₂)
when M is the midpoint of AC then

Question 17.
In the adjoining figure, P (3, 1) is the point on the line segment AB such that AP : PB = 2 : 3. Find the co-ordinates of A and B.

Solution:
A lies on x-axis and
B lies on y-axis
Let co-ordinates of A be (x, 0) and B be (0, y)
and P (3, 1) divides it in the ratio of 2 : 3.

Question 18.
Given, O, (0, 0), P(1, 2), S( – 3, 0) P divides OQ in the ratio of 2 : 3 and OPRS is a parallelogram.
Find : (i) the co-ordinates of Q.
(ii)the co-ordinates of R.
(iii) the ratio in which RQ is divided by y-axis.

Solution:
(i) Let co-ordinates of Q be (x’, y’) and of R (x”, y”)
Point P (1, 2) divides OQ in the ratio of 2 : 3

Question 19.
If A (5, – 1), B ( – 3, – 2) and C ( – 1, 8) are the vertices of a triangle ABC, find the length of the median through A and the co-ordinates of the centroid of triangle ABC.
Solution:
A (5, -1), B (-3, -2) and C (-1, 8) are the vertices of ∆ABC
D, E and F are the midpoints of sides BC, CA and AB respectively
and G is the centroid of the ∆ABC

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

Question 1.
Find the equation of a line whose inclination is 60° and y-intercept is – 4.
Solution:
Angle of inclination = 60°
Slope = tan θ = tan 60° = √3
Equation of the line will be,
y = mx + c = √3x + ( – 4)
⇒ y – √3x – 4

Question 2.
Write down the gradient and the intercept on the y-axis of the line 3y + 2x = 12.
Solution:
Slope of the line 3y + 2x = 12
⇒ 3y = 12 – 2x
⇒ 3y = -2x + 12

Question 3.
If the equation of a line is y – √3x + 1, find its inclination.
Solution:
In the line
y = √3 x + 1
Slope = √3
⇒ tan θ = √3
⇒ θ = 60° (∵ tan 60° = √3)

Question 4.
If the line y = mx + c passes through the points (2, – 4) and ( – 3, 1), determine the values of m and c.
Solution:
The equation of line y = mx + c
∵ it passes through (2, – 4) and ( – 3, 1)
Now substituting the value of these points -4 = 2m + c …(i)
and 1 = -3m + c …(ii)
Subtracting we get,

Question 5.
If the point (1, 4), (3, – 2) and (p, – 5) lie on a st. line, find the value of p.
Solution:
Let the points to be A (1, 4), B (3, -2) and C (p, -5) are collinear and let B (3, -2)
divides AC in the ratio of m₁ : m₂

Question 6.
Find the inclination of the line joining the points P (4, 0) and Q (7, 3).
Solution:
Slope of the line joining the points P (4, 0) and Q (7, 3)

Question 7.
Find the equation of the line passing through the point of intersection of the lines 2x + y = 5 and x – 2y = 5 and having y-intercept equal to \(– \frac { 3 }{ 7 } \)
Solution:
Equation of lines are
2x + y = 5 …(i)
x – 2y = 5 …(ii)
Multiply (i) by 2 and (ii) by 1, we get
4x + 2y = 10
x – 2y = 5
Adding we get,

Question 8.
If point A is reflected in the y-axis, the co-ordinates of its image A₁, are (4, – 3),
(i) Find the co-ordinates of A
(ii) Find the co-ordinates of A₂, A₃ the images of the points A, A₁, Respectively under reflection in the line x = – 2
Solution:
(i) ∵ A is reflected in the y-axis and its image is A₁ (4, -3)
Co-ordinates of A will be (-4, -3)

Question 9.
If the lines \(\frac { x }{ 3 } +\frac { y }{ 4 } =7 \) and 3x + ky = 11 are perpendicular to each other, find the value of k.
Solution:
Given Equation of lines are

Question 10.
Write down the equation of a line parallel to x – 2y + 8 = 0 and passing through the point (1, 2).
Solution:
The equation of the line is x – 2y + 8 = 0
⇒ 2y = x + 8

Question 11.
Write down the equation of the line passing through ( – 3, 2) and perpendicular to the line 3y = 5 – x.
Solution:
Equations of the line is
3y = 5 – x ⇒ 3y = -x + 5

Question 12.
Find the equation of the line perpendicular to the line joining the points A (1, 2) and B (6, 7) and passing through the point which divides the line segment AB in the ratio 3 : 2.
Solution:
Let slope of the line joining the points A (1, 2) and B (6, 7) be m₁

Question 13.
The points A (7, 3) and C (0, – 4) are two opposite vertices of a rhombus ABCD. Find the equation of the diagonal BD.
Solution:
Slope of line AC (m₁)

Question 14.
A straight line passes through P (2, 1) and cuts the axes in points A, B. If BP : PA = 3 : 1, find:

(i) the co-ordinates of A and B
(ii) the equation of the line AB
Solution:
A lies on x-axis and B lies on y-axis
Let co-ordinates of A be (x, 0) and B be (0, y)
and P (2, 1) divides BA in the ratio 3 : 1.

Question 15.
A straight line makes on the co-ordinates axes positive intercepts whose sum is 7. If the line passes through the point ( – 3, 8), find its equation.
Solution:
Let the line make intercept a and b with the
x-axis and y-axis respectively then the line passes through

Question 16.
If the coordinates of the vertex A of a square ABCD are (3, – 2) and the quation of diagonal BD is 3 x – 7 y + 6 = 0, find the equation of the diagonal AC. Also find the co-ordinates of the centre of the square.
Solution:
Co-ordinates of A are (3, -2).

Diagonals AC and BD of the square ABCD
bisect each other at right angle at O.
∴ O is the mid-point of AC and BD Equation

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

Choose the correct answer from the given four options (1 to 13) :

Question 1.
The slope of a line parallel to y-axis is
(a) 0
(b) 1
(c) – 1
(d) not defined
Solution:
Slope of a line parallel to y-axis is not defined. (b)

Question 2.
The slope of a line which makes an angle of 30° with the positive direction of x-axis is
(a) 1
(b) \(\frac { 1 }{ \sqrt { 3 } } \)
(c) √3
(d) \(– \frac { 1 }{ \sqrt { 3 } } \)
Solution:
Slope of a line which makes an angle of 30°
with positive direction of x-axis = tan 30°
= \(\frac { 1 }{ \sqrt { 3 } } \) (b)

Question 3.
The slope of the line passing through the points (0, – 4) and ( – 6, 2) is
(a) 0
(b) 1
(c) – 1
(d) 6
Solution:
Slope of the line passing through the points (0, -4) and (-6, 2)
\(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { 2+4 }{ -6-0 } =\frac { 6 }{ -6 } =-1 \) (c)

Question 4.
The slope of the line passing through the points (3, – 2) and ( – 7, – 2) is
(a) 0
(b) 1
(c) \(– \frac { 1 }{ 10 } \)
(d) not defined
Solution:
Slope of the line passing through the points (3, -2) and (-7, -2)
\(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { -2+2 }{ -7-3 } =\frac { 0 }{ -10 } =0 \) (a)

Question 5.
The slope of the fine passing through the points (3, – 2) and (3, – 4) is
(a) – 2
(b) 0
(c) 1
(d) not defined
Solution:
The slope of the line passing through (3, -2) and (3, -4)
\(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { -4+2 }{ 3-3 } =\frac { -2 }{ 0 } \) (d)

Question 6.
The inclination of the line y = √3x – 5 is
(a) 30°
(b) 60°
(c) 45°
(d) 0°
Solution:
The inclination of the line y = √3x – 5 is
√3 = tan 60° = 60° (b)

Question 7.
If the slope of the line passing through the points (2, 5) and (k, 3) is 2, then the value of k is
(a) -2
(b) -1
(c) 1
(d) 2
Solution:
Slope of the line passing through the points (2, 5) and (k, 3) is 2, then

Question 8.
The slope of a line parallel to the line passing through the points (0, 6) and (7, 3) is
(a) \(– \frac { 1 }{ 5 } \)
(b) \(\\ \frac { 1 }{ 5 } \)
(c) -5
(d) 5
Solution:
Slope of the line parallel to the line passing through (0, 6) and (7, 3)
Slope of the line = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { 3-6 }{ 7-0 } =\frac { -3 }{ 7 } \) (b)

Question 9.
The slope of a line perpendicular to the line passing through the points (2, 5) and ( – 3, 6) is
(a) \(– \frac { 1 }{ 5 } \)
(b) \(\\ \frac { 1 }{ 5 } \)
(c) -5
(d) 5
Solution:
Slope of the line joining the points (2, 5), (-3, 6)

Question 10.
The slope of a line parallel to the line 2x + 3y – 7 = 0 is
(a) \(– \frac { 2 }{ 3 } \)
(b) \(\\ \frac { 2 }{ 3 } \)
(c) \(– \frac { 3 }{ 2 } \)
(d) \(\\ \frac { 3 }{ 2 } \)
Solution:
The slope of a line parallel to the line 2x + 3y – 7 = 0
slope of the line

Question 11.
The slope of a line perpendicular to the line 3x = 4y + 11 is
(a) \(\\ \frac { 3 }{ 4 } \)
(b) \(– \frac { 3 }{ 4 } \)
(c) \(\\ \frac { 4 }{ 3 } \)
(d) \(– \frac { 4 }{ 3 } \)
Solution:
slope of a line perpendicular to the line 3x = 4y + 11 is

Question 12.
If the lines 2x + 3y = 5 and kx – 6y = 7 are parallel, then the value of k is
(a) 4
(b) – 4
(c) \(\\ \frac { 1 }{ 4 } \)
(d) \(– \frac { 1 }{ 4 } \)
Solution:
lines 2x + 3y = 5 and kx – 6y = 7 are parallel
Slope of 2x + 3y = 5 = Slope of kx – 6y = 7
⇒ 3y – 2x + 5

Question 13.
If the line 3x – 4y + 7 = 0 and 2x + ky + 5 = 0 are perpendicular to each other, then the value of k is
(a) \(\\ \frac { 3 }{ 2 } \)
(b) \(– \frac { 3 }{ 2 } \)
(c) \(\\ \frac { 2 }{ 3 } \)
(d) \(– \frac { 2 }{ 3 } \)
Solution:
line 3x – 4y + 7 = 0 and 2x + ky + 5 = 0
are perpendicular to each other

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test

Question 1.
In the given figure, ∠1 = ∠2 and ∠3 = ∠4. Show that PT x QR = PR x ST.
Solution:
Given: In the given figure,
∠1 = ∠1 and ∠3 = ∠4

To prove : PT × QR = PR × ST
Proof: ∠1 = ∠2
Adding ∠6 to both sides
∠1 + ∠6 = ∠2 + ∠6
∠SPT = ∠QPR
In ∆PQR and ∆PST

Question 2.
In the adjoining figure, AB = AC. If PM ⊥ AB and PN ⊥ AC, show that PM x PC = PN x PB.

Solution:
Given : In the given figure,
AB = AC, PM ⊥ AB and PN ⊥ AC
To prove : PM × PC = PN × PB
Proof: In ∆ABC, AB = AC
∠B = ∠C
Now in ∆CPN and ∆BPM,

Question 3.
(a) In the figure (1) given below. ∠AED = ∠ABC. Find the values of x and y.
(b) In the fig. (2) given below, CD = \(\\ \frac { 1 }{ 2 } \) AC, B is mid-point of AC and E is mid-point of DF. If BF || AG, prove that :
(i) CE || AG
(ii) 3 ED = GD.

Solution:
(a) Given : In following figure, ∠AED = ∠ABC
Required: The values of x and y.
Now, in ∆ABC and ∆ADE
∠AED = ∠ABC (given)
∠A = ∠A (common)
∴ ∆ABC ~ ∆ADE
(By A.A. axiom of similarity)

Question 4.
In the given figure, 2 AD = BD, E is mid-point of BD and F is mid-point of AC and EC || BH. Prove that:
(i) DF || BH
(ii) AH = 3 AF.

Solution:
Given: E is the mid-point of BD
and F is mid-point of AC
also 2 AD = BD and EC || BH
To Prove : (i) DF || BH
(ii) AH = 3 AF

Question 5.
In a ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = 2.4 cm, AE = 3.2 cm, DE = 2 cm and BC = 5 cm, find BD and CE.
Solution:
Given : In ∆ABC, D and E are the points
on the sides AB and AC respectively
DE || BC
AD = 2.4 cm, AE = 3.2 cm,
DE = 2 cm, BC = 5 cm

Question 6.
In a ∆ABC, D and E are points on the sides AB and AC respectively such that AD = 5.7cm, BD = 9.5cm, AE = 3.3cm and AC = 8.8cm. Is DE || BC? Justify your answer.
Solution:
In ∆ABC, D and E are points on the sides AB and AC respectively
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and AC = 8.8 cm

Question 7.
In a ∆ABC, DE is parallel to the base BC, with D on AB and E on AC. If \(\frac { AD }{ DB } =\frac { 2 }{ 3 } ,\frac { BC }{ DE } \)
Solution:
In ∆ABC, DE || BC
D is on AB and E is on AC

Question 8.
If the area of two similar triangles are 360 cm² and 250 cm² and if one side of the first triangle is 8 cm, find the length of the corresponding side of the second triangle.
Solution:
Let ∆ABC and ∆DEF are similar and area of
∆ABC = 360 cm²

Question 9.
In the adjoining figure, D is a point on BC such that ∠ABD = ∠CAD. If AB = 5 cm, AC = 3 cm and AD = 4 cm, find
(i) BC
(ii) DC
(iii) area of ∆ACD : area of ∆BCA.

Solution:
In ∆ABC and ∆ACD
∠C = ∠C (Common)
∠ABC = ∠CAD (given)
∴ ∆ABC ~ ∆ACD

Question 10.
In the adjoining figure the diagonals of a parallelogram intersect at O. OE is drawn parallel to CB to meet AB at E, find area of DAOE : area of ||gm ABCD.

Solution:
(a) In the figure
Diagonals of parallelogram ABCD are
AC and BD which intersect each other at O.
OE is drawn parallel to CB to meet AB in E.

Question 11.
In the given figure, ABCD is a trapezium in which AB || DC. If 2AB = 3DC, find the ratio of the areas of ∆AOB and ∆COD.

Solution:
In the given figure, ABCD is trapezium in
which AB || DC, 2AB = 3DC

Question 12.
In the adjoining figure, ABCD is a parallelogram. E is mid-point of BC. DE meets the diagonal AC at O and meet AB (produced) at F. Prove that .

(i) DO : OE = 2 : 1
(ii) area of ∆OEC : area of ∆OAD = 1 : 4.
Solution:
Given : In || gm ABCD,
E is the midpoint of BC and DE meets the diagonal AC at O
and meet AB produced at F.
To prove : (i) DO : OE = 2 : 1
(ii) area of ∆OEC : area of ∆OAD = 1 : 4
Proof: In ∆AOD and ∆EDC
∠AOD = ∠EOC (vertically opposite angle)
∠OAD = ∠OCB (alt. angles)
∆AOD ~ ∆EOC (AA postulate)

Question 13.
A model of a ship is made to a scale of 1 : 250. Calculate :
(i) the length of the ship, if the length of model is 1.6 m.
(ii) the area of the deck of the ship, if the area of the deck of model is 2.4 m².
(iii) the volume of the model, if the volume of the ship is 1 km³.
Solution:
Scale factor (k) of the model of the ship = \(\\ \frac { 1 }{ 250 } \)
(i) Length of model = 1.6 m

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test

Choose the correct answer from the given four options (1 to 22):

Question 1.
In the given figure, ∆ABC ~ ∆QPR. Then ∠R is
(a) 60°
(b) 50°
(c) 70°
(d) 80°

Solution:
In the given figure,
∆ABC ~ ∆QPR
∴ ∠A = ∠Q, ∠B = ∠P and ∠C = ∠R
But ∠A = 70°, ∠B = 50°
∴ ∠C = 180° – (70° + 500) = 180° – 120° = 60°
∠C = ∠R
∴ ∠R = ∠C = 60°

Question 2.
In the given figure, ∆ABC ~ ∆QPR. The value of x is
(a) 2.25 cm
(b) 4 cm
(c) 4.5 cm
(d) 5.2 cm

Solution:
In the given figure
∆ABC ~ ∆QPR

Question 3.
In the given figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to
(a) 50°
(b) 30°
(c) 60°
(d) 100°

Solution:
In the given figure two line segments AC and BD intersect each other at P
and PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°
In ∆APB and ∆CPD

Question 4.
If in two triangles ABC and PQR,
\(\frac { AB }{ QR } =\frac { BC }{ PR } =\frac { CA }{ PQ } \)
then
(a) ∆PQR ~ ∆CAB
(b) ∆PQR ~ ∆ABC
(c) ∆CBA ~ ∆PQR
(d) ∆BCA ~ ∆PQR
Solution:
In two ∆ABC and ∆PQR

Question 5.
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE, then the two triangles are
(a) congruent but not similar
(b) similar but not congruent
(c) neither congruent nor similar
(d) congruent as well as similar
Solution:
In ∆ABC and ∆DEF
∠B = ∠E, ∠F = ∠C
AB = 3DE
∵ Two angles of the one triangles are equal
to corresponding two angles of the other
But sides are not equal
∵ Triangles are similar but not congruent, (b)

Question 6.
In the given figure, if D, E and F are midpoints of the sides BC, CA and AB respectively, then the two triangles ABC and DEF are
(a) similar
(b) congruent
(c) both similar and congruent
(d) neither similar nor congruent

Solution:
D, E and F are the mid-points of the sides BC, CA and AB of ∆ABC
then two triangles ABC and DEF are similar. (a)

Question 7.
The given figure, AB || DE. The length of CD is
(a) 2.5 cm
(b) 2.7 cm
(c) \(\\ \frac { 10 }{ 3 } \) cm
(d) 3.5 cm

Solution:
In the given figure, AB || DE
∆ABC ~ ∆DCE

Question 8.
If in triangles ABC and DEF,\(\frac { AB }{ DE } =\frac { BC }{ FD } \) , then they will be similar when
(a) ∠B = ∠E
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠A = ∠F
Solution:
In two triangles ABC and DEF
\(\frac { AB }{ DE } =\frac { BC }{ FD } \)
They will be similar if their included angles are equal
∠B = ∠D (c)

Question 9.
If ∆PQR ~ ∆ABC, PQ = 6 cm, AB = 8 cm and perimeter of ∆ABC is 36 cm, then perimeter of ∆PQR is
(a) 20.25 cm
(b) 27 cm
(c) 48 cm
(d) 64 cm
Solution:
∆PQR ~ ∆ABC
PQ = 6 cm, AB = 8 cm
Perimeter of ∆ABC = 36 cm
Let perimeter of ∆PQR be x cm

Question 10.
In the given figure, DE || BC and all measurements are in centimetres. The length of AE is
(a) 2 cm
(b) 2.25 cm
(c) 3.5 cm
(d) 4 cm

Solution:
In the given figure,
DE || BC

Question 11.
In the given figure, PQ || CA and all lengths are given in centimetres. The length of BC is
(a) 6.4 cm
(b) 7.5 cm
(c) 8 cm
(d) 9 cm

Solution:
In the given figure,
PQ || CA
Let BC = x

Question 12.
In the given figure, MN || QR. If PN = 3.6 cm, NR = 2.4 cm and PQ = 5 cm, then PM is
(a) 4 cm
(b) 3.6 cm
(c) 2 cm
(d) 3 cm

Solution:
In the given figure, MN || QR
PN = 3.6 cm, NR = 2.4 cm and PQ = 5 cm
Let PM = x cm

Question 13.
D and E are respectively the points on the sides AB and AC of a ∆ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then the length of DE is
(a) 2.5 cm
(b) 3 cm
(c) 5 cm
(d) 6 cm
Solution:
D and E are the points on sides AB and AC of ∆ABC,
AD = 2 cm, BD = 3 cm,
BC = 7.5 cm

Question 14.
It is given that ∆ABC ~ ∆PQR with \(\frac { BC }{ QR } =\frac { 1 }{ 3 } \) then \(\frac { area\quad of\quad \Delta PQR }{ area\quad of\quad \Delta ABC } \) equal to
(a) 9
(b) 3
(c) \(\\ \frac { 1 }{ 3 } \)
(d) \(\\ \frac { 1 }{ 9 } \)
Solution:
∆ABC ~ ∆PQR
\(\frac { BC }{ QR } =\frac { 1 }{ 3 } \)

Question 15.
If the areas of two similar triangles are in the ratio 4 : 9, then their corresponding sides are in the ratio
(a) 9 : 4
(b) 3 : 2
(c) 2 : 3
(d) 16 : 81
Solution:
Ratio in the areas of two similar triangles = 4 : 9
Ratio in their corresponding sides
= √4 : √9
= 2 : 3 (c)

Question 16.
If ∆ABC ~ ∆PQR, BC = 8 cm and QR = 6 cm, then the ratio of the areas of ∆ABC and ∆PQR is
(a) 8 : 6
(b) 3 : 4
(c) 9 : 16
(d) 16 : 9
Solution:
∆ABC ~ ∆PQR, BC = 8 cm, QR = 6 cm
\(\frac { area\quad of\quad \Delta ABC }{ area\quad of\quad \Delta PQR } =\frac { { BC }^{ 2 } }{ { QR }^{ 2 } } \)
= \(\frac { { 8 }^{ 2 } }{ { 6 }^{ 2 } } =\frac { 64 }{ 36 } =\frac { 16 }{ 9 } \) (d)

Question 17.
If ∆ABC ~ ∆QRP \(\frac { area\quad of\quad \Delta ABC }{ area\quad of\quad \Delta PQR } \) AB = 18 cm and BC = 15 cm, then the length of PR is equal to
(a) 10 cm
(b) 12 cm
(c) \(\\ \frac { 20 }{ 3 } \)
(d) 8 cm
Solution:
∆ABC ~ ∆QRP
\(\frac { area\quad of\quad \Delta ABC }{ area\quad of\quad \Delta PQR } \)

Question 18.
If ∆ABC ~ ∆PQR, area of ∆ABC = 81 cm², area of ∆PQR = 144 cm² and QR = 6 cm, then length of BC is
(a) 4 cm
(b) 4.5 cm
(c) 9 cm
(d) 12 cm
Solution:
∆ABC ~ ∆PQR,
area of ∆ABC = 81 cm² and area of ∆PQR = 144 cm²,
QR = 6 cm, BC = ?

Question 19.
In the given figure, DE || CA and D is a point on BD such that BD : DC = 2 : 1. The ratio of area of ∆ABC to area of ∆BDE is
(a) 4 : 1
(b) 9 : 1
(c) 9 : 4
(d) 3 : 2

Solution:
In the given figure, DE || CA ,
D is a point on BC and BD : DC = 2 : 1
BD : BC = 2 : (2 + 1) = 2 : 3
In ∆ABC, DE || CA
∆ABC ~ ∆BDE

Question 20.
If ABC and BDE are two equilateral triangles such that D is mid-point of BC, then the ratio of the areas of triangles ABC and BDE is
(a) 2 : 1
(b) 1 : 2
(c) 1 : 4
(d) 4 : 1
Solution:
∆ABC and ∆BDE are an equilateral triangles

Question 21.
The areas of two similar triangles are 81 cm² and 49 cm² respectively. If an altitude of the smaller triangle is 3.5 cm, then the corresponding altitude of the bigger triangle is
(a) 9 cm
(b) 7 cm
(c) 6 cm
(d) 4.5 cm
Solution:
Areas of two similar triangles are 81 cm² and 49 cm²
The altitude of the smaller triangle is 3.5 cm
Let the altitude of the bigger triangle is x, then

Question 22.
Given ∆ABC ~ ∆PQR, area of ∆ABC = 54 cm² and area of ∆PQR = 24 cm². If AD and PM are medians of ∆’s ABC and PQR respectively, and length of PM is 10 cm, then length of AD is
(a) \(\\ \frac { 49 }{ 3 } \) cm
(b) \(\\ \frac { 20 }{ 3 } \) cm
(c) 15 cm
(d) 22.5 cm
Solution:
∆ABC ~ ∆PQR
area of ∆ABC = 54 cm²
and of ∆PQR = 24 cm²
AD and PM are their median respectively
PM = 10 cm
Let AD = x cm, then

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

Question 1.
State which one of the following is true : The straight lines y = 3x – 5 and 2y = 4x + 7 are
(i) parallel
(ii) perpendicular
(iii) neither parallel nor perpendicular.
Solution:
Slope of line y = 3x – 5 = 3
and slope of line 2y = 4x + 7
⇒ y = 2x + \(\\ \frac { 7 }{ 2 } \) = 2.
∴ Slope of both the lines are neither equal nor their product is – 1.
∴ These line are neither parallel nor perpendicular.

Worksheets for Class 10 Maths

Question 2.
If 6x + 5y – 7 = 0 and 2px + 5y + 1 = 0 are parallel lines, find the value of p.
Solution:
In equation
6x + 5 y – 7 = 0
⇒ 5y = -6x + 7

Question 3.
Lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel. Find the relation connecting a and b. (1991)
Solution:
In equation 2x – by + 5 = 0
⇒ – by = – 2x – 5
⇒ y = \(\\ \frac { 2 }{ b } \) + \(\\ \frac { 5 }{ b } \)

Question 4.
Given that the line \(\\ \frac { y }{ 2 } \) = x – p and the line ax + 5 = 3y are parallel, find the value of a. (1992)
Solution:
In equation y = x – p
⇒ y = 2x – 2p
Slope (m₁) = 2
In equation ax + 5 = 3y

Question 5.
If the lines y = 3x + 7 and 2y + px = 3 perpendicular to each other, find the value of p. (2006)
Solution:
Gradient m₁ of the line y = 3x + 7 is 3
2y + px = 3

Question 6.
Find the value of k for which the lines kx – 5y + 4 = 0 and 4x – 2y + 5 = 0 are perpendicular to each other. (2003)
Solution:
Given
In equation, kx – 5y + 4 = 0

Question 7.
If the lines 3x + by + 5 = 0 and ax – 5y + 7 = 0 are perpendicular to each other, find the relation connecting a and b.
Solution:
Given
In the equation 3x + by + 5 = 0

Question 8.
Is the line through ( – 2, 3) and (4, 1) perpendicular to the line 3x = y + 1 ?
Does the line 3x = y + 1 bisect the join of ( – 2, 3) and (4, 1). (1993)
Solution:
Slope of the line passing through the points
(-2, 3) and (4, 1) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-x_{ 1 } } \)

Hence the line 3x = y + 1 bisects the line joining the points (-2, 3), (4, 1).

Question 9.
The line through A ( – 2, 3) and B (4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Solution:
Gradient (m₁) of the line passing through the
points A (-2, 3) and B (4, b)

Question 10.
If the lines 3x + y = 4, x – ay + 7 = 0 and bx + 2y + 5 = 0 form three consecutive sides of a rectangle, find the value of a and b.
Solution:
In the line 3x + y = 4 …(i)
⇒ y = – 3x + 4
Slope (m₁) = – 3
In the line x – ay + 7 = 0…..(ii)

⇒ -b = -6 ⇒ b = 6
Hence a = 3, b = 6

Question 11.
Find the equation of a line, which has the y-intercept 4, and is parallel to the line 2x – 3y – 7 = 0. Find the coordinates of the point where it cuts the x-axis. (1998)
Solution:
In the given line 2x – 3y – 7 = 0
⇒ 3y = 2x – 7
⇒ \(y=\frac { 2 }{ 3 } x-\frac { 7 }{ 3 } \)

Question 12.
Find the equation of a straight line perpendicular to the line 2x + 5y + 7 = 0 and with y-intercept – 3 units.
Solution:
In the line 2x + 5y + 7 = 0
⇒ 5y = – 2x – 7
⇒ \(y=\frac { -2 }{ 5 } x-\frac { 7 }{ 5 } \)

Question 13.
Find the equation of a st. line perpendicular to the line 3x – 4y + 12 = 0 and having same y-intercept as 2x – y + 5 = 0.
Solution:
In the given line 3x – 4y + 12 = 0
⇒ 4y = 3x + 12
⇒ y = \(\\ \frac { 3 }{ 4 } x+3\)

Question 14.
Find the equation of the line which is parallel to 3x – 2y = – 4 and passes through the point (0, 3). (1990)
Solution:
In the given line 3x – 2y = – 4
⇒ 2y = 3x + 4
⇒ y = \(\\ \frac { 3 }{ 2 } x+2\)

Question 15.
Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0. (1999)
Solution:
In the given equation 3x + 5y + 15 = 0
⇒ 5y = – 3x – 15
⇒ y = \(\\ \frac { -3 }{ 5 } x-3\)

Question 16.
The equation of a line is y = 3x – 5. Write down the slope of this line and the intercept made by it on the y-axis. Hence or otherwise, write down the equation of a line which is parallel to the line and which passes through the point (0, 5).
Solution:
In the given line y = 3x – 5
Here slope (m₁) = 3
Substituting x = 0, then y = – 5
y-intercept = – 5
The slope of the line parallel to the given line
will be 3 and passes through the point (0, 5).
Equation of the line will be

Question 17.
Write down the equation of the line perpendicular to 3x + 8y = 12 and passing through the point ( – 1, – 2).
Solution:
In the given line 3x + 8y = 12
⇒ 8y = -3x + 12
⇒ \(y=\frac { -3 }{ 8 } x+\frac { 12 }{ 8 } \)

Question 18.
(i) The line 4x – 3y + 12 = 0 meets the x-axis at A. Write down the co-ordinates of A.
(ii) Determine the equation of the line passing through A and perpendicular to 4x – 3y + 12 = 0. (1993)
Solution:
(i) In the line 4x – 3y + 12 = 0 …(i)
3y = 4x + 12
⇒ y = \(\\ \frac { 4 }{ 3 } x+4\)

Question 19.
Find the equation of the line that is parallel to 2x + 5y – 7 = 0 and passes through the mid-point of the line segment joining the points (2, 7) and ( – 4, 1).
Solution:
The given line 2x + 5y – 7 = 0
5y = -2x + 7
⇒ \(y=\frac { -2 }{ 5 } x+\frac { 7 }{ 5 } \)

Question 20.
Find the equation of the line that is perpendicular to 3x + 2y – 8 = 0 and passes through the mid-point of the line segment joining the points (5, – 2), (2, 2).
Solution:
In the given line 3x + 2y – 8=0
⇒ 2y = – 3x + 8
⇒ y = \(\\ \frac { -3 }{ 2 } x+4\)

Question 21.
Find the equation of a straight line passing through the intersection of 2x + 5y – 4 = 0 with x-axis and parallel to the line 3x – 7y + 8 = 0.
Solution:
Let the point of intersection of the line 2x + 5y – 4 = 0 and x-axis be (x, 0)
Substituting the value of y in the equation
2x + 5 × 0 – 4 = 0
⇒ 2x – 4 = 0
⇒ 2x = 4
⇒ x = \(\\ \frac { 4 }{ 2 } \) = 2
Coordinates of the points of intersection will be (2, 0)

Question 22.
The equation of a line is 3x + 4y – 7 = 0. Find
(i) the slope of the line. .
(ii) the equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0. (2010)
Solution:
(i) Equation of the line is 3x + 4y – 1 = 0
⇒ 4y = 7 – 3x

Question 23.
Find the equation of the line perpendicular from the point (1, – 2) on the line 4x – 3y – 5 = 0. Also find the co-ordinates of the foot of perpendicular.
Solution:
In the equation 4x – 3y – 5 = 0,
⇒ 3y = 4x – 5
⇒ \(y=\frac { 4 }{ 3 } x-\frac { 5 }{ 3 } \)

Question 24.
Prove that the line through (0, 0) and (2, 3) is parallel to the line through (2, – 2) and (6, 4).
Solution:
Given that
Slope of the line through (0, 0) and (2, 3)

Question 25.
Prove that the line through,( – 2, 6) and (4, 8) is perpendicular to the line through (8, 12) and (4, 24).
Solution:
Given that
Slope of the line through (-2, 6) and (4, 8)

Question 26.
Show that the triangle formed by the points A (1, 3), B (3, – 1) and C ( – 5, – 5) is a right angled triangle by using slopes.
Solution:
Slope (m₁) of line by joining the points
A(1, 3), B (3, -1) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ x_{ 2 }-{ x }_{ 1 } } \)

Question 27.
Find the equation of the line through the point ( – 1, 3) and parallel to the line joining the points (0, – 2) and (4, 5).
Solution:
Slope of the line joining the points (0, -2) and (4, 5) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ x_{ 2 }-{ x }_{ 1 } } \)
= \(\frac { 5+2 }{ 4-0 } =\frac { 7 }{ 4 } \)
Slope of the line parallel to it passing through (-1, 3) = \(\\ \frac { 7 }{ 4 } \)

Question 28.
A ( – 1, 3), B (4, 2), C (3, – 2) are the vertices of a triangle.
(i) Find the coordinates of the centroid G of the triangle.
(ii) Find the equation of the line through G and parallel to AC
Solution:
Given, A (-1, 3), B (4, 2), C (3, -2)
(i) Coordinates of centroid G

Question 29.
The line through P (5, 3) intersects y-axis at Q.
(i) Write the slope of the line.
(ii) Write the equation of the line.
(iii) Find the coordinates of Q.

Solution:
(i) Here θ = 45°
So, slope of the line = tan θ = tan 45° = 1
(ii) Equation of the line through P and Q is
y – 3 = 1(x – 5) ⇒ y – x + 2 = 0
(iii) Let the coordinates of Q be (0, y)

Question 30.
In the adjoining diagram, write down
(i) the co-ordinates of the points A, B and C.
(ii) the equation of the line through A parallel to BC. (2005)

Solution:
From the given figure, it is clear that
co-ordinates of A are (2, 3) of B are ( -1, 2)
and of C are (3, 0).

Question 31.
Find the equation of the line through (0, – 3) and perpendicular to the line joining the points ( – 3, 2) and (9, 1).
Solution:
The slope (m₁) of the line joining the points (-3, 2) and (9, 1)

Question 32.
The vertices of a triangle are A (10, 4), B (4, – 9) and C ( – 2, – 1). Find the equation of the altitude through A. The perpendicular drawn from a vertex of a triangle to the opposite side is called altitude.
Solution:
Vertices of ∆ABC are A (10, 4), B (4, -9) and C( – 2, – 1)
Slope of the line BC (m₁) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)

Question 33.
A (2, – 4), B (3, 3) and C ( – 1, 5) are the vertices of triangle ABC. Find the equation of :
(i) the median of the triangle through A
(ii) the altitude of the triangle through B
Solution:
(i) D is the mid-point of BC
Co-ordinates of D will

Question 34.
Find the equation of the right bisector of the line segment joining the points (1, 2) and (5, – 6).
Solution:
Slope of the line joining the points (1, 2) and (5, -6)
\({ m }_{ 1 }=\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { -6-2 }{ 5-1 } =\frac { -8 }{ 4 } =-2\)

Question 35.
Points A and B have coordinates (7, – 3) and (1, 9) respectively. Find
(i) the slope of AB.
(ii) the equation of the perpendicular bisector of the line segment AB.
(iii) the value of ‘p’ if ( – 2, p) lies on it.
Solution:
Coordinates of A are (7, -3), of B = (1, 9)
(i) ∴ slope (m)

Question 36.
The points B (1, 3) and D (6, 8) are two opposite vertices of a square ABCD. Find the equation of the diagonal AC.
Solution:
Slope of BD (m₁) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
= \(\frac { 8-3 }{ 6-1 } =\frac { 5 }{ 5 } =1\)
Diagonal AC is perpendicular bisector of diagonal BD

Question 37.
ABCD is a rhombus. The co-ordinates of A and C are (3, 6) and ( – 1, 2) respectively. Write down the equation of BD. (2000)
Solution:
Co-ordinates of A (3, 6), C (-1, 2)
Slope of AC (m₁) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
= \(\frac { 2-6 }{ -1-3 } =\frac { -4 }{ -4 } =1\)

Question 38.
Find the equation of the line passing through the intersection of the lines 4x + 3y = 1 and 5x + 4y = 2 and
(i) parallel to the line x + 2y – 5 = 0
(ii) perpendicular to the x-axis.
Solution:
4x + 3y = 1 …(i)
5x + 4y = 2 …(ii)
Multiplying (i) by 4 and (ii) by 3

Question 39.
(i) Write down the co-ordinates of the point P that divides the line joining A ( – 4, 1) and B (17, 10) in the ratio 1 : 2.
(ii) Calculate the distance OP where 0 is the origin
(iii) In what ratio does the y-axis divide the line AB?
Solution:
(i) Co-ordinate A (-4, 1) and B (17, 10) P divides it in the ratio of 1 : 2
Let the co-ordinates of P will be (x, y)

Question 40.
Find the image of the point (1, 2) in the line x – 2y – 7 = 0
Solution:
Draw a perpendicular from the point P(1, 2) on the line, x – 2y – 7 = 0
Let P’ is the image of P and let its
co-ordinates sue (α, β) slope of line x – 2y – 7 = 0

Question 41.
If the line x – 4y – 6 = 0 is the perpendicular bisector of the line segment PQ and the co-ordinates of P are (1, 3), find the co-ordinates of Q.
Solution:
Let the co-ordinates of Q be (α, β) and let the line x – 4y – 6 = 0 is the

perpendicular bisector of PQ and it intersects the line at M.
M is the mid point of PQ Now slope of line x – 4y – 6 = 0

Question 42.
OABC is a square, O is the origin and the points A and B are (3, 0) and (p, q). If OABC lies in the first quadrant, find the values of p and q. Also write down the equations of AB and BC.
Solution:
OA = \(\sqrt { { (3-0) }^{ 2 }+{ (0-0) }^{ 2 } } \)
\(\sqrt { { (3-0) }^{ 2 }+{ (0) }^{ 2 } } \)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.
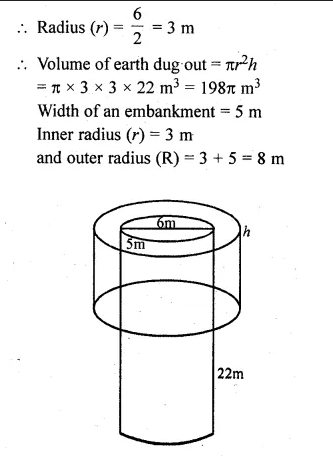
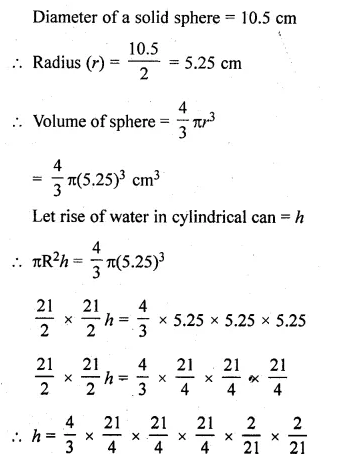
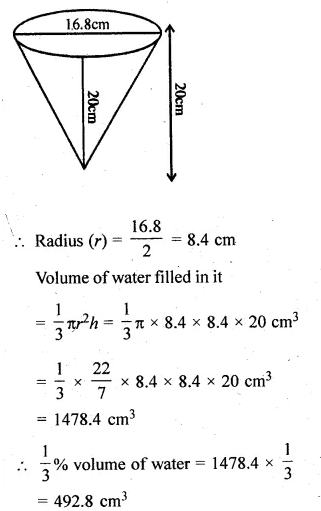
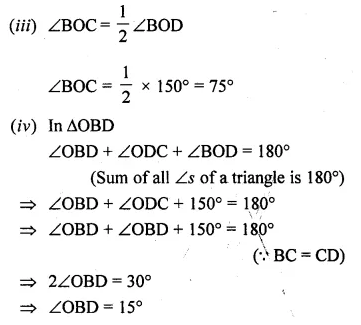
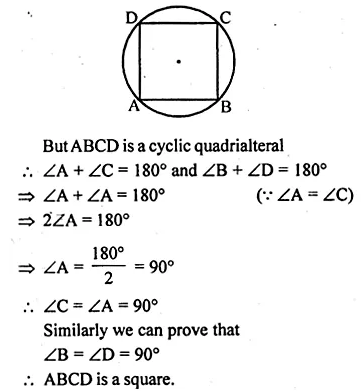
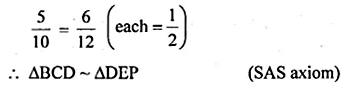
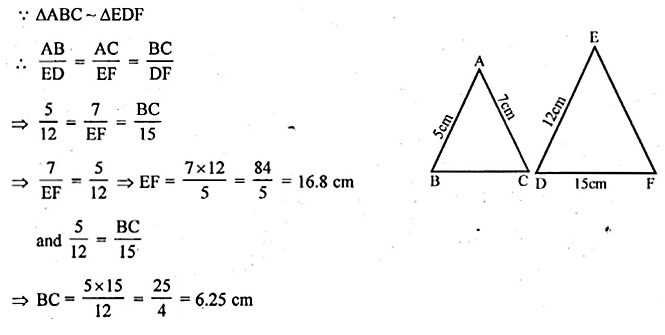
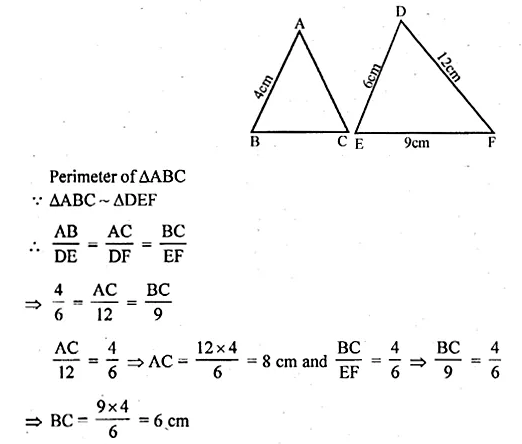
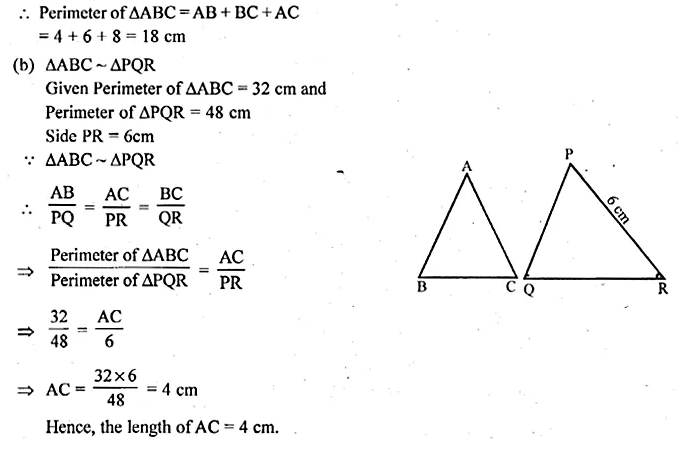
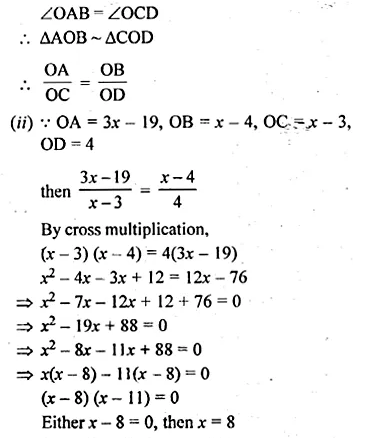
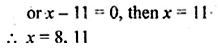