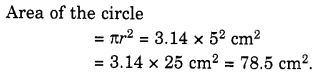Tag: NCERT Solutions for Class 7 Maths

NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1.

• Congruence of Triangles Class 7 Ex 7.2
• Congruence of Triangles Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 7
Chapter Name	Congruence of Triangles
Exercise	Ex 7.1
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1

Question 1.
Complete the following statements:
(a) Two line segments are congruent if……..
(b) Among two congruent angles, one has a measure of 70°; the measure of the other angle is…….
(c) When we write ∠A = ∠B, we actually mean….
Solution:
(a) they have the same length
(b) 70°
(c) m∠A = m∠B

Question 2.
Give any two real-life examples for congruent shapes.
Solution:

1. Two coins or notes of the same denomination.
2. Two keys of the same lock.

Question 3.
If ∆ ABC = ∆ FED under the correspondence ABC ↔ FED, write all the corresponding congruent parts of the triangles.
Solution:
Corresponding vertices: A and F; B and E; C and D.
Corresponding sides : \(\overline { AB } \) and \(\overline { FE } \) ; \(\overline { BC } \) and \(\overline { ED } \); \(\overline { CA } \) and \(\overline { DF } \).
Corresponding angles: ∠A and ∠F; ∠B and ∠E; ∠C and ∠D.

Question 4.
If ∆ DEF = ∆ BCA, write the part(s) of ∆ BCA that correspond to

1. ∠E
2. \(\overline { EF } \)
3. ∠F
4. \(\overline { DF } \)

Solution:

1. ∠C
2. \(\overline { CA } \)
3. ∠A
4. \(\overline { BA } \)

We hope the NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1.

• Lines and Angles Class  7 Ex 5.2
• Lines and Angles Class  7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 5
Chapter Name	Lines and Angles
Exercise	Ex 5.1, Ex 5.2.
Number of Questions Solved	14
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1

Question 1.
Find the complement of each of the following angles:

Solution:
Since, the sum of the measures of an angle and its complement is 90°, therefore,

1. The complement of an angle of measure 20° is the angle of (90° – 20°), f.e., 70°.
2. The complement of an angle of measure 63° is the angle of (90° – 63°), i.e., 27°.
3. The complement of an angle of measure 57° is the angle of (90° – 57°), i.e., 33°.

Question 2.
Find the supplement of each of the following angles:

Solution:

1. Supplement of the angle 105° = 180° – 105° = 75°
2. Supplement of the angle 87° = 180° – 87° = 93°
3. Supplement of the angle 154° = 180° – 154° = 26°

Question 3.
Identify which of the following pairs of angles are complementary and which are supplementary.

1. 65°, 115°
2. 63°, 27°
3. 112°, 68°
4. 130°, 50°
5. 45°,45°
6. 80°, 10°.

Solution:

1. Since, 65°+ 115° = 180°
   So, this pair of angles are supplementary.
2. Since, 63°+ 27° = 90°
   So, this pair of angles are complementary.
3. Since, 112° + 68° = 180°
   So, this pair of angles are supplementary.
4. Since, 130°+50° = 180°
   So, this pair of angles are supplementary.
5. Since, 45°+ 45° = 90°
   So, this pair of angles are complementary.
6. Since, 80°+ 10° = 90°
   So, this pair of angles are complementary.

Question 4.
Find the angle which is equal to its complement.
Solution:
Let the measure of the angle be x°. Then, the measure of its complement is given to be x°.
Since, the sum of the measures of an angle and its complement is 90°, therefore,
x° + x° = 90°
⇒ 2x° = 90°
⇒ x° = 45°
Thus, the required angle is 45°.

Question 5.
Find the angle which is equal to its supplement.
Solution:
Let the measure of the angle be x°. Then,
a measure of its supplement = x°
Since, the sum of the measures of an angle and its supplement is 180°, therefore,
x° + x° = 180°
⇒ 2x° =180°
⇒ x° = 90°
Hence, the required angle is 90°.

Question 6.
In the given figure, ∠ 1 and ∠ 2 are supplementary angles.

If ∠1 is decreased, what changes should take place in ∠ 2 so that both the angles still remain supplementary?
Solution:
∠ 2 will increase as much as ∠ 1 decreases.

Question 7.
Can two angles be supplementary if both of them are:

1. acute?
2. obtuse?
3. right?

Solution:

1. No! two acute angles cannot be a supplement.
2. No! Two obtuse angles cannot be supplementary.
3. Yes! Two right angles are always supplementary.

Question 8.
An angle is greater than 45°. Is its complementary angle greater than 45° or equal to 45° or less than 45°.
Solution:
Since the sum of the measure of ah angle and its complement is 90°.
∴ The complement of an angle of measures 45° + x°,
where x > 0 is the angle of [90° – (45° + x°)] = 90° – 45° – x°= 45° – x°.
Clearly, 45° + x° > 45° – x°
Hence, the complement of an angle > 45° is less than 45°.

Question 9.
In the adjoining figure:

1. Is ∠1 adjacent to ∠2 ?
2. Is ∠ AOC adjacent to ∠ AOE?
3. Do ∠ COE and ∠ EOD form a linear pair?
4. Are ∠ BOD and ∠ DOA supplementary?
5. Is ∠ 1 vertically opposite to ∠ 4?
6. What is the vertically opposite angle of ∠ 5?

Solution:

1. Yes ! ∠ 1 is adjacent to ∠ 2.
2. No ! ∠ AOC is not adjacent to ∠ AOE.
3. Yes! ∠ COE and ∠ EOD form a linear pair.
4. Yes ! ∠ BOD and ∠ DOA are supplementary.
5. Yes ! ∠ 1 is vertically opposite to ∠ 4.
6. The vertically opposite angle of ∠ 5 is ∠ 2 + ∠ 3, i.e., ∠ COB.

Question 10.
Indicate which pairs of angles are:

1. Vertically opposite angles.
2. Linear pairs.

Solution:

1. The pair of vertically opposite angles are ∠1, ∠4; ∠5, ∠2 + ∠3.
2. The pair of linear angles are ∠1, ∠5; ∠4, ∠5.

Question 11.
In the following figure, is ∠ 1 adjacent to ∠ 2? Give reasons.

Solution:
∠1 is not adjacent to ∠2 because they have no common vertex.

Question 12.
Find the values of the angles x, y, and z in each of the following:

Solution:

Question 13.
Fill in the blanks:

1. If two angles are complementary, then the sum of their measures is
2. If two angles are supplementary, then the sum of their measures is
3. Two angles forming a linear pair are
4. If two adjacent angles are supplementary, they form a
5. If two lines intersect at a point, then the vertically opposite angles are always
6. If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are

Solution:

1. 90°
2. 180°
3. supplementary
4. linear pair
5. equal
6. obtuse angles

Question 14.
In the adjoining figure, name the following pairs of angles.

1. Obtuse vertically opposite angles
2. Adjacent complementary angles
3. Equal supplementary angles
4. Unequal supplementary angles
5. Adjacent angles that do not form a linear pair.

Solution:

1. Obtuse vertically opposite angles are ∠AOD and ∠BOC.
2. Adjacent complementary angles are ∠BOA and ∠AOE.
3. Equal supplementary angles are ∠BOE and ∠EOD.
4. Unequal supplementary angles are ∠BOA and ∠AOD, ∠BOC and ∠COD, ∠EOA, and ∠EOC.
5. Adjacent angles that do not form a linear pair are ∠AOB and ∠AOE, ∠AOE and ∠EOD; ∠EOD and ∠COD.

We hope the NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Ex 8.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Ex 8.1.

• Comparing Quantities Class 7 Ex 8.2
• Comparing Quantities Class 7 Ex 8.3
• Comparing Quantities Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 8
Chapter Name	Comparing Quantities
Exercise	Ex 8.1
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Ex 8.1

Question 1.
Find the ratio of:
(a) ₹ 5 to 50 paise
(b) 15 kg to 210 g
(c) 9 m to 27 cm
(d) 30 days to 36 hour

Solution:
(a) ₹ 5 : 50 paise
= ₹ 5 : 50 paise
= 5 × 100 paise : 50 paise
= 500 paise : 50 paise
= 10 : 1.

(b) 15 kg to 210g
= 15 kg : 210g
= 15 × 1000 g : 210g
= 15000 g : 210g = 500:7.

(c) 9 m to 27 cm
= 9m : 27 cm = 9 × 100 cm : 27 cm
= 900 cm : 27 cm
900 : 27 = 100 : 3.

(d) 30 days to 36 hours
= 30 days : 36 hours
30 × 24 hours : 36 hours
= 720 hours : 36 hours
= 720 : 36 = 20 : 1.

Question 2.
In a computer lab, there are 3 computers for every 6 students. How many computers will be needed for 24 students?
Solution:
Let x computers be needed for 24 students.

Hence, 12 computers will be needed for
24 students.
Aliter:
In a computer lab,
Every 6 students need 3 computers.
∴ Every 1 student needs \(\frac { 3 }{ 6 } \) computers.
∴ Every 24 students need \(\frac { 3 }{ 6 } \) × 24 = 3 × 4 = 12 computers

Question 3.
Population of Rajasthan = 570 lakhs
and population of UP = 1660 lakhs.
Area of Rajasthan =3 lakh km2
and area of UP = 2 lakh km2.
(i) How many people are there per km2 in both these States?
(ii) Which State is less populated?
Solution:
(i) Number of people per sq. km. in Rajasthan state

(ii) The Rajasthan State is less populated.

We hope the NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Ex 8.1 helps you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Ex 8.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.1.

• The Triangle and its Properties Class 7 Ex 6.2
• The Triangle and its Properties Class 7 Ex 6.3
• The Triangle and its Properties Class 7 Ex 6.4
• The Triangle and its Properties Class 7 Ex 6.5
• The Triangle and its Properties Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 6
Chapter Name	The Triangle and its Properties
Exercise	Ex 6.1
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.1

Question 1.
In ∆PQR, D is the mid-point of \(\overline { QR } \).

Solution:
\(\overline { PM } \) is the altitude.
PD is the median.
No! QM ≠ MR.

Question 2.
Draw rough sketches for the following:

(a) In ∆ ABC, BE is a median.
(b) In ∆ PQR, PQ and PR are altitudes of the triangle.
(c) In ∆ XYZ, YL is an altitude in the exterior of the triangle.

Solution:

Question 3.
Verify by drawing a diagram if the median and altitude of an isosceles triangle can be the same.
Solution:
AD is the median.
AL is the altitude.

Draw a line segment BC. By paper folding, locate the perpendicular bisector of BC. The folded crease meets BC at D, its mid-point.
Take any point A on this perpendicular bisector. Join AB and AC. The triangle thus obtained is an isosceles ∆ABC in which AB = AC.
Since D is the mid-point of BC, so AD is its median. Also, AD is the perpendicular bisector of BC. So, AD is the altitude of ∆ABC.
Thus, it is verified that the median and altitude of an isosceles triangle are the same.

We hope the NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and it’s Properties Ex 6.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1.

• Algebraic Expressions Class 7 Ex 12.2
• Algebraic Expressions Class 7 Ex 12.3
• Algebraic Expressions Class 7 Ex 12.4
• Algebraic Expressions Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 12
Chapter Name	Algebraic Expressions
Exercise	Ex 12.1
Number of Questions Solved	7
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1

Question 1.
Get the algebraic expressions in the following cases using variables, constants, and arithmetic operations.
(i) Subtraction of z from y.
Solution:
y – z

(ii) One-half of the sum of numbers x and y.
Solution:
\(\frac{1}{2}\)  (x -y)

(iii) The number z multiplied by itself.
Solution:
z × z i.e., z²

(iv) One-fourth of the product of numbers p and q.
Solution:
\(\frac{1}{4}\) pq

(v) Numbers x and y both squared and added.
Solution:
x² + y²

(vi) Number 5 added to three times the product of numbers m and n.
Solution:
3mn + 5

(vii) Product of numbers y and z subtracted from 10.
Solution:
10 – yz

(viii) Sum of numbers a and 6 subtracted from their product.
Solution:
ab – (a + b)

Question 2.
(i) Identify the terms and their factors in the following expressions. Show the terms and factors by tree diagrams :

(a) x – 3
(b) 1 + x + x²
(c) y – y³
(d) 5xy² + 7x²y
(e) -ab + 2b² -3a²

(ii) Identify terms and factors in the expressions given below :

(a) – 4x + 5
(b) – 4x + 5y
(c) 5y + 3y²
(d) xy + 2x²y²
(e) pq + q
(f) 1.2 ab -2.4 b + 3.6 a
(g) \(\frac { 3 }{ 4 } \) x + \(\frac { 1 }{ 4 } \)
(h) 0.1 p² + 0.2 q²

Solution:

Question 3.
Identify the numerical coefficients of terms (other than constants) in the following expressions :

1. 5 – 3t²
2. 1 + t + t² + t³
3. x + 2xy + 3y
4. 100m + 1000n
5. -p²q² + 7pq
6. 1.2 a + 0.8 b
7. 3.14 r²
8. 2 (l + b)
9. 0.1 y + 0.01 y².

Solution:

Question 4.
(a) Identify terms which contain x and give the coefficient of x.

1. y²x + y
2. 13y² – 8yx
3. x + y + 2
4. 5 + z + zx
5. 1 + x + xy
6. 12xy² + 25
7. 7x + xy².

(b) Identify terms which contain y² and give the coefficient of y².

1. 8 – xy²
2. 5y² + 7x
3. 2x²y – 15xy² + 7y²

Solution:

Question 5.
Classify into monomials, binomials and trinomials.

1. 4y – 7z
2. y²
3. x + y – xy
4. 100
5. ab – a – b
6. 5 – 3t
7. 4p²q – 4pq²
8. 7mn
9. z² – 3z + 8 a² + b²
10. z² + z
11. 1 + x+ x²

Solution:
We know that an algebraic expression containing only one term is called a monomial. So, the monomials are : (ii), (iv), and (viii).

We know that an algebraic expression containing two terms is called a binomial. So, the binomials are : (i), (vi), (vii), (x) and (xi).

We know that an algebraic expression containing three terms is called a trinomial. So, the trinomial are : (iii), (v), (ix) and (xii).

Question 6.
State whether a given pair of terms is of like or unlike terms :
(i) 1, 100
Solution:
Like

(ii) -7x, \(\frac{5}{2}\)x
Solution:
Like

(iii) – 29x, – 29y
Solution:
Unlike

(iv)14xy, 42yx
Solution:
Like

(v) 4m²p, 4mp²
Answer:
Unlike

(vi) 12xz, 12x²z²
Solution:
Unlike

(i) 4y – 7z.
This expression is a binomial because it contains two terms: 4y and – Iz.
(ii) y².
This expression is a monomial because it contains only one term: y²
(iii) x + y – xy.
This expression is a trinomial because it contains three terms: x, y, and – xy.
(iv) 100.
This expression is a monomial because it contains only one term: 100
(v) ab – a – b.
This expression is a trinomial because it contains three terms: ab, -a, and -b
(vi) 5 – 3t.
This expression is a binomial because it contains two terms : 5 and – 31.
(vii) 4p²q – 4pq².
This expression is a binomial because it contains two terms: 4p²q and – 4pq².
(viii) 7mn.
This expression is a monomial because it contains only one term : 7mn.
(ix) z² – 3z + 8.
This expression is a trinomial because it contains three terms : z², – 3z and 8.
(x) a² + b².
This expression is a binomial because it contains two terms: a² and b².
(xi) z² + z.
This expression is a binomial because it contains two terms : z² and z.
(xii) 1 + x + x².
This expression is a trinomial because it contains three terms: 1, x, and x².

Question 6.
State whether a given pair of terms is of like or unlike terms :
(i) 1, 100
Solution:
Like

(ii) -7x, \(\frac{5}{2}\)x
Solution:
Like

(iii) – 29x, – 29y
Solution:
Unlike

(iv)14xy, 42yx
Solution:
Like

(v) 4m²p, 4mp²
Answer:
Unlike

(vi) 12xz, 12x²z²
Solution:
Unlike

Question 7.
Identify like terms in the following :

Solution:

We hope the NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1.

• Fractions and Decimals Class 7 Ex 2.2
• Fractions and Decimals Class 7 Ex 2.3
• Fractions and Decimals Class 7 Ex 2.4
• Fractions and Decimals Class 7 Ex 2.5
• Fractions and Decimals Class 7 Ex 2.6
• Fractions and Decimals Class 7 Ex 2.7
• Fractions and Decimals Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 2
Chapter Name	Fractions and Decimals
Exercise	Ex 2.1
Number of Questions Solved	8
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1

Question 1.
Solve :

Solution:

Question 2.
Arrange the following in descending order

Solution:
(i) Converting the given fractions into like fractions, we have


(ii) Converting the given fractions into like fractions, we have

Question 3.
In a “magic square”, the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?

Solution:
Yes ! this is a magic square.

Question 4.
A rectangular sheet of paper is 12 \(\frac { 1 }{ 2 } \) cm long 10 \(\frac { 2 }{ 3 } \) cm wide. find its perimeter
Solution:
Perimeter of the rectangular sheet of paper

Question 5.
Find the perimeters of (i) A ABE (ii) the rectangle BCDE in this figure. Whose perimeter is greater?
Solution:
(i) Perimeter of ∆ ABE = AB + BE + EA

(ii) Perimeter of the rectangle BCDE = BC + CD + DE + EB

So, the perimeter of A ABE is greater than the perimeter of the rectangle BCDE.

Question 6.
Salil wants to put a picture in a frame. The picture is 7 \(\frac { 3 }{ 5 } \) cm wide. To fit in the frame the picture cannot be more than 7 \(\frac { 3 }{ 10 } \) cm wide. How much should the picture be trimmed?
Solution:
The picture should be trimmed by

Question 7.
Ritu are \(\frac { 3 }{ 5 } \) part of an apple and the remaining apple was eaten by her brother Somu. How much part of the apple did Somu eat? Who had the larger share? By how much?
Solution:
Part of the apple ate by Somu

Question 8.
Michael finished colouring a picture in \(\frac { 7 }{ 12 } \) hour. Vaibhav finished colouring the same picture in \(\frac { 3 }{ 4 } \) hour. Who worked longer? By what fraction was it longer?
Solution:

We hope the NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1.

• Data Handling Class 7 Ex 3.2
• Data Handling Class 7 Ex 3.3
• Data Handling Class 7 Ex 3.4
• Data Handling Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 3
Chapter Name	Data Handling
Exercise	Ex 3.1
Number of Questions Solved	9
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1

Question 1.
Find the range of heights of any ten students of your class.
Solution:
Let the heights (in cm) of 10 students in the class be 150, 152, 151, 148, 149, 149, 150, 152, 153, 146.
Arranging the heights in ascending order, we have 146, 148, 149, 149, 150, 150, 151, 152, 152, 153.
Range of height of students = 153 – 146 = 7

Question 2.
Organize the following marks in a class assessment, in a tabular form.
4, 6, 7, 5, 3, 5, 4, 5, 2, 6, 2, 5, 1, 9, 6, 5, 8, 4, 6, 7
(i) Which number is the highest?
(ii) Which number is the lowest?
(iii) What is the range of the data?
(iv) Find the arithmetic mean.
Solution:

(i) Highest number is 9.
(ii) Lowest number is 1.
(iii) Range of the data = Highest observation – Lowest observation
= 9 – 1
= 8

Question 3.
Find the mean of the first five whole numbers.
Solution:
The first 5 whole numbers are 0, 1, 2, 3, and 4.
Their arithmetic mean

Question 4.
A cricketer scores the following runs in eight innings:
58, 76, 40, 35, 46, 45, 0, 100.
Find the mean score.
Solution:

Question 5.
Following table shows the points of each player scored in four games:

Now answer the following questions:

1. Find the mean to determine A’s average number of points scored per game.
2. To find the mean number of points per game for C, would you divide the total points by 3 or by 4? Why?
3. B played in all four games. How would you find the mean?
4. Who is the best performer?

Solution:

So, A’s average number of points scored per game is 12.5.
(ii) To find the mean number of points per game for C, we shall divide the total points by 3 because the number of games under consideration is 4 but ‘C’ did not play game 3.

Question 6.
The marks (out of 100) obtained by a group of students in a science test are 85, 76, 90, 85, 39, 48, 56, 95, 81 and 75. Find the:

1. Highest and the lowest marks obtained by the students.
2. Range of the marks obtained.
3. Mean marks obtained by the group.

Solution:

1. Highest marks obtained by the students = 95
   Lowest marks obtained by the students = 39
2. Range of the marks obtained = Highest marks – Lowest marks = 95 – 39 = 56
3. Mean marks obtained by the group
   

Question 7.
The enrolment of a school during six consecutive years was as follows:
1555, 1670, 1750, 2013, 2540, 2820.
Find the mean enrolment of the school for this period.
Solution:
Mean enrolment of the school for this period.

Question 8.
The rainfall (in mm) in a city on 7 days of a certain week was recorded as follows:

(i) Find the range of the rainfall in the above data.
(ii) Find the mean rainfall for the week.
(iii) On how many days was the rainfall less than the mean rainfall?
Solution:
(i) Range of the rainfall = Highest rainfall – Lowest rainfall = 20.5 mm – 0.0 mm = 20.5 mm
(ii) Mean rainfall for the week

(iii) The rainfall was less than the mean rainfall on 5 days.

Question 9.
The heights of 10 girls were measured in cm and the results are as follows:
135, 150, 139, 128, 151, 132, 146, 149, 143, 141.
(i) What is the height of the tallest girl?
(i) What is the height of the shortest girl?
(iii) What is the range of the data?
(iv) What is the mean height of the girls?
(v) How many girls have heights more than the mean height?

Solution:
(i) Height of the tallest girl = 151 cm
(ii) Height of the shortest girl = 128 cm
(iii) Range of the data

(v) 5 girls have heights more than the mean height.

We hope the NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1 helps you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.1.

• Integers Class 7 Ex 1.2
• Integers Class 7 Ex 1.3
• Integers Class 7 Ex 1.4
• Integers Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 1
Chapter Name	Integers
Exercise	Ex 1.1
Number of Questions Solved	10
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.1

Question 1.
Following number line shows the temperature in degree Celsius (°C) at different places on a particular day:

(a) Observe this number line and write the temperature of the places marked on it.
(b) What is the temperature difference between the hottest and the coldest places among the above?
(c) What is the temperature difference between Lahul-Spiti and Srinagar?
(d) Can we say temperature of Srinagar and Shimla taken together is less than the temperature at Shimla? Is it also less than the temperature at Srinagar?
Solution:
(a)

(b) The hottest place is Bangalore (22 °C) and the coldest place is Lahulspiti (-8°C). The temperature difference between the hottest and the coldest places
= 22 °C – (-8 °C)
= 22 °C + 8 °C
= 30 °C

(c) Temperature difference between Lahul-Spiti and Srinagar
= Temperature of Srinagar
– Temperature of Lahul-Spiti
= – 2°C – (- 8°C)
= – 2°C + 8°C
= 6°C

(d) Yes, we can say that the temperature of Srinagar and Shimla took together is less than the temperature at Shimla as -2 + 5 = 3 and 3 < 5.
This temperature is not less than the temperature at Srinagar.

Question 2.
In a quiz, positive marks are given for correct answers and negative marks are given for incorrect answers. If Jack’s scores in five successive rounds were 25, -5, -10, 15 and 10, what was his total at the end?
Solution:
Total at the end
= 25 + (- 5) + (- 10) + 15 + 10
= (25 + 15 + 10) + {(- 5) + (- 10))
= 50 + (- 15) = 35

Question 3.
At Srinagar, the temperature was – 5°C on Monday and then it dropped by 2°C on Tues¬day. What was the temperature of Srinagar on Tuesday? On Wednesday, it rose by 4°C. What was the temperature on this day?
Solution:
At Srinagar, the temperature was on Monday = -5 °C
Since the temperature was dropped by 2 °C on Tuesday, therefore, the temperature was on Tuesday = (-5-2) °C = -7°C
Also, on Wednesday the temperature rose by 4 °C.
∴ Temperature on Wednesday= (-7 + 4) °C = -3 °C

Question 4.
A plane is flying at the height of 5000 m above sea level. At a particular point, it is e×actly above a submarine floating 1200 m below sea level. What is the vertical distance between them?

Solution:
The vertical distance between the plane and submarine.
= 5000 m – (- 1200 m)
= 5000 m + 1200 m
= 6200 m.

Question 5.
Mohan deposits ₹ 2,000 in his bank account and withdraws ₹1,642 from it, the next day. If the withdrawal of the amount from the account is represented by a negative integer, then how will you represent the amount deposited?
Find the balance in Mohan’s account after the withdrawal.
Solution:
The amount deposited will be represented by a positive integer.
Balance in Mohan’s account after withdrawal
= (+ ₹ 2000) + (- ₹ 1642)
= ₹ (2000-1642)
= ₹ 358

Question 6.
Rita goes 20 km towards the east from point A to point B. From B, she moves 30 km towards the west along the same road. If the distance towards the east is represented by a positive integer then, how will you represent the distance travelled towards the west? By which integer will you represent her final position from A?

Solution:
The distance towards the west = -30 km
Her final position from A
= + 20 km + (- 30) km
= – (30 – 20) km
= – 10 km.

Question 7.
In a magic square each row, column, and diagonal have the same sum. Check which of the following is a magic square.

Solution:

I. Row, Sum = 5 + (- 1) + (- 4)
= 5 + (- 5) = 0
II. Row, Sum = (- 5) + (- 2) + 7
= (- 7) + 7 = 0
III. Row, Sum = 0 + 3 + (- 3)
= 0 + 0 = 0
I. Column, Sum = 5 + (- 5) + 0
= 0 + 0 = 0
II. Column, Sum = (- 1) + (- 2) + 3
= (- 3) + 3 = 0
III. Column, Sum = (- 4) + 7 + (- 3)
= 7 + (- 4) + (- 3)
= 7 + (- 7) = 0
One Diagonal, Sum = 5 + (- 2) + (- 3) = 5 + (- 5) = 0
Other Diagonal, Sum = 0 + (- 2) + (- 4) = 0 + (- 6) = -6 ≠ 0
Therefore, the given square is not a magic square.

I. Row, Sum = 1 + (- 10) + 0 = – 9
II. Row, Sum = (- 4) + (- 3) + (- 2) = – 9
III. Row, Sum = (- 6) + 4 + (- 7)
= 4 + (- 6) + (- 7)
= 4 + (- 13)
= – (13-4) = -9
I. Column, Sum = 1 + (- 4) + (- 6)
= 1 + (- 10)
= -(10 – 1) = – 9
II. Column, Sum = (- 10) + (- 3) + 4
= (-13)+ 4
= – (13-4) = -9
III. Column, Sum = 0 + (- 2) + (- 7)
= 0 + (- 9) = – 9
One Diagonal, Sum = 1 + (- 3) + (- 7)
= 1 + (- 10)
= -(10-1) = -9
Other Diagonal, Sum = (- 6) + (- 3) + 0
= (- 9) + 0 = – 9
Since each row, column, and diagonal ‘ have the same sum, therefore, the given square is a magic square.

Question 8.
Verify a – (- b) = a + b for the following values of a and b.
(i) a = 21, b = 18
(ii) a = 118, b = 125
(iii) a = 75, b = 84
(iv) a = 28, b = 11.
Solution:
(i) a = 21, b = 18
L.H.S. = a – (- b) = 21 – (- 18) = 21 + 18 = 39 …..(1)
R.H.S. = a + b = 21 + 18 = 39 …..(2)
From (1) and (2), we get a -(-b) = a + b

(ii) a = 118, b = 125
L.H.S. = a – (- b) = 118 – (- 125) = 118 + 125 = 243 …(1)
R.H.S. = a + b = 118 + 125 = 243 …(2)
From (1) and (2), we get a -(- b) = a + b

(iii) a = 75, b = 84
L.H.S. = a – (- b) = 75 – (- 84) = 75 + 84 = 159 …(1)
R.H.S. = a + b = 75 + 84 = 159 …(2)
From (1) and (2), we get a – (- b) = a + b

(iv) a = 28, b = 11
L.H.S. = a – (- b) = 28 -(-11) = 28 + 11 = 39 …(1)
R.H.S. = a + b = 28 + 11 = 39 …(2)
From (1) and (2), we get a – (- b) = a + b.

Question 9.
Use the sign of >, < or = in the bo× to make the statements true.
(a) (- 8) + (-4) …… (- 8) – (- 4)
(b) (-3) +7 – (19) …… 15-8 +(-9)
(c) 23 – 41 + 11 …… 23-41- 11
(d) 39 + (-24) – (15) …… 36+ (-52) – (- 36)
(e) – 231 + 79 + 51 …… -399 + 159 + 81.
Solution:
(a) L.H.S. = (- 8) + (- 4)
= – (8 + 4) = – 12
R.H.S. = (- 8) – (- 4)
= – 8 + 4 = – (8 – 4) = – 4
∴ (-8) + (-4) < (-8)-(-4)

(b) L.H.S. = (-3) + 7 – (19)
= + 4 – (19)
= + 4 – 19
= -15
R.H.S. = 15 – 8 + (- 9)
= 7 + (-9) = 7- 9 = -2
∴ (- 3) + 7 – (19) < 15 – 8 + (- 9)

(c) L.H.S. = 23 – 41 + 11
= 23 + 11- 41
= 34 – 41 = – (41 – 34)
= – 7
R.H.S. = 23 – 41 – 11
= 23 – (41 + 11)
= 23 – 52
= – (52 – 23)
= – 29
∴ 23 – 41 + > 23 – 41 – 11

(d) L.H.S. = 39 + (- 24) – (15)
= 39 – 24 – (15)
= 15 – (15) = 0
R.H.S. = 36 + (- 52) – (- 36)
= – (52 – 36) – (- 36)
= – 16 – (- 36)
= – 16 + 36 = 20
∴ 39 + (- 24) – (15) < 36 + (- 52) – (- 36)

(e) L.H.S. = – 231 + 79 + 51
= – 231 + 130
= – (231 – 130) = – 101
R.H.S. = – 399 + 159 + 81
= – 399 + 240
= – (399 – 240)
= – 159
∴ – 231 + 79 + 51 > – 399 + 159 + 81.

Question 10.
A water tank has stepped inside it. A monkey is sitting on the topmost step (i.e., the first step The water level is at the ninth step.

(i) He jumps 3 steps down and 2 steps up. In how many jumps will he reach the water level?
(ii) After drinking water he wants to go back. For this, he jumps 4 steps up and then jumps back 2 steps down in every move. In how many jumps will he reach back the top step?
(iii) If the number of steps moved down is represented by negative integers and the number of steps moved up by positive integers, represent his moves in part (i) and (ii) by completing the following;
(a) -3 + 2 – …………. = -8
(b) 4 – 2 + = 8.
In (a) the sum (-8) represents going down by eight steps. So, what will the sum 8 in (b) represent?
Solution:
(i) While going down the monkey jumps 3 steps down and then jumps back 2 steps up. To reach the water level he is to jump as under:
-3+ 2 -3 + 2 – 3 +2 – 3 + 2 – 3 + 2 – 3 = -8 Hence, he takes 11 jumps to reach the water level.
(ii) After drinking water, he jumps back as under to reach the top step as under : 4 – 2+ 4 – 2+ 4 = 8
Hence, he takes 5 jumps to reach back the top.
(iii) (a) – 3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3 + 2 – 3 = -8
(b) 4 – 2 + 4 – 2 + 4 = 8
In (b) the sum 8 represents going up 8 steps.

We hope the NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.1 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.1 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.1.

• Practical Geometry Class 7 Ex 10.2
• Practical Geometry Class 7 Ex 10.3
• Practical Geometry Class 7 Ex 10.4
• Practical Geometry Class 7 Ex 10.5

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 10
Chapter Name	Practical Geometry
Exercise	Ex 10.1
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.1

Question 1.
Draw a line, say, AB, take a point C outside it. Through C, draw a line parallel to AB using ruler and compasses only.
Solution:
Steps of Construction

1. Draw a line AB.
2. Take a point C outside it.
3. Take any point D on AB.
4. Join C to D.
   
5. with D as centre and a convenient radius, draw an arc cutting AB at F and CD at E.
6. Now with C as centre and the same radius as in step 5, draw an arc GH cutting CD at I.
7. Place the pointed tip of the compasses at F and adjust the opening so that the pencil tip is at E.
8. With the same opening as in step 7 and with I as centre, draw an arc cutting the arc GH at J.
9. Now join CJ to draw a line ‘KL’. Then KL is the required line.

Question 2.
Draw a line l. Draw a perpendicular to l at any point on l. On this perpendicular choose a point X, 4 cm away from l. Through X, draw a line m parallel to l.
Solution:
Steps of Construction

1. Draw a line l.
2. Take any point A on line l.
   
3. Construct an angle of 90° at point A of line l and draw a line AL perpendicular to line l.
4. Mark a point X on AL such that AX = 4 cm.
5. At X construct an angle of 90° and draw a line XC perpendicular to line AL.
6. Then line XC (line m) is the required line through X such that m || l.

Question 3.
Let l be a line and P be a point not on l. Through P, draw a line m parallel to l. Now join P to any point Q on l. Choose any other point R on m. Through R, draw a line parallel to PQ. Let this meet l at S. What shape do the two sets of parallel lines enclose?
Solution:
Steps of Construction

1. Draw a line l and take a point P not on it.
2. Take any point Q on l.
3. Join Q to P.
   
4. Draw a line m parallel to line l, as shown in the figure. Then line m || line l.
5. Join P to any point Q on l.
6. Choose any point R on m.
7. Join R to Q.
8. Through R, draw a line n parallel to the line PQ.
9. Let the line n meet the line l at S.
10. Then, the shape enclosed by the two sets of parallel lines is a parallelogram.

We hope the NCERT Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.1 helps you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 10 Practical Geometry EX 10.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.3 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.3.

• Perimeter and Area Class 7 Ex 11.1
• Perimeter and Area Class 7 Ex 11.2
• Perimeter and Area Class 7 Ex 11.4
• Perimeter and Area Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 11
Chapter Name	Perimeter and Area
Exercise	Ex 11.3
Number of Questions Solved	17
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.3

Question 1.
Find the circumference of the circles with the following radus (Take π = \(\frac { 22 }{ 7 } \))
(a) 14 cm
(b) 28 mm
(c) 21 cm
Solution:

Question 2.
Find the area of the following circles, given that: ( Take π = \(\frac { 22 }{ 7 } \) )
(a) radius = 14 mm
(b) diameter = 49 m
(c) radius = 5 cm.
Solution:

Question 3.
If the circumference of a circular sheet is 154 m, find its radius. Also find the area of the sheet ( Take π = \(\frac { 22 }{ 7 } \) )
Solution:
Circumference of the circular sheet = 154 m
Let the radius of the circular sheet be r cm
Then, its circumference = 2nr m According to the question,
Circumference = 2πr = 154

Question 4.
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase if he makes 2 rounds of offense. Also find the cost of the rope, if it costs ₹ 4 per meter. ( Take π = \(\frac { 22 }{ 7 } \) )
Solution:
The diameter of the circular garden (r) = 21 m
Radius of the circular garden (r) = \(\frac { 21 }{ 2 } \) m
∴ Circumference of the circular garden = 2πr
= 2 × \(\frac { 22 }{ 7 } \) × \(\frac { 21 }{ 2 } \) m = 66m
⇒ Length of the rope needed to make 1 round of fence = 66 m
⇒ Length of the rope needed to make 2 rounds of fence
= 66 × 2 m = 132 m
Cost of rope per meter = ₹ 4
∴ Cost of the rope = ₹ 132 × 4 = ₹ 528.

Question 5.
From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Solution:

Here, Outer radius, r = 4 cm
Inner radius, r = 3 cm
Area of the remaining sheet = Outer area – Inner area
= π (R² – r²) = 3.14 (4² – 3²) cm²
= 3.14 (16 – 9) cm²
= 3.14 × 7 cm² = 21.98 cm²

Question 6.
Saima wants to put lace on the edge of a circular table cover of a diameter of 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs ₹ 15. (Take π = 3.14)
Solution:
Diameter of the table cover = 1.5 m
⇒ Radius of the table cover (r) = \(\frac { 1.5 }{ 2 } \) m
⇒ Circumference of the table cover = 2πr
= 2 × 3.14 × \(\frac { 1.5 }{ 2 } \) m = 4.71 m
⇒ Length of the lace required = 4.71 m
∵ Cost of lace per meter = ₹ 15
∴ Cost of the lace = ₹ 4.71 × 15 = ₹ 70.65

Question 7.
Find the perimeter of the following figure, which is a semicircle including its diameter.
Solution:

Question 8.
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m². (Take π = 3.14)
Solution:
Diameter of the table-top = 1.6 m
⇒ Radius of the table-top (r) = \(\frac { 1.6 }{ 2 } \) m = 0.8 m
∴ Area of the table-top = πr²
= 3.14 × (0.8)2 m²
= 3.14 × 0.64 m²
= 2.0096 m²
∵ Rate of polishing = ₹ 15 per m²
∴ Cost of polishing the table-top = ₹ 2.0096 × 15
= ₹ 30.144
= ₹ 30.14 (approx.).

Question 9.
Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its side? Which figure encloses more area, the circle or the square? ( Take π = \(\frac { 22 }{ 7 } \) )
Solution:

Question 10.
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed (as shown in the following figure). Find the area of the remaining sheet. ( Take π = \(\frac { 22 }{ 7 } \) )

Solution:

Question 11.
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the leftover aluminium sheet? (Take π = 3.14)
Solution:

Question 12.
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
Solution:

Question 13.
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)

Solution:

Question 14.
A circular flower garden has an area of about 314 m². A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Taken π = 3.14)
Solution:
The circular area of the sprinkler = πr²
= 3.14 × 12 × 12
= 3.14 × 144 = 452.16 m²
Area of the circular flower garden = 314 m²
Since the area of the circular flower garden is smaller than by sprinkler
Therefore, the sprinkler will water the entire garden.

Question 15.
Find the circumference of the inner and the outer circles as shown in the following figure? (Take π = 3.14)

Solution:
Radius of inner circle = 19 – 10 = 9 m
∴ Circumference of the inner circle = 2 πr = 2 × 3.14 × 9 m = 56.52 cm
The radius of the outer circle = 19 m
∴ Circumference of the outer circle = 2πr = 2 × 3.14 × 19 m = 119.32 m.

Question 16.
How many times a wheel of radius 28 cm must rotate to go 352 m? ( Take π = \(\frac { 22 }{ 7 } \) )
Solution:

Question 17.
The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour? (Take π = 3.14)
Solution:
We know that the minute hand describes one complete revolution in one hour.
∴ Distance covered by its tip = Circumference of the circle of radius 15 cm
= (2 × 3.14 × 15) cm
= 94.2 cm

We hope the NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.3 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.2 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.2.

• Data Handling Class 7 Ex 3.1
• Data Handling Class 7 Ex 3.3
• Data Handling Class 7 Ex 3.4
• Data Handling Class 7 MCQ

Board	CBSE
Textbook	NCERT
Class	Class 7
Subject	Maths
Chapter	Chapter 3
Chapter Name	Data Handling
Exercise	Ex 3.2
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.2

Refer to our free online Polynomial in Ascending Order Calculator.

Question 1.
The scores in mathematics test (out of 25) of 15 students is as follows:
19, 25, 23, 20, 9, 20, 15, 10, 5, 16, 25, 20, 24, 12, 20
Find the mode and median of this data. Are they the same?
Solution:
For Median. We arrange the data in ascending order, we get
5, 9, 10, 12, 15, 16, 19, 20,
20, 20, 20, 23, 24, 25, 25
Median is the middle observation.
Therefore, 20 is the median.
For Mode.
Mode = Observation with highest frequency = 20
Yes, they are the same.

Question 2.
The runs scored in a cricket match by 11 players is as follows:
6, 15, 120, 50, 100, 80, 10, 15, 8, 10, 15.
Find the mean, mode, and median of this data. Are the three same?
Solution:

(ii) For Median. We arrange the data in ascending order, we get
6, 8, 10, 10, 15, 15, 15, 50, 80, 100, 120
Median is the middle observation. Therefore, 15 is the median.

(iii) For Mode. Mode = observation with highest frequency = 15
No! They are not the same.

Question 3.
The weights (in kg.) of 15 students of a class are:
38, 42, 35, 37, 45, 50, 32, 43,
43, 40, 36, 38, 43, 38, 47

1. Find the mode and median of this data.
2. Is there more than one mode?

Solution:
(i) For Median. We arrange the data in ascending order, we get
32, 35, 36, 37, 38, 38, 38, 40, 42, 43, 43,
43, 45, 47, 50
Median is the middle observation.
Therefore, 40 kg is the median.
For Mode. Mode = observation with highest frequency = 38 kg and 43 kg.
(ii) Yes! there are 2 (more than one) modes.

Question 4.
Find the mode and median of the data:
13, 16, 12, 14, 19, 12, 14, 13, 14.
Solution:
For Median. We arrange the data in ascending order, we get 12, 12, 13, 13, 14, 14, 14, 16, 19.
Median is the middle observation.
Therefore, 14 is the median.
For Mode. Mode = observation with highest frequency = 14.

Question 5.
Tell whether the statement is true or false:

1. The mode is always one of the numbers in data.
2. The mean is one of the numbers in a data.
3. The median is always one of the numbers in a data.
4. The data 6, 4, 3, 8, 9, 12, 13, 9 has a mean of 9.

Solution:

1. True
2. False
3. True
4. False.

 

We hope the NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.2 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.2, drop a comment below and we will get back to you at the earliest.