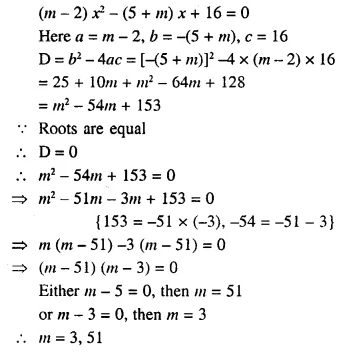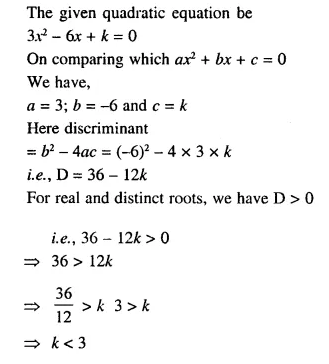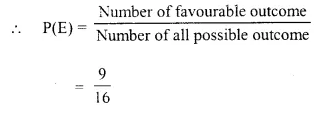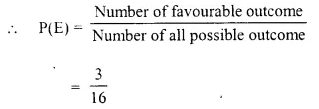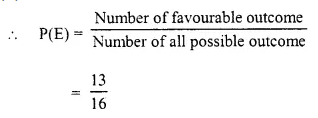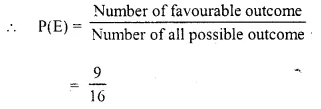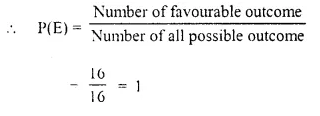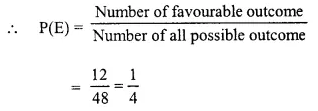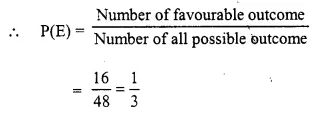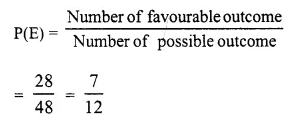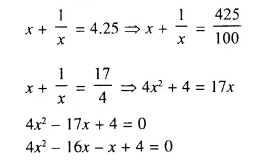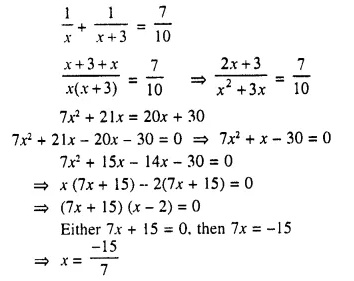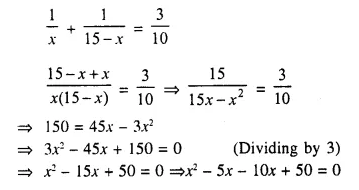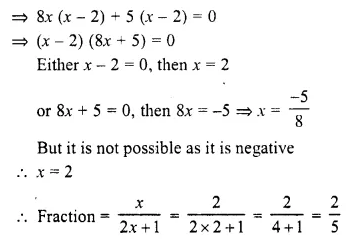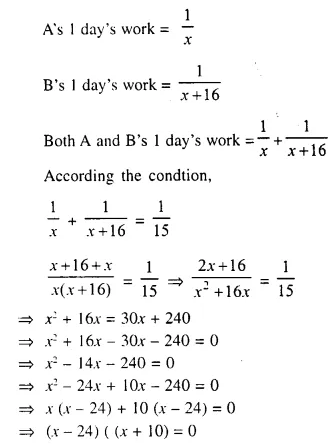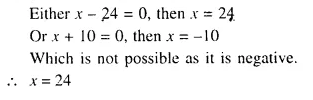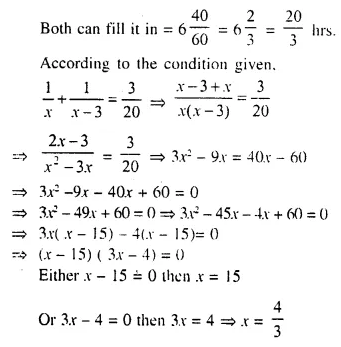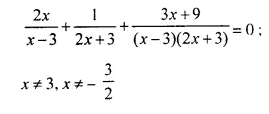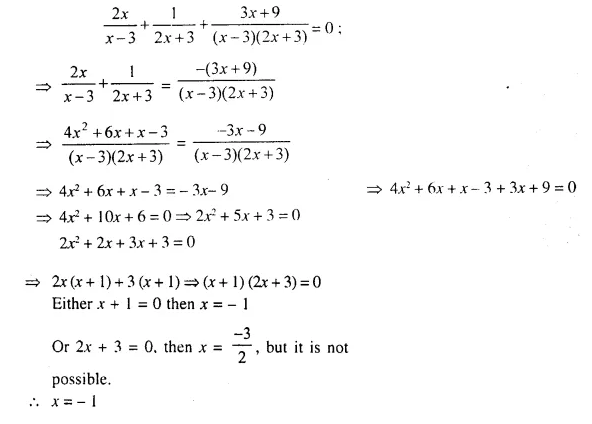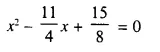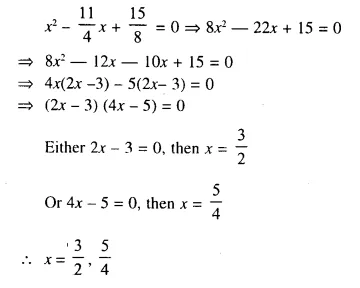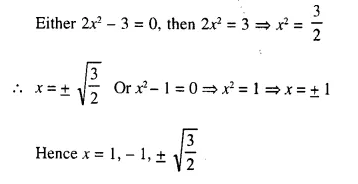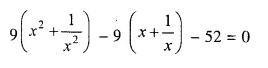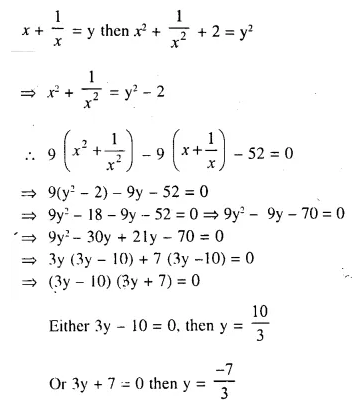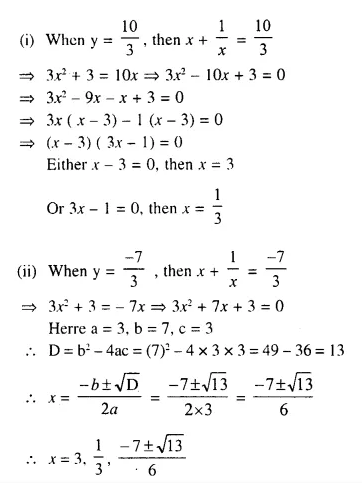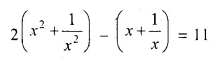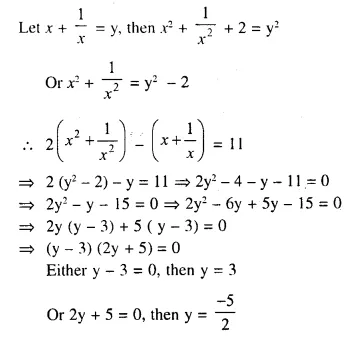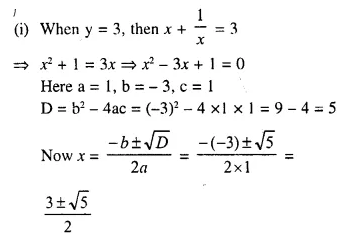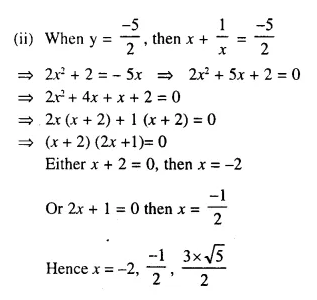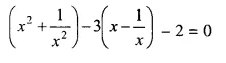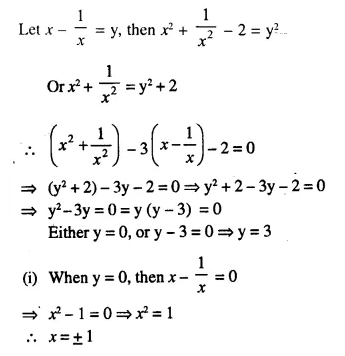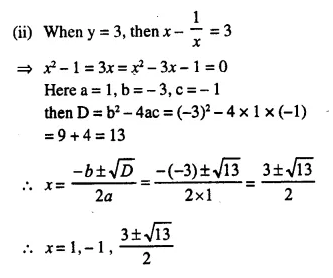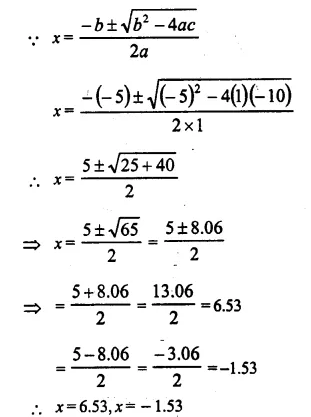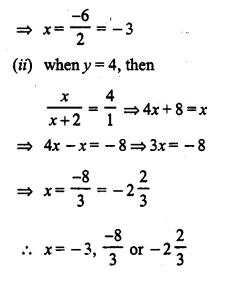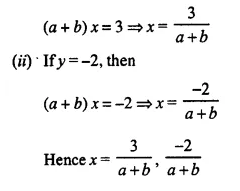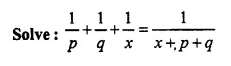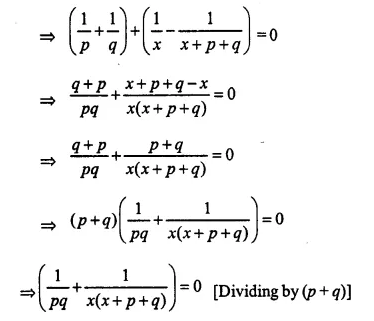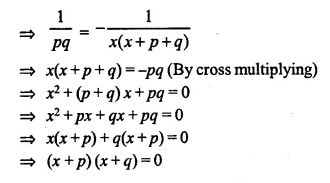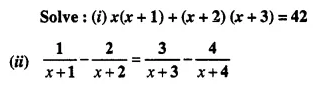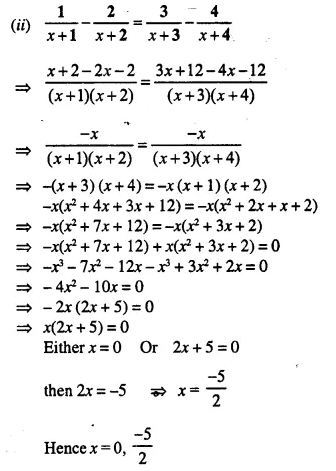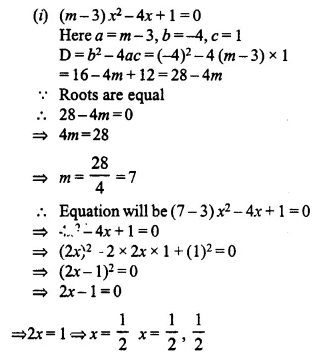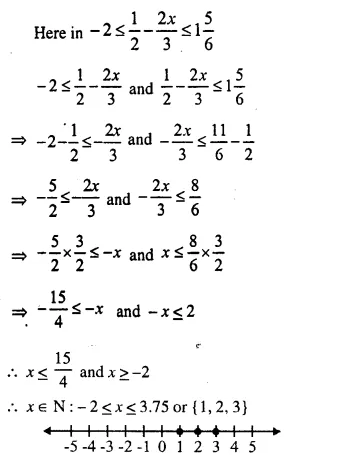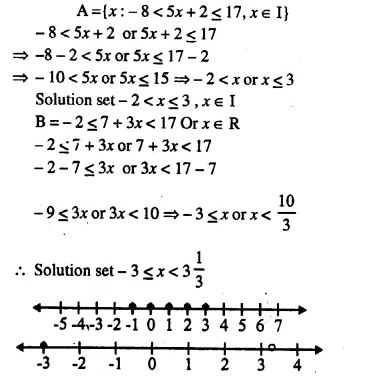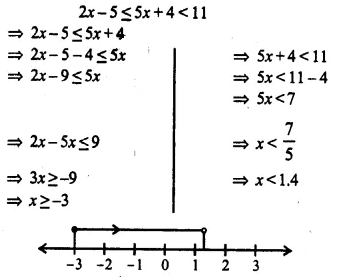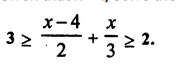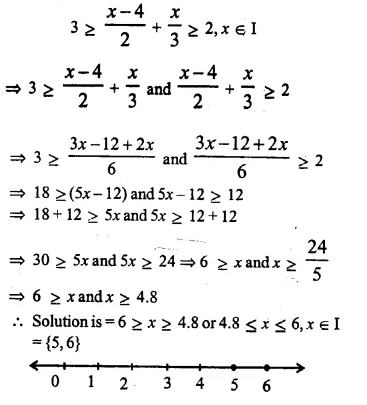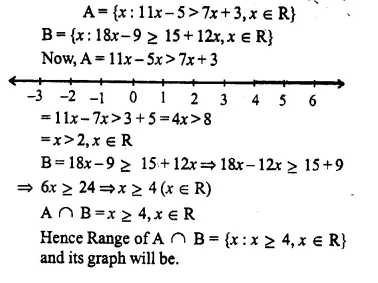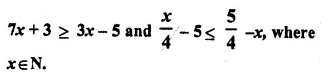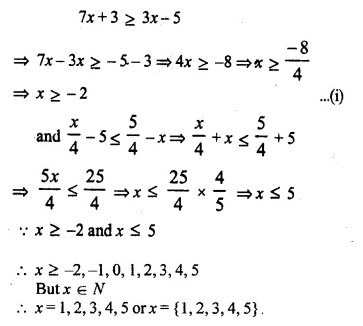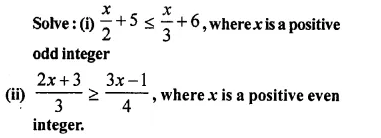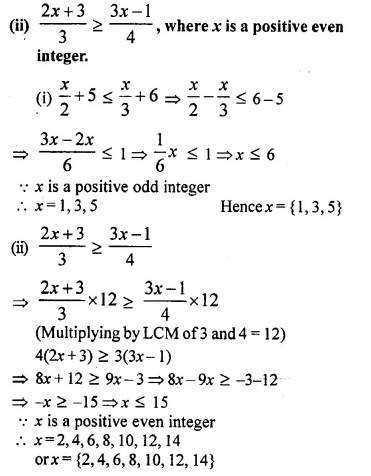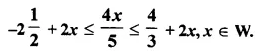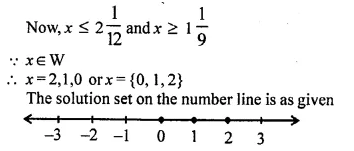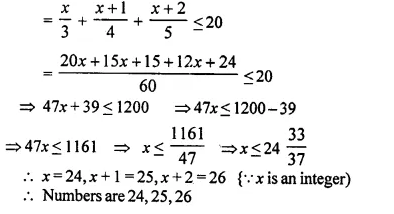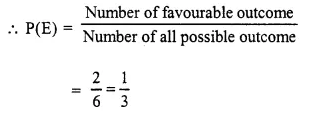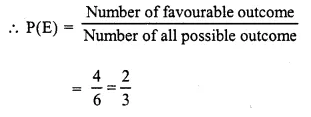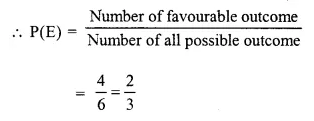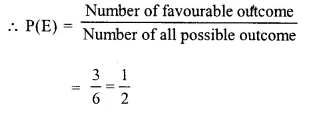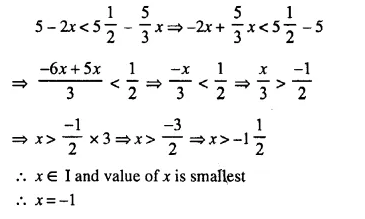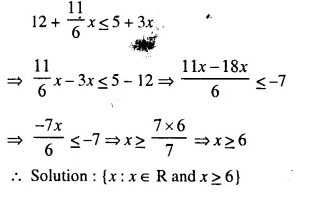Tag: Selina Concise ICSE Maths Solutions Class 10

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D

Solve equations, number 1 to number 20, given below, using factorisation method :
Question 1.
x² – 10x – 24 = 0
Solution:
x² – 12x + 2x – 24 = 0
⇒ x (x – 12) + 2 (x – 12) = 0
⇒ (x – 12) (x + 2) = 0
Either x – 12 = 0, then x = 12
or x + 2 = 0, then x = – 2
x = 12, – 2

Question 2.
x² – 16 = 0
Solution:
⇒ x² – (4)² = 0
⇒ (x + 4) (x – 4) = 0
Either x + 4 = 0, then x = – 4
or x – 4 = 0, then x = 4
x = 4, – 4

Question 3.
2x² – \(\frac { 1 }{ 2 }\) x = 0
Solution:
⇒ 4x² – x = 0
⇒ x (4x – 1) = 0
Either x = 0,
or 4x – 1 = 0, then 4x = 1 ⇒ x = \(\frac { 1 }{ 4 }\)
x = 0, \(\frac { 1 }{ 4 }\)

Question 4.
x (x – 5) = 24
Solution:
⇒ x² – 5x – 24 = 0
⇒ x² – 8x + 3x – 24 = 0
⇒ x (x – 8) + 3 (x – 8) = 0
⇒ (x – 8) (x + 3) = 0
Either x – 8 = 0, then x = 8
or x + 3 = 0, then x = – 3
x = 8, – 3

Question 5.
\(\frac { 9 }{ 2 }\) x = 5 + x²
Solution:
⇒ 9x = 10 + 2x²
⇒ 2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x (x – 2) – 5 (x – 2) = 0
⇒ (x – 2) (2x – 5) = 0
Either x – 2 = 0, then x = 2
or 2x – 5 = 0, then 2x = 5 ⇒ x = \(\frac { 5 }{ 2 }\)
x = 2, \(\frac { 5 }{ 2 }\)

Question 6.
\(\frac { 6 }{ x }\) = 1 + x
Solution:
⇒ 6 = x + x²
⇒ x² + x – 6 = 0
⇒ x² + 3x – 2x – 6 = 0
⇒ x (x + 3) – 2 (x + 3) = 0
⇒ (x + 3) (x – 2) = 0
Either x + 3 = 0, then x = – 3
or x – 2 = 0, then x = 2
x = 2, – 3

Question 7.
x = \(\frac { 3x + 1 }{ 4x }\)
Solution:
⇒ 4x² = 3x + 1
⇒ 4x² – 3x – 1 = 0
⇒ 4x² – 4x + x – 1 = 0
⇒ 4x (x – 1) + 1 (x – 1) = 0
⇒ (x – 1) (4x + 1) = 0
Either x – 1 = 0, then x = 1
or 4x + 1 = 0, then 4x = -1 ⇒ x = \(\frac { -1 }{ 4 }\)
x = 1, \(\frac { -1 }{ 4 }\)

Question 8.
x + \(\frac { 1 }{ x }\) = 2.5
Solution:

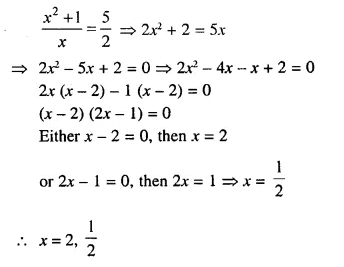
Question 9.
(2x – 3)² = 49
Solution:
⇒ 4x² – 12x + 9 = 49
⇒ 4x² – 12x + 9 – 49 = 0
⇒ 4x² – 12x – 40 = 0
⇒ x² – 3x – 10 = 0 (Dividing by 4)
⇒ x² – 5x + 2x – 10 = 0
⇒ x (x – 5) + 2 (x – 5) = 0
⇒ (x – 5) (x + 2) = 0
Either x – 5 = 0, then x = 5
or x + 2 = 0, then x = – 2
x = 5, – 2

Question 10.
2 (x² – 6) = 3 (x – 4)
Solution:
⇒ 2x² – 12 = 3x- 12
⇒ 2x² – 3x – 12 + 12 = 0
⇒ 2x² – 3x = 0
⇒ x (2x – 3) = 0
Either A = 0,
or 2x – 3 = 0, then 2x = 3 ⇒ x = \(\frac { 3 }{ 2 }\)
x = 0, \(\frac { 3 }{ 2 }\)

Question 11.
(x + 1) (2x + 8) = (x + 7) (x + 3)
Solution:

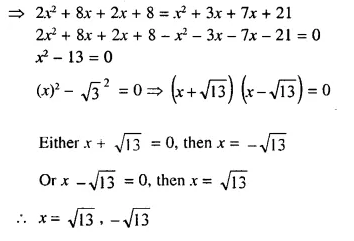
Question 12.
x² – (a + b) x + ab = 0
Solution:
⇒ x² – ax – bx + ab = 0
⇒ x (x – a) – b (x – a) = 0
⇒ (x – a) (x – b) = 0
Either x – a = 0, then x = a
or x – b = 0, then x = b
x = a, b

Question 13.
(x + 3)² – 4 (x + 3) – 5 = 0
Solution:
Let x + 3 = y, then
⇒ y² – 4y – 5 = 0
⇒y² – 5y + y – 5 = 0
⇒ y (y – 5) + 1 (y – 5) = 0
⇒ (y – 5) (y + 1) = 0
Substituting the value of y,
⇒ (x + 3 – 5) (x + 3 + 1) = 0
⇒ (x – 2) (x + 4) = 0
Either x – 2 = 0, then x = 2
or x + 4 = 0, then x = – 4
x = 2, -4

Question 14.
4 (2x – 3)² – (2x – 3) – 14 = 0
Solution:
Let 2x – 3 = y, then
⇒ 4y² – y – 14 = 0
⇒ 4y² – 8y + 7y – 14 = 0
⇒ 4y (y – 2) + 7 (y – 2) = 0
⇒ (y – 2) (4y + 7) = 0
Substituting the value of y,
⇒ (2x – 3 – 2) (8x – 12 + 7) = 0
⇒ (2x – 5) (8x – 5) = 0
Either 2x – 5 = 0, then 2x = 5 ⇒ x = \(\frac { 5 }{ 2 }\)
or 8x – 5 = 0, then 8x = 5 ⇒ x = \(\frac { 5 }{ 8 }\)
x = \(\frac { 5 }{ 2 }\) , \(\frac { 5 }{ 8 }\)

Question 15.

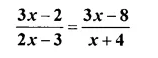
Solution:
⇒ (3x – 2) (x + 4) = (3x – 8) (2x – 3)
⇒ 3x² + 12x – 2x – 8 = 6x² – 9x – 16x + 24
⇒ 3x² + 12x – 2x – 8 – 6x² + 9x + 16x – 24 = 0
⇒ – 3x² + 35x – 32 = 0
⇒ 3x² – 35x + 32 = 0
⇒ 3x² – 3x – 32x + 32 = 0
⇒ 3x (x – 1) – 32 (x – 1) = 0
⇒ (x – 1) (3x – 32) = 0
⇒ 3x (x – 1) – 32 (x – 1) = 0
⇒ (x – 1) (3x – 32) – 0
Either x – 1 = 0, then x = 1
or 3x – 32 = 0, then 3x = 32 ⇒ x = \(\frac { 32 }{ 3 }\)
x = 1, \(\frac { 32 }{ 3 }\) or 1, 10\(\frac { 2 }{ 3 }\)

Question 16.
2x² – 9x + 10 = 0, when :
(i) x ∈ N
(ii) x ∈ Q.
Solution:
2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x (x – 2) – 5 (x – 2) = 0
⇒ (x – 2) (2 – 5) = 0
Either x – 2 = 0, then x = 2
or 2x – 5 = 0, then 2x = 5 ⇒ x = \(\frac { 5 }{ 2 }\)
(i) When x ∈ N, then x = 2
(ii) When x ∈ Q, then x = 2 , \(\frac { 5 }{ 2 }\)

Question 17.

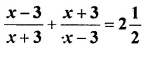
Solution:

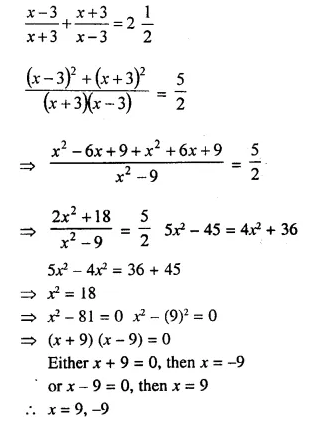
Question 18.

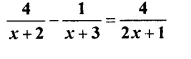
Solution:

Question 19.

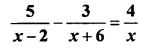
Solution:

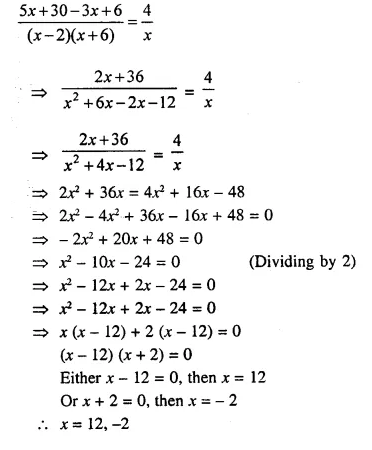
Question 20.

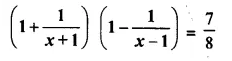
Solution:

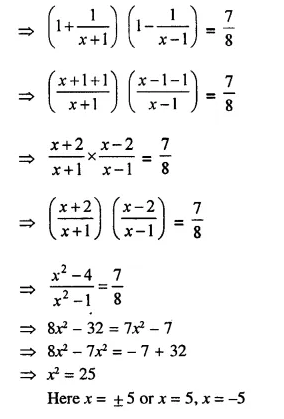
Question 21.
Find the quadratic equation, whose solution set is :
(i) {3, 5}
(ii) {-2, 3}
Solution:
(i) Solution set is {3, 5} or x = 3 and x = 5
Equation will be
(x – 3) (x – 5) = 0
⇒ x² – 5x – 3x + 15 = 0
⇒ x² – 8x + 15 = 0
(ii) Solution set is {-2, 3} or x = -2, x = 3
Equation will be
(x + 2) (x – 3) = 0
⇒ x² – 3x + 2x – 6 = 0
⇒ x² – x – 6 = 0

Question 22.

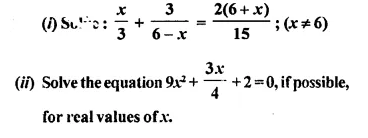
Solution:


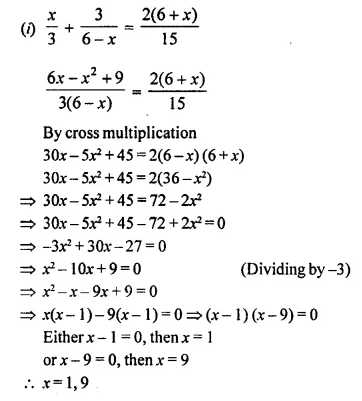
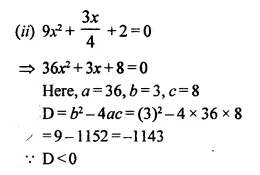
Roots are not real.
Hence there is no possible real value of x.

Question 23.
Find the value of x, if a + 1 = 0 and x² + ax – 6 = 0.
Solution:
a + 1 = 0 ⇒ a = -1
Now the equation x² + ax – 6 = 0 will be x² + (-1) x – 6 = 0
⇒ x² – x – 6 = 0
⇒ x² – 3x + 2x – 6 = 0
⇒ x (x – 3) + 2 (x – 3) = 0
Either x – 3 = 0, then x = 3
or x + 2 = 0, then x = – 2
x = 3, – 2

Question 24.
Find the value of x, if a + 7 = 0; b + 10 = 0 and 12x² = ax – b.
Solution:
a + 7 = 0, then a = -7
and b + 10 = 0, then b = -10
Now, substituting the value of a and b in
12x² = ax – b
⇒ 12x² = – 7x – (-10)
⇒ 12x² = – 7x + 10
⇒ 12x² + 7x – 10 = 0
⇒ 12x² + 15x – 8x – 10 = 0
⇒ 3x (4x + 5) – 2 (4x + 5) = 0
⇒ (4x + 5) (3x – 2) = 0
Either 4x + 5 = 0, then 4x = -5 ⇒ x = \(\frac { 5 }{ 4 }\)
or 3x – 2 = 0, then 3x = 2 ⇒ x = \(\frac { 2 }{ 3 }\)
x = \(\frac { 5 }{ 4 }\), \(\frac { 2 }{ 3 }\)

Question 25.
Use the substitution y = 2x + 3 to solve for x, if 4 (2x + 3)² – (2x + 3) – 14 = 0.
Solution:
y = 2x + 3, then equation
4 (2x + 3)² – (2x + 3) – 14 = 0 will be 4y² – y – 14 = 0
⇒ 4y² – 8y + 7y – 14 = 0
⇒ 4y (y – 2) + 7 (y – 2) = 0
⇒ (y – 2) (4y + 7) = 0
Either y – 2 = 0, then y = 2

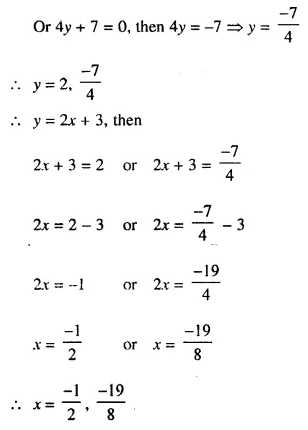
Question 26.
Without solving the quadratic equation 6x² – x – 2 = 0, find whether x = \(\frac { 2 }{ 3 }\) is a solution of this equation or not.
Solution:

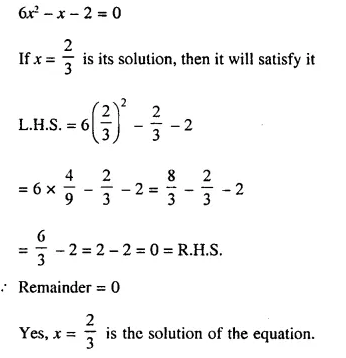
Question 27.
Determine whether x = -1 is a root of the equation x² – 3x + 2 = 0 or not.
Solution:
x² – 3x + 2 = 0
x = -1
Substituting the value of x = -1, in the quadratic equation
L.H.S. = x² – 3x + 2 = (-1)² – 3(-1) + 2 = 1 + 3 + 2 = 6 ≠ 0
Remainder is not equal to zero
x = -1 is not its root.

Question 28.
If x = \(\frac { 2 }{ 3 }\) is a solution of the quadratic equation 7x² + mx – 3 = 0; find the value of m.
Solution:

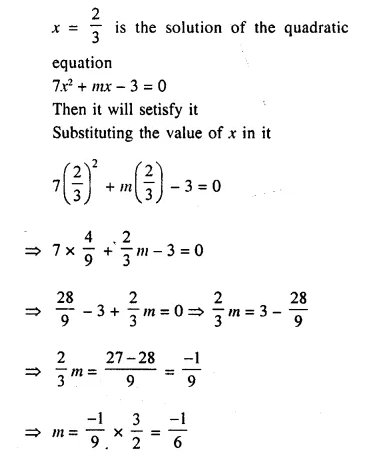
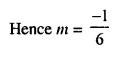
Question 29.
If x = -3 and x = \(\frac { 2 }{ 3 }\) are solutions of quadratic equation mx² + 7x + n = 0, find the values of m and n.
Solution:
x = -3, x = \(\frac { 2 }{ 3 }\) are the solution of the quadratic equation, mx² + 7x + n = 0
Then these values of x will satisfy it
(i) If x = -3, then mx² + 7x + n = 0
⇒ m(-3)² + 7(-3) + n = 0
⇒ 9m – 21 + n = 0
⇒ n = 21 – 9m ……(i)

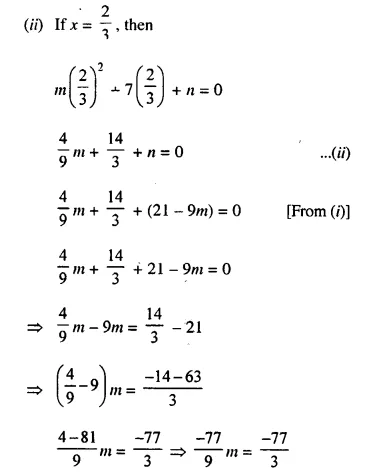
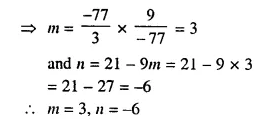
Question 30.
If quadratic equation x² – (m + 1) x + 6 = 0 has one root as x = 3; find the value of m and the other root of the equation.
Solution:
In equation, x² – (m + 1) x + 6 = 0
x = 3 is its root, then it will satisfy it
⇒ (3)² – (m + 1) x 3 + 6 = 0
⇒ 9 – 3m – 3 + 6 = 0
⇒ -3m + 12 = 0

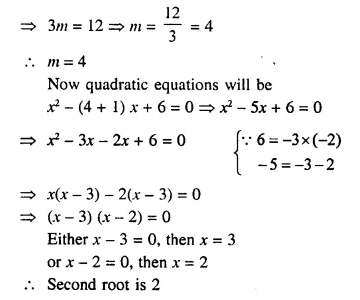
Question 31.
Give that 2 is a root of the equation 3x² – p (x + 1) = 0 and that the equation px² – qx + 9 = 0 has equal roots, find the values of p and q.
Solution:
3x² – p (x + 1) = 0
⇒ 3x² – px – p = 0
2 is a root of the equal It will satisfy it
3(2)² – p(2) – p = 0
⇒ 3 x 4 – 2p – p = 0
⇒ 12 – 3p = 0
⇒ 3p = 12
⇒ p = 4
px² – qx + 9 = 0
Here, a = p, b = -q, c = 9
D = b² – 4ac = (-q)² – 4 x p x 9 = q² – 36p
Roots are equal.
D = 0
⇒ q² – 36p = 0
⇒ q² – 36 x 4 = 0
⇒ q² = 144
⇒ q² = (±12)²
⇒ q = ± 12
Hence, p = 4 and q = ±12

Question 32.

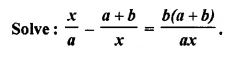
Solution:

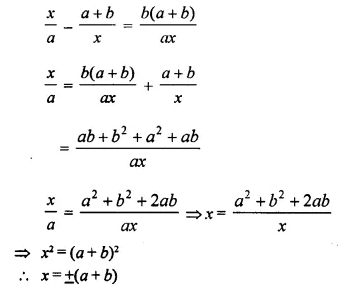
Question 33.
Solve: ( \(\frac { 1200 }{ x }\) + 2 ) (x – 10) – 1200 = 60
Solution:

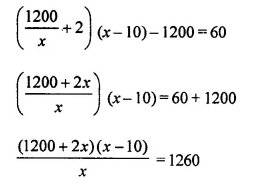
By cross multiplication,
⇒ 1200x – 12000 + 2x² – 20x – 1260x = 0
⇒ 2x² + 1200x – 20x – 1260x – 12000 = 0
⇒ 2x² – 80x – 12000 = 0
⇒ x² – 40x – 6000 = 0
⇒ x² – 100x + 60x – 6000 = 0
⇒ x (x – 100) + 60 (x – 100) = 0
⇒ (x – 100) (x + 60) = 0
Either x – 100 = 0, then x = 100
or x + 60 = 0, then x = -60
x = 100, -60

Question 34.
If -1 and 3 are the roots of x² + px + q = 0, find the values of p and q.
Solution:
-1 and 3 are the roots of the equation
x² + px + q = 0
Substituting the value of x = -1 and also x = 3, then
(-1 )² + p(-1) + q = 0
⇒ 1 – p + q = 0
⇒ p – q = 1
⇒ p = 1 + q …(i)
and (3)² + p x 3 + q = 0
⇒ 9 + 3p + q = 0
⇒ 9 + 3 (1 + q) + q = 0 [From(i)]
⇒ 9 + 3 + 3q + q = 0
⇒ 12 + 4q = 0
⇒ 4q = -12
⇒ q = -3
p = 1 + q = 1 – 3 = -2
Hence, p = -2, q = -3

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D

Question 1.
Without solving, comment upon the nature of roots of each of the following equations:
(i) 7x² – 9x + 2 = 0
(ii) 6x² – 13x + 4 = 0
(iii) 25x² – 10x + 1 = 0
(iv) x² + 2√3 x – 9 = 0
(v) x² – ax – b² = 0
(vi) 2x² + 8x + 9 = 0
Solution:

Question 2.
Find the value of ‘p’, if the following quadratic equations have equal roots :
(i) 4x² – (p – 2) x + 1 = 0
(ii) x² + (p – 3) x + p = 0
Solution:

Question 3.
The equation 3x² – 12x + (n – 5) = 0 has equal roots. Find the value of n.
Solution:
3x² – 12x + (n – 5) = 0
Here a = 3, b = -12, c = (n – 5)
D = b² – 4ac

Question 4.
Find the value of ‘m’, if the following equation has equal roots :
(m – 2) x² – (5 + m) x + 16 = 0
Solution:

Question 5.
Find the value of k for the which the equation 3x² – 6x + k = 0 has distinct and real root.
Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Chapter 25 Probability Ex 25B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25C

Question 1.
Nine cards (identical in all respects) are numbered 2 to 10. A card is selected from them at random. Find the probability that the card selected will be :
(i) an even number.
(ii) a multiple of 3 ,
(iii) an even number and a multiple of 3.
(iv) an even number or a multiple of 3.
Solution:
No. of cards = 9
Having numbers marked on it = 2 to 10
∴ Number of possible outcomes = 9
(i) An even number i.e. 2, 4, 6, 8, 10 = 5
∴ Number of even numbers = 5

(ii) A multiple of 3 are 3, 6, 9
Number of multiple of 3 = 3

(iii) An even number and a multiple of 3 are 6
which is one in number

(iv) An even number or a multiple of 3 are 2, 3, 4, 6, 8, 9, 10
which are 7 in numbers

Question 2.
Hundred identical cards are numbered from 1 to 100. The cards are well shuffled and then a card is drawn. Find the probability that the number on the card drawn is :
(i) a multiple of 5.
(ii) a multiple of 6.
(iii) between 40 and 60.
(iv) greater than 85.
(v) less than 48.
Solution:
Number of cards = 100
Marked with numbers from 1 to 100
∴ Number of possible outcome = 100
(i) A multiple of 5 are 5, 10, 15 95, 100
which are 20 in numbers.
∴ Number of favourable outcome = 20

(ii) A multiple of 6 are 6, 12, 18, 24, 90, 96
which are 16 in numbers.
∴ Number of favourable outcome =16

(iii) Between 40 and 60 are 41, 42, ……. , 58, 59,
which are 19

(iv) Greater than 85 are 86 to 100 which are 15 in numbers.

(v) Less than 48 are 1 to 47 which are 47 in numbers

Question 3.
From 25 identical cards, numbered, 1, 2, 3, 4, 5 ,…………, 24, 25 ; one card is drawn at random.
Find the probability that the number on the card drawn is a multiple of :
(i) 3
(ii) 5
(iii) 3 and 5
(iv) 3 or 5
Solution:
Number of identical cards = 25
Numbers marked on their are 1 to 25 i.e.
1, 2, 3, 4, 5, …. 21, 22, 23, 24, 25
∴ Number of possible outcome = 25
(i) Multiple of 3 are 3, 6, 9, 12, 15, 18, 21, 24
Which are 8 in numbers.

(ii) Multiple of 5 are 5, 10, 15, 20, 25
which are 5 in numbers

(iii) Multiple of 3 and 5 are = 15
which is 1 in number

(iv) Multiple of 3 or 5 are 3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25
which are 12 in numbers

Question 4.
A die is thrown once. Find the probability of getting a number :
(i) less than 3.
(ii) greater than or equal to 4.
(iii) less than 8
(iv) greater than 6.
Solution:
A die has 6 numbers i.e., 1, 2, 3, 4, 5, 6
∴ Number of possible outcome = 6
(i) Less than 3 are 1, 2 which are 2 in numbers

(ii) Greater than or equal to 4 are 4, 5, 6
which are 3 in number.

(iii) Less than 8 are 1, 2, 3, 4, 5, 6
which are 6 in numbers

(iv) Greater than 6 is nothing on the die

Question 5.
A book contains 85 pages. A page is chosen at random. What is the probability that the sum of the digits on the page is 8 ?
Solution:
Number of pages of the book = 85
which are from 1 to 85
Number of possible outcome = 85
∴ Number of pages whose sum of its page is 8 are : 17, 26, 35, 44, 53, 62, 71, 80 and 8

Question 6.
A pair of dice is thrown. Find the probability of getting a sum of 10 or more if 5 appears on the first die.
Solution:
Numbers marked on each die = 6
∴ Total number of cases = 6 x 6 = 36
∵ Favourable come are (5, 5), (5, 6) as 5 appears on the first, which are 2 in number

Question 7.
If two coins are tossed once, what is the probability of getting :
(i) 2 heads
(ii) at least one head
(iii) both heads or both tails.
Solution:
∵ A coins has two faces Head and Jail or H, T
∴ Two coins are tossed
∴ Number of coins = 2 x 2 = 4
which are HH, HT, TH, TT
(i) When both are Head, then
∴ Number of outcome = 1

(ii) At least one head, then
Number of outcomes = 3

(iii) When both head or both tails, then 1
Number of outcomes = 2

Question 8.
Two dice are rolled together. Find the probability of getting :
(i) a total of at least 10.
(ii) a multiple of 2 on one die and an odd number on the other die.
Solution:
∵ A die has 6 faces which are 1, 2, 3, 4, 5,6
∴ On rolling two dice at a time, number of comes = 6 x 6 = 36
∴ Number of possible outcome = 36
(i) a total of atleast 10, the favourable can be (4,6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6) which are 6 in number

(ii) A multiple of 2 on one die and an odd number on the other
∴ Outcome can be (2, 1), (2, 3), (g, 5), (4, 1), (4,3) , (4, 5), (6, 1), (6, 3), (6, 5), (1, 2), (3, 2), (5, 2), (1, 4), (3, 4), (5, 4), (1, 6), (3, 6), 5, 6) which are 18 in numbers.
Number of favourable outcome

Question 9.
A card is drawn from a well-shuffled pack of 52 cards. Find the probability that the card drawn is :
(i) a spade.
(ii) a red card.
(iii) a face card.
(iv) 5 of heart or diamond.
(v) Jack or queen.
(vi) ace and king.
(vii) a red and a king.
(viii) a red or a king.
Solution:
A pack of playing card has 52 cards
∴ Number of possible outcome = 52
(i) A spade
∵ there are 13 cards of spade
∴ Number of favourable outcome = 13

(ii) A red card.
∵ There are 13 + 13 = 26 red card

(iii) A face card.
∵ There are 3 x 4 = 12 faces which are red.

(iv) 5 of heart or diamond.
∴ Number of cards =1 + 1=2

(v) Jack or queen
There are 4 + 4 = 8 such cards

(vi) ace and king.
There is no such card which is ace and king both
∴ P(E) = 0.
(vii) a red and a king
There are 2 such cards which are red kings

(viii) a red or a king
There are 26 cards which are red in which 2 kings are red and 2 more kings which are black = 26 + 2 = 28

Question 10.
A bag contains 16 coloured balls. Six are green, 7 are red and 3 are white. A ball is chosen, without looking into the bag. Find the probability that the ball chosen is :
(i) red
(ii) not red
(iii) white
(iv) not white
(v) green or red
(vi) white or green
(vii) green or red or white.
Solution:
Number of balls in a bag = 16
Green balls = 6
White balls = 3
Red balls = 7
∴ Total possible outcome =16
(i) Red balls = 7

(ii) Not red balls = 16-7 = 9

(iii) White balls = 3

(iv) Not white balls = 16 – 3= 13

(v) Green or red balls = 6 + 7 = 13

(vi) White or green balls = 3 + 6 = 9

(vii) Green or red or white balls =16

Question 11.
A ball is drawn at random from a box .ontammg 12 white. 16 red and 20 green balls. Determine the probability that the ball drawn is:
(i) white
(ii) red
(iii) not green
(iv) red or white.
Solution:
Number of balls in a box
White = 12
Red = 16
Green = 20
Total balls = 12 + 16 +20 = 48
∴ Total possible outcome = 48
(i) White balls = 12
∴ Number of favourable outcome =12

(ii) Red balls = 16
∴ Number of favourable outcome =16

(iii) Not green
Number of balls =12 + 16 = 28
∴ Number of favourable outcome = 28

(iv) Red or white balls =12 + 16 = 28
∴ Number of favourable outcome = 28

Question 12.
A card is drawn from a pack of 52 cards. Find the probability that the card drawn is :
(i) a red card
(ii) a black card
(iii) a spade
(iv) an ace
(v) a black ace
(vi) ace of diamonds
(vii) not a club
(viii) a queen or a jack
Solution:
Number of cards in playing card deck = 52
∴ Number of possible outcome = 52
(i) A red card
There are 13 + 13 = 26 red cards in the deck
∴ Number of favourable outcome = 26

(ii) A black card
There are 13 + 13 = 26 black cards
∴ Number of favourable outcome = 26

(iii) A spade
There are 13 spade cards in the deck
∴ Number of favourable outcome = 13

(iv) An Ace
There use 4 aces in the deck
Number of favourable outcome = 4

(v) A black ace
There are two black aces in a deck
∴ Number of favourable outcome = 2
Number of cards in playing card deck = 52

(vi) Ace of diamonds
∴ There are only one ace of diamonds
∴ Number of favourable of outcome = 1

(vii) Not a club
There are 13 x 3 = 39 cards which are not a club
∴ Number of favourable outcome = 39

(viii) A queen or a Jack
There are 4 queen cards and 4 Jack cards
∴ Number of favourable outcome = 4 + 4 = 8

Question 13.
Thirty identical cards are marked with numbers 1 to 30. If one card is drawn at random, find the probability that it is :
(i) a multiple of 4 or 6.
(ii) a multiple of 3 and 5
(iii) a multiple of 3 or 5
Solution:
There are 30 cards which are marks with numbers 1 to 30 and one card is drawn
(i) A multiple of 4 or 6.
∴ There are multiple of 4 or 6 = 4,6, 8, 12, 16, 18, 20, 24, 28, 30 which are 10
∴ Number of favourable outcome = 10

(ii) A multiple of 3 and 5 are 15, 30 which are 2
∴ Number of favourable outcome = 2

(iii) A multiple of 3 or 5
which are 3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25, 27, 30 which are 14
∴ Number of favourable outcome = 14

Question 14.
In a single throw of two dice, find the probability of :
(i) a doublet
(ii) a number less than 3 on each dice.
(iii) an odd number as a sum.
(iv) a total of at most 10.
(v) an odd number on one dice and a number less than or equal to 4 on the other dice.
Solution:
Number of dice thrown = 2
Each die has 1 to 6 numbers on its faces Number of possible outcomes = 6 X 6 = 36
(i) A doublet : These can be (1, 1), (2, 2),(3, 3), (4, 4), (5, 5) and (6, 6) which are 6
∴ Number of favourable outcome = 6

(ii) A number less than 3 on each die which can be (1, 1), (1, 2), (2, 1), (2, 2) which are 4 in numbers
∴ Number of favourable outcome = 4

(iii) An odd number as a sum which can be (1, 1), (1,3), (1,5), (2, 1), (2,3), (2,5), (3, 1), (3,3), (3,5), (4, 1), (4,3), (4, 5), (5,1),(5,3), (5,5), (6, 1), (6, 3), (6, 5) which are 18 in numbers.
∴ Number of favourable outcome = 18

(iv) Total of at most 10
Which can be = 36 – 3 (which can be (5, 6), (6, 6), (6, 5) = 33
∴ Number of favourable outcome = 33

(v) An odd number on one die and a number less than or equal to 4 on the other die
(1, 1), (1,2), (1,3), (1,4), (3,1), (3,2), (3, 3), (3,4) , (5, 1), (5, 2), (5, 3), (5, 4), (2, 1), (3, 1), (4, 1),(1, 3), (2, 3), (2, 5), (3, 1), (3, 5), (4, 1), (4, 3), (4,5) which are 23 in numbers
∴ Number of favourable outcome = 23

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25B  are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems (Based on Quadratic Equations) Ex 6A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6E

Question 1.
The product of two consecutive integers is 56. Find the integers.
Solution:
Let the first integer = x
Then second integer = x + 1
Now according to the condition given
x (x + 1) = 56
⇒ x² + x – 56 = 0
⇒ x² + 8x – 7x – 56 = 0
⇒ x (x + 8) – 7 (x + 8) = 0
⇒ (x + 8) (x – 7) = 0
Either x + 8 = 0, then x = – 8
or x – 7 = 0, then x = 7
(i) If x = -8, then
first integer = -8
and second integer = – 8 + 1 = – 7
(ii) If x = 7, then
first integer = 7
and second integer = 7 + 1 = 8
Integers are 7, 8 or -8, -7

Question 2.
The sum of the squares of two consecutive natural numbers is 41. Find the numbers.
Solution:
Let the first natural number = x
Then second natural number = x + 1
Now according to the condition given,
(x)² + (x + 1)² = 41
⇒ x² + x² + 2x + 1 = 41
⇒ 2x² + 2x + 1 – 41 = 0
⇒ 2x² + 2x – 40 = 0
⇒ x² + x – 20 = 0 (Dividing by 2)
⇒ x² + 5x – 4x – 20 = 0
⇒ x (x + 5) – 4 (x + 5) = 0
⇒ (x + 5) (x – 4) = 0
Either x + 5 = 0 then x = – 5 But it is not a natural number
or x – 4 = 0, Then x = 4
Numbers are 4 and 5

Question 3.
Find the two natural numbers which differ by 5 and the sum of whose squares is 97.
Solution:
Let the first natural number = x
Then second natural number = x + 5
Now according to the given condition,
(x)² + (x + 5)² = 97
⇒ x² + x² + 10x + 25 – 97 = 0
⇒ 2x² + 10x – 72 = 0
⇒ x² + 5x – 36 = 0 (Dividing by 2)
⇒ x² + 9x – 4x – 36 = 0
⇒ x (x + 9) – 4 (x + 9) = 0
⇒ (x + 9) (x – 4) = 0
Either x + 9 = 0, then x = – 9 But it is not a natural number
or x – 4 = 0, then x = 4
First number = 4
and second number = 4 + 5 = 9

Question 4.
The sum of a number and its reciprocal is 4.25. Find the number.
Solution:
Let the number = x
Now according to the condition,

⇒ 4x (x – 4) – 1 (x – 4) = 0
⇒ (x – 4) (4x – 1) = 0
Either x – 4 = 0, then x = 4
or 4x – 1 = 0, 4x = 1 then x = \(\frac { 1 }{ 4 }\)
Number is 4 or \(\frac { 1 }{ 4 }\)

Question 5.
Two natural numbers differ by 3. Find the numbers, if the sum of their reciprocals is \(\frac { 7 }{ 10 }\)
Solution:
Let the first natural number = x
Then second natural number = x + 3
Now according to the given condition,

But it is not a natural number
or x – 2 = 0, then x = 2
First number = 2
and second number = 2 + 3 = 5

Question 6.
Divide 15 into two parts such that the sum of their reciprocals is \(\frac { 3 }{ 10 }\).
Solution:
Let first part = x
Then second part = 15 – x (sum = 15)
Now according to the given condition,

⇒ x (x – 5) – 10 (x – 5) = 0
⇒ (x – 5) (x – 10) = 0
Either x – 5 = 0, then x = 5
or x – 10 = 0, then x = 10
If x = 5, then first part = 15 – 5 = 10
If x = 10, then second part = 15 – 10 = 5
Parts are 5, 10

Question 7.
The sum of the squares of two positive integers is 208. If the square of the larger number is 18 times the smaller number, find the numbers.
Solution:
Let x be the larger number and y be the smaller number, then
According to the conditions x2 = 18 ….(i)
and x² + y² = 208 ….(ii)
⇒ 18y + y² = 208 [From (i)]
⇒ y² + 18y – 208 = 0
⇒ y² + 26y – 8y – 208 = 0
⇒ y (y + 26) – 8 (y + 26) = 0
⇒ (y + 26) (y – 8) = 0
Either y + 26 = 0, then y = -26
But it is not possible as it is not positive
or y – 8 = 0, then y = 8
Then x² = 18y ⇒ y² = 18 x 8 ⇒x² = 144 = (12)² ⇒ x = 12
Number are 12, 8

Question 8.
The sum of the squares of two consecutive positive even numbers is 52. Find the numbers.
Solution:
Let first even number = 2x
and second even number = 2x + 2
Now according to the given condition,
(2x)² + (2x + 2)² = 52
⇒ 4x² + 4x² + 8x + 4 = 52
⇒ 4x² + 4x² + 8x + 4 – 52 = 0
⇒ 8x² + 8x – 48 = 0
⇒ x² + x – 6 = 0 (Dividing by 8)
⇒ x² + 3x – 2x – 6 = 0
⇒ x (x + 3) – 2 (x + 3) = 0
⇒ (x + 3) (x – 2) = 0
Either x + 3 = 0, then x = – 3 But it is not possible because it is not positive.
or x – 2 = 0, then x = 2
First even number = 2 x 2 = 4
Second number = 4 + 2 = 6
Hence numbers are 4, 6

Question 9.
Find two consecutive positive odd numbers, the sum of whose squares is 74.
Solution:
Let first odd number = 2x -1
Second odd number = 2x – 1 + 2 = 2x + 1
Now according to the given condition,
(2x – 1)² + (2x + 1)² = 74
⇒ 4x² – 4x + 1 + 4x² + 4x + 1 = 74
⇒ 8x² + 2 – 74 = 0
⇒ 8x² – 72 = 0
⇒ x² – 9 = 0 (Dividing by 8)
⇒ (x + 3) (x – 3) = 0
Either x + 3 = 0, then x = -3 But it is not possible because it is not positive.
or x – 3 = 0, then x = 3
First odd number = 2x – 1 = 2 x 3 – 1 = 6 – 1 = 5
and second odd number = 5 + 2 = 7
Number are 5, 7

Question 10.
The denominator of a positive fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is 2.9; find the fraction.
Solution:
Let numerator of a fraction = x
Then denominator = 2x + 1

Question 11.
Three positive numbers are in the ratio \(\frac { 1 }{ 2 }\) : \(\frac { 1 }{ 3 }\) : \(\frac { 1 }{ 4 }\) Find the numbers; if the sum of their squares is 244.
Solution:
Multiply each ratio by L.C.M. of de-nominators i.e. by 12.
We get, 6 : 4 : 3
Let first positive number = 6x
Then second number = 4x
and third number = 3x
According to the given condition,
(6x)² + (4x)² + (3x)² = 244
⇒ 36x² + 16x² + 9x² = 244
⇒ 61x² = 244
⇒ x² – 4 = 0
⇒ (x + 2) (x – 2) = 0
Either x + 2 = 0, then x = -2 But it is not possible because it is not positive
or x – 2 = 0, then x = 2
First number = 6x = 6 x 2 = 12
Second number = 4x = 4 x 2 = 8
and third number = 3x = 3 x 2 = 6
Numbers are 12, 8, 6

Question 12.
Divide 20 into two parts such that three times the square of one part exceeds the other part by 10.
Solution:
Let first part = x
Then second part = 20 – x (Sum = 20)
Now, according to the given condition,
3(x)² – (20 – x) = 10
⇒ 3x² – 20 + x – 10 = 0
⇒ 3x² + x – 30 = 0
⇒ 3x² + 10x – 9x – 30 = 0
⇒ x (3x + 10) – 3 (3x + 10) = 0
⇒ (3x + 10) (x – 3) = 0
Either 3x + 10 = 0, then 3x = -10 ⇒ x = \(\frac { -10 }{ 3 }\)
But it is not possible.
or x – 3 = 0 then x = 3
Then first part = 3
and second part = 20 – 3 = 17

Question 13.
Three consecutive natural numbers are such that the square of the middle number exceeds the difference of the squares of the other two by 60. Assume the middle number to be x and form a quadratic equation satisfying the above statement Hence ; find the three numbers.
Solution:
Let middle number = x
Then, first number = x – 1
and third number = x + 1
Now according to the condition,
(x)²= [(x + 1)² – (x – 1)²] + 60
⇒ x² = [x² + 2x + 1 – x² + 2x – 1 ] + 60
⇒ x² = 4x + 60
⇒ x² – 4x – 60 = 0
⇒ x² – 10x + 6x – 60 = 0
⇒ x (x – 10) + 6 (x – 10) = 0
⇒ (x – 10) (x + 6) = 0
Either x – 10 = 0 then x = 10
or x + 6 = 0 then x = -6. But it is not a natural number.
Middle number = 10
First number = 10 – 1 = 9
and third number = 10 + 1 = 11
Hence numbers are 9, 10, 11

Question 14.
Out of three consecutive positive integers, the middle number is p. If three times the square of the largest is greater than the sum of the squares of the other two numbers by 67; calculate the value of p.
Solution:
Middle number = p
then smallest number = p – 1
and greatest number = p + 1
Now, according to the condition.
3 (p + 1)² – (p – 1)² – p² = 67
⇒ 3 (p² + 2p + 1) – (p² – 2p + 1) – p² = 67
⇒ 3p² + 6p + 3 – p² + 2p – 1 – p² – 67 = 0
⇒ p² + 8p + 2 – 67 = 0
⇒ p² + 8p – 65 = 0
⇒ p² + 13p – 5p – 65 = 0
⇒ p (p + 13) – 5 (p + 13) = 0
⇒ (p + 13) (p – 5) = 0
Either p + 13 = 0, then p = -13 But it is not possible.
or p – 5 = 0, then p = 5
p = 5

Question 15.
A can do a piece of work in ‘x’ days and B can do the same work in (x + 16) days. If both working together can do it in 15 days. Calculate ‘x’.
Solution:

Question 16.
One pipe can fill a cistern in 3 hours less than the other. The two pipes together can fill the cistern in 6 hours 40 minutes. Find the time that each pipe will take to fill the cistern.
Solution:
Let first pipe can fill the cistern in = x hrs.
Second pipe will fill the cistern in = x – 3 hrs.

But it is not possible.
x = 15
First pipe can fill in 15 hrs.
and second pipe in 15 – 3 = 12 hrs.

Question 17.
A positive number is divided into two parts such that the sum of the squares of the two parts is 20. The square of the larger part is 8 times the smaller part. Taking A as the smaller part of the two parts. Find the number. (2010)
Solution:
Let larger part = y
and smaller part = x
x² + y² = 20 ….(i)
and y² = 8x ….(ii)
Substituting the value of y² in „
x² + 8x = 20
⇒ x² + 8x – 20 = 0
⇒ x² + 10x – 1x – 20 = 0 {-20 = 10 x (-2), 8 = 10 – 2}
⇒ x (x + 10) – 2(x + 10) = 0
⇒ (x + 10) (x – 2) = 0
Either x + 10 = 0, then x = – 10 which is not possible because it is negative
or x – 2 = 0, then x = 2
Smaller number = 2
and larger number = y² = 8x = 8 x 2 = 16
⇒ y² = 16 = (4)²
⇒ y = 4
Number = x + y = 2 + 4 = 6

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency (Mean, Median, Quartiles and Mode) Ex 24A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Chapter 24 Measures of Central Tendency (Mean, Median, Quartiles and Mode) Ex 24A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24E

Question 1.
Find the mean of following set of numbers:
(i) 6, 9, 11, 12 and 7
(ii) 11, 14, 23, 26, 10, 12, 18 and 6.
Solution:

Question 2.
Marks obtained (in mathematics) by a students are given below :
60, 67, 52, 76, 50, 51, 74, 45 and 56
(a) Find the arithmetic mean
(b) If marks of each student be increased by 4;
what will be the new value of arithmetic mean.
Solution:
(a) Hence x = 9

(b) If marks of each students be increased by 4 then new mean will be = 59 + 4 = 63

Question 3.
Find the mean of natural numbers from 3 to 12.
Solution:
Numbers betweeen 3 to 12 are 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Here n = 10

Question 4.
(a) Find the means of 7, 11, 6, 5 and 6. (b) If each number given in (a) is diminished by 2; find the new value of mean.
Solution:
(a) The mean of 7, 11, 6, 5 and 6.

(b) If we subtract 2 from each number, then the mean will be 7 – 2 = 5

Question 5.
If the mean of 6, 4, 7, a and 10 is 8. Find the value of ‘a’.
Solution:
No. of terms = 5
Mean = 8
∴ Sum of number (Σx_i) = 5 x 8 = 40 …(i)
But Σx_i = 6 + 4 + 7 + a+10 = 27 + a ….(ii)
From (i) and (ii)
27 + a = 40 ⇒ a = 40 – 27
∴ a = 13

Question 6.
The mean of the number 6, y, 7, x and 14 is 8. Express y in terms of x.
Solution:
No. of terms = 5 and
mean = 8
∴ Sum of numbers (Σx_i) = 5 x 8 = 40 ….(i)
But sum of numbers given = 6 + y + 7 + x + 14
= 21 + y + x + ….(ii)
From (i) and (ii)
27 + y + x = 40
⇒ y = 40 – 27 – x
⇒ y= 13 – x

Question 7.
The ages of 40 students are given in the following table :

Find the arithmetic mean.
Solution:

Question 8.
If 69.5 is the mean of 72, 70, x, 62, 50, 71, 90, 64, 58 and 82, find the value of x.
Solution:
No. of terms = 10
Mean = 69.5
∴ Sum of numbers = 69,5 x 10 = 695 ….(i)
But sum of given number = 72 + 70 + x + 62 + 50 + 71 + 90 + 64 + 58 + 82 = 619+x ….(ii)
From (i) and (ii)
619 + x = 695
⇒ x = 695 – 619 = 76

Question 9.
The following table gives the heights of plants in centimeter. If the mean height of plants is 60.95 cm; find the value of ‘f’.

Solution:

Question 10.
From the data given below, calculate the mean wage, correct to the nearest rupee.

(i) If the number of workers in each category is doubled, what would be the new mean wage? [1995]
(ii) If the wages per day in each category are increased by 60%; what is the new mean wage?
(iii) If the number of workers in each category is doubled and the wages per day per worker are reduced by 40%. What would be the new mean wage?
Solution:

(i) Mean remains the same if the number of workers in each catagory is doubled.
∴ Mean = 80.
(ii) Mean will be increased by 60% if the wages per day per worker is increased by 60%.
∴ New mean = 80 x \(\frac { 160 }{ 100 }\)= 128
(iii) No change in the mean if the number of worker is doubled but if wages per worker is reduced by 40%, then
New mean = 80 x \(\frac { 60 }{ 100 }\)= 48

Question 11.
The contents of 100 match boxes were checked to determine the number of matches they contained.

(i) Calculate, correct to one decimal place, the mean number of matches per box.
(ii) Determine how many extra matches would have to be added to the total contents of the 100 boxes to bring the mean up to exactly 39 matches. [1997]
Solution:

(ii) In the second case,
New mean = 39 matches
∴ Total contents = 39 x 100 = 3900
But total no of matches already given = 3813
∴ Number of new matches to be added = 3900 – 3813 = 87

Question 12.
If the mean of the following distribution is 3, find the value of p.

Solution:
Mean = 3

Question 13.
In the following table, Σf= 200 and mean = 73. Find the missing frequencies f₁ and f₂.

Solution:

Question 14.
Find the arithmetic mean (correct to the nearest whole-number) by using step-deviation method.

Solution:
Let the Assumed mean = 30

Question 15.
Find the mean (correct to one place of decimal) by using short-cut method.

Solution:
Let the Assumed mean A = 45

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D

Solve each of the following equations :
Question 1.

Solution:

Question 2.
(2x + 3)² = 81
Solution:
(2x + 3)2 = 81
⇒ 4x² + 12x + 9 = 81
⇒ 4x² + 12x + 9 – 81 = 0
⇒ 4x² + 12x – 72 = 0
⇒ x² + 3x – 18 = 0 (Dividing by 4)
⇒ x² + 6x – 3x – 18 = 0
⇒ x (x + 6) – 3 (x + 6) = 0
⇒ (x + 6) (x – 3) = 0
Either x + 6 = 0, then x = -6
or x – 3 = 0, then x = 3
x = 3, – 6

Question 3.
a² x² – b² = 0
Solution:
a² x² – b² = 0
⇒ (ax)² – (b)² =0
⇒ (ax + b) (ax – b) =
Either ax + b = 0, then x = \(\frac { -b }{ a }\)
or ax – b = 0. then x = \(\frac { b }{ a }\)
x = \(\frac { b }{ a }\) , \(\frac { -b }{ a }\)

Question 4.

Solution:

Question 5.
x + \(\frac { 4 }{ x }\) = – 4; x ≠ 0
Solution:
x + \(\frac { 4 }{ x }\) = -4
⇒ x² + 4 = -4x
⇒ x² + 4x + 4 = 0
⇒ (x + 2)² = 0
⇒ x + 2 = 0
⇒ x = – 2

Question 6.
2x⁴ – 5x² + 3 = 0
Solution:
2x⁴ – 5x² + 3 = 0
⇒ 2(x²)² – 5x² + 3 = 0
⇒ 2(x²)² – 3x² – 2x² + 3 = 0
⇒ 2x⁴ – 3x² – 2x² + 3 = 0
⇒ x² (2x² – 3) – 1 (2x² – 3) = 0
⇒ (2x² – 3) (x² – 1) = 0

Question 7.
x⁴ – 2x² – 3 = 0
Solution:
x⁴ – 2x² – 3 = 0
⇒ (x²)² – 2x² – 3 = 0
⇒ (x²)² – 3x² + x² – 3 = 0
⇒ x² (x² – 3) + 1 (x² -3) = 0
⇒ (x² – 3) (x² + 1) = 0
Either x² – 3 = 0, then x² = 3 ⇒ x = √3
or x² + 1 = 0, then x² = – 1 In this case roots are not real
x = ±√3 or √3 , – √3

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.
(x² + 5x + 4)(x² + 5x + 6) = 120
Solution:
Let x² + 5x + 4 = y then x² + 5x + 6 = y + 2
Now (x² + 5x + 4) (x² + 5x + 6) = 120
⇒ y (y + 2) – 120 = 0
⇒ y² + 2y – 120 = 0
⇒ y² + 12y – 10y – 120 = 0
⇒ y (y + 12) – 10 (y + 12) = 0
⇒ (y + 12) (y – 10) = 0
Either y + 12 = 0, then y = – 12
or y – 10 = 0, then y = 10
(i) when y = -12, then x² + 5x + 4 = -12
⇒ x² + 5x + 4 + 12 = 0
⇒ x² + 5x + 16 = 0
Here a = 1, b = 5, c = 16
D = b² – 4ac = (5)² – 4 x 1 x 16 = 25 – 64 = -39
D < 0, then roots are not real
(ii) When y = 10, then x² + 5x + 4 = 10
⇒ x² + 5x + 4 – 10 = 0
⇒ x² + 5x – 6 = 0
⇒ x² + 6x – x – 6 = 0
⇒ x (x + 6) – 1 (x + 6) = 0
⇒ (x + 6) (x – 1) = 0
Either x + 6 = 0, then x = – 6
or x – 1 = 0, then x = 1
x = 1, -6

Question 12.
Solve each of the following equations, giving answer upto two decimal places:
(i) x² – 5x – 10 = 0 [2005]
(ii) 3x² – x – 7 = 0 [2004]
Solution:
(i) Given Equation is : x² – 5x – 10 = 0
On comparing with, ax² + bx + c = 0
a = 1, b = -5 , c = -10

Question 13.

Solution:

Question 14.
Solve:
(i) x² – 11x – 12 = 0; when x ∈ N
(ii) x² – 4x – 12 = 0; when x ∈ I
(iii) 2x² – 9x + 10 = 0; when x ∈ Q.
Solution:
(i) x² – 11x – 12 = 0
⇒ x² – 12x + x – 12 = 0
⇒ x (x – 12) + 1 (x – 12) = 0
⇒ (x – 12) (x + 1) = 0
Either x – 12 = 0, then x = 12
or x + 1 = 0, then x = -1
x ∈ N
x = 12
(ii) x² – 4x – 12 = 0
⇒ x² – 6x + 2x – 12 = 0
⇒ x (x – 6) + 2 (x – 6)=0
⇒ (x – 6) (x + 2) = 0
Either x – 6 = 0, then x = 6
or x + 2 = 0, then x = -2
x ∈ I
x = 6, -2
(iii) 2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x (x – 2) – 5 (x – 2) = 0
⇒ (x – 2) (2x – 5) = 0
Either x – 2 = 0, then x = 2
or 2x – 5 = 0, then 2x = 5 ⇒ x = \(\frac { 1 }{ 2 }\)
x ∈ Q
x = 2, \(\frac { 5 }{ 2 }\) or 2, 2.5

Question 15.
Solve: (a + b)² x² – (a + b) x – 6 = 0, a + b ≠ 0.
Solution:
(a + b)² x² – (a + b) x – 6 = 0
Let (a + b) x = y, then y² – y – 6 = 0
⇒ y² – 3y + 2y – 6 = 0
⇒ y (y – 3) + 2 (y – 3) = 0
⇒ (y – 3) (y + 2) = 0
Either y – 3 = 0, then y = 3
or y + 2 = 0, then y = – 2
(i) If y = 3, then

Question 16.

Solution:


Either x + p = 0, then x = -p
or x + q = 0, then x = -q
Hence x = -p, -q

Question 17.

Solution:
(i) x (x + 1) + (x + 2) (x + 3) = 42
⇒ x² + x + x² + 3x + 2x + 6 – 42 = 0
⇒ 2x² + 6x – 36 = 0
⇒ x² + 3x – 18 = 0
⇒ x² + 6x – 3x – 18 = 0
⇒ x (x + 6) – 3(x + 6) = 0
⇒ (x + 6) (x – 3) = 0
Either x + 6 = 0, then x = -6
or x – 3 = 0, then x = 3
Hence x = 3, -6

Question 18.
For each equation, given below, find the value of ‘m’ so that the equation has equal roots. Also, find the solution of each equation:
(i) (m – 3) x² – 4x + 1 = 0
(ii) 3x² + 12x + (m + 7) = 0
(iii) x² – (m + 2) x + (m + 5) = 0
Solution:

Question 19.
Without solving the following quadratic equation, find the value of ‘p’ for which the roots are equal. px² – 4x + 3 = 0.
Solution:
px² – 4x + 3 = 0 …..(i)
Compare (i) with ax² + bx + c = 0
Here a = p, b = -4, c = 3
D = b² – 4ac = (-4)² – 4.p.(3) = 16 – 12p
As roots are equal, D = 0
16 – 12p = 0
⇒ \(\frac { 16 }{ 12 }\) = p
⇒ p = \(\frac { 4 }{ 3 }\)

Question 20.
Without solving the following quadratic equation, find the value of m for which the given equation has real and equal roots : x² + 2 (m – 1) x + (m + 5) = 0.
Solution:
x² + 2 (m – 1) x + (m + 5) = 0.
Here, a = 1, b = 2 (m – 1), c = m + 5
So, discriminant, D = b² – 4ac
= 4(m – 1)² – 4 x 1 (m + 5)
= 4m² + 4 – 8m – 4m – 20
= 4m² – 12m – 16
For real and equal roots D = 0
So, 4m² – 12m – 16 = 0
⇒ m² – 3m – 4 = 0 (Dividingby4)
⇒ m² – 4m + m – 4 = 0
⇒ m (m – 4) + 1 (m – 4) = 0
⇒ (m – 4) (m + 1) = 0
⇒ m = 4 or m = -1

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16A

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B

Question 1.
Given— PQ is perpendicular bisector of side AB of the triangle ABC

Solution:

Question 2.
Given— CP is bisector of angle C of A ABC.

Prove: p is equidistant from AC and BC
Solution:

Question 3.
Given— AX bisects angle BAG and PQ is perpendicular bisector of AC which meets AX at point Y.

Prove:
(i) X is equidistant from AB and AC.
(ii) Y is equidistant from A and C.
Solution:
Construction: From X, draw XL ⊥ AC and XM ⊥ AB and join YC.

Question 4.
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
Solution:
Given: In Δ ABC, AB, = 4.2 cm, BC = 6.3 cm and AC = 5cm

Steps of Construction:
(i) Draw a line segment BC = 6.3 cm.
(ii) With centre B-and radius 4.2 cirr draw mi are.
(iii) With centre C mid radius 5 cm, draw another arc which intersect the first arc at A.
(iv) Join AB mid AC.
A ABC is the required triangle.
(v) Again with centre B mid C mid radius greater
than \(\frac { -1 }{ 2 }\) BC, draw arcs which intersects each other at L mid M.
(vi) Join LM intersecting AC at D mid BC at E.
(vii) Join DB.

Question 5.
In each of the given figures: PA = PH and QA = QB.

Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of points equidistant from two given fixed points.
Solution:
(i) Construction: Join PQ which meets AB in D.

Proof:
P is equidistant from A mid B
∴ P lies on die perpendicular bisector of AB similarly Q is equidistant from A mid B.
∴ Q lies on perpendicular bisector of AB P mid Q both lies on the perpendicular bisector of AB.
∴ PQ is Hie perpendicular bisector of AB

Hence locus of die points which are equidistant from two fixed points, is a perpendicular, bisector of die line joining die fixed points.         Q.E.D.

Question 6.
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
Solution:

Steps of Construction
(i) Draw a line segment QR = 4.5 cm.
(ii) At Q, draw a ray QX making an angle of 90°.
(iii) With centre P mid radius 8 cm, draw mi arc which intersects QX at P.
(iv) Join RP.
A-PQR is the required triangle.
(v) Draw the bisector of ∠PQR which meets PR in T.
(vi) From T, draw perpendicular PL and PM respec- lively on PQ and QR.

Question 7.
Construct a triangle ABC in which angle ABC = 75°. AB = 5 cm and BC = 6.4 cm.
Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisectors intersect each other at point P ; prove that P is equidistant from B and C ; and also from AC and BC.
Solution:

Steps of Construction:
(i) Draw a line segment BC = 6.4 cm.
(ii) At B, draw a ray BX making an angle of 75° with BC and cut off BA = 5 cm.
(iii) Join AC.
Δ ABC is the required triangle.
(iv) Draw the perpendicular bisector of BC.
(v) Draw the angle bisector of ∠ACB which intersects the perpendicular bisector of ,BC at P
(vi) Join PB and draw PL ⊥ AC.

Question 8.
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B.
Prove that P is equidistant from AB and BC.

Solution:
Given:  In || gm ABCD. AB > BC and bisector of ∠B meets diagonal AC at P.
To Prove:  P is equidistant from AB and BC.
Construction: From P, draw PL ⊥ AB and PM ⊥ BC.

Question 9.
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A.
Prove that:
(i) point A is equidistant from all the three sides of the triangle.
(ii) AM bisects angle LMN.
Solution:

Given: In A LMN, angle bisectors of ∠L and ∠N
meet at A, AM is joined.
To Prove:
(i) A is equidistant from all the sides of A LMN.
(ii) AM is the bisector of ∠M.
Proof: ∴ A lies on the bisector of ∠N
∴ A is equidistant from MN and LN Again
∴ A lies on the bisector of ∠L A is equidistant from LN and LM Hence
∴ A is equidistant from all sides of the triangle LMN.
∴ A lies on the bisector of ∠M                               Q.E.D.

Question 10.
Use ruler and compasses only for this question:
(i) construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB. (2010)
Solution:
Steps of construction:
1. Draw a line BC = 6 cm and an angle CBX = 60°. Cut off AB = 3.5 cm. Join AC, ΔABC is the required triangle.
2. Draw ⊥ bisector of BC and bisector of ∠B.
3. Bisector of ∠B meets bisector of BC at P
∴ BP is the required length, where PB = 3.5 cm
4. P is the point which is equidistant from BA and BC, also equidistant fromB and C

Question 11.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point E Prove that:

(i) F is equidistant from A and B.
(ii) F is equidistant from AB and AC.
Solution:
Given : In the figure,
In ΔABC, AD is the bisector of ∠BAC Which meets BC at D EG is the perpendicular bisector of AB which intersects AD at F
To prove :
(i) F is equidistant from A and B.
(ii) F is equidistant from AB and AC.
Proof:
(i) ∴ F lies on the perpendicular bisector of AB F is equidistant from A and B
(ii) Again,
∴ F lies onthe bisector of ∠BAC
∴ F is equidistant from AB and AC.
(10 cm theorem)
Hence proved.

Question 12.
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect each other at point P. Show that P is equidistant from the opposite sides AB and CD.
Solution:
In quadrilateral ABCD, the bisectors of ∠B and ∠C meet each other at P.

To prove : D is equidistant from the sides AB and CD.
Proof:
∴ P lies on the bisector of ∠B P is equidistant from AB and BC ….(i)
Similarly, P lies on the bisector of ∠C P is equidistant from BC and CD ….(ii)
From (i) and (ii),
∴ P is equidistant from AB and CD
Hence proved.

Question 13.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Solution:
Steps of Construction:
(i) Draw a line segment AB = 6 cm
(ii) Draw perpendicular bisector LM of AB. LM is the required locus.
(iii) Take any point on LM say P.
(iv) Join PA and PB
∵ P lies on the right bisector of line AB

∴ P is equidistant from A and B.
∴ PA = PB
∴ Perpendicular bisector of AB is the locus of all points which are equidistant from A and B.

Question 14.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
Solution:

Steps of Construction:
(I) Draw a ray BC.
(ii) Construct a ray RA making an angle of 750 with BC.
(iii) ∴ ∠ABC = 75°
(iv) Draw the angle bisector BP of ∠ABC. BP is the required locus.
(v) Take any point D on BP.
(vi) From D, draw DE ⊥ AB and DF ⊥ BC.
∵ D lies on the angle bisector ∠ABC.
∴ D is equidistant from AB and BC.
∴ DE = DF
Similarly any point on BP, is equidistant from AB and BC.
∴BP is the locus of all points which are equidistant from AB and BC.

Question 15.
Draw an angle ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC ; and also equidistant from A and B
Solution:

Steps of Construction:
(i) Draw a line segment BC = 5 cm.
(ii) At B, draw a ray BX making an angle of 60° and cut off BA = 4.6 cm.
(iii) Draw the angle bisector of ∠ABC.
(iv) Draw the perpendicular bisector of AB which intersects the angle bisector at P.
P is the required point which is equidistant from AB and BC as well as from points A and B.

Question 16.
In the figure given below, find a point P on CD equidistant from points A and B.

Solution:

Steps of Construction:
(i) In the figure AB and CD are two line segments.
(ii) Draw the perpendicular bisector of AB which intersects CD in P.
P is the required point which is equidistant from A and B
∵ P lies on the perpendicular bisector of AB.
∴ PA = PB.

Question 17.
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.

Solution:

Steps of Construction:
(i) In the given triangle, draw the angle bisector of ∠BAC.
(ii) Draw the perpendicular bisector of BC which intersects the angle bisector of ∠A at P.
P is the required point which is equidistant from AB and AC as well as from B and C.
∵ P lies on the angle bisector of ∠BAC.
∴ It is equidistant from AB and AC. Again
∵ P lies on the perpendicular bisector of BC.
∴ P is equidistant from B and C.

Question 18.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that :
(i) P is equidistant from B and C.
(ii) P is equidistant from AB and BC.
(iii) Measure and record the length of PB.
(2000)
Solution:
Steps of Construction :
1. Draw a line segment AB = 7 cm.
2. Draw angle ∠ABC = 60° with the help of compass.
3. Cut off BC = 8 cm.
4. Join A and C.
5. The triangle ABC so formed is required triangle.
(i) Draw perpendicular bisector of line BC. The point situated on this line will be equidistant from B and C.
(ii) Draw angular bisector of ∠ABC. Any
point situated on this angular bisector is equidistant from lines AB and BC.

The point which fulfills the condition required in (i) and (ii) is the intersection point of bisector of line BC and angular bisector of ∠ABC.
(iii) Length of PB is 4.5 cm.

Question 19.
On a graph paper, draw the lines x = 3 and y = -5. Now, on the same graph paper, draw the locus of the point which is equidistant from the given lines.
Solution:
On the graph paper, draw axis XOX’ and YOY’ Draw a line l, x = 3 which is parallel to y-axis and another line m, y = -5, which is parallel to x-axis

These two lines intersect eachother at P.
Now draw the angle bisector p of ∠P
∵ p is the bisector of ∠P
∴ Any point on P, is equidistant from l and m
∴ This line p is equidistant from l and m.

Question 20.
On a graph paper, draw the line x = 6. Now, on the same graph paper, draw the locus of the point which moves in such a way that its distance from the given line is always equal to 3 units.
Solution:

On the graph, draw axis XOX’ and YOY’
Draw a line l, x = 6
Which is parallel to -axis
Take point P and Q which are at a distance of 3units from the line l
Draw line rn and n from P and Q parallel to P respectively
The line m and n are the required locus of the points P and Q
Which arc always 3 units from the line l.
Hence proved.

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B  are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations (In one variable) Ex 4B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4B

Question 1.
Represent the following inequalities on real number lines:
(i) 2x – 1 < 5
(ii) 3x + 1 ≥ – 5
(iii) 2 (2x – 3) ≤ 6
(iv) -4 < x < 4
(v) -2 ≤ x < 5 (vi) 8 ≥ x > -3
(vii) -5 < x ≤ -1
Solution:

Question 2.
For each graph given below, write an inequation taking x as the variable :

Solution:

Question 3.
For the following inequations, graph the solution set on the real number line :
(i) – 4 ≤ 3x – 1 < 8
(ii) x – 1 < 3 – x ≤ 5
Solution:

Question 4.
Represent the solution of each of the following inequalities on the real number line :
(i) 4x – 1 > x + 11
(ii) 7 – x ≤ 2 – 6x
(iii) x + 3 ≤ 2x + 9
(iv) 2 – 3x > 1 – 5x
(v) 1 + x ≥ 5x – 11
(vi) \(\frac { 2x + 5 }{ 2 }\) > 3x – 3
Solution:

Question 5.
x ∈ {real numbers} and -1 < 3 – 2x ≤ 7, evaluate x and represent it on a number line.
Solution:

Question 6.
List the elements of the solution set of the inequation – 3 < x – 2 ≤ 9 -2x ; x ∈ N.
Solution:

Question 7.
Find the range of values of x which satisfies

Graph these values of x on the number line.
Solution:

Question 8.
Find the values of x, which satisfy the inequation:

Graph the solution on the number line. (2007)
Solution:

Question 9.
Given x ∈ {real numbers}, find the range of values of x for which – 5 ≤ 2x – 3 < x + 2 and represent it on a real number line.
Solution:

Question 10.
If 5x – 3 ≤ 5 + 3x ≤ 4x + 2, express it as a ≤ x ≤ b and then state the values of a and b.
Solution:
Here in, 5x – 3 ≤ 5 + 3x ≤ 4x + 2
⇒ 5x – 3 ≤ 5 + 3x and 5 + 3x ≤ 4x + 2
⇒ 5x – 3x ≤ 5 + 3 and 3x – 4x ≤ 2 – 5
⇒ 2x ≤ 8 and – x ≤ – 3
⇒ x ≤ 4 and x ≥ 3
Solution is 3 ≤ x ≤ 4
a = 3 and b = 4

Question 11.
Solve the following inequation and graph the solution set on the number line :
2x – 3 < x + 2 ≤ 3x + 5; x ∈ R.
Solution:

Question 12.
Solve and graph the solution set of:
(i) 2x – 9 < 7 and 3x + 9 ≤ 25; x ∈ R.
(ii) 2x – 9 ≤ 7 and 3x + 9 > 25; x ∈ I.
(iii) x + 5 ≥ 4 (x – 1) and 3 – 2x < -7; x ∈ R.
Solution:
(i) 2x – 9 < 7 and 3x + 9 ≤ 25; x ∈ R.

Question 13.
Solve and graph the solution set of:
(i) 3x – 2 > 19 or 3 – 2x ≥ – 7; x ∈ R.
(ii) 5 > p – 1 > 2 or 7 ≤ 2p – 1 ≤ 17; p ∈ R.
Solution:

Question 14.
The diagram represents two inequations A and B on real number lines :

(i) Write down A and B in set builder notation.
(ii) Represent A ∩ B and A ∩ B’ on two different number lines.
Solution:

Question 15.
Use real number line to find the range of values of x for which :
(i) x > 3 and 0 < x < 6
(ii) x < 0 and -3 ≤ x < 1
(iii) -1 < x ≤ 6 and -2 ≤ x ≤ 3
Solution:

Question 16.
Illustrate the set {x : -3 ≤ x < 0 or x > 2 ; x ∈ R} on a real number line.
Solution:

Question 17.
Given A = {x : -1 < x < 5, x ∈ R} and B = {x : – 4 < x < 3, x ∈ R}
Represent on different number lines:
(i) A ∩ B
(ii) A’ ∩ B
(iii) A – B
Solution:

Question 18.
P is the solution set of 7x – 2 > 4x + 1 and Q is the solution set of 9x – 45 ≥ 5 (x – 5); where x ∈ R. Represent:
(i) P ∩ Q
(ii) P – Q
(iii) P ∩ Q’ on different number lines.
Solution:

Question 19.
If P = {x : 7x – 4 > 5x + 2, x ∈ R} and Q = {x : x – 19 ≥ 1 – 3x , x ∈ R}: find the range of set P ∩ Q and represent it on a number line.
Solution:

Question 20.
Find the range of values of x, which satisfy:

Graph, in each of the following cases, the values of x on the different real number lines:
(i) x ∈ W
(ii) x ∈ Z
(iii) x ∈ R.
Solution:

Question 21.
Given A = {x : – 8 < 5x + 2 ≤ 17, x ∈ I}, B = {x : -2 ≤ 7 + 3x < 17, x ∈ R}
Where R = {real numbers} and I = {integers}
Represent A an B is on two different number lines. Write down the elements of A ∩ B.
Solution:

Question 22.
Solve the following inequation and represent the solution set on the number line 2x – 5 ≤ 5x + 4< 11, where x ∈ I.
Solution:

Question 23.
Given that x ∈ I, solve the inequation and graph the solution on the number line:

Solution:

Question 24.
Given:
A = {x : 11x – 5 > 7x + 3, x ∈ R} and B = {x : 18x – 9 ≥ 15 + 12x, x ∈ R}.
Find the range of set A ∩ B and represent it on a number line. (2005)
Solution:

Question 25.
Find the set of values of x, satisfying:

Solution:

Question 26.

Solution:

Question 27.
Solve the inequation:

Graph the solution set on the number line.
Solution:

Question 28.
Find three consecutive largest positive integers such that the sum of one-third of first, one-fourth of second and one-fifth of third is atmost 20.
Solution:
Let first positive integer = x
Then, second integer = x + 1
and third integer = x + 2
According to the condition,

Question 29.
Solve the given inequation and graph the solution on the number line.
2y – 3 < y + 1 < 4y + 7; y ∈ R (2008)
Solution:

Question 30.
Solve the inequation:
3z – 5 ≤ z + 3 < 5z – 9; z ∈ R.
Graph the solution set on the number line.
Solution:

Question 31.
Solve the following inequation and represent the solution set on the number line.

Solution:

Question 32.
Solve the following inequation and represent the solution set on the number line:

Solution:

Question 33.
Solve the following inequation, write the solution set and represent it on the number

Solution:

Question 34.

Solution:

Question 35.
Solve the following inequation and write the solution set:
13x – 5 < 15x + 4 < 7x + 12, x ∈ R
Represent the solution on a real number line. (2015)
Solution:

Question 36.
Solve the following inequation, write the solution set and represent it on the number line.
-3 (x – 7) ≥ 15 – 7x > \(\frac { x + 1 }{ 3 }\), x ∈ R. (2016)
Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Chapter 25 Probability Ex 25A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25C

Question 1.
A coin is tossed once. Find the probability of:
(i) getting a tail
(ii) not getting a tail
Solution:
On tossing a coin once,
number of possible outcome = 2
(i) Favourable outome getting a tail = 1
⇒ number of favourable outcome = 2

(ii) Similarly favourable outcome not getting a tail = 1
But no. of possible out come = 2

Question 2.
A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is :
(i) a black ball.
(ii) a red ball.
(iii) a white ball.
(iv) not a red ball.
(v) not a black ball.
Solution:
In a bag, 3 balls are white
2 balls are red
5 balls are black
Total number of balls = 3 + 2 + 5 = 10
(i) Number of possible outcome of one black ball = 10
and number of favouable outcome of one black ball = 5

(ii) Number of possible outcome of one red ball = 10
and number of favourable outcome = 2

(iii) Number of possible outcome of white ball = 10
and number of favourable outcome = 3

(iv) Number of possible outcome = 10
Number of favourable outcome = 3+5 = 8
not a red ball

(v) Number of possible outcomes =10 Number of favourable outcome
not a black ball = 3 + 2 = 5

Question 3.
In a single throw of a die, find the probability of getting a number :
(i) greater than 4.
(ii) less than or equal to 4.
(iii) not greater than 4.
Solution:
A die has numbers 1, 2, 3, 4, 5, 6 on its sides
∴ Number of possible outcome = 6
(i) Number of favourable outcome = greater than four i.e. two number 5 and 6

(ii) Number of favourable outcome = less than or equal to 4 i.e. 1, 2, 3, 4 which are 4 in number

(iii) Number of favourable outcome = not greater than 4 or numbers will be 1, 2, 3, 4 which are 4 in numbers

Question 4.
In a single throw of a die, find the probability that the number :
(i) will be an even number.
(ii) will not be an even number.
(iii) will be an odd number.
Solution:
A die has six numbers : 1, 2, 3, 4, 5, 6
∴ Number of possible outcome = 6
(i) Number of favourable outcome = an even number i.e. 2, 4, 6 which are 3 in numbers

(ii) & (iii) Number of favourable outcome = not an even number i.e. odd numbers : 1, 3, 5 which are 3 in numbers

Question 5.
From a well-shuffled deck of 52 playing-cards, one card is drawn. Find the probability that the card drawn will :
(i) be a black card.
(ii) not be a red card.
(iii) be a red card.
(iv) be a face card.
(v) be a face card of red color.
Solution:
Number of cards in a playing card deck =52
number of possible outcomes = 52
(i) Number of favourable outcomes = black cards = 26 cards

(ii) Number of favourable outcomes = Not be a red card = black cards = 26

(iii) Number of favourable outcome = Number of red cards = 26

(iv) Number of favourable outcome = face cards = 3×4=12

(v) Number of favourable outcome = face cards of red colour = 3 x2 = 6

Question 6.
(i) If A and B are two complementary events then what is the relation between P(A) and P(B)?
(ii) If the probability of happening of an event A is 0.46. What will be the probability of not happening of the event A ?
Solution:
(i) A and B are two complementary events
Then A = P(E) and B = P(\(\bar { E }\) )
ButP(E) + P(\(\bar { E }\)) = 1
or P(A) + P(B) = 1
(ii) ∵ P(A) + P(B) = 1 (Complementary events)
But P(A) = 0.46
∴ P(B) = 1 – P (A)
= 1 – 0.46 = 0.54

Question 7.
In a T.T. match between Geeta and Ritu, the probability of the winning of Ritu is 0.73. Find the probability of :
(i) winning of Geeta.
(ii) not winning of Ritu.
Solution:
∵ Match of T.T. is played between Geeta and Ritu
∴ Probability of winning of Geeta + Probability of winning of Ritu = 1
Probability of winning of Ritu = 0.73
(i) Probability of winning of Geeta
= 1 – probability of winning of Ritu
= 1 – 0.73 = 0.27
(ii) Probability of not winning of Ritu
= Probability of winning of Geeta = 0.27

Question 8.
In a race between Mahesh and John ; the probability that John will lose the race is 0.54.
Find the probability of :
(i) winning of Mahesh.
(ii) winning of John.
Solution:
∵ A Race is run between Mahesli and John
∴ P(E) + P(\(\bar { E }\) )=1
Where P(E) is the probability of lose the race by John
and P(\(\bar { E }\) ) is the probability of not losing or winning the race by Mahesh
But P( \(\bar { E }\) ) = 0.54
then 0.54 + P(E) = 1
⇒ P(E) = 1 – 0.54 = 0.46
∴ Probability of winning the race by John = 0.46 .

Question 9.
(i) Write the probability of a sure event.
(ii) Write the probability of an event which is impossible.
(iii) For an event E. write a relation representing the range of values of P(E).
Solution:
(i) We know that if the probability of an event is 1 then the probability is called a certain event or a sure event
Hence probability of a sure event = 1
(ii) The probability of an event which is impossible = 0
(iii) Probability of no event can be less than 0 and more than 1 and E be any event then
0 ≤ P(E) ≤ 1

Question 10.
In a single throw of a die, find the probability of getting :
(i) 5 (ii) 8
(in) a number less than 8.
(iv) a prime number.
Solution:
On a die the numbers are 1, 2, 3, 4, 5, 6 i.e. six.
∴ Number of possible outcome = 6
(i) Number of favourable outcome = 1 i.e. 5

(ii) Number of favourable outcome = 0 (∵ 8 is not possible)

(iii) Number less than 8 will be 1,2, 3, 4, 5, 6

(iv) A prime number will be = 2. 3, 5

Question 11.
A die is thrown once. Find the probability of getting :
(i) an even number.
(ii) a number between 3 and 8.
(iii) an even number or a multiple of 3.
Solution:
The number on die are 1. 2. 3. 4. 5. 6
(i) Number of even numbers on the die = 2, 4, 6 = 3

(ii) A number between 3 and 8 on the die = 3, 4, 5, 6 = 4

(iii) An even number or a multiple of 3 = 2, 3, 4, 6 = 4

Question 12.
Which of the following cannot be the probability of an event ?
(i) \(\frac { 3 }{ 5 }\)
(ii) 2.7
(iii) 43%
(iv) -0.6
(v) -3.2
(vi) 0.35
Solution:
We know that probability of no event can be less than 0 and more than 1
∴ If probability of any event can be less than 0 or more than 1 now
(i) \(\frac { 3 }{ 5 }\) which is between 0 and 1
∴ It is the probability of an event
(ii) 2.7 which is greater than 1
∴ It is not the probability of an event.
(iii) 43% = \(\frac { 43 }{ 100 }\) which is between 0 and 1
∴ It is the probability of an event.
(iv) -0.6 which is less than 0
∴ It is not the probability of an event
(v) -3.2 which is less than 0.
∴ It is not the probability of an event
(vi) 0.35 = \(\frac { 35 }{ 100 }\) which is between 0 and 1
∴ It is the probability of an event
Hence (ii), (iv) and (v) are not probability of an event Ans.

Question 13.
A bag contains six identical black balls. A child withdraws one ball from the bag without looking into it. What is the probability that he takes out:
(i) a white ball
(ii) a black ball
Solution:
∵ There are 6 black balls in a bag
∴ number of possible outcome = 6
(i) A white ball
As there is no white ball in the bag
∴ Its probability is zero (0) = or P(E) = 0
(ii) a black ball
∴ Number of favourable outcome = 1

Question 14.
A single letter is selected at random from the word ‘Probability’. Find the probability that it is a vowel.
Solution:
In the word, Probability, number of letters are
i.e. P, R, O, B, A, I, L, T, Y
and number of favourable outcome = o.a.i = 3

Question 15.
Ramesh chooses a date at random in January for a party (see the following figure).

Find the probability that he chooses :
(i) A Wednesday (ii) A Friday (iii) A Tuesday or a Saturday
Solution:
We are given the days of the month of January which has 31 days.
∴ Number of possible outcome = 31
(i) Number of Wednesday in the month = 5

(ii) Number of Friday in the month = 5

(iii) Number of Tuesday = 4
and number of Saturday = 4
Total number of Tuesday and Saturday = 4 + 4 = 8

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations (In one variable) Ex 4A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4B

Question 1.
State, true or false :

Solution:

Question 2.
State whether the following statements are true or false:
(i) If a < b, then a – c < b – c (ii) If a > b, then a + c > b + c
(iii) If a < b, then ac > bc
(iv) If a > b, then \(\frac { a }{ b }\) < \(\frac { b }{ c }\) (v) If a – c > b – d; then a + d > b + c
(vi) If a < b, and c > 0, then a – c > b – c where a, b, c and d are real numbers and c ≠ 0.
Solution:
(i) True
(ii) True
(iii) False
(iv) False
(v) True
(vi) False

Question 3.
If x ∈ N, find the solution set of inequations,
(i) 5x + 3 ≤ 2x + 18
(ii) 3x – 2 < 19 – 4x
Solution:

x = {1, 2}

Question 4.
If the replacement set is the set of whole numbers, Solve:
(i) x + 7 ≤ 11
(ii) 3x – 1 > 8
(iii) 8 – x > 5
(iv) 7 – 3x ≥ – \(\frac { 1 }{ 2 }\)
(v) x – \(\frac { 3 }{ 2 }\) < \(\frac { 3 }{ 2 }\) – x
(vi) 18 ≤ 3x – 2
Solution:

Question 5.
Solve the inequation :
3 – 2x ≥ x – 12 given that x ∈ N. [1987]
Solution:
3 – 2x ≥ x – 12
⇒ – 2x – x ≥ – 12 – 3
⇒ – 3x ≥ -15
⇒ – x ≥ – 5
⇒ x ≤ 5
Solution Set= {1, 2, 3, 4, 5} or {x ∈ N : x ≤ 5}

Question 6.
If 25 – 4x ≤ 16, find:
(i) the smallest value of x, when x is a real number
(ii) the smallest value of x, when x is an integer.
Solution:
25 – 4x ≤ 16
⇒ – 4x ≤ 16 – 25
⇒ – 4x ≤ – 9
⇒ 4x ≥ 9
x ≥ \(\frac { 9 }{ 4 }\)
(i) The smallest value of x, when x is a real number \(\frac { 9 }{ 4 }\) or 2.25
(ii) The smallest value of x, when x is an integer 3.

Question 7.
If the replacement set is the set of real numbers, solve:

Solution:

Question 8.
Find the smallest value of x for which 5 – 2x < 5\(\frac { 1 }{ 2 }\) – \(\frac { 5 }{ 3 }\) x, where x is an integer.
Solution:

Question 9.
Find the largest value of x for which 2 (x – 1) ≤ 9 – x and x ∈ W.
Solution:
2 (x – 1) ≤ 9 – x
⇒ 2x – 2 ≤ 9 – x
⇒ 2x + x ≤ 9 + 2
⇒ 3x ≤ 11
⇒ x ≤ \(\frac { 11 }{ 3 }\)
⇒ x ≤ 3\(\frac { 2 }{ 3 }\)
x ∈ W and value of x is largest x = 3

Question 10.
Solve the inequation:
12 + 1\(\frac { 5 }{ 6 }\) x ≤ 5 + 3x and x ∈ R. (1999)
Solution:

Question 11.
Given x ∈ (integers), find the solution set of: -5 ≤ 2x – 3 < x + 2.
Solution:
-5 ≤ 2x – 3 < x + 2
(i) -5 ≤ 2x – 3
⇒ -2x ≤ -3 + 5
⇒ -2x ≤ 2
⇒ x ≤ -1
⇒ -1 ≤ x
(ii) 2x – 3 < x + 2
⇒ 2x – x < 2 + 3
⇒ x < 5
From (i) and (ii),
-1 ≤ x < 5
x = {-1, 0, 1, 2, 3, 4}

Question 12.
Given x ∈ (whole numbers), find the solution set of: -1 ≤ 3 + 4x < 23.
Solution:
-1 ≤ 3 + 4x < 23
(i) -1 ≤ 3 + 4x
⇒ -1 – 3 ≤ 4x
⇒ -4 < 4x
⇒ -1 ≤ x
(ii) 3 + 4x < 23
⇒ 4x < 23 – 3
⇒ 4x < 20
⇒ x < 5
From (i) and (ii)
-1 ≤ x < 5 and x ∈ W
Solution set = {0, 1, 2, 3, 4}

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.