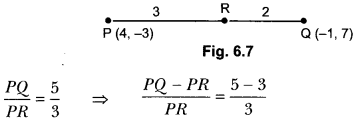
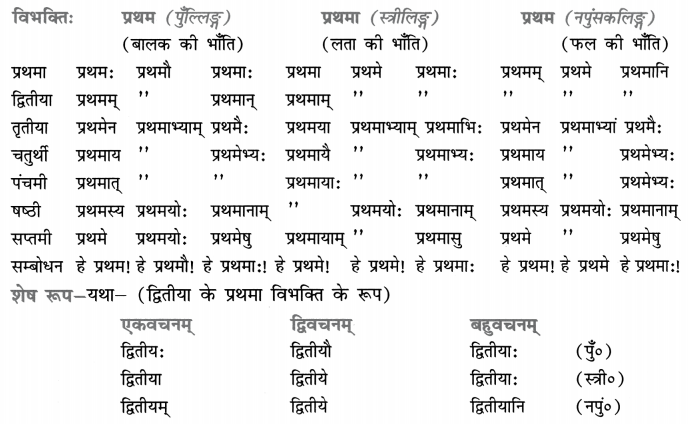
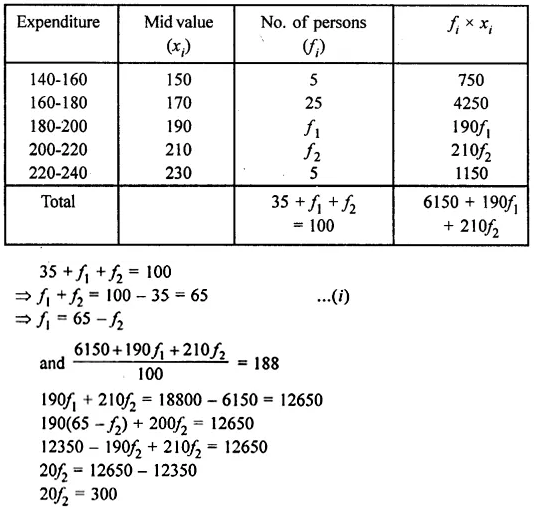
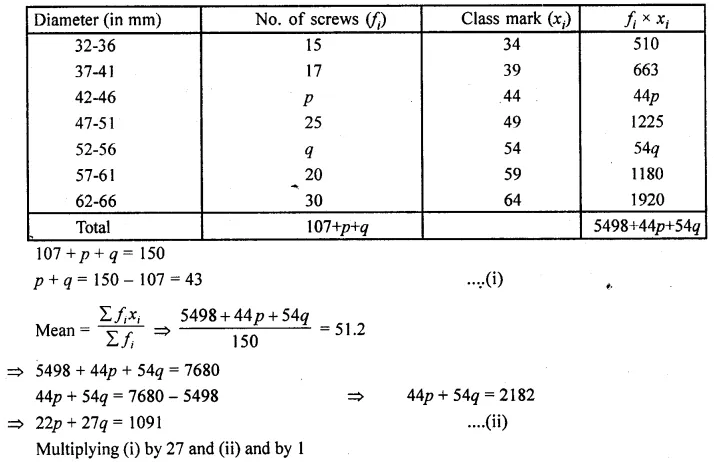
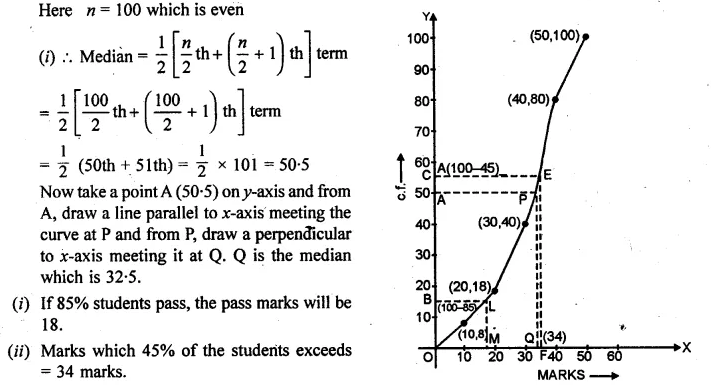
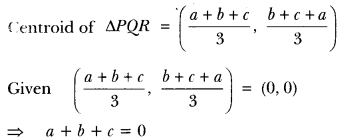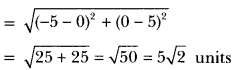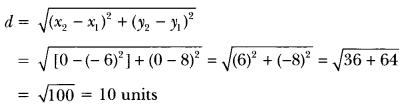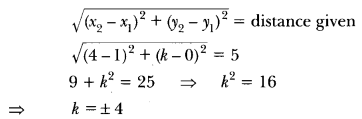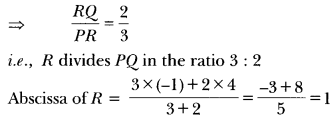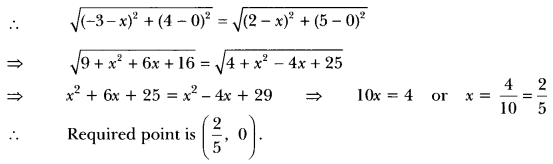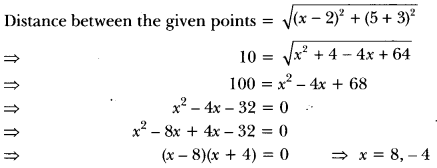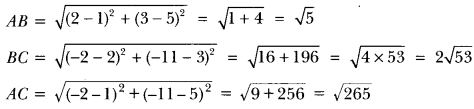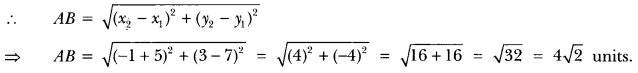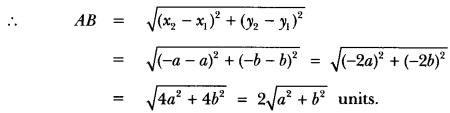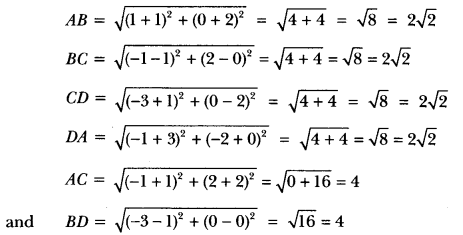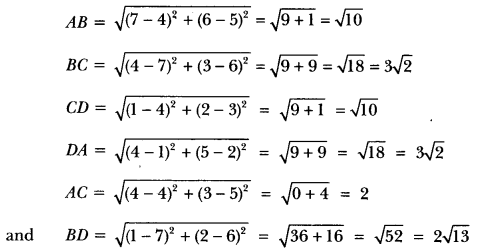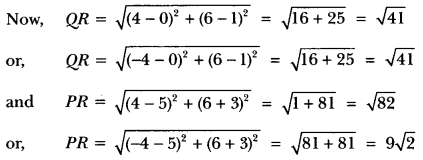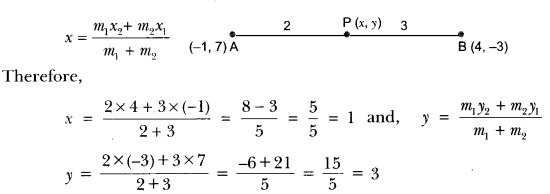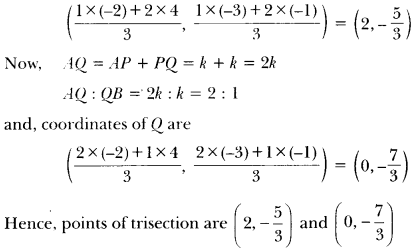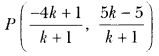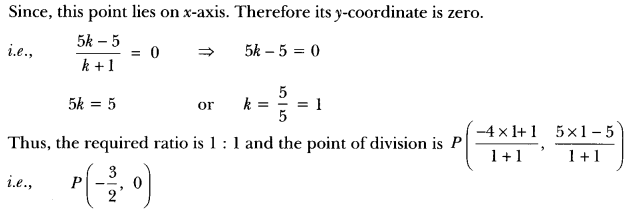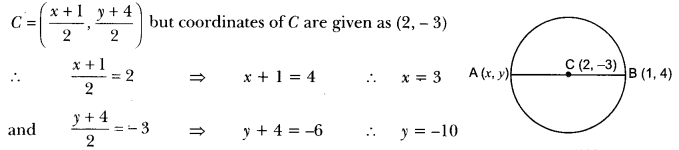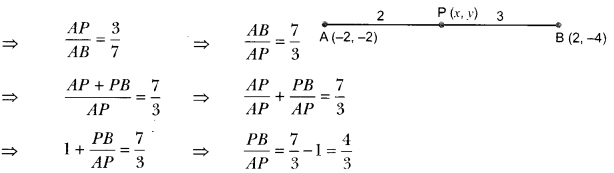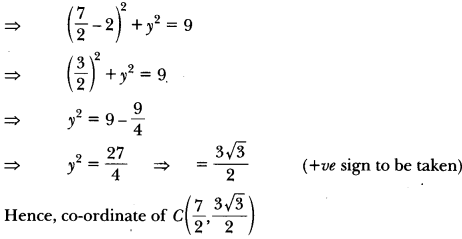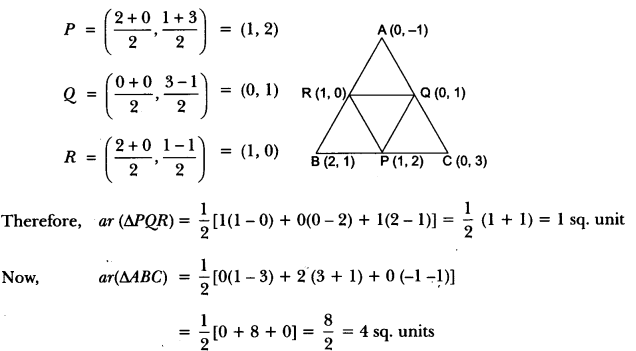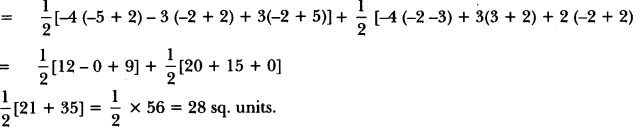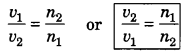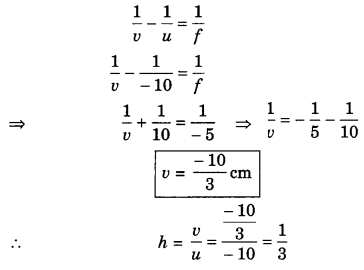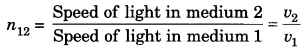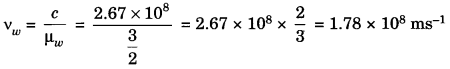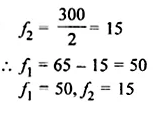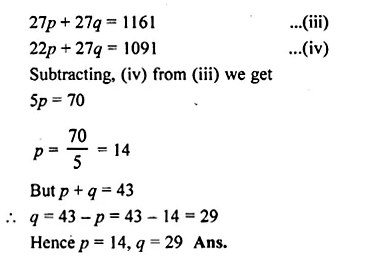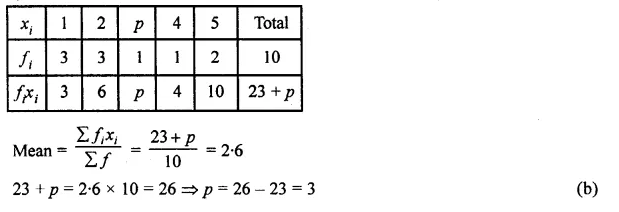ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 8 Simple and Compound Interest Ex 8.1
Question 1.
Find the simple interest on ₹4000 at 7.5% p.a. for 3 years 3 months. Also, find the amount.
Solution:
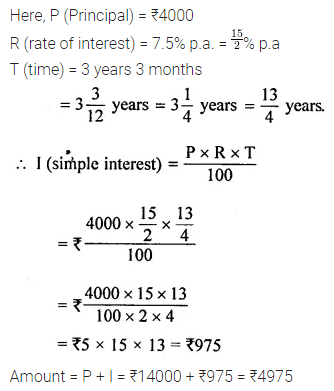
Question 2.
What sum of money will yield ₹170·10 as simple interest in 2 years 3 months at 6% per annum?
Solution:
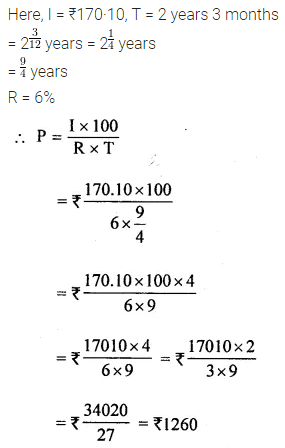
Question 3.
Find the rate of interest when ₹800 fetches ₹130 as a simple interest in 2 years 6 months.
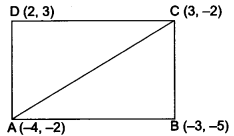
Solution:
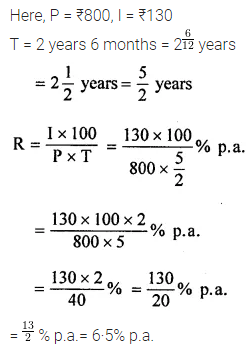
Question 4.
Find the time when simple interest on ₹3·3 lakhs at 6·5% per annum is ₹75075.
Solution:
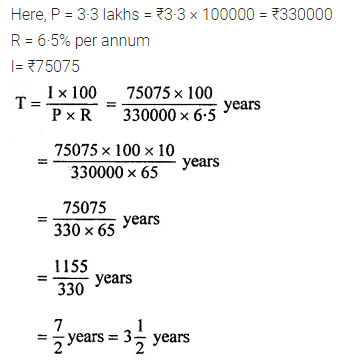
Question 5.
Find the sum of money when
(i) simple interest at 7\(\frac{1}{4}\)% p.a. for years is ₹2356·25
(ii) the final amount is ₹ 11300 at 4% p.a. for 3 years 3 months.
Solution:
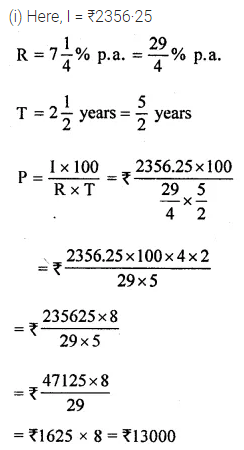
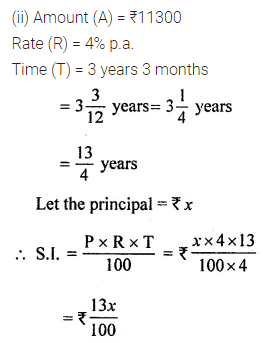
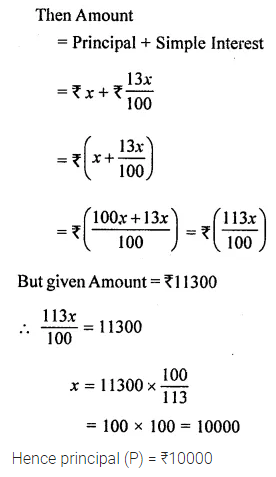
Question 6.
How long will it take a certain sum of money to triple itself at 13\(\frac{1}{3}\)% per annum simple interest?
Solution:
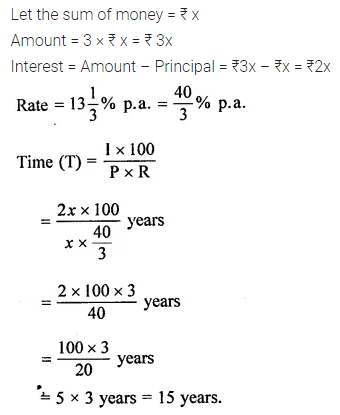
Question 7.
At a certain rate of simple interest ₹4050 amounts to ₹4576·50 in 2 years. At the same rate of simple interest, how much would ₹1 lakh amount to in 3 years?
Solution:

Question 8.
What sum of money invested at 7.5% p.a. simple interest for 2 years produces twice as much interest as ₹9600 in 3 years 6 months at 10% p.a. simple interest?
Solution: