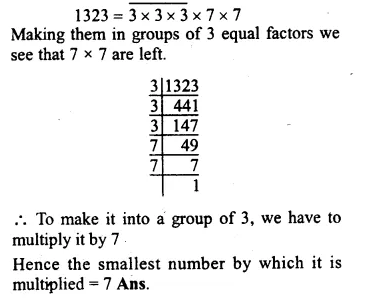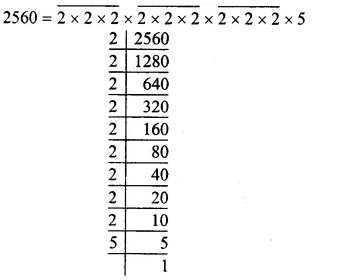Prasanna – Page 261

RS Aggarwal Class 8 Solutions Chapter 5 Playing with Numbers Ex 5B

January 23, 2023

RS Aggarwal Class 8 Solutions Chapter 5 Playing with Numbers Ex 5B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5B.

Other Exercises

Question 1.
Solution:
We know that a number is divisible by 2 if its unit digit is 0, 2, 4, 6 or 8
Therefore, (i) 94, (ii) 570, (iv) 2398,(v) 79532 and (vi) 13576 are divisible by 2.

Question 2.
Solution:
We know that a number is divisible by 5 if its unit digit is 0 or 5.
Therefore, (i) 95, (ii) 470, (iv) 2735, (vi) 35790, (vii) 98765 and (ix) 77990 are divisible by 5.

Question 3.
Solution:
We know that a number is divisible by 10 if its unit digit is zero.
Therefore, (ii) 90 and (iv) 57930 are divisible by 10.

Question 4.
Solution:
We know that a number is divisible by 3 if the sum of its digits is divisible by 3. Therefore
(i) 83 – 8 + 3 = 11,not divisible by 3
(ii) 378 – 3 + 7 + 8 = 18, is divisible by 3
(iii) 474 – 4 + 7 + 4 = 15, is divisible by 3
(iv) 1693 – 1 + 6 + 9 + 3 = 19, is divisible by 3
(v) 20345 – 2 + 0 + 3 + 4 + 5 = 14 is not divisible by 3
(vi) 67035 – 6 + 7 + 0 + 3 + 5 = 21 is divisible by 3
(vii)591282 – 5 + 9 + 1 + 2 + 8 = 27 is divisible by 3
(viii)903164 – 9 + 0 + 3 + 1 + 6 + 4 = 23,is not divisible by 3
(ix) 100002 – 1 + 0 + 0 + 0 + 0 + 2 = 3,is divisible by 3

Question 5.
Solution:
We know that a number is divisible by 9, if the sum of its digits is divisible by 9. Therefore,
(i) 327 = 3 + 2 + 7 = 12,is not divisible by 9
(ii) 7524 = 7 + 5 + 2 + 4 = 18, is divisible by 9
(iii) 32022 = 3 + 2 + 0 + 2 + 2 = 9,is divisible by 9
(iv) 64302 = 6 + 4 + 3 + 0 + 2 = 15, is not divisible by 9
(v) 89361= 8 + 9 + 3 + 6 + 1 = 27 is divisible by 9
(vi)14799 = 1 + 4 + 7 + 9 + 9 = 30,is not divisible by 9
(vii) 66888 = 6 + 6 + 8 + 8 + 8 = 36, is divisible by 9
(viii) 30006 = 3 + 0 + 0 + 0 + 6 = 9, is divisible by 9
(ix) 33333 = 3 + 3 + 3 + 3 + 3 = 15 is not divisible by 9

Question 6.
Solution:
We know that a number is divisible by 4, only when the number formed by its last two digits is divisible by 4.
Therefore,
(i) 134, is not divisible by 4 as last two digits 34 is not divisible by 4.
(ii) 618, is not divisible by 4 as last two digits 18 is not divisible by 4.
(iii) 3928, is divisible by 4 as last two digits 28 is divisible by 4.
(iv) 50176, is not divisible by 4 as last two digits 76 is not divisible by 4.
(y) 39392, is not divisible by 4 as last two digits 92 is not divisible by 4.
(vi) 56794, is not divisible by 4 as last two digits 94 is not divisible by 4.
(vii) 86102, is not divisible by 4 as last two digits 02 is not divisible by 4.
(viii) 66666, is not divisible by 4 as last two digits 66 is not divisible by 4.
(ix) 99918, is not divisible by 4 as last two digits 18 is not divisible by 4.
(x) 77736, is divisible by 4 as last two digits 36 is divisible by 4.

Question 7.
Solution:
A given number is divisible by 8 only when the number formed by its last three digits is divisible by 8.
(i) 6132, is not divisible by 8 as last three digits 132 is not divisible by 8.
(ii) 7304, is divisible by 8 as last three digits 304 is not divisible by 8.
(iii) 59312, is divisible by 8 as last three digits 312 is divisible by 8.
(iv) 66664, is divisible by 8 as last three digits 664 is divisible by 8.
(v) 44444, is not divisible by 8 as last three digits 444 is not divisible by 8.
(vi) 154360, is divisible by 8 as last three digits 360 is not divisible by 8.
(vii) 998818, is not divisible by 8 as last three digits 818 is not divisible by 8.
(viii) 265472, is divisible by 8 as last three digits 472 is divisible by 8.
(ix) 7350162, is not divisible by 8 as last three digits 162 is not divisible by 8.

Question 8.
Solution:
A given number is divisible by 11, if the difference between the sum of its digits at odd places and the sum of its digits at even places, is either O or a number divisible by 11.
(i) 22222
Sum of digit at odd places = 2 + 2 + 2 = 6
Sum of digit at even places = 2 + 2 = 4
Difference of the above sum = 6 – 4 =2,
which is not divisible by 11
22222 is not divisible by 11

(ii) 444444
Sum of digit at odd places = 4 + 4 + 4 = 12
Sum of digit at even places = 4 + 4 + 4 = 12
Difference of the above sum =(12 – 12) = O
444444 is divisible by 11

(iii) 379654
Sum of digit at odd places = 7 + 6 + 4 = 17
Sum of digit at even places = 3 + 9 + 5 = 17
Difference of the above sum = (17 – 17) = 0
379654 is divisible by 11

(iv) 1057982
Sum of digit at odd places = 1 + 5 + 9 + 2 = 17
Sum of digit at even places = 0 + 7 + 8 = 15
Difference of the above sum = (17 – 15) = 2, which is not divisible by 11
1057982 is not divisible by 11

(v) 6543207
Sum of digit at odd places = 6 + 4 + 2 + 7 = 19
Sum of digit at even places = 5 + 3 + 0 = 8
Difference of the above sum = (19 – 8) = 11, Which is divisible by 11
6543207 is divisible by 11

(vi) 818532
Sum of digital to odd places = 1 + 5 + 2 = 8
Sum of digit at even places = 8 + 8 + 3 = 19
Difference of the above sum = 19 – 8 = 11, which is divisible by 11
818532 is divisible by 11

(vii) 900163
Sum of digit at odd places = 0 + 1 + 3 = 4
Sum of digit at even places = 9 + 0 + 6 = 15
Difference of the above sum = (15 – 4) = 11, which is divisible by 11
900163 is divisible by 11

(viii) 7531622
Sum of digit at odd places = 7 + 3 + 6 + 2 = 18
Sum of digit at even places = 5 + 1 + 2 = 8
Difference of the above sum = (18 – 8) = 10, which is not divisible by 11
7531622 is not divisible by 11

Question 9.
Solution:
For testing the divisibility of a number by 7, we proceed according to the
following steps:
Step 1: Double the unit digit of the given number.
Step 2 : Subtract the above number from the number formed by excluding the unit digit of the given number.
Step 3 : 1f the number so obtained is divisible by 7 then the given number is divisible by 7.
(i) 693
Now, 69 – (2 x 3) = 63, which is divisible by 7
693 is divisible by 7

(ii) 7896
Now 789 – (6 x 2) = 777, which is divisible by 7
7896 is divisible by 7

(iii) 3467
Now, 346 – (7 x 2) = 332, which is not divisible by 7
3467 is not divisible by 7

(iv) 12873
Now,1287 – (3 x 2) = 1281, which is divisible by 7
12873 is divisible by 7

(v) 65436
Now, 6543 – (6 x 2) = 6531, which is divisible by 7
65436 is divisible by 7

(vi) 54636
Now, 5463 – (6 x 2) 5451, which is not divisible by 7
54636 is not divisible by 7

(vii) 98175
Now, 9817 – (5 x 2) 9807, which is divisible by 7
98175 is divisible by7

(viii) 88777
Now, 8877 – (7 x 2) = 8863, which is not divisible by 7
88777 is not divisible by 7

Question 10.
Solution:
The given number 7×3 is divisible by 3
The sum of its digits is divisible by 3
7 + x + 3 =>10 + x is divisible by 3
Value of x can be 2, 5, 8
The numbers can be 723, 753, 783

Question 11.
Solution:
The given number 53yl is divisible by 3
Sum of its digits is divisible by 3
i.e., 5 + 3 + y + 1 or 9 + y is divisible by 3
Values of y can be 0, 3, 6, 9
Then the numbers can be 5301, 5331, 5361, 5391

Question 12.
Solution:
Number x806 is divisible by 9
The sum of its digits is also divisible by 9
or x + 8 + 0 + 6 or 14 + x is divisible by 9
x can be 4
Number will be 4806

Question 13.
Solution:
The number 471z8 is divisible by 9
The sum of its digits is also divisible by 9
471z8 = 4 + 7 + 1 + z + 8
=> 20 + z is divisible by 9
Value of z can be 7
Number will be 47178

Question 14.
Solution:
Let the number 21, sum of digits 2 + 1 = 3
which is divisible by 3 not by 9
Let the number 24, sum of digits 2 + 4 = 6
which is divisible by 3 not by 9
Let the number 30, sum of digits 3+0 = 3
which is divisible by 3 not by 9
Let the number 33, sum of digits 3 + 3 = 6
which is divisible by 3 not by 9
Let the number by 39 sum of digits 3 + 9 = 12
which is divisible by 3 not by 9

Question 15.
Solution:
Consider numbers as 28, 36,44, 52,60 as these numbers are divisible by 4 not by 8.
Let the number 39, sum of digits 3 + 9 = 12
which is divisible by 3 not by 9

Hope given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 7 Factorisation Ex 7A

January 23, 2023

RS Aggarwal Class 8 Solutions Chapter 7 Factorisation Ex 7A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 7 Factorisation Ex 7A.

Other Exercises

Factorize :

Question 1.
Solution:
(i) 12x + 15 = 3(4x + 5) {HCF of 12 and 15 = 3)
(ii) 14m – 21 = 7(2m – 3) {HCF of 14 and 21 = 7)
(iii) 9n – 12n² = 3n(3 – 4n) Ans.{HCF of 9 and 12 = 3}

Question 2.
Solution:
(i) 16a² – 24ab = 8a(2a – 3b) { HCF of 16 and 24 = 8)
(ii) 15ab² – 20a²b = 5ab(3b – 4a) {HCF of 15 and 20 5}
(iii) 12x²y³ – 21x³y²= 3x²y²(4y – 7x) Ans. {HCF of 12 and 21 = 3)

Question 3.
Solution:
(i) 24x³ – 36x²y = 12x²(2x – 3y) {HCF of 24 and 36 = 12}
(ii) 10x³ – 15x² = 5x²(2x – 3) {HCF of 10, 15 = 5}
(iii) 36x³y – 60x²y³z = 12x²y (3x – 5y²z) {HCF of 36 and 60 = 12}

Question 4.
Solution:
(i)9x³ – 6x² + 12x
= 3x(3x² – 2x + 4) {HCF of 9, 6, 12 = 3)
(ii)8x² – 72xy + 12x
= 4x(2x – 18y + 3) (HCF of 8, 72, 124)
(iii)18a³b³ – 27a²b³ + 36a³b²
= 9a²b²(2ab – 3b + 4a) Ans.{HCF of 10, 27, 36 = 9)

Question 5.
Solution:
(i) 14x³ + 21x⁴y – 28x²y²
= 7x² (2x + 3x²y – 4y²) {HCF of 14, 21 28 = 7)
(ii) – 5 – 10t + 20t²
= – 5(1 + 2t – 4t²) Ans. {HCF of 5, 10, 20=5)

Question 6.
Solution:
(i) x(x + 3) + 5(x + 3)
=(x + 3)(x + 5)
(ii) 5x(x – 4) – 7(x – 4)
= (x – 4) (5x – 7)
(iii) 2m (1 – n) + 3(1 – n)
= (1 – n) (2m + 3) Ans.

Question 7.
Solution:
6a(a – 2b) + 5b(a – 2b)
= (a – 2b) (6a + 5b) Ans.

Question 8.
Solution:
x³(2a – b) + x²(2a – b)
=x²(2a – b)(x + 1)Ans.

Question 9.
Solution:
9a(3a – 5b) – 12a²(3a – 5b)
= 3a (3a – 5b) (3 – 4a) Ans.

Question 10.
Solution:
(x + 5)² – 4(x + 5)
= (x + 5)(x + 5 – 4)
=(x + 5)(x + 1)Ans.

Question 11.
Solution:
3(a – 2b)² – 5 (a – 2b)
= (a – 2b) {3(a – 2b) – 5}
= (a – 2b) (3a – 6b – 5) Ans.

Question 12.
Solution:
2a + 6b – 3 (a + 3b)²
= 2(a + 3b) – 3(a + 3b)²
= (a + 3b){ 2 – 3 (a + 3b)}
= (a + 3b) (2 – 3a – 9b) Ans.

Question 13.
Solution:
16(2p – 3q)² – 4 (2p – 3q)
= 4(2p – 3q) {4(2p – 3q) – 1}
= 4(2p – 3q) (8p – 12q – 1) Ans.

Question 14.
Solution:
x(a – 3) + y (3 – a)
= x(a – 3) – y(a – 3)
= (a – 3) (x – y) Ans.

Question 15.
Solution:
12(2x – 3y)² – 16(3y – 2x)
= 12(2x – 3y)² + 16(2x – 3y)
= 4(2x – 3y) {3(2x – 3y) + 4}
= 4(2x – 3y) (6x – 9y + 4) Ans.

Question 16.
Solution:
(x + y)(2x + 5) – (x + y)(x + 3)
= (x + y)(2 + 5 – x – 3)
= (x + y)(x + 2) Ans.

Question 17.
Solution:
ar + br + at + bt
= r(a + b) + t(a + b)
= (a + b) (r + t) Ans.

Question 18.
Solution:
x² – ax – bx + ab
= x(x – a) – b(x – a)
= (x – a)(x – b)Ans.

Question 19.
Solution:
ab² – bc² – ab + c²
= ab² – ab – bc² + c²
= ab(b – 1) – c²(b – 1)
= (b – 1) (ab – c²) Ans.

Question 20.
Solution:
x² – xz + xy – yz
= x(x – z) + y(x – z)
= (x – z)(x + y)Ans.

Question 21.
Solution:
6ab – b² + 12ac – 2bc
6ab + 12ac – b² – 2bc
= 6a(b + 2c) – b(b + 2c)
= (b + 2c) (6a – b) Ans.

Question 22.
Solution:
(x – 2y)² + 4x – 8y
= (x – 2y)² + 4(x – 2y)
= (x – 2y)(x – 2y + 4)Ans.

Question 23.
Solution:
y² – xy(1 – x) – x³
y² – xy + x²y – x²
= y(y – x) + x² (y – x)
= (y – x)(y + x²)Ans.

Question 24.
Solution:
(ax + by)² + (bx – ay)²
= a²x² + b²y² + 2abxy + b²x² + a²y² – 2abxy
= a²x² + b²y² + b²x² + a²y²
= a²x² + b²x² + a²y² + b²y²
= x²(a² + b²) + y²(a² + b²)
= (a² + b²) (x² + y²) Ans.

Question 25.
Solution:
ab² + (a – 1)b – 1
= ab² + ab – b – 1
= ab(b + 1) – 1(b + 1)
= (b + 1) (ab – 1) Ans.

Question 26.
Solution:
x³ – 3x² + x – 3
= x²(x – 3) + 1(x – 3)
(x – 3)(x² + 1)Ans.

Question 27.
Solution:
ab (x² + y²) – xy (a² + b²)
= abx² + aby² + xya² – xyb²
= abx² – xya² – xyb² + aby2
=ax(bx – ay) – by(bx – ay)
= (bx – ay) (ax – by) Ans.

Question 28.
Solution:
x² – x (a + 2b) + 2ab
= x² – xa – 2bx + 2ab
= x(x – a) – 2b(x – a)
= (x – a)(x – 2b)

Hope given RS Aggarwal Solutions Class 8 Chapter 7 Factorisation Ex 7A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3G

January 23, 2023

RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3G

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3G.

Other Exercises

Evaluate:

Question 1.
Solution:
\(\sqrt { \frac { 16 }{ 81 } } \)
= \(\frac { \sqrt { 16 } }{ \sqrt { 81 } } \)
= \(\sqrt { \frac { 4X4 }{ 9X9 } } \)
= \(\\ \frac { 4 }{ 9 } \)

Worksheets for Class 8 Maths

Question 2.
Solution:
\(\sqrt { \frac { 64 }{ 225 } } \)
= \(\frac { \sqrt { 64 } }{ \sqrt { 225 } } \)
= \(\sqrt { \frac { 8X8 }{ 15X15 } } \)
= \(\\ \frac { 8 }{ 15 } \)

Question 3.
Solution:
\(\sqrt { \frac { 121 }{ 256 } } \)
= \(\frac { \sqrt { 121 } }{ \sqrt { 256 } } \)
= \(\sqrt { \frac { 11X11 }{ 16X16 } } \)
= \(\\ \frac { 11 }{ 16 } \)

Question 4.
Solution:
\(\sqrt { \frac { 625 }{ 729 } } \)
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3G Q4.1

Question 5.
Solution:
\(\sqrt { 3\frac { 13 }{ 36 } } \)
= \(\sqrt { \frac { 3X36+13 }{ 36 } } \)
= \(\sqrt { \frac { 108+13 }{ 36 } } \)
= \(\sqrt { \frac { 121 }{ 36 } } \)
= \(\sqrt { \frac { 11X11 }{ 6X6 } } \)
= \(\\ \frac { 11 }{ 6 } \)

Question 6.
Solution:
\(\sqrt { 4\frac { 73 }{ 324 } } \)
= \(\sqrt { \frac { 4X324+73 }{ 324 } } \)
= \(\sqrt { \frac { 1296+73 }{ 324 } } \)
= \(\sqrt { \frac { 1369 }{ 324 } } \)
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3G Q6.1

Question 7.
Solution:
\(\sqrt { 3\frac { 33 }{ 289 } } \)
= \(\sqrt { \frac { 3X289+33 }{ 289 } } \)
= \(\sqrt { \frac { 867+33 }{ 289 } } \)
= \(\sqrt { \frac { 900 }{ 289 } } \)
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3G Q7.1

Question 8.
Solution:
\(\frac { \sqrt { 80 } }{ \sqrt { 405 } } \)
= \(\sqrt { \frac { 80 }{ 405 } } \)
= \(\sqrt { \frac { 16 }{ 81 } } \)
= \(\frac { \sqrt { 16 } }{ \sqrt { 81 } } \)
= \(\\ \frac { 4 }{ 9 } \)

Question 9.
Solution:
\(\frac { \sqrt { 1183 } }{ \sqrt { 2023 } } \)
= \(\sqrt { \frac { 1183 }{ 2023 } } \)
= \(\sqrt { \frac { 1183\div 7 }{ 2023\div 7 } } \)
= \(\frac { \sqrt { 169 } }{ \sqrt { 289 } } \)
= \(\frac { \sqrt { 13X13 } }{ \sqrt { 17X17 } } \)
= \(\\ \frac { 13 }{ 17 } \)

Question 10.
Solution:
\(\sqrt { 95 } \times \sqrt { 162 } \)
= \(\sqrt { 98\times 162 }\)
= \(\sqrt { 2\times 7\times 7\times 2\times 3\times 3\times 3\times 3 } \)
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3G Q10.1

Hope given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3G are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 5 Playing with Numbers Ex 5D

January 23, 2023

RS Aggarwal Class 8 Solutions Chapter 5 Playing with Numbers Ex 5D

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5D.

Other Exercises

Question 1.
Solution:
5×6 is exactly divisible by 3
Sum of its digits must be divisible by 3
5 + x + 6 = 11 + x is divisible by 3
Least value of x = 1 as 12 is divisible by 3 (b)

Question 2.
Solution:
64y8 is exactly divisible by 3 then the sum of its digits must be divisible by 3
6 + 4 + y + 8 or 18 + y is divisible by 3
Least value of y = 0
18 is divisible by 3 (a)

Question 3.
Solution:
7 x 8 is exactly divisible by 9
Sum of its digits must be divisible by 9
7 + x + 8 = 15 + x must be divisible by 9
Least value of x = 3 as 15 + 3 = 18 is divisible by 9 (c)

Question 4.
Solution:
37y4 is exactly divisible by 9
The sum of its digits must be divisible by
3 + 7 + y + 4 or 14 + y is divisible by 9
Least value of y = 4
As 14 + 4 = 18 is divisible by 9 (d)

Question 5.
Solution:
4xy7 is exactly divisible by 3
The sum of its digits must be divisible by 9
or 4 + x + y + 7 or 11 + (x + y) is divisible by 9
Least value of x + y = 7
as 11 + 7 = 18 is divisible by 9 (d)

Question 6.
Solution:
x7y5 is exactly divisible by 3
Sum of its digits must be divisible by 3
x + 7 + y + 512 + (x + y) is divisible by 3
Least value of x + y = 0 as
12 + 0 = 12 is divisible by 3 (b)

Question 7.
Solution:
x4y5z is exactly divisible by 9
The sum of its digits must be divisible by 9
x + 4 + y + 5 + z or 9 + (x + y + z) must be divisible by 9
Least value of x + y + z = 0 as 9 + 0 = 9 is divisible by 9 (d)

Question 8.
Solution:
A2B5 is exactly divisible by 9
Sum of its digits must be divisible by 9
A + 2 + B + 5 = 7 + A + B is divisible by 9
Least value of A + B = 2 as 7 + 2 = 9 is divisible by 9

Question 9.
Solution:
x27y is exactly divisible by 9
The sum of its digits must be divisible by 9
x + 2 + 7 + y = x + y + 9 is divisible by 9
Least value of x + y = 0 as 0 + 99 is exactly divisible by 9 (a)

Hope given RS Aggarwal Solutions Class 8 Chapter 5 Playing with Numbers Ex 5D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4A

January 23, 2023

RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4A.

Other Exercises

Question 1.
Solution:
(i) (8)³ = 8 x 8 x 8 = 512
(ii) (15)³ = 15 x 15 x 15 = 3375
(iii) (21)³ = 21 x 21 x 21 = 9261
(iv) (60)³ = 60 x 60 x 60 = 216000 Ans.

Question 2.
Solution:
(i)(1.2)³= 1.2 x 1.2 x 1.2 = 1.728
(ii) (3.5)³ = 3.5 x 3.5 x 3.5 = 42.875
(iii) (0.8)³ = 0.8 x 0.8 x 0.8 = 0.512
(iv) (0.05)³ = 0.05 x 0.05 x 0.05 = 0.000125

Question 3.
Solution:
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4A Q3.1

Question 4.
Solution:
(i) 125
= \(\overline { 5\times 5\times 5 } ={ \left( 5 \right) }^{ 3 }\)
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4A Q4.1

Question 5.
Solution:
We know that cube of an even number is also even.
216, 1000 and 512 are the cubes of even numbers as these are all even numbers. Ans.

Question 6.
Solution:
We know that cube of an odd number is also odd.
125, 343 and 9261 are the cubes of odd natural numbers as these are also odd numbers. Ans.

Question 7.
Solution:
Factorising 1323 into prime factors,
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4A Q7.1

Question 8.
Solution:
Factorising 2560 into prime factors.
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4A Q8.1
Making them in groups of 3 equal factors, we are left 5
To make it into a group of 3, we have to multiply it by 5 x 5 i.e. by 25.
Hence, the smallest number by which it is multiplied = 25 Ans.

Question 9.
Solution:
Factorising 1600 into prime factors
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4A Q9.1

Question 10.
Solution:
Factorising 8788 into prime factors
RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4A Q10.1
Making them in groups of 3 equal factors, we are left with 2 x 2
2 x 2 i.e. 4 is to be divided.
Hence least number to be divided for getting perfect cube = 4 Ans.

Hope given RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3

January 23, 2023

RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3

Other Exercises

Question 1.
In a parallelogram ABCD, determine the sum of angles ZC and ZD.
Solution:
In a ||gm ABCD,
∠C + ∠D = 180°
(Sum of consecutive angles)
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3 Q1.1

Question 2.
In a parallelogram ABCD, if ∠B = 135°, determine the measures of its other angles.
Solution:
In a ||gm ABCD, ∠B = 135°
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3 Q2.1
∴ ∠D = ∠B = 135° (Opposite angles of a ||gm)
But ∠A + ∠B = 180° (Sum of consecutive angles)
⇒ ∠B + 135° = 180°
∴ ∠A = 180° – 135° = 45°
But∠C = ∠B = 45° (Opposite angles of a ||gm)
∴ Angles are 45°, 135°, 45°, 135°.

Question 3.
ABCD is a square, AC and BD intersect at O. State the measure of ∠AOB.
Solution:
In a square ABCD,
Diagonal AC and BD intersect each other at O
∵ Diagonals of a square bisect each other at right angle
∵∠AOB = 90°
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3 Q3.1

Question 4.
ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC.
Solution:
In rectangle ABCD,
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3 Q4.1
∠B = 90°, BD is its diagonal
But ∠ABD = 40°
and ∠ABD + ∠DBC = 90°
⇒ 40° + ∠DBC = 90°
⇒ ∠DBC = 90° – 40° = 50°
Hence ∠DBC = 50°

Question 5.
The sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
Solution:
Given : In ||gm ABCD, E and F are the mid points of the side AB and CD respectively
DE and BF are joined
To prove : EBFD is a ||gm
Construction : Join EF
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3 Q5.1
Proof : ∵ ABCD is a ||gm
∴ AB = CD and AB || CD
(Opposite sides of a ||gm are equal and parallel)
∴ EB || DF and EB = DF (∵ E and F are mid points of AB and CD)
∴ EBFD is a ||gm.

Question 6.
P and Q are the points of trisection of the diagonal BD of the parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
Solution:
Given : In ||gm, ABCD. P and Q are the points of trisection of the diagonal BD
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3 Q6.1
To prove : (i) CQ || AP
AC bisects PQ
Proof: ∵ Diagonals of a parallelogram bisect each other
∴ AO = OC and BO = OD
∴ P and Q are point of trisection of BD
∴ BP = PQ = QD …(i)
∵ BO = OD and BP = QD …(ii)
Subtracting, (ii) from (i) we get
OB – BP = OD – QD
⇒ OP = OQ
In quadrilateral APCQ,
OA = OC and OP = OQ (proved)
Diagonals AC and PQ bisect each other at O
∴ APCQ is a parallelogram
Hence AP || CQ.

Question 7.
ABCD is a square. E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
Solution:
Given : In square ABCD
E, F, G and H are the points on AB, BC, CD and DA respectively such that AE = BF = CG = DH
To prove : EFGH is a square
Proof : E, F, G and H are points on the sides AB, BC, CA and DA respectively such that
AE = BF = CG = DH = x (suppose)
Then BE = CF = DG = AH = y (suppose)
Now in ∆AEH and ∆BFE
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3 Q7.1
AE = BF (given)
∠A = ∠B (each 90°)
AH = BE (proved)
∴ ∆AEH ≅ ∆BFE (SAS criterion)
∴ ∠1 = ∠2 and ∠3 = ∠4 (c.p.c.t.)
But ∠1 + ∠3 = 90° and ∠2 + ∠4 = 90° (∠A = ∠B = 90°)
⇒ ∠1 + ∠2 + ∠3 + ∠4 = 90° + 90° = 180°
⇒ ∠1 + ∠4 + ∠1 + ∠4 = 180°
⇒ 2(∠1 + ∠4) = 180°
⇒ ∠1 + ∠4 = \(\frac { { 180 }^{ \circ } }{ 2 }\) = 90°
∴ ∠HEF = 180° – 90° = 90°
Similarly, we can prove that
∠F = ∠G = ∠H = 90°
Since sides of quad. EFGH is are equal and each angle is of 90°
∴ EFGH is a square.

Question 8.
ABCD is a rhombus, EABF is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles.
Solution:
Given : ABCD is a rhombus, EABF is a straight line such that
EA = AB = BF
ED and FC are joined
Which meet at G on producing
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3 Q8.1
To prove: ∠EGF = 90°
Proof : ∵ Diagonals of a rhombus bisect
each other at right angles
AO = OC, BO = OD
∠AOD = ∠COD = 90°
and ∠AOB = ∠BOC = 90°
In ∆BDE,
A and O are the mid-points of BE and BD respectively.
∴ AO || ED
Similarly, OC || DG
In ∆ CFA, B and O are the mid-points of AF and AC respectively
∴ OB || CF and OD || GC
Now in quad. DOCG
OC || DG and OD || CG
∴ DOCG is a parallelogram.
∴ ∠DGC = ∠DOC (opposite angles of ||gm)
∴ ∠DGC = 90° (∵ ∠DOC = 90°)
Hence proved.

Question 9.
ABCD is a parallelogram, AD is produced to E so that DE = DC = AD and EC produced meets AB produced in F. Prove that BF = BC.
Solution:
Given : In ||gm ABCD,
AB is produced to E so that
DE = DA and EC produced meets AB produced in F.
To prove : BF = BC
Proof: In ∆ACE,
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3 Q9.1
O and D are the mid points of sides AC and AE
∴ DO || EC and DB || FC
⇒ BD || EF
∴ AB = BF
But AB = DC (Opposite sides of ||gm)
∴ DC = BF
Now in ∆EDC and ∆CBF,
DC = BF (proved)
∠EDC = ∠CBF
(∵∠EDC = ∠DAB corresponding angles)
∠DAB = ∠CBF (corresponding angles)
∠ECD = ∠CFB (corresponding angles)
∴ AEDC ≅ ACBF (ASA criterion)
∴ DE = BC (c.p.c.t.)
⇒ DC = BC
⇒ AB = BC
⇒ BF = BC (∵AB = BF proved)
Hence proved.

Hope given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A

January 23, 2023

RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6A.

Other Exercises

Add:

Question 1.
Solution:
8ab + ( – 5ab) + (3ab) + ( – ab)
= 8ab – 5ab + 3ab – ab = 11 ab – 6ab
= 5ab Ans.

Question 2.
Solution:
7x + ( – 3x) + 5x + ( – x) + ( – 2x)
= 7x – 3x + 5x – x – 2x
= 12x – 6x = 6x Ans.

Question 3.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 3.1

Question 4.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 4.1

Question 5.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 5.1

Question 6.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 6.1

Question 7.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 7.1

Question 8.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 8.1

Subtarct:

Question 9.
Solution:
-5a²b – 3a²b = – 8a²b Ans.

Question 10.
Solution:
6pq – ( – 8pq) = 6pq + 8pq

Question 11.
Solution:
– 8abc – ( – 2abc)
= – 8abc + 2abc
= – 6abc Ans.

Question 12.
Solution:
– 11p – ( – 16p)
= – 11p + 16p
= 5p Ans.

Question 13.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 13.1

Question 14.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 14.1

Question 15.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 15.1

Question 16.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 16.1

Question 17.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 17.1

Question 18.
Solution:
RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6A 18.1

Question 19.
Solution:
Let length of rectangle = 5x² – 3y²
and breadth = x² + 2xy
Perimeter = 2(Length + Breadth)
= 2(5x² – 3y² + x² + 2xy)
= 2(6x² – 3y² + 2xy)
= 12x² – 6y² + 4xy Ans.

Question 20.
Solution:
Perimeter of a triangle = 6p² – 4p + 9
Sum of two sides of it = 3p² – 5p + 3 + p² – 2p + 1 = 4p² – 7p – 4
Third side = (6p² – 4p + 9) – (4p² – 7p + 4)
= 6p² – 4p + 9 – 4p² + 7p – 4
= 2p² + 3p + 5 Ans

Hope given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS

January 23, 2023

RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS

Other Exercises

Mark the correct alternative in each of the following:
Question 1.
The opposite sides of a quadrilateral have
(a) no common point
(b) one common point
(c) two common points
(d) infinitely many common points
Solution:
The opposite sides of a quadrilateral have no common point. (a)

Question 2.
The consecutive sides of a quadrilateral have
(a) no common point
(b) one common point
(c) two common points
(d) infinitely many common points
Solution:
The consecutive sides of a quadrilateral have one common point. (b)

Question 3.
PQRS is a quadrilateral, PR and QS intersect each other at O. In which of the following cases, PQRS is a parallelogram?
(a) ∠P = 100°, ∠Q = 80°, ∠R = 100°
(b) ∠P = 85°, ∠Q = 85°, ∠R = 95°
(c) PQ = 7 cm, QR = 7 cm, RS = 8 cm, SP = 8 cm
(d) OP = 6.5 cm, OQ = 6.5 cm, OR = 5.2 cm, OS = 5.2 cm
Solution:
PQRS is a quadrilateral, PR and QS intersect each other at O. PQRS is a parallelogram if ∠P = 100°, ∠Q = 80°, ∠R = 100° (a)

Question 4.
Which of the following quadrilateral is not a rhombus?
(a) All four sides are equal
(b) Diagonals bisect each other
(c) Diagonals bisect opposite angles
(d) One angle between the diagonals is 60°
Solution:
A quadrilateral is not a rhombus if one angle between the diagonals is 60°. (d)

Question 5.
Diagonals necessarily bisect opposite angles in a
(a) rectangle
(b) parallelogram
(c) isosceles trapezium
(d) square
Solution:
Diagonals necessarily bisect opposite angles in a square. (d)

Question 6.
The two diagonals are equal in a
(a) parallelogram
(b) rhombus
(c) rectangle
(d) trapezium
Solution:
The two diagonals are equal in a rectangle. (c)

Question 7.
We get a rhombus by joining the mid-points of the sides of a
(a) parallelogram
(b) rhombus
(c) rectangle
(d) triangle
Solution:
We get a rhombus by joining the mid points of the sides of a rectangle. (c)

Question 8.
The bisectors of any two adjacent angles of a parallelogram intersect at
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution:
The bisectors of any two adjacent angles of a parallelogram intersect at 90°. (d)

Question 9.
The bisectors of the angle of a parallelogram enclose a
(a) parallelogram
(b) rhombus
(c) rectangle
(d) square
Solution:
The bisectors of the angles of a parallelogram enclose a rectangle. (c)

Question 10.
The figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a
(a) parallelogram
(b) rectangle
(c) square
(d) rhombus
Solution:
The figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a parallelogram. (a)

Question 11.
The figure formed by joining the mid-points of the adjacent sides of a rectangle is a
(a) square
(b) rhombus
(c) trapezium
(d) none of these
Solution:
The figure formed by joining the mid-points of the adjacent sides of a rectangle is a rhombus. (b)

Question 12.
The figure formed by joining the mid-points of the adjacent sides of a rhombus is a
(a) square
(b) rectangle
(c) trapezium
(d) none of these
Solution:
The figure formed by the joining the mid-points of the adjacent sides of a rhombus is a rectangle. (b)

Question 13.
The figure formed by joining the mid-points of the adjacent sides of a square is a
(a) rhombus
(b) square
(c) rectangle
(d) parallelogram
Solution:
Tire figure formed by joining the mid-points of the adjacent sides of a square is a square. (b)

Question 14.
The figure formed by joining the mid-points of the adjacent sides of a parallelogram is a
(a) rectangle
(b) parallelogram
(b) rhombus
(d) square
Solution:
The figure formed by joining the mid-points of the adjacent sides of a parallelogram is a parallelogram. (b)

Question 15.
If one angle of a parallelogram is 24° less than twice the smallest angle, then the measure of the largest angle of the parallelogram is
(a) 176°
(b) 68°
(c) 112°
(d) 102°
Solution:
Let the smallest angle be x
The largest angle = 2x – 24°
But sum of two adjacent angles = 180°
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q15.1

Question 16.
In a parallelogram ABCD, If ∠DAB = 75° and ∠DBC = 60°, then ∠BDC =
(a) 75°
(b) 60°
(c) 45°
(d) 55°
Solution:
In ||gm ABC,
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q16.1
∠A = 75°, ∠DBC = 60°
But ∠A + ∠B = 180° (Sum of two consecutive angles)
⇒ 75° + ∠B = 180°
⇒ ∠B = 180°- 75“= 105°
But ∠DBC = 60°
∴ ∠DBA = 105°-60° = 45°
But ∠BDC = ∠DBA (Alternate angles)
∴ ∠BDC = 45° (c)

Question 17.
ABCD is a parallelogram and E and F are the centroids of triangles ABD and BCD respectively, then EF =
(a) AE
(b) BE
(c) CE
(d) DE
Solution:
In ||gm ABCD, BD is joined forming two triangles ABD and BCD
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q17.1
E and F are the centroid of ∆ABD and ∆BCD
Now E and F trisect AC
i.e. AE = EF = FC
∴ EF = AE (a)

Question 18.
ABCD is a parallelogram, M is the mid¬point of BD and BM bisects ∠B. Then, ∠AMB =
(a) 45°
(b) 60°
(c) 90°
(d) 75°
Solution:
In ||gm ABCD, M is mid-point of BD and
BM bisects ∠B
AM is joined
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q18.1
∴AM bisects ∠A
But ∠A + ∠B = 180° (Sum of two consecutive angles)
∴ ∠AMB = 90° (c)

Question 19.
If an angle of a parallelogram is two-third of its adjacent angle, the smallest angle of the parallelogram is
(a) 108°
(b) 54°
(c) 12°
(d) 81°
Solution:
Let adjacent angle of a ||gm = x
Then second angle = \(\frac { 2 }{ 3 }\) x
∴ x+ \(\frac { 2 }{ 3 }\) x= 180°
(Sum of two adjacent angles of a ||gm is 180°)
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q19.1

Question 20.
If the degree measures of the angles of quadrilateral are Ax, lx, 9x and 10JC, what is the sum of the measures of the smallest angle and largest angle?
(a) 140°
(b) 150°
(c) 168°
(d) 180°
Solution:
Sum of the angles of a quadrilateral = 360°
∴ 4x + 1x + 9x + 10x = 360°
⇒ 30x = 360°
⇒ x = \(\frac { { 360 }^{ \circ } }{ 30 }\) = 12°
Now sum of smallest and largest angle = 4 x 12° + 10 x 12°
= 48° + 120° = 168° (c)

Question 21.
If the diagonals of a rhombus are 18 cm and 24 cm respectively, then its side is equal to
(a) 16 cm
(b) 15 cm
(c) 20 cm
(d) 17 cm
Solution:
Diagonals of a rhombus are 18 cm and 24 cm But diagonals of a rhombus bisect each other at right angles
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q21.1

Question 22.
ABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC = 35°, then ∠ABC =
(a) 70°
(b) 110°
(c) 90°
(d) 120°
Solution:
In ||gm ABCD, AC is its diagonal which bisect ∠BAD
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q22.1
∠BAD = 35°
∴ ∠BAD = 2 x 35° = 70°
But ∠A + ∠B = 180° (Sum of consecutive angles)
⇒ 70° + ∠B = 180°⇒ ∠B = 180° – 70°
∴ ∠B = 110°
⇒ ABC = 110° (b)

Question 23.
In a rhombus ABCD, if ∠ACB = 40°, then ∠ADB =
(a) 70°
(b) 45°
(c) 50°
(d) 60°
Solution:
In rhombus ABCD, ∠ACB = 40°
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q23.1
∴ ∠BCD = 2 x ∠ACB
= 2 x 40° = 80°
But ∠BCD + ∠ADC = 180° (Sum of consecutive angles of ||gm)
⇒ 80° + ∠ADC = 180°
⇒ ∠ADC = 180° – 80° = 100°
∴ ∠ADB = \(\frac { 1 }{ 2 }\)∠ADC = \(\frac { 1 }{ 2 }\)x 100° = 50° (c)

Question 24.
In ∆ABC, ∠A = 30°, ∠B = 40° and ∠C = 110°. The angles of the triangle formed by joining the mid-points of the sides of this triangle are
(a) 70°, 70°, 40°
(b) 60°, 40°, 80°
(c) 30°, 40°, 110°
(d) 60°, 70°, 50°
Solution:
In ∆ABC,
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q24.1
∠A = 30°, ∠B = 40°, ∠C = 110°
D, E and F are mid-points of the sides of the triangle. By joining them in order,
DEF is a triangle formed
Now BDEF, CDFE and AFDE are ||gms
∴ ∠A = ∠D = 30°
∠B = ∠E = 40°
∠C = ∠F= 110°
∴ Angles are 30°, 40°, 110° (c)

Question 25.
The diagonals of a parallelogram ABCD intersect at O. If ∠BOC = 90° and ∠BDC = 50°, then ∠OAB =
(a) 40°
(b) 50°
(c) 10°
(d) 90°
Solution:
In ||gm ABCD, diagonals AC and BD intersect each other at O
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q25.1
BOC = 90°, ∠BDC = 50°
∵ ∠BOC = 90°
∴ Diagonals of ||gm bisect each other at 90°
∴∠COD = 90°
In ∆COD,
∠OCD = 90° – 50° = 40°
But ∠OAB = ∠OCD (Alternate angles)
∴∠OAB = 40° (a)

Question 26.
ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and BC respectively. If AB = 12 cm, MN = 14 cm, then CD =
(a) 10 cm
(b) 12 cm
(c) 14 cm
(d) 16 cm
Solution:
In trapezium AB || DC
M and N are mid-points of sides AD and BC and MN are joined
AB = 12 cm, MN = 14 cm
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q26.1
∵ MN = \(\frac { 1 }{ 2 }\)(AB + CD)
⇒ 2MN = AB + CD
⇒ 2 x 14 = 12 + CD
CD = 2 x 14 – 12 = 28 – 12 = 16 cm (d)

Question 27.
Diagonals of a quadrilateral ABCD bisect each other. If ∠A = 45°, then ∠B =
(a) 115°
(b) 120°
(c) 125°
(d) 135°
Solution:
Diagonals AC and BD of quadrilateral ABCD bisect each other at O
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q27.1
∴ AO = OC, BO = OD
∴ ABCD is a ||gm ∠A = 45°
But ∠A + ∠B = 180° (Sum of consecutive angles)
∴ ∠B = 180° – ∠A = 180° – 45°
= 135° (d)

Question 28.
P is the mid-point of side BC of a paralleogram ABCD such that ∠BAP = ∠DAP. If AD = 10 cm, then CD =
(a) 5 cm
(b) 6 cm
(c) 8 cm
(d) 10 cm
Solution:
In ||gm ABCD, P is mid-point of BC
AD = 10cm
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q28.1
∠BAP = ∠DAP
Through P, draw PQ || AB
∴ ABPQ is rhombus
∴ AB = BP = AQ
= \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) x 10 = 5 cm
But CD = AB (Opposite sides of ||gm)
∴ CD = 5 cm (a)

Question 29.
In ∆ABC, E is the mid-point of median AD such that BE produced meets AC at E If AC = 10.5 cm, then AF =
(a) 3 cm
(b) 3.5 cm
(c) 2.5 cm
(d) 5 cm
Solution:
In ∆ABC, E is the mid-point of median AD
Such that BE produced meets AC at F
AC = 10.5 cm
Draw DG || AF
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q29.1
In ∆ADG
E is mid-point of AD and EF || DG
∴ F is mid-point of AG
⇒ AF = FG …(i)
In ∆BCF
D is mid-point of BC and DG || BF
∴ G is mid-point of FC
∴ FG = GC …(i)
From (i) and (ii)
AF = FG = GC = \(\frac { 1 }{ 3 }\) AC
But AC = 10.5 cm
∴ AF = \(\frac { 1 }{ 3 }\) AC = \(\frac { 1 }{ 3 }\) x 10.5 = 3.5 cm (b)

Question 30.
ABCD is a parallelogram and E is the mid-point of BC. DE and AB when produced meet at F. Then, AF =
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q30.2
Solution:
In ||gm ABCD, E is mid-point of BC DE and AB are produced to meet at F

∵ E is mid point of BC
∴ BE = EC
In ∆BEF and ∆CDE
BE = EC
∠BEF = ∠CED (Vertically opposite angle)
and ∠EBF = ∠ECD (Alternate angles)
∴ ∆BEF ≅ ∆CDE (ASA criterian)
∴ DC = BF
But DC = AB
∴ AB = BF
AF = AB + BF = AB + AB
= 2AB (b)

Question 31.
In a quadrilateral ABCD, ∠A + ∠C is 2 times ∠B + ∠D. If ∠A = 140° and ∠D = 60°, then ∠B =
(a) 60°
(b) 80°
(c) 120°
(d) None of these
Solution:
In quadrilateral ABCD
⇒ ∠A + ∠C = 2(∠B + ∠D)
⇒ ∠A + ∠C = 2∠B + 2∠D
Adding 2∠A + 2∠C both sides
2∠A + 2∠C + ∠A + ∠C = 2∠A + 2∠B + 2∠C + 2∠D
⇒ 3∠A + 3∠C = 2(∠A + ∠B + ∠C + ∠D)
⇒ 3(∠A + ∠C) = 2 x 360° = 720°
∴ ∠A + ∠C = \(\frac { { 720 }^{ \circ } }{ 3 }\) = 240°
⇒ 40° + ∠C = 240° (∵ ∠A = 40°)
∠C = 240° – 40° = 200°
Now 2(∠B + ∠D) = ∠A + ∠C = 240°
∠B + ∠D = \(\frac { { 240 }^{ \circ } }{ 2 }\) = 120°
∴ ∠B = 60° = 120°
∴ ∠B = 60° (a)

Question 32.
The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, then ∠DPC =
(a) 70°
(b) 90°
(c) 80°
(d) 100°
Solution:
In rectangle ABCD, diagonals AC and BD intersect each other at P
RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS Q32.1
∠ABD = 50°
∴ ∠CAB = ∠ABD = 50° (∵ AP = BP)
Now in ∆APB
∠CAB + ∠ABD + ∠APB = 180° (Angles of a triangle)
⇒ ∠PAB + ∠PBA + ∠APB = 180°
⇒ 50° + 50° + ∠APB = 180°
⇒ ∠APB = 180° – 50° – 50° = 80°
But ∠DPC = ADB (Vertically opposite angles)
∴ ∠DPC = 80° (c)

Hope given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS

January 23, 2023

RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS

Other Exercises

Question 1.
If ABC and BDE are two equilateral triangles such that D is the mid-ponit of BC, then find ar(∆ABC) : ar(∆BDE).
Solution:
ABC and BDE are two equilateral triangles and D is the mid-point of BC
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS Q1.1
Let each side of AABC = a
Then BD = \(\frac { a }{ 2 }\)
∴ Each side of triangle BDE will be \(\frac { a }{ 2 }\)

Question 2.
In the figure, ABCD is a rectangle in which CD = 6 cm, AD = 8 cm. Find the area of parallelogram CDEF.
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS Q2.1
Solution:
In rectangle ABCD,
CD = 6 cm, AD = 8 cm
∴ Area of rectangle ABCD = CD x AD
= 6 x 8 = 48 cm²
∵ DC || AB and AB is produced to F and DC is produced to G
∴ DG || AF
∵ Rectangle ABCD and ||gm CDEF are on the same base CD and between the same parallels
∴ ar(||gm CDEF) = ar(rect. ABCD)
= 48 cm²

Question 3.
In the figure of Q. No. 2, find the area of ∆GEF.
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS Q3.1
Solution:

Question 4.
In the figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ∆EFG.
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS Q4.1
Solution:
ABCD is a rectangle in which
AB = 10 cm, AD = 5 cm

∵ ABCD is a rectangle
∴DC || AB,
DC is produced to E and AB is produced to G
∴DE || AG
∵ Rectangle ABCD and ||gm ABEF are on the same base AB and between the same parallels
∴ ar(rect. ABCD) = ar(||gm ABEF)
= AB x AD = 10 x 5 = 50 cm²
Now ||gm ABEF and AEFG are on the same
base EF and between the same parallels
∴ area ∆EFG = \(\frac { 1 }{ 2 }\) ar(||gm ABEF)
= \(\frac { 1 }{ 2 }\) x 50 = 25 cm²

Question 5.
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then find or(∆RAS).
Solution:
In quadrant PLRM, rectangle PQRS is in scribed
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS Q5.1
Radius of the circle = 13 cm
A is any point on PQ
AR and AS are joined, PS = 5 cm
In right ∆PRS,
PR² = PS² + SR²
⇒ (13² = (5)²+ SR²
⇒ 169 = 25 + SR²
⇒ SR² = 169 – 25 = 144 = (12)²
∴ SR = 12 cm
Area of rect. PQRS = PS x SR = 5x 12 = 60 cm²
∵ Rectangle PQRS and ARAS are on the same
base SR and between the same parallels
∴ Area ARAS = \(\frac { 1 }{ 2 }\) area rect. PQRS 1
= \(\frac { 1 }{ 2 }\) x 60 = 30 cm²

Question 6.
In square ABCD, P and Q are mid-point of AB and CD respectively. If AB = 8 cm and PQ and BD intersect at O, then find area of ∆OPB.
Solution:
In sq. ABCD, P and Q are the mid points of sides AB and CD respectively PQ and BD are joined which intersect each other at O
Side of square AB = 8 cm
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS Q6.1
∴ Area of square ABCD = (side)²
∵ Diagonal BD bisects the square into two triangle equal in area
∴ Area ∆ABD = \(\frac { 1 }{ 2 }\) x area of square ABCD
= \(\frac { 1 }{ 2 }\) x 64 = 32 cm²
∵ P is mid point of AB of AABD, and PQ || AD
∴ O is the mid point of BD
∴ OP = \(\frac { 1 }{ 2 }\)AD = \(\frac { 1 }{ 2 }\) x 8 = 4 cm
and PB = \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) x 8 = 4 cm
∴ Area ∆OPB = \(\frac { 1 }{ 2 }\)PB x OP
= \(\frac { 1 }{ 2 }\) x4x4 = 8 cm²

Question 7.
ABC is a triangle in which D is the mid-point of BC. E and F are mid-points of DC and AE respectively. If area of ∆ABC is 16 cm², find the area of ∆DEF.
Solution:
In ∆ABC, D is mid point of BC. E and F are the mid points of DC and AE respectively area of ∆ABC = 16 cm²
FD is joined
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS Q7.1
∵ D is mid point of BC
∴ AD is the median and median divides the triangle into two triangles equal in area
area ∆ADC = \(\frac { 1 }{ 2 }\) ar(∆ABC)
= \(\frac { 1 }{ 2 }\) x 16 = 8 cm²
Similarly, E is mid point of DC
∴ area (∆ADE) = \(\frac { 1 }{ 2 }\) ar(∆ADC)
= \(\frac { 1 }{ 2 }\) x 8 = 4 cm²
∵ F is mid point of AE of ∆ADE
∴ ar(∆DEF) = \(\frac { 1 }{ 2 }\)area (∆ADE)
= \(\frac { 1 }{ 2 }\) x 4 = 2 cm²

Question 8.
PQRS is a trapezium having PS and QR as parallel sides. A is any point on PQ and B is a point on SR such that AB || QR. If area of ∆PBQ is 17 cm2, find the area of ∆ASR.
Solution:
In trapezium PQRS,
PS || QR
A and B are points on sides PQ and SR
Such that AB || QR
area of ∆PBQ = 17 cm²
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS Q8.1
∆ABQ and ∆ABR are on the same base AB and between the same parallels
∴ ar(∆ABQ) = ar(∆ABR) …(i)
Similarly, ∆ABP and ∆ABS are on the same base and between the same parallels
∴ ar(ABP) = ar(∆ABS) …(ii)
Adding (i) and (ii)
ar( ∆ABQ) + ar( ∆ABP)
= ar(∆ABR) + ar(∆ABS)
⇒ ar(∆PBQ) = ar(∆ASR)
Put ar(PBQ) = 17 cm²
∴ ar(∆ASR) = 17 cm²

Question 9.
ABCD is a parallelogram. P is the mid-point of AB. BD and CP intersect at Q such that CQ : QP = 3 : 1. If ar(∆PBQ) = 10 cm2, find the area of parallelogram ABCD.
Solution:
In ||gm ABCD, P is mid point on AB,
PC and BD intersect each other at Q
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS Q9.1
CQ : QP = 3 : 1
ar(∆PBQ) = 10 cm²
In ||gm ABCD,
BD is its diagonal
∴ ar(∆ABD) = ar(∆BCD) = \(\frac { 1 }{ 2 }\) ar ||gm ABCD
∴ ar(||gm ABCD) = 2ar(∆ABD) …(i)
In ∆PBC CQ : QP = 3 : 1
∵ ∆PBQ and ∆CQB have same vertice B
∴ 3 x area ∆PBQ = ar(∆CBQ)
⇒ area(∆CBQ) = 3 x 10 = 30 cm²
∴ ar(∆PBC) = 30 + 10 = 40 cm²
Now ∆ABD and ∆PBC are between the
same parallel but base PB = \(\frac { 1 }{ 2 }\) AB
∴ ar(∆ABD) = 2ar(∆PBC)
= 2 x 40 = 80 cm²
But ar(||gm ABCD) = 2ar(∆ABD)
= 2 x 80 = 160 cm²

Question 10.
P is any point on base BC of ∆ABC and D is the mid-point of BC. DE is drawn parallel to PA to meet AC at E. If ar(∆ABC) = 12 cm², then find area of ∆EPC.
Solution:
P is any point on base of ∆ABC
D is mid point of BC
DE || PA drawn which meet AC at E
ar(∆ABC) = 12 cm²
AD and PE are joined
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS Q10.1
∵ D is mid point of BC
∴ AD is median
∴ ar(∆ABD) = ar(∆ACD)
= \(\frac { 1 }{ 2 }\) (∆ABC) = \(\frac { 1 }{ 2 }\) x 12 = 6 cm² …(i)
∵ ∆PED and ∆ADE are on the same base DE and between the same parallels
∴ ar(∆PED) = ar(∆ADE)
Adding ar(∆DCE) to both sides,
ar(∆PED) + ar(∆DCE) = ar(∆ADE) + ar(∆DCE)
ar(∆EPC) = ar(∆ACD)
⇒ ar(∆EPC) = ar(∆ABD) = 6 cm2 [From (i)]
∴ ar(∆EPC) = 6 cm²

Hope given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms

January 23, 2023

NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms

These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms

Question 1.
Write true (T) or false (F)
(a) Wittaker proposed five kingdom classification.
(b) Monera is divided into Archaebacteria and Eubacteria.
(c) Starting from Class, Species comes before Genus.
(d) Anabaena belongs to kingdom Monera.
(e) Blue-green algae belong to kingdom Protista.
(f) All prokaryotes are classified under Monera.
Answer:
(a) —T
(b) —T,
(c) — F
(d) —T,
(e) —F,
(f) —T.

More Resources

Question 2.
Fill in the blanks :
(a) Fungi show ……………. mode of nutrition.
(b) Cell wall of fungi is made up of ……………… .
(c) Association between blue-green algae and fungi is called as …………….. .
(d) Chemical nature of chidn is ……………… .
(e) ………………. has smallest number of organisms with maximum number of similar characters.
(f) ……………… are called amphibians of plant kingdom.
Answer:
(a) saprophytic
(b) chitin
(c) lichen
(d) carbohydrate
(e) Species
(f) Bryophytes.

Question 3.
You are provided with seeds of Gram, Wheat, Rice Pumpkin, Maize and Pea. Classify them whether they are monocot or dicot ?
Answer:
Gram-Dicot.
Wheat-Monocot.
Rice-Monocot.
Pumpkin-Dicot.
Maize-Monocot.
Pea-Dicot.

Question 4.
Match the items of Column A with items of Column B.
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 1
Answer:
(a) —(ii),
(b) —(i),
(c) — (iv),
(d) —(iii),
(e) — (vi),
(f) —(v),
(g) — (vii).

Question 5.
Match the articles of Column A with those of column B
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 2
Answer:
a —(iii),
b —(ii),
c—(vi),
d —(i),
e —(v),
f—(iv).

Question 6.
Classify the following organisms based on absence or presence of true coelom as acoelomate, pseudocoelomate and coelomate : Spongilla, Sea Anemone, Planaria, Liver Fluke, Wuchereria, Ascaris, Nereis, Earthworm, Scorpion, Birds, Fishes and Horse.
Answer:

Spongilla-Acoelomaxe
Sea Anemone-Acoelomate
Planaria-Acoelomate
Liver Fluke-Acoelomate
Wuchereria— Pseudocoelomate
Aszvzris-Pseudocoelomate
Nereis-Coelomate
Scorpion—Coelomate
Earthworm-Coelomate
Birds-Coelomate
Fishes-Coelomate
Horse-Coelomate.

Question 7.
Endoskeleton of fishes is made up of cartilage and bone. Classify the following fishes as cartilaginous or bony : Xorpedo, Sting Ray, Dog fish, Rohu, Angler Fish, Exocoetus.
Answer:

Xorpedo—Cartilaginous
Sting Ray-Cartilaginous
Dog Fish-Cartilaginous
Rohu-Bony
Angler fish-Bony
Exocoetus—Bony.

Question 8.
Classify the following based on number of chambers in their heart : Rohu, Scolidon, Salamander, Flying Lizard, King Cobra, Crocodile, Ostrich, Pigeon, Bat, Whale.
Answer:

Rohu. 2-Chambered.
Scoliodon. 2-chambered
Frog. 3-chambered
Salamander. 3-chambered
Flying Lizard. Incompletely 4-chambered.
King Cobra. Incompletely 4-chambered.
Crocodile. 4-chambered
Ostrich. 4-chambered
Pigeon. 4-chambered
Bat. 4-chambered
Whale. 4-chambered.

Question 9.
Classify Rohu, Scoliodon, Flying Lizard, King Cobra, Frog, Salamander, Ostrich, Pigeon, Bat, Crocodile and Whale into cold blooded and warm blooded animals.
Answer:

Rohu. Cold blooded
Scoliodon. Cold blooded
Flying Lizard. Cold blooded
King Cobra. Cold Blooded
Frog. Cold blooded
Salamander. Cold blooded
Ostrich. Warm blooded
Pigeon. Warm blooded
Bat. Warm blooded,
Crocodile. Cold blooded
Whale. Warm blooded.

Question 10.
Name two egg laying mammals.
Answer:

Duck Billed Platypus
Echidna

Question 11.
Fill in the blanks.
(a) Five Kingdom classification of living organisms is given by …………….. .
(b) Basic smallest unit of classification is …………. .
(c) Prokaryotes are grouped in kingdom …………. .
(d) Paramoecium is a protistan because of its ……………. .
(e) Fungi do not contain ……………. .
(f ) A fungus ………….. can be seen without microscope.
(g) Common fungus used in preparing the bread is …………… .
(h) Algae and fungi form symbiotic association called ……………. .
Answer:
(a) Whittaker
(b) species
(c) Monera
(d) unicellular eukaryotic nature
(e) chlorophyll
(f) like mushroom
(g) Yeast
(h) lichen.

Question 12.
Give True (T) and Flase (F) :
(a) Gymnosperms differ from angiosperms in having covered seeds.
(b) Non-flowering plants are called cryptogamae.
(c) Bryophytes have conducting tissue.
(d) Funaria is a moss.
(e) Compound leaves are found in many ferns.
(f) Seeds, contain embryo.
Answer:
(a) —F,
(b) —F,
(c) —F,
(d) —T,
(e) —T,
(f) —T.

Question 13.
Give examples for the following :
(a) Bilateral, dorsiventral symmetry is found in ……………. .
(b) Worm causing disease elephantiasis is ……………… .
(c) Open circulatory system is found in ………………. where coelomic cavity is filled with blood.
(d) …………….. are known to have pseudocoelom.
Answer:
(a) Liver Fluke/Lizard
(b) Wuchereria (Filarial Worm)
(c) Arthropods
(d) Nematodes (roundworms).

Question 14.
Label a, b, c and d in the given figure. Give the function of b.
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 3
Answer:
a —pectoral fin.
b —caudal fin.
c—posterior dorsal fin,
d —anterior dorsal fin.
Function of b. Swimming and steering.

Question 15.
Fill the boxes with appropriate characteristics/plant group(s)
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 4
Answer:
a —Thallophyta.
b —Without specialized vascular tissue (non-vascular)
c —Pteridophyta.
d —Phanerogemae.
e —Bear naked seeds.
f—Angiosperms.
g—Have seeds with two cotyledons,
h —Monocots.

Question 16.
Write name of a few thallophytes. Draw a labelled diagram of Spirogyra.
Answer:
Ulothrix, Cladophora, JJlva, Spirogyra, Chara,
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 5

Question 17.
Thallophyta, bryophyta and pteridophyta one called “cryptogams.” Gymnosperms and angiosperns are called “phanerogams”. Discuss why ? Draw one example of gymnosperm. (CCE 2011)
Answer:
(a) Thallophyta, bryophyta and pteridophyta are called cryptogams because they are seedless and possesss inconspicuous or hidden reproductive organs.
(b) Gymnosperms and angiosperms are called phanerogams as they have conspicuous reproductive organs with seeds containing an embryo and reserve food.
(c)
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 6

Question 18.
Define the terms and give one example of each
(a) Bilateral symmetry
(b) Coelom
(c) Triploblastic. (CCE 2011, 2012)
Answer:
(a) Bilateral Symmetry: It is a type of symmetry in which appendages and organs of the body are paired with one of each pair being present in right and left halves of the body, e.g., Lizard, Human.
(b) Coelom: It is mesoderm lined, fluid filled internal body cavity that lies between alimentary canal and skin. It provides a shock proof environment to the contained body organs, e.g, chordates, annelids.
(c) Triploblastic: They are animals having three germinal layers — outer ectoderm, middle mesoderm and inner endoderm, e.g, nematodes, arthropods, star fish.

Question 19.
You are given Leech, Nereis, Scolopendra, Prawn and Scorpio/i. All have segmented body organisation. Will you classify them in one group ? If not give the important characters based on which you will separate these, organisms into different groups.
(CCE 2012)
Answer:
No,

Leech and Nereis have metameric segmentation (external segmentation corresponding to internal segmentation), closed circulatory system and unjointed appendages. They belong to annelida.
Scolopendra, Prawn and Scorpion have open circulatory system and jointed appendages. They belong to arthropoda.

Question 20.
Which organism is more complex and evolved among bacteria, Mushroom and Mango tree ? Give reasons. (CCE 2012)
Answer:
Mango tree is more complex and evolved among bacteria, Mushroom and Mango because of the

Differentiated sporophyte
Vascular tissues
Embryo stage
Seeds present inside fruit. Bacteria are procaryotic. Mushroom is eucaryotic (fungus) but without any differentiation of stem leaves and roots, absence of vascular tissues and embryo stage.

Question 21.
Differentiate between flying Lizard and Bird. Draw the diagram.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 7

Question 22.
List out some common features in Cat, Rat and Bat. (CCE2012, 2013)
Answer:
Cat, Rat and Bat belong to same class of mammalia. The common features are

Hair
Mammary glands
Integumentary glands
Seven cervical vertebrae
Diaphragm
4-Chambered heart
External pinnae
Vivipary.

Question 23.
Why do we keep both snake and turtle in the same class ? (CCE 2012)
Answer:
Both Snake and Turtle have been placed in class reptilia because of the common characteristics :

Skin without glands
Three chambered (incompletely four chambered) heart
Respiration through lungs
Cold blooded
Hard shelled eggs
Embryo protected by extra embryonal membranes.

Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3

January 23, 2023

RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3

Other Exercises

Question 1.
In the figure, compute the area of the quadrilateral.
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q1.1
Solution:
In the quadrilateral ABCD,
∠A = 90°, ∠CBD = 90°, AD = 9 cm, BC = 8 cm and CD = 17 cm

In right ∆BCD,
CD = BC² + BD² (Pythagoras Theorem)
⇒ (17)² = (8)² + BD²
⇒ 289 = 64 + BD²
⇒ BD² = 289 – 64 = 225 = (15)²
∴ BD = 15 cm
Now in right ∆ABD,
BD² = AB² + AD²
⇒ (15)² = AB² + (9)²
⇒ 225 = AB² + 81
⇒ AB²= 225 – 81 = 144 = (12)²
∴ AB = 12 cm
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q1.3

Question 2.
In the figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR. Find the area of ∆OTS if PQ = 8 cm.
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q2.1
Solution:
In square PQRS, T and U are the mid-points of the sides PS and QR
TU, QS and US are joined
PQ = 8 cm
∴ T and U are mid-points of the opposites sides PS and QR
∴ TU || PQ TO || PQ
In RQS,
T is mid-point of PS and TO || PQ
∴ O is the mid point of SQ 1 1
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q2.2

Question 3.
Compute the area of trapezium PQRS in the figure.
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q3.1
Solution:
In ∆TQR, ∠RTQ = 90°
∴ QR² = TQ² + RT²
⇒ (17)² = (8)² + RT²
⇒ 289 = 64 + RT²
⇒ RT² = 289 – 64 = 225 = (15)²
∴ RT = 15 cm
and PQ = 8 + 8 = 16 cm

Question 4.
In the figure, ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of ∆AOB.
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q4.1
Solution:
In ∆AOB, ∠AOB = 90°
C is a point on AB such that AC = BC Join OC

Since C is the mid-point of hypotenuse of right ∆AOB
∴ AC = CB = OC = 6.5 cm
∴ AB = 6.5 + 6.5 = 13 cm
Now in right ∆AOB
⇒ AB² = AO² + OB²(Pythagoras Theorem)
⇒ (13)² = (12)² + OB²
⇒ 169 = 144 + OB²
⇒ OB² = 169 – 144 = 25 = (5)²
∴ OB = 5 cm
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q4.3

Question 5.
In the figure, ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm, and distance between AB and DC is 4 cm. Find the value of x and area of trapezium ABCD.
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q5.1
Solution:
In the trapezium ABCD,
AB = 7 cm
AL = BM = 4 cm
AD = BC = 5 cm

Question 6.
In the figure, OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm.If OE = 2 \(\sqrt { 5 } \) , find the area of the rectangle.
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q6.1
Solution:
Radius of the quadrant of circle = 2\(\sqrt { 5 } \) units
∴ OD diagonal of rectangle = 10 units (∵ OD = OB = OA = 10 cm)
DE = 2 \(\sqrt { 5 } \) cm
∴ In right ∆OED,
OD² = OE² + DEv
(10)² = OE² + (2\(\sqrt { 5 } \))²
100 = OE2 + 20
OE² = 100 – 20 = 80
⇒ OE² = (4\(\sqrt { 5 } \))²
∴ OE = 4\(\sqrt { 5 } \) cm
∴ Area of rectangle = lxb
= DE x OE
= 2\(\sqrt { 5 } \) x 4\(\sqrt { 5 } \)
= 8 x 5 = 40 cm2

Question 7.
In the figure, ABCD is a trapezium in which AB || DC. Prove that ar( ∆AOD = ar(∆BOC).
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q7.1
Solution:
In trapezium ABCD, diagonals AC and BD intersect each other at O
∴ ∆ADB and ∆ACB are on the same base AB and between the same parallels
∴ ar(∆ADB = ar(∆ACD)
Subtracting, ar(AAOB) from both sides,
ar(∆ADB) – ar(∆AOB) = ar(∆ACD) – ar(∆AOB)
⇒ ar(∆AOD) = ar(∆BOC)

Question 8.
In the figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(∆ADE) = ar(∆BCF) [NCERT]
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q8.1
Solution:
Given : In the figure, ABCD, ABEF and CDEF are ||gms
To prove : ar(∆ADE) = ar(∆BCF)
Proof: ∴ ABCD is a ||gm
∴ AD = BC
Similarly, in ||gm ABEF
AE = BF
and in ||gm CDEF,
DE = CF
Now, in ∆ADE and ∆BCF
AD = BC (proved)
DE = CF (proved)
AE = BF (proved)
∴ ∆ADE ≅ ∆BCF
∴ ar(∆ADE) = ar(∆BCF) (∵ Congruent triangles are equal in area)

Question 9.
In the figure, ABC and ABD are two triangles on the base AB. If line segment CD is bisected by AB at O, show that ar(∆ABC) = ar(∆ABC)
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q9.1
Solution:
Given : In the figure, ∆ABC and ∆ABD are on the same base AB and line CD is bisected by AB at O i.e. CO = OD
To prove : ar(∆ABC) = ar(∆ABD)
Construction : Draw CL ⊥ AB and DM ⊥ AB

Question 10.
If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in area. If G is the mid point of median AD, prove that ar(∆BGC) = 2ar(∆AGC).
Solution:
Given : In ∆ABC, AD is its median. G is mid point of AD. BG and CF are joined
To prove :
(i) ar(∆ADB) = ar(∆ADC)
(ii) ar(∆BGC) = 2ar(∆AGC)
Construction : Draw AL ⊥ BC
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q10.1

Question 11.
A point D is taken on the side BC of a AABC such that BD = 2DC. Prove that ar(∆ABD) = 2ar(∆ADC)
Solution:
Given : In ∆ABC, D is a point on BC such that
BD = 2DC
AD is joined
To prove : ar(∆ABD) = 2ar(∆ADC)
Construction : Draw AL ⊥ BC
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q11.1

Question 12.
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that
(i) ar(∆ADO) = or (∆CDO)
(ii) ar(∆ABP) = ar(∆CBP).
Solution:
Given : In ||gm ABCD, Diagonals AC and BD intersect each other at O
P is any point on BO
AP and CP are joined
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q12.1
To prove :
(i) ar(∆ADO) = ar(∆CDO)
(ii) ar(∆ABP) = ar(∆CBP)
Proof:
(i) In ∆ADC,
O is the mid point of AC
∴ ar(∆ADO) = ar(∆CDO)
(ii) Since O is the mid point of AC
∴ PO is the median of ∆APC
∴ af(∆APO) = or(∆CPO) …(i)
Similarly, BO is the median of ∆ABC
∴ ar(∆ABO) = ar(∆BCO) …(ii)
Subtracting (i) from (ii),
ar(∆ABO) – ar(∆APO) = ar(∆BCO) – ar( ∆CPO)
⇒ ar(∆ABP) = ar(∆CBP)
Hence proved.

Question 13.
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F.
(i) Prove that ar(∆ADF) = ar(∆ECF)
(ii) If the area of ∆DFB = 3 cm2, find the area of ||^gm ABCD.
Solution:
Given : In ||gm ABCD, BC is produced to E such that CE = BC
AE intersects CD at F
To prove :
(i) ar(∆ADF) = ar(∆ECF)
(ii) If ar(∆DFB) = 3 cm2, find the area of (||gm ABCD)
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q13.1

Question 14.
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar(∆POA) = ar(∆QOC).
Solution:
Given : In ||gm ABCD, diagonals AC and BD intersect at O
A line through O intersects AB at P and CD at Q
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q14.1
To prove : ar(∆POA) = ar(∆QOC)
Proof : In ∆POA and ∆QOC,
OA = OC (O is mid-point of AC)
∠AOD = ∠COQ (Vertically opposite angles)
∠APO = ∠CQO (Alternate angles)
∴ ar(∆POA) ≅ ar(∆QOC) (AAS criterian)
∴ ar(∆POA) = ar(∆QOC)

Question 15.
In the figure, D and E are two points on BC such that BD = DE = EC. Show that ar(∆ABD) = ar(∆ADE) = ar(∆AEC). [NCERT]
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q15.1
Solution:
Given : D and E are two points on BC such that BD = DE = EC
AD and AE are joined
To prove : ar(∆ABD) = ar(∆ADE) = ar(∆AEC)
Construction : From A, draw AL ⊥ BC and XAY || BC

Proof: ∵ BD = DE = EC
and ∆ABD, ∆ADE and ∆AEC have equal bases and from the common vertex A
∴ ar(∆ABD) = ar(∆ADE) = ar(∆AEC)

Question 16.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P.
Show that: ar(∆APB) x ar(∆CPD) = ar(∆APD) x ar(∆BPC)
Solution:
Given : In quadrilateral ABCD, diagonal AC and BD intersect each other as P
To prove : ar(∆APB) x ar(∆CPD) = ar(APD) x ar(∆BPC)
Construction : Draw AL and CN perpendiculars on BD
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q16.1

Question 17.
If P is any point in the interior of a parallelogram ABCD, then prove that area of the triangle APB is less than half the area of parallelogram.
Solution:
Given : In ||gm ABCD, P is any point in the ||gm
AP and BP are joined
To prove : ar(∆APB) < \(\frac { 1 }{ 2 }\) ar(||gm ABCD)
Construction : Draw DN ⊥AB and PM ⊥ AM
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q17.1

Question 18.
ABCD is a parallelogram. E is a point on BA such that BE = 2EA and F is a point on DC such that DF = 2FC. Prove that AECF is a parallelogram whose area is one third of the area of parallelogram ABCD.
Solution:
Given : In ||gm ABCD, E is a point on AB such that BE = 2EA and F is a point on CD such that DF = 2FC. AE and CE are joined
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q18.1

Question 19.
In a ∆ABC, P and Q are respectively, the mid-points of AB and BC and R is the mid-point of AP. Prove that
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q19.1
Solution:
Given : In ∆ABC,
P and Q are mid-pionts of AB and BC R is mid-point of AP, PQ, RC, RQ are joined

Question 20.
ABCD is a parallelogram, G is the point on AB such that AG = 2GB, E is a point of DC such that CE = 2DE and F is the point of BC such that BF = 2FC. Prove that:
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q20.1
(v) Find what portion of the area of parallelogram is the area of AEFG.
Solution:
Given : ABCD is a parallelogram and AG = 2GB, CE = 2DE and BF = 2FC
To prove :

(v) Find what portion of the area of parallelogram is the area of AFEG.
Construction : Draw EP ⊥ AB and EQ ⊥ BC
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q20.3

Question 21.
In the figure, CD || AE and CY || BA.
(i) Name a triangle equal in area of ACBX.
(ii) Prove that or(∆ZDE) = ar(∆CZA).
(iii) Prove that ar(∆CZY) = ar(∆EDZ).
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q21.1
Solution:
Given : In the figure,
CP || AE and CY || BA

To prove :
(i) Name a triangle equal in area of ∆CBX
(ii) Prove that ar(∆ZDE) = ar(∆CZA)
(iii) ar(BCZY) = ar(∆EDZ)
Proof:
(i) ∆CBX and ∆CYX are on the same base BY and between same parallels.
∴ ar(∆CBX) = ar(∆CYX)
(ii) ∆ADE and ∆ACE are on the same base AE
and between the same parallels (AE || CD)
∴ ar(∆ADE) = ar(∆ACE)
Subtracting ar(∆AZE) from both sides
⇒ ar(∆ADE) – ar(∆AZE) = ar(∆ACE) – ar(∆AZE)
⇒ ar(∆ZDE) = ar(∆ACZ)
⇒ ar∆ZDE = ar∆CZA
(iii) ∵ As ACY and BCY are on the same base CY and between the same parallels
∴ ar(∆ACY) = ar(∆BCY)
Now ar(∆ACZ) = ar(∆ZDE) (Proved)
⇒ ar(∆ACY) + ar(∆CYZ) = ar(∆EDZ)
⇒ ar(∆BCY) + ar(∆CYZ) = ar(∆EDZ)
∴ ar quad. (BCZY) = ar(EDZ)
Hence proved.

Question 22.
In the figure, PSD A is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove that ar(∆PQE) = ar(∆CFD).
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q22.1
Solution:
Given : In the figure, PSDA is a ||gm in
which PQ = QR = RS and
AP || BQ || CR || DS
To prove : ar(∆PQE) = ar(∆CFD)
Construction : Join PD
Proof : ∵ PA || BQ || CR || DS
and PQ – QR = RS (Given)
∴ AB = BC = CD
∴ PQ = CD
Now in ABED, F is mid point of ED
∴ EF = FD
Similarly, EF = PE
⇒ PE = FD
In ∆PQE and ∆CFD,
∴ ∠EPQ = ∠FDC (Alternate angles)
PQ = CD
PE = FD (Proved)
∴ APQE ≅ ACFD (SAS cirterion)
∴ ar(∆PQE) = ar(∆CFD)

Question 23.
In the figure, ABCD is a trapezium in which AB || DC and DC = 40 cm and AB = 60 cm. If X and Y are, respectively the mid-points of AD and BC, prove that:
(i) XY = 50 cm
(ii) DCYX is a trapezium
(iii) ar(trap. DCYX) = \(\frac { 9 }{ 11 }\) ar(trap. XYBA)
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q23.1
Solution:
Given : In the figure, ABCD is a trapezium in which AB || DC
DC = 40 cm, AB = 60 cm
X and Y are the mid-points of AD and BC respectively
To prove :
(i) XY = 50 cm
(ii) DCYX is a trapezium
(iii) ar(trap. DCYX) = \(\frac { 9 }{ 11 }\) m(trap. XYBA)
Construction : Join DY and produce it to meet AB produced at P
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q23.2

Question 24.
D is the mid-point of side BC of ∆ABC and E is the mid-point of BD. If O is the mid-point of AE, prove that ar(∆BOE) = \(\frac { 1 }{ 8 }\) ar(∆ABC).
Solution:
Given : In ∆ABC, D is mid point of BC, E is mid point BE and O is the mid point of AE. BO, AE, AD are joined.
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q24.1

Question 25.
In the figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar(∆ABP) = ar(∆ACQ).
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q25.1
Solution:
Given : In ∆ABC, X and Y are the mid pionts of AC and AB respectively. Through A, a line parallel to BC is drawn. Join BX and CY and produce them to meet the parallel line through A, at P and Q respectively and intersect each other at O.
To prove : ar(∆ABP) = ar(∆ACQ)
Construction : Join XY and produce it to both sides
Proof : ∵ X and Y are mid points of sides AC and AB
∴ XY || BC
Similarly, XY || PQ
∆BXY and ∆CXY are on the same base XY and between the same parallels
∴ ar(∆BXY) = ar(∆CXY) …(i)
Now, trap. XYAP and trap. XYAQ are on the same base XY and between the same parallels
∴ ar(XYAP) = ar(XYAQ) …(ii)
Adding (i) and (ii),
∴ ar(∆BXY) + ar(∆YAP)
= ar(CXY) + ar(XYAQ)
⇒ ar(∆ABP) = ar(∆ACQ)

Question 26.
In the figure, ABCD and AEFD are two parallelograms. Prove that
(i) PE = FQ
(ii) ar(∆APE) : ar(∆PFA) = ar(∆QFD) : ar(∆PFD)
(iii) ar(∆PEA) = ar(∆QFD).
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q26.1
Solution:
Given : Two ||gm ABCD and ||gm AEFD are on the same base AD. EF is produced to meet CD at Q. Join AF and PD also
To prove :
(i) PE = FQ
(ii) ar(∆APE) : ar(∆PFA) = ar(∆QFD) : ar(∆PFD)
(iii) ar(∆PEA) = ar(∆QFD)
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q26.2
Proof:
(i) In ∆AEP and DFQ,
AE = DF (Opposite sides of a ||gm)
∠AEP = ∠DFQ (Corresponding angles)
∠APE = ∠DQF (Corresponding angles)
∴ ∆AEP ≅ ∆DFQ (AAS axiom)
∴ PE = QF (c.p.c.t.)
(ii) and ar(∆AEP) = ar(∆DFQ) …(i)
(iii) ∵ ∆PFA and ∆PFD are on the same base PF and between the same parallels
∴ ar(∆PFA) = ar(∆PFD) …(ii)
From (i) and (ii),
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q26.3

Question 27.
In the figure, ABCD is a ||gm. O is any point on AC. PQ || AB and LM || AD. Prove that ar(||gm DLOP) = ar(||gm BMOQ).
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q27.1
Solution:
Given : In ||gm ABCD, O is any point on diagonal AC. PQ || AB and LM || BC
To prove : ar(||gm DLOP) = ar(||gm BMOQ)
Proof : ∵ Since, a diagonal of a parallelogram divides it into two triangles of equal area.
∴ ar(∆ADC) = or(∆ABC)
⇒ ar(∆APO) + or(||gm DLOP) + ar(∆OLC)
= ar(∆AOM) + ar(||^gm BMOQ) + ar( ∆OQC) …(i)
Since, AO and OC are diagonals of parallelograms AMOP and OQCL respectively,
∴ ar(∆APO) = ar(∆AMO) …(ii)
And, ar(∆OLC) = ar(∆OQC) …(Hi)
Subtracting (ii) and (iii) from (i), we get ar(||^gm DLOP) = ar(||^gm BMOQ)

Question 28.
In a ∆ABC, if L and M are points on AB and AC respectively such that LM || BC.
Prove that:
(i) ar(∆LCM) = ar(∆LBM)
(ii) ar(∆LBC) = ar(∆MBC)
(iii) ar(∆ABM) = ar(∆ACL)
(iv) ar(∆LOB) = ar(∆MOC).
Solution:
Given : In ∆ABC,
L and M are mid points on AB and AC
LM, LC and MB are joined
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q28.1
To prove :
(i) ar(∆LCM) = or(∆LBM)
(ii) ar(∆LBC) = ar(∆MBC)
(iii) ar(∆ABM) = ar(∆ACL)
(iv) ar(∆LOB) = ar(∆MOC)
Proof: ∵ L and M are the mid points of AB and AC
∴ LM || BC
(i) Now ∆LBM and ∆LCM are on the same base LM and between the same parallels
∴ar(∆LBM) = ar(∆LCM) …(i)
⇒ ar(∆LCM) = ar(∆LBM)
(ii) ∵ ∆LBC and ∆MBC are on the same base
BC and between the same parallels
∴ ar(∆LBC) = ar(∆MBC) …(ii)
(iii) a(∆LMB) = ar(∆LMC) [From (i)]
⇒ ar(∆ALM) + ar(∆LMB)
= ar(∆ALM) + ar(∆LMC) [Adding or(∆ALM) to both sides]
⇒ ar(∆ABM) = ar(∆ACL)
(iv) ∵ ar(∆LBC) = ar(∆MBC) [From (ii)]
⇒ ar(∆LBC) – ar(∆BOC) = ar(∆MBC) – ar(∆BOC)
ar(∆LBO) = ar(∆MOC)

Question 29.
In the figure, ABC and BDC are two equilateral triangles such that D is the mid-point of BC. AE intersects BC in F.
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q29.1

Solution:
Given : ABC and BDE are two equilateral triangles and D is mid point of BC. AE intersects BC in F
To prove :

Question 30.
In the figure, ABC is a right triangle right angled at A, BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that [NCERT]
(i) ∆MBC ≅ ∆ABD
(ii) ar(BYXD) = ar(∆MBC)
(iii) ar(BYXD) = ar(ABMN)
(iv) ∆FCB ≅ ∆ACE
(v) ar(CYXE) = 2ar(∆FCB)
(vi) ar(CYXE) = ar(∆CFG)
(vii) ar(BCED) = ar(AMBN) + ar(ACFG)
RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 Q30.1
Solution:
Given : In ∆ABC, ∠A = 90°
BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively
AX ⊥ DE meeting DE at X
To prove :
(i) ∆MBC ≅ ∆ABD
(ii) ar(BYXD) = 2ar(∆MBC)
(iii) ar(BYXD) = ar(ABMN)
(iv) ∆FCB ≅ ∆ACE
(v) ar(CYXE) = 2ar(∆FCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = or(AMBN) + ar(ACFG)
Construction : Join AD, AE, BF and CM
Proof:
(i) In ∆MBC and ∆ABD,
MB=AB (Sides of square)
BC = BD
∠MBC = ∠ABD (Each angle = 90° + ∠ABC)
∴ ∆MBC ≅ ∆ABD (SAS criterian)
∴ ar(∆MBC) = ar(∆ABD) …(i)
(ii) ∵ ∆ABD and rectangle BYXD are on the same base BD and between the same parallels
∴ ar(∆ABD) = \(\frac { 1 }{ 2 }\) ar(rect. BYXD)
⇒ ar(rect. BYXD) = 2ar(∆ABD)
⇒ ar(rect. BYXD) = 2ar(∆MBC) …(ii)
(iii) Similarly, ∆MBC and square MBAN are on the same base MB and between the same parallels
∴ ar(∆MBC) = ar(sq. ABMN) …(iii)
From (ii) and (iii)
ar(sq. ∆BMN) = ar(rect. BYXD)
(iv) In AFCB and ∆ACE,
FC = AC
CB = CE (Sides of squares)
∠FCB = ∠ACE (Each = 90° + ∠ACB)
∴ ∆FCB = ∆ACE (SAS criterian)
(v) ∵ ∆FCB ≅ ∆ACE (Proved)
∴ ar(∆FCB) = ar(∆ACE)
∵∆ACE and rectangle CYXE are on the same base and between the same parallels
∴ 2ar(∆ACE) = ar(CYXC)
⇒ 2ar(∆FCB) = ar(CYXE) …(iv)
(vi) ∵ AFCB and rectangle FCAG are on the base FC and between the same parallels
∴ 2ar(∆FCB) = ar(FCAG) …(v)
From (iv) and (v)
ar(CMXE) = ar(ACFG)
(vii) In ∆ACB.
BC2 = AB2 + AC2 (By Pythagoras Theorem)
⇒ BC x BD = AB x MB + AC x FC
⇒ ar(BCED) = ar(ABMN) + ar(ACFG)
Hence proved.

Hope given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.