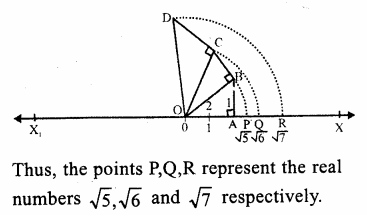
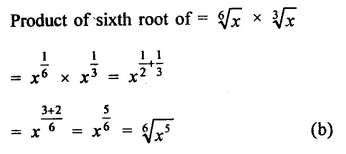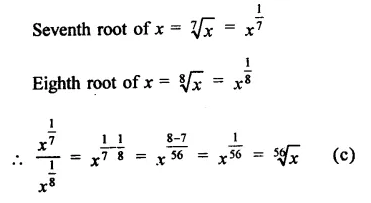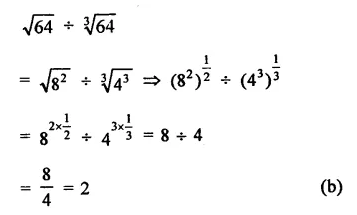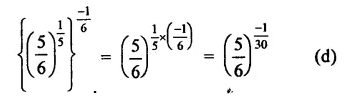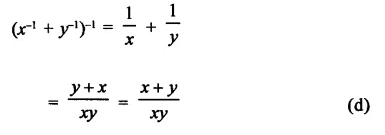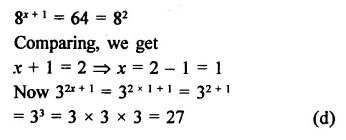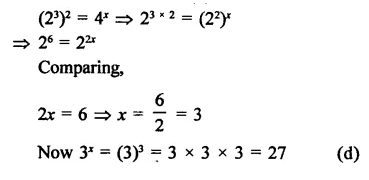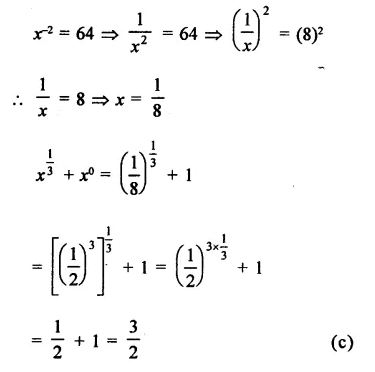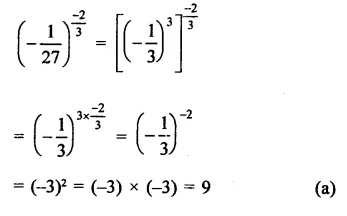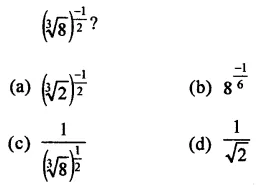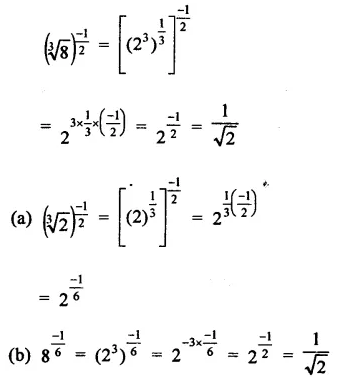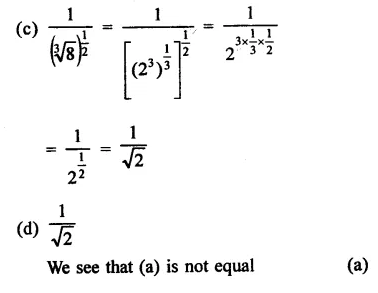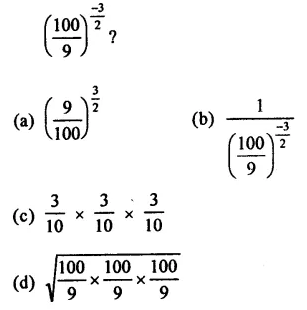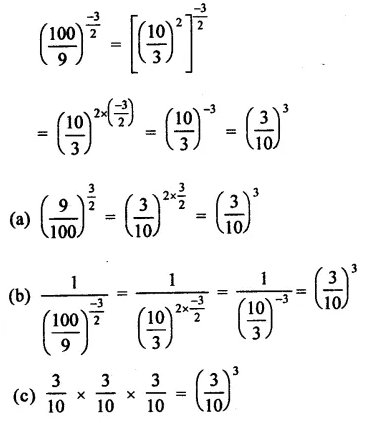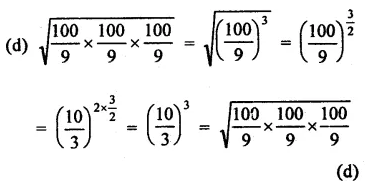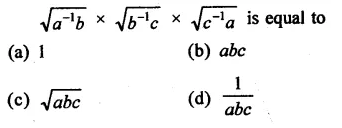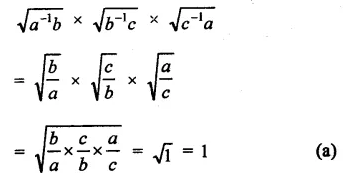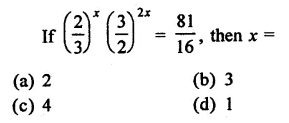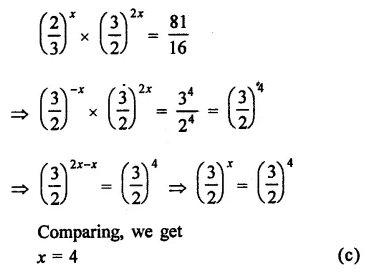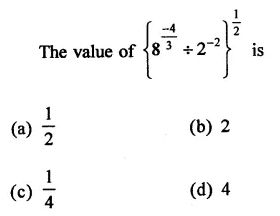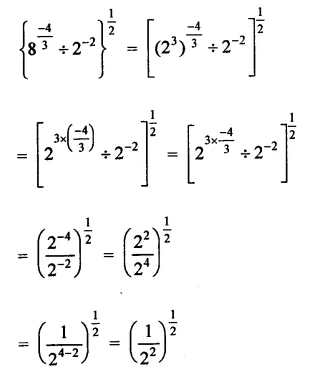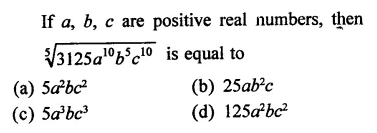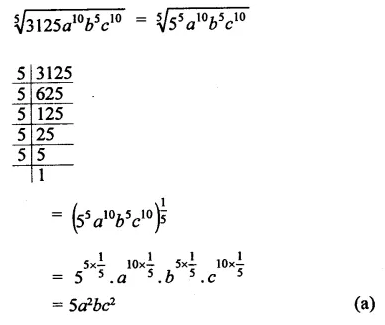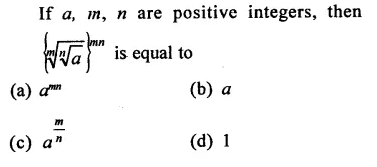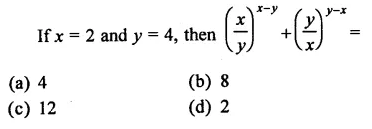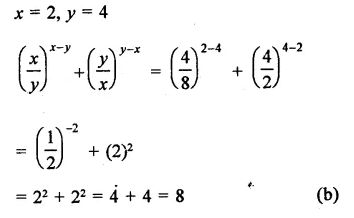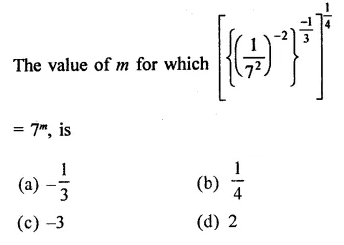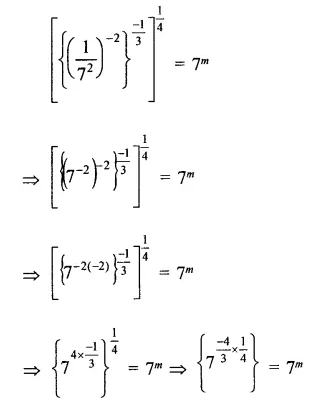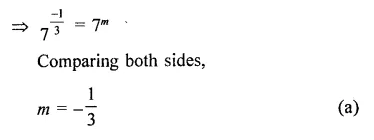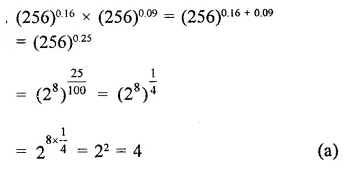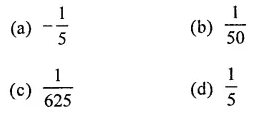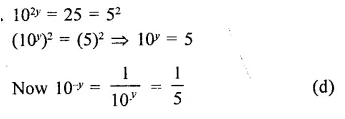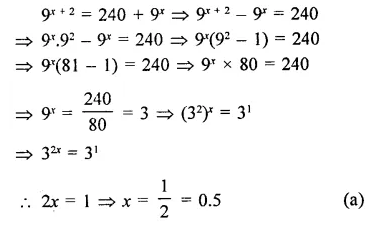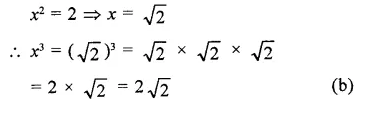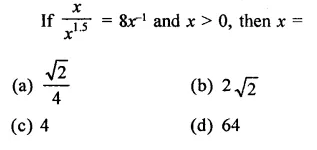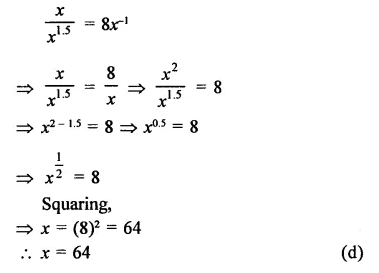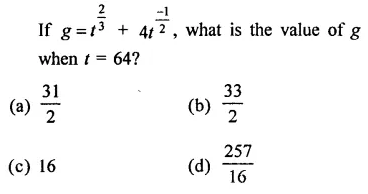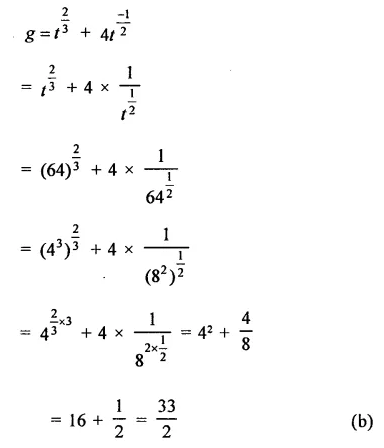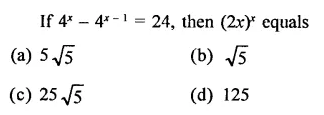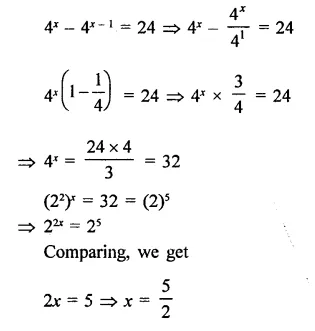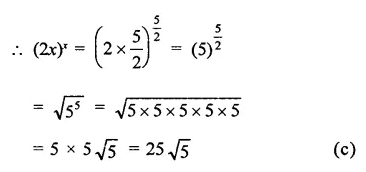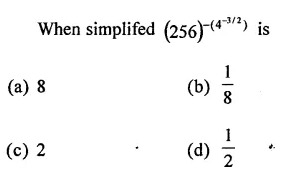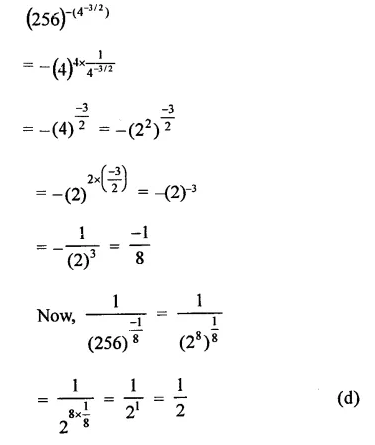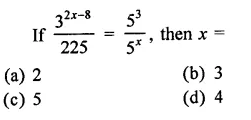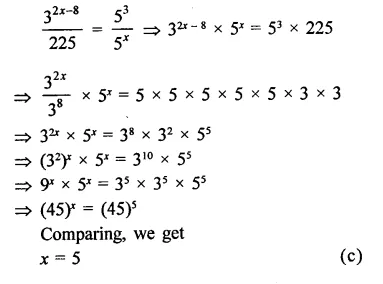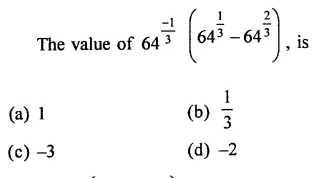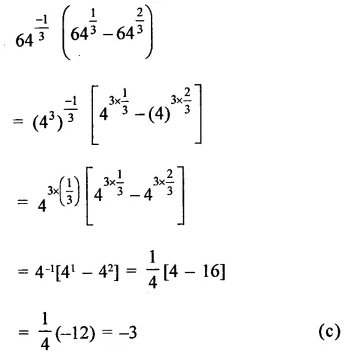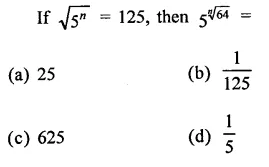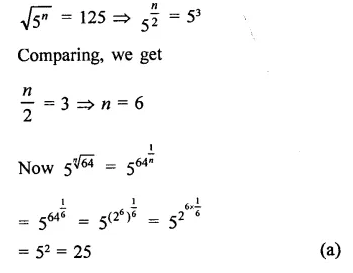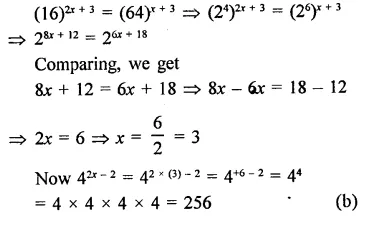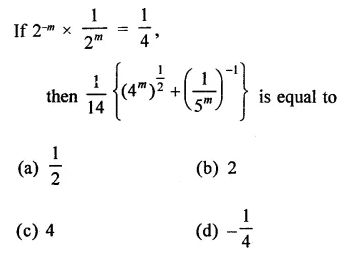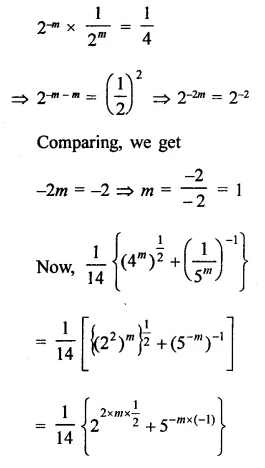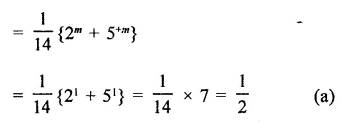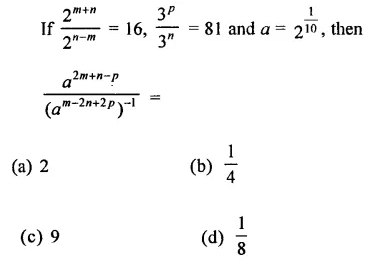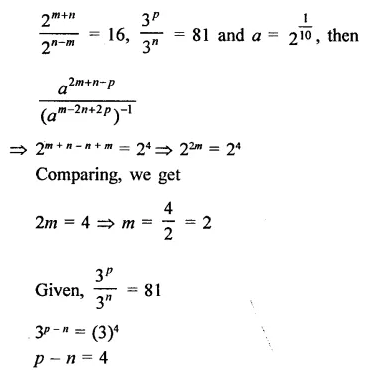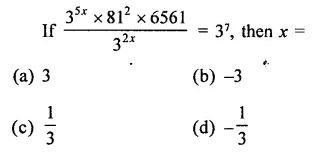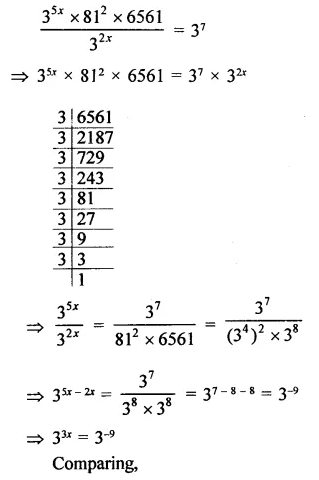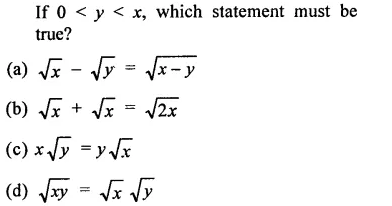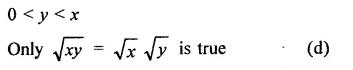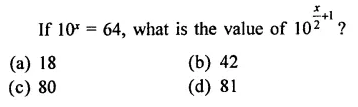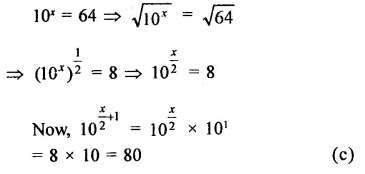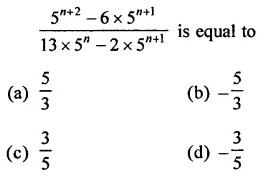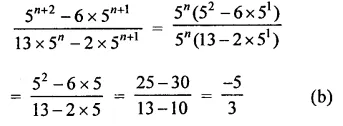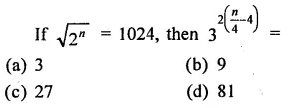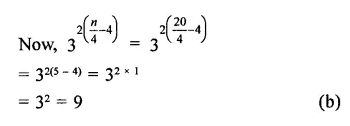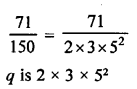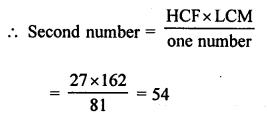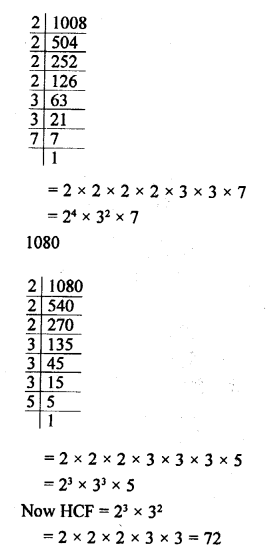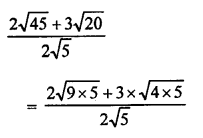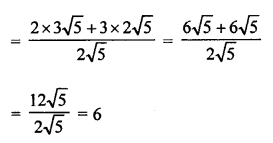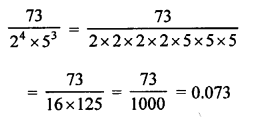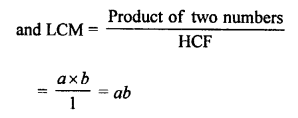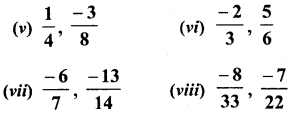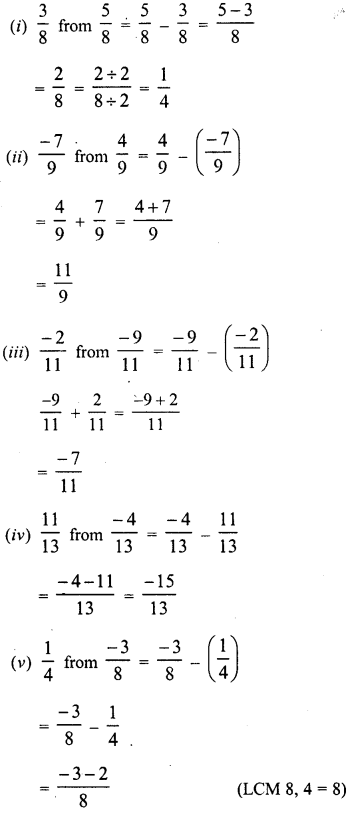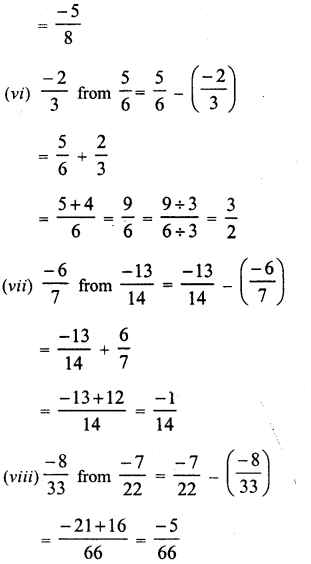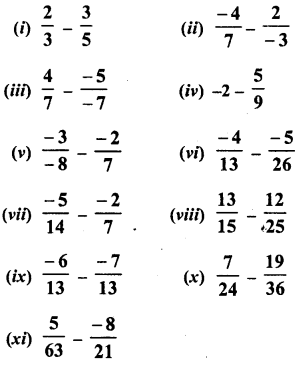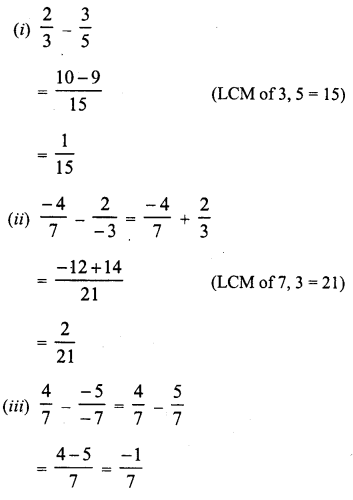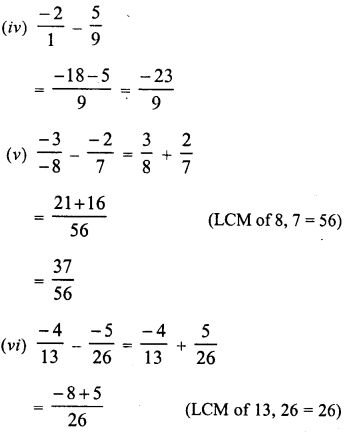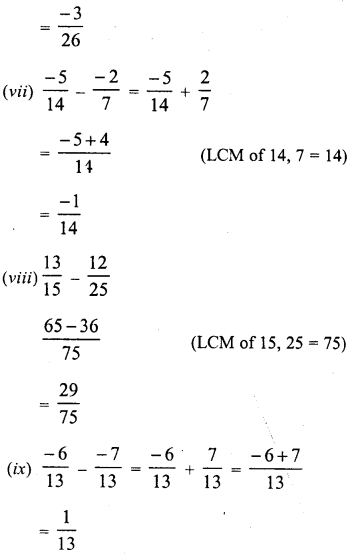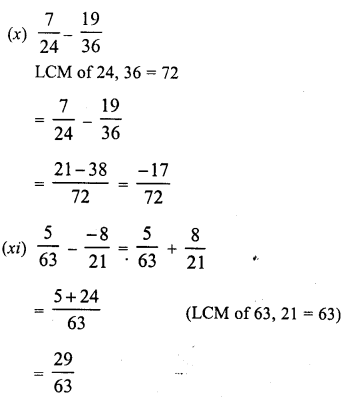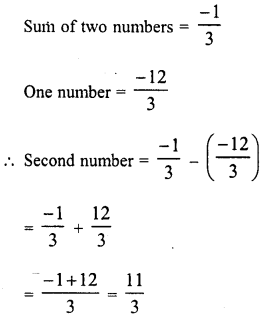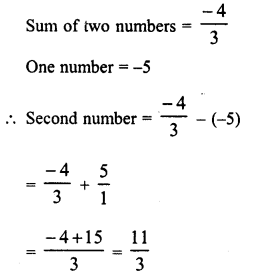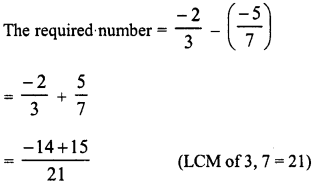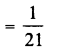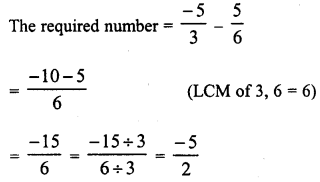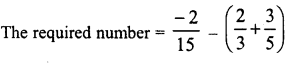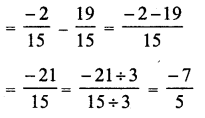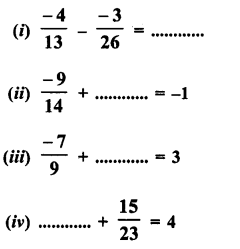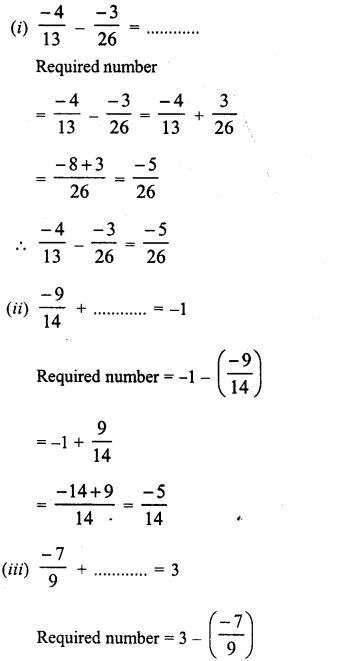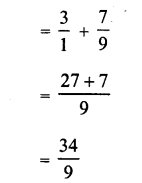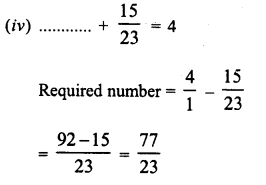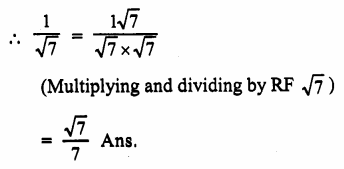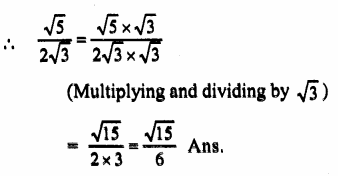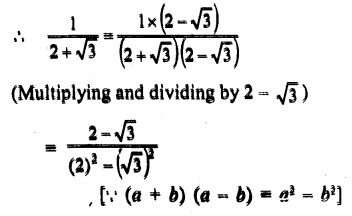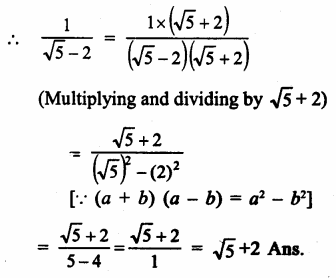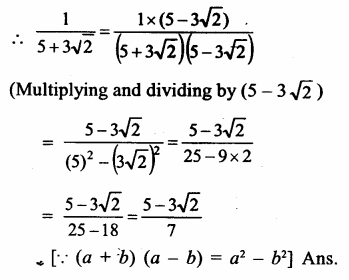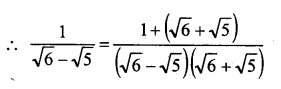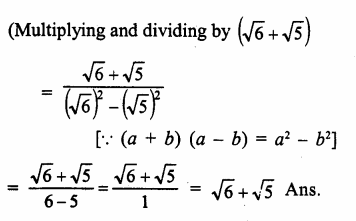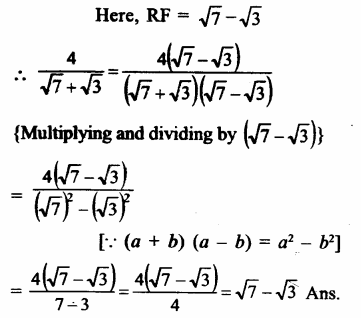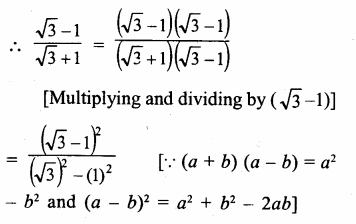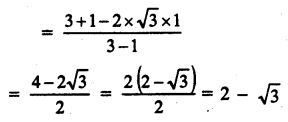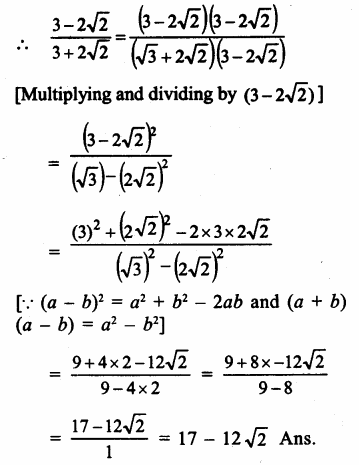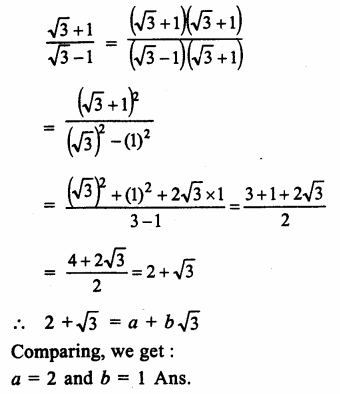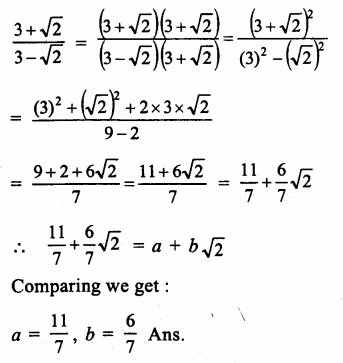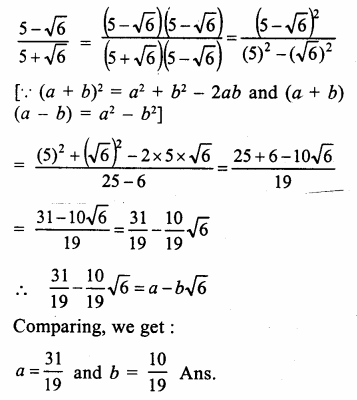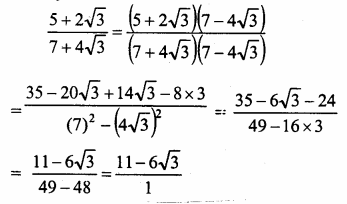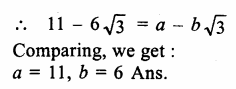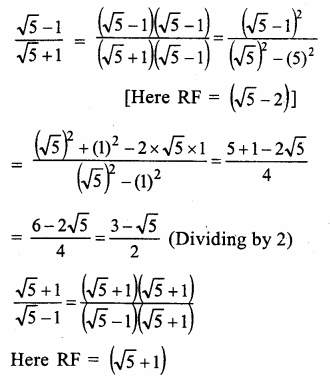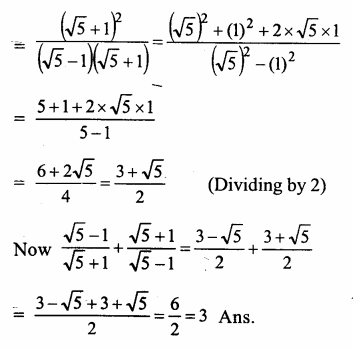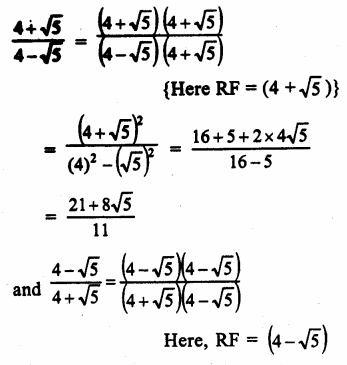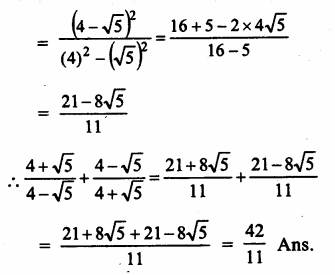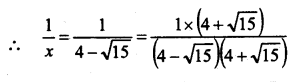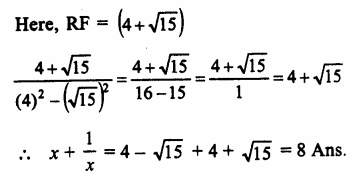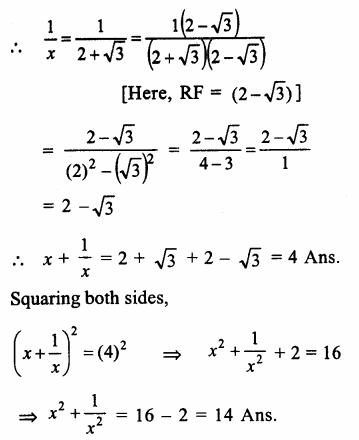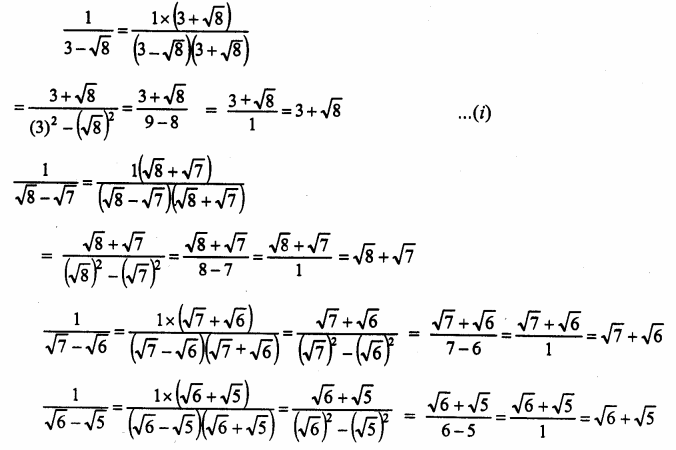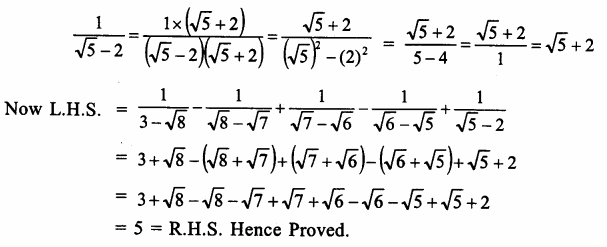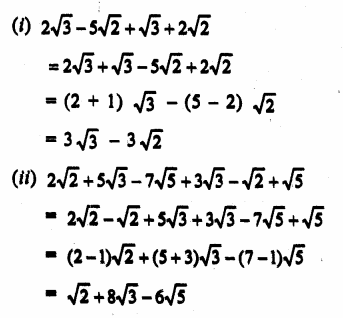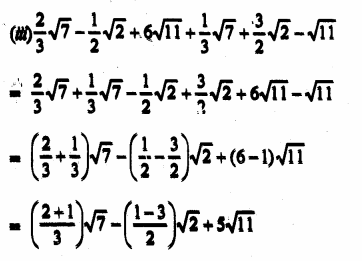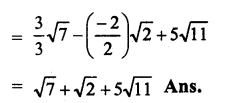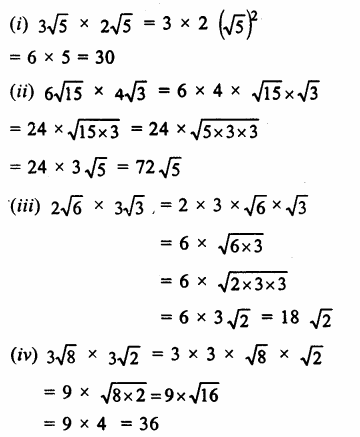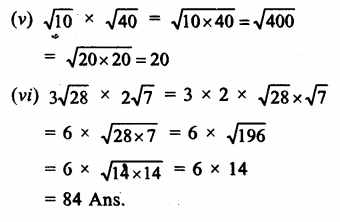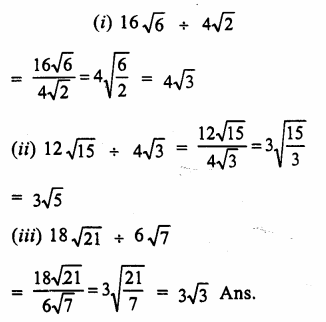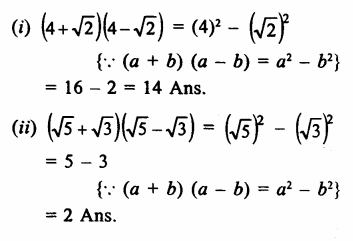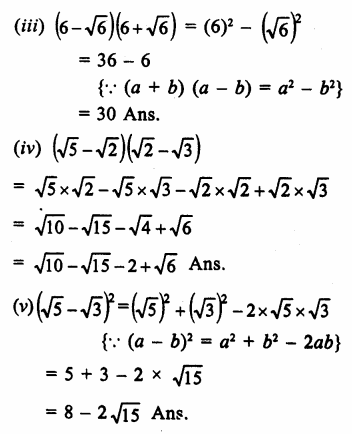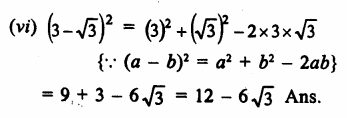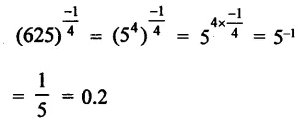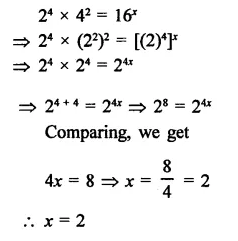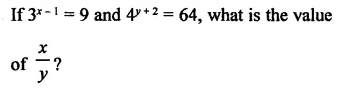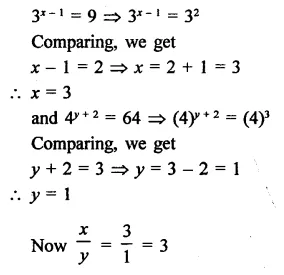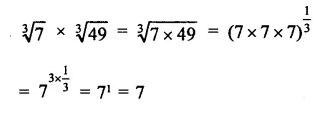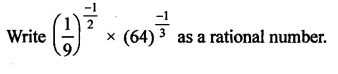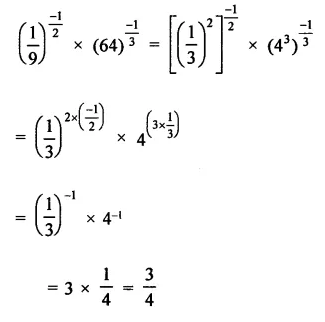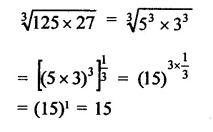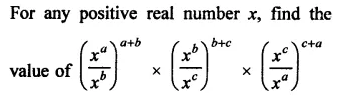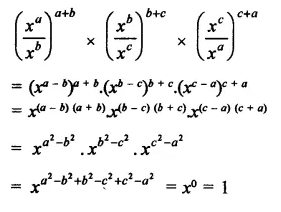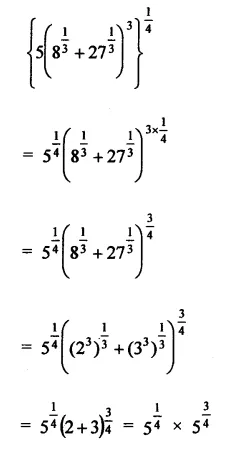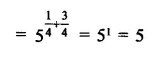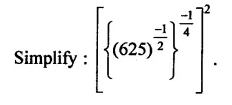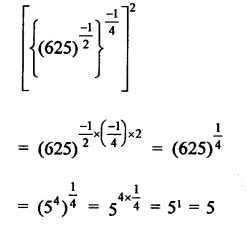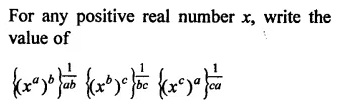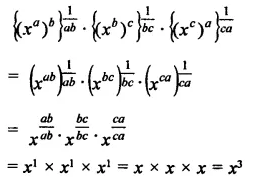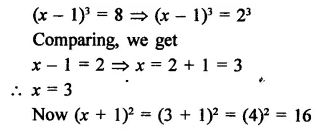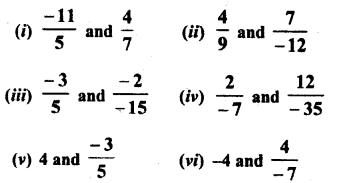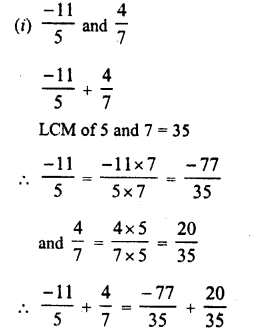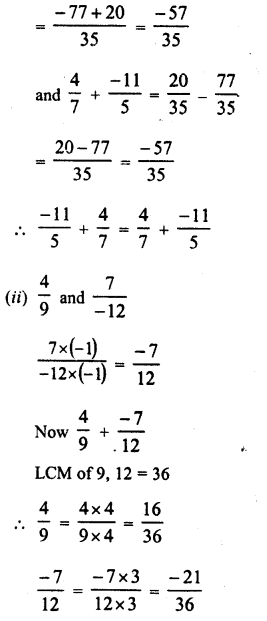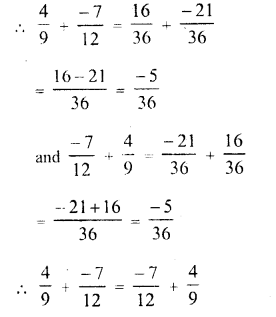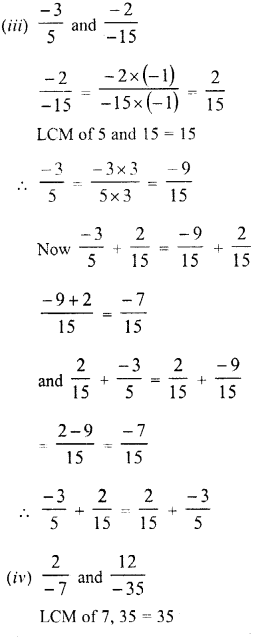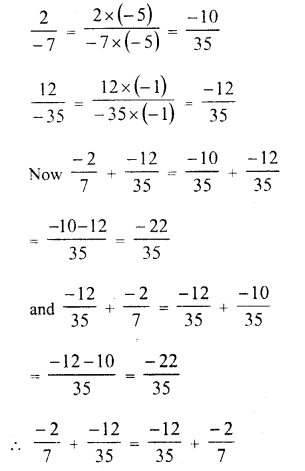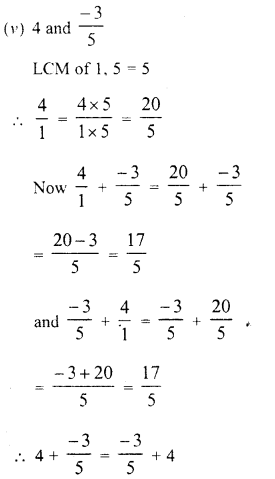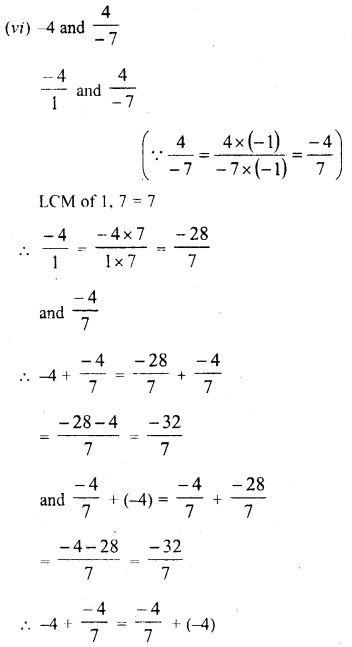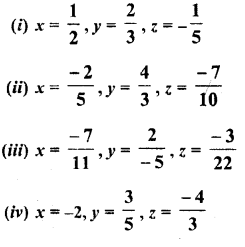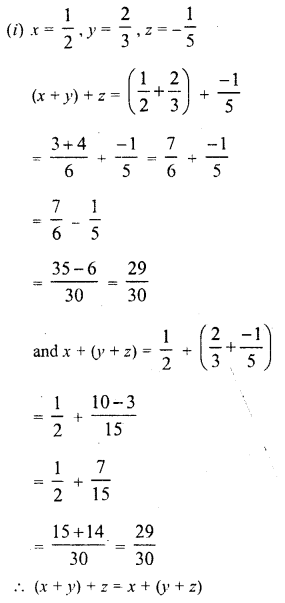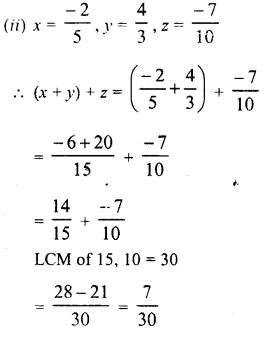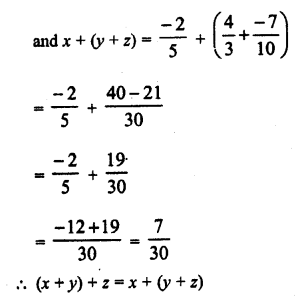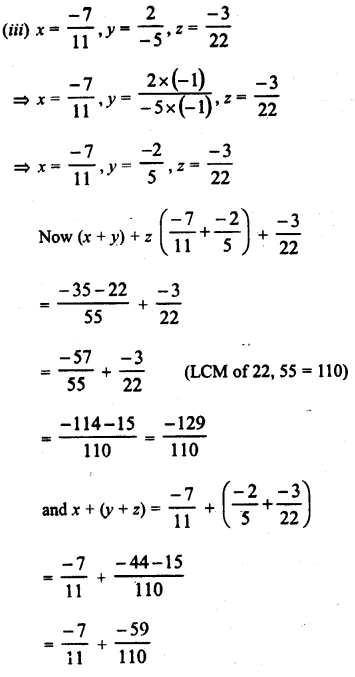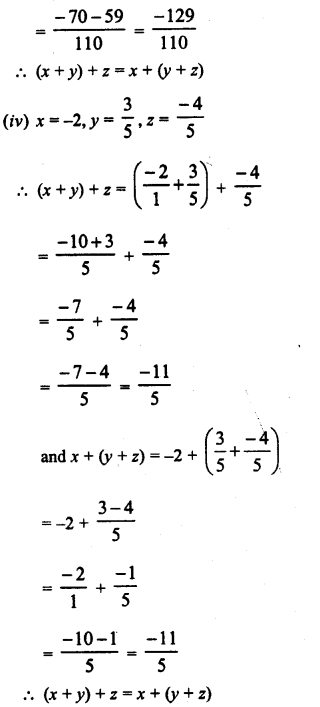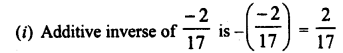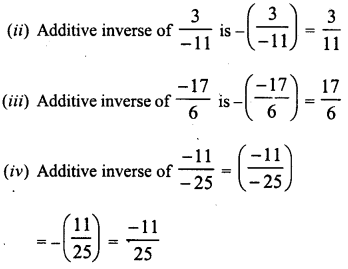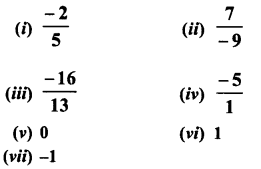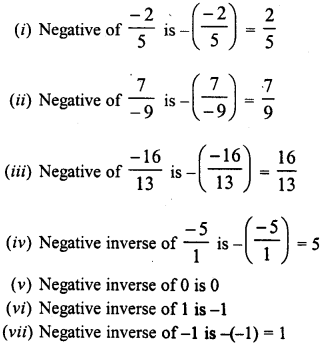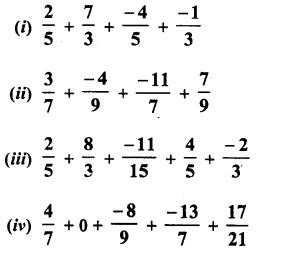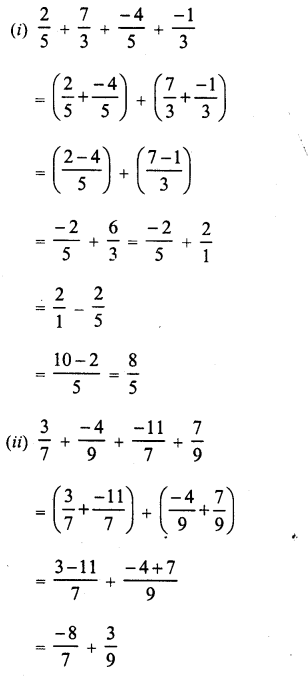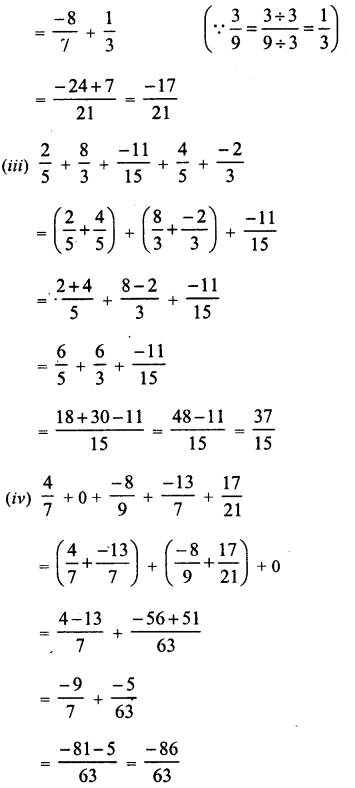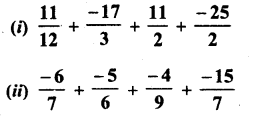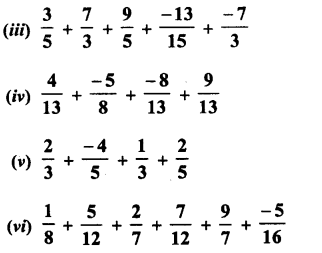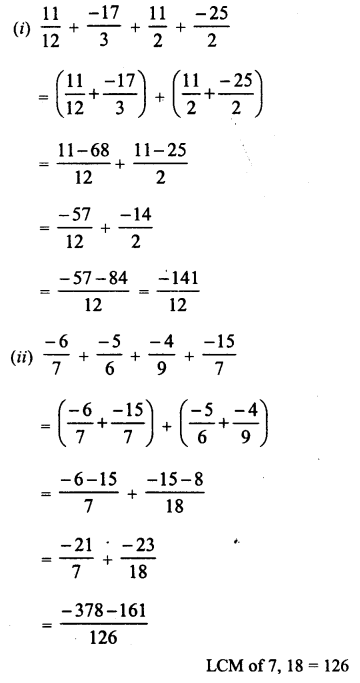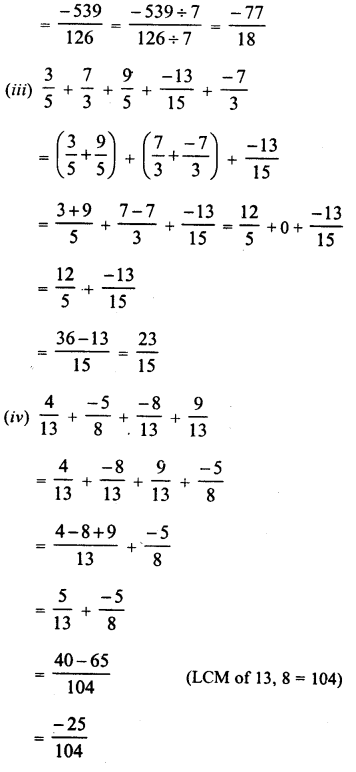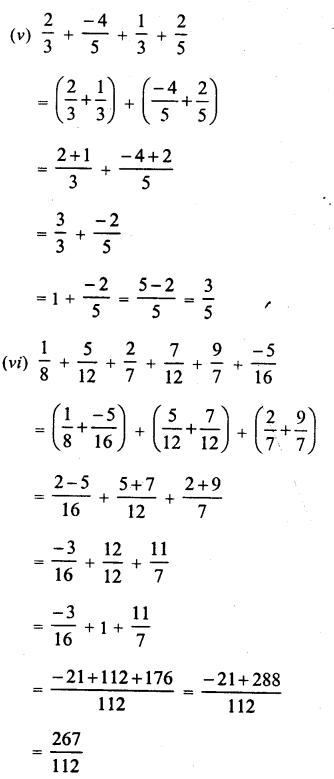RS Aggarwal Class 9 Solutions Chapter 1 Real Numbers Ex 1F
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1F.
Other Exercises
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1A
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1B
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1C
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1D
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1E
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1F
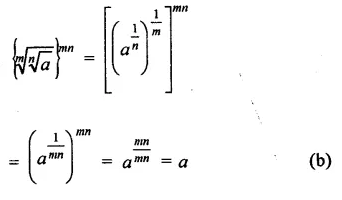
Question 1.
Solution:
We know that
ap x aq = ap+q
∴ Therefore
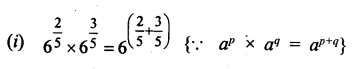
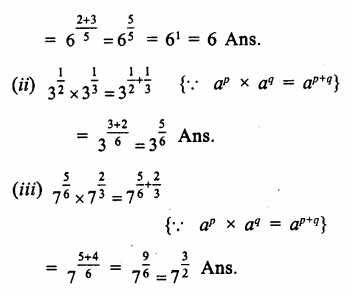
Question 2.
Solution:
We know that
ap ÷ aq = ap-q
Therefore
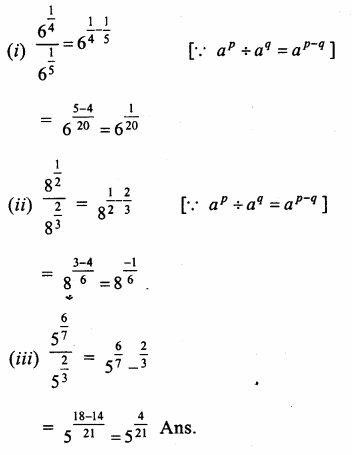
Question 3.
Solution:
We know that
ap x bp = (ab)p
Therefore
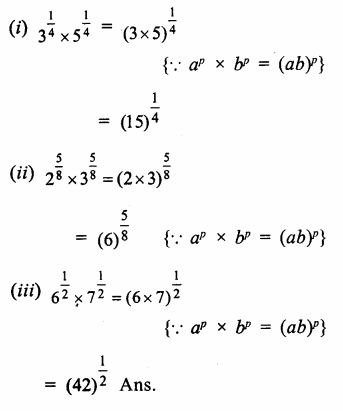
Question 4.
Solution:
We know that
(ap)q =apq
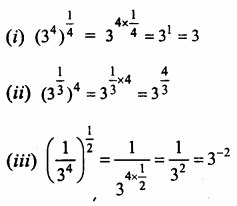
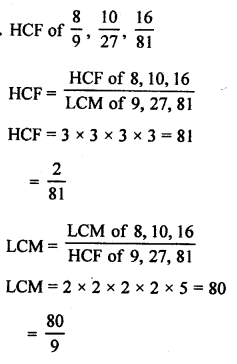
Question 5.
Solution:

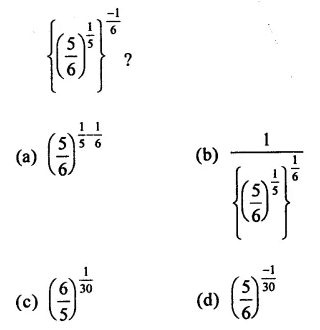
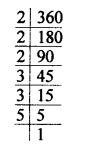
Question 6.
Solution:
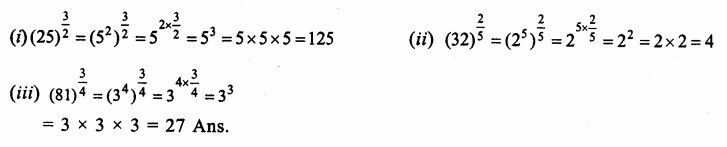
Question 7.
Solution:
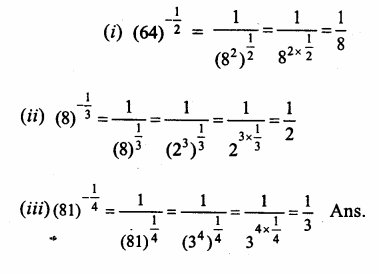
Hope given RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1F are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.