Here we are providing Class 11 chemistry Important Extra Questions and Answers Chapter 7 Equilibrium. Chemistry Class 11 Important Questions are the best resource for students which helps in Class 11 board exams.
Class 11 Chemistry Chapter 7 Important Extra Questions Equilibrium
Equilibrium Important Extra Questions Very Short Answer Type
Question 1.
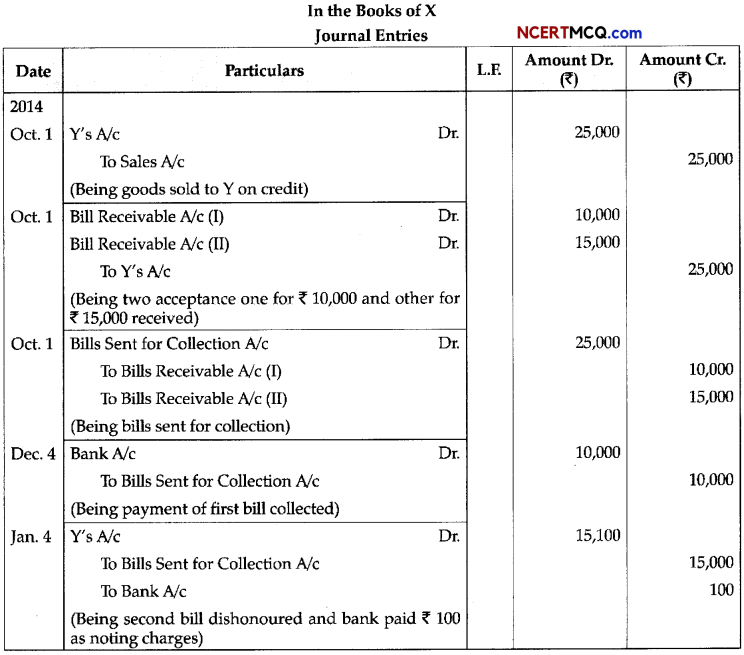
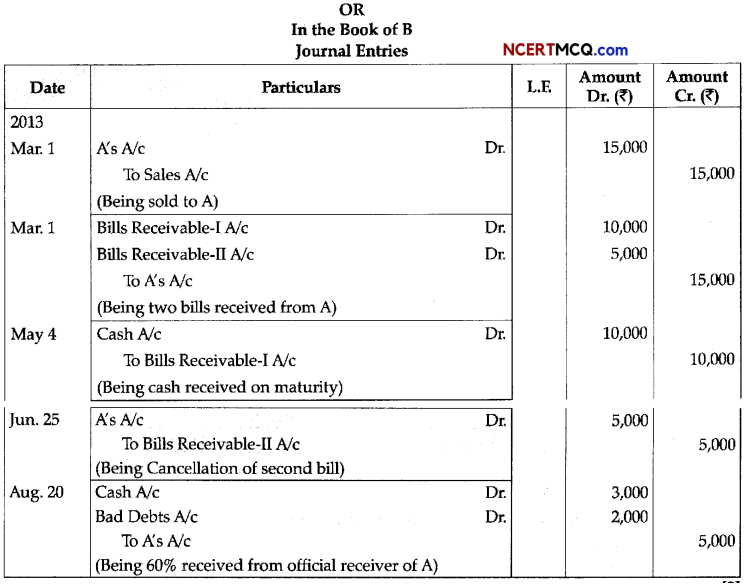
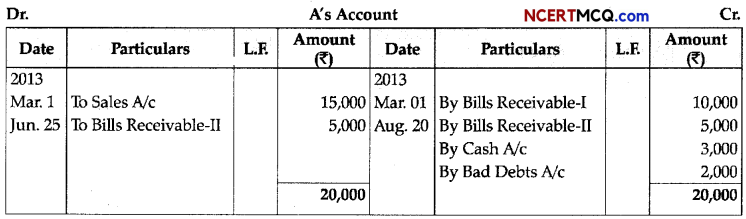
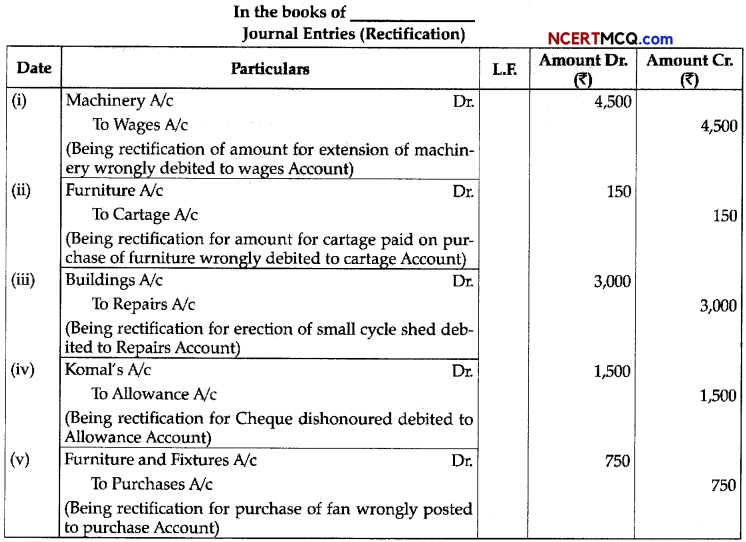
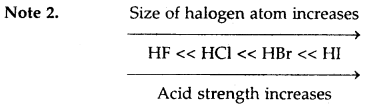
Write the expression for the equilibrium constant Kp for the reaction 3Fe (s) + 4H2O (g) ⇌ Fe3O4 (s) + 4H2 (g)
Answer:
Kp = \(\frac{p_{\mathrm{H}_{2}}^{4}}{p_{\mathrm{H}_{2} \mathrm{O}}^{4}}=\frac{p_{\mathrm{H}_{2}}}{p_{\mathrm{H}_{2} \mathrm{O}}}\)
Question 2.
How are Kc and Kp related to each other in the reaction
N2 (g) + O2 (g) ⇌ 2NO (g)
Answer:
Kp = Kc.
Question 3.
What is the equilibrium constant expression for the reaction
Al (s) + 3H+ (aq) ⇌ Al3+ (aq) + \(\frac{3}{2}\)H2 (g)
Answer:
Kc = [Al3+ (aq)][H2 (g)3/2/[H+ (aq)]3.
Question 4.
What happens to the equilibrium
PCl5 (g) ⇌ PCl3 (g) + Cl2 (g) if nitrogen is added to it
(i) at constant volume
Answer:
The state of equilibrium remains unaffected.
(ii) at constant pressure?
Answer:
Dissociation increases, i.e., the equilibrium shifts forward.
Question 5.
What does the equilibrium K < I indicate? ,
Answer:
The reaction does not proceed much in the forward direction.
Question 6.
For an exothermic reaction, what happens to the equilibrium constant if the temperature is increased?
Answer:
K = K/Kb.
Kb increases much more than when the temperature is increased in an exothermic reaction. Hence K decreases.
How to find Kp from Best fit line.
Question 7.
Under what conditions, a reversible process becomes irreversible?
Answer:
If one of the products (gaseous) is allowed to escape out (i.e., in the open vessel).
Question 8.
What is the effect of increasing pressure on the equilibrium?
N2 (g) + 3H2 (g) ⇌ 2NH3 (g)?
Answer:
Equilibrium will shift in the forward direction forming more ammonia.
Question 9.
What is- the effect of increasing pressure on the equilibrium.
CaCO3 (s) ⇌ CaO (s) + CO2 (g)
Answer:
Kc = [CaO (s)][CO2 (g)J/[CaCO3 (s)]
Kc = [CO2 (g)]
Similarly, Kp = PCO2.
Question 10.
The equilibrium constant for the reaction SO3 (g) ⇌ SO2 (g) + \(\frac{1}{2}\) O2 (g) is 0.18 at 900 K. What will be the equilibrium
constant for the reaction SO2 (g) + \(\frac{1}{2}\) O2 (g) ⇌ SO3 (g)?
Answer:
K = \(\frac{1}{0.18}\) = 5.55.
350 Degrees F to C 176.667 °C The Celsius (ºC) degree or Fahrenheit (ºF) degree […..] by Helen C.
Question 11.
For which of the following cases does the reaction go farthest to completion: K = 1, K = 1010, K = 10-10.
Answer:
The reaction having K = 1010 will go farthest to completion because the ratio (product)/(reactants) is maximum in this case.
Question 12.
Under what conditions ice water system is in equilibrium?
(a) at 273 K
(b) below 273 K
(c) above 273 K.
Answer:
(a) At 273 K.
Question 13.
The equilibrium constant for the reaction
N2 (g) + 3H2 (g) ⇌ 2NH3-(g) is K. How is the equilibrium constant for the reaction
NH3 (g) ⇌ \(\frac{1}{2}\)N2 (g) + \(\frac{3}{2}\) H2 (g) related to K?
Answer:
If K’ is the equilibrium constant for the reaction
NH33(g) = \(\frac{1}{2}\)N2(g)+ \(\frac{3}{2}\)H2(g)
Then, K’ = \(\frac{1}{K}\).
Question 14.
Write the relation between Kc and Kp for the reaction
PCl5 (g) ⇌ PCl3 (g) + Cl2 (g)
Answer:
Δn (g) = 2 – 1 = 1
Hence Kp = Kc × (RT)Δn = K × RT.
Question 15.
The equilibrium constant of a reaction is 2 × 10-3 at 25°C and 2 × 10-2 at 50°C. Is the reaction exothermic or endothermic? ,
Answer:
It is endothermic as the equilibrium constant has increased with temperature.
Question 16.
What is the thermodynamic criterion for the state of equilibrium?
Answer:
At equilibrium, (ΔG)TP = 0.
Question 17.
Which measurable property becomes constant in water ⇌ water vapor equilibrium at constant temperature?
Answer:
Vapour pressure.
Question 18.
What happens to the dissociation of PCl5 in a closed vessel if helium gas is introduced into it at the same temperature?
Answer:
No effect.
Question 19.
What are the conditions for getting NH33 by Haber’s process?
N2 (g) + 3H2 (g) 2NH3 (g); ΔH = – Q.
Answer:
High concentration of N2 and H2, low temperature, and high pressure.
Question 20.
What happens if ferric salt is added to the equilibrium of the reaction between Fe3+ and SCN̅ ions?
Answer:
The red color deepens. Equilibrium shifts in the forward direction.
Question 21.
Does the value of equilibrium constant change on adding, a catalyst?
Answer:
No.
Question 22.
Name the factors which affect the equilibrium state.
Answer:
Temperature, pressure, and concentration.
Ionic Strength Calculator … Ionic strength is used to measure the concentration of the ions in a solution.
Question 23.
What happens to the ionic product of water if some acid is added into the water?
Answer:
It remains unchanged.
Question 24.
What is the pH of 0.1 M HCl?
Answer:
pH = – log [H+] = – log 10-1 = 1.
Question 25.
Which conjugate base is stronger: CN̅ or F̅?
Answer:
CN̅ is a stronger base than F̅
Question 26.
The dimethyl ammonium ion (CH3)2 NH2+ is a weak acid. What is its conjugate base?
Answer:
(CH3)2NH.
Question 27.
Write the solubility product expression for:
Ag2CrO4 (s) ⇌ 2Ag+ (aq) + CrO42- (aq)
Answer:
Ksp = [Ag+]2[CrO42-].
Question 28.
When does salt get precipitated in solution?
Answer:
When the Ionic product of its ions exceeds its solubility product.
Question 29.
The Ksp value of salt is high. What does it indicate?
Answer:
This means that the salt is highly soluble in water.
Question 30.
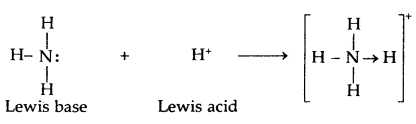
Select the Lewis acid and Lewis base in
SnCl4 + 2Cl– → [SnCl66]2-.
Answer:
SnCl4 is acid and Cl is a base.
Question 31.
Out of pure water and 0.1. KCl solution in which AgCl will dissolve more?
Answer:
Pure water.
Question 32.
Write the conjugate acid and conjugate base of water?
Answer:
Conjugate acid H3O+ and conjugate base OH̅.
Question 33.
Select Lewis acids and Lewis bases from the following: Cu2+, H2O, BF3, OH.
Answer:
Lewis acids: Cu2+, BF3
Lewis base: H2O, OH.
Question 34.
Give two examples of cations that can act as Lewis acids.
Answer:
Ag+, H+.
Question 35.
What is the difference between a conjugate acid and a conjugate base?
Answer:
A conjugate acid and its conjugate base differ from each other by a proton.
Question 36.
What is the active mass of water?
Answer:
55.5 mol L-1
Question 37.
Whether the pH value of an aqueous solution of sodium acetate will be 7 or greater than 7?
Answer:
It is greater than 7.
Question 38.
An old sample of an aqueous solution of CuSO4 is acidic. Why?
Answer:
On keeping CuS04 solution undergoes hydrolysis to give H2SO4 a strong acid and a weak base Cu(OH)2
Question 39.
What happens to the pH of ammonium acetate solution when a few drops of acid are added to it?
Answer:
pH will remain unchanged as ammonium acetate (CH3COONH4) solution is a buffer.
Question 40.
What happens when HCl gas is passed through NaCl solution?
Answer:
NaCl will precipitate out.
Question 41.
What is the value of H3O+ ions and OH ions in water at 298 K?
Answer:
[H3O+] = [OH̅] 1.0 × 10-7 mL-1.
Question 42.
Will the ionic products of water increase or decrease on increasing the temperature?
Answer:
It increases with the increase in temperature.
Question 43.
Give one example of
(i) acidic buffer
Answer:
Acidic buffer: CH3COOH + CH3COONa
(ii) basic buffer.
Answer:
Basic buffer: NH4OH + NH4Cl.
Question 44.
Write down the conjugate base of [Al(H2O)6]3+.
Answer:
[Al(0H)(H2O)5]2+ is the conjugate base of [Al(H2O)6]3+.
Question 45.
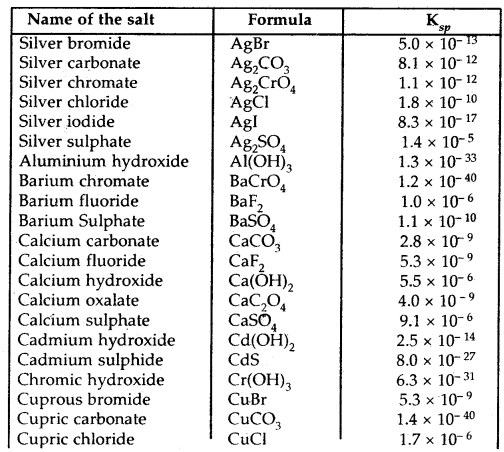
The Ksp of CuS, Ag2S, HgS is 10-31, 10-44, 10-54 respectively. What is the order of the solubility of these sulfides?
Answer:
CuS > Ag2S > HgS.
Question 46.
Ksp for HgSO4 is 6.4 × 10-5. What is the solubility of the salt?
Answer:
S = \(\sqrt{\mathrm{K}_{s p}}=\sqrt{6.4 \times 10^{-5}}\)= 8 × 10-3 mol L-1.
Question 47.
The solubility product (K ) of silver chloride is 1.8 × 10-10 at 298 K. What is the solubility of AgO in 0.01 M HCl in mol L-1?
Answer:
[Ag+] = \(\frac{\mathrm{K}_{s p}}{\left|\mathrm{Cl}^{-}\right|}=\frac{1.8 \times 10^{-10}}{0.01}\) = 1.8 × 10-8 mol L-1
∴ Solubility of AgCl = 1.8 × 10-8 Mol L-1.
Question 48.
How does dilution with water affect the pH of a buffer solution?
Answer:
Dilution with water of a buffer solution has no effect on the pH of a buffer solution.
Question 49.
What is the pH of our blood? Why does it not change in spite of the variety of foods and Spices we eat?
Answer:
the pH of our blood is about 7.4. It remains constant because blood is a buffer.
Question 50.
Why does boric acid act as Lewis acid?
Answer:
Boric a.cid acts as a Lewis acid by accepting electrons from hydroxyl ions.
B(OH)3 + 2HOH → B(OH)–4 + H3+O.
Question 51.
When a precipitate formed when solutions of BaCl2 and Na2SO4 are mixed?
Answer:
When in the final solution after mixing, the ionic product.
[Ba2+] [SO42- ] exceeds Ksp for BaSO4.
Question 52.
What is the common ion effect?
Answer:
The suppression of the dissociation of a weak electrolyte by the addition of a strong electrolyte having a common ion.
Question 53.
Arrange them in increasing order of the extent of hydrolysis.
CCl4, MgCl2, AlCl3 PCl5, SiCl4.
Answer:
The increasing order of the extent of hydrolysis is CCl4 < MgCl2 < AlCl3 < PCl5 < SiCl4.
Question 54.
Mention two different ways of drawing the following equilibrium towards the right
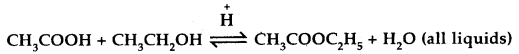
[W.B. JEE 2003]
Answer:
- By adding more of CH3COOH or CH3CH2OH.
- By removing the ester or water formed.
Question 55.
Give one example of everyday life in which there is gas ⇌ solution equilibrium.
Answer:
Soda-water bottle.
Question 56.
What is the relationship between pKa and pKb values where Ka, Kb represent ionization constants of the acid and its conjugate base respectively?
Answer:
pKa + pKb = pKw =14.
Question 57.
What is the relationship between pH and pOH?
Answer:
pH + pOH= pKw = 14.
Question 58.
What is the function of adding NH4OH in group V?
Answer:
It converts any NH4HCO3 present into (NH4)2CO3.
Question 59.
What happens to the solubility of AgCl in water if NaCl solution is added to it?
Answer:
Solubility of AgCl decreases due to the common ion effect.
Question 60.
Write the expression for comparison of relative strengths of two weak acids in terms of their ionization constants.
Answer:
\(\frac{\text { Strength of acid }_{1}}{\text { Strength of acid }_{2}}=\sqrt{\frac{\mathrm{K}_{a_{1}}}{\mathrm{~K}_{a_{2}}}}\)
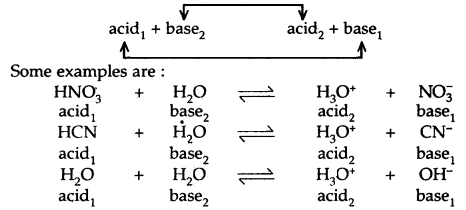
Equilibrium Important Extra Questions Short Answer Type
Question 1.
Justify the statement that water behaves like acid as well as a base on the basis of the protonic concept.
Answer:
Water ionizes as H2O + H2O ⇌ H3O+ + OH–
With strong acids, water behaves as a base by accepting a proton from an acid.
HCl + H2O ⇌ H3O+ (aq) + Cl– (aq)
While with bases, water behaves as an acid by liberating a proton
NH3 + H2O ⇌ NH4+ (aq) + OH (aq).
Question 2.
What is pOH? What is its value for pure water at 298 K?
Answer:
pOH = – log [OH–]
pH + pOH = 14 for pure water at 298 K
pH = 7
or
pOH of water at 298 = 7.
Question 3.
Calculate the pH of a buffer solution containing 0.1 moles of acetic acid and 0.15 mole of sodium acetate. The ionization constant for acetic acid is 1.75 × 10-5.
Answer:

Question 4.
An aqueous solution of CuSO4 is acidic while that of Na2SO4 is neutral. Explain.
Answer:
CuSO4 + 2H2O ⇌ Cu(OH)2 + H2SO4 (weak base strong acid)
CuS04 is the salt of weak base Cu(OH)2 and a strong acid H2SO4.
Thus the solution will have free H+ ions and will, therefore, be acidic.
Na2SO4, being the salt of a strong acid H2SO4 and a strong base.
NaOH does not undergo hydrolysis. The solution is, therefore, neutral.
Question 5.
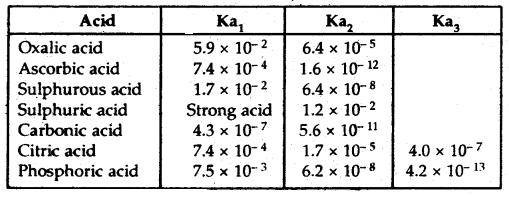
The dissociation constants of HCN, CH3COOH, and HF are 7.2 × 10-10, 1.8 × 10-5, and 6.7 × 10-4 respectively. Arrange them in increasing order of acid strength.
Answer:
More the value of Ka, the stronger the acid
Their Ka1S are 6.7 × 10-4 > 1.8 × 10-5 > 7.2 × 10-10
∴ HCN < CH3COOH < HF.
Question 6.
The dissociation of PCl5 decreases in presence of Cl2. Why?
Answer:
For PCl5 ⇌ PCl3 + Cl2.
According to Le Chatelier’s principle, an increase in the concentration of Cl2 (one of the products) at equilibrium will favor the backward reaction, and thus the dissociation of PCl5 into PCl3 and Cl2 decreases.
Question 7.
The dissociation of HI is independent of pressure while dissociation of PCl5 depends upon the pressure applied. Why?•
Answer:
For 2HI ⇌ H2 + I2
Kc = \(\frac{x^{2}}{4(1-x)^{2}}\)
where x = degree of dissociation
For PCl5 ⇌ PCl3 + Cl2
K = \(\frac{x^{2}}{V(1-x)^{2}}\); V = Volume of container.
Kc for HI does not have a volume factor- and dissociation is independent of volume and hence pressure.
Kc for PCl5 has volume in the denominator and hence dissociation of PCl5 depends upon the volume and consequently pressure.
Question 8.
The reaction between ethyl acetate and water attains a state of equilibrium in an open vessel, but not the decomposition of CaCO3. Explain.
Answer:
CH2 COOC2H5 (l) + H2O (l) ⇌ CH3COOH (l) + C2H5OH (l)
Here both reactants and products are liquids and they will not escape from the vessel even if it is open. Therefore equilibrium is attained.
CaSO3 (s) ⇌ CaO (s) + CO2 (g)
Here CO2 is a gas. It will escape from the vessel if it is open and so backward reaction cannot take place. Therefore equilibrium is attained.
Question 9.
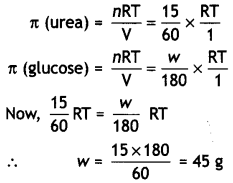
The degree of dissociation of N2O4 is α according to the reaction
N2O4 (g) ⇌ 2NO2 (g) at temperature T and total pressure P.
Find the expression for the equilibrium constant of this reaction.
Answer:
![]()
Total moles at eqbm. = 1 – α + 2α = 1 + α
If P is total pressure
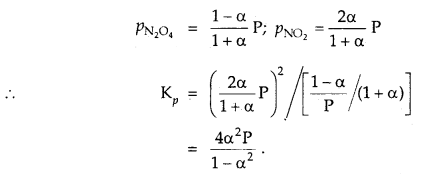
Question 10.
Why NH4Cl is added in precipitating III group hydroxides before the addition of NH4OH?
Answer:
To prevent precipitation of IV group hydroxides (especially Mn) along with III group hydroxides. NH4Cl decreases dissociation of NH4OH and thus limited OH ions are present in solution to precipitate III group cations only
NH4OH ⇌ NH4 (aq) + OH (aq) to a small extent
NH4Cl (aq) ⇌ NH4 (aq) + Cl (aq) to a large extent
Due to common ion affect the degree of dissociation of NH4OH decreases leaving only a small no. of OH̅ ions.
Question 11.
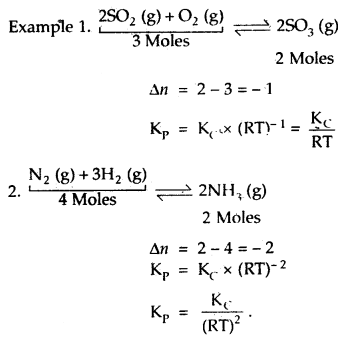
If concentrations are expressed in moles L-1 and pressures in atmospheres. What is the ratio of Kp to Kc for the
2SO2 + O2 (g) ⇌ 2SO3 (g)
Answer:
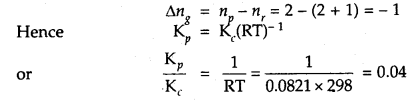
Question 12.
The equilibrium constants for the reactions
N2 + O2 ⇌ 2NOand
2NO + O2 ⇌ 2NO2 are K1 and K2 respectively, then what would be the equilibrium constant for the reactions.
N2 + 2O2 ⇌ 2NO2?
Answer:
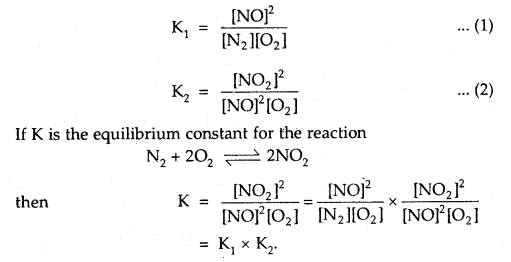
Question 13.
What qualitative information can be obtained from the magnitude of the equilibrium constant?
Answer:
- Large values of equilibrium constant (> 103) show that the forward direction is favored i.e. concentration of products is much larger than that of the reactants of equilibrium.
- Intermediate values of K (10-3 to 103) show that the concentrations of the reactants and products are comparable.
- The low value of K (< 10-3) shows that the backward reaction is favored, i.e., the concentration of reactants is much large than that of. products.
Question 14.
The following reaction has attained equilibrium
CO (g) + 2H2 (g) ⇌ CH3OH (g); ΔH° = – 92.0 kJ mol-1.
What will happen if
(i) the volume of the vessel is suddenly reduced to half?
Answer:
Kc = [CH3OH]/[CO][H2]2, Kp = PCH3OH/PCO × PH2
When the volume of the vessel is reduced to half, the concentration of each reactant or product becomes double. Thus
Qc = 2[CH3OH]/2[CO] × {2[H2]}2 = i K..
As Qc < Kp, equilibrium will shift in the forward direction.
(ii) The partial pressure of hydrogen is suddenly doubled (ii) an inert gas is added to the system.
Answer:
As volume remains constant, molar concentration will not change. Hence there is no effect on the state of equilibrium.
Question 15.
How does the degree of ionization of a weak electrolyte vary with concentration? Give exact relationship. What is this law called?
Answer:
α = \(\sqrt{\mathrm{K}_{i} / c}\) . It is called Ostwald’s dilution law.
(Ki is ionization constant and c is the molar concentration).
Question 16.
The ionization constant for formic acid and acetic acid is 17.7 × 10-5 and 1.77 × 10-5. Which acid is stronger and how many times the other if equimolar concentrations of the two are taken?
Answer:
Ka for HCOOH > Ka for CH3COOH. Hence formic acid is stronger.
Further \(\frac{\text { Strength of } \mathrm{HCOOH}}{\text { Strength of } \mathrm{CH}_{3} \mathrm{COOH}}=\sqrt{\frac{\mathrm{K}_{\mathrm{HCOOH}}}{\mathrm{K}_{\mathrm{CH}_{3} \mathrm{COOH}}}}\)
= \(\sqrt{10}\) = 3.16 times.
Question 17.
Out of CH3COO̅ and OH̅ which is the stronger base and why?
Answer:
OH̅ ions can combine with H+ ions more readily than CH3COO̅ ions can do. Hence OH̅ is a stronger base.
Question 18.
What is pKw? What is it? value at 25°C?
Answer:
pKw = – log Kw = – log 10-14 = 14.
Question 19.
What are pH and pOH values of a neutral solution at a temperature at which = 10-13?
Answer:
pKw = pH + pOH, But pKw =13
Hence pH = pOH = 6.5.
Question 20.
The ionization constants of HF = 6.8 × 10-4. Calculate the ionization constant of the corresponding conjugate base.
Answer:
Kb = \(\frac{\mathrm{K}_{w}}{\mathrm{~K}_{c}}=\frac{10^{-14}}{6.8 \times 10^{-4}}\) = 1.47 × 10-11.
Question 21.
What is the difference between an ionic product a rich solubility product?
Answer:
Solubility product is the product of the molar concentrations of the ions in a saturated solution, but the ionic product is for any solution.
Question 22.
Why common salt is added to precipitate soap from the solution during its manufacture?
Answer:
Soap is the sodium salt of higher fatty acid [RCOONa].
On adding common salt, Na+ ion concentration increases.
Hence the equilibrium RCOONa (s) ⇌ RCOO̅ + Na+ shifts in the backward direction, i.e., soap precipitates out.
Question 23.
Through a solution containing Cu2+ and Ni2+, H2S gas is passed after adding dil. HCl, which will precipitate out and why?
Answer:
Cu2+ ions will precipitate out because in the acidic medium only ionic product [Cu2+][S2-] exceeds the solubility product of CuS.
Question 24.
Why in Group V of qualitative analysis sufficient NH4OH solution should be added before adding (NH4)2CO3 solution?
Answer:
This is done to convert NH4HCO3 usually present in large amounts to (NH4)2CO3.
NH4HCO3 + NH4OH → (NH4)2CO3 + H2O.
Question 25.
The pH of an enzyme-catalyzed reaction has to be maintained between 7 and 8. What indicator should be used to monitor and control the pH?
Answer:
Bromothymol blue or phenol red or cresol red.
Question 26.
The ionization constant of formic acid is 1.8 × 10-4. Around what pH will its mixture with sodium formate give buffer solution of highest capacity?
Answer:
Buffer solution of highest capacity is formed at which
pH = PKa = – l0g 1.8 × 10-4 = 3.74.
Question 27.
Why PO4 ion is not amphiprotic?
Answer:
An amphiprotic ion is one that can donate proton as well as accept a proton. PO43- ion can accept a proton(s) but cannot donate any proton. Hence, PO43- is not amphiprotic.
Question 28.
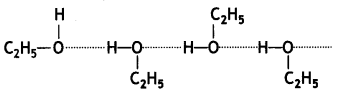
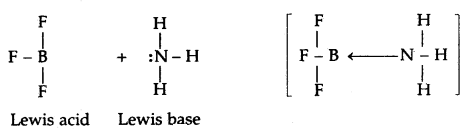
In the reaction between BF3 and C2H5OC2H5 which one of them will act as an acid. Justify your answer.
Answer:
The reaction between BF3 and C2H5OC2H5 is
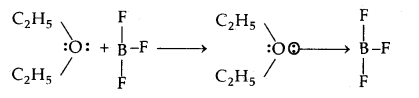
As BF3 is electron-deficient and accepts a pair of electrons from C2H5OC2H5, hence BF3 is the Lewis acid.
Question 29.
Will the water be the same at 4°C and 25°C? Explain. [IIT 2003]
Answer:
No. the pH of water is not the same at 4°C and 25°C. This is because with an increase in temperature dissociation of H20 molecules increases. Hence concentration of [H+] ions will increase, i.e., pH will decrease. Thus pH of H2O at 4°C will be more than at 25°C.
Question 30.
What type of salts are Na2HPO3 and NaHS? [W.B. /EE 2003]
Answer:
Na2HPO3 is obtained by the reaction between NaOH and H3PO3 a dibasic acid.
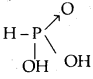
Both displaceable hydrogens are displaced by Na. No acidic hydrogen is left. Hence Na2HPO3 is a normal salt. NaHS is obtained by the replacement of one acidic hydrogen of H2S by Na (on reaction with NaOH)’. Hence NaHS is an acidic salt.
Question 31.
Explain why the pH of 0.1 molar solution of acetic acid will be higher than that of 0.1 molar solution of HCl.
Answer:
Acetic acid is a weak electrolyte. It is not completely ionized and hence gives less H+ ion concentration. HCl is a strong acid. It is completely ionized giving more H+ ions concentration. As pH = – log [H+], the lesser the no. of H+ ions, the more the value of pH. Therefore pH of 0.1 M acetic acid is more than that of 0.1 M HCl.
Question 32.
Benzoic acid is a monobasic acid. When 1.22 of its pure sample are dissolved in water and titrated against base 50 mL of 0.2 M NaOH are used up. Calculate the molar mass of benzoic acid.
Answer:
1000 ml of 1.0 M NaOH will neutralize acid
= \(\frac{1.22}{50 \times 0.2}\) × 1000 = 122 g.
But 1000 ml of 1.0 M NaOH contains 1 mole of NaOH and will neutralize 1 mole of monobasic acid. Hence the molar mass of benzoic acid is 122 g mol-1
Question 33.
Explain why ammonium chloride is acidic in liquid ammonia solvent.
Answer:
When NH4Cl is present in liquid ammonia, the following reaction takes place:
NH4 + NH3 ⇌ NH3 + NH4
Thus NH4Cl gives protons to liquid ammonia solvent.
Hence it is acidic.
Question 34.
Arrange the following in order of their increasing basicity.
H2O, OH̅, CH3OH, CH3 O̅.
Answer:
H2O < CH3OH < OH̅ < CH3 O̅.
Question 35.
The following can act both as Bronsted acid and Bronsted base. Write the formula in each case (of the product).
(i) HCO3-
Answer:
CO32-, H2CO3
(ii) H2PO4-
Answer:
HPO4–, H3PO4
(iii) NH3
Answer:
NH̅2, NH4+
(iv) HS̅.
Answer:
S2-, H2S.
Question 36.
NaCl solution is added to a saturated solution of PbCl2. What will happen to the concentration of Pb2+ ions?
Answer:
Pb2+ ion concentration will decrease to keep K constant.
Question 37.
Which is a stronger base in each of the following pairs and why?
(i) H2O, Cl–
Answer:
H2O is a stronger base being the conjugate base of a weak acid H3O+. Cl– ion is the conjugate base of a strong acid and so is weak.
(ii) CH3COO, OH.
Answer:
OH is the stronger base, being the conjugate base of H2O a very weak acid.
Question 38.
For an aqueous solution of NH4Cl, prove that [H3O]+ = \(\sqrt{\mathbf{K}_{h} c}\) [CBSE PMT 2004]
Answer:
For salt of a strong acid weak base
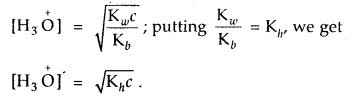
Question 39.
What are the conjugate bases of the following?
CH3OH, HN3, [Al(H2O)6]3+.
Answer:
CH3O (methoxide ion), N3 (azide ion), [Al(H2O)S(OH)]2+.
Question 40.
Write reaction for autoprotolysis of water. How is the ionic product of water-related to ionization constant of water? Derive the relationship.
Answer:
Autoprotolysis of H2O takes place as follows:
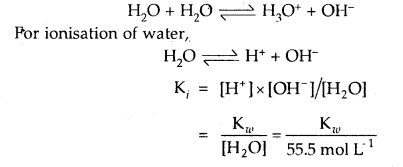
Question 41.
Glycine is an a-aminoacid that exists in the form of Zwitter ion as NH3CH2OO̅. Write the formula of its conjugate acid and conjugate base.
Answer:
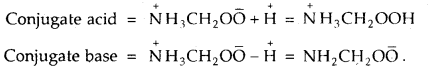
Equilibrium Important Extra Questions Long Answer Type
Question 1.
Explain chemical equilibrium with th^ help of an example of formation and decomposition of hydrogen iodide.
Answer:
Consider the reaction between hydrogen and iodide at a constant temperature of 720 K in a closed vessel. The reaction involved is:
H2(g) + I2(g) → 2HI(g)
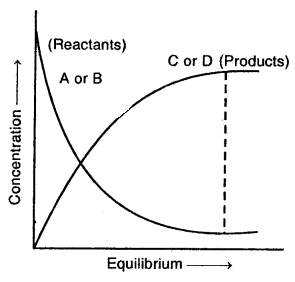
Accordingly, the effective collision amongst the reactant molecules will result in the production of HI. Since the product molecules are not permitted to leave the vessel (i.e., the reaction is carried out in a closed vessel), they will also collide amongst themselves leading to the formation of reactant molecules. Under these conditions, the reaction takes place in both directions. Hence, it is called a reversible reaction.
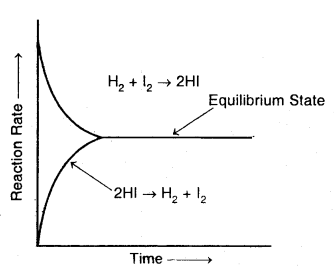
Graphical representation of the change of reaction rates with time for the formation and decomposition of hydrogen iodide
Forward reaction: H2 (g) + I2 (g) → 2HI (g)
Backward reaction: 2HI (g) → H2 (g) + I2 (g)
Reversible reaction: H2 (g) + I2 (g) ⇌ 2HI (g).
To begin with, with the concentration of the reactants being higher in comparison to the product molecules, the rate of the forward reaction will be high as compared to the backward reaction. As the reaction proceeds further, the molar concentration of the reactants will gradually decrease while that of the product will gradually increase.
Apparently, the rate of forwarding reaction goes on decreasing while that of the backward reaction. This state is the reversible chemical reaction is called a chemical equilibrium state.
Question 2.
Name and explain the factors which influence the equilibrium state.
Answer:
The various factors which influence the equilibrium state are:
1. Concentration: Concentration change influences the equilibrium state. If the concentration of the reactants is increased, the equilibrium will shift in such a direction in which more to the products are formed and vice-versa.
On the other hand, if the concentration of the products is increased, the equilibrium will shift in such a direction in which more of the reactants are formed.
2. Temperature: Like concentration, the temperature change also affects the equilibrium state. An increase in temperature of the system will shift the equilibrium in such a direction in which heat is absorbed (i.e. rate of endothermic reaction will increase).
On the other hand, a decrease in temperature of the system will shift the equilibrium in such a direction in which heat is evolved (i.e., rate of exothermic reaction will increase).
3. Pressure: Like concentration and temperature, the pressure also influences the equilibrium state only when the reaction proceeds with a change in volume. An increase in pressure of the system will shift the equilibrium in such a direction in which the volume of the system decreases.
On the other hand, a decrease in pressure of the system will shift the equilibrium in such a direction in which the volume of the system increases.
To explain the effect of temperature, pressure, and concentration on the equilibrium state, consider the combination of N2 and H2 to form NH3
N2 (g) + 3H2 (g) ⇌ 2NH3 (g); ΔH = – 93.6 kJ
The reaction is reversible, exothermic, and accompanied by a decrease in volume.
Effect of temperature: According to Le-Chatelier’s principle, an increase in temperature shifts the equilibrium in the direction in which heat is absorbed, and a decrease in temperature shifts the equilibrium in the direction in which heat is evolved. Since the formation of ammonia is accompanied by the evolution of heat, it is favored by a decrease in temperature.
Effect of pressure: According to Le-Chatelier’s principle, an increase of pressure on a system in equilibrium, favors the direction which is accompanied by a decrease in volume and vice-versa. While going from, left to right in the above reaction, there is a decrease in the number of moles or say volume, the formation of ammonia is favored by an increase in pressure.
Effect of concentration: According to Le-Chatelier’s principle, an increase of concentration of any of the substances in the system shifts the equilibrium in the direction in which the concentration of that substance is reduced. Thus, the addition of N2 or H2 favors the formation of ammonia.
Question 3.
What is salt hydrolysis? Explain hydrolysis of salts of
(i) strong acids and strong bases
(ii) strong acids and weak bases
(iii) strong bases and weak acids
(iv) strong acids and weak bases.
Answer:
Salt hydrolysis: Hydrolysis is a process in which a salt reacts with water to form acid and base.
Salt + Water ⇌ Acid + Base
B A + H2O ⇌ HA + BOH
That is the interaction of the cations of the salt with OH ions furnished by water and anions of the salt with H+ ions furnished by water to form an acidic or basic solution is called salt hydrolysis.
(i) Salts of strong acids and strong bases like NaCl, KCl, KNO3 NaNO3, Na2SO4, K2SO4 do not undergo hydrolysis because the acids an.d bases furnished by them in aqueous solutions are strong acids and strong bases which are completely dissociated.
NaCl + H2O ⇌ NaOH + HCl
NaOH (aq) ⇌ Na+ + OH–
HCl (Aq) ⇌ H+ + Cl–
Since [H+] = [OH–] the resulting solution is neutral and its pH = 7.
(iii) Hydrolysis of salts of strong acids and weak bases:
The salts belonging to this type are NH4NO3, NH4Cl, (NH4)2SO4, CuSO4, AlCl3, Ca(NO3)2, etc.
Let us take the case of NH4NO3
NH4NO3 + H2O ⇌ NH4OH + HNO3
NH4+ + NO3– + H2O ⇌ NH4OH + HNO3
or
NH4+ + H2O ⇌ NH4OH + H+
The resulting solution after hydrolysis is basic (pH > 7). Since only the anions of the salt have taken place in the hydrolysis, it is called anionic hydrolysis.
(iv) Hydrolysis of salts of weak acids and weak bases:
The salts belonging to this type are:
CH3COONH4, (NH4)2CO3, Ca3(PO4)2 etc.
Let us take the case of hydrolysis of CH3COONH4
CH3COONH4 + H3O ⇌ CH3COOH + NH4OH
or
CH3COO̅ + NH4 + H2O ⇌ CH3COOH + NH4OH
Since both the cations and anions of the salt have participated in the hydrolysis, it is known as cationic as well as anionic hydrolysis. The nature of the solution or pH depends upon the relative strengths of the acid and base that are formed on hydrolysis.
Equilibrium Important Extra Questions Numerical Problems
Question 1.
Calculate the pH of \(\frac{N}{1000}\) sodium hydroxide solution assuming complete ionisation (Kw = 1.0 × 10-14).
Answer:
Since NaOH is completely ionized
∴ [NaOH] = [OH–] = 10-3 N = 10-3 M
Now [H2O+][OH–] = Kw = 10-14 [Given]
∴ [H3O+] = \(\frac{\mathrm{K}_{w}}{\left[\mathrm{OH}^{-}\right]}=\frac{10^{-14}}{10^{-3}}\) = 10-11
pH = – log [H3O+] = – log 10-11 = 11.
Question 2.
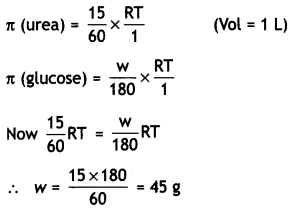
Calculate the pH of a 0.01 N solution of acetic acid. Ka for acetic acid is 1.8 × 10-5 at 25°C.
Answer:
![]()
Applying the law of chemical equilibrium
Ka = [CH3COO̅][H3O+]/[CH3COOH]
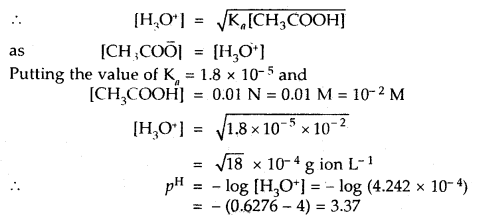
Question 3.
Calculate the pH value of a solution of 0.1 M NH3 (Kb = 1.8 × 10-5). ,
Answer:
NH3 H2O ⇌ NH4+ + OH–
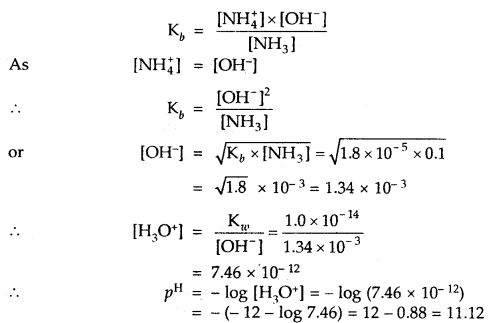
Question 4.
Equal volumes of solutions with pH = 4 and pH = 10 are mixed. Calculate the pH of the resulting solution?
Answer:
pH = 4
∴ [H3O+] = 10-4 M
pH = 10
∴ [H3O+] = 10-10 M
or [OH–] = 10-4 M
Thus, they will exactly neutralize each other, and the pH of the resulting solution will be = 7.
Question 5.
An aqueous solution of 0.02 g of NaOH in 50 mL has been prepared. What is its pH and pOH.
Answer:
50 mL of NaOH contains 0.02 g of it
1000 mL of it contains = \(\frac{0.02}{50}\) × 1000 = 0.4 g
Strength of NaOH = 0.4 gL-1
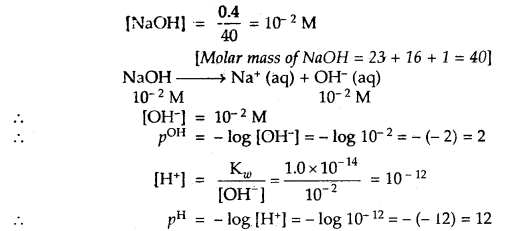
Question 6.
A reaction mixture containing N2 at 0.50 atm, H2 at 3.0 atm and NH3 at 0.50 atm is heated to 450°C, in which direction the reaction N2 (g) + 3H2 (g) ⇌ 2NH3 (g) will go if Kp = 4.28 × 10-5?
Answer:
Concentration quotient Q = \(\frac{p^{2} \mathrm{NH}_{3}}{p_{\mathrm{N}_{2}} \times p_{\mathrm{H}_{2}}^{3}}=\frac{(0.50)^{2}}{0.5 \times(3.0)^{3}}\) = 0.018
Kp = 4.28 × 10-5
As Q > > Kp reaction will go in the backward direction.
Question 7.
Under what pressure must an equimolar mixture of PCl3 and Cl2 be placed at 250°C in order to obtain PCl5 at 1 atm > Kp for dissociation of PCl5 = 1.78.
Answer:
Let partial pressure of PCl3 at eqbm. = p atm
Then partial pressure of Cl2 at eqbm. = p atm
Partial pressure of PCl5 at eqbm. = 1 atm
Then for PCl5 ⇌ PCl3 + Cl2
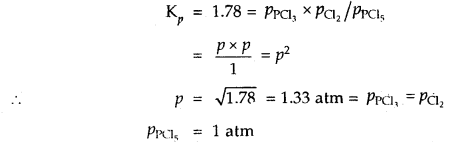
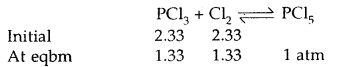
∴ Total initial pressure of PCl3 and Cl2 = 2.33 + 2.33 = 4.66 atm.
Question 8.
At 773 K, the equilibrium constant Kc for the reaction N2 (g) + 3H2 (g) ⇌ 2NH3 (g) is 6.02 × 10-2 L2 mol-2. Calculate the value of Kp at the same temperature.
Answer:
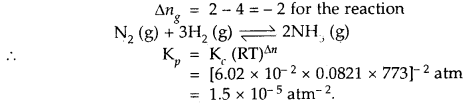
Question 9.
Kp for the reaction N2 (g) + 3H2 (g) ⇌ 2NH3 (g) is 49 at a certain temperature. Calculate the value of Kp at the same
temperature for the reaction NH3 ⇌ \(\frac{1}{2}\)N2 + \(\frac{3}{2}\)H2 (g)
Answer:
Given for the reaction N2 (g) + 3H2 (g) ⇌ 2NH3 (g), Kp = 49
∴ for the reverse reaction 2NH3 (g) ⇌ N2 (g) + 3H2 (g)
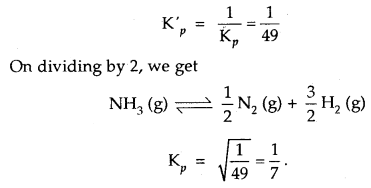
Question 10.
In the equilibrium CaCO3 (s) ⇌ CaO (s) + CO2 (g) at 1073 K, the pressure of CO2 is formed to be 2.5 × 104 Pa. What is the equilibrium constant for this reaction at 1073 K.
Answer:
With reference to the standard state pressure of 1 bar which is = 105 Pa
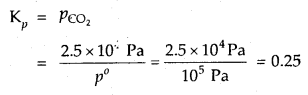
Question 11.
Determine the concentration of CO2 which will be in equilibrium with 2.5 × 10-2, mol L-1 of CO at 100°C for the reaction FeO (s) + CO (g) ⇌ Fe (s) + CO2 (g); Kc = 5.0.
Answer:
Kc = \(\frac{\left[\mathrm{CO}_{2}\right]}{[\mathrm{CO}]}\)
i.e., 5 = \(\frac{\left[\mathrm{CO}_{2}\right]}{2.5 \times 10^{-2}}\)
or
[CO2] = 5 × 2.5 × 10-2 = 12.5 × 10-2 mol L-1
Question 12.
In a reaction between hydrogen and iodine, 6.34 moles of hydrogen and 4.02 moles of iodine are found to be in equilibrium with 42.85 moles of hydrogen iodide at 350°C. Calculate the equilibrium constant.
Answer:
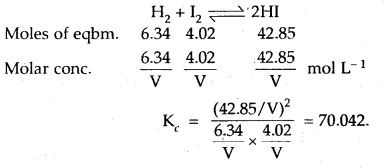
Question 13.
Prove that the pressure necessary to obtain 50% dissociation of PCl5 at 500 K is numerically equal to the three times the value of the equilibrium constant, Kp.
Answer:
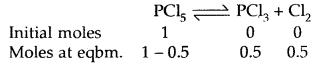
Total no. of moles = 1.5
If P is the total required pressure, then
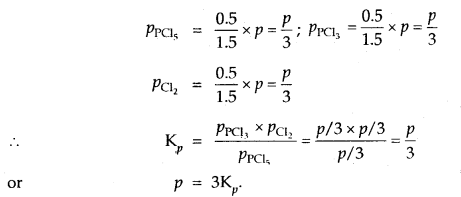
Question 14.
The equilibrium constant for the reaction A2 + B2 ⇌ 2AB is Kp. What will be the equilibrium constant for the reaction AB ⇌ \(\frac{1}{2}\)A2 + \(\frac{1}{2}\) B22? [A, B and AB are all gases] [WB JEE 2004]
Answer:
For A2 + B2 ⇌ 2AB, eqbm. constant = Kp
For the reverse reaction 2AB ⇌ A2 + B2 eqmb. constant = \(\frac{1}{\mathbf{K}_{p}}\)
On dividing by 2, AB ⇌ \(\frac{1}{2}\)A2 + \(\frac{1}{2}\)B2
eqbm. constant = \(\sqrt{\frac{1}{K_{p}}}\)
Question 15.
The concentration of hydronium ions in a cup of black coffee is 1.3 × 10-5 M. Find the pH of the coffee. Is this coffee acidic or alkaline?
Answer:
Here, given [H3O+] = 1.3 × 10-5 M
pH = – log [H3O+] = – log (1.3 × 10-5-5)
= 5 – log 1.3 = 5 – 0.1139 = 4.8861
As pH is less than 7, the black coffee is acidic.
Question 16.
A solution is found to contain 0.63 g of nitric acid in 100 mL of the solution. What is the pH of the solution.
Answer:
HNO3 → H+ + NO3 completely
∴ [HNO3] = [H+] as nitric acid is a strong acid.
Cone, of HNO3 = 0.63 g per 100 mL
Strength L-1 = 6.3
[HNO3] = \(\frac{6.3}{63}\) = 0.1 = 10-1 M
∴ [H+] = 10-1 M
∴ pH = – log 10-1 = 1.
Question 17.
The value of Kw is 9.55 × 10-14 at a certain temperature. Calculate the pH of water at this temperature.
Answer:
Kw = 9.55 × 10-14
Now for water [H3O+] = [OH–]
∴ Kw = [H3O+] × [OH–] = [H3O+]2
or
[H3O+] = \(\sqrt{\mathrm{K}_{w}}=\sqrt{9.55 \times 10^{-14}}\) = 3.09 × 10-7M
pH = – log (3.09 × 10-7) = – (- 7 – log 3.09) = 7 – log 3.09 = 7 – 0.49 = 6.51
Question 18.
Calculate the mass of HCl to be dissolved per litre of the solution so that its pH = 1.301.
pH = – log [H3O+]
[H3+O] = antulog (- 1.301) = antilog 2.699
= 5.0 × 10-2 × 36.5 gL-1 = 1.825 gL-1
Question 19.
Calculate the pH of 0 001 N H2SO4 solution.
Answer:
H2SO4 is completely ionised as
H2SO4 + 2H2O ⇌ 2H3O+ + SO42- as it is, a strong acid.
[H3O+] = 2[H2SO4] as one molecule of H2SO4 gives 2 H3O+ ions
But H2SO4 is given to be 0.001 N = 0.001 × 49 g L-1 [Eq. wt of H2SO4 = 49]
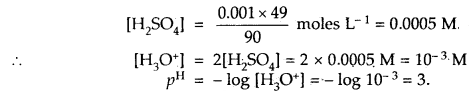
Question 20.
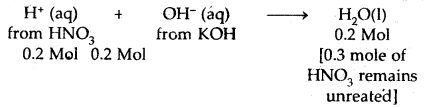
What would be the pH of a solution obtained by mixing 100 mL of 0.1 NHCl and 9.9 mL of 1.0 N NaOH solution?
Answer:
100 mL of 0.1 N HCl = 100 × 0.1 = 10 millieq.
9.9 mL of 1 N NaOH = 9.9 × 1 = 9.9 millieq.
∴ HCl left unneutralized = 10 – 9.9 = 0.1 millieq
Volume of solution = 100 + 9.9 = 109.9 mL
Normality of resulting HCl solution
= \(\frac{0.1}{109.9}=\frac{0.1}{110}\) = 0.09 × 10-4 N
Molarity = 9.09 × 10-4 M = [H+] = [HCl]
pH = – log(9.09 × 10-4) = 3.05
Question 21.
Calculate the pH of 10-8 M HCl solution.
Answer:
From acid [H+] = 10-8 M as HCl is completely ionised
Now the concentration of [H+] = 10-7 M cannot be ignored as compared to [H+] = 10-8 M from HCl as HCl is very dilute solution.
∴ Total [H+] = 10-8 + 10-7 = 10-8(1 + 10)
= 11 × 10-8 M
pH = – log (11 × 10-8) = 8 – log 11
= 8 – 1.04 = 6.96.
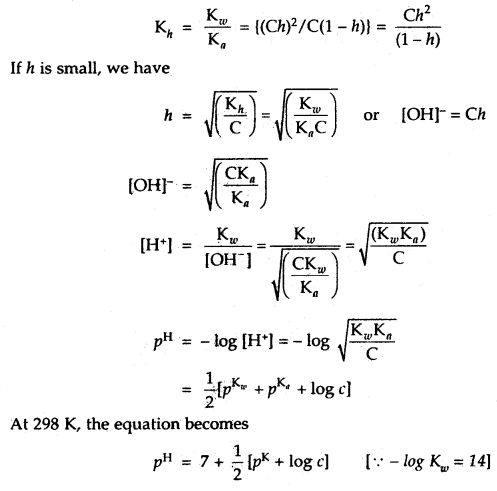
Question 22.
Calculate the hydrolysis constant and degree of hydrolysis and pH of 0.10 M KCN solution at 25°C. Ka for HCN = 6.2 × 10-10.
Answer:
KCN is the salt of a weak acid HCN and strong base KOH
∴ Kh = Hydrolysis constant
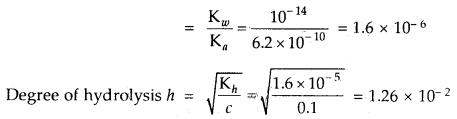
The hydrolysis reaction of KCN is

Question 23.
Calculate the pH of 0.01 M solution of NH4CN. Given that the Ka for HCN = 6.2 × 10-10 and Kb for NH3 = 1.6 /10“5.
Answer:
Applying the formula
PH = 7+ [pKa – pKb] = 7 + [- log Ka + log Kb]
= 7 + \(\frac{1}{2}\)[- log (6.2 × 10-10) + log (1.6 × 10-5)]
= 7+ \(\frac{1}{2}\)[(10- 0.7924) + (5 – 0.2041)]
pH = 9,31
Question 24.
The solubility product of AgCl in water is 1.5 × 10-10. Calculate its solubility in 0.01 M NaCl solution.
Answer:
As NaCl dissociates completely
∴ [NaCl] = [Cl] = 0.01 M
If solubility of AgCl in 0.01 M is s mol L-1, then
[Ag+] = [Cl] = s mol L-1
∴ Total [Cl] = 0.01 + s ≈ 0.01 M
Ksp for AgCl = [Ag+][Cl- ] = s × 0.01 = 0.01 s
∴ 0.01 s = 1.5 × 10-10
s = 1.5 × 10-8 M.
Question 25.
Given that the solubility product of BaSO4 is 1 × 10-10. Will a precipitate form when
(i) Equal volumes of 2 × 10-3 M BaCl2 solution and 2 × 10-4 M NaSO4 solutions are mixed?
Answer:
BaCl2 ionizes completely in solution
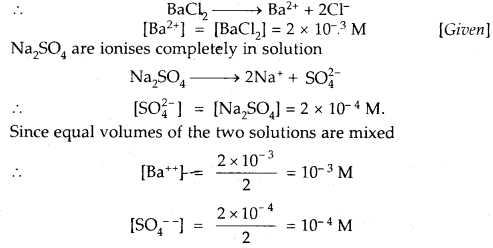
Ionic product of BaSO4 = [Ba++][SO4—]
= 10-3 × 10-4 = 10-7
As Ionic product 10-7 is > Ksp 1 × 10-10
Hence a precipitate of BaSO4 will be formed.
(ii) Equal volumes of 2 × 10-8 M BaCl2 solution and × 2 × 10-3 M Na2SO4 solutions are mixed?
Answer:
Similarly [Ba++] = \(\frac{2 \times 10^{-8}}{2}\) = 10-8 M
[SO4—] = \(\frac{2 \times 10^{-3}}{2}\) = 10-3
Ionic product of BaSO4 = 108 × 10 = 10-11
It is less than the solubility product Ksp × 1 × 10-10
Hence, no precipitate will be formed in this case.



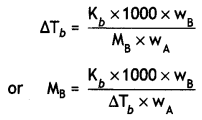

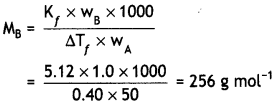
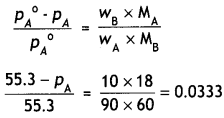
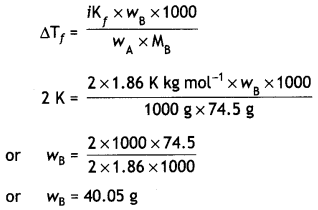
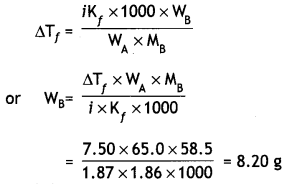
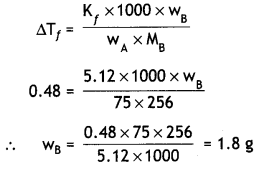

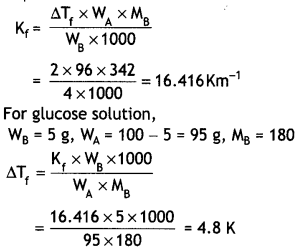
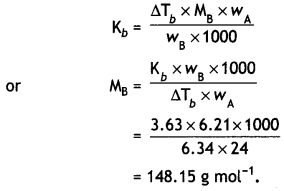



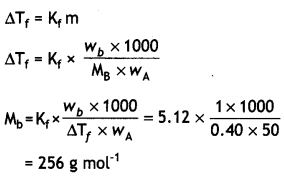


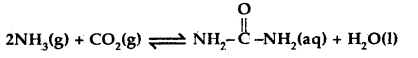
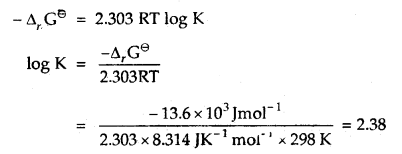
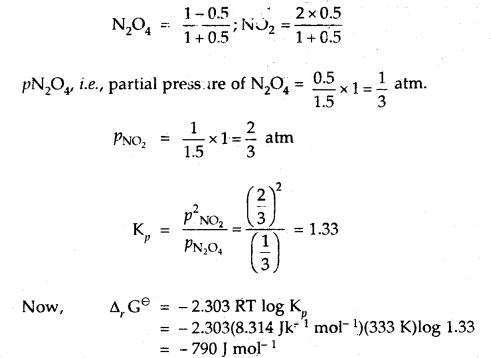
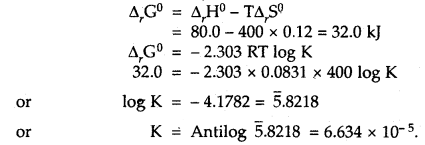
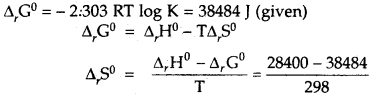
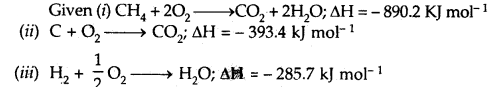
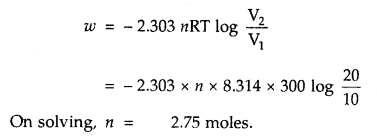

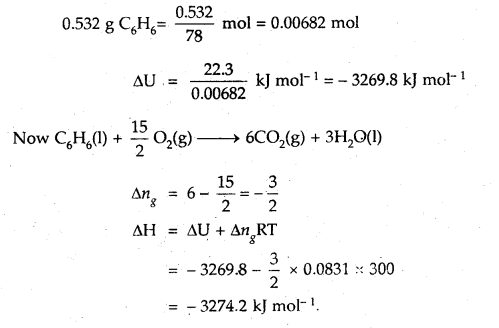

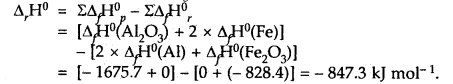
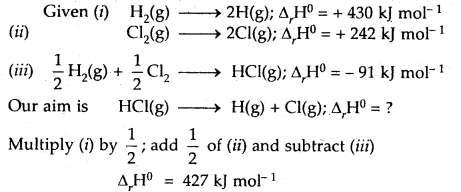
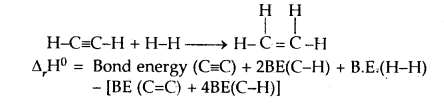





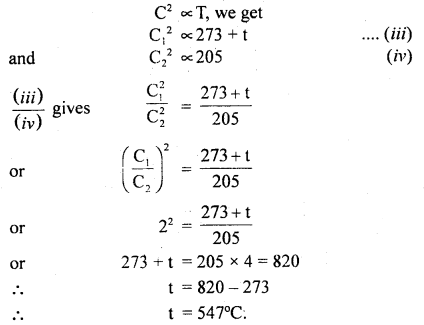
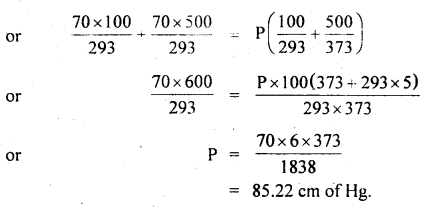
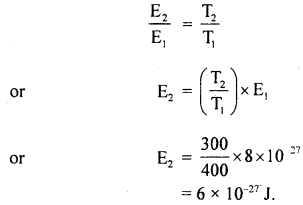
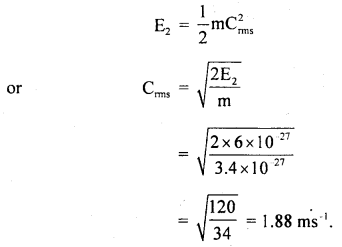
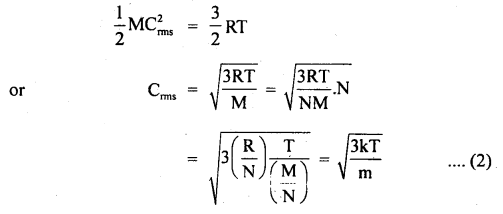

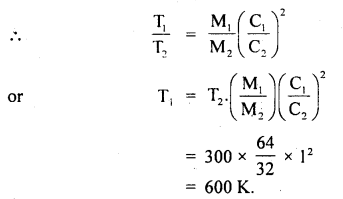
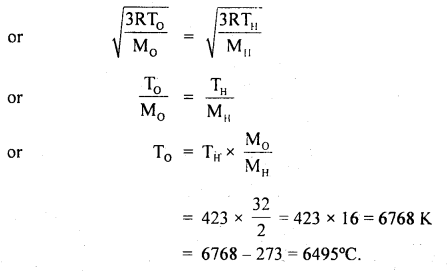
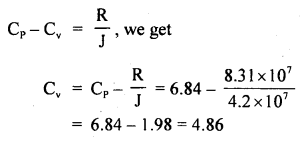
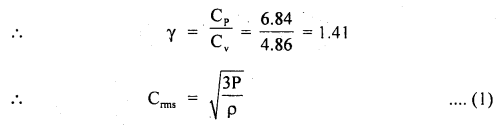

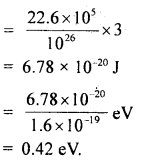

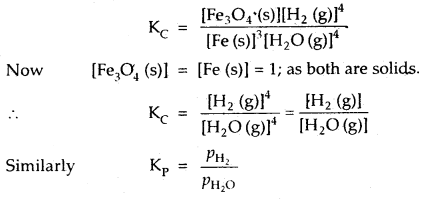

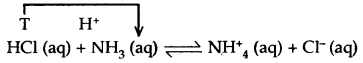
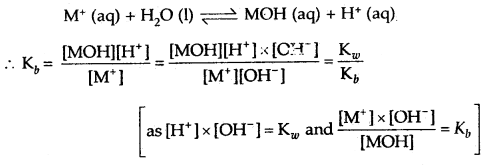
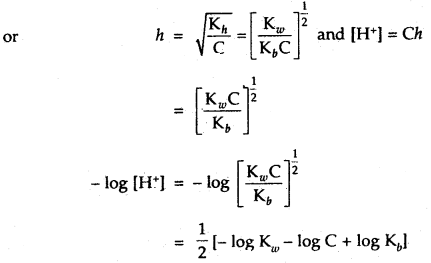
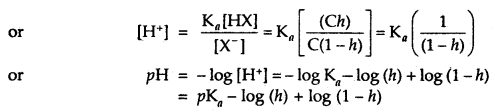
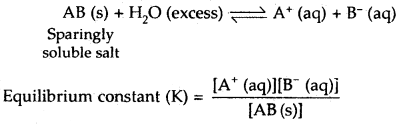

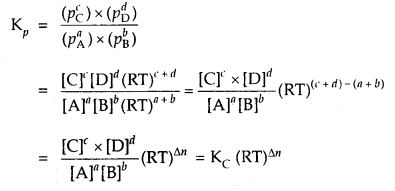

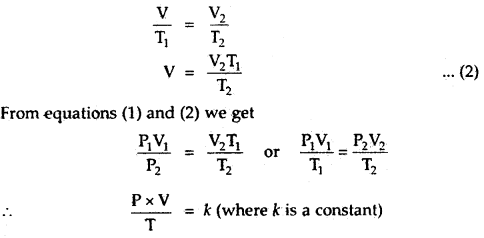
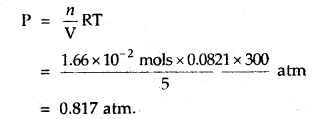
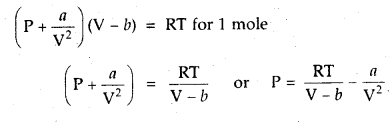
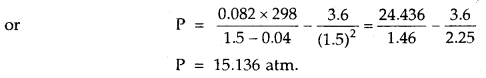
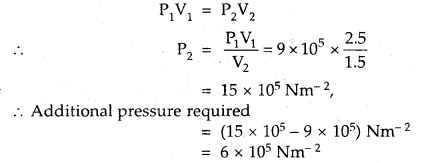
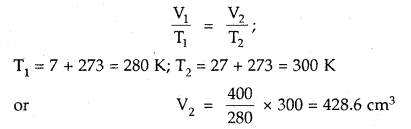
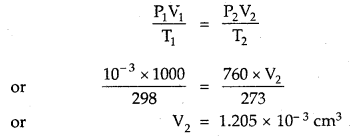
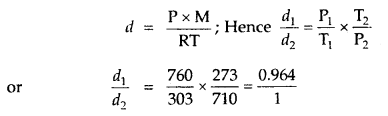
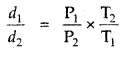
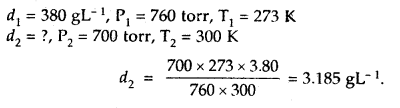


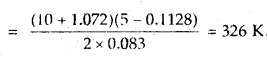
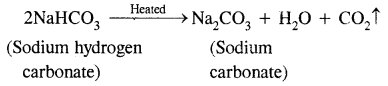
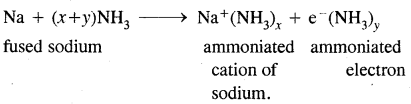
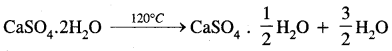
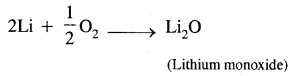

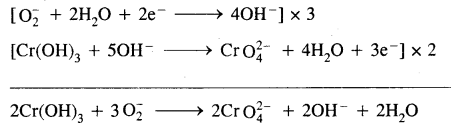






 (3)
(3)









 (5)
(5)