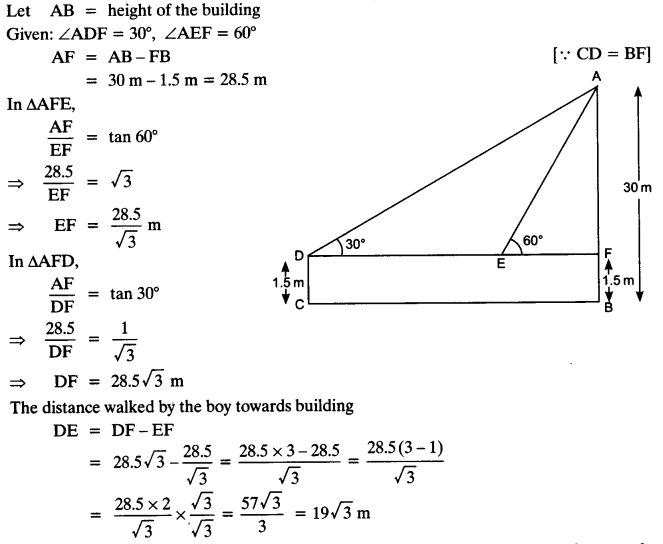
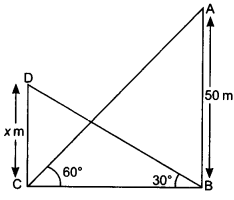
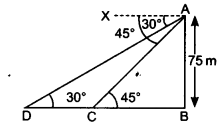
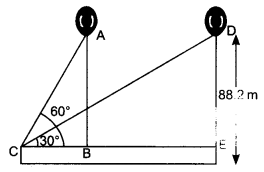
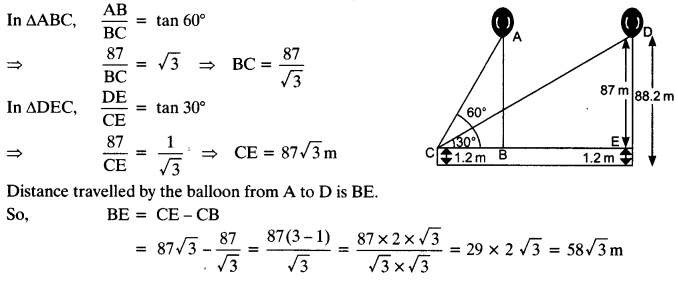
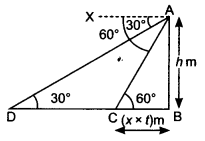
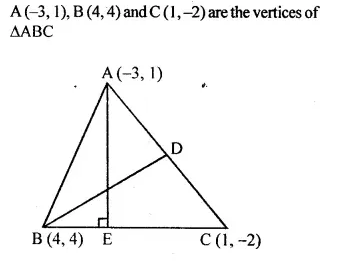
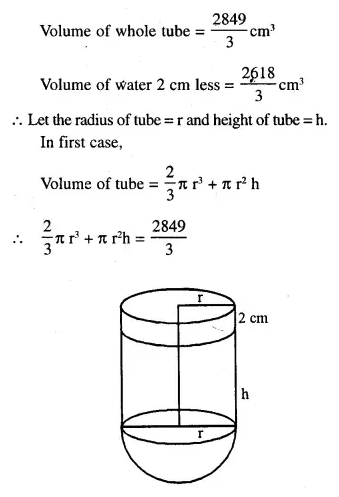
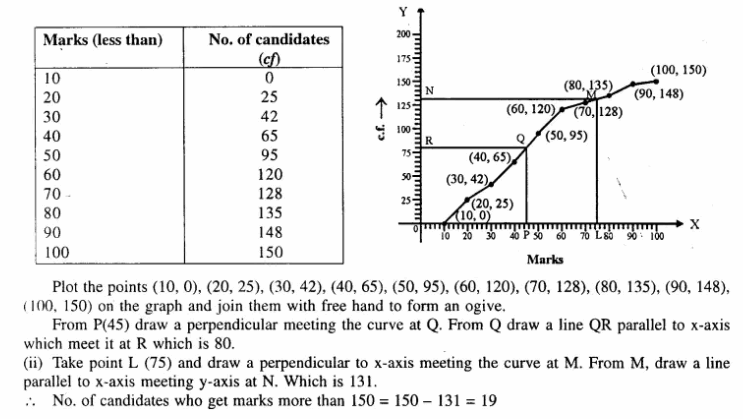
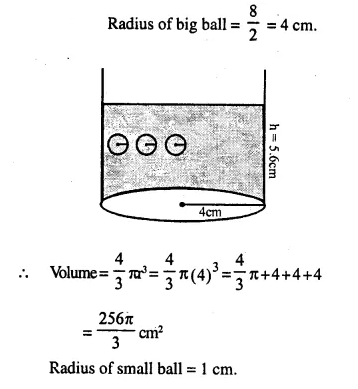
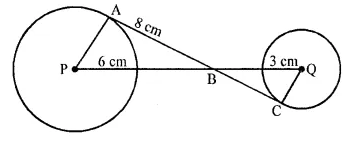
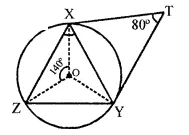
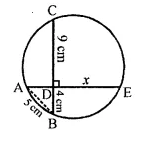
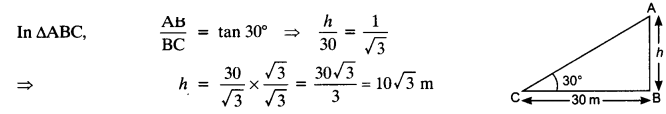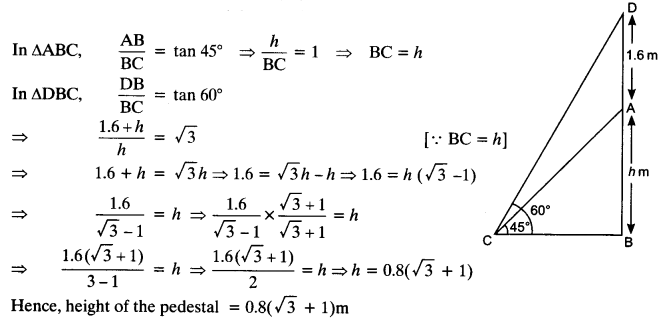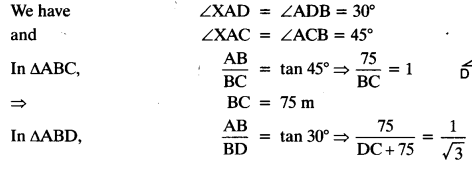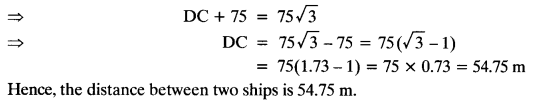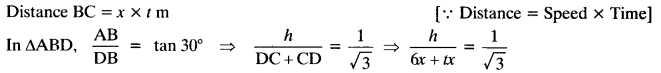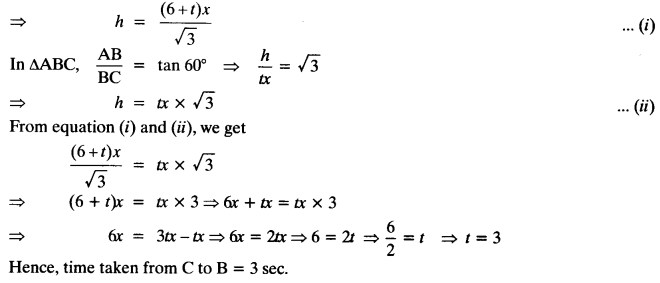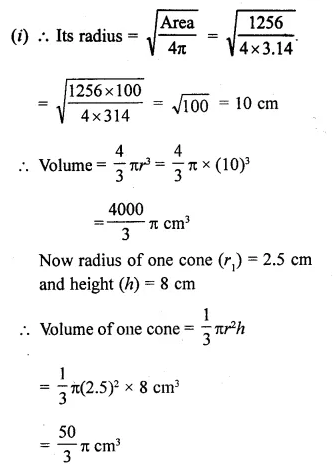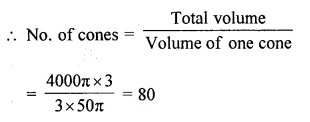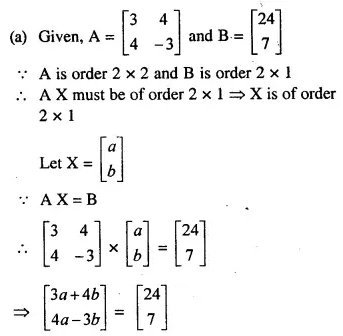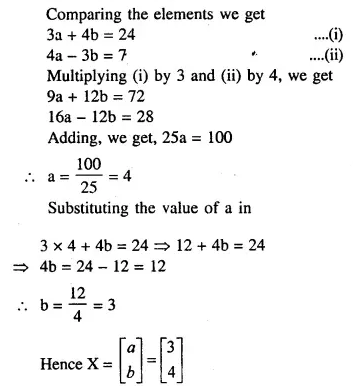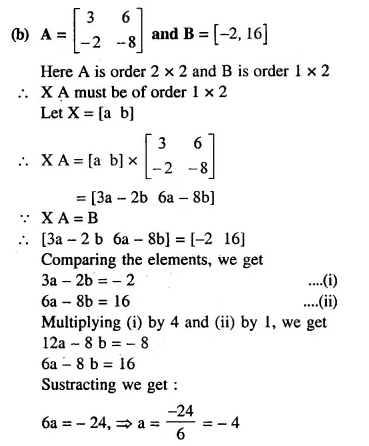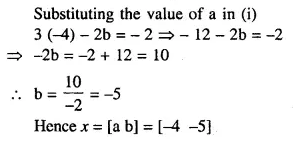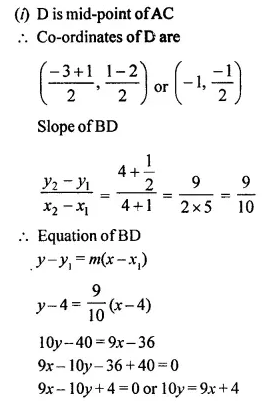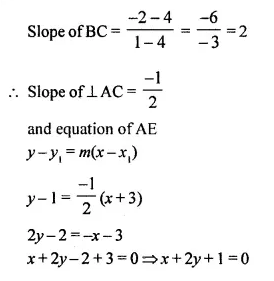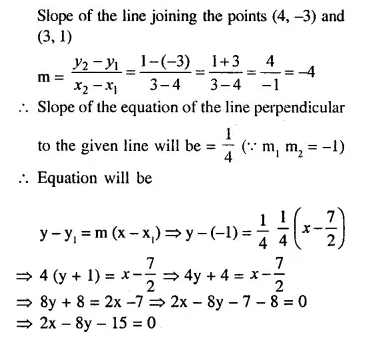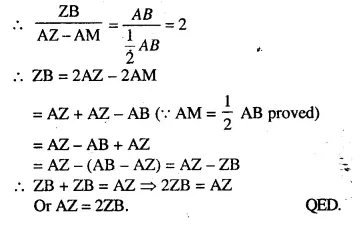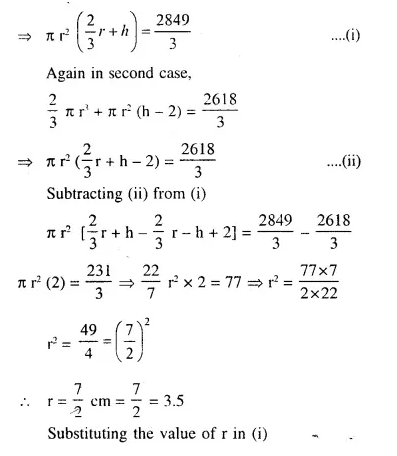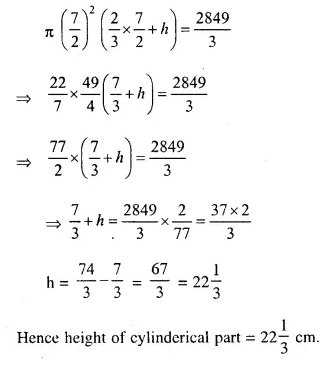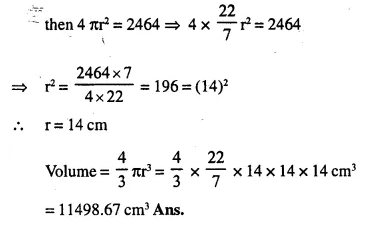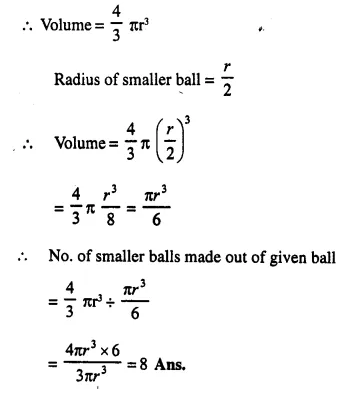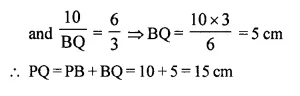NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.1 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.1.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 6 |
| Chapter Name | Triangles |
| Exercise | Ex 6.1 |
| Number of Questions Solved | 3 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.1
Question 1.
Fill in the blanks by using the correct word given in brackets.
(i) All circles are ……………. . (congruent/similar)
(ii) All squares are …………… . (similar/congruent)
(iii) All …………….. triangles are similar. (isosceles/equilateral)
(iv) Two polygons of the same number of sides are similar, if
(a) their corresponding angles are …………… and
(b) their corresponding sides are …………… (equal/proportional)
Solution:
Fill in the blanks.
(i) All circles are similar.
(ii) All squares are similar.
(iii) All equilateral triangles are similar.
(iv) Two polygons of the same number of sides are similar, if
(a) their corresponding angles are equal and
(b) their corresponding sides are proportional.
Question 2.
Give two different examples of pair of
(i) similar figures.
(ii) non-similar figures.
Solution:
(i) Examples of similar figures:
- Square
- Regular hexagons
(ii) Examples of non-similar figures:
- Two triangles of different angles.
- Two quadrilaterals of different angles.
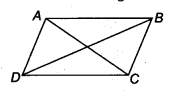
Question 3.
State whether the following quadrilaterals are similar or not.
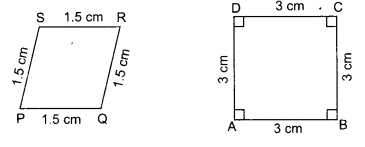
Solution:
No, the sides of quadrilateral PQRS and ABCD are proportional but their corresponding angles are not equal.
We hope the NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.1 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.1, drop a comment below and we will get back to you at the earliest.