RS Aggarwal Class 7 Solutions Chapter 9 Unitary Method Ex 9A
These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A.
Other Exercises
- RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A
- RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B
- RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C
- RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper
Question 1.
Solution:
Cost of 15 oranges = Rs. 110
Cost of 1 orange = Rs. \(\frac { 110 }{ 15 }\)
and cost of 39 oranges = Rs. \(\frac { 110 }{ 15 }\) x 39
= Rs. 22 x 13 = Rs. 286
Question 2.
Solution:
In Rs. 260, the sugar is bought = 8 kg
and in Re. 1, the sugar is bought = \(\frac { 8 }{ 260 }\) kg
Then in Rs. 877.50, the sugar will be bought = \(\frac { 8 }{ 260 }\) x 877.50 kg
= \(\frac { 8 }{ 260 }\) x \(\frac { 87750 }{ 100 }\)
= 27 kg
Question 3.
Solution:
In Rs. 6290, silk is purchased = 37 m
and in Re. 1, silk is purchased = \(\frac { 37 }{ 6290 }\) m
and in Rs. 4420, silk will be purchased 37
= \(\frac { 37 }{ 6290 }\) x 4420 m = 26 m
Question 4.
Solution:
Rs. 1110 is wages for = 6 days.
Re. 1 will be wages for = \(\frac { 6 }{ 1110 }\) days
and Rs. 4625 will be wages for
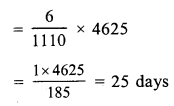
Question 5.
Solution:
In 42 litres of petrol, a car covers = 357 km
and in 1 litre, car will cover = \(\frac { 357 }{ 42 }\) km
and in 12 litres, car will cover = \(\frac { 357 }{ 42 }\) x 12 = 102 km
Question 6.
Solution:
Cost of travelling 900 km is = Rs. 2520
and cost of 1 km will be = Rs. \(\frac { 2520 }{ 900 }\)
andcostof360kmwillbe = Rs. \(\frac { 2520 }{ 900 }\) x 360 = Rs. 1008
Question 7.
Solution:
To cover a distance of 51 km, time is taken = 45 minutes


Question 8.
Solution:
If weight is 85.5 kg, then length of iron rod = 22.5 m
If weight is 1 kg, then length of rod will be
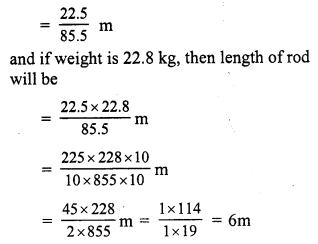
Question 9.
Solution:
In 162 grams, sheets are = 6

Question 10.
Solution:
1152 bars of soap can be packed in 8 cartons
1 bar of soap coil be packed in

Question 11.
Solution:
In 44 mm of thickness, cardboards are = 16
In 1 mm of thickness, cardboards will be

Question 12.
Solution:
If length of shadow is 8.2 m, then
height of flag staff is = 7 m
If length of shadow is 1 m, then height will

Question 13.
Solution:
16.25 m long wall is build by = 15 men

Question 14.
Solution:
1350 litres of milk cm be consumed by = 60 patients
1 litres of milk can be consumed by = \(\frac { 60 }{ 1350 }\) patients
and 1710 litres of milk can be consumed
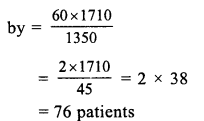
Question 15.
Solution:
2.8 cm extension is produced by = 150 g.
1 cm extension will be produced by = \(\frac { 150 }{ 2.8 }\) g
and 19.6 cm extension will be produced by
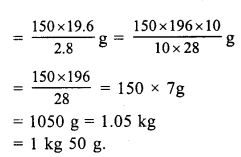
Hope given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.