Category: CBSE Class 6

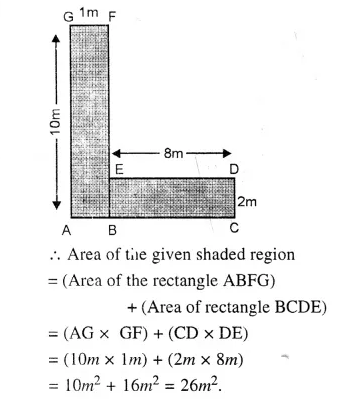
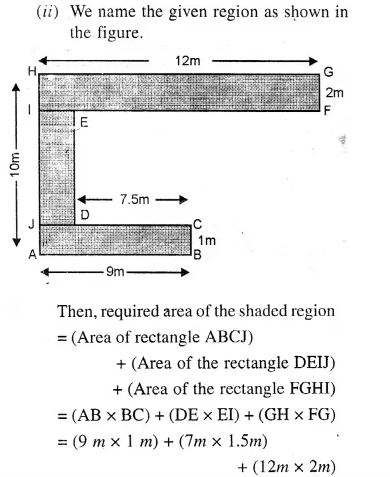
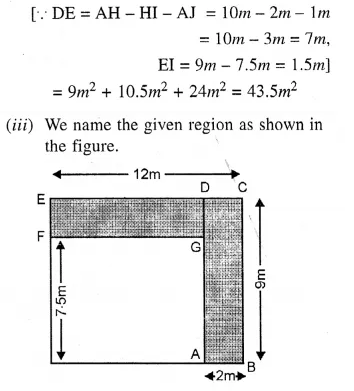
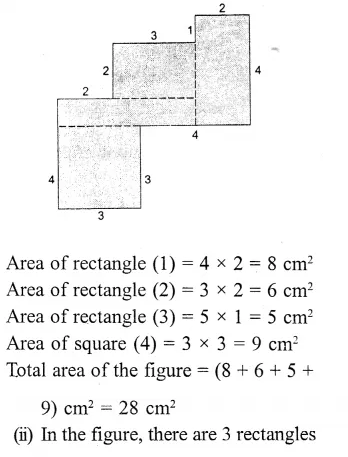
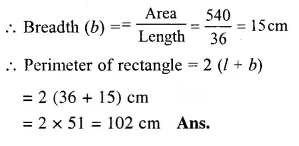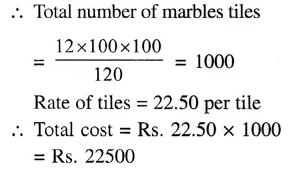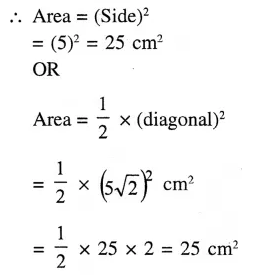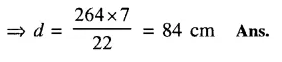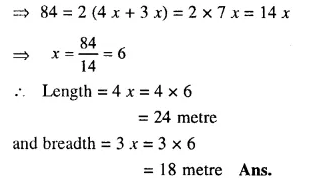RS Aggarwal Class 6 Solutions Chapter 21 Concept of Perimeter and Area Ex 21E

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21E

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21A
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21B
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21C
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21D
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21E

Objective questions
Mark against the correct answer in each of the following :

Question 1.
Solution:
Ratio in the sides of a rectangle = 7 : 5
and perimeter = 96 cm

Question 2.
Solution:
Area of a rectangle = 650 cm²
and breadth (b) = 13 cm

Question 3.
Solution:
Length of a rectangular field (l) = 34 m
and breadth (b) = 18 m
Circumference = 2 (l + b)
= 2 (34 + 18)m
= 2 x 52
= 104 m
Rate of fencing = Rs. 22.50 per m
Total cost = Rs. 22.50 x 104
= Rs. 2340 (b)

Question 4.
Solution:
Total cost of fencing = Rs. 2400
Rate = Rs. 30 per m
Perimeter of the rectangular field

Question 5.
Solution:
Area of rectangular carpet =120 cm²
Perimeter = 46 m
Now 2 (l + b)
= 46 m

Question 6.
Solution:
Let width of a rectangle = x
Then length = 3x
and diagonal = 6√10 cm

Question 7.
Solution:
Ratio in length and perimeter of a rectangle = 1 : 3
Let length = x,
then perimeter = 3x

Question 8.
Solution:
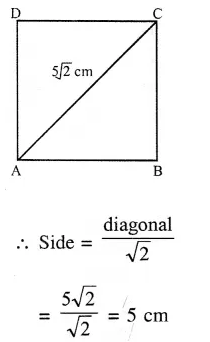
Length of diagonal of a square = 20 cm

Question 9.
Solution:
Total cost of fencing around a square field = Rs. 2000
and rate = Rs. 25 per metre

Question 10.
Solution:
Circumference = πd
= \(\\ \frac { 22 }{ 7 } \) x 7
= 22 cm (b)

Question 11.
Solution:
(a) Diameter = \(\frac { circumference }{ \pi } \)
= \(\\ \frac { 88\times 7 }{ 22 } \)
= 28 cm

Question 12.
Solution:
Circumference = πd
= \(\\ \frac { 22 }{ 7 } \) x 70
= 220 cm

Question 13.
Solution:
Length of the lane = 150 m
Breadth of the lane = 9 m
Area of the lane = (150 x 9) m²
= 1350 m²
Area of the brick = 22.5 cm x 7.5 cm
= 168.75 cm²

Question 14.
Solution:
Length of a rectangular room (l) = 5 m 40 cm = 5.4 m
and breadth (b) = 4 m 50 cm
= 4.5 m
Area = l x b = 5.4 x 4.5 m²
= 24.3 m² (b)

Question 15.
Solution:
Length of a sheet (l) = 72 cm
and breadth (b) = 48 cm
Area = l x b = 72 x 48 cm²
Area of paper for one envelope = 18 x 12 cm²
No. of envelopes = \(\\ \frac { 72\times 48 }{ 18\times 12 } \) =16 (d)

 

Hope given RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 21 Concept of Perimeter and Area Ex 21D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21D

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21A
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21B
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21C
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21D
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21E

Question 1.
Solution:
(i) Length (l) = 46 cm
Breadth (b) = 25 cm
Area of rectangle = l x b
= 46 x 25 sq. cm
= 1150 sq.cm.
(ii) Length (l) = 9 m
Breadth (b) = 6 m
Area = l x b = 9 x 6
= 54 sq. metre Ans.
(iii) Length (l) = 14.5 m
Breadth (b) = 6.8 m
Area = l x b
= 14.5 x 6.8 sq. m
= 98.6 sq. m Ans.
(iv) Length (l) = 2m 5cm
= 2x 100 cm + 5 cm
= 200 cm + 5 cm
= 205 cm
Breadth = 60 cm
Area = l x b
= 205 cm x 60 cm
= 12300 cm²
(v) Length (l) = 3.5 km
Breadth (b) = 2 km
Area = l x b
= 3.5 x 2
= 7 sq. km. Ans.

Question 2.
Solution:
Side of a square plot = 14 m
Area = (Side)²
= (14)²
= 196 m²

Question 3.
Solution:
Length of top of table (l) = 2 m, 25 cm = 2.25 m
Breadth (l) = 1 m 20 cm = 1.20 m
Area of the top of the table = l x b
= (2.25 x 1.20) sq. m
= 2.7 sq. m. Ans.

Question 4.
Solution:
Length of carpet (l) = 30 m 75 cm
= 30.75 m
Breadth (b) = 80 cm = 0.80 m
Area of the carpet = l x b
= (30.75 x 0.80) sq. m
= 24.6 sq. m
Cost of one square metre = Rs. 20
Total cost = 24.6 x 150
= Rs. 3690. Ans

Question 5.
Solution:
Length of the sheet of paper 3 m 24 cm
= 300 cm + 24 cm
= 324 cm
Breadth of the sheet of the paper 1 m 72 cm
= 100 cm + 72 cm
= 172 cm
Area of the sheet of paper = (324 x 172) cm²
Also, area of the piece of paper required for an envelope = (18 x 12) cm².
Number of envelopes that can be made
= \(\\ \frac { 324\times 172 }{ 18\times 12 } \)
= 258

Question 6.
Solution:
Length of room (l) = 12.5 m
Breadth (b) = 8 m
Area = l x b
= (12.5 x 8) sq. m
= 100 sq. m
Side of square carpet (a) = 8 m
Area of carpet = a² = (8 x 8) sq. m.
= 64 square metre
Area left without carpet = 100 sq. m – 64 sq. m
= 36 sq. m Ans.

Question 7.
Solution:
Length of the lane = 150 m
Breadth of the lane = 9 m
Area of the lane = (150 x 9) m²
= 1350 m²
Area of the brick = 22.5 cm x 7.5 cm
= 168.75 cm²

Question 8.
Solution:
Length of room (l) = 13 m
Breadth (b) = 9 m
Area of floor or carpet = l x b
= 13 x 9
= 117 sq. m

Question 9.
Solution:
Let the length of the rectangular park = 5x metres
and the breadth of the rectangular park = 3x metres

Question 10.
Solution:
Side of the square plot = 64 m
Perimeter of the square plot = 4 x Side
= 4 x 64
= 256 m
Perimeter of the rectangular plot = Perimeter of the square plot = 256 m
Length of the rectangular plot = 70 m
Perimeter = 2 x (Length + Breadth)
256 = 2 (70 + b)
256 = 140 + 2b
=> 2b = 256 – 140
=> 2b = 116
b = \(\\ \frac { 116 }{ 2 } \) = 58 cm
Area of the rectangular plot = (length x breadth)]
= (70 x 58) m²
= 4060 m²
Area of the square plot = Side x Side
= (64 x 64) m²
= 4096 m².
Square plot has the greater area than that of the rectangular plot by
(4096 – 4060)
= 36 m².

Question 11.
Solution:
Total cost of cultivating the rectangular field = Rs. 71400
Rate of cultivating = Rs. 35 per sq. m

Question 12.
Solution:
Area of rectangle = 540 sq. cm
Length (l) = 36 cm

Question 13.
Solution:
Measure of a marble tile = 12cm x 10cm
Area of wall = 4 m x 3 m
= 12 m²
Area of one marble tile
= 12 x 10
= 120 cm²

Question 14.
Solution:
Area of a rectangle = 600 cm²
Breadth = 25 cm

Question 15.
Solution:
diagonal of square = 5 √2

Question 16.
Solution:
(i) We name the given region as shown in the figure

Question 17.
Solution:
Measures are in cm
(i) In the figure, there are three rectangles and one square



= 5(6 x 6) cm²
= 180 cm²

 

Hope given RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 21 Concept of Perimeter and Area Ex 21C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21C

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21A
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21B
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21C
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21D
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21E

Question 1.
Solution:
1. In the given figure, there are 12 complete squares, so its area is 12 cm².
2. In the given figure, there are 18 complete squares, so its area is 18 cm².
3. In the given figure, there are 14.5 complete squares, so its area is 14.5 cm² .
4. In the given figure, there are 6 complete squares and four half parts of a square, the area of the figure is 8 cm².
5. The given figure contains 9 complete squares and 6 half parts of a square. So the area of the figure is
\(\left( 9+\frac { 6 }{ 2 } \right) \) = 9 + 3 = 12 cm².
6. The given figure contains 16 complete squares. So, its area is 16 cm².
7. The given figure contains 4 complete squares, 8 more than half parts and 4 less than half parts of a square. Neglecting the less than half parts and considering the more than half parts as complete squares, the approximate area of the figure is 12 cm².
8. The given figure contains 7 complete squares and 5 more than half parts and some less than half parts of a square. Neglecting the less than half parts and considering more than half parts as complete square, the area of the figure is 12 cm² approximately.
9. The given figure contains 14 complete squares and four half parts of a square. So, the area of the figure is
\(\left( 14+\frac { 4 }{ 2 } \right) \) cm² = (14 + 2) cm² = 16 cm².

Hope given RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 21 Concept of Perimeter and Area Ex 21B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21B

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21A
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21B
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21C
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21D
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21E

Question 1.
Solution:
(i) Radius of the circle (r) = 28 cm
Circumference = 2 πr
= 2 x \(\\ \frac { 22 }{ 7 } \) x 28 cm
= 176 cm Ans.

Question 2.
Solution:
(i) Diameter of the circle (d) = 14 cm
Circumference = πd
= \(\\ \frac { 22 }{ 7 } \) x 14
= 44 cm

Question 3.
Solution:
Circumference of the circle = 176 cm
Let r be the radius, then

Question 4.
Solution:
Circumference of a wheel = 264 cm
Let d be its diameter, then
πd = 264
=> \(\\ \frac { 22 }{ 7 } d\)
= 264

Question 5.
Solution:
Diameter of the wheel (d) = 77 cm
Circumference = πd

Question 6.
Solution:
Diameter of the wheel = 70 cm
circumference = πd

Hope given RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G

Question 1.
Solution:
(i) \(\\ \frac { 2 }{ 3 } \)
= \(\\ \frac { 2X2 }{ 3X2 } \)
= \(\\ \frac { 4 }{ 6 } \)

Question 2.
Solution:
(i) In \(\\ \frac { 5 }{ 6 } \) and \(\\ \frac { 20 }{ 24 } \)
\(\\ \frac { 5 }{ 6 } \) = \(\\ \frac { 20 }{ 24 } \)

Question 3.
Solution:
Equivalent fraction of \(\\ \frac { 3 }{ 5 } \) having
(i) Denominator = 30 and 30 = 5 x 6

Question 4.
Solution:
(i) Denominator = 54, and 54 = 9 x 6

Question 5.
Solution:
Equivalent fraction of \(\\ \frac { 6 }{ 11 } \) having
(i) Denominator = 77 and 77 = 11 = 7
\(\\ \frac { 6 }{ 11 } \)
= \(\\ \frac { 6X7 }{ 11X7 } \)
= \(\\ \frac { 42 }{ 77 } \)
(ii) Numerator = 60 and 60 = 6 x 10
\(\\ \frac { 6 }{ 11 } \)
= \(\\ \frac { 6X10 }{ 11X10 } \)
= \(\\ \frac { 60 }{ 110 } \)

Question 6.
Solution:
Let \(\\ \frac { 24 }{ 30 } \) = \(\\ \frac { 4 }{ x } \)
In order to get 4, divide 24 by 6,

Question 7.
Solution:
Equivalent fraction of \(\\ \frac { 36 }{ 48 } \), with
(i) Numerator 9 and 9 = 36 + 4
\(\frac { 36 }{ 48 } =\frac { 36\div 4 }{ 48\div 4 } =\frac { 9 }{ 12 } \)
(ii) Denominator = 4 and 4 = 48 ÷ 12
\(\frac { 36 }{ 48 } =\frac { 36\div 12 }{ 48\div 12 } =\frac { 3 }{ 4 } \)

Question 8.
Solution:
Equivalent fraction of \(\\ \frac { 56 }{ 70 } \) with
(i) Numerator 4 and = 56 ÷ 14
\(\frac { 56 }{ 70 } =\frac { 56\div 14 }{ 70\div 14 } =\frac { 4 }{ 5 } \)
(ii) Denominator =10 and 10 = 70 ÷ 7
\(\frac { 56 }{ 70 } =\frac { 56\div 7 }{ 70\div 7 } =\frac { 8 }{ 10 } \)

Question 9.
Solution:
(i) In \(\\ \frac { 9 }{ 15 } \), HCF of 9 and 15 = 3
Now, dividing each term by 3, we get:
\(\frac { 9 }{ 15 } =\frac { 9\div 3 }{ 15\div 3 } =\frac { 3 }{ 5 } \)

Question 10.
Solution:
We know that a fraction is in its simplest form if its HCF of numerator and denominator is 1.

Question 11.
Solution:

Hope given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G

Question 1.
Solution:
We know that, a fraction is proper if its denominator is greater than its numerator. Therefore,
\(\\ \frac { 1 }{ 2 } \), \(\\ \frac { 3 }{ 5 } \) and \(\\ \frac { 10 }{ 11 } \) are proper fractions. Ans.

Question 2.
Solution:
We know that a fraction is improper if its denominator is less than its numerator
Therefore,

are improper fractions. Ans.

Question 3.
Solution:
Six improper fractions with denominator 5 can be

Question 4.
Solution:
Six improper fraction with denominator 13 can be

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Hope given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G

Question 1.
Solution:
(i) \(\\ \frac { 3 }{ 4 } \)
(ii) \(\\ \frac { 1 }{ 4 } \)
(iii) \(\\ \frac { 2 }{ 3 } \)
(iv) \(\\ \frac { 3 }{ 10 } \)
(v) \(\\ \frac { 4 }{ 9 } \)
(vi) \(\\ \frac { 3 }{ 8 } \)

Question 2.
Solution:
In the figure, \(\\ \frac { 4 }{ 9 } \) is shaded

Question 3.
Solution:
In the figure, whole rectangle is not divided into four equal parts.

Question 4.
Solution:
(i) Three-fourths = \(\\ \frac { 3 }{ 4 } \)
(ii) Four-sevenths = \(\\ \frac { 4 }{ 7 } \)
(iii) Two-fifths = \(\\ \frac { 2 }{ 5 } \)
(iv) Three-tenths = \(\\ \frac { 3 }{ 10 } \)
(v) One-eighth = \(\\ \frac { 1 }{ 8 } \)
(vi) three-tenths = \(\\ \frac { 5 }{ 6 } \)
(vii) five-sixths = \(\\ \frac { 8 }{ 9 } \)
(vii) seven-twelfths = \(\\ \frac { 7 }{ 12 } \)

Question 5.
Solution:
(i) In \(\\ \frac { 4 }{ 9 } \), numerator is 4 and denominator is 9.
(ii) In \(\\ \frac { 6 }{ 11 } \), numerator is 6 and denominator is 11.
(iii) In \(\\ \frac { 8 }{ 15 } \), numerator is 8 and denominator is 15.
(iv) In \(\\ \frac { 12 }{ 17 } \), numerator is 12 and denominator is 17.
(v) \(\\ \frac { 5 }{ 1 } \) , numerator is 5 and denominator is 1.

Question 6.
Solution:
(z) Numerator = 3, Denominator = 8, then fraction = \(\\ \frac { 3 }{ 8 } \).
(ii) Numerator = 5, Denominator = 12, then fraction = \(\\ \frac { 5 }{ 12 } \)
(iii) Numerator = 7, Denominator = 16, then fraction = \(\\ \frac { 7 }{ 16 } \).
(iv) Numerator = 8, Denominator = 15, then fraction = \(\\ \frac { 8 }{ 15 } \)

Question 7.
Solution:
(i) \(\\ \frac { 2 }{ 3 } \) = two-thirds
(ii) \(\\ \frac { 4 }{ 9 } \) = four-ninths
(iii) \(\\ \frac { 2 }{ 5 } \) = two-fifths
(iv) \(\\ \frac { 7 }{ 10 } \) = seven-tenths
(v) \(\\ \frac { 1 }{ 3 } \) = one-thirds
(vi) \(\\ \frac { 3 }{ 4 } \) = three-fourth
(vii) \(\\ \frac { 3 }{ 8 } \) = three-eighths
(viii) \(\\ \frac { 9 }{ 14 } \) = nine-fourteenths
(ix) \(\\ \frac { 5 }{ 11 } \) = five-elevanths
(x) \(\\ \frac { 6 }{ 15 } \) = six-fifteenths

Question 8.
Solution:
24 minutes is the fraction of 1 hour i.e.,
60 minutes = \(\\ \frac { 24 }{ 60 } \)

Question 9.
Solution:
Natural number between 2 to 10 are 2, 3, 4, 5, 6, 7, 8, 9, 10 = 9
Out of these prime number are 2, 3, 5, 7 = 4
Fraction = \(\\ \frac { 4 }{ 9 } \)

Question 10.
Solution:
(i) \(\\ \frac { 2 }{ 3 } \) of 15 pens = \(\\ \frac { 2 }{ 3 } \) x 15 = 2 x 5 = 10 pens.
(ii) \(\\ \frac { 2 }{ 3 } \) of 27 balls = \(\\ \frac { 2 }{ 3 } \) x 27 = 2 x 9 = 18 balls.
(iii) \(\\ \frac { 2 }{ 3 } \) of 36 balloons = \(\\ \frac { 2 }{ 3 } \) x 36 = 2 x 12 = 24 balloons. Ans.

Question 11.
Solution:
(i) \(\\ \frac { 3 }{ 4 } \) of 16 cups = \(\\ \frac { 3 }{ 4 } \) x 16 = 3 x 4
= 12 cups.
(ii) \(\\ \frac { 3 }{ 4 } \) of 28 rackets = \(\\ \frac { 3 }{ 4 } \) x 28 = 3 x 7
= 21 rackets.
(iii) \(\\ \frac { 3 }{ 4 } \) of 32 books = \(\\ \frac { 3 }{ 4 } \) x 32 = 3 x 8
= 24 books. Ans.

Question 12.
Solution:
Total number of pencils Neelam has = 25
No. of pencils given to Meena
= \(\\ \frac { 4 }{ 5 } \) of 25
= \(\\ \frac { 4 }{ 5 } \) x 25 – 20
No. of pencils left with Neelam = 25 – 20 = 5

Question 13.
Solution:
(i) \(\\ \frac { 3 }{ 8 } \)
Take a line segment OA = one unit of length
Divide it into 8 equal parts and take 3 parts at P, then P represents \(\\ \frac { 3 }{ 8 } \).

(ii) \(\\ \frac { 5 }{ 9 } \)
(a) Take a line segment OA = one unit of length.
(b) Divide it into nine equal parts and take 5 parts at P, then P represents \(\\ \frac { 5 }{ 9 } \).

(iii) \(\\ \frac { 4 }{ 7 } \)
(a) Take a line segment OA = one unit of length.
(b) Divide it into 7 equal parts and take 4 parts at P then P represents \(\\ \frac { 4 }{ 7 } \).

(iv) \(\\ \frac { 2 }{ 5 } \)
(a) Take a line segment OA = 1 unit of length.
(b) Divide it with 5 equal parts and take 2 parts and P then P represents \(\\ \frac { 2 }{ 5 } \).

(v) \(\\ \frac { 1 }{ 4 } \)
(a) Take a line segment OA = 1 unit of length.
(b) Divide it with 4 equal parts and take 1 parts and P then P represents \(\\ \frac { 1 }{ 4 } \).

Hope given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4F

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4F.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4A
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4B
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4C
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4D
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4E
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4F

OBJECTIVE QUESTIONS
Tick the correct answer in each of the following :

Question 1.
Solution:
(b) Because – 4 < – 3.

Question 2.
Solution:
Because – 3 – 2 = – 5.

Question 3.
Solution:
(c) Because 4 + ( – 5) = – 1.

Question 4.
Solution:
(a) Because – 7 – 2 = – 9.

Question 5.
Solution:
(b) Because 7 + | – 3| = 7 + 3 = 10.

Question 6.
Solution:
(c) Because – 42 + ( – 35) = – 42 – 35 = – 77.

Question 7.
Solution:
(b) Because ( – 37) + 6 = – 31.

Question 8.
Solution:
(c) Because 49 + ( – 27) = 49 – 27 = 22.

Question 9.
Solution:
(c) Because successor of – 18 = – 18 + 1 = – 17.

Question 10.
Solution:
(b) Because predecessor of – 16 is = – 16 – 1 = – 17.

Question 11.
Solution:
(a) Because additive inverse of – 5 is = – ( – 5) = 5.

Question 12.
Solution:
(b) Because – 12 – ( – 5) = – 12 + 5 = – 7

Question 13.
Solution:
(b) Because 5 – ( – 8) = 5 + 8 = 13.

Question 14.
Solution:
(c) Because other – 25 – 30 = – 55.

Question 15.
Solution:
(a) Because other 20 – ( – 5) = 20 + 5 = 25.

Question 16.
Solution:
(b) Because other – 13 – 8 = – 21.

Question 17.
Solution:
(b) Because 0 – ( – 8) = 0 + 8 = 8

Question 18.
Solution:
(c) Because 8 + ( – 8) = 8 – 8 = 0.

Question 19.
Solution:
(c)Because- 6 + 4 – ( – 3) = – 6 + 4 + 3 = 7 – 6 = 1.

Question 20.
Solution:
(c) Because 6 – ( – 4) = 6 + 4 = 10.

Question 21.
Solution:
(a) Because ( – 7) + ( – 9) + 12 + ( – 16) = – 7 – 9 + 12 – 16 = – 32 + 12 = – 20.

Question 22.
Solution:
(c) Because – 4 – (8) = – 4 – 8 = – 12.

Question 23.
Solution:
(c) Because – 6 – ( – 9) = – 6 + 9 = 3.

Question 24.
Solution:
(c) Because 10 – ( – 5) = 10 + 5 = 15.

Question 25.
Solution:
(b) Because ( – 6) x 9 = 54.

Question 26.
Solution:
(a) Because ( – 9) x 6 + ( – 9) x 4
= – 54 – 36 = – 90.

Question 27.
Solution:
(b) Because 36 + ( – 9) = \(\\ \frac { 36 }{ -9 } \) = – 4.

Hope given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4E

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4E.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4A
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4B
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4C
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4D
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4E
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4F

Question 1.
Solution:
(i) 85 ÷ ( – 17) = \(\\ \frac { 85 }{ -17 } \) = – 5
(ii) ( – 72) ÷ 18 = \(\\ \frac { -72 }{ 18 } \) = – 4
(iii) ( – 80) ÷ 16 = \(\\ \frac { -80 }{ 16 } \) = – 5
(iv) ( – 121) ÷ 11 = \(\\ \frac { -121 }{ 11 } \) = – 11
(v) 108 ÷ ( – 12) = \(\\ \frac { 108 }{ -12 } \) = – 9
(vi) ( – 161) ÷ 23 = \(\\ \frac { -161 }{ 23 } \) = – 7
(vii) ( – 76) ÷ ( – 19) = \(\\ \frac { -76 }{ -19 } \) = 4
(viii) ( – 147) + ( – 21) = \(\\ \frac { -147 }{ -21 } \) = 7
(ix) ( – 639) ÷ ( – 71) = \(\\ \frac { -639 }{ -71 } \) = 9
(x) ( – 15625) ÷ ( – 125) = \(\\ \frac { -15625 }{ -125 } \)

(xi) 2067 ÷ ( – 1) = \(\\ \frac { 2067 }{ -1 } \) = – 2067
(xii) 1765 ÷ ( – 1765) = \(\\ \frac { 1765 }{ -1765 } \) = – 1
(xiii) 0 ÷ ( – 278) = \(\\ \frac { 0 }{ -278 } \) = 0
(xiv) 3000 ÷ ( – 100) = \(\\ \frac { 3000 }{ -100 } \) = – 30

Question 2.
Solution:
(i) 80 ÷ (…..) = – 5
Let 80 ÷ a = – 5
then, a = 80 ÷ ( – 5) = – 16
80 ÷ ( – 16) = – 5
(ii) – 84 + (…..) = – 7
Let – 84 ÷ a = – 7
then a = \(\\ \frac { -84 }{ -7 } \) = 12s
– 84 ÷ 12 = – 7
(iii)(….) ÷ ( – 5) = 25
Let a + ( – 5) = 25
a = 25 x ( – 5) = – 125
( – 125) ÷ ( – 5) = 25
(iv)(……) ÷ 372 = 0
Let a ÷ 372 = 0
Then a = 6 x 372 = 0
(0) ÷ 372 = 0
(v)(….) ÷ 1 = – 186
Let a ÷ 1 = – 186
Then a = – 186 x 1 = – 186
( – 186) ÷ 1 = – 186
(vi)(…..) ÷ 17 = – 2
Let a ÷ 17 = – 2
Then a = – 2 x 17 = – 34
( – 34) ÷ 17 = – 2
(vii) (….) ÷ 165 = – 1
Let a ÷ 165 = – 1
Then a = – 1 x 165 = – 165
( – 165) ÷ 165 = – 1
(viii) (….) + ( – 1) = 73
Let a ÷ ( – 1) = 73
Then a = 73 ( – 1) = – 73
( – 73) + ( – 1) = 73
(ix) 1 ÷ (…..) = – 1
Let 1 ÷ (a) = – 1
Then a = – 1 x 1 = – 1
1 ÷ ( – 1) = – 1 Ans.

Question 3.
Solution:
(i) True : as if zero is divided by any non-zero integer, then quotient is always zero.
(ii) False : As division by zero is not admissible.
(iii) True : As dividing by one integer by another having opposite signs is negative.
(iv) False : As dividing one integer by another having the same signs is positive not negative.
(v) True : As dividing one integer by another with same sign is always positive.
(vi) True : As dividing one integer by another having opposite signs is always negative.
(vii) True : As dividing one integer by another having opposite signs is always negative.
(viii) True : As dividing one integer by another having opposite signs is always negative.
(ix) False : As dividing one integer by another having same signs is always positive not negative

 

Hope given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 21 Concept of Perimeter and Area Ex 21A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21A

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21A
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21B
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21C
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21D
• RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21E

Question 1.
Solution:
(i) Length (l) = 16.8 cm
Breadth (b) = 6.2 cm
Perimeter = 2 (l + b)
= 2 (16.8 + 6.2) cm
= 2 x 23
= 46 cm


= 30m 6 dm

Question 2.
Solution:
Length of rectangular field (l) = 62 m
and breadth (b) = 33 m

Question 3.
Solution:
Perimeter of field = 128 m
Length + Breadth = \(\\ \frac { 128 }{ 2 } \) = 64 m
Ratio in length and breadth = 5:3
Let length (l) = 5x
Then breadth = 3x
5x + 3x = 64
=> 5x = 64
=> x = \(\\ \frac { 64 }{ 8 } \) = 8
Length of the field = 5x = 5 x 8 = 40m
and breadth = 3x = 3 x 8 = 24m

Question 4.
Solution:
Cost of fencing a rectangular field
= Rs. 18 per m
Total cost = Rs. 1980

Question 5.
Solution:
Total cost of fencing a rectangular field
= Rs 3300
Rate of fencing = Rs 25 per m

Question 6.
Solution:
(i) Side of square = 3.8 cm
Perimeter = 4 x side
= 4 x 3.8 cm
= 15.2 cm
(ii) Side of a square = 4.6 m
Perimeter = 4 x side
= 4 x 4.6 m
= 18.4 m
(iii) Side of a square = 2 m 5 dm
= 2.5 m
Perimeter = 4 x side
= 4 x 2.5 m
= 10 m

Question 7.
Solution:
Total cost of fencing a square field = Rs. 4480
Rate of fencing = Rs. 35 per m

Question 8.
Solution:
Side of a square field (a) = 21 m
Perimeter = 4a = 4 x 21 = 84m
Perimeter of rectangular field = 84 m
Ratio in length and breadth = 4 : 3
Let length (l) = 4x
and breadth (b) = 3x
Perimeter = 2 (l + b)

Question 9.
Solution:
(i) Sides of a triangle are 7.8 cm, 6.5 cm and 5.9 cm

Question 10.
Solution:
(i) Each side of a regular pentagon
= 8 cm
Perimeter = 5 x Side
= 5 x 8
= 40 cm
(ii) Each side of an octagon = 4.5 cm
Perimeter = 8 x Side
= 8 x 4.5
= 36 cm
(iii) Each side of a regular decagon = 3.6 cm
Perimeter = 10 x Side
= 10 x 3.6
= 36 cm

Question 11.
Solution:
We know that perimeter of a closed figure or a polygon = Sum of its sides
(i) In the figure, sides of a quadrilateral are 45 cm, 35 cm, 27 cm, 35 cm
Its perimeter = Sum of its sides
= (45 + 35 + 27 + 35) cm
= 142 cm
(ii) Sides of a quadrilateral (rhombus) are 18 cm, 18 cm, 18 cm, 18 cm
i.e., each side = 18 cm Perimeter
= 4 x Side
= 4 x 18
= 72 cm
(iii) Sides of the polygon given are 16 cm, 4 cm, 12 cm, 12 cm, 4 cm, 16 cm and 8 cm
Its perimeter = Sum of its sides
= (16 + 4 + 12 + 12 + 4 + 16 + 8) cm
= 72 cm

 

Hope given RS Aggarwal Solutions Class 6 Chapter 21 Concept of Perimeter and Area Ex 21A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 20 Two-Dimensional Reflection Symmetry (Linear Symmetry) Ex 20

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 20 Two-Dimensional Reflection Symmetry (Linear Symmetry) Ex 20

Mark against the correct answer in each of Q. 1 to Q. 8.

Question 1.
Solution:
(d)∵ A square has four lines of symmetry, two diagonals and two lines joining the mid-points of opposite sides.

Question 2.
Solution:
(c) ∵ A rectangle has two lines of symmetry, each one of which being the line joining of mid-points of opposite sides.

Question 3.
Solution:
(b) ∵ A rhombus has two lines of symmetry namely two diagonals.

Question 4.
Solution:
(d) Each diameter of a circle is its line of symmetry which are unlimited numbers.

Question 5.
Solution:
(a) ∵ A scalene triangle has no line of symmetry.

Question 6.
Solution:
(a) ∵ It is a figure of kite ; so AC is its line of symmetry.

Question 7.
Solution:
(c) ∵ Letter O has two lines of symmetry, one vertical and second horizontal

Question 8.
Solution:
(a) ∵ Letter Z has no line of symmetry.

Question 9.
Solution:

Question 10.
Solution:
(i) True (T) Parallelogram has no line of symmetry.
(ii) True (T) Bisector of an angle of*equal sides is the line of symmetry.
(iii) True (T)  Perpendiculars from each vertices’s of an equilateral-triangle to its opposite side is its line of symmetry.
(iv) False (F) Rhombus has two lines of symmetry which are its -diagonals.
(v) True (T) Square has four lines of symmetry, two diagonals and two perpendicular bisectors of opposite sides.
(vi) True (T) A rectangle has two lines of symmetry which are the perpendicular bisectors of its opposite sides.
(vii) True (T) H, I, O and X has two lines of symmetry.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 20 Two-Dimensional Reflection Symmetry (Linear Symmetry) Ex 20 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.