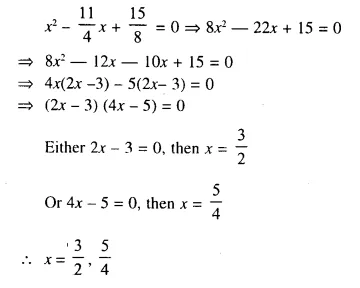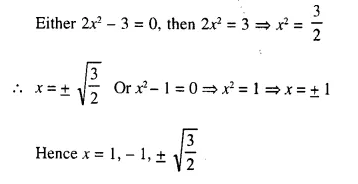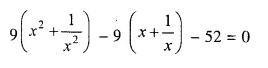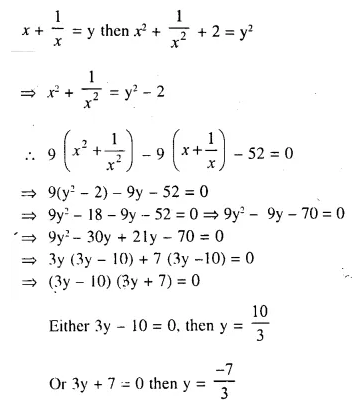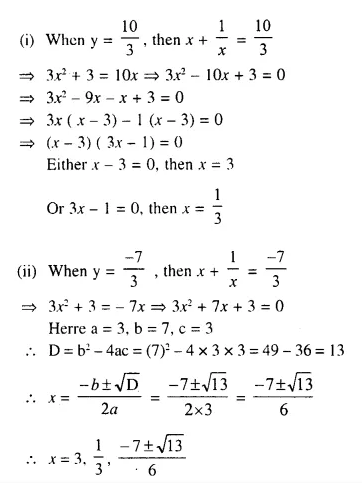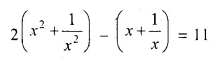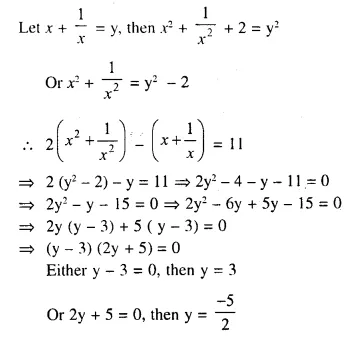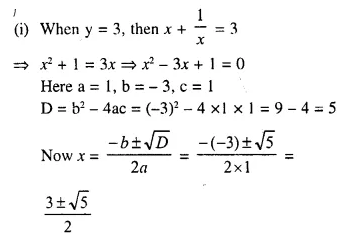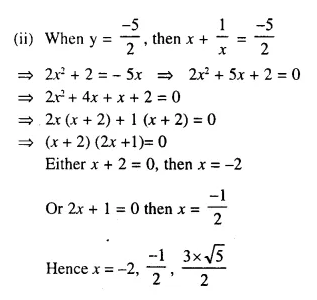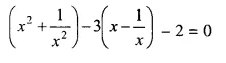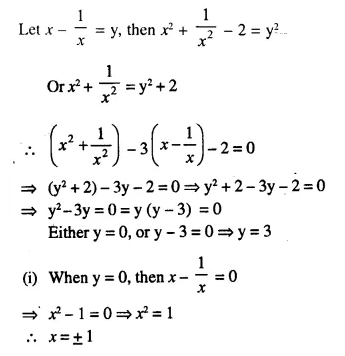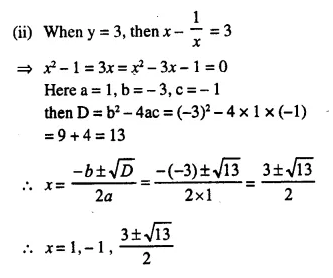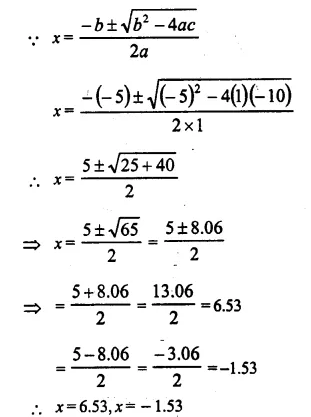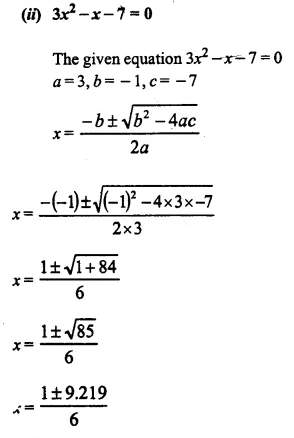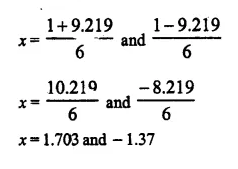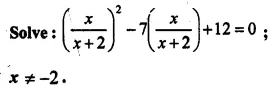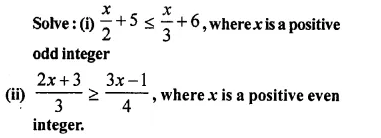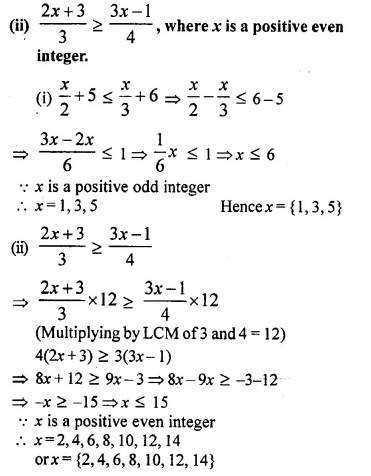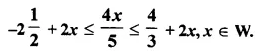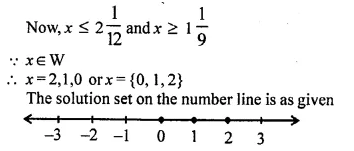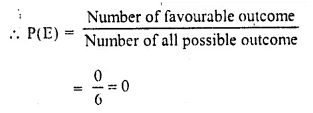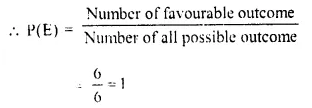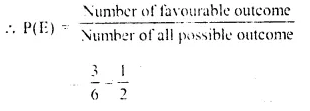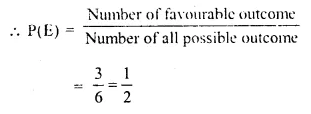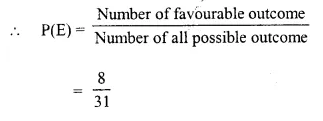Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems (Based on Quadratic Equations) Ex 6B
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6B.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6E
Question 1.
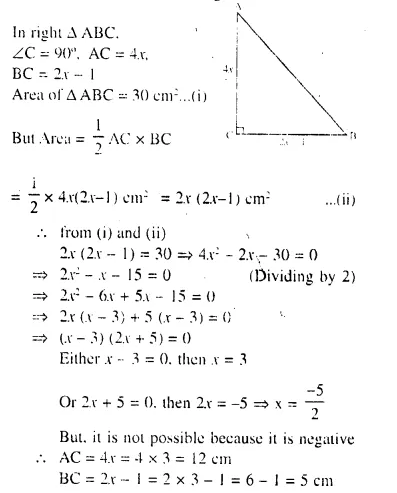
The sides of a right-angled triangle containing the right angle are 4x cm and (2x – 1) cm. If the area of the triangle is 30 cm²; calculate the lengths of its sides
Solution:
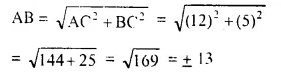
But -13 is not possible.
Sides are 5 cm, 12 cm and 13 cm.
Question 2.
The hypotenuse of a right-angled triangle is 26 cm and the sum of other two sides is 34 cm. Find the lengths of its sides.
Solution:
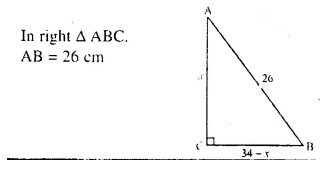
AC + BC = 34 cm
Let AC = x cm Then BC = (34 – x) cm
But AC² + BC² = AB² (By Pythagoras Theorem)
⇒ (x)² + (34 – x)² = (26)²
⇒ x² + 1156 + x² – 68x = 676
⇒ 2x² – 68x + 1156 – 676 = 0
⇒ 2x² – 68x + 480 = 0
⇒ x² – 34x + 240 = 0 (Dividing by 2)
⇒ x² – 24x – 10x + 240 = 0
⇒ x (x – 24) – 10 (x – 24) = 0
⇒ (x – 24) (x- 10) = 0
Either x – 24 = 0, then x = 24
or x – 10 = 0, then x = 10
If one side is 24 cm, then second will be 34 – 24 = 10 cm
If one side is 10 cm, then second side will be 34 – 10 = 24
Sides are 24 cm and 10 cm
Question 3.
The sides of a right-angled triangle are (x – 1) cm, 3x cm and (3x + 1) cm. Find :
(i) The value of x,
(ii) the lengths of its sides,
(iii) its area.
Solution:
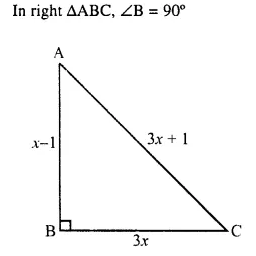
AB = x – 1, BC = 3x and AC = 3x +1
According to Pythagoras Theorem,
AC² = AB² + BC²
⇒ (3x + 1)² = (x – 1)² + (3x)²
⇒ 9x² + 6x + 1 = x² – 2x + 1 + 9x²
⇒ 9x² + 6x + 1 – x² + 2x -1 – 9x² = 0
⇒ – x² + 8x = 0
⇒ x² – 8x = 0
⇒ x (x – 8) = 0
Either x = 0 but it is not possible.
or x – 8 = 0, then x = 8
(i) x = 8
(ii) Side AB = x – 1 = 8 – 1 = 7cm
BC = 3x = 3 x 8 = 24 cm
AC = 3x + 1 = 3 x 8 + 1 = 24 + 1 = 25 cm
(iii) Area = \(\frac { 1 }{ 2 }\) x AB x BC = \(\frac { 1 }{ 2 }\) x 7 x 24 cm² = 84 cm²
Question 4.
The hypotenuse of a right-angled triangle exceeds one side by 1 cm and the other side by 18 cm; find the lengths of the sides of the triangle.
Solution:
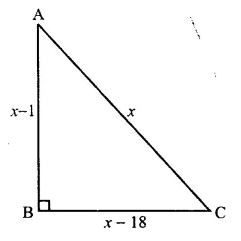
In right triangle ABC, ∠B = 90°
Let hypotenuse AC = x, then AB = x – 1 and BC = x – 18
Now, according to Pythagoras Theorem,
AC² = AB² + BC²
⇒ x² = (x – 1)² + (x – 18)²
⇒ x² = x² – 2x + 1 + x² – 36x + 324
⇒ x² = 2x² – 38x + 325
⇒ 2x² – 38x + 325 – x² = 0
⇒ x² – 38x + 325 = 0
⇒ x² – 13x – 25x + 325 =0
⇒ x (x – 13) – 25 (x – 13) = 0
⇒ (x – 13) (x – 25) = 0
Either x – 13 = 0, then x = 13 But it is not possible.
x – 18 = 13 – 18 = -5 cannot be possible.
or x – 25 = 0, then x = 25
AC = 25,
AB = x – 1 = 25 – 1 = 24
and BC = x – 18 = 25 – 18 = 7
Sides are 25, 24, 7
Question 5.
The diagonal of a rectangle is 60 m more than its shorter side and the larger side is 30 m more than the shorter side. Find the sides of the rectangle.
Solution:
Let shorter side of a rectangle (b) = x m
Longer side (l) = (x + 30) m
and length of diagonal = (x + 60) m
According to the condition,
(Diagonal)² = (Longer side)² + (Shorter side)² (Pythagoras Theorem)
⇒ (x + 60)² = (x + 30)² + x²
⇒ x² + 120x + 3600 = x² + 60x + 900 + x²
⇒ 2x² + 60x + 900 – x² – 120x – 3600 = 0
⇒ x² – 60x – 2700 = 0
⇒ x² – 90x + 30x – 2700 = 0 {-2700 = -90 x 30, -60 = -90 + 30}
⇒ x (x – 90) (x + 30) = 0
Either x – 90 = 0, then x = 90
or x + 30 = 0, then x = -30 but is not possible being negative
Length = x + 30 = 90 + 30 = 120 m
Breadth = x = 90 m
Question 6.
The perimeter of a rectangle is 104 m and its area is 640 m². Find its length and breadth.
Solution:
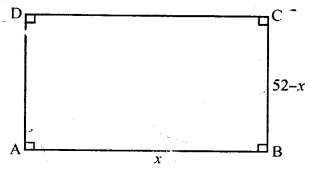
Perimeter = 104 m
⇒ 2 (l + b) = 104 m
l + b = 52 m
Let length of the rectangular plot = x m
Breadth = 52 – x
Area = l x b = x (52 – x)
But area of plot = 640 m²
x (52 – x) = 640
⇒ 52x – x² = 640
⇒ – x² + 52x – 640 = 0
⇒ x² – 52x + 640 = 0
⇒ x² – 20x – 32x + 640 = 0
⇒ x (x – 20) – 32 (x – 20) = 0
⇒ (x – 20) (x – 32) = 0
Either x – 20 = 0, then x = 20
or x – 32 = 0, then x = 32
Length = 32 m
and breadth = 52 – 32 = 20 m
Question 7.
A footpath of uniform width runs round the inside of a rectangular field 32 m long and 24 m wide. If the path occupies 208 m², find the width of the footpath.
Solution:
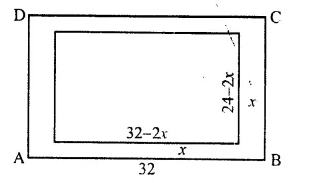
Length of field = 32m
and width = 24 m
Area of the field = 32 x 24 m² = 768m²
Area of path = 208 m²
Let width of path = x m
Inner length = 32 – 2x
and inner width = 24 – 2x
and inner area = (32 – 2x) (24 – 2x) m²
Area of path = 768 – (32 – 2x) (24 – 2x)
Now, according to the condition,
768 – (32 – 2x) (24 – 2x) = 208
⇒ 768 – (768 – 64x – 48x + 4x²) = 208
⇒ 768 – 768 + 64x + 48x – 4x² = 208
⇒ -4x² + 112x – 208 = 0
Dividing by -4 , we get:
⇒ x² – 28x + 52 = 0
⇒ x² – 26x – 2x + 52 = 0
⇒ x (x – 26) – 2 (x – 26) = 0
⇒ (x – 26 ) (x – 2) = 0
Either x – 26 = 0 , then x = 26 But it is not possible.
or x – 2 – 0 then x = 2
Width of path = 2 m
Question 8.
Two squares have sides x cm and (x + 4 ) cm. The sum of their areas is 656 sq. cm. Express this as an algebraic equation in x and solve the equation to find the sides of the squares.
Solution:
Side of first square = x cm
Area = x² cm²
Side of second square = (x + 4) cm
Area = (x + 4)² cm²
Sum of squares = 656 cm²
⇒ x² + (x + 4)² = 656
⇒ x² + x² + 8x + 16 – 656 = 0
⇒ 2x² + 8x – 640 = 0
⇒ x² + 4x- 320 = 0 (Dividing by 2)
⇒ x² + 20x – 16x – 320 = 0
⇒ x (x + 20) – 16 (x + 20) = 0
⇒ (x + 20) (x – 16) = 0
Either x + 20 = 0, then x = – 20 But it is not possible.
or x – 16 = 0, then x = 16
Side of first square = 16 cm
and side of second square = 16 + 4 = 20 cm
Question 9.
The dimensions of a rectangular field are 50 m by 40 m. A flower bed is prepared inside this field leaving a gravel path of uniform width all around the flower bed. The total cost of laying the flower bed and gravelling the path at Rs. 30 and Rs. 20 per square metre, respectively, is Rs. 52,000. Find the width of the gravel path.
Solution:
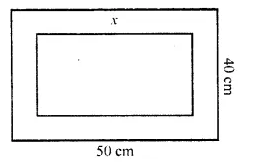
Length of the field (l) = 50 m
and width (b) = 40 m
Area of rectangular field = l x b = 50 x 40 = 2000 m²
Let width of gravel path be x
Then inner length = 50 – 2x
and width = 40 – 2x
Area of inner flower bed = (50 – 2x) (40 – 2x)
= 2000 – 80x – 100x + 4x² = 4x² – 180x + 2000 sq m
and Area of gravel path = 2000 – (4x² – 180x + 2000)
= 2000 – 4x² + 180x – 2000 = -4x² + 180x
Now rate of gravelling = Rs. 20 per m²
and rate of laying flowers = Rs. 30 per m²
and total cost = Rs. 52000
According to the condition,
(-4x² + 180x) x 20 + (4x² -180x + 2000) x 30 = 52000
-80x² + 3600x + 120x² – 5400x + 60000 = 52000
⇒ 40x² – 1800x – 60000 – 52000 = 0
⇒ 40x² – 1800x + 8000 = 0
⇒ x² – 45x + 200 = 0 (Dividing by 40)
⇒ x² – 40x – 5x + 200 = 0 (200= -40 x (- 5), -45 = -40 – 5)
⇒ x (x – 40) – 5 (x – 40) = 0
⇒ (x – 40) (x – 5) = 0
Either x – 40 = 0, then x = 40
or x – 5 = 0, then x = 5
But x = 40 is not possible
x = 5
Width of gravel path = 5 m
Question 10.
An area is paved with square tiles of a certain size and the number required is 128. If the tiles had been 2 cm smaller each way, 200 tiles would have been needed to pave the same area. Find the size of the larger tiles.
Solution:
No. of square tiles = 128
Let the size of square tile = x cm
Area of one square tile = x² cm²
Area of total tiles = 128 x x² = 128x² cm²
If the size of square tile is reduced by 2 cm
Then size of square tile = (x – 2) cm
Area of one tile = (x – 2)² cm²
Now number of tiles will be = 200
⇒ 128x² = 200 (x – 2)²
⇒128x² = 200x² – 800x + 800
⇒ 200x² – 800x + 800 – 128x² = 0
⇒ 72x² – 800x + 800 = 0
⇒ 9x² – 100x + 100 = 0 (Dividing by 8)
⇒ 9x² – 90x – 10x + 100 = 0
⇒ 9x (x – 10) – 10 (x – 10) = 0
⇒ (x – 10) (9x – 10) = 0
Either x- 10 = 0, then x = 10
or 9x – 10 = 0, then 9x = 10 ⇒ x = \(\frac { 10 }{ 9 }\)
Which is not possible x = 10
Size of square tile = 10 cm
Question 11.
A farmer has 70 m. of fencing, with which he encloses three sides of a rectangular sheep pen; the fourth side being a wall. If the area of the pen is 600 sq. m, find the length of its shorter side.
Solution:
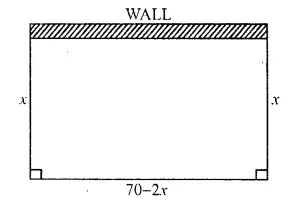
Length of fencing = 70 m.
Area of rectangular pen = 600 sq. m
(i) Let the length of shorter side = x m
Length of larger side = 70 – 2x
Area of rectangular pen = x ( 70 – 2x) ….(ii)
From (i) and (ii)
x (70 – 2x) = 600
⇒ 70x – 2x² = 600
⇒ -2x² + 70x – 600 = 0
⇒ x² – 35x + 300 = 0 (Dividing by -2)
⇒ x² – 15x – 20x + 300 = 0
⇒ x (x – 15) – 20 (x – 15) = 0
⇒ (x – 15) (x – 20) = 0
Either x – 15 = 0 then x = 15
or x – 20 = 0 then x = 20
Shorter side = 15 m
Question 12.
A square lawn is bounded on three sides by a path 4 m wide. If the area of the path is \(\frac { 7 }{ 8 }\) that of the lawn, find the dimensions of the lawn.
Solution:
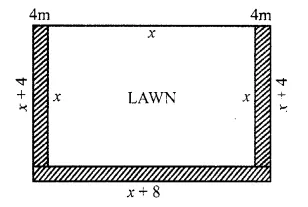
Let the side of square lawn = x m
Area of lawn = x² m²
Width of path = 4 m.
Area of path = 4 x x + 4 x x + (x + 8) x 4 = 8x + 4x + 32 = 12x + 32
But 12x + 32 = \(\frac { 7 }{ 8 }\) x2
⇒ 96x + 256 = 7x²
⇒ 7x² – 96x – 256 = 0
⇒ 7x² – 112x + 16x – 256 = 0
⇒ 7x (x – 16) + 16 (x – 16) = 0
⇒ (x – 16 ) (7x + 16) = 0
Either x – 16 = 0, then x = 16
0r 7x + 16 = 0, then 7x = -16 ⇒ x = \(\frac { -16 }{ 7 }\)
But it is not possible.
Side of square lawn = 16 m
Question 13.
The area of a big rectangular room is 300 m². If the length were decreased by 5m and the breadth increased by 5 m; the area would be unaltered. Find the length of the room.
Solution:
Area of big rectangular room = 300 m²
Let length of the room = x m.
Width = m
In second case,
Length = (x – 5) m
and width = (\(\frac { 300 }{ x }\) + 5) m
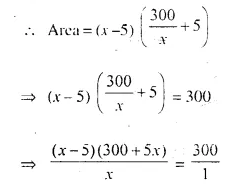
⇒ (x – 5) ( 300 + 5x) = 300x
⇒ 300x + 5x² – 1500 – 25x = 300x
⇒ 5x² + 300x – 25x – 300x – 1500 = 0
⇒ 5x² – 25x – 1500 = 0
⇒ x² – 5x – 300 = 0 (Dividing by 5)
⇒ x² – 20x + 15x – 300 = 0
⇒ x (x – 20) + 15 (x – 20) = 0
⇒ (x – 20) (x + 15) = 0
Either x – 20 – 0 then x = 20
or x + 15 = 0 then x = -15 But it is not possible.
Length of room = 20 m
and width = \(\frac { 300 }{ 20 }\) = 15 m
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.