Tag: Class 7 Maths RS Aggarwal Solutions

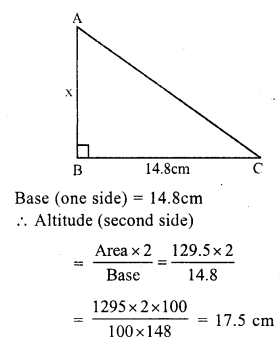
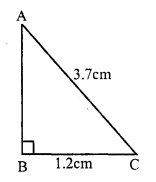
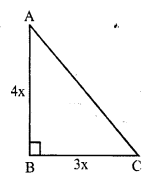
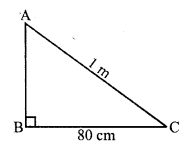
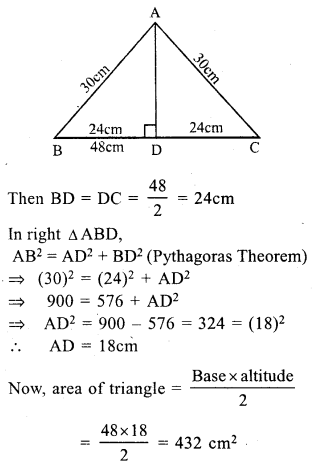
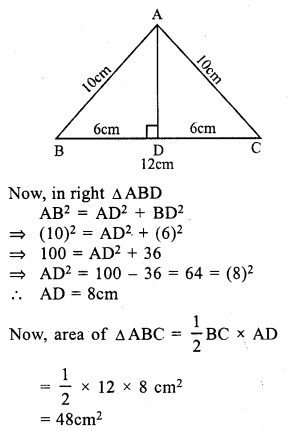
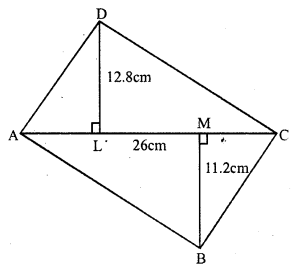
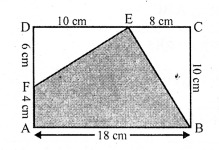
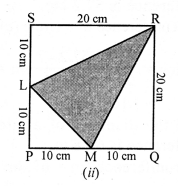
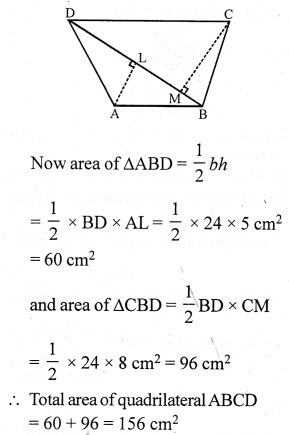
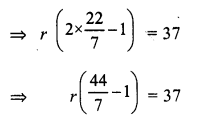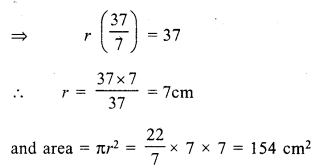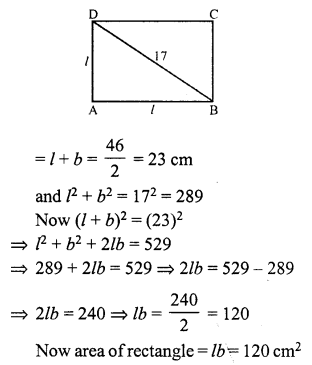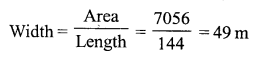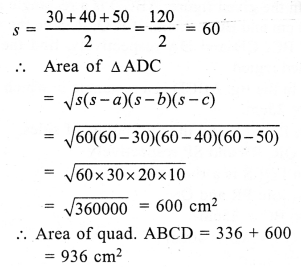RS Aggarwal Class 7 Solutions Chapter 18 Reflection and Rotational Symmetry Ex 18B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18A
• RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18B

Question 1.
Solution:
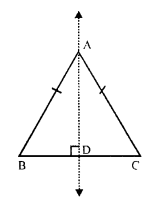
(a) An equilateral triangle has three lines of symmetry which are the angle bisectors.
(b) It has three order of rotational symmetry.

Question 2.
Solution:
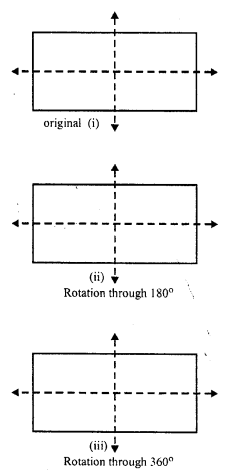
The rectangle should be rotated through 180° and 360° to be in symmetrical position with the original position as given below :

Question 3.
Solution:
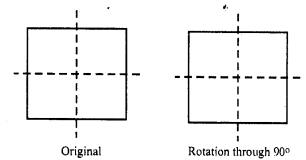
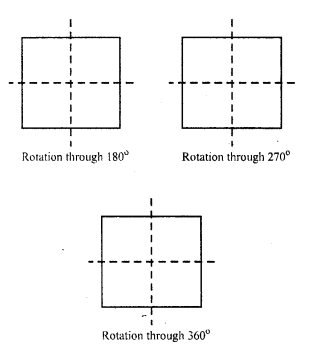
A square has four orders of rotational symmetry and angles through which the rotational symmetry are 90°, 180°, 270° and 360° as given below:

Question 4.
Solution:
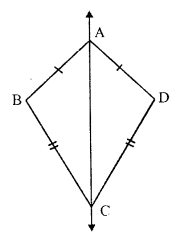
(i) A rhombus has two lines of symmetry which are its diagonal.
(ii) Order of rotational symmetry of a rhombus is not possible. Therefore it has no rotational symmetry.

Question 5.
Solution:
Three letters of the English Alphabet which have two lines of symmetry and rotational symmetry of order 2 are H, I and N.

Question 6.
Solution:
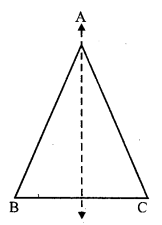
The figure which has only on line of symmetry but no rotational symmetry order is an isosceles triangle.

Question 7.
Solution:
No, only isosceles trapezium has a line of symmetry but not every trapezium.

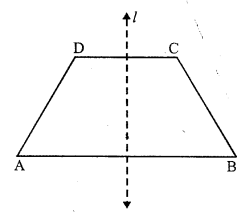
Question 8.
Solution:
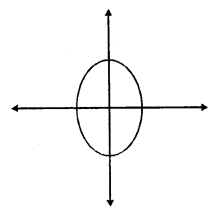
The line of symmetry of a semicircle is the perpendicular bisector of the diameter No, it has not any rotational symmetry.

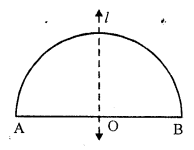
Question 9.
Solution:
A scalene triangle has neither any line of symmetry nor a rotational symmetry.

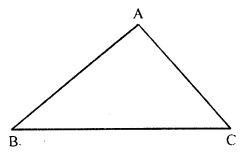
Question 10.
Solution:
In the given figure, the line of symmetry has been drawn which is one. There is no rotational symmetry of this figure.

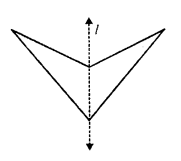
Question 11.
Solution:
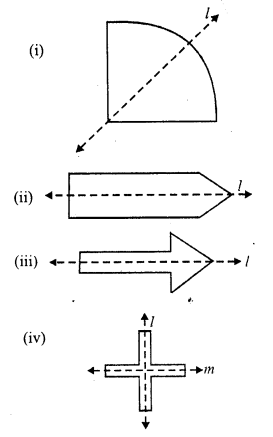
(i) The given figure has two lines of symmetry which has been drawn.

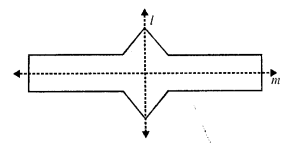
(ii) It has three orders of the rotational symmetry which are 90°, 270° and 360°.

Question 12.
Solution:
There is one letter of the English Alphabet Z which has no line of symmetry but it has order two of rotational symmetry of 180° and 360°.

Hope given RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 18 Reflection and Rotational Symmetry Ex 18A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18A
• RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18B

Tick (✓) the correct answer in each of Q.1 to Q.9
Question 1.
Solution:
(a) A scalene triangle has no line of symmetry

Question 2.
Solution:
(c) A rectangle has two lines of symmetry which are the lines joining the mid points of opposite sides.

Question 3.
Solution:
(d) A square has four lines of symmetry which are two diagonal and two the lines joining the mid points of opposite sides.

Question 4.
Solution:
(b) A rhombus has two lines of symmetry which are the diagonals.

Question 5.
Solution:
(d) A circle has an unlimited number of lines of symmetry as its lines of symmetry is its diameter which are infinite in number.

Question 6.
Solution:
(a) ∆ABC in which AB = AC, is an isosceles triangle and AD ⊥ BC.

AD is the line of symmetry

Question 7.
Solution:
(a) ABCD is a kite in which AB = AD and BC = DC

Its line of symmetry will be one diagonal AC.

Question 8.
Solution:
(c) The letter O of the English Alphabet has two lines of symmetry as shown here in the figure.

Question 9.
Solution:
(a) The letter Z of the English Alphabet has no line of symmetry.

Question 10.
Solution:
The line/lines of symmetry have been drawn as given below :

Question 11.
Solution:
(i) True
(ii) True
(iii) True : The bisectors of angles are its lines of symmetry.
(iv) False : A rhombus has two lines of symmetry which are its diagonals.
(v) True : The two diagonals and two perpendicular bisector of its opposite sides are the lines of symmetry.
(vi) True : The perpendicular bisectors of opposite sides are the two lines of symmetry of the rectangle.
(vii) True : Each of the English Alphabet H, I, O and X has two lines of symmetry.

Hope given RS Aggarwal Solutions Class 7 Chapter 18 Reflection and Rotational Symmetry Ex 18A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 17 Constructions CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 17 Constructions CCE Test Paper.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17A
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17B
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17C
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions CCE Test Paper

Question 1.
Solution:
Given, ∠ABO = 60°
∠CDO = 40°
⇒ ∠ABO = ∠BOC = 60° [alternate angles]

Question 2.
Solution:
Here, AB || EC
∠BAC = ∠ACE = 70° (alternate angles)
⇒ ∠BCA = 180° – ∠BAC
⇒ ∠BCA = 180°- 120°
⇒ ∠BCA = 60°

Question 3.
Solution:
(i) ∠AOC = ∠BOD = 50° [vertically opposite angles]
(ii) ∠BOC = 180° – 50° (linear pair)
= 130°

Question 4.
Solution:
Here, 3x + 20 + 2x – 10 = 180
⇒ 5x + 10 = 180
⇒ 5x = 170
⇒ x = 34
∠AOC = (3 x 34 + 20)° = (102 + 20)° = 122°
∠BOC = (2 x 34 – 10)° = (68 – 10)° = 58°

Question 5.
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180°
⇒ 65° + 45° + ∠C= 180°
⇒ ∠C = 180° – 110° = 90°

Question 6.
Solution:
Let x = 2k and y = 3k
2k + 3k = 120° [Exterior angle property]
⇒ 5k = 120°
⇒ k = 24°
x = 2 x 24° = 48° and y = 3 x 24° = 72°
In ∆ABC :
∠A + ∠B + ∠C = 180°
⇒ 48° + 72° + ∠C = 180°
⇒ ∠C = 180°- 120°
⇒ ∠C = 60°
z = 60°

Question 7.
Solution:
Since it is a right triangle, by using the Pythagoras theorem:
Length of the hypotenuse = √(8² + 15²) = √(64 + 225) = √289 = ± 17 cm
The length of the side can not be negative.

Question 8.
Solution:
Given:
∠BAD = ∠DAC …..(i)
To show that ∆ABC is isosceles, we should show that ∠B = ∠C
AD ⊥ BC, ∠ADB = ∠ADC = 90°
∠ADC = ∠ADB
∠BAD + ∠ABD = ∠DAC + ∠ACD (exterior angle property)
∠DAC + ∠ABD = ∠DAC + ∠ ACD [from equation (i)]
∠ABD = ∠ACD
This is because opposite angles of a triangle ∆ABC are equal.
Hence, ∆ABC is an isosceles triangle.

Mark (✓) against the correct answer in each of the following :
Question 9.
Solution:
(c) 145°
The supplement of 35° = 180° – 35° = 145°

Question 10.
Solution:
(d) 124
x° + 56° = 180° (linear pair)
⇒ x = 180° – 56°
⇒ x = 124
x = 124°

Question 11.
Solution:
(c) 65°
∠ACD = 125°
∠ACD = ∠CAB + ∠ABC (the exterior angles are equal to the sum of its interior opposite angles)
∠ABC = 125° – 60° = 65°

Question 12.
Solution:
(c) 105°
∠A + ∠B + ∠C = 180°
⇒ ∠A = 180° – (40° + 35°)
⇒ ∠A = 105°

Question 13.
Solution:
(c) 60°
Given:
2∠A = 3∠B

Question 14.
Solution:
(b) 55°
In ∆ABC :
A + B + C = 180° …(i)
Given, A – B = 33°
A = 33° + B …(ii)
B – C = 18°
C = B + 18° …(iii)
Putting the values of A and B in equation (i):
⇒ B + 33° + B + B – 18° = 180°
⇒ 3B = 180°
⇒ B = 55°

Question 15.
Solution:
(b) 3√2 cm
Here, AB = AC
In right angled isosceles triangle:
BC² = AB² + AC²
⇒ BC² = AB² + AB²
⇒ BC² = 2AB²
⇒ 36 = 2AB²
⇒ AB² = 18
⇒ AB = √18
⇒ AB = 3√2

Question 16.
Solution:
(i) The sum of the angles of a triangle is 180°.
(ii) The sum of any two sides of a triangle is always greater than the third side.
(iii) In ∆ABC, if ∠A = 90°, then BC² = (AB²) + (BC²)
(iv) In ∆ABC :
AB = AC
AD ⊥ BC
Then, BD = DC
This is because in an isosceles triangle, the perpendicular dropped from the vertex joining the equal sides, bisects the base.
(v) In the given figure, side BC of ∆ABC has produced to D and CE || BA.
If ∠ABC = 50°, then ∠ACE = 50°
AB || CE
∠BAC = ∠ACE = 50° (alternate angles)

Question 17.
Solution:
(i) True
(ii) True
(iii) False. Each acute angle of an isosceles right triangle measures 45°.
(iv) True.

Hope given RS Aggarwal Solutions Class 7 Chapter 17 Constructions CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20G

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper

Objective Questions
Mark (✓) against the correct answer in each of the following :
Question 1.
Solution:
(c)
Length of rectangle AB = 16 cm
and diagonal BD = 20 cm

But, in right ∆ABD
BD² = AB² + AD²
⇒ (20)² = (16)² + AD²
⇒ 400 = 256 + AD²
⇒ AD² = 400 – 256 = 144 = (12)²
⇒ AD = 12 cm
Area = l x b = 16 x 12 = 192 cm²

Question 2.
Solution:
(b)
Diagonal of square = 12 cm
Let side = 9
diagonal = √2 a

Question 3.
Solution:
(b)
Area = 200 cm²
side = √200 =√2 x 10
and diagonal = √2 a = √2 x √2 x 10 = 20

Question 4.
Solution:
(a)
Area of square = 0.5 hectare = 0.5 x 10000 = 5000 m²
= √10000 = 100 m

Question 5.
Solution:
(c)
Perimeter of rectangle = 240m
l + b = \(\frac { 240 }{ 2 }\) = 120 m
Let breadth = x, then length = 3x .
3x + x = 120
⇒ 4x = 120
⇒ x = 30
Length = 3x = 3 x 30 = 90 m

Question 6.
Solution:
Answer = (d)
Let original side of square = x
area = x²

Question 7.
Solution:
(b)
Let side of square = a
Then its diagonal = √2 a
Now, area of square = a²
and area of square on diagonal = (√2 a)² = 2a²
Ratio = a² : 2a² = 1 : 2

Question 8.
Solution:
(c)
If perimeters of a square and a rectangle are equal Then the area of the square will be greater than that of a rectangle
A > B

Question 9.
Solution:
(b)
Perimeter of rectangle = 480m

Question 10.
Solution:
(a)
Total cost of carpet = Rs. 6000
Rate per metre = Rs. 50

Question 11.
Solution:
(a)
Sides are 13 cm, 14 cm, 15 cm

Question 12.
Solution:
(b)
Base of triangle = 12 m
and height = 8m
Area= \(\frac { 1 }{ 2 }\) x Base x height
= \(\frac { 1 }{ 2 }\) x 12 x 8 = 48 m²

Question 13.
Solution:
(b)
Let side = a
then area = \(\frac { \surd 3 }{ 4 }\) a²

Question 14.
Solution:
(c)
Side of an equilateral triangle = 8cm

Question 15.
Solution:
(b)
Let a be the side of an equilateral triangle

Question 16.
Solution:
(b)
One side (Base) of parallelogram = 16 cm
and altitude = 4.5 cm
Area = base x altitude = 16 x 4.5 = 72 cm²

Question 17.
Solution:
(b)
Length of diagonals of a rhombus are 24 cm and 18 cm

Question 18.
Solution:
(c)
Let r be the radius of the circle Then
c = 2πr
2πr – r = 37

Question 19.
Solution:
(c) Perimeter of room = 18 m
and height = 3 m
Area of 4 walls = Perimeter x height = 18 x 3 = 54 m²

Question 20.
Solution:
(a) Area of floor = l x b = 14 x 9 = 126 m²
Area of carpet = 126 m²

Question 21.
Solution:
(c)
Perimeter = 46 cm

Question 22.
Solution:
(b)
Ratio in area of two squares = 9 : 1
Let area of bigger square = 9x²
and of smaller square = x²
Side of bigger square = √9x² = 3x
and perimeter = 4 x side = 4 x 3x = 12x
Side of smaller square = √x² = x
Perimeter = 4x
Now ratio in their perimeter = 12x : 4x = 3 : 1

Question 23.
Solution:
(d)
Let the diagonals of two square be 2d and d
Area of bigger square 2 (2d)² = 8d²
and of smaller = 2 (d)² = 2d²
Ratio in their area = \(\frac { 8{ d }^{ 2 } }{ 2{ d }^{ 2 } } =\frac { 4 }{ 1 }\)
= 4 : 1

Question 24.
Solution:
(c)
Side of square = 84 m
Area of square = (84)² = 7056 m²
Area of rectangle = 7056 m²
Length of rectangle = 144 m

Question 25.
Solution:
(d)
Side of a square = a
Area = a²
Side of equilateral triangle = a

Question 26.
Solution:
(a)
Let a be the side of a square
Area = a²
Then area of circle = a²
Let r be the radius

Question 27.
Solution:
(b)
Let each side of an equilateral triangle = a
Then area = \(\frac {\surd 3 }{ 4 }\) a²
Now radius of the circle = a
Then area = πr² = πa²

Question 28.
Solution:
(c)
Area of rhombus = 36 cm²
Length of one diagonal = 6 cm
Length of second diagonal

Question 29.
Solution:
(d)
Area of a rhombus =144 cm²
Let one diagonal (d1) = a
then Second diagonal (d2) = 2a

Larger diagonal = 2a = 2 x 12 = 24 cm

Question 30.
Solution:
(c)
Area of a circle = 24.64 m²

Question 31.
Solution:
(c)
Let original radius = r
Then its area = πr²
Radius of increased circle = r + 1

2r = 7 – 1 = 6
⇒ r = \(\frac { 6 }{ 2 }\) = 3
Radius of original circle = 3 cm

Question 32.
Solution:
(c)
Radius of a circular wheel (r) = 1.75 m

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20F

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper

Question 1.
Solution:
(i) Radius of the circle (r) = 21 cm

Question 2.
Solution:
(i) Diameter of the circle = 28 cm

Question 3.
Solution:
Circumference of a circle = 264 cm

Question 4.
Solution:
Circumference of the circle (c) = 35.2 m

Question 5.
Solution:
Area of the circle = 616 cm²

Question 6.
Solution:
Area of a circle = 1386 m²

Question 7.
Solution:
Ratio in the radii of two circles = 4 : 5
Let radius of first circle (r1) = 4x
and radius of the second circle (r2) = 5x

Question 8.
Solution:
Length of rope (r) = 21 m
Area of the circle = πr² = \(\frac { 22 }{ 7 }\) x 21 x 21 m² = 1386 m²
The horse will graze on 1386 m² area

Question 9.
Solution:
Area of a square made of a wire = 121 cm²
Side = √Area = √121 = 11 m
Perimeter of wire = 4 x side = 4 x 11 = 44 cm
Circumference of circular wire = 44 cm

Question 10.
Solution:
Radius of circular wire = 28 cm
Circumference = 2πr = 2 x \(\frac { 22 }{ 7 }\) x 28 cm = 176 cm
Perimeter of the square formed by this wire = 176 cm
Side (a) = \(\frac { 176 }{ 4 }\) = 44 cm .
Area of square so formed = a² = (44)² cm² = 1936 cm²

Question 11.
Solution:
Length of rectangular sheet (l) = 34 cm
and breadth (b) = 24 cm
Area = l x b = 34 x 24 cm² = 816 cm²
Diameter of one button = 3.5 cm
Radius (r) = \(\frac { 3.5 }{ 2 }\) cm
and area of one button = πr²

Area of 64 buttons = 9.625 x 64 cm² =616 cm²
Area of remaining sheet = 816 – 616 = 200 cm²

Question 12.
Solution:
Length of ground (l) = 90 m
and breadth (b) = 32 m
Area = l x b = 90 x 32 m² = 2880 m²
Radius of circular tank (r) = 14 m

= 616 m²
Area of remaining portion = 2880 – 616 = 2264 m²
Rate of turfing = Rs. 50 per sq.m.
Total cost = Rs. 50 x 2264 = Rs. 113200

Question 13.
Solution:
Each side of square = 14 cm
Area of square = a² = 14 x 14 = 196 cm²
Radius of each circle at each corner of square = \(\frac { 14 }{ 2 }\) = 7 cm

Area of shaded portion = Area of square – area of 4 quadrants
= 196 – 154 = 42 cm²

Question 14.
Solution:
Length of field = 60 m
and breadth = 40 m
Length of rope = 14 m
Area covered by the horse

Question 15.
Solution:
Diameter of largest circle (outer circle) = 21 cm


Area of shaded portion = 346.5 – (154 + 38.5) = (346.5 – 192.5) = 154 cm²

Question 16.
Solution:
Length of plot (l) = 8m
and breadth (b) = 6m
Area of plot = l x b = 8 x 6 = 48 m²
Radius of each quadrant at the corner = 2 m

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20E

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper

Question 1.
Solution:
Radius of the circle (r) = 28 cm

Question 2.
Solution:
(i) Diameter of circle (d) = 35 cm

Question 3.
Solution:
Radius of a circle = 15 cm

Circumference = 2πr = 2 x 3.14 x 15 = 94.20 cm = 94.2 cm

Question 4.
Solution:
Circumference of a circle (c) = 57.2 cm

Question 5.
Solution:
Circumference (c) = 63.8 m

Question 6.
Solution:
Let c be the circumference and d be the diameter of the circle.
c = d + 30
⇒ dπ = d + 30
⇒ dπ – d = 30
⇒ d (π – 1) = 30

Question 7.
Solution:
The ratio of the radii of the circles = 5 : 3
Let radius of first circle = 5x
and radius of second circle = 3x
Circumference of first circle = 2πr = 2π x 5x = 10πx
and circumference of second circle = 2π x 3x = 6πx
Ratio = 10πx : 6πx = 10 : 6 = 5 : 3

Question 8.
Solution:
Radius of circular field (r) = 21 m
Circumference = 2πr

Question 9.
Solution:
Outer circumference = 616 m

Width of track = R – r = 98 – 84 = 14m

Question 10.
Solution:
Inner circumference of the circular track = 330 m

Rate of fencing = Rs. 20 per metre
Total cost = Rs. 20 x 396 = Rs. 7920

Question 11.
Solution:
Radius of inner circle (r) = 98 cm
Inner circumference = 2πr = 2 x \(\frac { 22 }{ 7 }\) x 98 cm = 616 cm

Radius of the outer circle (R) = 1 m 26cm = 126 cm
Outer circumference = 2πR = 2 x \(\frac { 22 }{ 7 }\) x 126 cm = 792 cm

Question 12.
Solution:
Side of equilateral triangle = 8.8 cm
Its perimeter = 8.8 x 3 = 26.4 cm
By bending their wire into a circular shape,
the circumference = 26.4 cm
Let d be the diameter,
Then C = dπ

Question 13.
Solution:
Each side of rhombus = 33 cm
Perimeter = 4 x 33 = 132 cm
Perimeter of circle = 132 cm
Let r be the radius

Question 14.
Solution:
Length of rectangle (l) = 18.7 cm
Breadth (b) = 14.3 cm
Perimeter = 2 (l + b) = 2 (18.7 + 14.3) cm = 2 x 33 = 66 cm
Circumference of the so formed circle = 66 cm

Question 15.
Solution:
Radius of the circle (r) = 35 cm
Its circumference (c) = 2πr

Question 16.
Solution:
Diameter of well (d) = 140 cm
Outer circumference of parapet = 616 cm
Let D be the diameter, then

Question 17.
Solution:
Diameter of wheel (d) = 98 cm

Question 18.
Solution:
Diameter of cycle wheel (d) = 70 cm

Question 19.
Solution:
Diameter of car wheel (d) = 77 cm
Circumference = πd = \(\frac { 22 }{ 7 }\) x 77 cm

Question 20.
Solution:
No. of revolutions = 5000
Distance covered = 11 km = 11 x 1000 = 11000 m

Question 21.
Solution:
Length of hour hand (r) = 4.2 cm
and length of minutes hand (R) = 7cm

Distance covered by hour hand in 24 hours = 2πR
= 2 x \(\frac { 22 }{ 7 }\) x 4.2
= 26.4 cm
But distance covered by minute hand in one hour = 2πR = 2 x \(\frac { 22 }{ 7 }\) x 7 = 44 cm
and distance covered by minute hand in 24 hours = 44 x 24 cm = 1056 cm
Sum of distance covered by these hands = 26.4 + 1056 = 1082.4 cm

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20D

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper

Question 1.
Solution:
(i) Base of the triangle = 42 cm

Height = 25 cm
Area = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x 42 x 25 = 525 cm²
(ii) Base of the triangle = 16.8 m
and height = 75 cm = 0.75 m
Area = \(\frac { 1 }{ 2 }\) x Base x height
= \(\frac { 1 }{ 2 }\) x 16.8 x 0.75 m2 = 6.3 m²
(iii) Base of a triangle (b) = 8 m = 80 cm
and height (h) = 35 cm
Area = \(\frac { 1 }{ 2 }\) bh = \(\frac { 1 }{ 2 }\) x 80 x 35 = 1400 cm²

Question 2.
Solution:
Base of triangle = 16 cm
area of the triangle = 72 cm²

Question 3.
Solution:
Area of triangular region = 224 m²
Base = 28 m

Question 4.
Solution:
Area of triangle = 90 cm²
and height (h) = 12 cm

Question 5.
Solution:
Let height of a triangular field = x m
Then base (b) = 3x m
and area = \(\frac { 1 }{ 2 }\) bh = \(\frac { 1 }{ 2 }\) x 3x x x

Question 6.
Solution:
Area of the right angled triangle = 129.5 cm²

Question 7.
Solution:
In right angled ∆ABC,
Base BC = 1.2 m

and hypotenuse AC = 3.7 m
But AC² = AB² + BC² (Pythagoras Theorem)
⇒ (3.7)² = AB² + (1.2)²
⇒ 13.69 = AB² + 1.44
⇒ AB² = 13.69 – 1.44
⇒ AB² = 12.25 = (3.5)²
⇒ AB = 3.5 m
Now, area of ∆ABC = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x 1.2 x 3.5 m² = 2.1 m²

Question 8.
Solution:
Legs of a right angled triangle = 3 : 4
Let one leg (base) = 3x

Then second leg (altitude) = 4x
Area = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x 3x x 4x = 6x²
6x² = 1014
⇒ x² = \(\frac { 1014 }{ 6 }\) = 169 = (13)²
x = 13
one leg'(Base) = 3x = 3 x 13 = 39 cm
and second leg (altitude) = 4x = 4 x 13 = 52 cm

Question 9.
Solution:
One side BC of a right triangular scarf = 80 cm

and longest side AC = 1 m = 100 cm
By Pythagoras Theorem,
AC² = AB² + BC²
⇒ (100)² = AB² + (80)²
⇒ 10000 = AB² + 6400
⇒ AB² = 10000 – 6400
⇒ AB² = 3600 = (60)²
⇒ AB = 60
Second side = 60 cm
Area of the scarf = \(\frac { 1 }{ 2 }\) x b x h
= \(\frac { 1 }{ 2 }\) x 80 x 60 cm2 = 2400 cm²
Rate of cost = Rs. 250 per m²
Total cost =\(\frac { 2400 }{ 100 x 100 }\) x 250 = Rs. 60

Question 10.
Solution:
(i) Side of the equilateral triangle (a) = 18 cm

Question 11.
Solution:
Area of equilateral triangle = 16√3 cm²
Let each side = a
then \(\frac { \surd 3 }{ 4 }\) a² = 16√3
⇒ a² = \(\frac { 16\surd 3\times 4 }{ \surd 3 }\)
⇒ a² = 64 = (8)²
a = 8 cm
Each side = 8 cm

Question 12.
Solution:
Each side of an equilateral triangle = 24cm
Length of altitude = \(\frac { \surd 3 }{ 2 }\) a = \(\frac { \surd 3 }{ 2 }\) x 24
= 12√3 cm = 12 (1.73) = 20.76 cm

Question 13.
Solution:
(i) a = 13 m, b = 14 m, c = 15 m

= 2 x 2 x 3 x 7 x 7 x 7 = 4116 m²

Question 14.
Solution:
Let a = 33 cm, b = 44 cm, c = 55 cm

Question 15.
Solution:
Perimeter of the triangle = 84 cm
Ratio in side = 13 : 14 : 15
Sum of ratios =13 + 14 + 15 = 42
Let then first side = \(\frac { 84 x 13 }{ 42 }\) = 26 cm

Question 16.
Solution:
Let a = 42 cm, b = 34 cm, c = 20 cm

Question 17.
Solution:
In isosceles ∆ABC
Base BC = 48 cm.
and AB = AC = 30cm.
Let AD ⊥ BC

Question 18.
Solution:
Perimeter of an isosceles triangle = 32 cm
Base = 12 cm
Sum of two equal sides = 32 – 12 = 20 cm
Length of each equal side = \(\frac { 20 }{ 2 }\) = 10cm
Let AD ⊥ BC
BD = DC = \(\frac { 12 }{ 2 }\) = 6 cm

Question 19.
Solution:
In quadrilateral ABCD,
diagonal AC = 26 cm.

and perpendiculars DL = 12.8cm, BM = 11.2 cm
Area of quadrilateral ABCD
= \(\frac { 1 }{ 2 }\) (Sum of perpendicular) x diagonal
= \(\frac { 1 }{ 2 }\) (12.8 + 11.2) x 26 cm²
= \(\frac { 1 }{ 2 }\) x 24 x 26 = 312 cm²

Question 20.
Solution:
In quad. ABCD,
AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm
and diagonal AC = 30 cm
In ∆ABC,

Question 21.
Solution:
ABCD is a rectangle in which AB = 36 m
and BC = 24m
In ∆AED,
EF = 15 m
AD = BC = 24 m.
Now area of rectangle ABCD = l x b = 36 x 24 cm² = 864 cm²
Area of ∆AED = \(\frac { 1 }{ 2 }\) x AD x EF
= \(\frac { 1 }{ 2 }\) x 24 x 15 cm² = 180 cm²
Area of shaded portion = 864 – 180 = 684 m²

Question 22.
Solution:
In the fig. ABCD is a rectangle in which AB = 40 cm, BC = 25 cm.
P, Q, R and S and the mid points of sides, PQ, QR, RS and SP respectively
Then PQRS is a rhombus.
Now, join PR and QS.
PR = BC = 25cm and QS = AB = 40cm
Area of PQRS = \(\frac { 1 }{ 2 }\) x PR x QS
= \(\frac { 1 }{ 2 }\) x 25 x 40 = 500 cm²

Question 23.
Solution:
(i) Length of rectangle (l) = 18 cm
and breadth (b) = 10 cm
Area = l x b = 18 x 10 = 180 cm²

Area of right ∆EBC = \(\frac { 1 }{ 2 }\) x 10 x 8 = 40 cm²
and area of right ∆EDF = \(\frac { 1 }{ 2 }\) x 10 x 6 = 30 cm²
Area of shaded region = 180 – (40 + 30) = 180 – 70 = 110 cm²
(ii) Side of square = 20 cm

Area of square = a² = (20)² = 400 cm²
Area of right ∆LPM = \(\frac { 1 }{ 2 }\) x 10 x 10 cm² = 50 cm²
Area of right ∆RMQ = \(\frac { 1 }{ 2 }\) x 10 x 20 = 100 cm²
and area of right ∆RSL = \(\frac { 1 }{ 2 }\) x 20 x 10 = 100 cm²
Area of shaded region = 400 – (50 + 100 + 100) cm2 = 400 – 250 = 150 cm²

Question 24.
Solution:
In the quadrilateral ABCD
BD = 24 cm
AL ⊥ BD and CM ⊥ BD
AL = 5 cm and CM = 8 cm

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 17 Constructions Ex 17A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17A
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17B
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17C
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions CCE Test Paper

Question 1.
Solution:
Steps of construction :
(i) Draw a line segment AB
(ii) From a point P outside AB, draw a line PQ meeting AB at Q.

(iii) At P, draw a line PQ making an angle
∠QPC equal to ∠PQB with the help of compass and ruler and produce it to D.
Then the line CD is parallel to AB. Which is the required line.

Question 2.
Solution:
Steps of construction :
(i) Draw a line AB and take a point P on it.
(ii) From P, draw a perpendicular PX and cut off PQ = 3.5 cm.
(iii) From Q, draw a perpendicular line CD and produce it to both sides.

Then, CD is the required line which is parallel to AB.

Question 3.
Solution:
Steps of construction :
(i) Draw a line / and take a point P on it.
(ii) At P, draw a perpendicular line PX and cut off PQ = 4.3 cm.
(iii) From Q, draw a line m which is perpendicular on PX, and produce it to both sides.
Then m is the required line which is parallel to l.

 

Hope given RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 16 Congruence Ex 16

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 16 Congruence Ex 16.

Question 1.
Solution:
(i) ∆ABC ≅ ∆EFD, Then
A ↔ E, B ↔ F and C ↔ D
AB = EF, BC = FD and CA = DE
∠A = ∠E, ∠B = ∠F and ∠C = ∠D
(ii) ∆CAB ≅ ∆QRP
C ↔ Q, A ↔ R and B ↔ P
CA = QR, AB = RP and BC = PQ
∠C = ∠Q, ∠A = ∠R and ∠B = ∠P
(iii) ∆XZY ≅ ∆QPR
X ↔ Q, Z ↔ P, Y ↔ R
XZ = QP, ZY = PR and YX = RQ
∠X = ∠Q, ∠Z = ∠P and ∠Y = ∠R
(iv) ∆MPN ≅ ∆SQR
M ↔ S, P ↔ Q and N ↔ R
MP = SQ, PN = QR and NM = RS
∠M = ∠S, ∠P = ∠Q and ∠N = ∠R.

Question 2.
Solution:
(i) In fig (i)
In ∆ABC and ∆DEF
∠C = ∠E
CA = ED
CB = EF
∆ACB ≅ ∆DEF (SAS condition)
(ii) In fig (ii)
In ∆RPQ and ∆LNM
Side PQ = NM
Hyp. RQ = LM
∆RPQ ≅ ∆LNM (RHS condition)
(iii) In ∆YXZ and ∆TRS
XY = RT
∠X = SR and YZ = TS
∆YXZ ≅ ∆TRS (SSS condition)
(iv) In ∆DEF and ∆PNM
∠E = ∠N
∠F = ∠M
EF = NM
∆DEF ≅ ∆PNM (ASA condition)
(v) In ∆ABC and ∆ADC
AC = AC (common)
∠ CAB = ∠ CAD (each 50°)
∠ ACB = ∠ DCA (each 60°)
∆ABC ≅ ∆ADC (ASA condition)

Question 3.
Solution:
In fig,
PL ⊥ OA and PM ⊥ OB and PL = PM
Now in right ∆PLO and ∆PMO,
Side PL = PM (given)
Hypotenuse OP = OP (common)
∆PLO ≅ ∆PMO (RHS condition)
Yes ∆PLO ≅ ∆PMO
Hence proved.

Question 4.
Solution:
In the figure,
AD = BC and AD || BC.
In ∆ABC and ∆ADC,
AC = AC (common)

BC = AB (given)
∠ACB = ∠CAD (Alternate angles)
∆ABC ≅ ∆ADC (SAS condition)
AB = DC (c.p.c.t)
Hence proved.

Question 5.
Solution:
In ∆ABD and ∆ACD,
AD = AD (common)
AB = AC (given)
BD = CD (given)
∆ABD ≅ ∆ADC (SSS condition)
∠BAD = ∠CAD (c.p.c.t.)
and ∠ADB = ∠ADC (c.p.c.t.)
But ∠ADB + ∠ADC = 180° (Linear pair)
∠ADB = ∠ADC = 90°
Hence proved.

Question 6.
Solution:
given : In ∆ABC, AD is the bisector of ∠A i.e. ∠BAD = ∠CAD
AD ⊥ BC.
To prove : ∆ABC is an isosceles
Proof : In ∆ADB and ∆ADC.
AD = AD (common)
∠ BAD = ∠ CAD (AD is the bisector of ∠A)
∠ ADB = ∠ ADC (each = 90°, AD ⊥ BC)
∆ADM ≅ ∆ADC (ASA condition)
AB = AC (c.p.c.t)
Hence ∆ABC is an isosceles triangle.
Hence proved.

Question 7.
Solution:
In the figure,
AB = AD, CB = CD
To prove : ∆ABC ≅ ∆ADC
Proof : In ∆ABC and ∆ADC
AC = AC (common)
AB = AD (given)
CB = CD (given)
∆ABC ≅ ∆ADC (SSS condition)
Hence proved.

Question 8.
Solution:
Given : In the figure,
PA ⊥ AB, QB ⊥ AB and PA = QB.
To prove : ∆OAP ≅ ∆OBQ,
Is OA = QB ?
Proof : In ∆OAP and ∆OBQ,
∠ A = ∠ B (each 90°)
AP = BQ (given)
∠AOP = ∠BOQ (vertically opposite angles)

∆OAP ≅ ∆OBQ (AAS condition)
OA = OB (c.p.c.t.)
Hence proved.

Question 9.
Solution:
Given : In right triangles ABC and DCB right angled at A and D respectively and AC = DB

To prove : ∆ABC ≅ ∆DCB.
Proof: In right angled ∆ABC and ∆DCB,
Hypotenuse BC = BC (common)
side AC = DB (given)
∆ABC ≅ ∆DCB (RHS condition)
Hence proved.

Question 10.
Solution:
Given: ∆ABC is an isosceles triangle in which AB = AC.
E and F are the midpoints of AC and AB respectively.

To prove : BE = CF
Proof : In ∆BCF and ∆CBE,
BC = BC (common)
BF = CE (Half of equal sides AB and AC)
∠CBF = ∠BCF (Angles opposite to equal sides)
∆BCF ≅ ∆CBE (SAS condition)
CF = BE (c.p.c.t.)
or BE = CF
Hence proved.

Question 11.
Solution:
Given : In isosceles ∆ABC,
AB = AC.
P and Q are the points on AB and AC respectively such that AP = AQ.
To prove : BQ = CP

Proof : In ∆ABQ and ∆ACP,
AB = AC (given)
AQ = AP (given)
∠ A = ∠ A (common)
∆ABQ ≅ ∆ACP (SAS condition)
BQ = CP (c.p.c.t.)
Hence proved.

Question 12.
Solution:
Given : ∆ABC is an isosceles triangle in which AB = AC.
AB and AC are produced to D and E respectively such that BD = CE.
BE and CD are joined.
To prove : BE = CD.
Proof : AB = AC and BD = CE
Adding we get:
AB + BD = AC + CE
AD = AE
Now, in ∆ACD and ∆ABE
AC = AB (given)
AD = AE (proved)
∠ A = ∠ A (common)
∆ACD ≅ ∆ABE (SSA condition)
CD = BE (c.p.c.t.)
Hence, BE = CD.

Question 13.
Solution:
Given : In ∆ABC,
AB = AC.
D is a point such that BD = CD.
AD, BD and CD are joined.
To prove : AD bisects ∠A and ∠D.
Proof : In ∆ABD and ∆CAD,
AD = AD (common)
AB = AC (given)
BD = CD (given)
∆ABD ≅ ∆CAD (SSS condition)
∠BAD = ∠CAD (c.p.c.t.)
and ∠BDA = ∠CDA (c.p.c.t.)
Hence AD is the bisector of ∠A and Z D.
Hence proved.

Question 14.
Solution:
Two triangles whose corresponding angles are equal, it is not necessarily that they should be congruent. It is possible if atleast one side must be equal. Below given a pair of triangles whose angles are equal but these are not congruent.

Question 15.
Solution:
In two triangles, if two sides and and included angle of the one equal to the corresponding two sides and included angle, then the two triangles are congruent.

If another angle except included angles are equal to each other and two sides are also equal these are not congruent. In the above figures, in ∆ABC and ∆PQR, two corresponding sides and one angle are equal, but these are not congruent.

Question 16.
Solution:
In ∆ABC,

Area = \(\frac { 1 }{ 2 }\) x BC x AL = \(\frac { 1 }{ 2 }\) x 5 x 4 = 10 cm²
and in ∆PQR
Area = \(\frac { 1 }{ 2 }\) x QR x PR = \(\frac { 1 }{ 2 }\) x 5 x 4 = 10 cm²
In these triangles
Areas of both triangles are equal but are not congruent to each other

Question 17.
Solution:
(i) Two line segments are congruent if they have the same length.
(ii) Two angles are congruent if they have equal measure.
(iii) Two squares are congruent if they have same side length.
(iv) Two circles are congruent if they have equal radius.
(v) Two rectangles are congruent if they have the same length and same breadth.
(vi) Two triangles are congruent if they have all parts equal.

Question 18.
Solution:
(i) False : Only those squares are congruent which have the same side.
(ii) True :
(iii) False : It is not necessarily, that those figures which have equal areas, must be congruent.
(iv) False : It is not necessarily that those triangles whose areas are equal, must be congruent.
(v) False : It is not necessarily that such triangles must be congruent.
(vi) True : It two angles and one side of a triangle are equal to the corresponding two angles and one side of the other are equal they are congruent.
(vii) False : Only three angles of one are equal the three angles of is not necessarily that these must be congruent.
(viii) True.
(ix) False : Only hypotenuse and one right angle of the one are equal to the hypotenuse and one right angles of the other, the triangles are not necessarily congruent, one side except them, must be equal.
(x) True : It is the definition of congruency of two triangles.

 

Hope given RS Aggarwal Solutions Class 7 Chapter 16 Congruence Ex 16 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 15 Properties of Triangles Ex 15D

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D

Question 1.
Solution:
In right triangle ABC, ∠B = 90° AB = 9cm, BC = 12cm

By Pythagoras Theorem,
AC² = AB² + BC² = (9)² + (12)² = 81 + 144 = 225
AC = √225 = 15 cm

Question 2.
Solution:
In right ∆ABC, ∠B = 90°
AC = 26cm, AB = 10cm
By Pythagoras Theorem
AC² = AB² + BC²

⇒ (26)² = (10)² + BC²
⇒ 676 = 100 + BC²
⇒ BC² = 676 – 100 = 576 = (24)²
⇒ BC = 24 cm

Question 3.
Solution:
In right ∆ABC, ∠C = 90°,
AB = 7.5cm, BC = 4.5cm
By Pythagoras Theorem
AB² = BC² + AC²

⇒ (7.5)² = (4.5)² + AC²
⇒ 56.25 = 20.25 + AC²
⇒ AC² = 56.25 – 20.25 = 36.00 = (6)²
⇒ AC = 6cm

Question 4.
Solution:
In ∆ABC, ∠B = 90°
Let each leg = x cm

By Pythagoras Theorem,
x² + x² = AC²
⇒ 2x² = 50
⇒ x² = 25 = (5)²
⇒ x = 5
Length of each equal leg = 5cm

Question 5.
Solution:
A triangle is a right-angled,
If (Hypotenuse)² = sum of squares or other two sides
If (39)² = (15)² + (36)² (Hypotenuse is the longest side)
If 1521 = 225 + 1296
If 1521 = 1521 Which is true.
It is a right-angled triangle.

Question 6.
Solution:
In ∆ABC, ∠C = 90°

a = 6cm, b = 4.5cm.
By Pythagoras Theorem
c² = a² + b² = (6)² + (4.5)² = 36.00 + 20.25 = 56.25 = (7.5)²
c = 7.5 cm

Question 7.
Solution:
A triangle will be a right angled
if (longest side)² = Sum of squares of other two sides
(i) a = 15cm, b = 20cm, c = 25cm.
Here, longest side = c ,
The triangle will be right angled
if c² = a² + b²
if (25)² = (15)² + (20)²
if 625 = 225 + 400 = 625 Which is true.
It is a right angled triangle.
(ii) a = 9cm, b = 12cm, c = 16cm
∆ABC is a right angled triangle if
c² = a² + b²
if (16)² = (9)² + (12)²
if 256 = 81 + 144 = 225
⇒ 256 = 225
Which is not true
Triangle is not a right angled triangle.
(iii) a = 10cm, b = 24cm, c = 26cm
The triangle ABC is a right angled triangle
if c² = a² + b²
if (26)² = (10)² + (24)²
if 676 = 100 + 576
if 676 = 676 Which is true.
The triangle is a right angled triangle.

Question 8.
Solution:
In ∆ABC,
∠B = 35° and ∠C = 55°
∠A = 180°- (∠B + ∠C) = 180° – (35° + 55°) = 180° – 90° = 90°
∆ABC is a right angled triangle
By Pythagoras Theorem,
BC² = AB² + AC²
(iii) is hue

Question 9.
Solution:
AB is a ladder and it is 15 m long B is window and BC = 12 m
In right ∆ABC
AB² = AC² + BC² (By Pythagoras Theorem)
⇒ (15)² = x² + (12)²
⇒ (15)² = x² + (12)²
⇒ 225 = x² + 144
⇒ x² = 225 – 144
⇒ x² = 81 = (9)²
x = 9 m
Distance of the foot of ladder from the wall = 9 m

Question 10.
Solution:
Let AB be the ladder and AC be the height.

Length of ladder AB = 5m
and height CA = 4.8m
Let distance of the ladder from the wall BC = x
Now in right angled ∆ABC, ∠C = 90°
AB² = AC² + BC² (By Pythagoras Theorem)
⇒ (5)² = (4.8)² + x²
⇒ 25 = 23.04 + x²
⇒ x² = 25.00 – 23.04 = 1.96 = (1.4)²
⇒ x = 1.4
The foot of ladder are 1.4m away from the wall.

Question 11.
Solution:
Let AB be the tree which broke at D and its top A touches the ground at C
their BD = 5m, BC = 12m,
Let AD = x m, then CD = x m
Now, in right ∆ABC,
CD² = BD² + BC²
(By Pythagoras Theorem)

CD² = (9)² + (12)² = 81 + 144 = 225 = (15)²
CD = 15m,
AD = x = 15m
Height of the tree AB = AD + BD = 15 + 9 = 24m

Question 12.
Solution:
AB and CD are two poles and they are 12,m apart
AB = 18 m, CD = 13m and BD = 12 m

From C, draw CE || BD Then
CE = BD = 12 m
and AE = AB – EB = AB – CD = 18 – 13 = 5 m
Join AC
Now in right ∆ACE
AC² = CE² + AE²
(By Pythagoras Theorem)
AC² = (12)² + (5)² = 144 + 25 = 169 = (13)²
AC = 13 m
Distance between their tops = 13 m

Question 13.
Solution:
A man starts from O and goes 35m due west and then 12m due north, then
In rights ∆OAB,
OA = 35 m
AB = 12 m

OB² = OA² + AB² (By Pythagoras Theorem)
= (35)² + (12)² = 1225 + 144 = 1369 = (37)²
OB = 37
Hence he is 37m away from the starting point

Question 14.
Solution:
A man goes 3km due north and then 4km east.

In right angled ∆OAB,
OA = 3km.
AB = 4km.
OB² = OA² + AB² (By Pythagoras Theorem)
= (3)² + (4)² = 9 + 16 = 25 = (5)²
OB = 5km
Hence he is 5km from the initial position.

Question 15.
Solution:
ABCD is a rectangle whose sides
AB = 16cm and BC = 12cm.
AC is its diagonal
In right angled ∆ABC
AC² = AB² + BC²
(By Pythagoras Theorem)
= (16)² + (12)² = 256 + 144 = 400 = (20)²
AC = 20cm
Hence length of diagonal AC = 20 cm

Question 16.
Solution:
ABCD is a rectangle and AC is its diagonal

AB = 40 cm and AC = 41 cm
Now in right ∆ABC
AC² = AB² + BC² (By Pythagoras Theorem)
⇒ (41)² = (40)² + BC²
⇒ 1681 = 1600 + BC²
⇒ BC² = 1681 – 1600 = 81 = (9)²
⇒ BC = 9 cm
Now perimeter of rectangle ABCD = 2 (AB + BC)
= 2 (40 + 9) = 2 x 49 = 98 cm

Question 17.
Solution:
Perimeter of rhombus ABCD = 4 x Side
Diagonal AC = 30 cm and BD = 16 cm
The diagonals of rhombus bisect each other at right angles
AO = OC = \(\frac { 30 }{ 2 }\) = 15 cm
and BO = OD = \(\frac { 16 }{ 2 }\) = 8 m
Now in right ∆AOB,
AB² = AO² + BO² = (15)² + (8)² = 225 + 64 = 289 = (17)²
AB = 17 cm
Now perimeter = 4 x side = 4 x 17 = 68 cm

Question 18.
Solution:
(i) In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
(ii) If the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right angled.
(iii) Of all the line segments that can be drawn to a given line from a given point outside it, the perpendicular is the shortest.

Hope given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 15 Properties of Triangles Ex 15C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D

Question 1.
Solution:
We know that in a triangle, sum of any two sides is greater than the third side. Therefore :
(i) 1cm, 1cm, 1cm
It is possible to draw a triangle
(1 + 1) cm > 1cm (sum of two sides is greater than the third)
(ii) 2cm, 3cm, 4cm
It is also possible to draw the triangle
(2 + 3) cm > 4cm (sum of two sides is greater than third side)
(iii) 7cm, 8cm, 15cm
It is not possible to draw the triangle
(7 + 8)cm not > 15cm
But (7 + 8) cm = 15 cm
(iv) 3.4 cm, 2.1 cm, 5.3 cm
It is possible to draw the triangle
(3.4 + 2.1) cm > 5.3 cm
⇒ 5.5cm > 5.3 cm
(v) 6cm, 7cm, 14cm
It is not possible to draw
(6 + 7) cm not > 14cm
i.e. 13cm not > 14cm (13cm < 14cm)

Question 2.
Solution:
Two sides of a triangle are 5 cm and 9 cm long
Then the third side will be less then (5 + 9) or less than 14 cm

Question 3.
Solution:
(i) In ∆APB,
PA + PB > AB (sum of two sides is greater than its third side)
(ii) In ∆PBC,
PB + PC > BC (sum of two sides is greater than its third side)
(iii) In ∆PAC,
AC < PA + PC (PA + PC > AC)

Question 4.
Solution:
Proof: AM is the median of ∆ABC
M is mid-point of BC

In ∆ABM,
AB + BM > AM ….(i)
(Sum of any two sides of a triangle is greater than its third side)
Similarly in ∆ACM,
AC + MC > AM ….(ii)
Adding (i) and (ii)
AB + BM + AC + MC > 2 AM
⇒ AB + AC + BM + MC > 2AM
⇒ AB + AC + BC > 2AM
Hence proved.

Question 5.
Solution:
Given: In ∆ABC, P is a point on BC.
AP is joined.
To prove :
(AB + BC + AC) > 2AP
Proof : In ∆ABP,
AB + BP > AP …(i) (Sum of two sides is greater than third)
Similarly in ∆ACP,

AC + PC > AP …(ii)
Adding (i) and (ii)
AB + BP + AC + PC > AP + AP
⇒ AB + BP + PC + CA > 2AP
⇒ AB + BC + CA > 2AP
Hence proved.

Question 6.
Solution:
ABCD is a quadrilateral AC and BD are joined.
Proof: Now in ∆ABC
AB + BC > AC ….(i)

(Sum of any two sides of a triangle is greater than its third side)
Similarly in ∆ADC,
AD + CD > AC ….(ii)
In ∆ABD,
AB + AD > BD ….(iii)
and in ∆BCD,
BC + CD > BD ……..(iv)
Adding (i), (ii), (iii) and (iv)
AB + BC + CD + AD + AB + AD + BC + CD > AC + AC + BD + BD
⇒ 2 (AB + BC + CD + AD) > 2(AC + BD)
⇒ AB + BC + CD + AD > AC + BD
Hence proved.

Question 7.
Solution:
Given : O is any point outside of the ∆ABC
To prove : 2(OA + OB + OC) > (AB + BC + CA)
Construction : Join OA, OB and DC.
Proof: In ∆AOB,

OA + OB > AB ….(i) (Sum of two sides of a triangle is greater than its third side)
Similarly in ∆BOC,
OB + OC > BC …(ii)
and in ∆COA
OC + OA > CA …(iii)
Adding (i), (ii) and (iii), we get:
OA + OB + OB + OC + OC + OA > AB + BC + CA
2 (OA + OB + OC) > (AB + BC + CA)
Hence proved.

Hope given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.