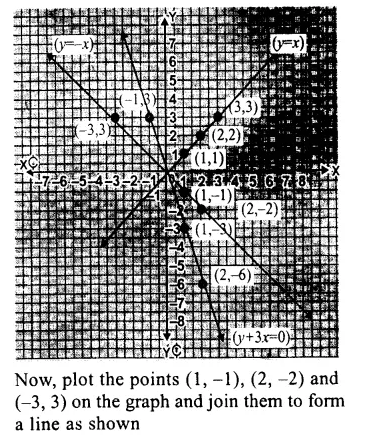
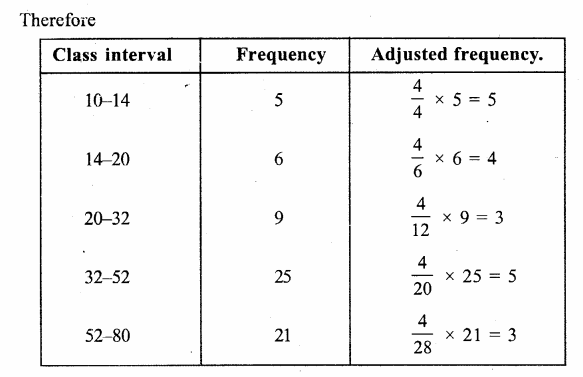
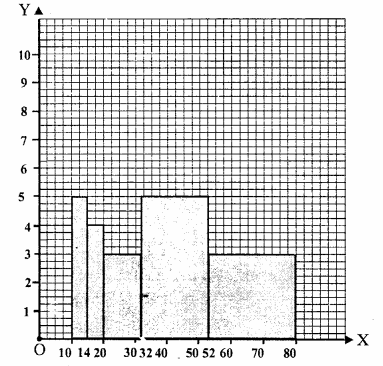
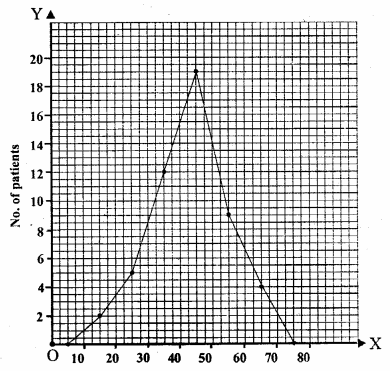
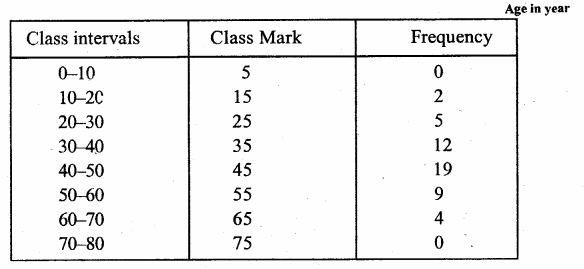
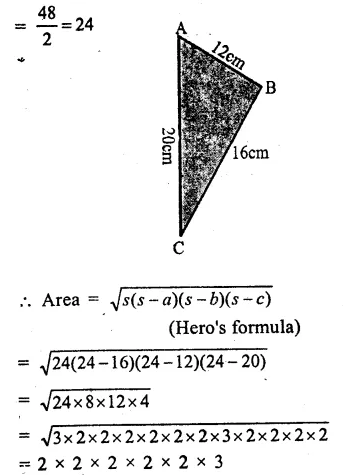
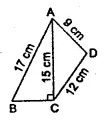
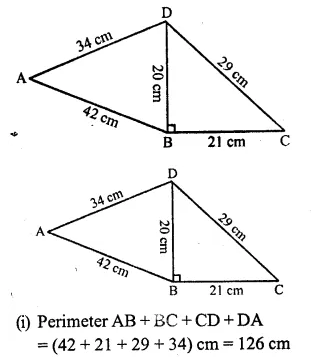
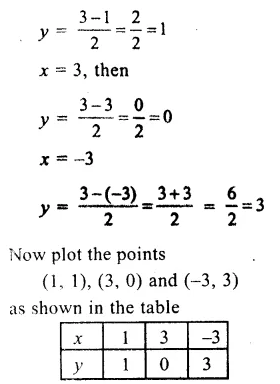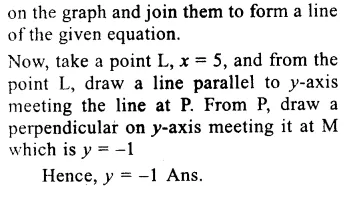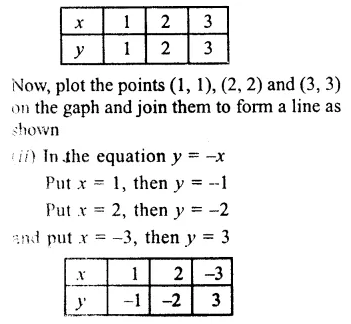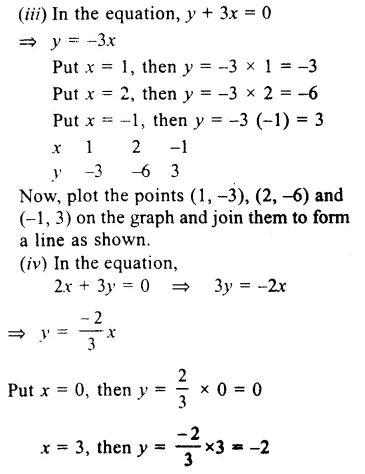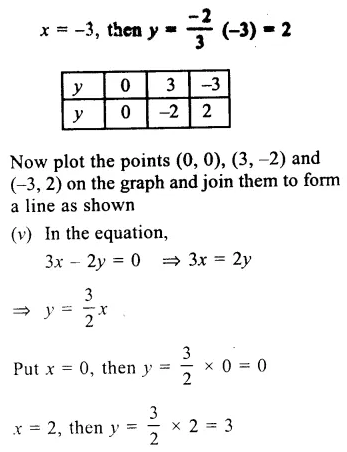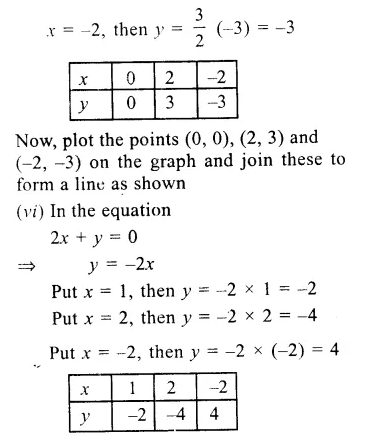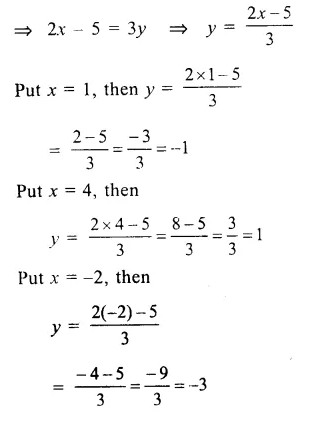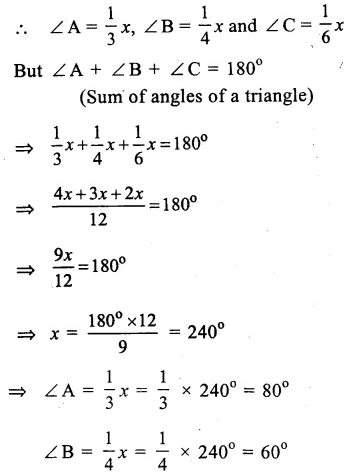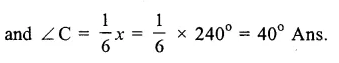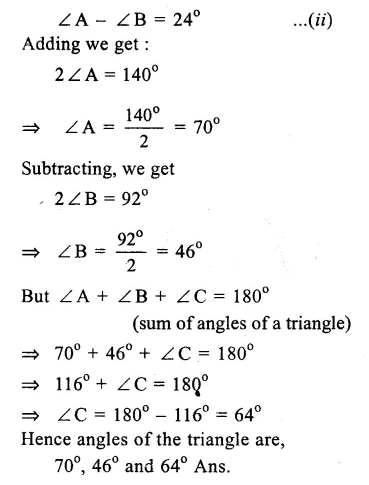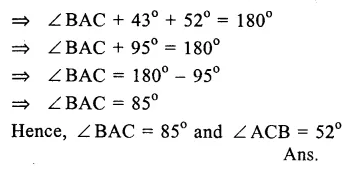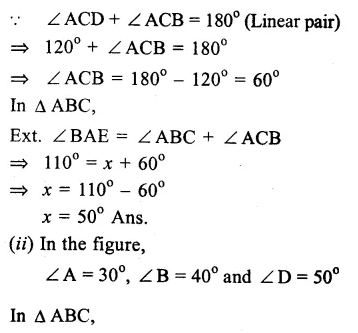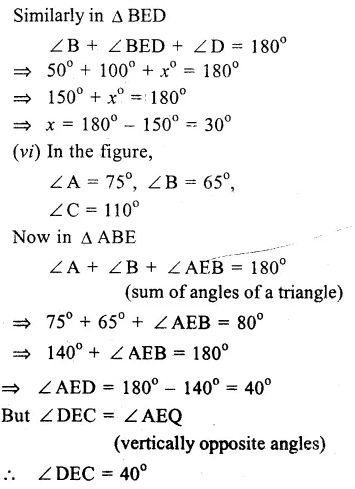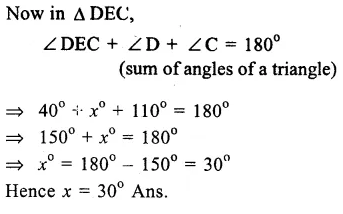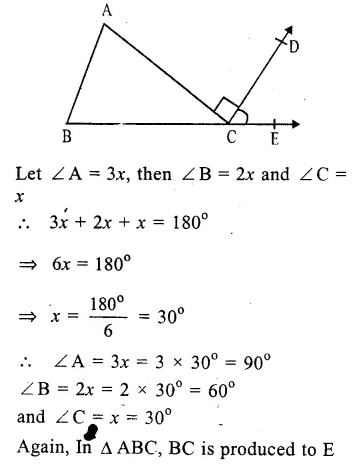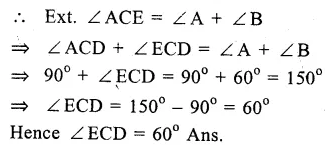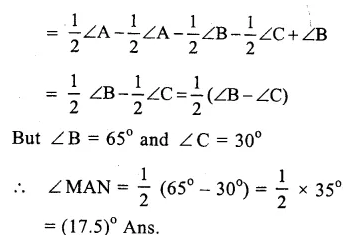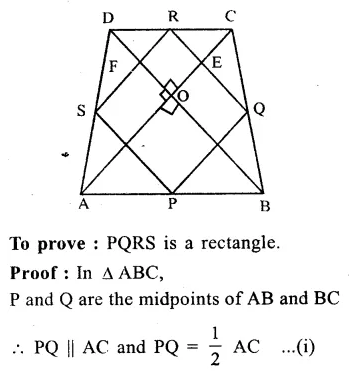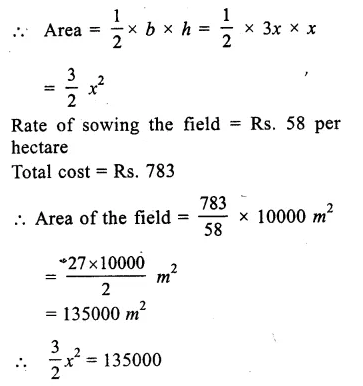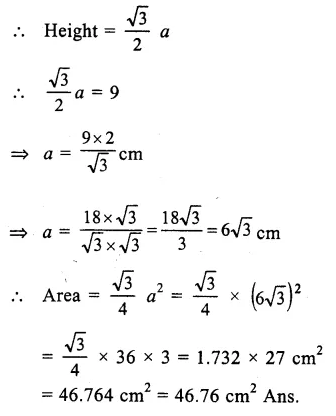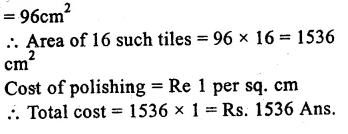RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14B
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14B.
Other Exercises
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14A
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14B
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14C
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14D
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14E
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14F
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14G
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14H
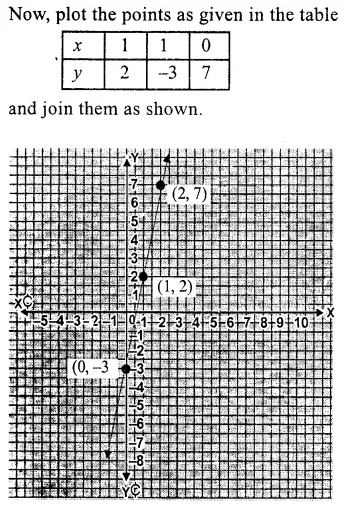
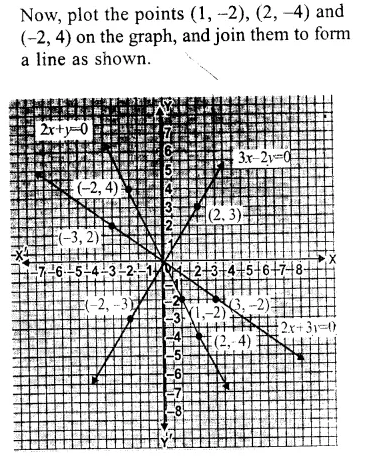
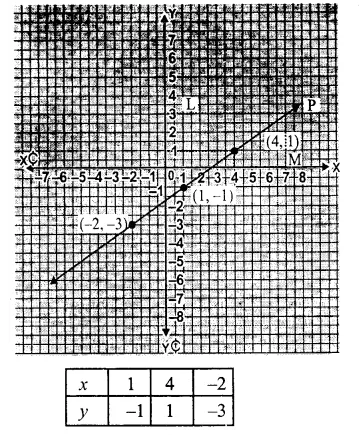
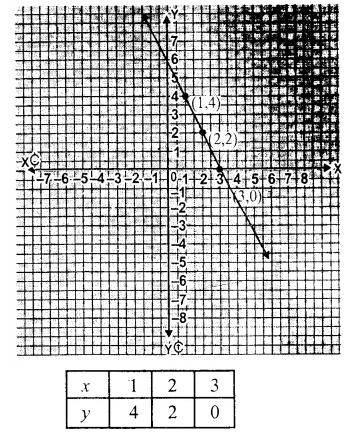
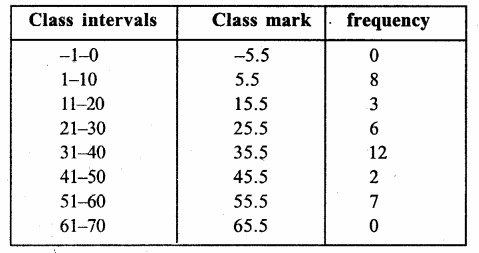
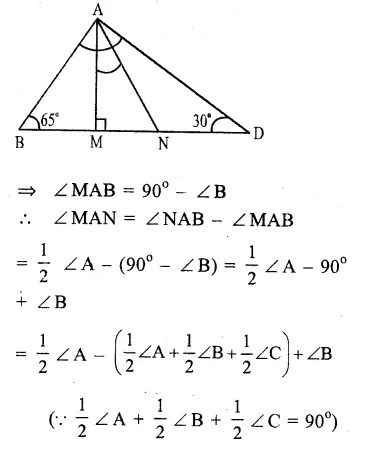
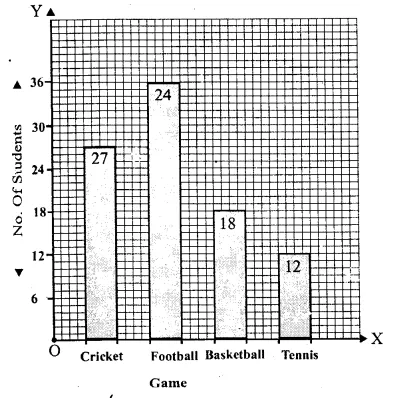
Question 1.
Solution:
We shall take the game along x-axis and number of students along y-axis.
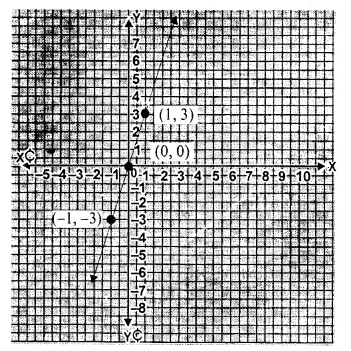
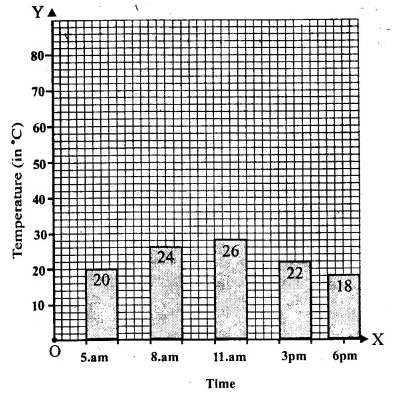
Question 2.
Solution:
We shall take the time on x-axis and temperature (in °C) on y-axis.
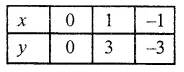
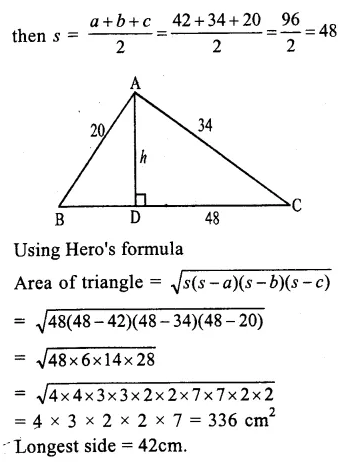
Question 3.
Solution:
We shall take name of vehicle on x-axis and velocity (in km/hr) on y-axis
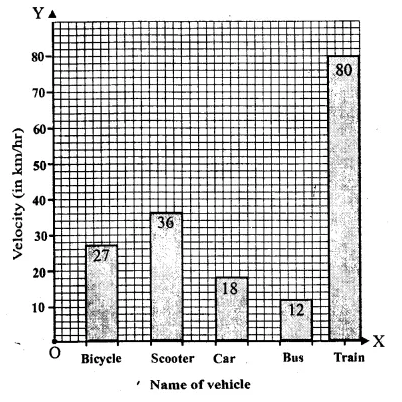
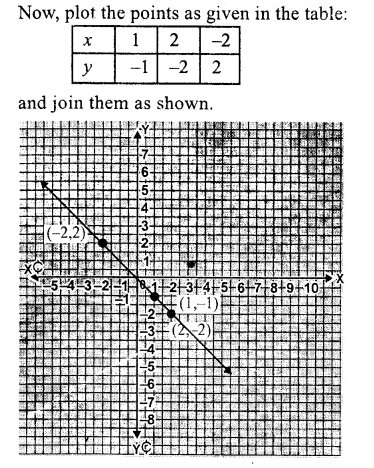
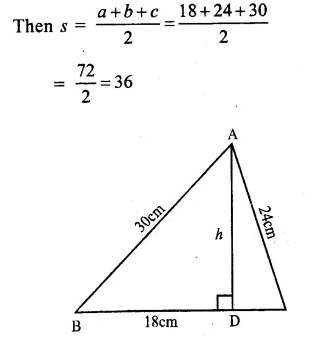
Question 4.
Solution:
We shall take sports on x-axis and number of students on y-axis.
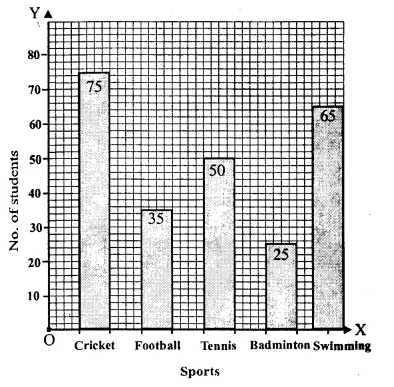
Question 5.
Solution:
We shall take years on x-axis and number of students on y-axis.
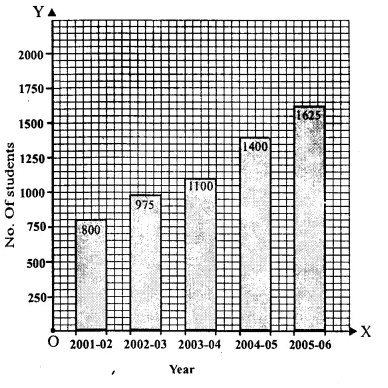
Question 6.
Solution:
We shall take years on x-axis and number of students on y-axis.
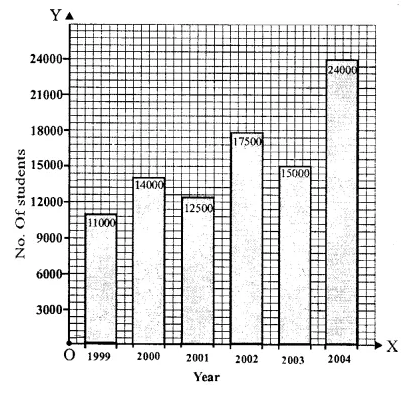
Question 7.
Solution:
We shall take years on x-axis and number of students on y-axis.
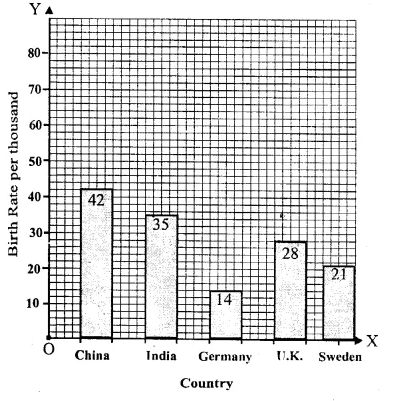
Question 8.
Solution:
We shall take years on x-axis and number of students on y-axis.
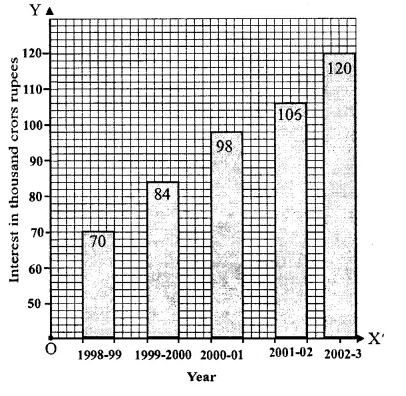
Question 9.
Solution:
We shall take years on x-axis and number of students on y-axis.
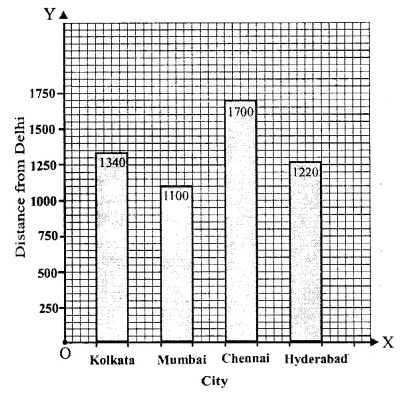
Question 10.
Solution:
We shall take years on x-axis and number of students on y-axis.
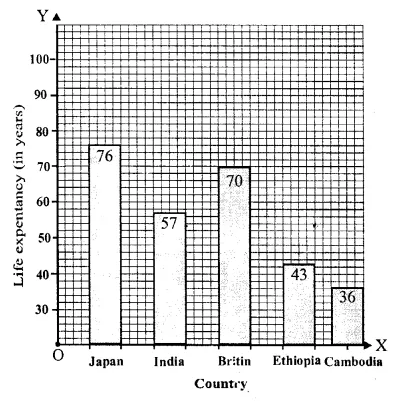
Question 11.
Solution:
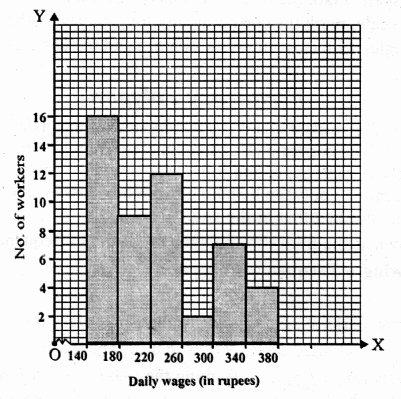
We shall take week on x-axis and Rate per 10g (in Rs.) on y-axis.
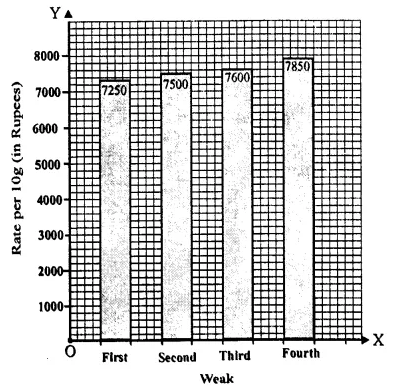
Question 12.
Solution:
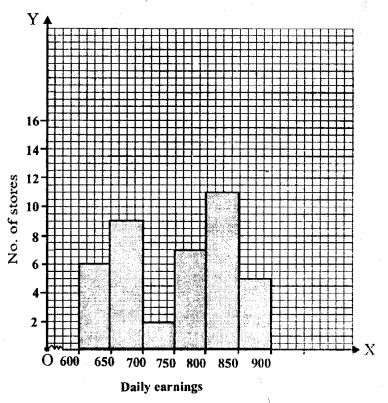
We shall take mode of transport on x-axis and number of students on y-axis.
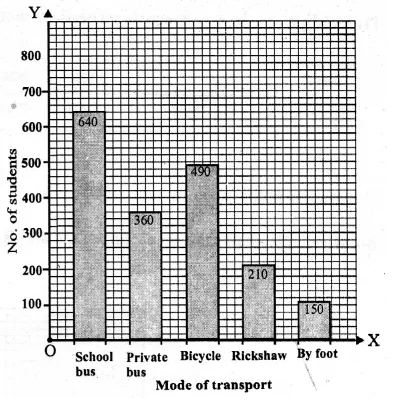
Question 13.
Solution:
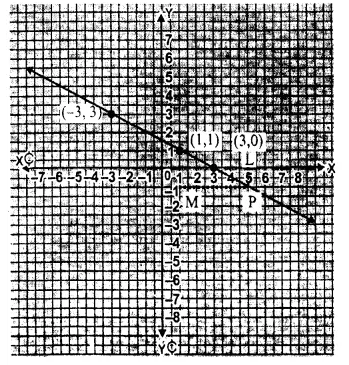
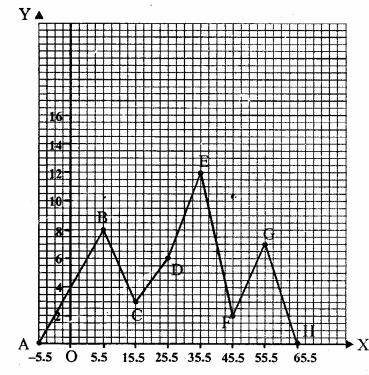
We see from the graph that
(i) It shows the marks obtained by a student in various subjects.
(ii) The student is very well in mathematics.
(iii) The student is very’ poor, in Hindi.
(iv) Average marks
= \(\frac { 60+35+75+50+60 }{ 5 } \) (Here x = 5)
= \(\frac { 280 }{ 5 } \)
= 56 marks
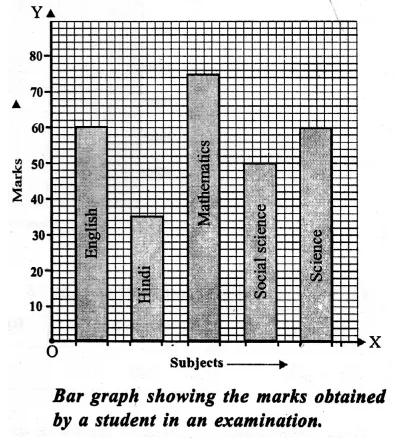
Hope given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.