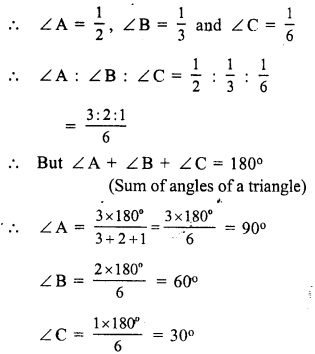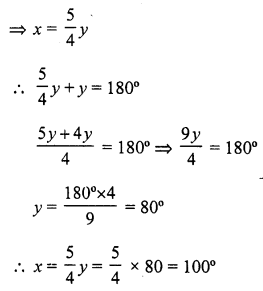Tag: Maths Class 7 RS Aggarwal Solutions

RS Aggarwal Class 7 Solutions Chapter 15 Properties of Triangles Ex 15B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D

Question 1.
Solution:
In ∆ABC,
∠A = 75°, ∠B = 45°
side BC is produced to D

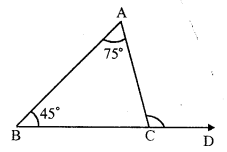
forming exterior ∠ ACD
Exterior ∠ACD = ∠A + ∠B (Exterior angle is equal to sum of its interior opposite angles)
= 75° + 45° = 120°

Question 2.
Solution:
In ∆ABC, BC is produced to D forming an exterior angle ACD
∠ B = 68°, ∠ A = x°, ∠ ACB = y° and ∠ACD = 130°

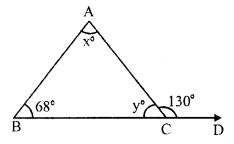
In triangle,
Exterior angles is equal to sum of its interior opposite angles
∠ACD = ∠A + ∠B
⇒ 130° = x + 68°
⇒ x = 130° – 68° = 62°
But ∠ACB + ∠ACD = 180° (Linear pair)
⇒ y + 130° = 180°
⇒ y = 180° – 130° = 50°
Hence x = 62° and y = 50°

Question 3.
Solution:
In ∆ABC, side BC is produced to D forming exterior angle ACD.
∠ACD = 65°, ∠A = 32°
∠B = x, ∠ACB = y

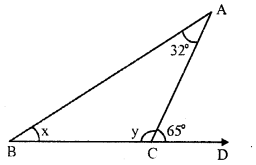
In a triangle, the exterior angles is equal to the sum of its interior opposite angles
∠ACD = ∠A + ∠B
⇒ 65° = 32° + x
⇒ x = 65° – 32° = 33°
But ∠ ACD + ∠ ACB = 180° (Linear pair)
⇒ 65° + y = 180°
⇒ y = 180°- 65° = 115°
x = 33° and y = 115°

Question 4.
Solution:
In ∆ABC, side BC is produced to D forming exterior ∠ ACD

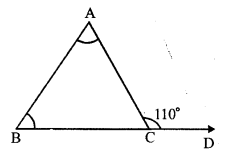
∠ACD = 110°, and ∠A : ∠B = 2 : 3
In a triangle, exterior angles is equal to the sum of its interior opposite angles
⇒ ∠ACD = ∠A + ∠B
⇒ ∠A + ∠B = 110°
But ∠A : ∠B = 2 : 3

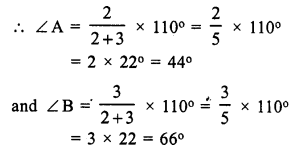
But ∠A + ∠B + ∠C = 180° (sum of angles of a triangle)
⇒ 44° + 66° + ∠C = 180°
⇒ 110° + ∠C = 180°
⇒ ∠C = 180° – 110° = 70°
Hence ∠ A = 44°, ∠ B = 66° and ∠ C = 70°

Question 5.
Solution:
In ∆ABC, side BC is produced to forming exterior angle ACD.
∠ACD = 100° and ∠A = ∠B
Exterior angle of a triangle is equal to the sum of its interior opposite angles.

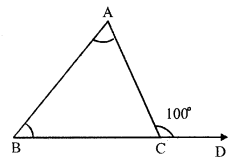
∠ACD = ∠A + ∠B But ∠A = ∠B
∠A + ∠A = ∠ACD = 100°
⇒ 2 ∠A = 100°
⇒ ∠A = 50°
∠B = ∠A = 50°
But ∠A + ∠B + ∠ ACB = 180° (sum of angles of a triangle)
⇒ 50° + 50° + ∠ ACB = 180°
⇒ 100° + ∠ ACB = 180°
⇒ ∠ ACB = 180° – 100° = 80°
Hence ∠ A = 50°, ∠ B = 50° and ∠ C = 80°

Question 6.
Solution:
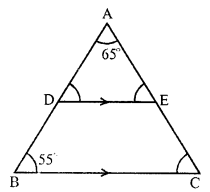
In ∆ABC, side BC is produced to D From D, draw a line meeting AC at E so that ∠D = 40°
∠A = 25°, ∠B = 45°
In ∆ABC,

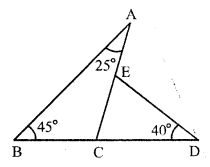
Exterior ∠ACD = ∠A + ∠B = 25° + 45° = 70°
Again, in ∆CDE,
Exterior ∠ AED = ∠ ECD + ∠ D = ∠ACD + ∠D = 70° + 40° = 110°
Hence ∠ACD = 70° and ∠AED = 110°

Question 7.
Solution:
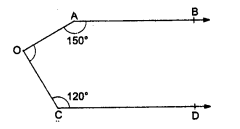
In ∆ABC, sides BC is produced to D and BA to E
∠CAD = 50°, ∠B = 40° and ∠ACB = 100°
∠ ACB + ∠ ACD = 180° (Linear pair)
⇒ 100° + ∠ ACD = 180°
⇒ ∠ ACD = 180° – 100° = 80°

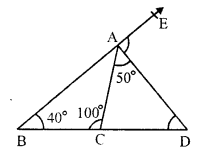
In ∆ACD,
∠ CAD + ∠ ACD + ∠ ADC = 180° (sum of angles of a triangle)
⇒ 50° + 80° + ∠ ADC = 180°
⇒ 130° + ∠ ADC = 180°
⇒ ∠ ADC = 180° – 130° = 50°
Now, in ∆ABD, BA is produced to E
Exterior ∠DAE = ∠ACD + ∠ADC = 80° + 50° = 130°
Hence ∠ ACD = 80°, ∠ ADC = 50° and ∠DAE = 130°

Question 8.
Solution:
In ∆ABC, BC is produced to D forming exterior ∠ ACD

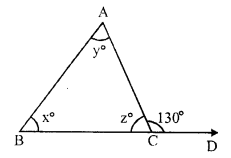
∠ACD = 130°, ∠A = y°, ∠B = x° and ∠ACB = z°.
x : y = 2 : 3
Now, in ∆ABC,
Exterior ∠ACD = ∠A + ∠B

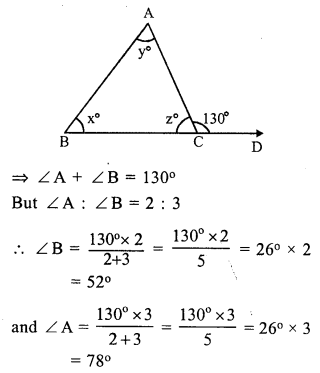
But ∠A + ∠B + ∠ACB = 180° (sum of angles of a triangle)
⇒ 78° + 52° + ∠ACB = 180°
⇒ 130° + ∠ACB = 180°
⇒ ∠ACB = 180° – 130°
⇒ ∠ACB = 50°
⇒ ∠ = 50°
Hence x = 52°, y = 78° and z = 50°

Hope given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 15 Properties of Triangles Ex 15A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D

Question 1.
Solution:
In ∆ABC,
∠A = 72°, ∠B = 63°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ 72° + 63° + ∠C = 180°
⇒ 135° + ∠C = 180°
⇒ ∠C= 180°- 135° = 45°

Question 2.
Solution:
In. ∆PQR,
∠E = 105°, and ∠F = 40°
But ∠D + ∠E+ ∠F= 180° (sum of angles of a triangle)
⇒ ∠D + 105°+ 40°= 180°
⇒ ∠ D + 145° = 180°
⇒ ∠D = 180°- 145°
⇒ ∠D = 35°

Question 3.
Solution:
In ∆XYZ,
∠ X = 90°, ∠ Z = 48°
But ∠X + ∠Y + ∠Z = 180° (Sum of angles of a triangle)
⇒ 90° + ∠ Y + 48° = 180°
⇒ 138°+ ∠ Y = 180°
⇒ ∠Y = 180° – 138° = 42°
⇒ ∠Y = 42°

Question 4.
Solution:
Sum of angles of a triangle = 180°
and ratio in the three angles = 4 : 3 : 2

Question 5.
Solution:
In a right triangle
Sum of the two acute angles = 90°
One angle = 30°
Second angle = 90° – 36° = 54°

Question 6.
Solution:
In a right triangle
Sum of two acute angles = 90°
and ratio of these two angles = 2 : 1
Let first angle = 2x
Then second angle = x
2x + x = 90°
⇒ 3x = 90°
⇒ x = \(\frac { 90 }{ 3 }\) = 30°
First angle = 2x = 2 x 30° = 60°
and second angle = x = 1 x 30° = 30°

Question 7.
Solution:
In a triangle,
Measure of one angle = 100°
Sum of other two angles = 180° – 100° = 80°
(Sum of angles of a triangles)
But, these two angles are equal.
Measure of each angle = \(\frac { 80 }{ 2 }\) = 40°

Question 8.
Solution:
Sum of angles of a triangle = 180°
Let third angle = x
then, each equal angles = 2x
x + 2x + 2x = 180°
⇒ 5x = 180°
⇒ x = \(\frac { 180 }{ 5 }\) = 36°
Each equal angle = 2x = 2 x 36° = 72°
and third angle = 36°

Question 9.
Solution:
In a triangle ABC,
Let ∠A = ∠B + ∠C
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ ∠A + ∠A = 180° (∠B + ∠C = ∠A)
⇒ 2A = 180°
⇒ ∠ A = \(\frac { 180 }{ 2 }\) = 90°
∠ A = 90°
Hence, ∆ABC is a right triangle.

Question 10.
Solution:
In a ∆ABC,
2 ∠A = 3 ∠B = 6 ∠C = 1 (suppose)

Question 11.
Solution:
In an equilateral triangle,
All sides are equal.
All angles are also equal.
Each angle = \(\frac { 180 }{ 3 }\) = 60°
(Sum of angles of a triangle = 180°)

Question 12.
Solution:
In the given figure,
ABC is a triangle in which DE || BC,
∠A = 65° and ∠B = 55°
DE || BC and ADB is the transversal
⇒ ∠ ADE = ∠ B (corresponding angles) = 55° (∠B = 55°)
In ∆ADE,
∠A + ∠ADE + ∠AED = 180° (sum of angles of a triangle)

⇒ 65° + 55° + ∠AED = 180°
⇒ ∠ 120° + ∠AED = 180°
⇒ ∠AED = 180°- 120° = 60°
∠AED = 60°
D || BC and AEC is the transversal
∠ C = ∠ AED (A corresponding angles)
∠C = 60°
Hence ∠ADE = 55°, ∠AED = 60° and ∠ C = 60°

Question 13.
Solution:
(i) No. In a triangle, only one right angle is possible as if there are two right angles, then The third angle will be ∠ero which is not possible.
(ii) No. In a triangle only one obtuse angle is possible as if there are two obtuse angles, then the sum of these two angles will be greater than 180° which is not possible.
(iii) Yes. two acute can arc possible.
(iv) No. The sum of these three angles will be greater than 180° which is not possible in a triangle.
(v) No. The sum of these angles will be less than 180° which is not possible.
(vi) Yes. The sum of there three angle will be in 180° which is possible.

Question 14.
Solution:
(i) Yes, it can be a right triangle also
(ii) Yes, if right triangle has its sides different then it is possible.
(iii) No, a right triangle cannot be an equilateral triangle as an equilateral triangle has each side 60°.
(iv) Yes, it is possible, if its sides opposite to acute angles are equal.

Question 15.
Solution:
(i) A right triangle cannot have an obtuse angle.
(ii) The acute angles of a right triangle are complementary.
(iii) Each acute angle of an isosceles right triangle measures 45°.
(iv) Each angle of an equilateral triangle measures 60°.
(v) The side opposite the right angle of the right triangle is called the hypotenuse.
(vi) The sum of the lengths of the sides of a triangle is called its perimeter.

 

Hope given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 17 Constructions Ex 17C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17A
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17B
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17C
• RS Aggarwal Solutions Class 7 Chapter 17 Constructions CCE Test Paper

Mark (✓) against the correct answer in each of the following:
Question 1.
Solution:
(c) Supplement of 45° is 135°
135°+ 45° = 180°

Question 2.
Solution:
(b) Complement of 80° is 10°
10° + 80° = 90°

Question 3.
Solution:
(b) The angle is its own complement.
The measure of the angles will be 45° (45° + 45° = 90°)

Question 4.
Solution:
(a) The angle is one-fifth of its supplement
Let angle be x, then
x + 5x = 180°
⇒ 6x = 180°
⇒ x = 30°
Angle is 30°

Question 5.
Solution:
(b) Let angle is x
Then its complement angle=x-24° But x + x- 24° = 90°
⇒ 2x = 90° + 24° = 114°
⇒ x = 57°
The required angle is 57°

Question 6.
Solution:
(b) Let required angle = x
Then its supplement angle = x + 32
But x + x + 32° = 180°
⇒ 2x = 180° – 32 = 148°
⇒ x = 74°
Required angle = 74°

Question 7.
Solution:
(c) Two supplementary angle are in the ratio = 3 : 2
Let first angle = 3x
Second angle = 2x
But 3x + 2x = 180°
⇒ 5x = 180°
⇒ x = 36°
Smaller angle = 2x = 2 x 36° = 72°

Question 8.
Solution:
(b) In the figure ∠BOC = 132°
But ∠AOC + ∠BOC =180° (Linear pair)
⇒ ∠AOC + 132° = 180°
⇒ ∠AOC = 180° – 132° = 48°

Question 9.
Solution:
(c) In the figure, ∠AOC = 68°
But ∠AOC + ∠BOC = 180° (Linear pair)
⇒ 68° + x = 180°
⇒ x = 180° – 68° = 112°

Question 10.
Solution:
(b) In the figure,
AOB is a straight line
∠AOC + ∠BOC = 180° (Linear pair)
⇒ 2x – 10° + 3x + 15° = 180°
⇒ 5x = 180° + 10° – 15° = 175°
⇒ x = 35°
x = 35

Question 11.
Solution:
(d) In the figure,
AOB is a straight line
∠AOC + ∠COD + ∠DOB = 180°
⇒ 55° + x + 45° = 180°
⇒ x + 100° = 180°
⇒ x = 180° – 100° = 80°

Question 12.
Solution:
(a) AOB is a straight line
x + y = 180°
But 4x = 5y

Question 13.
Solution:
(b) AB and CD intersect each other at O and ∠AOC = 50°
∠BOD = ∠AOC = 50° (Vertically opposite angles)

Question 14.
Solution:
(a) AOB is a straight line
∠AOC + ∠COD + ∠DOB = 180°
⇒ 3x – 8° + 50° + x + 10° = 180°
⇒ 4x = 180° + 8° – 50° – 10°
⇒ 4x = 128°
⇒ x = 32°

Question 15.
Solution:
(b) In ∆ABC, side BC is produced to D
∠ACD = 132° and ∠A = 54°
Ext. ∠ACD = ∠A + ∠B
⇒ 132° = 54° + ∠B
⇒ ∠B = 132° – 54° = 78°

Question 16.
Solution:
(c) In ∆ABC,
Side BC is produced to D
∠A = 45°, ∠B = 55°
Ext. ∠ACD = ∠A + ∠B = 45° + 55° = 100°

Question 17.
Solution:
(b) In ∆ABC, side BC is produced to D
∠ABC = 70° and ∠ACD = 120°
Ext. ∠ACD = ∠BAC + ∠ABC
⇒ 120° = ∠BAC + 70°
⇒ ∠BAC = 120° – 70° = 50°

Question 18.
Solution:
(c) In the figure,
∠AOB = 50°, ∠BOC = 90°
∠COD = 70°, ∠AOD = x.
But ∠AOB + ∠BOC + ∠COD + ∠DOA = 360° (Angles at a point)
⇒ 50° + 90° + 70° + x = 360°
⇒ 210 + x = 360°
⇒ x = 360° – 210°
⇒ x = 150°

Question 19.
Solution:
(c) In the figure,
Side BC of ∆ABC is produced to D
CE || BA is drawn
∠A = 50° and ∠ECD = 60°
AB || CE
∠ABC = ∠ECD (corresponding angle) = 60°
But in ∆ABC,
∠A + ∠B + ∠ACB = 180° (Angles of a triangles)
⇒ 50° + 60° + ∠ACB = 180°
⇒ ∠ACB = 180° – 50° – 60° = 70°

Question 20.
Solution:
(b) In ∆ABC,
∠A = 65°, ∠C = 85°
But ∠A + ∠B + ∠C = 180° (Angles of a triangle)
⇒ 65° +∠B+ 85° = 180°
⇒ 150° + ∠B = 180°
⇒ ∠B = 180° – 150° = 30°

Question 21.
Solution:
(d) Sum of angles of a triangle = 180°

Question 22.
Solution:
(c) Sum of angles of a quadrilateral = 360°

Question 23.
Solution:
(b) In the figure, AB || CD
∠OAB = 150°, ∠OCD = 120°

From O, draw OE || AB or CD
AB || DE
∠OAB + ∠AOE =180°
⇒ 150° + ∠AOE = 180°
⇒ ∠AOE = 180° – 150° = 30°
Similarly DE || CD
∠EOC + ∠OCD = 180°
⇒ ∠EOC + 120° = 180°
⇒ ∠EOC = 180° – 120° = 60°
Now ∠AOC = ∠AOE + ∠EOC = 30° + 60° = 90°

Question 24.
Solution:
(a) In the given figure,
PQ || RS,
∠PAB = 60° and ∠ACS = 100°
PQ || RS
∠ABC = ∠PAB (alternate angles) = 60°
But Ext. ∠ACS = ∠BAC + ∠ABC
⇒ 100° = ∠BAC + 60°
⇒ ∠BAC = 100° – 60° = 40°

Question 25.
Solution:
(c) In the figure, AB || CD || EF
∠ABG =110° and ∠GCD = 100°
∠BGC = x°
AB || EF
∠ABG + ∠BGE = 180°
⇒ 110° + ∠BGE = 180°
⇒ ∠BGE = 180° – 110° = 70°
Similarly CD || EF
∠GCD + ∠CGF = 180°
⇒ 100° + ∠CGF = 180°
⇒ ∠CGF = 180° – 100° = 80°
But ∠BGE + ∠BGC + ∠CGF = 180°
⇒ 70° + x + 80° = 180°
⇒ 150° + x = 180°
⇒ x = 180° – 150° = 30°

Question 26.
Solution:
(d) Sum of any two sides of a triangle is always greater than the third side

Question 27.
Solution:
(d) The diagonals of a rhombus always bisect each other at right angles.

Question 28.
Solution:
(c) In ∆ABC, ∠B = 90°
AB = 5 cm and AC = 13 cm
But AC² = AB² + BC² (By Pythagoras Theorem)
⇒ (13)² = (5)² + BC²
⇒ 169 = 25 + BC2
⇒ BC² = 169 – 25 = 144 = (12)²
BC = 12 cm

Question 29.
Solution:
(c) In ∆ABC, ∠B = 37°, ∠G = 29°
But ∠A + ∠B + ∠C = 180° (angles of a triangle)
⇒ ∠A + 37° + 29° = 180°
⇒ ∠A + 66° = 180°
⇒ ∠A = 180° – 66° = 114°

Question 30.
Solution:
(c) The ratio of angles of a triangle is 2 : 3 : 7
But sum of angles of a triangle = 180°

Question 31.
Solution:
In ∆ABC,
Let 2∠A = 3∠B = 6∠C = x

Question 32.
Solution:
(a) In ∆ABC,
∠A + ∠B = 65°, ∠B + ∠C = 140°
∠A = 65°
∠C = 140° – ∠B
But ∠A + ∠B + ∠C = 180° (Angles of a triangle)
⇒ 65° – ∠B + 140° – ∠B + ∠B = 180°
⇒ 205° – ∠B = 180°
⇒ ∠B = 205° – 180° = 25°

Question 33.
Solution:
(b) In ∆ABC, ∠A – ∠B = 33°
and ∠B – ∠C = 18°
∠A = 33° + ∠B and ∠C = ∠B – 18°
But ∠A + ∠B + ∠C = 180°
⇒ 33° + ∠B + ∠B + ∠B – 18° = 180°
⇒ 3∠B = 180° – 33° + 18° = 165°
⇒ ∠B = 55°

Question 34.
Solution:
(c) In ∆ABC
∠A + ∠B + ∠C= 180° (Sum of angles of a triangle)
But angles are (3x)°, (2x – 7)° and (4x – 11)°
3x + (2x – 7) + (4x – 11)° = 180°
⇒ 3x + 2x – 7 + 4x – 11° = 180°
⇒ 9x – 18° = 180°
⇒ 9x = 180° + 18° = 198°
⇒ x = 22°

Question 35.
Solution:
(c) ∆ABC is a right angled, ∠A = 90°
AB = 24 cm, AC = 7 cm

but BC² = AB² + AC²
⇒ BC² = (24)² + (7)² = 576 + 49 = 625 = (25)²
BC = 25 cm

Question 36.
Solution:
(b) Let AB is a ladder and A is the window
BC = 15 m, AC = 20 m

Now in right ∆ABC
AB² = BC² + AC² = (15)² + (20)² = 225 + 400 = 625 = (25)²
AB = 25 m
Length of ladder = 25 m

Question 37.
Solution:
(a) Let AB and CD are two poles such that
AB = 6 m, CD = 11 m
and distance between two poles BD = 12m
From A, draw AE || BD
AE = BD = 12m
CE = CD – ED = 11 – 6 = 5 m

Now in right ∆AEC
AC² = AE² + CE² = (12)² + (5)² = 144 + 25 = 169 = (13)²
AC = 13 m
Distance between tops of poles = 13 m

Question 38.
Solution:
(d) ∆ABC is an isosceles triangle
∠C = 90°,
AC = 5 cm
BC = AC = 5 cm

In right ∆ABC
AB² = AC² + BC² = (5)² + (5)² = 25 + 25 = 50 = 2 x 25
AB = √(2 x 25) = 5√2 cm

Hope given RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 12 Simple Interest CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest CCE Test Paper.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12A
• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12B
• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest CCE Test Paper

Question 1.
Solution:

Question 2.
Solution:
Let the sum be ₹ x

Question 3.
Solution:
P = ₹ 3625, A = ₹ 4495, T = 2 years
S.I. = A – P = ₹ 4495 – ₹ 3625 = ₹ 870

Question 4.
Solution:
P = ₹ 3600, A = ₹ 4410, R = 9%
S.I. = A – P = ₹ 4410 – ₹ 3600 = ₹ 810

Question 5.
Solution:
Let the sum be ₹ x
Amount = ₹ 2x
S.I. = (2x – x) = ₹ x
Time = 12 years
P = x, S.I. = x, T = 12 years

Question 6.
Solution:
Let the sum be ₹ 4

Mark (✓) against the correct answer in each of the following :
Question 7.
Solution:
(c) 9%
Let the sum be ₹ x
A = \(\frac { 49x }{ 40 }\)
We know:
A = P + S.I.
S.I. = A – P

Question 8.
Solution:
(c) ₹ 3500
A = ₹ 3626, R = 6%,

Question 9.
Solution:
(a) 9 months
P = ₹ 6000, A = ₹ 6360
S.I. = A – P = 6300 – 6000 = ₹ 360

Question 10.
Solution:
(c) 12%
Let the sum be ₹ x

Question 11.
Solution:

P = ₹ \(\frac { 100 }{ x }\)

Question 12.
Solution:
(b) 10%
Let the sum be ₹ x
Amount ₹ 2x
Time =10 years
S.I. = A – P = 2x – x = ₹ x

Question 13.
Solution:

Question 14.
Solution:
(i) False

Hope given RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 12 Simple Interest Ex 12B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12A
• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12B
• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest CCE Test Paper

Question 1.
Solution:
Principal (P) = Rs. 6250
Rate of (R) = 4% p.a.
Period (T) = 6 months = \(\frac { 1 }{ 2 }\) year

Question 2.
Solution:
Amount (A) = Rs. 3605
Rate (R) = 5% p.a.

Question 3.
Solution:
Let sum (P) = Rs. 100

Question 4.
Solution:
Principal (P) = Rs. 8000
Amount (A) – Rs. 8360
S.I. = A – P = Rs. 8360 – Rs. 8000 = Rs. 360
Rate (R) = 6% p.a.

Question 5.
Solution:
Let sum (P) = Rs. 100
Then amount (A) = Rs. 100 x 2 = Rs. 200
S.I. = A – P = Rs. 200 – Rs. 100 = Rs. 100
Period (T) = 10 years

Question 6.
Solution:
S.I. = Rs. x
Rate (R) = x% p.a.
Time (T) = x year

Rs. \(\frac { 100 }{ x }\) (c)

Question 7.
Solution:
Let sum (P) = Rs. 100

Question 8.
Solution:
A’s principal (P) = Rs. 8000
Rate (R) = 12% p.a.
B’s principal = Rs. 9100
Rate = 10%
Let after x years, then amount will be equal

Question 9.
Solution:
Amount (A) = Rs. 720
Principal (P) = Rs. 600
S.I. = A – P = Rs. 720 – 600 = Rs. 120
Period (T) = 4 years

Question 10.
Solution:

Question 11.
Solution:
Let sum (P) = Rs. 100
Their S.I. = 0.125 of Rs. 100

Question 12.
Solution:
S.I. = Rs. 210

Hope given RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 12 Simple Interest Ex 12A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12A
• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12B
• RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest CCE Test Paper

Find the simple interest and the amount when :
Question 1.
Solution:
Principal (P) = Rs. 6400
Rate (r) = 6% p.a.
Time (t) = 2 years

Question 2.
Solution:
Principal (P) = Rs. 2650
Rate (r) = 8% p.a.

Question 3.
Solution:
Principal (P) = Rs. 1500
Rate (r) = 12% p.a.

Question 4.
Solution:
Principal (P) = Rs. 9600

Question 5.
Solution:
Principal (P) = Rs. 5000
Rate (r) = 9% p.a.

Find the time when :
Question 6.
Solution:
Principal (P) = Rs. 6400
S.I. = Rs. 1152
Rate (r) = 6% p.a.

Question 7.
Solution:
Principal (P) = Rs. 9540
S.I. = Rs. 1908
Rate (r) = 8% p.a.

Question 8.
Solution:
Amount (A) = Rs. 6450
Principal (P) = Rs. 5000
S.I. = A – P = Rs. (6450 – 5000) = Rs. 1450
Rate (r) = 12% p.a.

Find the rate when :
Question 9.
Solution:
Principal (P) = Rs. 8250
S.I. = Rs. 1100
Time (t) = 2 years

Question 10.
Solution:
Principal (P) = Rs. 5200
S.I. = Rs. 975

Question 11.
Solution:
Principal (P) = Rs. 3560
Amount (A) = Rs. 4521.20
S.I. = A – P = Rs. 4521.20 – 3560 = Rs. 961.20
Time (t) = 3 years

Question 12.
Solution:
Principal (P) = Rs. 6000
Rate (r) = 12% p.a.

Question 13.
Solution:
Principal = Rs. 12600
Rate (A) = 15% p.a.
Time (t) = 3 years

Amount = P + S.I. = Rs. 12600 + Rs. 5670 = Rs. 18270
Amount paid in cash = Rs. 7070
Balance = Rs. 18270 – 7070 = Rs. 11200
Price of goat = Rs. 11200

Question 14.
Solution:
S.I. = Rs. 829.50
Rate (r) = 10% p.a.
Time (t) = 3 years

Question 15.
Solution:
Amount (A) = Rs. 3920

Question 16.
Solution:
Amount = Rs. 4491
Let principal (P) = Rs. 100
Rate (r) =11% p.a.
Time (t) = 2 years 3 months = 2\(\frac { 1 }{ 4 }\) = \(\frac { 9 }{ 4 }\) years

Question 17.
Solution:
Amount = Rs. 12122
Let principal (P) = Rs. 100
Rate (r) = 8% p.a.
Time (t) = 2 years

Question 18.
Solution:
Amount (A) = Rs. 4734
Principal (P) = Rs. 3600
S.I. = A – P = Rs. 4734 – Rs. 3600 = Rs. 1134

Question 19.
Solution:
In first case,
Amount (A) = Rs. 768
Principal (P) = Rs. 640
S.I. = A – P = Rs. 768 – 640 = Rs. 128

Question 20.
Solution:
Principal (P) = Rs. 5600
Amount (A) = Rs. 6720
S.I. = A – P = Rs. 6720 – 5600 = Rs. 1120
Rate (r) = 8% p.a.

Question 21.
Solution:
Let principal (P) = Rs. 100
then amount (A) = Rs. 100 x \(\frac { 8 }{ 5 }\) = Rs. 160
S.I. = A – P = Rs. 160 – 100 = Rs. 60
Time (t) = 5 years

Question 22.
Solution:
Amount in 3 years = Rs. 837
Amount in 2 years = Rs. 783
Difference = Rs. 837 – Rs. 783 = Rs. 54
Rs. 54 is interest for 1 year
Interest for 2 years = 2 x 54 = Rs. 108
Principal = Rs. 783 – 108 = Rs. 675

Question 23.
Solution:
Amount in 5 years = Rs. 5475
Amount in 3 years = Rs. 4745
Interest for 2 years = Rs. 5475 – 4745 = Rs. 730

Question 24.
Solution:
Total sum = Rs. 3000
Let first part = Rs. x
Then second part = Rs. (3000 – x)
Now, interest on first part at the rate of

Question 25.
Solution:
Total sum =Rs. 3600
Let first part = Rs. x
Then second part = Rs. (3600 – x)
Interest on first part for 1 year at 9% p.a.

⇒ 9x + 10 (3600 – x) = 33300
⇒ 9x + 36000 – 10x = 33300
⇒ -x = 33300 – 36000
⇒ -x = – 2700
⇒ x = 2700
First part = Rs. 2700
and second part = Rs. 3600 – 2700 = Rs. 900

Hope given RS Aggarwal Solutions Class 7 Chapter 12 Simple Interest Ex 12A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 11 Profit and Loss CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss CCE Test Paper.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11A
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11B
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss CCE Test Paper

Question 1.
Solution:
SP of the chair = ₹ 1375
Gain% = 10
CP of the chair

Question 2.
Solution:
Let the cost of each pen be ₹ 1
CP of 10 pens = ₹ 10
SP of 10 pens = CP of 14 pens = ₹ 14
Gain = SP – CP = 14 – 10 = ₹ 4

Question 3.
Solution:
Let the cost price of the fan be ₹ x

Question 4.
Solution:
Cost price of six lemons = ₹ 10

Question 5.
Solution:
SP of the bat = ₹ 486
Loss = 10%
CP of the bat

Mark (✓) against the correct answer in each of the following :
Question 6.
Solution:
(b) ₹ 85
SP of a football = ₹ 100
Gain = ₹ 15
Gain = SP – CP
⇒ 15 = 100 – CP
⇒ CP = ₹ (100 – 15)
⇒ CP = ₹ 85

Question 7.
Solution:
(c) 15.2%
Cost price of 12 bananas = ₹ 25
Cost price of one banana = ₹ \(\frac { 25 }{ 12 }\)
Cost price of five bananas = 5 x \(\frac { 25 }{ 12 }\)
= \(\frac { 125 }{ 12 }\) = 10.42
He shells five bananas at the cost (SP) of ₹ 12.
Gain = SP – CP = ₹ (12 – 10.42) = ₹ 1.58

Question 8.
Solution:
(c) ₹ 196
Let the cost price of the jug be ₹ x

Question 9.
Solution:
(c) 66\(\frac { 2 }{ 3 }\) %
Let the cost price of each banana be ₹ 1
Cost price of three bananas = ₹ 3
SP of three bananas = CP of five bananas = ₹ 5
Gain = SP – CP = ₹ (5 – 3) = ₹ 2

Question 10.
Solution:
(i) Loss = (CP) – (SP).

Question 11.
Solution:
(i) False
Gain or loss is always reckoned on the cost price.
(ii) True
(iii) True
(iv) True

Hope given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 11 Profit and Loss Ex 11B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11A
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11B
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss CCE Test Paper

Objective Questions :
Mark (✓) against the correct answer in each of the following :
Question 1.
Solution:
(b)
C.P. = Rs. 80
S.P. = Rs. 100
Gain = S.P. – C.P. = Rs. 100 – 80 = Rs. 20

Question 2.
Solution:
(a)
C.P. = Rs. 120
S.P. = Rs. 105
Loss = C.P. – S.P. = Rs. 120 – 105 = Rs. 15

Question 3.
Solution:
(b)
S.P. = Rs. 100
Gain = Rs. 20
C.P. = S.P. – gain = Rs. 100 – 20 = Rs. 80

Question 4.
Solution:
(a)
S.P. = Rs. 198
Gain = 10%

Question 5.
Solution:
(a)
First S.P. of jug = Rs. 144
Loss = \(\frac { 1 }{ 7 }\) of C.P.
Let C.P. = x

Question 6.
Solution:
(d)
First S.P. of a pen = Rs. 48
Loss = 20%

Question 7.
Solution:
(a)
C.P. of 12 pencils = S.P. of 15 pencils = Re 1 (suppose)

Question 8.
Solution:
(d)
Let CP of 4 toffees = SP of 3 toffee = Rs. 12
(LCM of 4, 3 = 12)
CP of 1 toffee = Rs. \(\frac { 12 }{ 4 }\) = Rs. 3
SP of 1 toffee = Rs. \(\frac { 12 }{ 3 }\) = 4
Gain = Rs. 4 – 3 = Re 1

Question 9.
Solution:
(c) SP of an article = Rs. 144
Loss% = 10%

Question 10.
Solution:
(a)
CP of 6 lemons = Re 1
CP of 1 lemon = Re \(\frac { 1 }{ 6 }\)
SP of 4 lemons = Re 1
SP of 1 lemon = Re \(\frac { 1 }{ 4 }\)

Question 11.
Solution:
(d)
SP of chair = Rs. 720
Gain% = 20%

Question 12.
Solution:
(c)
SP of stool = Rs. 630
Loss% = 10%

Hope given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 11 Profit and Loss Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11A
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11B
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss CCE Test Paper

Question 1.
Solution:
(i) C.P. = Rs. 950

Question 2.
Solution:
(i) CP = Rs. 2400
SP = Rs. 2592
Gain = SP – CP = Rs. 2592 – Rs. 2400 = Rs. 192

Question 3.
Solution:
(i) S.P. = Rs. 924
Gain% = 10%

Question 4.
Solution:
C.P. of an almirah = Rs. 13600
Amount spent on transportation = Rs. 400
Total cost price (CP) = Rs. 13600 + Rs. 400 = Rs. 14000
SP = Rs. 16800
Total gain = SP – CP
= Rs. 16800 – Rs. 14000 = Rs. 2800

Question 5.
Solution:
CP of an old house = Rs. 765000
Amount spent on repairs = Rs. 115000
Total cost price (CP) = Rs. 765000 + Rs. 115000 = Rs. 880000
Gain = 5%

Question 6.
Solution:
CP of 1 dozen or 12 lemons = Rs. 25
SP of 5 lemons = Rs. 12

Question 7.
Solution:
SP of 12 pens = CP of 15 pens
Let CP of 1 pen = Re. 1
The CP of 15 pens = Rs. 15
and SP of 12 pens = Rs. 12

Question 8.
Solution:
SP of 16 spoons = CP of 15 spoons
Let CP of 1 spoon = Re. 1
Then CP of 15 spoons = Rs. 15
and SP of 16 spoons = Rs. 15

Question 9.
Solution:
For Manoj
CP of video = Rs. 12000
Gain = 10%

Question 10.
Solution:
SP of sofa set = Rs. 21600
Gain = 8%

Question 11.
Solution:
SP of a watch = Rs. 11400
Loss = 5%

Question 12.
Solution:
SP of calculator = Rs. 1325
Gain = 6%

Question 13.
Solution:
SP of computer = Rs. 24480
Loss = 4%

Question 14.
Solution:
In first case gain =15%
and in second case, gain = 20%
Difference = 20 – 15 = 5%
Now 5% of the CP = Rs. 108
CP = \(\frac { 108 x 100 }{ 5 }\) = Rs. 2160

Question 15.
Solution:
In first case, loss = 8%
and in second case gain = 6%
Difference = 8 + 6 = 14%
Now 14% of CP = Rs. 3360
CP = Rs. \(\frac { 3360 x 100 }{ 14 }\) = Rs. 24000

Question 16.
Solution:
SP of first cycle = Rs. 2376
Gain = 10%

Question 17.
Solution:
SP of an exhaust fan = Rs. 7350

Question 18.
Solution:
Let CP of watch for Mohit = Rs. 100
Gain =10%
SP for Mohit = Rs. 100 + 10 = Rs. 110
CP for Karim = Rs. 110
Gain = 4%

Question 19.
Solution:
Retail price or S.P. of the machine for retailer = Rs. 37950
Gain = 25%

Question 20.
Solution:
CP of video = Rs. 20000
and CP of television = Rs. 30000
Loss on video = 5%
and gain on TV = 8%

Total CP of video and TV = Rs. 20000 + 30000 = Rs. 50000
and SP of video and TV = Rs. 190000 + 32400 = RS. 51400
Gain = SP – CP = Rs. 51400 – 50000 = Rs. 1400

Question 21.
Solution:
SP of 36 oranges = CP of 36 oranges – loss = CP of 36 oranges – SP of 4 oranges
⇒ SP of 36 oranges + SP of 4 oranges = CP of 3 6 oranges
⇒ SP of 40 oranges = CP of 36 oranges
Let CP of each orange = Re. 1
CP of 36 oranges = Rs. 36
and SP of 40 of 40 oranges = Rs. 36

Question 22.
Solution:
We know that C.P. = S.P. – gain
C.P. of 8 dozen pencils = S.P. of 8 dozen pencils – S.P. of 1 dozen pencils
= S.P. of 7 dozen pencils = Rs. 100 (suppose)
C.P. of 1 dozen = Rs.\(\frac { 100 }{ 8 }\)

 

Hope given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 10 Percentage CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 10 Percentage CCE Test Paper.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10A
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10B
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10C
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage CCE Test Paper

Question 1.
Solution:
We have :

Question 2.
Solution:
(i) Let x% of 1 kg be 125 g

Question 3.
Solution:

Question 4.
Solution:
(i) Let x be the required number.

Question 5.
Solution:
Let x be the number
The number is increased by 10%
Increased number = 110% of x

Question 6.
Solution:
The present value of the machine = ₹ 10000
The decrease in its value after the 1 st year = 10% of ₹ 10000
\(\frac { 10 }{ 100 }\) x 10000 = ₹ 1000
The depreciated value of the machine after the 1 st year = ₹ (10000 – 1000) = ₹ 9000
The decrease in its value after th 2nd year = 10% of ₹ 9000
\(\frac { 10 }{ 100 }\) x 9000 = 900
The depreciated value of the machine after the 2nd year = ₹ (9000 – 900) = ₹ 8100
Hence, the value of the machine after two years will be ₹ 8100.

Question 7.
Solution:
The present population of the town = 16000
Increase in population after 1 year = 5% of 16000
= (\(\frac { 5 }{ 100 }\) x 16000) = 800
Thus, population after one year = 16000 + 800 = 16800
Increase in population after 2 years = 5% of 16800
= \(\frac { 5 }{ 100 }\) x 16800 = 840
Population after two years = 16800 + 840 = 17640
Hence, the population of the town after two years will be 17,640.

Question 8.
Solution:
Let us assume that the original price of the tea set is Increase in price = 5%
So, value increased on the tea set = 5% of ₹ x

Hence, the original price of the tea set is ₹ 420.

Mark (✓) against the correct answer in each of the following :
Question 9.
Solution:

Question 10.
Solution:
(c) 12
Given that x% of 75 = 12

Question 11.
Solution:
(c) 25
Let the number be x. Then, we have:
120% of x = increased number

Question 12.
Solution:
(d) 180
Let the required number be x.
Then, we have :
5% of x = 9

Question 13.
Solution:
(a) 60
Let the number be x According to question, we get:
(35 % of x) + 39 = x

Question 14.
Solution:
(c) 500
Let x be the maximum marks Pass marks = (160 + 20) = 180
36 % of x = 180

Question 15.
Solution:
(i) 3 : 4 = (75) %
Explanation:
3 : 4 = \(\frac { 3 }{ 4 }\)
= (\(\frac { 3 }{ 4 }\) x 100) %
= (3 x 25)% = 75%
(ii) 0.75 = (75)%
Explanation : (0.75 x 100)% = 75%
(iii) 6% = 0.06 (express in decimals)
Explanation :
6% = \(\frac { 6 }{ 100 }\) = 0.06
(iv) If x decreased by 40% gives 135, then x = 225
Explanation :
Let the number be x.
According to question, we have :
x – 40% of x = 135

Question 16.
Solution:
(i) True (T)

Hope given RS Aggarwal Solutions Class 7 Chapter 10 Percentage CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 10 Percentage Ex 10C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10A
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10B
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10C
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage CCE Test Paper

Objective Questions :
Mark (✓) against the correct answer in each of the following :
Question 1.
Solution:
(b) \(\frac { 3 }{ 4 }\) = \(\frac { 3 }{ 4 }\) x 100 = 75 %

Question 2.
Solution:
(c)
2 : 5 = \(\frac { 2 }{ 5 }\) = \(\frac { 2 }{ 5 }\) x 100 = 40%

Question 3.
Solution:
(c)

Question 4.
Solution:
(c) x% of 75 = 9

Question 5.
Solution:
(d)

Question 6.
Solution:
(b)
Let x% of 1 day = 36 minutes

Question 7.
Solution:
(a)
Let x be the required number

Question 8.
Solution:
(b)
Let x be the required number, then

Question 9.
Solution:
(d)
Let ore = x, then
5% of x = 400g
\(\frac { x x 5 }{ 100 }\) 400

Question 10.
Solution:
(b)
Let gross value of T.V = x
Commission = 10%
After deducting commission, the value

Question 11.
Solution:
(b)
Increase in salary = 25%
Let original salary = x

Question 12.
Solution:
(c)
Let x be the number of total examinees
No. of examinees passed

Question 13.
Solution:
(c)
Let total number of apples = x

Question 14.
Solution:
(b)
Present value of machine = Rs. 25000
Rate of depreciation = 10% p.a.
Value of machine after one year

Question 15.
Solution:
(c) Let x be numbers

Question 16.
Solution:
(c) 60% of 450
= \(\frac { 60 }{ 100 }\) x 450 = 270

Question 17.
Solution:
(d) Rate of reduction = 6%
Price after reduction = Rs. 658

Question 18.
Solution:
(b) Boys = 70% of students
No. of girls = 240
Girls percentage = 100 – 70 = 30%

Question 19.
Solution:
(c) Let number = x
11% of x – 7% of x = 18

Question 20.
Solution:
(a) Let number = x
35% of x + 39 = x

Question 21.
Solution:
(c) Pass marks = 36%
A students get =145 marks
But failed by 3 5 marks
Then pass marks = 145 + 35 = 180
Maximum marks = \(\frac { 180 x 100 }{ 36 }\) = 500

Question 22.
Solution:
(d) Let number be = x
Then decreasing by 40%

Hope given RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.