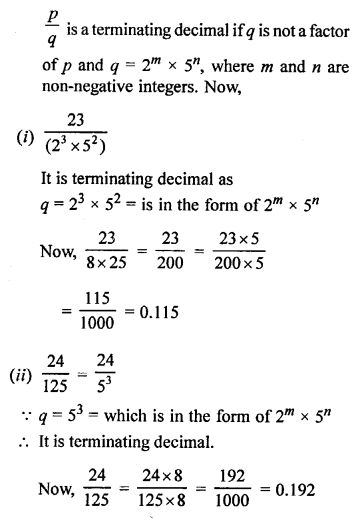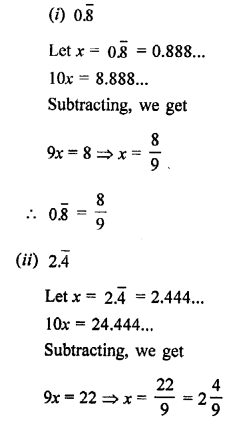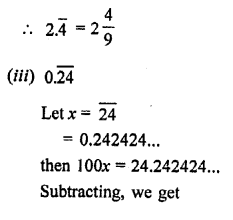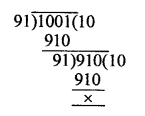RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself
Very-Short-Answer and Short-Answer Questions
Question 1.
Solution:
Two properties for similarity of two triangles are:
(i) Angle-Angle-Angle (AAA) property.
(ii) Angle-Side-Angle (ASA) property.
Question 2.
Solution:
In a triangle, if a line parallel to one side is drawn, it will divide the other two sides proportionally.
Question 3.
Solution:
If a line divides any two sides of a triangle in the same ratio. Then, the line must be parallel to the third side.
Question 4.
Solution:
The line joining the midpoints of two sides of a triangle, is parallel to the third side.
Question 5.
Solution:
In two triangles, if three angles of the one triangle are equal to the three angles of the other, the triangles are similar.
Question 6.
Solution:
In two triangles, if two angles of the one triangle are equal to the corresponding angles of the other triangle, then the triangles are similar.
Question 7.
Solution:
In two triangles, if three sides of the one are proportional to the corresponding sides of the other, the triangles are similar.
Question 8.
Solution:
In two triangles, if two sides of the one are proportional to the corresponding sides of the other and their included angles are equal, the two triangles are similar.
Question 9.
Solution:
In a right angled triangle, the square on the hypotenuse is equal to the sum of squares on the other two sides.
Question 10.
Solution:
In a triangle, if the square on the longest side is equal to the sum of the squares on the other two sides, then the angle opposite to the hypotenuse is a right angle.
Question 11.
Solution:
The ratio of their areas will be 1 : 4.
Question 12.
Solution:
In two triangles ∆ABC and ∆PQR,
AB = 3 cm, AC = 6 cm, ∠A = 70°
PR = 9 cm, ∠P = 70° and PQ= 4.5 cm
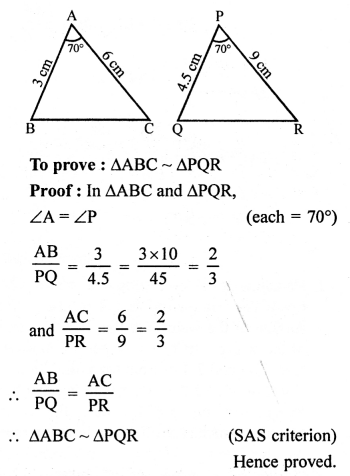
Question 13.
Solution:
∆ABC ~ ∆DEF
2AB = DE, BC = 6 cm
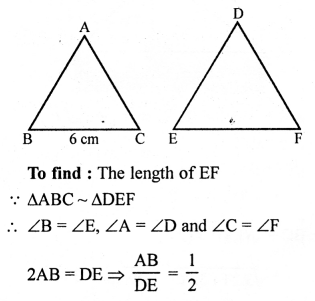

Question 14.
Solution:
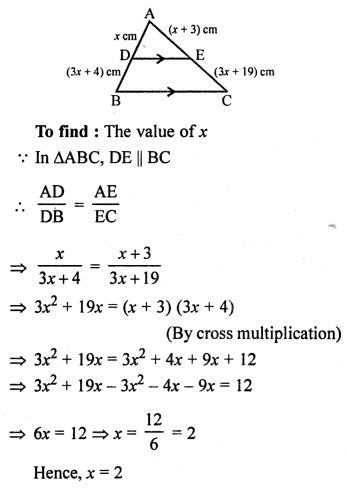
In the given figure,
DE || BC
AD = x cm, DB = (3x + 4) cm
AE = (x + 3) cm and EC = (3x + 19) cm
Question 15.
Solution:
AB is the ladder and A is window.
AB =10 m, AC = 8 m
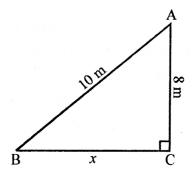
We have to find the distance of BC
Let BC = x m
In right ∆ABC,
AB² = AC² + BC² (Pythagoras Theorem)
(10)² = 8² + x²
⇒ 100 = 64 + x²
⇒ x² = 100 – 64 = 36 = (6)²
x = 6
Distance between foot of ladder and base of the wall = 6 m.
Question 16.
Solution:
∆ABC is an equilateral triangle with side = 2a cm
AD ⊥ BC
and AD bisects BC at D
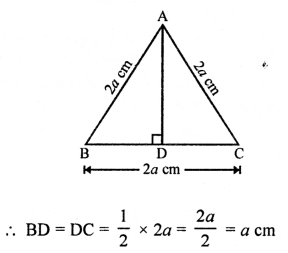
Now, in right ∆ABD,
AB² = AD² + BD² (Pythagoras Theorem)
⇒ (2a)² = AD² + (a)²
⇒ 4a² = AD² + a²
⇒ AD² = 4a² – a² = 3a²
AD = √3 a² = √3 a cm
Question 17.
Solution:
Given : ∆ABC ~ ∆DEF
and ar (∆ABC) = 64 cm²
and ar (∆DEF) = 169 cm², BC = 4 cm.
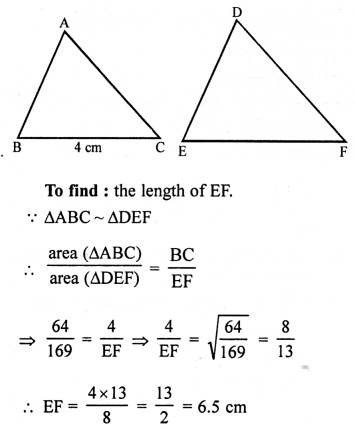
Question 18.
Solution:
In trape∠ium ABCD,
AB || CD
AB = 2CD
Diagonals AC and BD intersect each other at O
and area(∆AOB) = 84 cm².
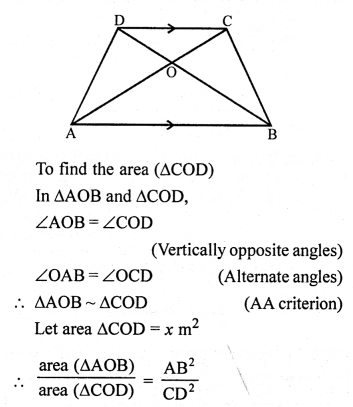

Question 19.
Solution:
Let ∆ABC ~ ∆DEF

Question 20.
Solution:
In an equiangular ∆ABC,
AB = BC = CA = a cm.
Draw AD ⊥ BC which bisects BC at D.
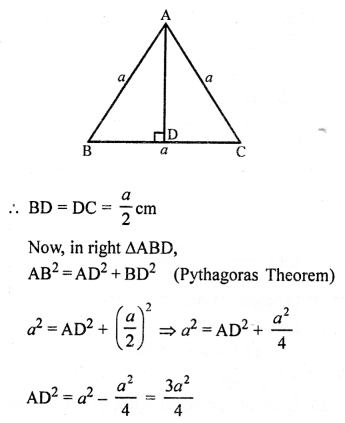

Question 21.
Solution:
ABCD is a rhombus whose sides are equal and diagonals AC and BD bisect each other at right angles.
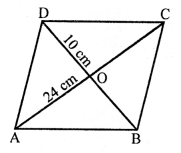
∠AOB = 90° and AO = OC, BO = OD
AO = \(\frac { 24 }{ 2 }\) = 12 cm
and BO = \(\frac { 10 }{ 2 }\) = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² (Pythagoras Theorem)
= (12)² + (5)² = 144 + 25 = 169 = (13)²
AB = 13
Each side of rhombus = 13 cm
Question 22.
Solution:
∆DEF ~ ∆GHK
∠D = ∠G = 48°
∠E = ∠H = 57°
∠F = ∠K
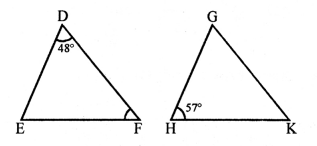
Now, in ∆DEF,
∠D + ∠E + ∠F = 180° (Angles of a triangle)
⇒ 48° + 57° + ∠F = 180°
⇒ 105° + ∠F= 180°
⇒ ∠F= 180°- 105° = 75°
Question 23.
Solution:
In the given figure,
In ∆ABC,
MN || BC
AM : MB = 1 : 2

Question 24.
Solution:
In ∆BMP,
PB = 5 cm, MP = 6 cm and BM = 9 cm
and in ∆CNR, NR = 9 cm


Question 25.
Solution:
In ∆ABC,
AB = AC = 25 cm
BC = 14 cm
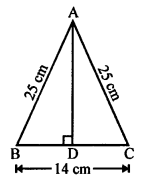
AD ⊥ BC which bisects the base BC at D.
BD = DC = \(\frac { 14 }{ 2 }\) = 7 cm
Now, in right ∆ABD,
AB² = AD² + BD² (Pythagoras Theorem)
(25)² = AD² + 7²
625 = AD² + 49
⇒ AD² = 625 – 49 = 576
⇒ AD² = 576 = (24)²
AD = 24 cm
Length of altitude = 24 cm
Question 26.
Solution:
A man goes 12 m due north of point O reaching A and then 37 m due west reaching B.
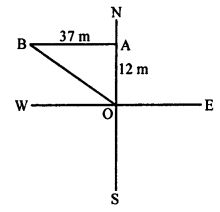
Join OB,
In right ∆OAB,
OB² = OA² + AB² (Pythagoras Theorem)
= (12)² + (35)² = 144 + 1225 = 1369 = (37)²
OB = 37 m
The man is 37 m away from his starting point.
Question 27.
Solution:
In ∆ABC, AD is the bisector of ∠A which meets BC at D.
AB = c, BC = a, AC = b
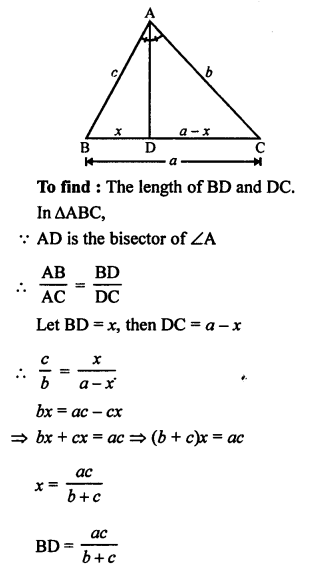
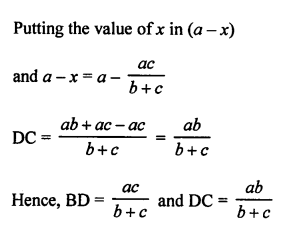
Question 28.
Solution:
In the given figure, ∠AMN = ∠MBC = 76°
p, q and r are the lengths of AM, MB and BC Express the length of MN in terms of p, q and r.
In ∆ABC,
∠AMN = ∠MBC = 76°
But there are corresponding angles
MN || BC
∆AMN ~ ∆ABC
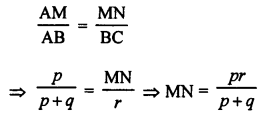
Question 29.
Solution:
In rhombus ABCD,
Diagonals AC and BD bisect each other at O at right angles.
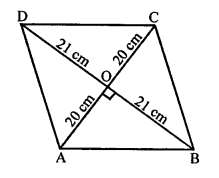
AO = OC = \(\frac { 40 }{ 2 }\) = 20 cm
BO = OD = \(\frac { 42 }{ 2 }\) = 21 cm
Now, in right ∆AOB,
AB2 = AO2 + BO2 = (20)2 + (21)2 = 400 + 441 = 841
AB = √841 cm = 29 cm
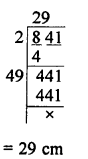
Each side of rhombus = 29 cm
For each of the following statements state whether true (T) or false (F):
Question 30.
Solution:
(i) True.
(ii) False, as sides will not be proportion in each case.
(iii) False, as corresponding sides are proportional, not necessarily equal.
(iv) True.
(v) False, in ∆ABC,
AB = 6 cm, ∠A = 45° and AC = 8 cm
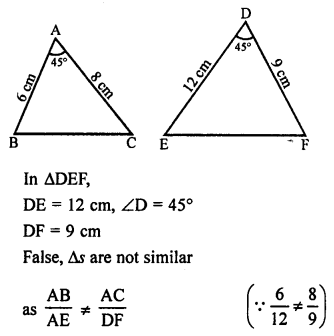
(vi) False, the polygon joining the midpoints of a quadrilateral is not a rhombus but it is a parallelogram.
(vii) True.
(viii) True.
(ix) True, O is any point in rectangle ABCD then
OA² + OC² = OB² + OD² is true.
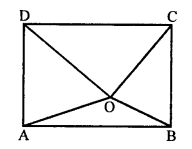
(x) True.
Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.