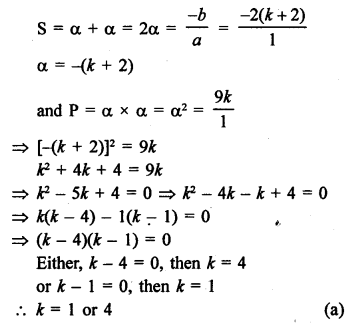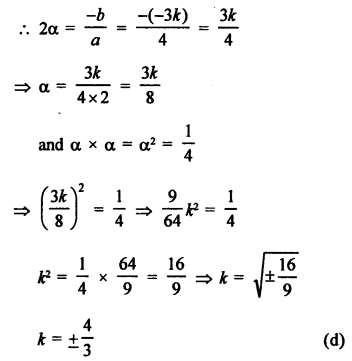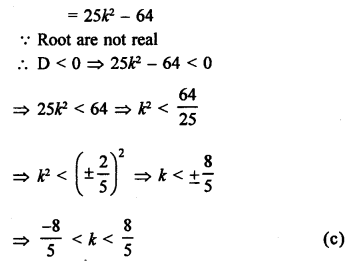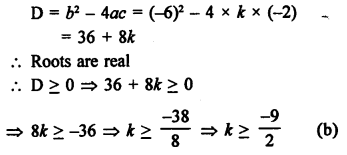RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers Ex 1A
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1B
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQs
- RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself
Question 1.
Solution:
For any two given positive integers a and b, there exist unique whole numbers q and r such that
a = bq + r, when 0 ≤ r < b.
Here, a is called dividend, b as divisor, q as quotient and r as remainder.
Dividend = (Divisor x Quotient) + Remainder.
Question 2.
Solution:
Using Euclid’s divison Lemma
Dividend = (Divisor x Quotient) + Remainder
= (61 x 27) + 32
= 1647 + 32
= 1679
Required number = 1679
Question 3.
Solution:
Let the required divisor = x
Then by Euclid’s division Lemma,
Dividend = (Divisor x Quotient) + remainder
1365 = x x 31 + 32
=> 1365 = 31x + 32
=> 31x= 1365 – 32 = 1333
x = \(\frac { 1331 }{ 31 }\) = 43
Divisor = 43
Question 4.
Solution:
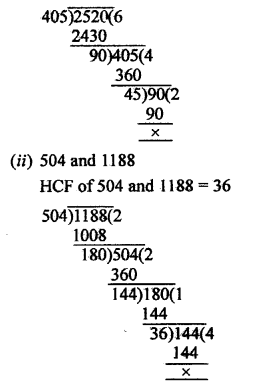
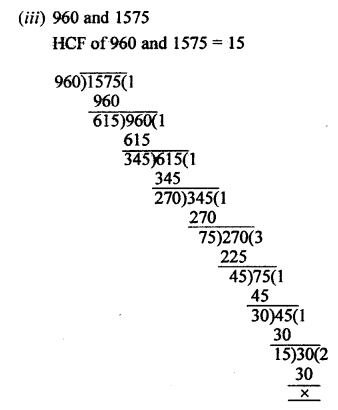
(i) 405 and 2520
HCF of 405 and 2520 = 45
Question 5.
Solution:
Let n be an arbitrary positive integer.
On dividing n by 2, let m be the quotient and r be the remainder, then by Euclid’s division lemma
n = 2 x m + r = 2m + r, 0 ≤ r < 2
n = 2m or 2m + 1 for some integer m.
Case 1 : When n = 2m, then n is even
Case 2 : When n = 2m + 1, then n is odd.
Hence, every positive integer is either even or odd.
Question 6.
Solution:
Let n be a given positive odd integer.
On dividing n by 6, let m be the quotient and r be the remainder, then by Euclid’s division Lemma.
n = 6m + r, where 0 ≤ r < 6 => n = 6m + r, where r = 0, 1, 2, 3, 4, 5
=> n = 6m or (6m + 1) or (6m + 2) or (6m + 3) or (6m + 4) or (6m + 5)
But n = 6m, (6m + 2) and (6m + 4) are even.
Thus when n is odd, it will be in the form of (6m + 1) or (6m + 3) or (6m + 5) for some integer m.
Question 7.
Solution:
Let n be an arbitrary odd positive integer.
On dividing by 4, let m be the quotient and r be the remainder.
So by Euclid’s division lemma,
n = 4m + r, where 0 ≤ r < 4
n = 4m or (4m + 1) or (4m + 2) or (4m + 3)
But 4m and (4m + 2) are even integers.
Since n is odd, so n ≠ 4m or n ≠ (4m + 2)
n = (4m + 1) or (4m + 3) for some integer m.
Hence any positive odd integer is of the form (4m + 1) or (4m + 3) for some integer m.
Question 8.
Solution:
Let a = n3 – n
=> a = n (n2 – 1)
=> a = n (n – 1) (n + 1) [(a2 – b2) = (a – b) (a + b)]
=> a = (n – 1 ) n (n + 1)
We know that,
(i) If a number is completely divisible by 2 and 3, then it is also divisible by 6.
(ii) If the sum of digits of any number is divisible by 3, then it is also divisible by 3.
(iii) If one of the factor of any number is an even number, then it is also divisible by 2.
a = (n – 1) n (n + 1) [From Eq. (i)]
Now, sum of the digits
= n – 1 + n + n + 1 = 3n
= Multiple of 3, where n is any positive integer.
and (n – 1) n (n +1) will always be even, as one out of (n – 1) or n or (n + 1) must be even.
Since, conditions (ii) and (iii) is completely satisfy the Eq. (i).
Hence, by condition (i) the number n3 – n is always divisible by 6, where n is any positive integer.
Hence proved.
Question 9.
Solution:
Let x = 2m + 1 and y = 2m + 3 are odd positive integers, for every positive integer m.
Then, x2 + y2 = (2m + 1)2 + (2m + 3)2
= 4m2 + 1 + 4 m + 4m2 + 9 + 12m [(a + b)2 = a2 + 2ab + b2]
= 8m2 + 16m + 10 = even
= 2(4m2 + 8m + 5) or 4(2m2 + 4m + 2) + 1
Hence, x2 + y2 is even for every positive integer m but not divisible by 4.
Question 10.
Solution:
We find HCF (1190, 1145) using the following steps:

(i) Since 1445 > 1190, we divide 1445 by 1190 to get 1 as quotient and 255 as remainder.
By Euclid’s division lemma, we get
1445 = 1190 x 1 + 255 …(i)
(ii) Since the remainder 255 ≠ 0, we divide 1190 by 255 to get 4 as a quotient and 170 as a remainder.
By Euclid’s division lemma, we get
1190 = 255 x 4 + 170 …(ii)
(iii) Since the remainder 170 ≠ 0, we divide 255 by 170 to get 1 as quotient and 85 as remainder.
By Euclid’s division lemma, we get
255 = 170 x 1 +85 …(iii)
(iv) Since the remainder 85 ≠ 0, we divide 170 by 85 to get 2 as quotient and 0 as remainder.
By Euclid’s division lemma, we get
170 = 85 x 2 + 0 …(iv)
The remainder is now 0, so our procedure steps
HCF (1190, 1445) = 85
Now, from (iii), we get
255 = 170 x 1 + 85
=> 85 = 255 – 170 x 1
= (1445 – 1190) – (1190 – 255) x 4
= (1445 – 1190) – (1190 – 255) x 4
= (1445 – 1190) x 2 + (1445 – 1190) x 4
= 1445 – 1190 x 2 + 1445 x 4 – 1190 x 4
= 1445 x 5 – 1190 x 6
= 1190 x (-6) + 1445 x 5
Hence, m = -6, n = 5
Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.