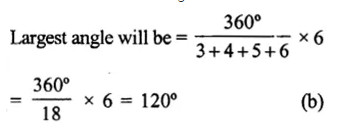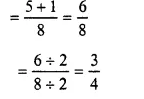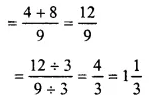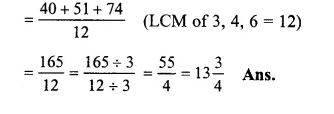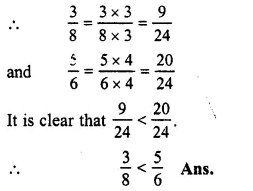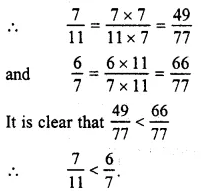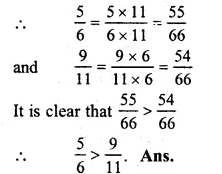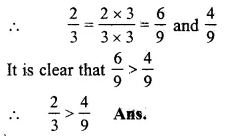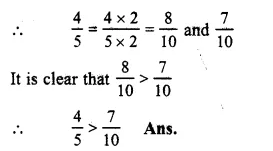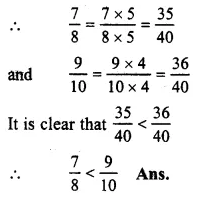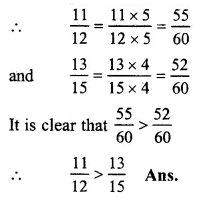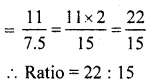RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5F
These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F.
Other Exercises
- RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A
- RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B
- RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C
- RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D
- RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E
- RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F
- RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G
Find the difference:
Question 1.
Solution:
\(\frac { 5 }{ 8 } -\frac { 1 }{ 8 } \)
= \(\\ \frac { 5-1 }{ 8 } \)
= \(\frac { 4 }{ 8 } \)
= \(\frac { 4\div 4 }{ 8\div 4 } \)
= \(\frac { 1 }{ 2 } \)
Question 2.
Solution:
\(\frac { 7 }{ 12 } -\frac { 5 }{ 12 } \)
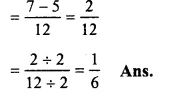
Question 3.
Solution:
\(4\frac { 3 }{ 7 } -2\frac { 4 }{ 7 } \)
= \(\frac { 31 }{ 7 } -\frac { 18 }{ 7 } \)
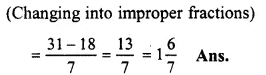
Question 4.
Solution:
\(\frac { 5 }{ 6 } -\frac { 4 }{ 9 } \)

Question 5.
Solution:
\(\frac { 1 }{ 2 } -\frac { 3 }{ 8 } \)

Question 6.
Solution:
\(\frac { 5 }{ 8 } -\frac { 7 }{ 12 } \)

Question 7.
Solution:
\(2\frac { 7 }{ 9 } -1\frac { 8 }{ 15 } \)
= \(\frac { 25 }{ 9 } -\frac { 23 }{ 15 } \)
(changing into improper fractions)

Question 8.
Solution:
\(3\frac { 5 }{ 8 } -2\frac { 5 }{ 12 } \)
= \(\frac { 29 }{ 8 } -\frac { 29 }{ 12 } \)

Question 9.
Solution:
\(2\frac { 3 }{ 10 } -1\frac { 7 }{ 15 } \)
= \(\frac { 23 }{ 10 } -\frac { 22 }{ 15 } \)

Question 10.
Solution:
\(6\frac { 2 }{ 3 } -3\frac { 3 }{ 4 } \)
= \(\frac { 20 }{ 3 } -\frac { 15 }{ 4 } \)

Question 11.
Solution:
\(7-5\frac { 2 }{ 3 } \)
= \(\frac { 7 }{ 1 } -\frac { 17 }{ 3 } \)
(changing into improper fractions)
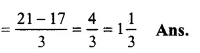
Question 12.
Solution:
\(10-6\frac { 3 }{ 8 } \)
= \(\frac { 10 }{ 1 } -\frac { 51 }{ 8 } \)
(changing into improper fractions)
![]()
Simpilify
Question 13.
Solution:
\(\frac { 5 }{ 6 } -\frac { 4 }{ 9 } +\frac { 2 }{ 3 } \)
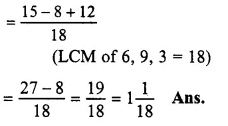
Question 14.
Solution:
\(\frac { 5 }{ 8 } +\frac { 3 }{ 4 } -\frac { 7 }{ 12 } \)
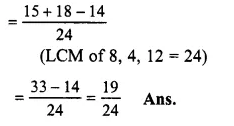
Question 15.
Solution:
\(2+\frac { 11 }{ 15 } -\frac { 5 }{ 9 } \)
= \(\frac { 90+33-25 }{ 45 } \)
(LCM of 15 and 9 = 45)
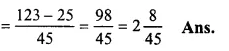
Question 16.
Solution:
\(5\frac { 3 }{ 4 } -4\frac { 5 }{ 12 } +3\frac { 1 }{ 6 } \)
= \(\frac { 23 }{ 4 } -\frac { 53 }{ 12 } +\frac { 19 }{ 6 } \)
(changing into improper fractions)
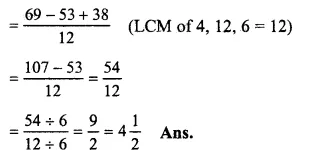
Question 17.
Solution:
\(2+5\frac { 7 }{ 10 } -3\frac { 14 }{ 15 } \)
= \(\frac { 2 }{ 1 } +\frac { 57 }{ 10 } -\frac { 59 }{ 15 } \)
(changing into improper fractions)
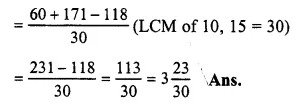
Question 18.
Solution:
\(8-3\frac { 1 }{ 2 } -2\frac { 1 }{ 4 } \)
= \(\frac { 8 }{ 1 } -\frac { 7 }{ 2 } -\frac { 9 }{ 4 } \)
(changing into improper fractions)
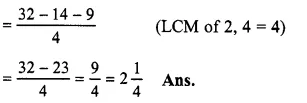
Question 19.
Solution:
\(8\frac { 5 }{ 6 } -3\frac { 3 }{ 8 } +2\frac { 7 }{ 12 } \)
= \(\frac { 53 }{ 6 } -\frac { 27 }{ 8 } +\frac { 31 }{ 12 } \)
(changing into improper fractions)
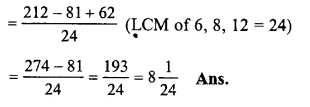
Question 20.
Solution:
\(6\frac { 1 }{ 6 } -5\frac { 1 }{ 5 } +3\frac { 1 }{ 3 } \)
= \(\frac { 37 }{ 6 } -\frac { 26 }{ 5 } +\frac { 10 }{ 3 } \)
(changing into improper fractions)
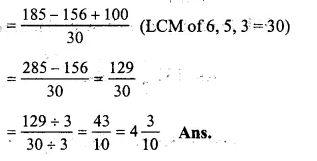
Question 21.
Solution:
\(3+1\frac { 1 }{ 5 } +\frac { 2 }{ 3 } -\frac { 7 }{ 15 } \)
= \(\frac { 3 }{ 1 } +\frac { 6 }{ 5 } +\frac { 2 }{ 3 } -\frac { 7 }{ 15 } \)
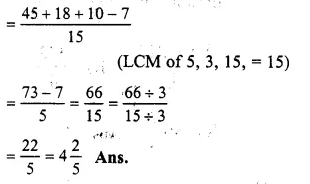
Question 22.
Solution:
By subtracting \(9 \frac { 2 }{ 3 } \) from 19, we get the required number
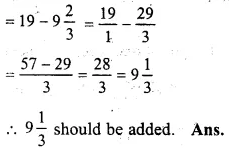
Question 23.
Solution:
By subtracting \(6 \frac { 7 }{ 15 } \) from \(8 \frac { 1 }{ 5 } \) we get the required number
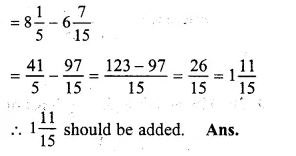
Question 24.
Solution:
Sum of \(3 \frac { 5 }{ 9 } \) and \(3 \frac { 1 }{ 3 } \)
= \(\frac { 32 }{ 9 } +\frac { 10 }{ 3 } \)
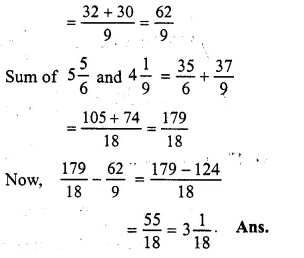
Question 25.
Solution:
\(\\ \frac { 3 }{ 4 } \), \(\\ \frac { 5 }{ 7 } \)

Question 26.
Solution:
Milk bought by Mrs. Soni = \(7 \frac { 1 }{ 2 } \) litres
and milk consumed by here = \(5 \frac { 3 }{ 4 } \) litres
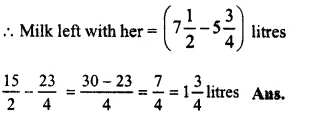
Question 27.
Solution:
Total time of film show = \(3 \frac { 1 }{ 3 } \) hours
Total spent on advertisement = \(1 \frac { 3 }{ 4 } \) hours
Duration of the film
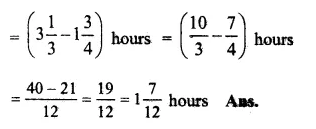
Question 28.
Solution:
On a day, rickshaw pullar earned
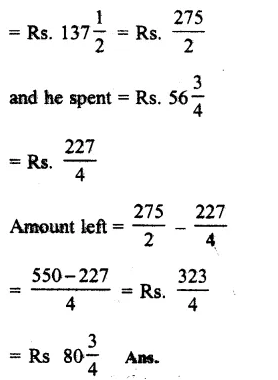
Question 29.
Solution:
Total length of wire =\(2 \frac { 3 }{ 4 } \)-metres
Length of one piece = \(\\ \frac { 5 }{ 8 } \) metre
Length of the other piece
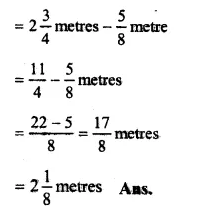
Hope given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.