Prasanna

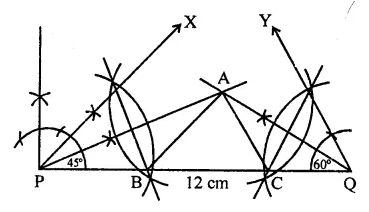
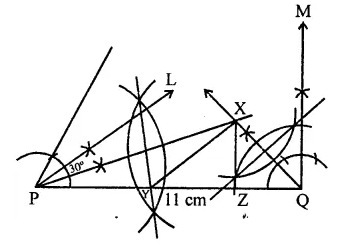
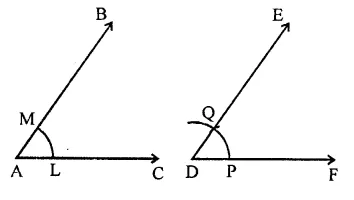
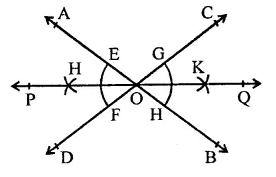
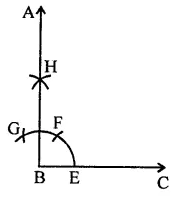
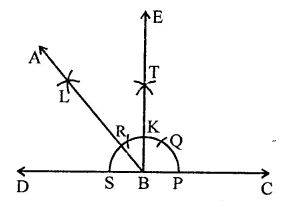
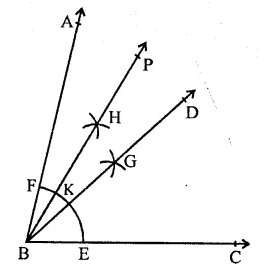
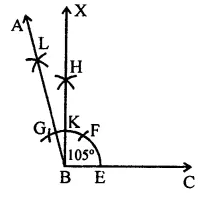
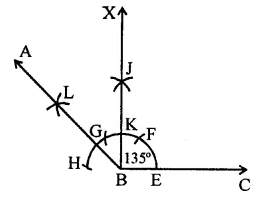
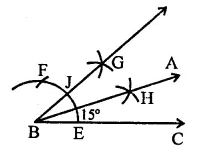
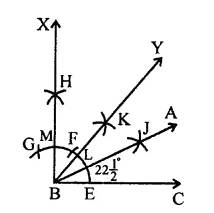
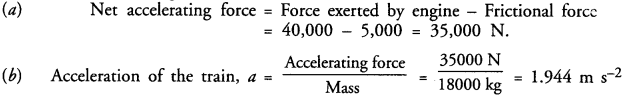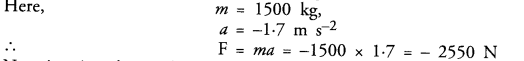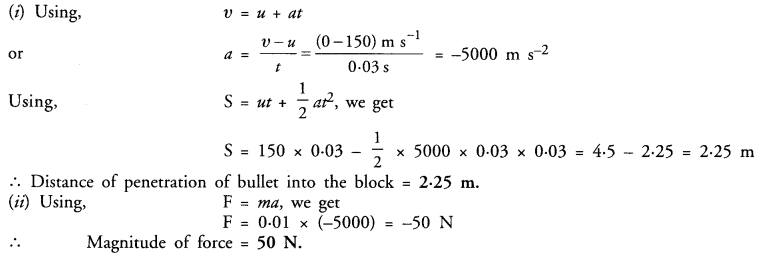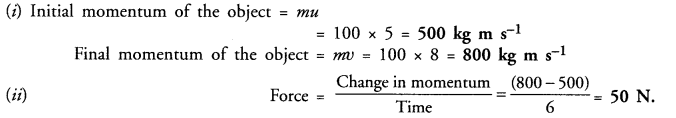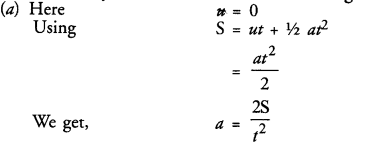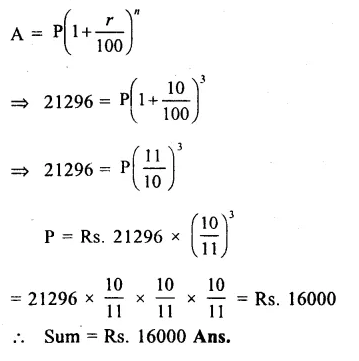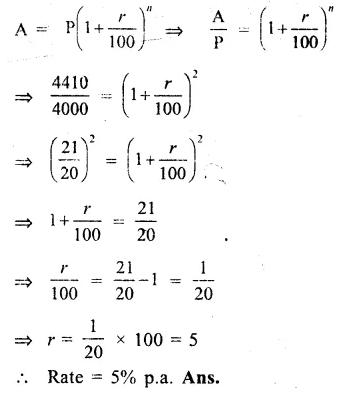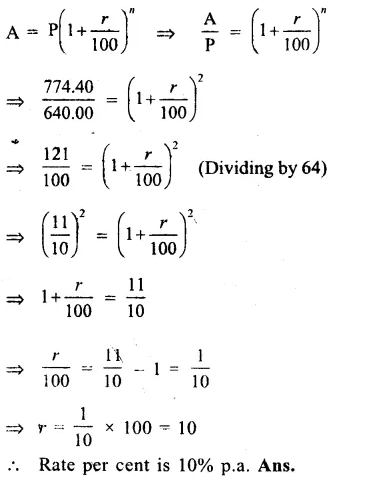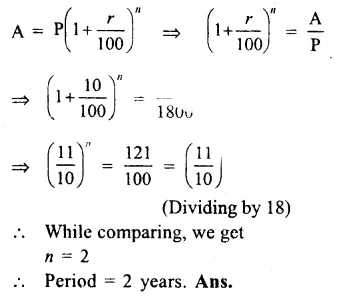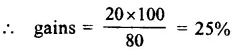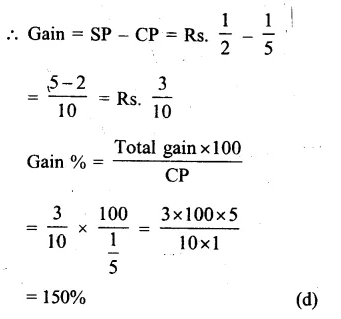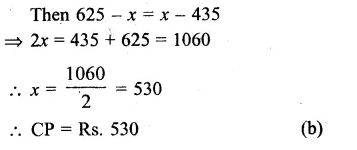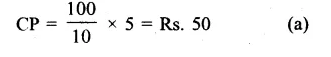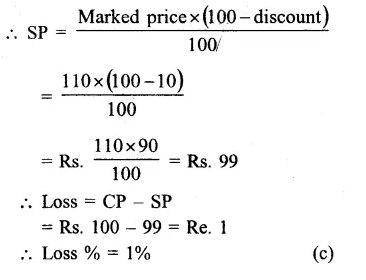RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1
• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2
• RD Sharma Class 9 Solutions Chapter 17 Constructions VSAQS
• RD Sharma Class 9 Solutions Chapter 17 Constructions MCQS

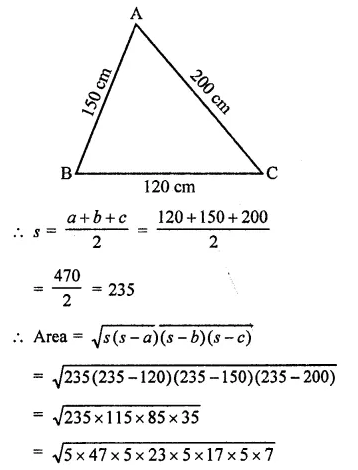
Question 1.
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm.
Solution:
Sides of triangle are 120 cm, 150 cm, 200 cm

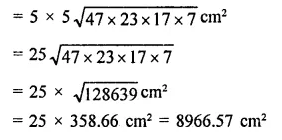
Question 2.
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm.
Solution:
Sides of a triangle are 9 cpi, 12 cm, 15 cm

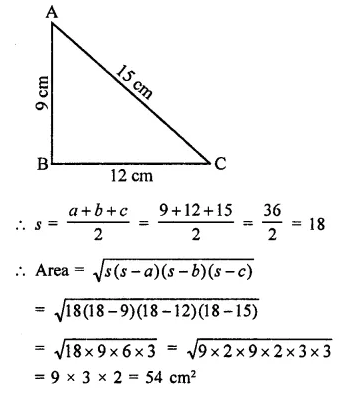
Question 3.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:
Perimeter of a triangle = 42 cm
Two sides are 18 cm and 10 cm
Third side = 42 – (18 + 10)
= 42 – 28 = 14 cm

Question 4.
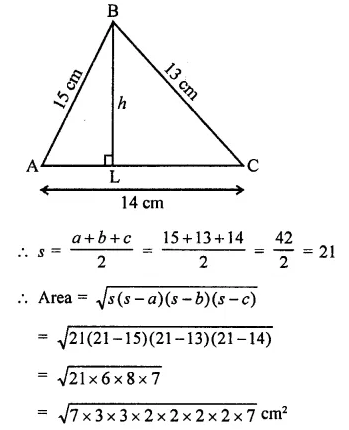
In a ∆ABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ∆ABC and hence its altitude on AC.
Solution:
Sides of triangle ABC are AB = 15 cm, BC = 13 cm, AC = 14 cm

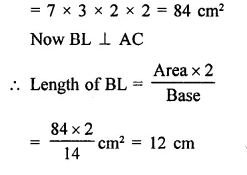
Question 5.
The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle. [NCERT]
Solution:
Perimeter of a triangle = 540 m
Ratio in sides = 25 : 17 : 12
Sum of ratios = 25 + 17 + 12 = 54

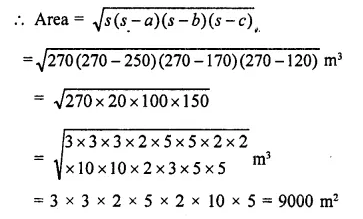
Question 6.
The perimeter of a triangle is 300 m. If its sides are in the ratio 3:5:7. Find the area of the triangle. [NCERT]
Solution:
Perimeter of a triangle = 300 m
Ratio in the sides = 3 : 5 : 7
∴ Sum of ratios = 3 + 5 + 7= 15

Question 7.
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
Solution:
Perimeter of a triangular field = 240 dm
Two sides are 78 dm and 50 dm
∴ Third side = 240 – (78 + 50)
= 240 – 128 = 112 dm

Question 8.
A triangle has sides 35 cm, 54 cm and 61 cm long. Find its area. Also, find the smallest of its altitudes.
Solution:
Sides of a triangle are 35 cm, 54 cm, 61 cm

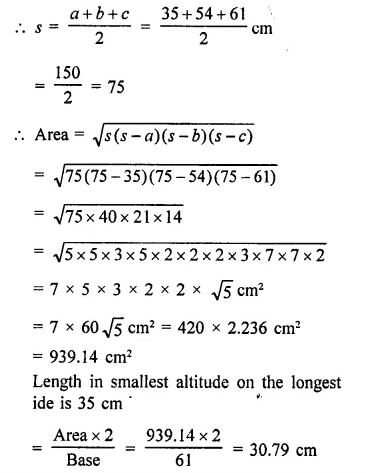
Question 9.
The lengths of the sides of a triangle are in the ratio 3:4:5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.
Solution:
Ratio in the sides of a triangle = 3:4:5

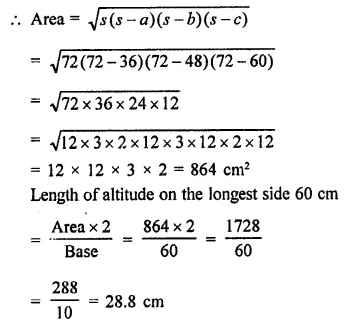
Question 10.
The perimeter of an isosceles triangle is 42 cm and its base is (3/2) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
Solution:
Perimeter of an isosceles triangle = 42 cm
Base = \(\frac { 3 }{ 2 }\) of its one of equal sides
Let each equal side = x, then 3
Base = \(\frac { 3 }{ 2 }\) x

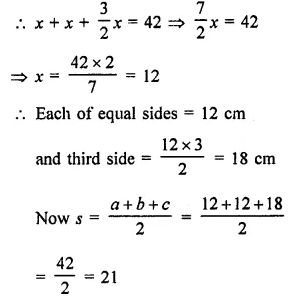
Question 11.
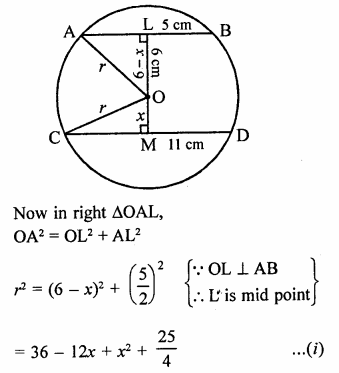
Find the area of the shaded region in figure.

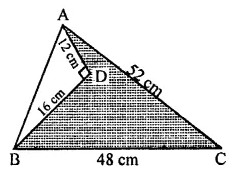
Solution:
In ∆ABC, AC = 52 cm, BC = 48 cm
and in right ∆ADC, ∠D = 90°
AD = 12 cm, BD = 16 cm
∴ AB²=AD² + BD² (Pythagoras Theorem)
(12)² + (16)² = 144 + 256 = 400 = (20)²
∴ AB = 20 cm

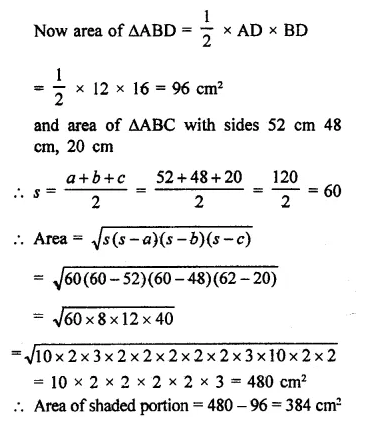
Hope given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
In the figure, O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

Solution:
Arc AB, subtends ∠AOB at the centre and ∠APB at the remaining part of the circle
∴∠AOB = 2∠APB = 2 x 50° = 100°
Join AB

∆AOB is an isosceles triangle in which
OA = OB
∴ ∠OAB = ∠OBA But ∠AOB = 100°
∴∠OAB + ∠OBA = 180° – 100° = 80°
⇒ 2∠OAB = 80°
80°
∴∠OAB = \(\frac { { 80 }^{ \circ } }{ 2 }\)  = 40°

Question 2.
In the figure, O is the centre of the circle. Find ∠BAC.

Solution:
In the circle with centre O
∠AOB = 80° and ∠AOC =110°
∴ ∠BOC = ∠AOB + ∠AOC
= 80°+ 110°= 190°
∴ Reflex ∠BOC = 360° – 190° = 170°
Now arc BEC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle.

∴ ∠BOC = 2∠BAC
⇒ 170° = 2∠BAC
⇒ ∠BAC = \(\frac { { 170 }^{ \circ } }{ 2 }\) = 85°
∴ ∠BAC = 85°

Question 3.
If O is the centre of the circle, find the value of x in each of the following figures:



Solution:
(i) A circle with centre O
∠AOC = 135°
But ∠AOC + ∠COB = 180° (Linear pair)
⇒ 135° + ∠COB = 180°
⇒ ∠COB = 180°- 135° = 45°
Now arc BC subtends ∠BOC at the centre and ∠BPC at the remaining part of the circle
∴ ∠BOC = 2∠BPC
⇒ ∠BPC = \(\frac { 1 }{ 2 }\)∠BOC = \(\frac { 1 }{ 2 }\) x 45° = \(\frac { { 45 }^{ \circ } }{ 2 }\)
∴ ∠BPC = 22 \(\frac { 1 }{ 2 }\)° or x = 22 \(\frac { 1 }{ 2 }\)°
(ii) ∵ CD and AB are the diameters of the circle with centre O
∠ABC = 40°
But in ∆OBC,
OB = OC (Radii of the circle)
∠OCB = ∠OBC – 40°
Now in ABCD,
∠ODB + ∠OCB + ∠CBD = 180° (Angles of a triangle)
⇒ x + 40° + 90° = 180°
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
∴ x = 50°
(iii) In circle with centre O,
∠AOC = 120°, AB is produced to D
∵ ∠AOC = 120°
and ∠AOC + convex ∠AOC = 360°
⇒ 120° + convex ∠AOC = 360°
∴ Convex ∠AOC = 360° – 120° = 240°
∴ Arc APC Subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle
∴ ∠ABC = \(\frac { 1 }{ 2 }\)∠AOC = \(\frac { 1 }{ 2 }\)x 240° = 120°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ 120° + x = 180°
⇒ x = 180° – 120° = 60°
∴ x = 60°
(iv) A circle with centre O and ∠CBD = 65°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ ∠ABC + 65° = 180°
⇒ ∠ABC = 180°-65°= 115°
Now arc AEC subtends ∠x at the centre and ∠ABC at the remaining part of the circle
∴ ∠AOC = 2∠ABC
⇒ x = 2 x 115° = 230°
∴ x = 230°
(v) In circle with centre O
AB is chord of the circle, ∠OAB = 35°
In ∆OAB,
OA = OB (Radii of the circle)
∠OBA = ∠OAB = 35°
But in ∆OAB,
∠OAB + ∠OBA + ∠AOB = 180° (Angles of a triangle)
⇒ 35° + 35° + ∠AOB = 180°
⇒ 70° + ∠AOB = 180°
⇒ ∠AOB = 180°-70°= 110°
∴ Convex ∠AOB = 360° -110° = 250°
But arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴∠ACB = \(\frac { 1 }{ 2 }\)∠AOB
⇒ x = \(\frac { 1 }{ 2 }\) x 250° = 125°
∴ x= 125°
(vi) In the circle with centre O,
BOC is its diameter, ∠AOB = 60°
Arc AB subtends ∠AOB at the centre of the circle and ∠ACB at the remaining part of the circle
∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB
= \(\frac { 1 }{ 2 }\) x 60° = 30°
But in ∆OAC,
OC = OA (Radii of the circle)
∴ ∠OAC = ∠OCA = ∠ACB
⇒ x = 30°
(vii) In the circle, ∠BAC and ∠BDC are in the same segment
∴ ∠BDC = ∠BAC = 50°
Now in ABCD,
∠DBC + ∠BCD + ∠BDC = 180° (Angles of a triangle)
⇒ 70° + x + 50° = 180°
⇒ x + 120° = 180° ⇒ x = 180° – 120° = 60°
∴ x = 60°
(viii) In circle with centre O,
∠OBD = 40°
AB and CD are diameters of the circle
∠DBA and ∠ACD are in the same segment
∴ ∠ACD = ∠DBA = 40°
In AOAC, OA = OC (Radii of the circle)
∴ ∠OAC = ∠OCA = 40°
and ∠OAC + ∠OCA + ∠AOC = 180° (Angles in a triangle)
⇒ 40° + 40° + x = 180°
⇒ x + 80° = 180° ⇒ x = 180° – 80° = 100°
∴ x = 100°
(ix) In the circle, ABCD is a cyclic quadrilateral ∠ADB = 32°, ∠DAC = 28° and ∠ABD = 50°
∠ABD and ∠ACD are in the same segment of a circle
∴ ∠ABD = ∠ACD ⇒ ∠ACD = 50°
Similarly, ∠ADB = ∠ACB
⇒ ∠ACB = 32°
Now, ∠DCB = ∠ACD + ∠ACB
= 50° + 32° = 82°
∴ x = 82°
(x) In a circle,
∠BAC = 35°, ∠CBD = 65°
∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 35°
In ∆BCD,
∠BDC + ∠BCD + ∠CBD = 180° (Angles in a triangle)
⇒ 35° + x + 65° = 180°
⇒ x + 100° = 180°
⇒ x = 180° – 100° = 80°
∴ x = 80°
(xi) In the circle,
∠ABD and ∠ACD are in the same segment of a circle
∴ ∠ABD = ∠ACD = 40°
Now in ∆CPD,
∠CPD + ∠PCD + ∠PDC = 180° (Angles of a triangle)
110° + 40° + x = 180°
⇒ x + 150° = 180°
∴ x= 180°- 150° = 30°
(xii) In the circle, two diameters AC and BD intersect each other at O
∠BAC = 50°
In ∆OAB,
OA = OB (Radii of the circle)
∴ ∠OBA = ∠OAB = 52°
⇒ ∠ABD = 52°
But ∠ABD and ∠ACD are in the same segment of the circle
∴ ∠ABD = ∠ACD ⇒ 52° = x
∴ x = 52°

Question 4.
O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A.
Solution:
Given : O is the circumcentre of ∆ABC.
OD ⊥ BC
OB is joined
To prove : ∠BOD = ∠A
Construction : Join OC.

Proof : Arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle
∴ ∠BOC = 2∠A …(i)
In right ∆OBD and ∆OCD Side OD = OD (Common)
Hyp. OB = OC (Radii of the circle)
∴ ∆OBD ≅ ∆OCD (RHS criterion)
∴ ∠BOD = ∠COD = \(\frac { 1 }{ 2 }\) ∠BOC
⇒ ∠BOC = 2∠BOD …(ii)
From (i) and (ii)
2∠BOD = 2∠A
∴∠BOD = ∠A

Question 5.
In the figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.

Solution:
Given : In the figure, a circle with centre O OB is the bisector of ∠ABC
To prove : AB = BC
Construction : Draw OL ⊥ AB and OM ⊥ BC

Proof: In ∆OLB and ∆OMB,
∠1 = ∠2 (Given)
∠L = ∠M (Each = 90°)
OB = OB (Common)
∴ ∆OLB ≅ ∆OMB (AAS criterion)
∴ OL = OM (c.p.c.t.)
But these are distance from the centre and chords equidistant from the centre are equal
∴ Chord BA = BC
Hence AB = BC

Question 6.
In the figure, O and O’ are centres of two circles intersecting at B and C. ACD is a straight line, find x.

Solution:
In the figure, two circles with centres O and O’ intersect each other at B and C.
ACD is a line, ∠AOB = 130°
Arc AB subtends ∠AOB at the centre O and ∠ACB at the remaining part of the circle.

∴ ∠ACB =\(\frac { 1 }{ 2 }\)∠AOB
= \(\frac { 1 }{ 2 }\) x 130° = 65°
But ∠ACB + ∠BCD = 180° (Linear pair)
⇒ 65° + ∠BCD = 180°
⇒ ∠BCD = 180°-65°= 115°
Now, arc BD subtends reflex ∠BO’D at the centre and ∠BCD at the remaining part of the circle
∴ ∠BO’D = 2∠BCD = 2 x 115° = 230°
But ∠BO’D + reflex ∠BO’D = 360° (Angles at a point)
⇒ x + 230° = 360°
⇒ x = 360° -230°= 130°
Hence x = 130°

Question 7.
In the figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.

Solution:
Arc AB subtend ∠ACB and ∠ADB in the same segment of a circle
∴ ∠ACB = ∠ADB = 40°
In ∆PDB,
∠DPB + ∠PBD + ∠ADB = 180° (Sum of angles of a triangle)
⇒ 120° + ∠PBD + 40° = 180°
⇒ 160° + ∠PBD = 180°
⇒ ∠PBD = 180° – 160° = 20°
⇒ ∠CBD = 20°

Question 8.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:
A circle with centre O, a chord AB = radius of the circle C and D are points on the minor and major arcs of the circle

∴ ∠ACB and ∠ADB are formed Now in ∆AOB,
OA = OB = AB (∵ AB = radii of the circle)
∴ ∆AOB is an equilateral triangle,
∴ ∠AOB = 60°
Now arc AB subtends ∠AOB at the centre and ∠ADB at the remainder part of the circle.
∴ ∠ADB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\)x 60° = 30°
Now ACBD is a cyclic quadrilateral,
∴ ∠ADB + ∠ACB = 180° (Sum of opposite angles of cyclic quad.)
⇒ 30° + ∠ACB = 180°
⇒ ∠ACB = 180° – 30° = 150°
∴ ∠ACB = 150°
Hence angles are 150° and 30°

Question 9.
In the figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

Solution:
In circle with centre O and ∠AOC = 150°
But ∠AOC + reflex ∠AOC = 360°
∴ 150° + reflex ∠AOC = 360°
⇒ Reflex ∠AOC = 360° – 150° = 210°
Now arc AEC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.

Reflex ∠AOC = 2∠ABC
⇒ 210° = 2∠ABC
∴ ∠ABC = \(\frac { { 210 }^{ \circ } }{ 2 }\)  = 105°

Question 10.
In the figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
Solution:
Given : In circle, O is centre

To prove : ∠x = ∠y + ∠z
Proof : ∵ ∠3 and ∠4 are in the same segment of the circle
∴ ∠3 = ∠4 …(i)
∵ Arc AB subtends ∠AOB at the centre and ∠3 at the remaining part of the circle
∴ ∠x = 2∠3 = ∠3 + ∠3 = ∠3 + ∠4 (∵ ∠3 = ∠4) …(ii)
In ∆ACE,
Ext. ∠y = ∠3 + ∠1
(Ext. is equal to sum of its interior opposite angles)
⇒ ∠3 – ∠y – ∠1 …(ii)
From (i) and (ii),
∠x = ∠y – ∠1 + ∠4 …(iii)
Similarly in ∆ADF,
Ext. ∠4 = ∠1 + ∠z …(iv)
From (iii) and (iv)
∠x = ∠y-∠l + (∠1 + ∠z)
= ∠y – ∠1 + ∠1 + ∠z = ∠y + ∠z
Hence ∠x = ∠y + ∠z

Question 11.
In the figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.

Solution:
In the figure, O is the centre of the circle,
PQ is the diameter and ∠ROS = 40°
Now we have to find ∠RTS
Arc RS subtends ∠ROS at the centre and ∠RQS at the remaining part of the circle

∴ ∠RQS = \(\frac { 1 }{ 2 }\) ∠ROS
= \(\frac { 1 }{ 2 }\) x 40° = 20°
∵ ∠PRQ = 90° (Angle in a semi circle)
∴ ∠QRT = 180° – 90° = 90° (∵ PRT is a straight line)
Now in ∆RQT,
∠RQT + ∠QRT + ∠RTQ = 180° (Angles of a triangle)
⇒ 20° + 90° + ∠RTQ = 180°
⇒ ∠RTQ = 180° – 20° – 90° = 70° or ∠RTS = 70°
Hence ∠RTS = 70°

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Question 1.
Construct a ∆ABC in which BC = 3.6 cm, AB + AC = 4.8 cm and ∠B = 60°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.6 cm.
(ii) At B, draw a ray BX making an angle of 60° and cut off BE = 4.8 cm.
(iii) Join EC.
(iv) Draw perpendicular bisector of CE which intersects BE at A.
(v) Join AC.
∆ABC is the required triangle.

Question 2.
Construct a ∆ABC in which AB + AC = 5.6 cm, BC = 4.5 cm and ∠B = 45°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 4.5 cm.
(ii) At B, draw a ray BX making an angle of 45° and cut off BE = 5.6 cm and join CE.
(iii) Draw the perpendicular bisector of CE which intersects BE at A.
(iv) Join AC.
∆ABC is the required triangle.

Question 3.
Construct a AABC in which BC = 3.4 cm, AB – AC = 1.5 cm and ∠B = 45°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.4 cm.
(ii) At B, draw a ray BX making an angle of 45° and cut off BE = 1.5 cm.
(iii) Join EC.
(iv) Draw the perpendicular bisector of CE which intersects BE produced at A.
(v) Join AC.
∆ABC is the required triangle.

Question 4.
Using ruler and compasses only, construct a ∆ABC, given base BC = 7 cm, ∠ABC = 60° and AB + AC = 12 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 7 cm!
(ii) At B, draw a ray BX making an angle of 60° and cut off BE = 12 cm.
(iii) Join EC.
(iv) Draw the perpendicular bisector of EC which intersects BE at A.
(v) Join AC.
∆ABC is the required triangle.

Question 5.
Construct a right-angled triangle whose perimeter is equal to 10 cm and one acute angle equal to 60°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 10 cm.
(ii) At P, draw a ray PX making an angle of 90° and at Q, QY making an angle of 60°.
(iii) Draw the angle bisectors of ∠P and ∠Q meeting each other at A.
(iv) Draw the perpendicular bisectors of AP and AQ intersecting PQ at B and C respectively,
(v) Join AB and AC.
∆ABC is the required triangle.

Question 6.
Construct a triangle ABC such that BC = 6cm, AB = 6 cm and median AD = 4 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm and bisect it at D.
(ii) With centre B and radius 6 cm and with centre D and radius 4 cm, draw arcs intersecting each other at A.
(iii) Join AD and AB and AC.
Then ∆ABC is the required triangle.

Question 7.
Construct a right triangle ABC whose base BC is 6 cm and the sum of hypotenuse AC and other side AB is 10 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm

(ii) At B, draw a ray BX making an angle of 90° and cut off BE = 10 cm.
(iii) Join EC and draw the perpendicular bisector of CE which intersects BE at A.
(iv) Join AC.
∆ABC is the required triangle.

Question 8.
Construct a triangle whose perimeter is 6.4 cm, and angles at the base are 60° and 45°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 6.4 cm.
(ii) At P draw a ray PX making an angle of 60° and at Q, a ray QY making an angle of 45°.
(iii) Draw the bisector of ∠P and ∠Q meeting each other at A.
(iv) Draw the perpendicular bisectors of PA and QA intersecting PQ at B and C respectively.
(v) Join AB and AC.
∆ABC is the required triangle.

Question 9.
Using ruler and compasses only, construct a ∆ABC, from the following data:
AB + BC + CA = 12 cm, ∠B = 45° and ∠C = 60°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 12 cm.
(ii) Draw ray PX at P making are angle of 45° and at Q, QY making an angle of 60°.
(Hi) Draw the angle bisectors of ∠P and ∠Q meeting each other at A.
(v) Draw the perpendicular bisector of AP and AQ intersecting PQ at B and C respectively.
(v) Join AB and AC.
∆ABC is the required triangle.

Question 10.
Construct a triangle XYZ in which ∠Y = 30° , ∠Z = 90° XY +YZ + ZX = 11
Solution:
Steps of construction :
(i) Draw a line segment PQ =11 cm.
(ii) At P, draw a ray PL making an angle of 30° and Q, draw another ray QM making an angle of 90°.
(iii) Draw the angle bisector of ∠P and ∠Q intersecting each other at X.
(iv) Draw the perpendicular bisector of XP and XQ. Which intersect PQ at Y and Z respectively.
(v) Join XY and XZ.
Then ∆XYZ is the required triangle

Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Question 1.
Draw an angle and label it as ∠BAC. Construct another angle, equal to ∠BAC.
Solution:
Steps of construction :
(i) Draw an angle BAC.
(ii) Draw a line DF.
(iii) With centre A and D, draw arcs of equal radius which intersect AC at L and AB at M and DF at P.
(iv) Cut off PQ = LM and join DQ and produce it to E, then
∠EDF = ∠BAC.

Question 2.
Draw an obtuse angle. Bisect it. Measure each of the angles so obtained.
Solution:
Steps of construction :
(i) Draw an angle ABC which is an obtuse i.e. more than 90°.
(ii) With centre B and a suitable radius draw an arc meeting BC at E and AB at F.
(iii) With centre E and F, and radius more than half of EF draw arcs intersecting each other at G.
(iv) Join BG and produce it to D.
ThenBD is die bisector of ∠ABC.
On measuring each part, we find each angle = 53°.

Question 3.
Using your protractor, draw an angle of measure 108°. With this angle as given, draw an angle of 54°.
Solution:
Steps of construction :
(i) With the help of protractor draw an angle ABC = 108°.
As 54° = \(\frac { 1 }{ 2 }\) x 108°
∴ We shall bisect it.

(ii) With centre B and a suitable radius, draw an arc meeting BC at E and AB at F.
(iii) With centre E and F, and radius more than half of EF, draw arcs intersecting each other at G
(iv) Join BG and produce it to D.
Then ∠DBC = 54°.

Question 4.
Using protractor, draw a right angle. Bisect it to get an angle of measure 45°.
Solution:
Steps of construction :
(i) Using protractor, draw a right angle ∆ABC.
i. e. ∠ABC = 90°.
(ii) With centre B and a suitable radius, draw an arc which meets BC at E and BA at F.
(iii) With centre E and F, draw arcs intersecting each other at G.
(iv) Join BG and produce it to D.
Then BD is the bisector of ∠ABC.
∴ ∠DBC =\(\frac { 1 }{ 2 }\) x 90° = 45°.

Question 5.
Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Solution:
Steps of construction :
(i) Draw a linear pair ∠DCA and ∠DCB.
(ii) Draw the bisectors of ∠DCA and ∠DCB. Forming ∠ECF on measuring we get ∠ECF = 90°.
Verification : ∵∠DCA + ∠DCB = 180°
⇒ \(\frac { 1 }{ 2 }\) ∠DCA + \(\frac { 1 }{ 2 }\) ∠DCB = 180° x \(\frac { 1 }{ 2 }\) = 90°
∴ ∠ECF = 90°
i.e. EC and FC are perpendicular to each other.

Question 6.
Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line
Solution:
Steps of construction :
(i) Draw two lines AB and CD intersecting each other at O.
(ii) Draw the bisector of ∠AOD and also the bisector of ∠BOC. Which are OP and OQ respectively. We see that OP and OQ are in the same straight line.

Question 7.
Using ruler and compasses only, draw a right angle.
Solution:
Steps of construction :
(i) Draw a line segment BC.
(ii) With centre B and a suitable radius, draw an arc meeting BC at E.
(iii) With centre E and same radius, cut off arcs EF and FG.
(iv) Bisect arc FG at H.
(v) Join BH and produce it to A.
Then ∠ABC = 90°.

Question 8.
Using ruler and compasses only, draw an angle of measure 135°.
Solution:
Steps of construction :
(i) Draw a line DC and take a point B on it.
(ii) With centre B and a suitable radius draw an arc meeting BC at P.
(iii) With centre P, cut off arcs PQ, QR and RS.
(iv) Bisect as QR at T and join BT and produce it to E.
(v) Now bisect the arc KS at RL.
(vi) Join BL and produce it to A.
Now ∠ABC = 135°.

Question 9.
Using a protractor, draw an angle of measure 72°. With this angle as given, draw angles of measure 36° and 54°.
Solution:
Steps of construction :
(i) Draw an angle ABC = 12° with the help of protractor.
(ii) With centre B and a suitable radius, draw an arc EF.
(iii) With centre E and F, draw arcs intersecting
each other at G and produce it to D.
Then BD is the bisector of ∠ABC.
∴ ∠DBC = 72° x \(\frac { 1 }{ 2 }\) = 36°.
(iv) Again bisect ∠ABD in the same way then PB is the bisector of ∠ABD.
∴ ∠PBC = 36° + \(\frac { 1 }{ 2 }\) x 36°
= 36° + 18° = 54°
Hence ∠PBC = 54°

Question 10.
Construct the following angles at the initial point of a given ray and justify the construction:
(i) 45°
(ii) 90°
Solution:
(i) 45°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) With centre E, cut off equal arcs EF and FG.
(d) Bisect FG at H.
(e) Join BH and produce to X so that ∠XBC = 90°.
(f) Bisect ∠XBC so that ∠ABC = 45°.

(ii) 90°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E and with centre E cut off arcs from E, EF = FG
(c) Now bisect the arc EG at H.
(d) Join BH and produce it to A.
∴ ∠ABC = 90°.

Question 11.
Construct the angles of the following measurements:
(i) 30°
(ii) 75°
(iii) 105°
(iv) 135°
(v) 15°
(vi) 22 \(\frac { 1 }{ 2 }\)°
Solution:
(i) 30°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) Cut off arcs EF and bisect it at G.
So that ∠ABC = 30°.

(ii) 75°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) Cut off arc EF = FG from E.
(d) Bisect the arc FG at K and join BK so that ∠KBC = 90°.
(e) Now bisect arc HF at L and join BL and produce it to A so that ∠ABC = 75°.

(iii) 105°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) From E, cut off arc EF = FG and divide FG at H.
(d) Join BH meeting the arc at K.
(e) Now bisect the arc KG at L.
Join BL and produce it to A.
Then ∠ABC = 105°.

(iv) 135°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) From E, cut off EF = FG = GH.
(d) Bisect arc FG at K, and join them.
(e) Bisect arc KH at L.
(f) Join BL and produce it to A, then ∠ABC = 135°.

(v) 15°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) Cut off arc EF from E and bisect it at G. Then ∠GBC = 30°.
(d) Again bisect the arc EJ at H.
(e) Join BH and produce it to A.
Then ∠ABC = 15°.

(vi) 22 \(\frac { 1 }{ 2 }\)°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc and from E, cut off EF = FG
(c) Bisect FG at H so that ∠HBC = 90°.
(d) Now bisect ∠HBC at K. So that ∠YBC = 45°.
(e) Again bisect ∠YBC at J. So thttt ∠ABC = 22 \(\frac { 1 }{ 2 }\)°

Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
Three girls Ishita, Isha and Nisha are playing a game by standing on a circle of radius 20 m drawn in a park. Ishita throws a ball to Isha, Isha to Nisha and Nisha to Ishita. If the distance between Ishita and Isha and between Isha and Nisha is 24 m each, what is the distance between Ishita and Nisha. [NCERT]
Solution:
∵ Distance between Isha and Ishita and Ishita and Nisha is same
∴ RS = SM = 24 m
∴They are equidistant from the centre
In right ∆ORL,
OL² = OR² – RL²


Hence distance between Ishita and Nisha = 38.4 m

Question 2.
A circular park of radius 40 m is situated in a colony. Three beys Ankur, Amit and Anand are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other. Find thelength of the string of each phone. [NCERT]
Solution:
Radius of circular park = 40 m
Ankur, Amit and Anand are sitting at equal distance to each other By joining them, an equilateral triangle ABC is formed produce BO to L which is perpendicular bisector of AC

∴ BL = 40 + 20 = 60 m (∵ O is centroid of ∆ABC also)
Let a be the side of ∆ABC

Hence the distance between each other = 40\(\sqrt { 3 } \) m

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
The radius of a circle is 8 cm and the length of one of its chords is 12 cm. Find the distance of the chord from the centre.
Solution:
Radius of circle with centre O is OA = 8 cm
Length of chord AB = 12 cm
OC ⊥ AB which bisects AB at C

∴ AC = CB = 12 x \(\frac { 1 }{ 2 }\) = 6 cm
In ∆OAC,
OA2 = OC2 + AC2 (Pythagoras Theorem)
⇒ (8)2 = OC2 + (6)2
⇒ 64 = OC2 + 36
OC2 = 64 – 36 = 28
∴ OC = \(\sqrt { 28 } \) = \(\sqrt { 4×7 } \) cm
= 2 x 2.6457 = 5.291 cm

Question 2.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 10 cm.
Solution:
Let AB be a chord of a circle with radius 10 cm. OC ⊥ AB
∴ OA = 10 cm
OC = 5 cm

∵ OC divides AB into two equal parts
i.e. AC = CB
Now in right AOAC,
OA2 = OC2 + AC2 (Pythagoras Theorem)
⇒ (10)2 = (5)2 + AC2
⇒ 100 = 25 + AC2
⇒ AC2 = 100 – 25 = 75
∴ AC = \(\sqrt { 75 } \)= \(\sqrt { 25×3 } \) = 5 x 1.732
∴ AB = 2 x AC = 2 x 5 x 1.732 = 10 x 1.732 = 17.32 cm

Question 3.
Find the length of a chord which is at a distance of 4 cm from the centre of the circle of radius 6 cm.
Solution:
In a circle with centre O and radius 6 cm and a chord AB at a distance of 4 cm from the centre of the circle
i.e. OA = 6 cm and OL ⊥ AB, OL = 4 cm

∵ Perpendicular OL bisects the chord AB at L 1
∴ AL = LB=\(\frac { 1 }{ 2 }\) AB
Now in right ∆OAL,
OA2 = OL2 + AL2 (Pythagoras Theorem)
(6)2 = (4)2 + AL2
⇒ 36=16+AL2
⇒ AL2 = 36 – 16 = 20
∴ AL = \(\sqrt { 20 } \) = \(\sqrt { 4×5 } \) = 2 x 2.236 = 4.472 cm
∴ Chord AB = 4.472 x 2 = 8.944 = 8.94 cm

Question 4.
Give a method to find the centre of a given circle.
Solution:
Steps of construction :

(i) Take three distinct points on the circle say A, B and C.
(ii) Join AB and AC.
(iii) Draw the perpendicular bisectors of AB and AC which intersect each other at O.
O is the required centre of the given circle

Question 5.
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Solution:
Given : In circle with centre O
CD is the diameter and AB is the chord
which is bisected by diameter at E
OA and OB are joined

To prove : ∠AOB = ∠BOA
Proof : In ∆OAE and ∆OBE
OA = OB (Radii of the circle)
OE = OE (Common)
AE = EB (Given)
∴ ∆OAE = ∆OBE (SSS criterian)
∴ ∠AOE = ∠BOE (c.p.c.t.)
Hence diameter bisect the angle subtended by the chord AB.

Question 6.
A line segment AB is of length 5 cm. Draw a circle of radius 4 cm passing through A and B. Can you draw a circle of radius 2 cm passing through A and B? Give reason in support of your answer.
Solution:
Steps of construction :
(i) Draw a line segment AB = 5 cm.
(ii) Draw a perpendicular bisector of AB.
(iii) With centre A and radius 4 cm, draw an arc which intersects the perpendicular bisector at O.
(iv) With centre O and radius 4 cm, draw a circle which passes through A and B.
With radius 2 cm, we cannot draw the circle passing through A and B as diameter
i. e. 2 + 2 = 4 cm is shorder than 5 cm.

Question 7.
An equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
Solution:
Steps of construction :
(i) Draw a line segment BC = 9 cm.
(ii) With centres B and C, draw arcs of 9 cm radius which intersect each other at A.
(iii) Join AB and AC.
∆ABC is the required triangle.
(iv) Draw perpendicular bisectors of sides AB and BC which intersect each other at O.
(v) With centre O and radius OB, draw a circle which passes through A, B and C.
This is the require circle in which ∆ABC is inscribed.

On measuring its radius, it is 5.2 cm

Question 8.
Given an arc of a circle, complete the circle.
Solution:
Steps of construction :
(i) Take three points A, B and C on the arc and join AB and BC.
(ii) Draw the perpendicular bisector of AB and BC which intersect each other at O.

(iii) With centre O and radius OA or OB, complete the circle.
This is the required circle.

Question 9.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
Below, three different pairs of circles are drawn:


(i) In the first pair, two circles do not intersect each other. Therefore they have no point in common. .
(ii) In the second pair, two circles intersect (touch) each other at one point P. Therefore they have one point in common.
(iii) In the third pair, two circles intersect each other at two points. Therefore they have two points in common.
There is no other possibility of two circles intersecting each other.
Therefore, two circles have at the most two points in common.

Question 10.
Suppose you are given a circle. Give a construction to find its centre.
Solution:
See Q. No. 4 of this exercise.

Question 11.
The length of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre? [NCERT]
Solution:
A circle with centre O and two parallel chords
AB and CD are AB = 6 cm, CD = 8 cm
Let OL ⊥ AB and OM ⊥ CD
∴ OL = 4 cm
Let OM = x cm
Let r be the radius of the circle

Question 12.
Two chords AB, CD of lengths 5 cm and 11 cm respectively of a circle are parallel. If the distance between AB and CD is 3 cm, find the radius of the circle.
Solution:
Let two chords AB and CD of length 5 cm and 11 cm are parallel to each other AB = 5 cm, CD = 11 cm
Distance between AB and LM = 3 cm
Join OB and OD
OL and OM are the perpendicular on CD and AB respectively. Which bisects AB and CD.
Let OL = x, then OM = (x + 3)

Now in right ∆OLD,
OD² = OL² + LD²
= x² + (5.5)²
Similarly in right ∆OMB,
OB² = OM² + MB² = (x + 3)² + (2.5)²
But OD = OB (Radii of the circle)
∴ (x + 3)² + (2.5)² = x² + (5.5)²
x² + 6x + 9 + 6.25 = x² + 30.25
6x = 30.25 – 6.25 – 9 = 15

Question 13.
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
Solution:
Given : A circle with centre O and a chord AB
Let M be the mid point of AB and OM is joined and produced to meet the minor arc AB at N
To prove : M is the mid point of arc AB
Construction : Join OA, OB

Proof: ∵ M is mid point of AB
∴ OM ⊥ AB
In AOAM and OBM,
OA = OB (Radii of the circle)
OM = OM (common)
AM = BM (M is mid point of AB)
∴ ∆OAM = ∆OBM (SSS criterian)
∴ ∠AOM = ∠BOM (c.p.c.t.)
⇒ ∠AOM = ∠BOM
But these are centre angles at the centre made by arcs AN and BN
∴ Arc AN = Arc BN
Hence N divides the arc in two equal parts

Question 14.
Prove that two different circles cannot intersect each other at more than two points.
Solution:
Given : Two circles
To prove : They cannot intersect each other more than two points
Construction : Let two circles intersect each other at three points A, B and C

Proof : Since two circles with centres O and O’ intersect at A, B and C
∴ A, B and C are non-collinear points
∴ Circle with centre O passes through three points A, B and C
and circle with centre O’ also passes through three points A, B and C
But one and only one circle can be drawn through three points
∴Our supposition is wrong
∴ Two circle cannot intersect each other not more than two points.

Question 15.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle. [NCERT]
Solution:
Let r be the radius of the circle with centre O.
Two parallel chords AB = 5 cm, CD = 11 cm
Let OL ⊥ AB and OM ⊥CD
∴ LM = 6 cm
Let OM = x, then
OL = 6 – x

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.