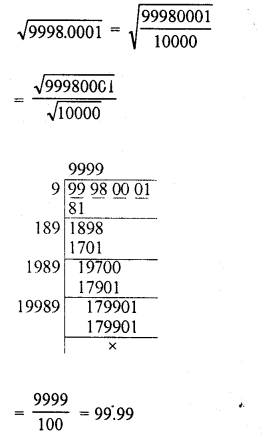
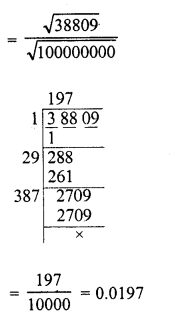
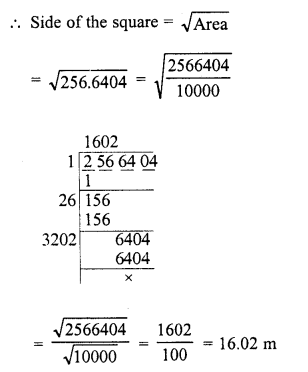
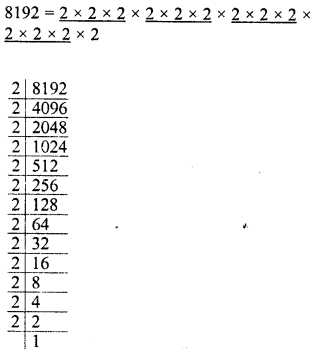
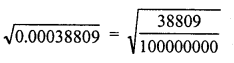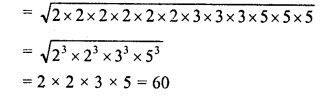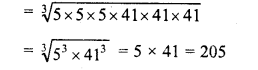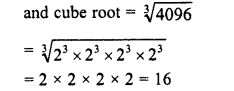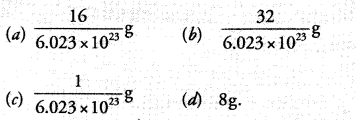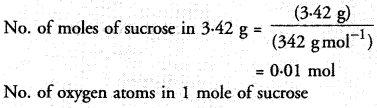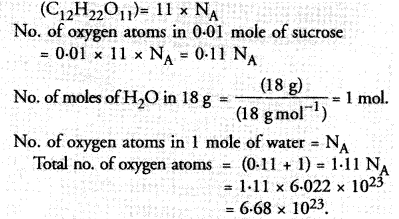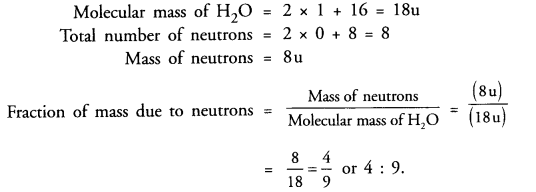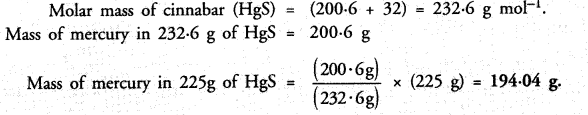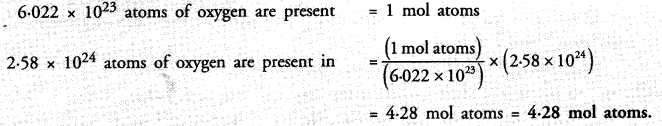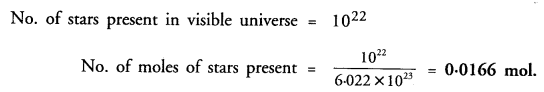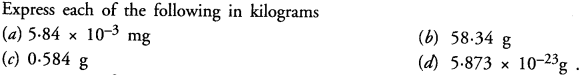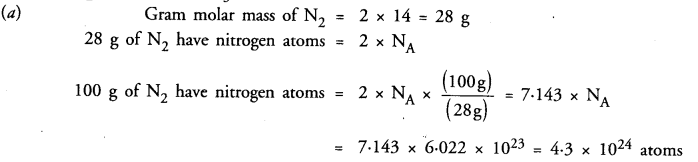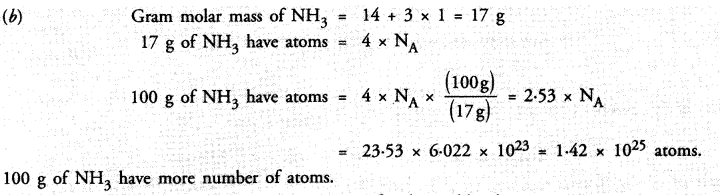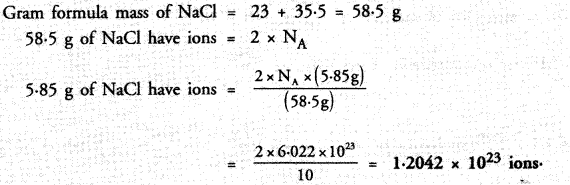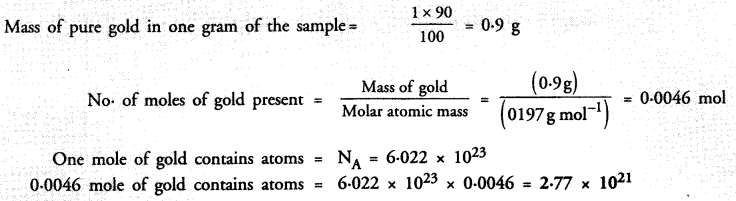Prasanna – Page 272

RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A

January 19, 2023

RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A.

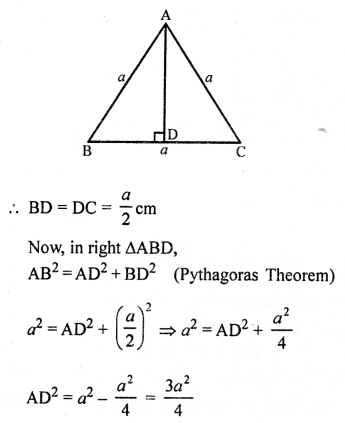
Question 1.
Solution:
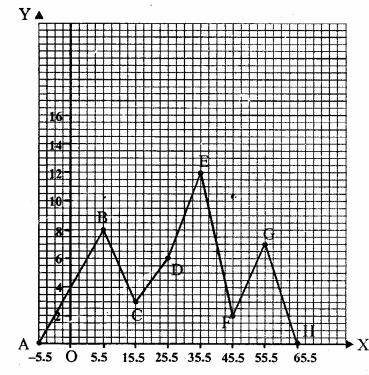
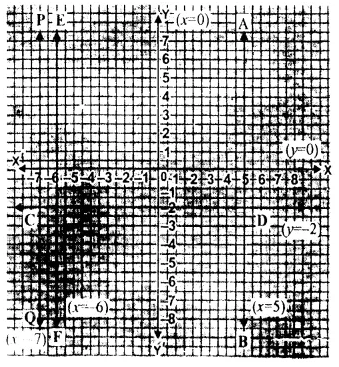
(i) x = 5 is the line AB parallel to the y-axis at a distance of 5 units.
(ii) y = – 2 is the line CD parallel to x-axis at a distance of – 2 units.
(iii) x + 6 = 0 => x = – 6 is the line EF parallel to y-axis at a distance of – 6 units.
(iv) x + 7 = 0 => x = – 7 is the line PQ parallel to y-axis at a distance of – 7 units.
(v) y = 0 is the equation of x-axis. The graph of y = 0 is the line X’OX
(vi) x = 0 is the equation of y-axis.The graph of x = 0 is the line YOY’
Ans.
RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A 1

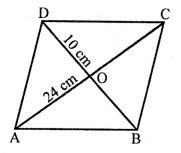
Question 2.
Solution:
In the given equation.
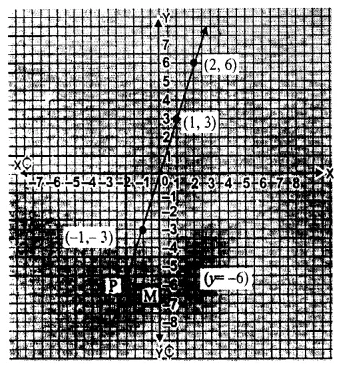
RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A 2
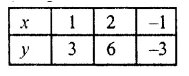
y = 3x
Put x = 1, then y = 3 x 1 = 3
Put x = 2, then y = 3 x 2 = 6
Put x = – 1, then y = 3 ( – 1) = – 3
Now, plot the points (1, 3), (2, 6) and ( – 1, – 3) as given the following table

and join them to form a line of the given equation.
Now from x = – 2,
draw a line parallel to y-axis at a distance of x = – 2, meeting the given line at P. From P, draw, a line parallel to x-axis joining y-axis at M, which is y = – 6 Hence, y = – 6 Ans.

Question 3.
Solution:
In the given equation x + 2y – 3 = 0
=> 2y = 3 – x
y = \(\frac { 3-x }{ 2 } \)
put x = 1,then
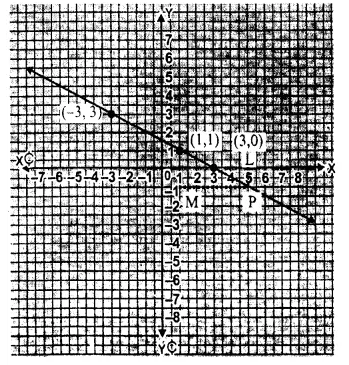
RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A 3

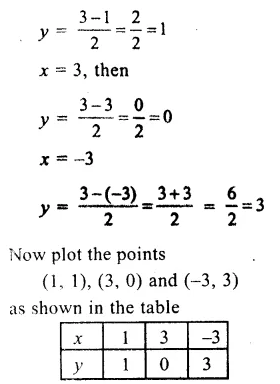
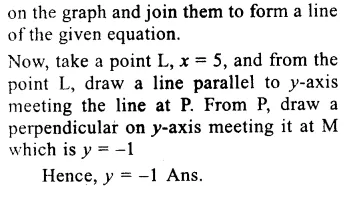
Question 4.
Solution:
(i) In the equation y = x
When x = 1, then y = 1
when x = 2, then y = 2
and when x = 3, then y = 3
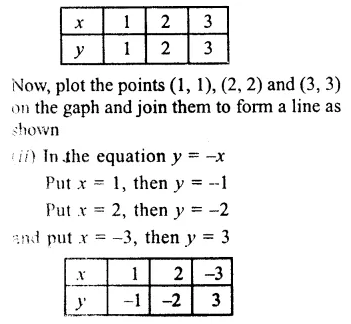
RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A 4

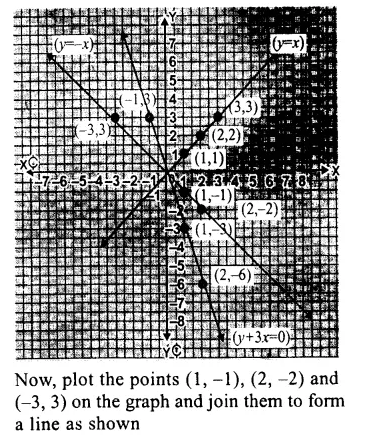
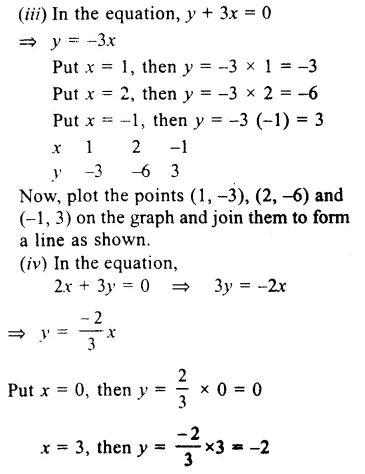
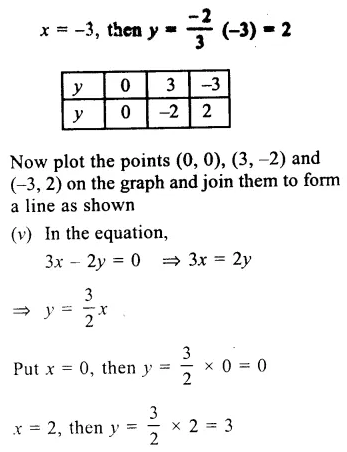
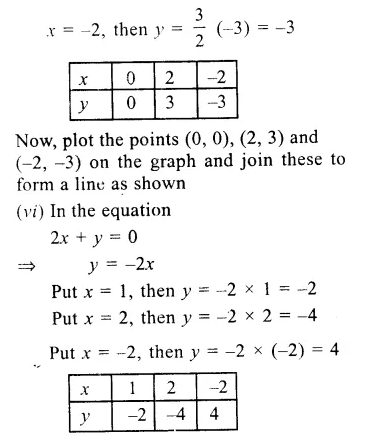
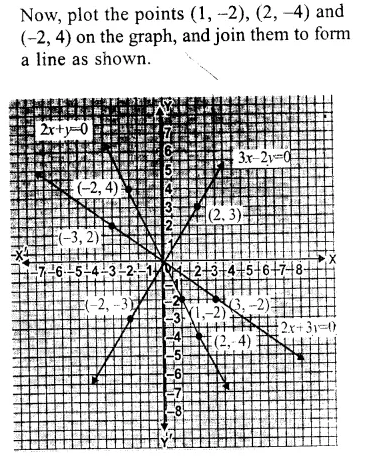
Question 5.
Solution:
In the given equation
2x – 3y = 5
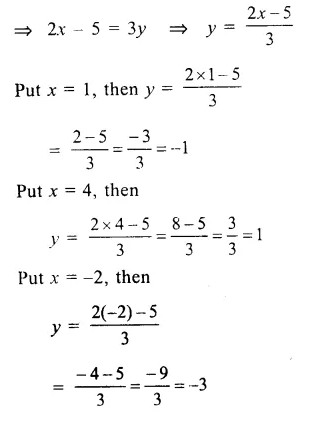
RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A 5

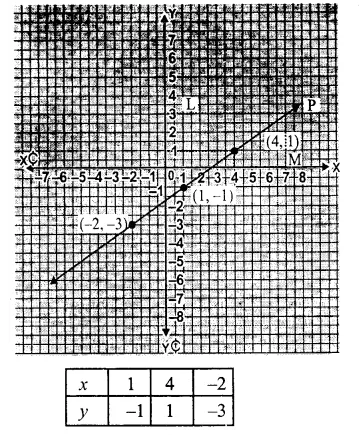
Question 6.
Solution:
In the given equation
2x + y = 6
=> y = 6 – 2x
Put x = 1, then y – 6 – 2 x 1 = 6 – 2 = 4
Put x = 2, then y = 6 – 2 x 2 = 6 – 4 = 2
Put x = 3, then y = 6 – 2 x 3 = 6 – 6 = 0
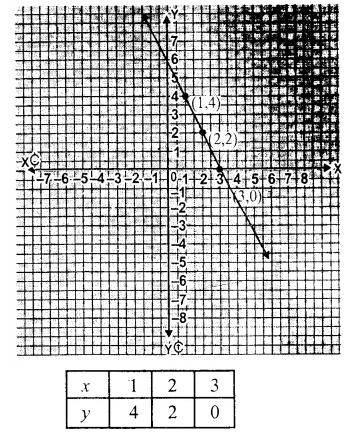
RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A 6

Question 7.
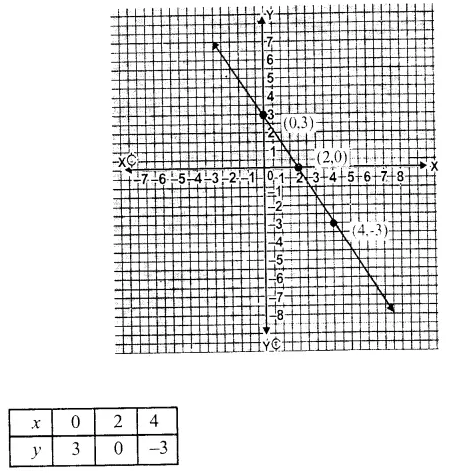
Solution:
In the given equation
3x + 2y = 6
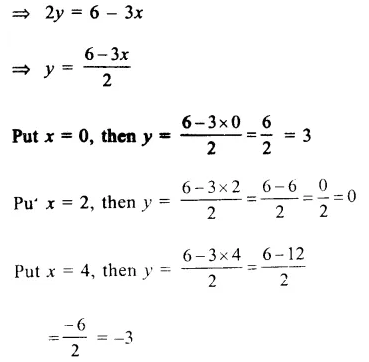
RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A 7

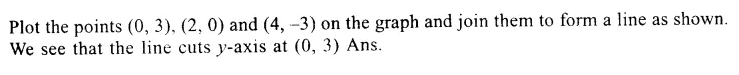
Hope given RS Aggarwal Class 9 Solutions Chapter 8 Linear Equations in Two Variables Ex 8A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E

January 19, 2023

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E.

Other Exercises

Very-Short-Answer and Short-Answer Questions
Question 1.
Solution:
Two properties for similarity of two triangles are:
(i) Angle-Angle-Angle (AAA) property.
(ii) Angle-Side-Angle (ASA) property.

Question 2.
Solution:
In a triangle, if a line parallel to one side is drawn, it will divide the other two sides proportionally.

Question 3.
Solution:
If a line divides any two sides of a triangle in the same ratio. Then, the line must be parallel to the third side.

Question 4.
Solution:
The line joining the midpoints of two sides of a triangle, is parallel to the third side.

Question 5.
Solution:
In two triangles, if three angles of the one triangle are equal to the three angles of the other, the triangles are similar.

Question 6.
Solution:
In two triangles, if two angles of the one triangle are equal to the corresponding angles of the other triangle, then the triangles are similar.

Question 7.
Solution:
In two triangles, if three sides of the one are proportional to the corresponding sides of the other, the triangles are similar.

Question 8.
Solution:
In two triangles, if two sides of the one are proportional to the corresponding sides of the other and their included angles are equal, the two triangles are similar.

Question 9.
Solution:
In a right angled triangle, the square on the hypotenuse is equal to the sum of squares on the other two sides.

Question 10.
Solution:
In a triangle, if the square on the longest side is equal to the sum of the squares on the other two sides, then the angle opposite to the hypotenuse is a right angle.

Question 11.
Solution:
The ratio of their areas will be 1 : 4.

Question 12.
Solution:
In two triangles ∆ABC and ∆PQR,
AB = 3 cm, AC = 6 cm, ∠A = 70°
PR = 9 cm, ∠P = 70° and PQ= 4.5 cm
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 1

Question 13.
Solution:
∆ABC ~ ∆DEF
2AB = DE, BC = 6 cm
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 2

Question 14.
Solution:
In the given figure,
DE || BC
AD = x cm, DB = (3x + 4) cm
AE = (x + 3) cm and EC = (3x + 19) cm
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 4

Question 15.
Solution:
AB is the ladder and A is window.
AB =10 m, AC = 8 m
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 5
We have to find the distance of BC
Let BC = x m
In right ∆ABC,
AB² = AC² + BC² (Pythagoras Theorem)
(10)² = 8² + x²
⇒ 100 = 64 + x²
⇒ x² = 100 – 64 = 36 = (6)²
x = 6
Distance between foot of ladder and base of the wall = 6 m.

Question 16.
Solution:
∆ABC is an equilateral triangle with side = 2a cm
AD ⊥ BC
and AD bisects BC at D
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 6
Now, in right ∆ABD,
AB² = AD² + BD² (Pythagoras Theorem)
⇒ (2a)² = AD² + (a)²
⇒ 4a² = AD² + a²
⇒ AD² = 4a² – a² = 3a²
AD = √3 a² = √3 a cm

Question 17.
Solution:
Given : ∆ABC ~ ∆DEF
and ar (∆ABC) = 64 cm²
and ar (∆DEF) = 169 cm², BC = 4 cm.
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 7

Question 18.
Solution:
In trape∠ium ABCD,
AB || CD
AB = 2CD
Diagonals AC and BD intersect each other at O
and area(∆AOB) = 84 cm².
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 8

Question 19.
Solution:
Let ∆ABC ~ ∆DEF
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 10

Question 20.
Solution:
In an equiangular ∆ABC,
AB = BC = CA = a cm.
Draw AD ⊥ BC which bisects BC at D.
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 12

Question 21.
Solution:
ABCD is a rhombus whose sides are equal and diagonals AC and BD bisect each other at right angles.
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 14
∠AOB = 90° and AO = OC, BO = OD
AO = \(\frac { 24 }{ 2 }\) = 12 cm
and BO = \(\frac { 10 }{ 2 }\) = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² (Pythagoras Theorem)
= (12)² + (5)² = 144 + 25 = 169 = (13)²
AB = 13
Each side of rhombus = 13 cm

Question 22.
Solution:
∆DEF ~ ∆GHK
∠D = ∠G = 48°
∠E = ∠H = 57°
∠F = ∠K
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 15
Now, in ∆DEF,
∠D + ∠E + ∠F = 180° (Angles of a triangle)
⇒ 48° + 57° + ∠F = 180°
⇒ 105° + ∠F= 180°
⇒ ∠F= 180°- 105° = 75°

Question 23.
Solution:
In the given figure,
In ∆ABC,
MN || BC
AM : MB = 1 : 2
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 16

Question 24.
Solution:
In ∆BMP,
PB = 5 cm, MP = 6 cm and BM = 9 cm
and in ∆CNR, NR = 9 cm
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 17

Question 25.
Solution:
In ∆ABC,
AB = AC = 25 cm
BC = 14 cm
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 19
AD ⊥ BC which bisects the base BC at D.
BD = DC = \(\frac { 14 }{ 2 }\) = 7 cm
Now, in right ∆ABD,
AB² = AD² + BD² (Pythagoras Theorem)
(25)² = AD² + 7²
625 = AD² + 49
⇒ AD² = 625 – 49 = 576
⇒ AD² = 576 = (24)²
AD = 24 cm
Length of altitude = 24 cm

Question 26.
Solution:
A man goes 12 m due north of point O reaching A and then 37 m due west reaching B.
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 20
Join OB,
In right ∆OAB,
OB² = OA² + AB² (Pythagoras Theorem)
= (12)² + (35)² = 144 + 1225 = 1369 = (37)²
OB = 37 m
The man is 37 m away from his starting point.

Question 27.
Solution:
In ∆ABC, AD is the bisector of ∠A which meets BC at D.
AB = c, BC = a, AC = b
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 21

Question 28.
Solution:
In the given figure, ∠AMN = ∠MBC = 76°
p, q and r are the lengths of AM, MB and BC Express the length of MN in terms of p, q and r.
In ∆ABC,
∠AMN = ∠MBC = 76°
But there are corresponding angles
MN || BC
∆AMN ~ ∆ABC
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 23

Question 29.
Solution:
In rhombus ABCD,
Diagonals AC and BD bisect each other at O at right angles.
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 24
AO = OC = \(\frac { 40 }{ 2 }\) = 20 cm
BO = OD = \(\frac { 42 }{ 2 }\) = 21 cm
Now, in right ∆AOB,
AB2 = AO2 + BO2 = (20)2 + (21)2 = 400 + 441 = 841
AB = √841 cm = 29 cm

Each side of rhombus = 29 cm

For each of the following statements state whether true (T) or false (F):
Question 30.
Solution:
(i) True.
(ii) False, as sides will not be proportion in each case.
(iii) False, as corresponding sides are proportional, not necessarily equal.
(iv) True.
(v) False, in ∆ABC,
AB = 6 cm, ∠A = 45° and AC = 8 cm
RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E 26
(vi) False, the polygon joining the midpoints of a quadrilateral is not a rhombus but it is a parallelogram.
(vii) True.
(viii) True.
(ix) True, O is any point in rectangle ABCD then
OA² + OC² = OB² + OD² is true.

(x) True.

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1

January 19, 2023

RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1

Other Exercises

Question 1.
Define the following tenns :
(i) Line segment
(ii) Collinear points
(iii) Parallel lines
(iv) Intersecting lines
(v) Concurrent lines
(vi) Ray
(vii) Half-line.
Solution:
(i) A line segment is a part of a line which lies between two points on it and it is denoted as \(\overline { AB }\) or only by AB. It has two end points and is measureable.

(ii) Three or more points which lie on the same straight line, are called collinear points.
(iii) Two lines which do not intersect each other at any point are called parallel lines.
(iv) If two lines have one point in common, are called intersecting lines.
(v) If two or more lines which pass through a common point are called concurrent lines.
(vi) Ray : A part of a line which has one end point.
(vii) Half line : If A, B, C, be the points on a line l, such that A lies between B and C and we delete the point from line l, two parts of l that remain are each called a half-line.
RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1 Q1.2

Question 2.
(i) How many lines can pass through a given point?
(ii) In how many points can two distinct lines at the most intersect?
Solution:
(i) Infinitely many lines can pass through a given point.
(ii) Two distinct lines at the most intersect at one point.

Question 3.
(i) Given two points P and Q, find how many line segments do they determine?
(ii) Name the line segments determined by the three collinear points P, Q and R.
Solution:
(i) Only one line segment can be drawn through two given points P and Q.
(ii) Three collinear points P, Q and R, three lines segments determine : \(\overline { PQ }\) , \(\overline { QR }\) and \(\overline { PR }\) .

Question 4.
Write the truth value (T/F) of each of the following statements:
(i) Two lines intersect in a point.
(ii) Two lines may intersect in two points.
(iii) A segment has no length.
(iv) Two distinct points always determine a line.
(v) Every ray has a finite length.
(vi) A ray has one end-point only.
(vii) A segment has one end-point only.
(viii) The ray AB is same as ray BA.
(ix) Only a single line may pass through a given point.
(x) Two lines are coincident if they have only one point in common.
Solution:
(i) False : As two lines do not intersect also any a point.
(ii) False : Two lines intersect at the most one point.
(iii) False : A line segment has definitely length.
(iv) True.
(v) False : Every ray has no definite length.
(vi) True.
(vii) False : A segment has two end point.
(viii)False : Rays AB and BA are two different rays.
(ix) False : Through a given point, infinitely many lines can pass.
(x) False : Two lines are coincident of each and every points coincide each other.

Question 5.
In the figure, name the following:
RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1 Q5.1

(i) Five line segments.
(ii) Five rays.
(iii) Four collinear points.
(iv) Two pairs of non-intersecting line segments.
Solution:
From the given figure,
(i) Five line segments are AC, PQ, PR, RS, QS.
(ii) Five rays : \(\xrightarrow { PA }\) , \(\xrightarrow { RB }\) , \(\xrightarrow { PB }\) , \(\xrightarrow { CS }\) , \(\xrightarrow { DS }\) .
(iii) Four collinear points are : CDQS, APR, PQL, PRB.
(iv) Two pairs of non-intersecting line segments an AB and CD, AP and CD, AR and CS, PR and QS.

Question 6.
Fill in the blanks so as to make the following statements true:
(i) Two distinct points in a plane determine a _____ line.
(ii) Two distinct_____ in a plane cannot have more than one point in common.
(iii) Given a line and a point, not on the line, there is one and only _____ line which passes through the given point and is_____ to the given line.
(iv) A line separates a plane into ____ parts namely the____ and the____ itself.
Solution:
(i) Two distinct points in a plane determine a unique line.
(ii) Two distinct lines in a plane cannot have more than one point in common.
(iii) Given a line and a point, not on the line, there is one and only perpendicular line which passes through the given point and is perpendicular to the given line.
(iv) A line separates a plane into three parts namely the two half planes, and the one line itself.

Hope given RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles Ex 9.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Value Based Questions in Science for Class 9 Chapter 3 Atoms and Molecules

January 19, 2023

Value Based Questions in Science for Class 9 Chapter 3 Atoms and Molecules

These Solutions are part of Value Based Questions in Science for Class 9. Here we have given Value Based Questions in Science for Class 9 Chapter 3 Atoms and Molecules

Question 1.
Kamla prepared aqueous solutions of barium chloride and sodium sulphate. She weighed them separately and then mixed them in a beaker. A white precipitate was immediately formed. She filtered the precipitate, dried it and then weighed it. After reading this narration, answer the following questions :

Will the weight of the precipitate be the same as that of the reactants before mixing ?
If not, what she should have done ?
Which law of chemical combination does this support ?
What is the value based information associated with it ?

Answer:

No, it will not be the same.
She should have weighed the total contents of the beaker after the reaction and not the precipitate alone.
It supports the law of conservation of mass.
Whenever the law of conservation of mass is to be verified in the laboratory, total mass of the reactants and also of products should be taken into account. Moreover, none of the species be allowed to leave the container.

More Resources

Question 2.
In order to verify the law of conservation of mass, a student mixed 6.3 g of sodium carbonate and 15.0 g of ethanoic acid in a conical flask. After experiment, he weighed the flask again. The weight of the residue in the flask was only 18.0 g. He approached the teacher who guided him to carry the experiment in a closed flask with a cork. There was no difference in weight of the flask before and after the experiment.

What was the mistake committed by the student ?
Why did not the two weights match earlier ?
How did the teacher help him ?
What lesson was learnt by the student ?

Answer:

He was carrying the experiment in an open flask.
CO₂ gas evolved in the reaction escaped from the flask
2CH₃COOH + Na₂CO₃ —-> 2CH₃COONa + H₂O + CO₂
Teacher asked him to cork the flask the moment the reactants were mixed.
The student learnt that in future he should not carry the experiment relating to the law of conservation of mass in an open container, particularly when one or more reactants or products are in the gaseous state.

Question 3.
A student was asked by his teacher a verify the law of conservation of mass in the laboratory. He prepared 5% aqueous solutions of NaCl and Na₂SO₄. He mixed 10 mL of both these solutions in a conical flask. He weighed the flask on a balance. He then stirred the flask with a rod and weighed it after sometime. There was no change in mass. Read this narration and answer the questions given below :

Was the student able to verify the law of conservation of mass ?
If not, what was the mistake committed by him ?
In your opinion, what he should have done ?
What is the value based information associated with this ?

Answer:

No, he could not verify the law of conservation of mass inspite of the fact that there was no change in mass.
No chemical reaction takes place between NaCl and Na₂SO₄. This means that no reaction actually took place in the flask.
He should have performed the experiment by using aqueous solutions of BaCl₂ and Na₂SO₄. A chemical reaction takes place in this case and a white precipitate of BaSO₄ is formed.
While working in the chemistry laboratory, a student must select those chemical substances which actually react with each other. Only then products will be formed.

Question 4.
Dalton was the first scientist to introduce symbols for the known elements. Modern symbols were given by J.J. Berzelius. A symbol in general may be defined as the short hand representation of the name of an element.

How do symbols help in identifying elements ?
Do we use symbols in daily life ?
What values do you attach for using symbols ?

Answer:

All the known elements are identified by their symbols.
For example, Symbol of calcium = Ca; Symbol of copper = Cu; Symbol of iron= Fe
Yes, these are very common in daily life. For example, all road signs such as diversions, dangerous, zones etc. are indicated by symbols. In playground, umpires, signify the various happenings such as ‘LBW’, ‘Out’ etc. in circket by symbols.
Symbols for road signs save many lives. The names of many complicated compounds are shown by the formulae which are collection of symbols. The chemical composition of all madicines are shown either on the strips or on the bottles by their formulae.

Question 5.
Mole concept is an important tool for dealing with chemical calculations. The elements have atomic masses while compounds have molecular masses or molar masses. Mole is in fact, a collection of Avogadro’s number (N_A) of the particles of a substance whether element or compound. The value of Avogadro’s number is 6-022 x 10²³.

Why is mole commonly called chemist’s dozen ?
What is the value associated with the term mole ?

Answer:

Just as a dozen represents 12 articles, a mole represents 6.022 x 10²³ or Avogadro’s number of particles. Therefore, it has been rightly called chemist’s dozen.
Since particles such as atoms, ions or molecules are very extremely small in size, it is very difficult to identify and express them individually. These are collectively represented as mole. For example, 3.011 x 10²³ molecules of CO₂ gas are shown as 0.5 mole which is very simple.

Hope given Value Based Questions in Science for Class 9 Chapter 3 Atoms and Molecules are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3

January 19, 2023

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3

Other Exercises

Question 1.
Find the squares of the following numbers using column method. Verify the result by finding the square using the usual multiplication :
(i) 25
(ii) 37
(iii) 54
(iv) 71
(v) 96
Solution:
(i) (25)²
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3 1

Question 2.
Find the squares of the following numbers using diagonal method :
(i) 98
(ii) 273
(iii) 348
(iv) 295
(v) 171
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3 3

Question 3.
Find the squares of the following numbers :
(i) 127
(ii) 503
(iii) 451
(iv) 862
(v) 265
Solution:
(i) (127)² = (120 + 7)²{(a + b)² = a² + lab + b²}
= (120)² + 2 x 120 x 7 + (7)²= 14400+ 1680 + 49 = 16129

(ii) (503)² = (500 + 3)²{(a + b)² = a² + lab + b¹}
= (500)² + 2 x 500 x 3 + (3)²= 250000 + 3000 + 9 = 353009

(iii) (451)² = (400 + 51)²{(a + b)² = a² + lab + b²}
= (400)² + 2 x 400 x 51 + (5l)²= 160000 + 40800 + 2601 = 203401

(iv) (451)² = (800 + 62)²{(a + b)² = a² + lab + b²}
= (800)² + 2 x 800 x 62 + (62)²= 640000 + 99200 + 3844 = 743044

(v) (265)²
{(a + b)² = a² + 2ab + b²}
(200 + 65)² = (200)² + 2 x 200 x 65 + (65)²= 40000 + 26000 + 4225 = 70225

Question 4.
Find the squares of the following numbers
(i) 425
(ii) 575
(iii) 405
(iv) 205
(v) 95
(vi) 745
(vii) 512
(viii) 995
Solution:
(i) (425)²Here n = 42
∴ n (n + 1) = 42 (42 + 1) = 42 x 43 = 1806
∴ (425)² = 180625

(ii) (575)²Here n = 57
∴ n (n + 1) = 57 (57 + 1) = 57 x 58 = 3306
∴ (575)² = 330625

(iii) (405)²Here n = 40
∴ n (n + 1) = 40 (40 + 1) -40 x 41 = 1640
∴ (405)² = 164025

(iv) (205)²Here n = 20
∴ n (n + 1) = 20 (20 + 1) = 20 x 21 = 420
∴ (205)² = 42025

(v) (95)²Here n = 9
∴ n (n + 1) = 9 (9 + 1) = 9 x 10 = 90
∴ (95)² = 9025

(vi) (745)²
Here n = 74
∴ n (n + 1) = 74 (74 + 1) = 74 x 75 = 5550
∴ (745)² = 555025

(vii) (512)²Here a = 1, b = 2
∴ (5ab)² = (250 + ab) x 1000 + (ab)²∴ (512)² = (250 + 12) x 1000 + (12)²= 262 x 1000 + 144
= 262000 + 144 = 262144

(viii) (995)²Here n = 99
∴ n (n + 1) = 99 (99 + 1) = 99 x 100 = 9900
∴ (995)² = 990025

Question 5.
Find the squares of the following numbers using the identity (a + b)1 = a2 + lab + b1
(i) 405
(ii) 510
(iii) 1001
(iv) 209
(v) 605
Solution:
a + b)² = a² + lab + b²

(i) (405)² = (400 + 5)²= (400)² + 2 x 400 x 5 + (5)²= 160000 + 4000 + 25 = 164025

(ii) (510)² = (500 + 10)²= (500)² + 2 x 500 x 10 x (10)²= 250000 + 10000 + 100
= 260100

(iii) (1001)² = (1000+1)²= (1000)² + 2 X 1000 x 1 + (1)= 1000000 + 2000 + 1
=1002001

(iv) (209)² = (200 + 9)²= (200)² + 2 x 200 x 9 x (9)²
= 40000 + 3600 +81
= 43681

(v) (605)² = (600 + 5)²= (600)² + 2 x 600 x 5 +(5)²= 360000 + 6000 25
=366025

Question 6.
Find the squares of the following numbers using the identity (a – b)² = a² – 2ab + b² :
(i) 395
(ii) 995
(iii) 495
(iv) 498
(v) 99
(vi) 999
(vii) 599
Solution:
a – b)² = a² – lab + b²

(i) (395)² = (400 – 5)²= (400)² – 2 x 400 x 5 + (5)²= 160000-4000 + 25
= 160025-4000
= 156025

(ii) (995)² = (1000 – 5)²
= (1000)² – 2 x 1000 x 5 + (5)²= 1000000- 10000 + 25
= 1000025- 10000
= 990025

(iii) (495)² = (500 – 5)²= (500)² – 2 x 500 x 5 + (5)²= 250000 – 5000 + 25
= 250025 – 5000
= 245025

(iv) (498)² = (500 – 2)²= (500)² – 2 x 500 x 2 + (2)²= 250000 – 2000 + 4
= 250004 – 2000
= 248004

(v) (99)² = (100 – l)²= (100)² – 2 x 100 x 1 + (1)²
= 10000 – 200 + 1
= 10001 – 200
= 9801

(vi) (999)² = (1000- l)²= (1000)² – 2 x 1000 x 1+ (1)2
= 1000000-2000+1
= 10000001-2000=998001

(vii) (599)² = (600 – 1)²= (600)²-2 x 600 X 1+ (1)2
= 360000 -1200+1
= 360001 – 1200 = 358801

Question 7.
Find the squares of the following numbers by visual method :
(i) 52
(ii) 95
(iii) 505
(iv) 702
(v) 99
Solution:
(a + b)² = a² – ab + ab + b²(i) (52)² = (50 + 2)²= 2500 + 100 + 100 + 4
= 2704
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3 6
(ii) (95)² = (90 + 5)²= 8100 + 450 + 450 + 25
= 9025

(iii) (505)² = (500 + 5)²= 250000 + 2500 + 2500 + 25
= 255025

(iv) (702)² = (700 + 2)²= 490000 + 1400+ 1400 + 4
= 492804

(v) (99)² = (90 + 9)²= 8100 + 810 + 810 + 81
= 9801
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3 10

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A

January 19, 2023

RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A.

Question 1.
Solution:
Given : In the figure, ABCD is a quadrilateral and
AB = CD = 5cm
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q1.1

Question 2.
Solution:
In ||gm ABCD,
AB = 10cm, altitude DL = 6cm
and BM is altitude on AD, and BM = 8 cm.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q2.1

Question 3.
Solution:
Diagonals of rhombus are 16cm and 24 cm.
Area = \(\frac { 1 }{ 2 } \) x product of diagonals
= \(\frac { 1 }{ 2 } \) x 1st diagonal x 2nd diagonal
= \(\frac { 1 }{ 2 } \) x 16 x 24
= 192 cm² Ans.

Question 4.
Solution:
Parallel sides of a trapezium are 9cm and 6cm and distance between them is 8cm
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q4.1

Question 5.
Solution:
from the figure
(i) In ∆ BCD, ∠ DBC = 90°
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q5.1

Question 6.
Solution:
In the fig, ABCD is a trapezium. AB || DC
AB = 7cm, AD = BC = 5cm.
Distance between AB and DC = 4 cm.
i.e. ⊥AL = ⊥BM = 4cm.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q6.1

Question 7.
Solution:
Given : In quad. ABCD. AL⊥BD and CM⊥BD.
To prove : ar(quad. ABCD)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q7.1

Question 8.
Solution:
In quad. ABCD, BD is its diagonal and AL⊥BD, CM⊥BD
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q8.1

Question 9.
Solution:
Given : ABCD is a trapezium in which AB || DC and its diagonals AC and BD intersect each other at O.
To prove : ar(∆ AOD) = ar(∆ BOC)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q9.1

Question 10.
Solution:
Given : In the figure,
DE || BC.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q10.1

Question 11.
Solution:
Given : In ∆ ABC, D and E are the points on AB and AC such that
ar( ∆ BCE) = ar( ∆ BCD)
To prove : DE || BC.
Proof : (∆ BCE) = ar(∆ BCD)
But these are on the same base BC.
Their altitudes are equal.
Hence DE || BC
Hence proved.

Question 12.
Solution:
Given : In ||gm ABCD, O is any. point inside the ||gm. OA, OB, OC and OD are joined.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q12.1

Question 13.
Solution:
Given : In quad. ABCD.
A line through D, parallel to AC, meets ‘BC produced in P. AP in joined which intersects CD at E.
To prove : ar( ∆ ABP) = ar(quad. ABCD).
Const. Join AC
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q13.1

Question 14.
Solution:
Given : ∆ ABC and ∆ DBC are on the same base BC with points A and D on , opposite sides of BC and
ar( ∆ ABC) = ar( ∆ DBC).
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q14.1

Question 15.
Solution:
Given : In ∆ ABC, AD is the median and P is a point on AD
BP and CP are joined
To prove : (i) ar(∆BDP) = ar(∆CDP)
(ii) ar( ∆ ABP) = ar( ∆ ACP)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q15.1

Question 16.
Solution:
Given : In quad. ABCD, diagonals AC and BD intersect each other at O and BO = OD
To prove : ar(∆ ABC) = ar(∆ ADC)
Proof : In ∆ ABD,
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q16.1

Question 17.
Solution:
In ∆ ABC,D is mid point of BC
and E is midpoint of AD and BE is joined.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q17.1

Question 18.
Solution:
Given : In ∆ ABC. D is a point on AB and AD is joined. E is mid point of AD EB and EC are joined.
To prove : ar( ∆ BEC) = \(\frac { 1 }{ 2 } \) ar( ∆ ABC)
Proof : In ∆ ABD,
E is midpoint of AD
BE is its median
ar(∆ EBD) = ar(∆ ABE)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q18.1

Question 19.
Solution:
Given : In ∆ ABC, D is midpoint of BC and E is die midpoint of BO is the midpoint of AE.
To prove that ar( ∆ BOE) = \(\frac { 1 }{ 8 } \) ar(∆ ABC).
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q19.1

Question 20.
Solution:
Given : In ||gm ABCD, O is any point on diagonal AC.
To prove : ar( ∆ AOB) = ar( ∆ AOD)
Const. Join BD which intersects AC at P
Proof : In ∆ OBD,
P is midpoint of BD
(Diagonals of ||gm bisect each other)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q20.1

Question 21.
Solution:
Given : ABCD is a ||gm.
P, Q, R and S are the midpoints of sides AB, BC, CD, DA respectively.
PQ, QR, RS and SP are joined.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q21.1

Question 22.
Solution:
Given : In pentagon ABCDE,
EG || DA meets BA produced and
CF || DB, meets AB produced.
To prove : ar(pentagon ABCDE) = ar(∆ DGF)
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q22.1

Question 23.
Solution:
Given ; A ∆ ABC in which AD is the median.
To prove ; ar( ∆ ABD) = ar( ∆ ACD)
Const : Draw AE⊥BC.
Proof : Area of ∆ ABD
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q23.1

Question 24.
Solution:
Given : A ||gm ABCD in which AC is its diagonal which divides ||gm ABCD in two ∆ ABC and ∆ ADC.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q24.1

Question 25.
Solution:
Given : In ∆ ABC,
D is a point on BC such that
BD = \(\frac { 1 }{ 2 } \) DC
AD is joined.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q25.1

Question 26.
Solution:
Given : In ∆ ABC, D is a point on BC such that
BD : DC = m : n
AD is joined.
RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A Q26.1

Hope given RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7

January 19, 2023

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7

Other Exercises

Find the square root of the following numbers in decimal form :

Question 1.
84.8241
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 1

Question 2.
0.7225
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 2

Question 3.
0.813604
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 3

Question 4.
0.00002025
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 5

Question 5.
150.0625
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 6

Question 6.
225.6004
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 7

Question 7.
3600.720036
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 8

Question 8.
236.144689
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 9

Question 9.
0.00059049
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 11

Question 10.
176.252176
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 12

Question 11.
9998.0001
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 14

Question 12.
0.00038809
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 15

Question 13.
What is that fraction which when multiplied by itself gives 227.798649 ?
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 17

Question 14.
square playground is 256.6404 square metres. Find the length of one side of the playground.
Solution:
Area of square playground = 256.6404 sq. m
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 18

Question 15.
What is the fraction which when multiplied by itself gives 0.00053361 ?
Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 19

Question 16.
Simplify :
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 20

Solution:

Question 17.
Evaluate \(\sqrt { 50625 }\) and hence find the value of \(\sqrt { 506.25 } +\sqrt { 5.0625 } \).
Solution:

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 24

Question 18.
Find the value of \(\sqrt { 103.0225 }\) and hence And the value of

Solution:
RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 26

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3

January 19, 2023

RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3

Other Exercises

Question 1.
Find the cube roots of the following numbers by successive subtraction of numbers : 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397,
(i) 64
(ii) 512
(iii) 1728
Solution:
(i) 64
64 – 1 = 63
63 – 7 = 56
56 – 19 = 37
37 – 37 = 0
∴ 64 = (4)³
∴ Cube root of 64 = 4

(ii) 512
512 -1 =511
511- 7 = 504
504 – 19 = 485
485 – 37 = 448
448 – 61 = 387
387 – 91 =296
296 – 127 = 169
169 – 169 = 0
∴ 512 = (8)³
∴ Cube root of 512 = 8

(iii) 1728
1728 – 1= 1727
1727 -7 = 1720
1720 -19 = 1701
1701 -37= 1664
1664 – 61 = 1603
1603 – 91 = 1512
1512 -127= 1385 .
1385 – 169= 1216
1216 – 217 = 999
999 – 271 =728
728 – 331 = 397
397 – 397=0
∴ 1728 = (12)³
∴ Cube root of 1728 = 1²

Question 2.
Using the method of successive subtraction, examine whether or not the following numbers are perfect cubes :
(i) 130
(ii) 345
(iii) 792
(iv) 1331
Solution:
(i) 130
130 – 1 = 129
129 -7 = 122
122 -19 = 103
103 -37 = 66
66 – 61 = 5
We see that 5 is left
∴ 130 is not a perfect cube.

(ii) 345
345 – 1 = 344
344 – 7 = 337
337 – 19 = 318
318 – 37 = 281
81 – 61 =220
220 – 91 = 129
129 – 127 = 2
We see that 2 is left
∴ 345 is not a perfect cube.

(iii) 792
792 – 1 = 791
791 – 7 = 784
784 – 19 = 765
765 – 37 = 728
728 – 61 = 667
667 – 91 = 576
576 – 127 = 449
449 – 169 = 280
∴ We see 280 is left as 280 <217
∴ 792 is not a perfect cube.

(iv) 1331
1331 – 1 = 1330
1330 -7 = 1323
1323 – 19 = 1304
1304 – 37 = 1267
1267 – 61 = 1206
1206 – 91 = 1115
1115 – 127 = 988
988 – 169 = 819
819 – 217 = 602
602 – 271 = 331
331 – 331 =0
∴ 1331 is a perfect cube

Question 3.
Find the smallest number that must be subtracted from those of the numbers in question 2, which are not perfect cubes, to make them perfect cubes. What are the corresponding cube roots ?
Solution:
We have examined in Question 2, the numbers 130, 345 and 792 are not perfect cubes. Therefore
(i) 130
130 – 1 = 129
129 -7= 122
122 -19 = 103
103 – 37 = 66
66 – 61 = 5
Here 5 is left
∴ 5 < 91 5 is to be subtracted to get a perfect cube.
Cube root of 130 – 5 = 125 is 5

(ii) 345
345 – 1 = 344
344 -7 = 337
337 – 19 = 318
318 – 37 = 281
281 – 61 =220
220 – 91 = 129
129 – 127 = 2
Here 2 is left ∵ 2 < 169
∴ Cube root of 345 – 2 = 343 is 7
∴ 2 is to be subtracted to get a perfect cube.

(iii) 792
792 – 1 = 791
791 – 7 = 784
784 – 19 = 765
765 – 37 = 728
728 – 61 =667
667 – 91 = 576 5
76 – 127 = 449
449 – 169 = 280
280 – 217 = 63
∴ 63 <217
∴ 63 is to be subtracted
∴ Cube root of 792 – 63 = 729 is 9

Question 4.
Find the cube root of each of the following natural numbers :
(i) 343
(ii) 2744
(iii) 4913
(iv) 1728
(v) 35937
(vi) 17576
(vii) 134217728
(viii) 48228544
(ix) 74088000
(x) 157464
(xi) 1157625
(xii) 33698267
Solution:
RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3 1

Question 5.
Find the smallest number which when multiplied with 3600 will make the product a perfect cube. Further, find the cube root of the product.
Solution:
RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3 11
Grouping the factors in triplets of equal factors, we see that 2, 3 x 3 and 5 x 5 are left
∴ In order to complete the triplets, we have to multiply it by 2, 3 and 5.
∴ The smallest number to be multiplied = 2×2 x 3 x 5 = 60
Now product = 3600 x 60 = 216000 and cube root of 216000
RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3 12

Question 6.
Multiply 210125 by the smallest number so that the product is a perfect cube. Also, find out the cube root of the product.
Solution:
RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3 13
Grouping the factors in triplets of equal factors, we see that 41 x 41 is left
∴ In order to complete the triplet, we have to multiply it by 41
∴ Smallest number to be multiplied = 41
∴ Product = 210125 x 41 = 8615125
∴ Cube root of 8615125
RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3 14

Question 7.
What is the smallest number by which 8192 must be divided so that quotient is a perfect cube ? Also, find the cube root of the quotient so obtained.
Solution:
RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3 15
Grouping the factors in triplets of equal factors, we see that 2 is left
∴ Dividing by 2, we get the quotient a perfect cube
∴ Perfect cube = 8192 + 2 = 4096

Question 8.
Three numbers are in the ratio 1:2:3. The sum of their cubes is 98784. Find the numbers.
Solution:
Ratio in numbers =1:2:3
Let first number = x
Then second number = 2x
and third number = 3x
∴ Sum of cubes of there numbers = (x)³ + (2x)³+(3x)³
RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3 17

Question 9.
The volume of a cube is 9261000 m³. Find the side of the cube.
Solution:
RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3 19

Hope given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C

January 19, 2023

RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14C.

Other Exercises

Question 1.
Solution:
It is clear that the given frequency distribution is in exclusive form, we represent the daily wages (in rupees) along x-axis and no. of workers along y-axis. Then we construct rectangles with class intervals as bases and corresponding frequencies as heights as shown given below:
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q1.1

Question 2.
Solution:
We shall take daily earnings along x-axis and number of stores along y-axis. Then we construct rectangles with the given class intervals as bases and corresponding frequency as height as shown in the graph.
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q2.1

Question 3.
Solution:
We shall take heights along x-axis and number of students along y-axis. Then we shall complete the rectangles with the given class intervals as bases and frequency as height and complete the histogram as shown below :
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q3.1

Question 4.
Solution:
We shall take class intervals along x-axis and frequency along y-axis Then we shall complete the rectangles with given class interval as bases and frequency as heights and complete the histogram as shown below.
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q4.1

Question 5.
Solution:
The given frequency distribution is in inclusive form first we convert it into exclusive form at given below.
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q5.1

Now, we shall take class intervals along x-axis and frequency along y-axis and draw rectangles with class intervals as bases and frequency as heights and complete the histogram as shown.

Question 6.
Solution:
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q6.1

Question 7.
Solution:
In the given distribution class intervals are different size. So, we shall calculate the adjusted frequency for each class. Here minimum class size is 4. We know that adjusted
frequency of the class is \(\frac { max\quad class\quad size }{ class\quad size\quad of\quad this\quad class } \) x its frequency
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q7.1

Question 8.
Solution:
We shall take two imagined classes one 0-10 at the beginning with zero frequency a id other 70-80 at the end with zero frequency.
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q8.1

Now, plot the points” (5, 0), (15, 2), (25, 5), (35, 12), (45, 19), (55, 9), (65, 4), (75, 0) on the graph and join them its order to get a polygon as shown below.

Question 9.
Solution:
We take Age (in years) along x-axis and number of patients along y-axis. First we complete the histogram and them join the midpoints of their tops in order
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q9.1
We also take two imagined classes. One 0-10 at the beginning and other 70-80 at the end and also join their midpoints to complete the polygon as shown.

Question 10.
Solution:
We take class intervals along x-axis and frequency along y-axis.
First we complete the histogram and then join the midpoints of the tops of adjacent rectangles in order. We shall take two imagined classes 15-20 at the beginning and 50-55 at the end.
We also join their midpoints to complete the polygon as shown
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q10.1

Question 11.
Solution:
We represent class interval on x-axis and frequency on y-axis. First we construct the histogram and then join the midpoints of the tops of each rectangle by line segments. We shall take two imagined class i.e. 560-600 at the beginning and 840-900 at the end. Join their midpoints also to complete
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q11.1

Question 12.
Solution:
We will take the imagined class 11-0 at the beginning and 61-70 at the end. Each with frequency zero. Thus, we have,
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14C Q12.1

Now we will mark the points A (-5.5, 0), B(5.5, 8), C(15.5, 3) D(25.5, 6), E(35.5, 12), F(45.5, 2), G(55.5, 7) and H(65.5, 0) on the graph and join them in order to get the required frequency polygon.

Hope given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles VSAQS

January 19, 2023

RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles VSAQS

Other Exercises

Question 1.
How many least number of distinct points determine a unique line?
Solution:
At least two distinct points determine a unique line.

Question 2.
How many lines can be drawn through both of the given points?
Solution:
Through two given points, one line can be drawn.

Question 3.
How many lines can be drawn through a given point?
Solution:
Through a given point, infinitely many lines can be drawn.

Question 4.
in how many points two distinct lines can intersect?
Solution:
Two distinct lines can intersect at the most one point.

Question 5.
In how many points a line, not in a plane, can intersect the plane?
Solution:
A line not in a plane, can intersect the plane at one point.

Question 6.
In how many points two distinct planes can intersect?
Solution:
Two distinct planes can intersect each other at infinite number of points.

Question 7.
In how many lines two distinct planes can intersect?
Solution:
Two distinct planes intersect each other in one line.

Question 8.
How many least number of distinct points determine a unique plane?
Solution:
Three non-collinear points can determine a unique plane.

Question 9.
Given three distinct points in a plane, how many lines can be drawn by joining them?
Solution:
Through three given points, one line can be drawn of they are collinear and three if they are non-collinear.

Question 10.
How many planes can be made to pass through a line and a point not on the line?
Solution:
Only one plane can be made to pass through a line and a point not on the line.

Question 11.
How many planes can be made to pass through two points?
Solution:
Infinite number of planes can be made to pass through two points.

Question 12.
How many planes can be made to pass through three distinct points?
Solution:
Infinite number of planes can be made of they are collinear and only one plane, if they are non-collinear.

Hope given RD Sharma Class 9 Solutions Chapter 9 Triangle and its Angles VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules

January 19, 2023

NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules

These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules

Question 1.
Which of the following correctly represents 360 g of water ?
(i) 2 moles of H₂O
(ii) 20 moles of water
(iii) 6.022 x 10²³ molecules of water
(iv) 1.2044 x 10²⁵ molecules of water
(a) (i)
(b) (i) and (iv)
(c) (ii) and (iii)
(d) (ii) and (iv).
Mass of water
Correct Answer:
(d)
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 1

More Resources

Question 2.
Which of the following statements is not true about atoms ?
(a) Atoms are not able to exist independently
(b) Atoms are the basic units from which molecules and ions are formed
(c) Atoms are always neutral in nature
(d) Atoms aggregate in large numbers to form the matter that we can see, feel or touch.
Correct Answer:
(a) Atoms of inert gas elements can exist independently. However, atoms of all other elements cannot exist independently.

Question 3.
The chemical symbol for nitrogen gas is :
(a) Ni
(b) N₂
(c) N⁺
(d) N
Correct Answer:
(b).

Question 4.
The chemical symbol for sodium is :
(a) So
(b) Sd
(c) NA
(d) Na.
Correct Answer:
(d ).

Question 5.
Which of the following would weigh the maximum ?
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 2
Correct Answer:
(c).
(a) 0.2 x 342 g = 68.4 g
(b) 2 x 44 g = 88 g
(c) 2 x 100 g = 200 g
(d) 10 x 18 g = 180 g.

Question 6.
Which of the following has maximum number of atoms ?
(a) 18 g of H₂O
(b) 18 g of O₂
(c) 18 g of CO₂
(d) 18 g of CH₄.
Correct Answer:
(d).
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 3

Question 7.
Which of the following contains maximum number of molecules ?
(a) 1g CO₂
(b) 1g N₂
(c) 1g H₂
(d) 1g CH₄.
Correct Answer:
(c).
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 4

Question 8.
Mass of one atom of oxygen is :
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 5
Correct Answer:
(a).

Question 9.
3.42 g of sucrose are dissolved in 18 g of water in a beaker. The number of oxygen atoms in the solution are
(a) 6.68 x 10²³
(b) 6.09 x 102²²(c) 6.022 x 10²³
(d) 6.022 x 10²¹.
Correct Answer:
(a).
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 6

Question 10.
A change in the physical state can be brought about :
(a) only when energy is given to the system
(b) only when energy is taken out from the system
(c) when energy is either given to, or taken out from the system
(d) without any energy change.
Correct Answer:
(c).

Short Answer Questions

Question 11.
Which of the following represents a correct chemical formula ? Name it.
(a) CaCl
(b) BiPO₄
(c) NaSO₄
(d) NaS.
Answer:
(b). Both Bi and PO₄ are trivalent ion (Bi³⁺ and PO₄^3- ).
It is known as bismuth phosphate.

Question 12.
Write the chemical formulae for the following compounds :
(a) Copper (II) bromide
(b) Aluminium (III) nitrate
(c) Calcium (II) phosphate
(d) Iron (III) sulphide
(e) Mercury (II) chloride
(f) Magnesium (II) acetate.
Answer:
(a) CuBr₂
(b) Al(NO₃)₃
(c) Ca₃(PO₄)₂
(d) Fe₂S₃
(e) HgCl₂
(f) Mg(CH₂COO)₂.

Question 13.
Write the chemical formulae of all the compounds that can be formed by the combination of following ions :
Cu²⁺, Na⁺, Fe³⁺, Cl^–, SO₄^2-, PO₄^3- .
Answer:
For Cu²⁺ ion : CuCl₂, CuSO₄, Cu₃(PO₄)₂
For Na⁺ ion : NaCl, Na₂SO₄, Na3PO₄
For Fe³⁺ um :FeCl₃, Fe₂(SO₄)₃, FePO₄.

Question 14.
Write the cations and anions present (if any) in the following compounds :
(a) CH₃COONa
(b) NaCl
(c) H₂
(d) NH₄NO₃.
Answer:
(a) CH₃O^– (anion), Na⁺ (cation)
(b) Na⁺ (cation), Cl^– (anion)
(c) Molecular compound (no ions)
(d) NH₄⁺(cation), NO₃^– (anion).

Question 15.
Give the formulae of the compounds formed from the following sets of elements :
(a) Calcium and fluorine
(b) Hydrogen and sulphur
(c) Nitrogen and hydrogen
(d) Carbon and chlorine
(e) Sodium and oxygen
(f) Carbon and oxygen.
Answer:
(a) CaF₂
(b) H₂S
(c) NH₃
(d) CCl₄
(e) Na₂O
(f) CO and CO₂.

Question 16.
Which of the following symbols of elements are incorrect ? Give their correct symbols :
(a) Cobalt Co
(b) Carbon C
(c) Aluminium Al
(d) Helium He
(e) Sodium So
Answer:
(a) Incorrect; correct symbol is Co
(b) Incorrect; correct symbol is C
(c) Incorrect; correct symbol is Al
(e) Incorrect; correct symbol is Na.

Question 17.
Give the chemical formulae for the following compounds and compute the ratio by mass of the combining elements in each one of them.
(a) Ammonia
(b) Carbon monoxide
(c) Hydogen chloride
(d) Aluminium fluoride
(e) Magnesium sulphide.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 8

Question 18.
State the number of atoms present in each of the following chemical species :
(a) CO₃^2-
(b) PO₄^3-
(c) P₂O₅
(d) CO.
Answer:
(a) Four
(b) Five
(c) Seven
(d) Two.

Question 19.
What is the fraction of mass of water (H₂O) due to neutrons ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 9

Question 20.
Does the solubility of a substance change with temperature ? Explain with the help of an example.
Answer:
In most of the cases, the solubility of a substance in a particular solvent such as water increases with the rise in temperature. For example, more of sugar can dissolve in a particular volume of water by increasing the temperature. .

Question 21.
Classify each of the following on the basis of their atomicity.
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 10
Answer:
(a) 2
(b) 3
(c) 3
(d) 8
(e) 4
(f) 4
(g) 14
(h) 3
(i) 2
(j) 5
(k) 1
(l) 1.

Question 22.
You are provided with a fine white coloured powder which is either sugar or salt. How would you identify it without tasting ?
Answer:
Dissolve both sugar and salt separately in water taken in two glass beakers. Pass electric current through both. In case, solution is conducting, it represents a salt dissolved in water. If it fails to conduct electricity, it represents a sugar solution.

Question 23.
Calculate the number of moles of magnesium present in a magnesium ribon weighing 12 g. Molar atomic mass of magnesium is 24 g mol^-1.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 11

Long Answer Questions

Question 24.
Verify by calculating that :
(a) 5 moles of CO₂ and 5 moles of H₂O do not have the same mass.
(b) 240 g of calcium and 240 g magnesium elements have mole ratio of 3 : 5.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 12

Question 25.
Find the ratio by mass of the combining elements in the following compounds :
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 13
Answer:

Question 26.
Calcium chloride when dissolved in water dissociates into its ions according to the following equation.

Calculate the number of ions obtained from CaCl₂ when 222 g of it is dissolved in water.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 16

Question 27.
The difference in the mass of 100 moles each of sodium atoms and sodium ions is 5.48002 g. Compute the mass of an electron.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 17

Question 28.
Cinnabar (HgS) is a prominent ore of mercury. How many grams of mercury are present in 225 g of pure HgS ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 18

Question 29.
The mass of one steel screw is 4.11 g. Find the mass of one mole of these steel screws. Compare this value with the mass of the Earth (5.98 x 10²⁴ kg). Which one of the two is heavier and by how many times ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 19

Question 30.
A sample of vitamin C is known to contain 2.58 x 10²⁴ oxygen atoms. How many moles of oxygen atoms are present in the sample ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 20

Question 31.
Raunak took 5 moles of carbon atoms in a container and Krish also took 5 moles of sodium atoms in another container of same weight.
(a) Whose container is heavier ?
(b) Whose container has more number of atoms ?
Answer:
(a) Molar atomic mass of carbon = 12 g
No. of moles of carbon carried by Raunak = 5
Mass of 5 moles of carbon = (12 x 5) = 60 g
Molar atomic mass of sodium = 23 g
No. of moles of sodium carried by Krish = 5
Mass of 5 moles of sodium = (23 x 5) = 115 g
This shows that the container carried by Krish is heavier.
(b) Since both the containers have same number of moles, the number of atoms present in these containers are also same i.e. 5 x N_A atoms.

Question 32.
Fill in the missing data in the given table
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 21
Answer:

Question 33.
The visible universe is estimated to contain 10²² stars. How many moles of stars are present in the visible universe ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 23

Question 34.
What is the SI prefix for each of the following multiples and submultiples of a unit ?
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 42
Answer:
(a) kilo
(b) deci
(c) centri
(d) micro
(e) nano
(f) pico

Question 35.
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 25
Answer:

Question 36.
Compute the difference in masses of 10³ moles each of magnesium atoms and magnesium ions.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 27

Question 37.
Which has more number of atoms ?
100 g of N₂ or 100 g of NH₃
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 28

Question 38.
Compare the number of ions present in 5.85 g of sodium chloride.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 30

Question 39:
A gold sample contains 90% of gold and the rest copper. How many atoms of gold are present in one gram of this sample of gold ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 31

Question 40.
What are ionic and molecular compounds ? Give examples.
Answer:
Simple ionic compounds are of binary nature. It means that both the positive and negative ions have one atom only. The symbols of these ions are written side by side with their valencies at their bottom. A common factor if any, is removed to get a simple ratio of the valencies of the combining atoms. The criss-cross method is then applied to arrive at the final chemical formula of the compound. Let us write the formulae of a few simple ionic compounds. For example,
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 32
The molecular compounds also called covalent compounds. The compounds listed above are heteroatomic in nature. It means that different elements participate in these compounds. They may be homoatomic also which means that these are formed from the atoms of the same element. For example, hydrogen molecule (H₂), chlorine molecule (Cl₂), oxygen molecule (0₂), nitrogen molecule (N₂), etc.
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 33

Question 41.
Compute the difference in masses of one mole each of aluminium atoms and one mole of its ions. (Mass of an electron is 9.1 x 10^-28 g). Which one is heavier ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 34

Question 42.
A silver ornament of mass ‘m’ gram is polished with gold equivalent to 1% of the mass of silver. Compute the ratio of the number of atoms of gold and silver in the ornament.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 35

Question 43.
A sample of ethane (C₂H₆) gas has the same mass as 1.5 x 10²⁰ molecules of methane (CH₄). How many C₂H₆ molecules does the sample of gas contain ?
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 37

Question 44.
Fill in the blanks
(a) In a chemical reaction, the sum of the masses of the reactants and products remains unchanged. This is called ………….. .
(b) A group of atoms carrying a fixed charge on them is called ………….. .
(c) The formula unit mass of Ca₃(PO₄)₂ is ………….. .
(d) Formula of sodium carbonate is ………… and that of ammonium sulphate is …………… .
Answer:
(a) Law of conservation of mass
(b) Polyatomic ions
(c) 3 x Atomic mass of Ca + 2 x Atomic mass of P + 8 x Atomic mass of O.
3 x 40 + 2 x 31 + 8 x 16 = 120 + 62 + 128 = 310 u
(d) Na₂CO₃, (NH₄)₂SO₄.

Question 45.
Complete the following crossword puzzle by using the name of the chemical elements. Use the data given in table.
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 38

Answer:

Question 46.
Write the formulae for the following and calculate the molecular mass for each one of them.
(a) Custic potash
(b) Baking powder
(c) Lime stone
(d) Caustic soda
(e) Ethanol
(f) Common salt.
Answer:
(a) KOH = 39 + 16 + 1 = 56 u
(b) NaHCO₃ = 23 + 1 + 12 + 3 x 16 = 84 u
(c) CaCO₃ = 12 + 12 x 3 x 16 = 100 u
(d) NaOH = 23 + 16 + 1 = 40 u
(e) C₂H₅OH = 2 x 12 + 6 x 1 + 16 = 46 u
(f) NaCl = 23 + 35.5 = 58.5 u

Question 47.
In photosynthesis, 6 molecules of carbon dioxide combine with an equal number of water molecules through a complex sereies of reactions to give a molecule of glucose having a molecular formula C₆H₁₂O₆ and a molecule of oxygen with molecular formula O₂. How many grams of water would be required to produce 18 g of glucose ? Compute the volume of water so consumed assuming the density of water to be 1 g cm^-3.
Answer:
NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules image - 41

Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.