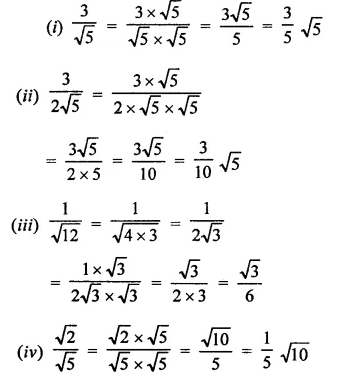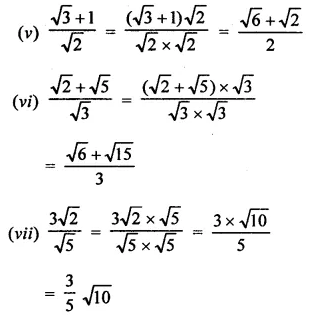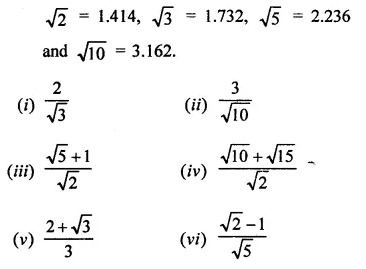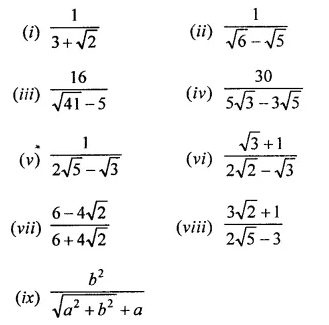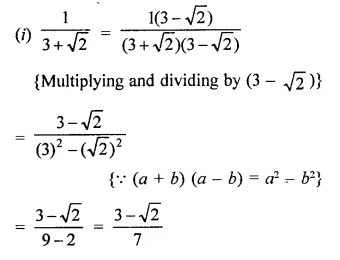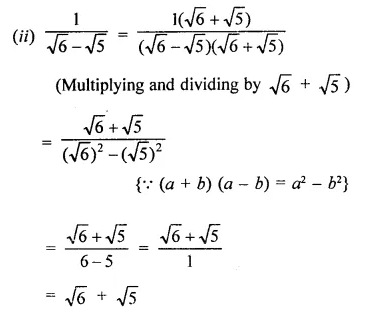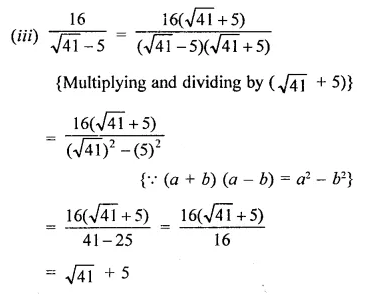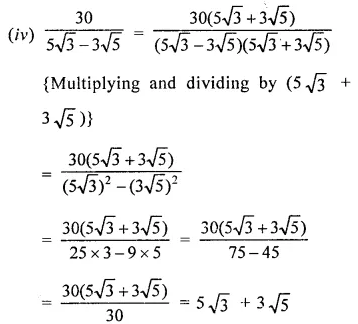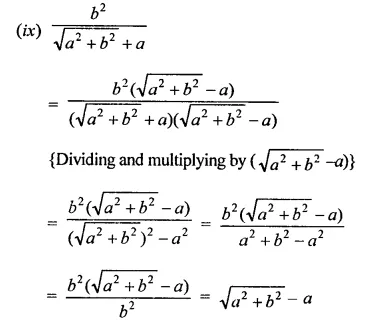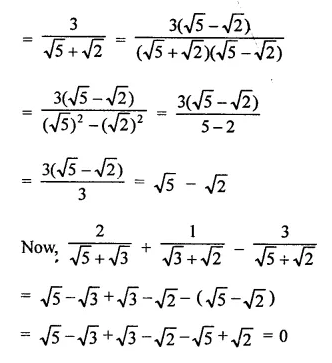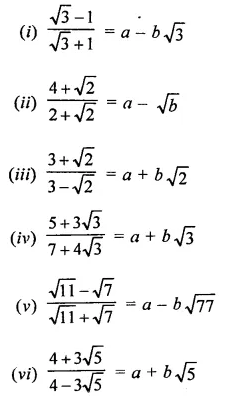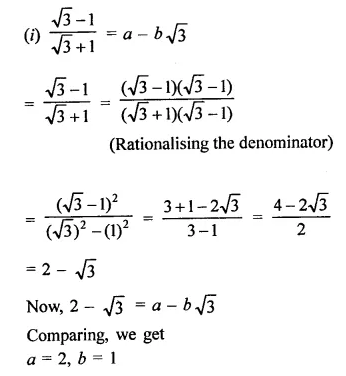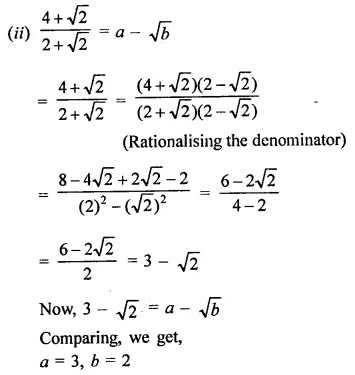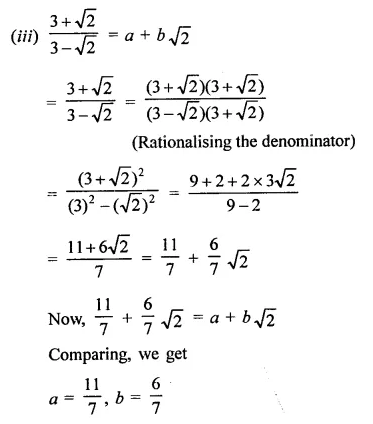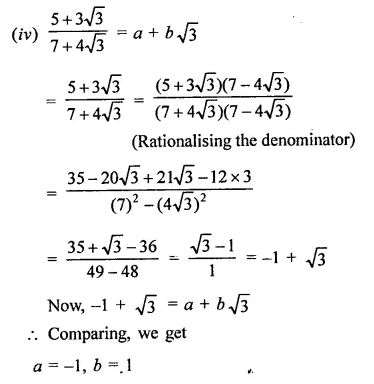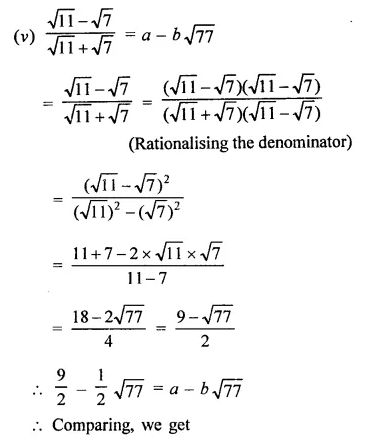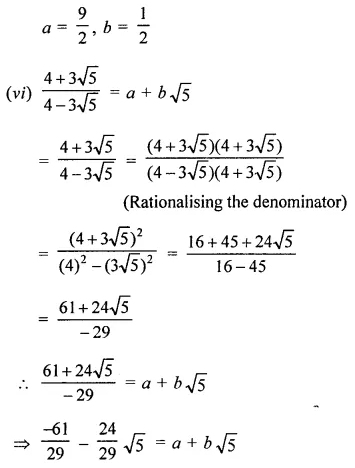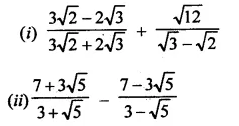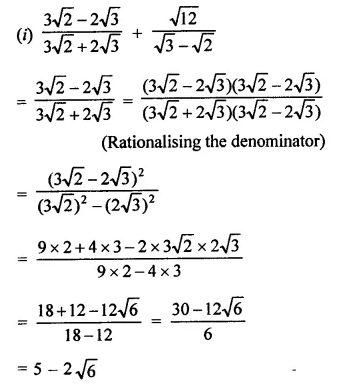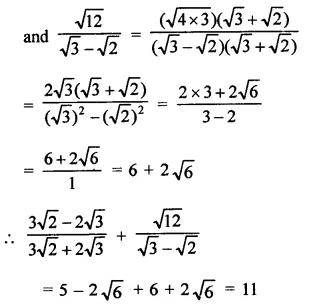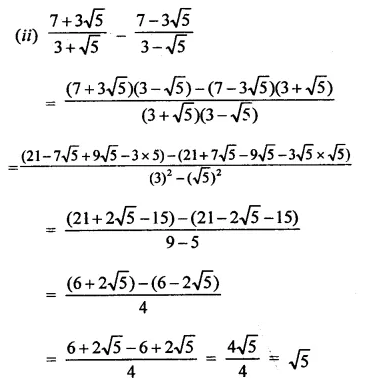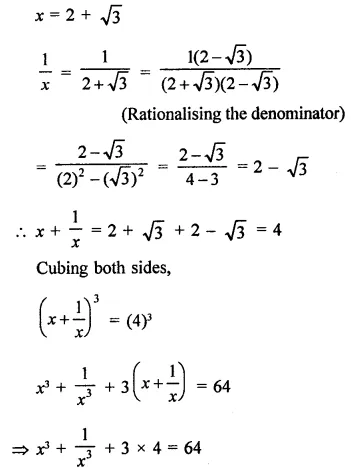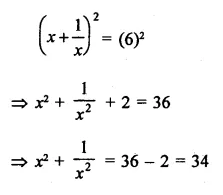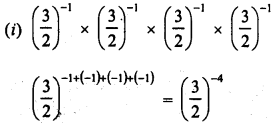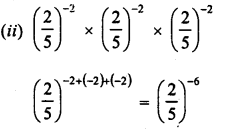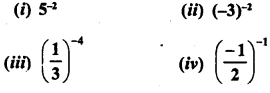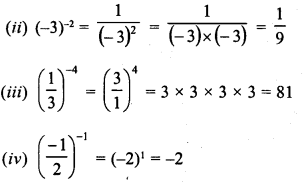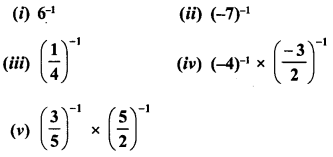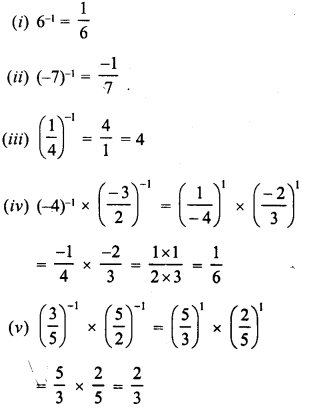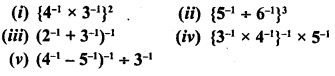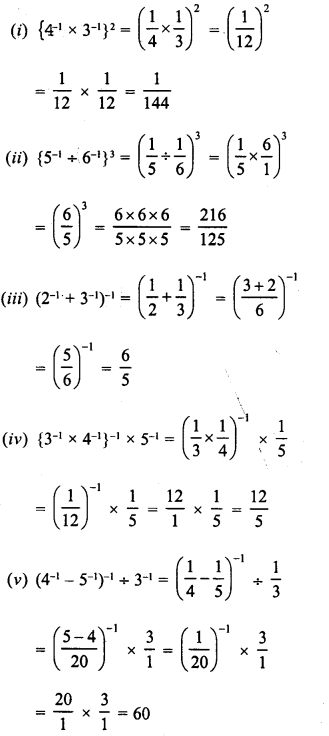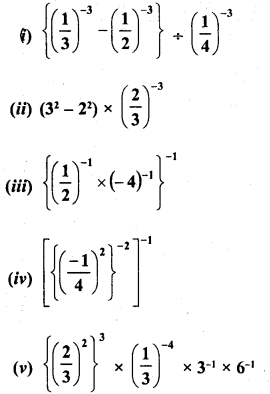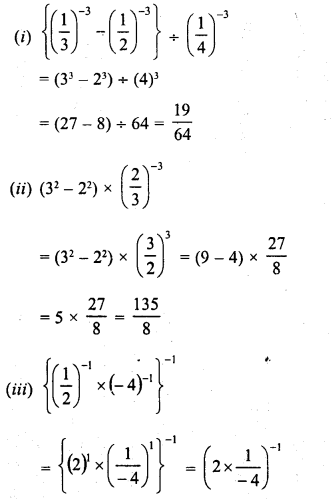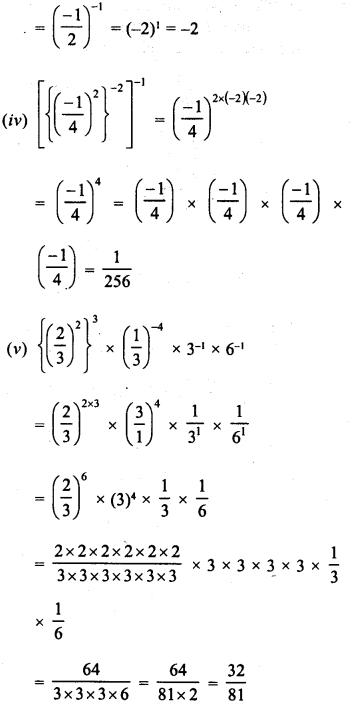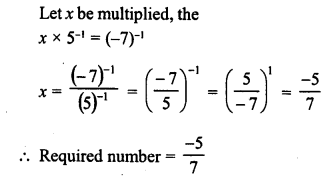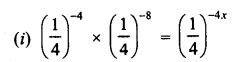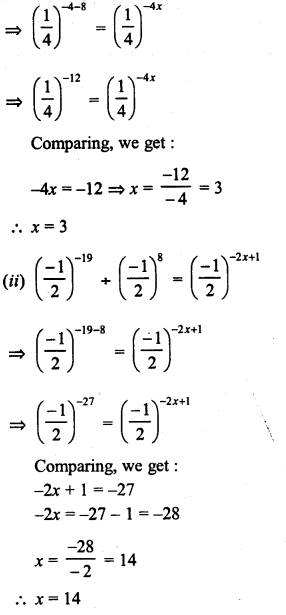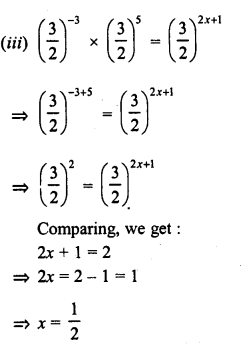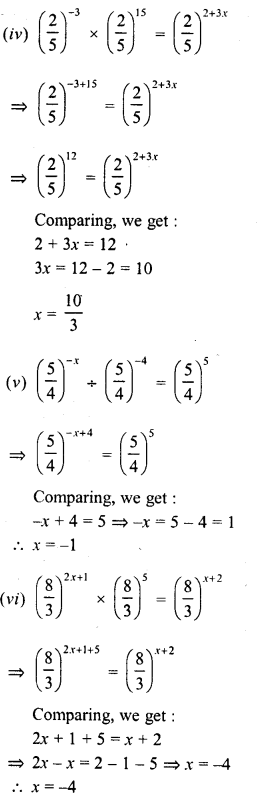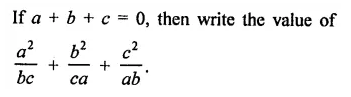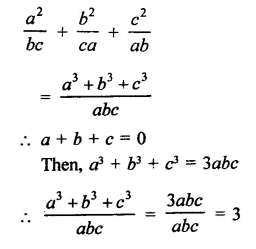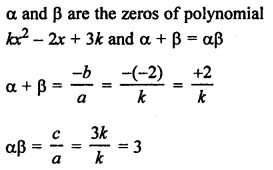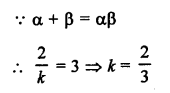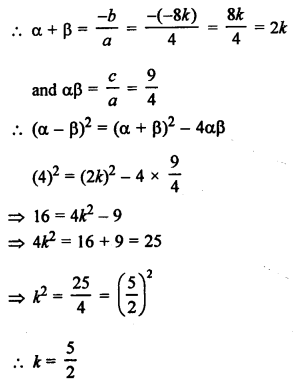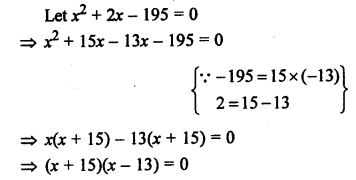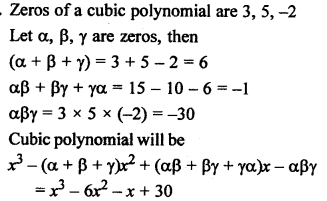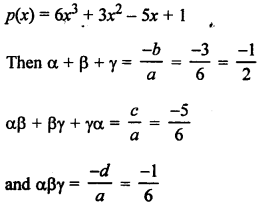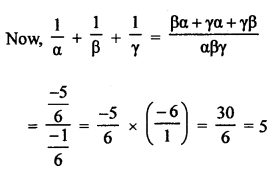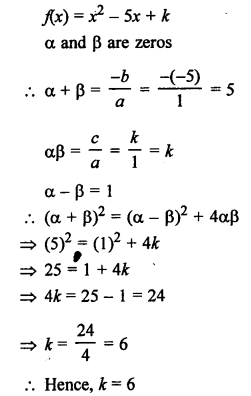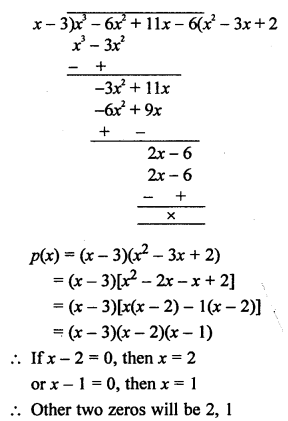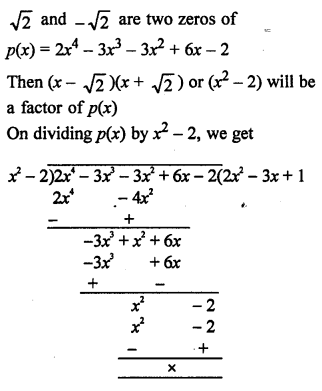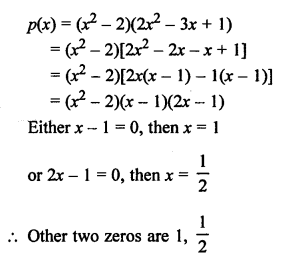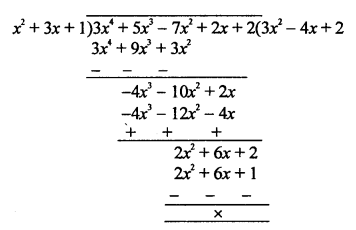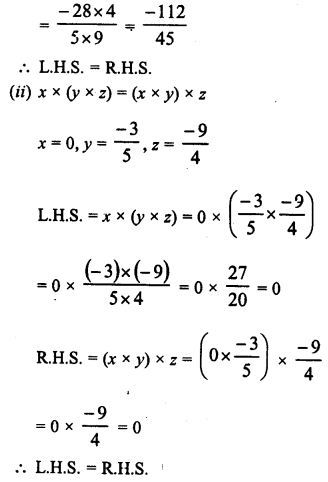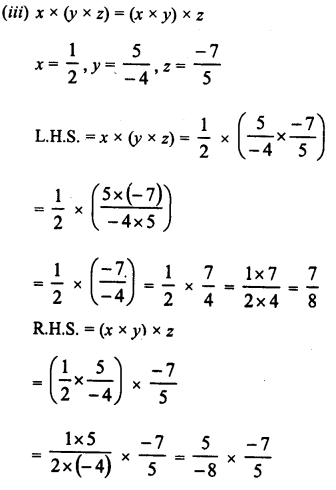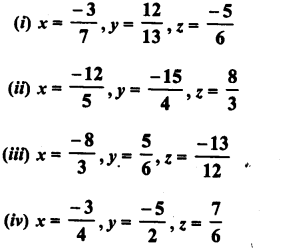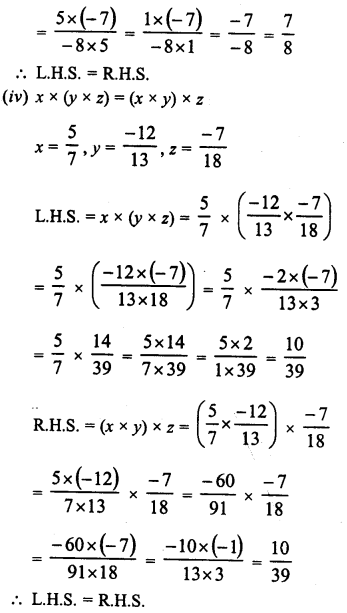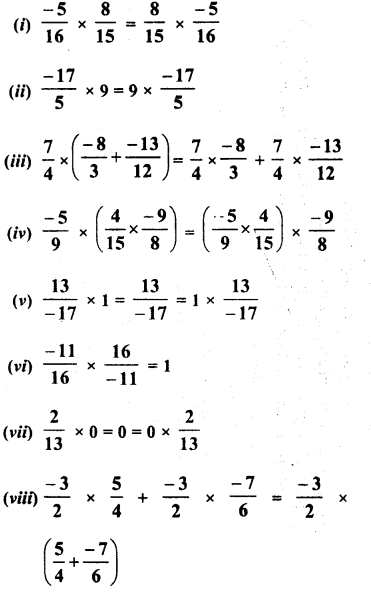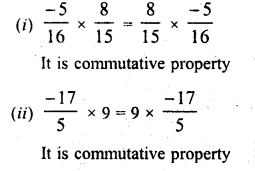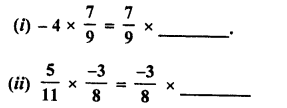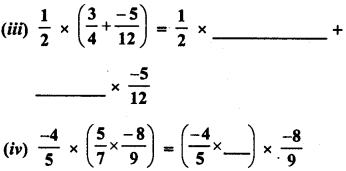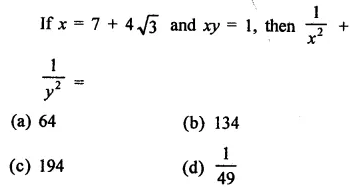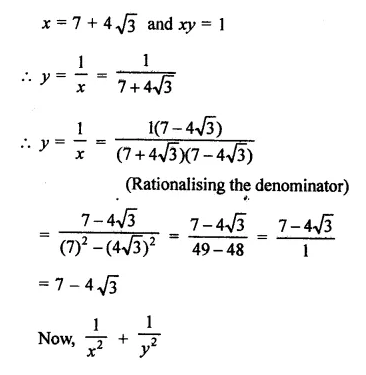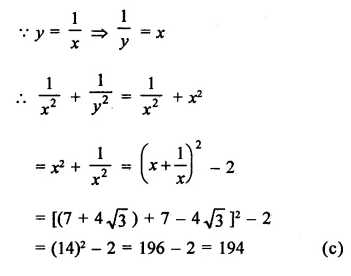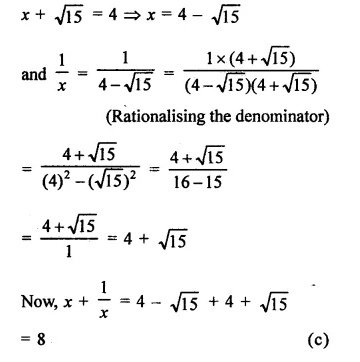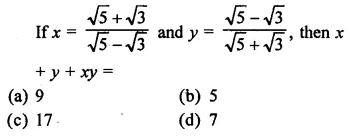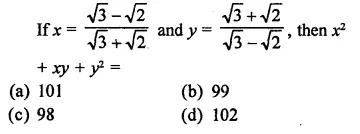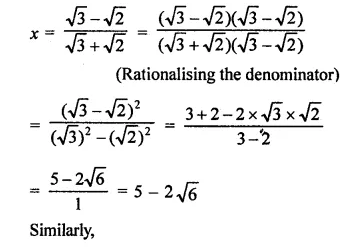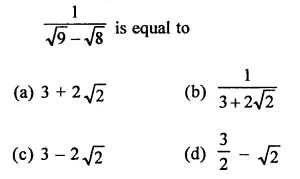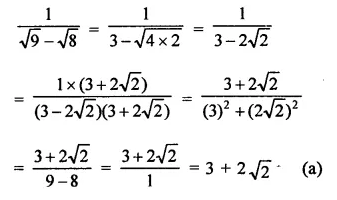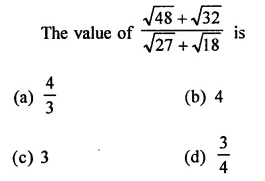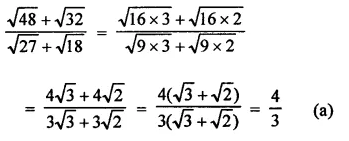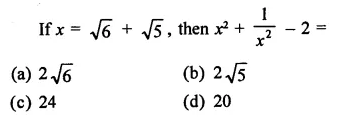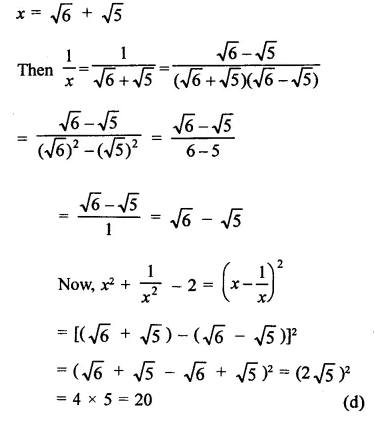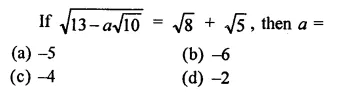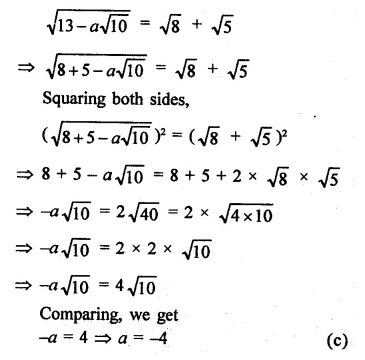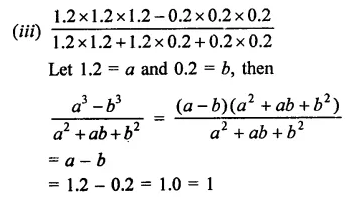RD Sharma Class 9 Solutions Chapter 8 Lines and Angles MCQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 8 Lines and Angles MCQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 8 Lines and Angles Ex 8.1
- RD Sharma Class 9 Solutions Chapter 8 Lines and Angles MCQS
Mark the correct alternative in each of the following:
Question 1.
The point of intersect of the co-ordiante axes is
(a) ordinate
(b) abscissa
(c) quadrant
(d) origin
Solution:
Origin (d)
Question 2.
The abscissa and ordinate of the origin are
(a) (0, 0)
(b) (1, 0)
(c) (0, 1)
(d) (1, 1)
Solution:
The abscissa and ordinate of the origin are (0, 0). (a)
Question 3.
The measure of the angle between the co-ordinate axes is
(a) 0°
(b) 90°
(c) 180°
(d) 360°
Solution:
The measure of the angle between the coordinates of axes is 90°. (b)
Question 4.
A point whose abscissa and ordinate are 2 and -5 respectively, lies in
(a) First quadrant
(b) Second quadrant
(c) Third quadrant
(d) Fourth quadrant
Solution:
The point whose abscissa is 2 and ordinate -5 will lies in fourth quadrant. (d)
Question 5.
Points (-4, 0) and (7, 0) lie
(a) on x-axis
(b) y-axis
(c) in first quadrant
(d) in second quadrant
Solution:
∵ The ordinates of both the points are 0
∴ They lie on x-axis (a)
Question 6.
The ordinate of any point on x-axis is
(a) 0
(b) 1
(c) -1
(d) any number
Solution:
The ordinate of any point lying on x-axis is 0. (a)
Question 7.
The abscissa of any point on y-axis is
(a) 0
(b) 1
(c) -1
(d) any number
Solution:
The abscissa of any point on y-axis is 0. (a)
Question 8.
The abscissa of a point is positive in the
(a) First and Second quadrant
(b) Second and Third quadrant
(c) Third and Fourth quadrant
(d) Fourth and First quadrant
Solution:
The abscissa of a point is positive in the fourth and First quadrant. (d)
Question 9.
A point whose abscissa is -3 and ordinate 2 lies in
(a) First quadrant
(b) Second quadrant
(c) Third quadrant
(d) Fourth quadrant
Solution:
A point (-3, 2) will lies in second quadrant. (b)
Question 10.
Two points having same abscissae but different ordinates lie on
(a) x-axis
(b) y-axis
(c) a line parallel to y-axis
(d) a line parallel to x-axis
Solution:
Two points having same abscissae but different ordinates is a line parallel to y- axis. (c)
Question 11.
The perpendicular distance of the point P (4, 3) from x-axis is
(a) 4
(b) 3
(c) 5
(d) none of these
Solution:
The perpendiculat distance of the point P (4, 3) from x-axis is 3. (b)
Question 12.
The perpendicular distance of the point P (4, 3) from y-axis is
(a) 4
(b) 3
(c) 5
(d) none of these
Solution:
perpendicular distance of the point P (4, 3) from y-axis is 4. (a)
Question 13.
The distance of the point P (4, 3) from the origin is
(a) 4
(b) 3
(c) 5
(d) 7
Solution:
The distance of the point P (4, 3) from origin is \(\sqrt { { 4 }^{ 2 }+{ 3 }^{ 3 } }\)
= \(\sqrt { 16+9 }\)
= \(\sqrt { 25 }\) = 5 (c)
Question 14.
The area of the triangle formed by the points A (2, 0), B (6, 0) and C (4, 6) is
(a) 24 sq. units
(b) 12 sq. units
(c) 10 sq. units
(d) none of these
Solution:
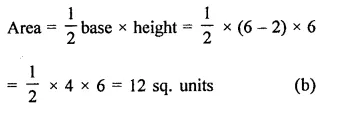
Question 15.
The area of the triangle formed by the points P (0, 1), Q (0, 5) and R (3, 4) is
(a) 16 sq. units
(b) 8 sq. units
(c) 4 sq. units
(d) 6 sq. units
Solution:
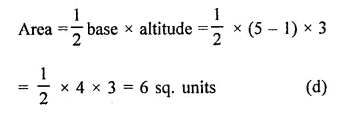
Hope given RD Sharma Class 9 Solutions Chapter 8 Lines and Angles MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.













 >
>