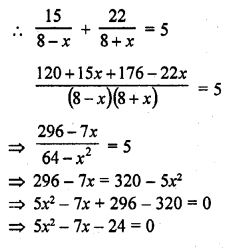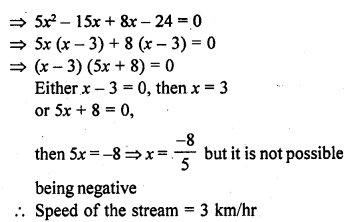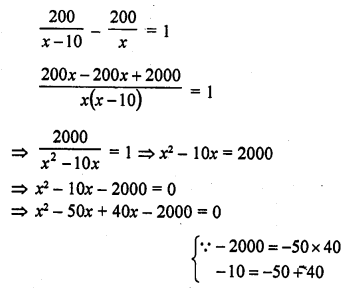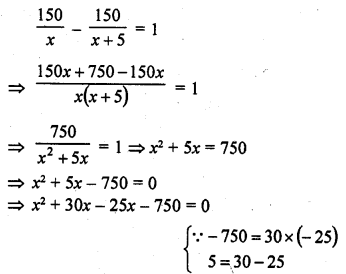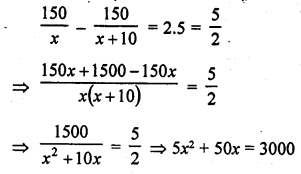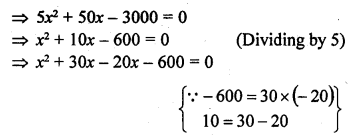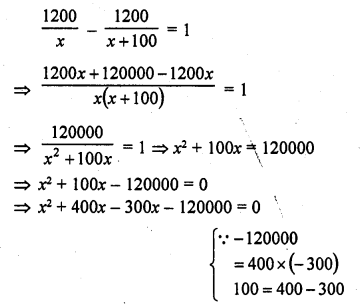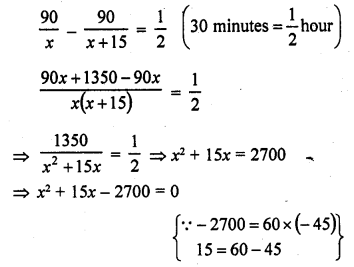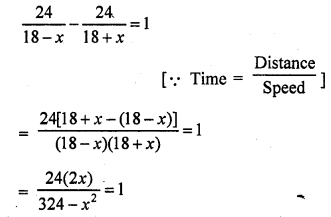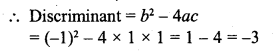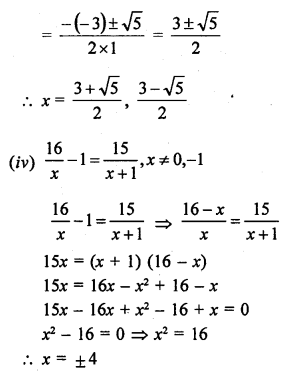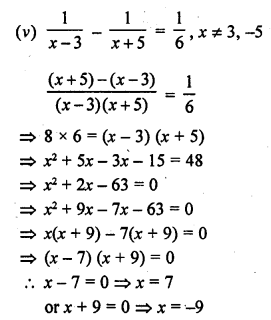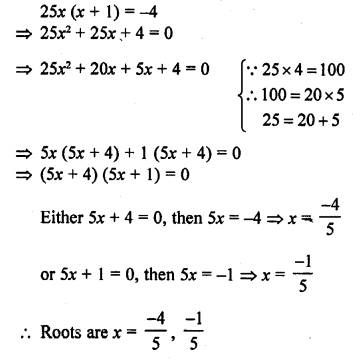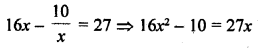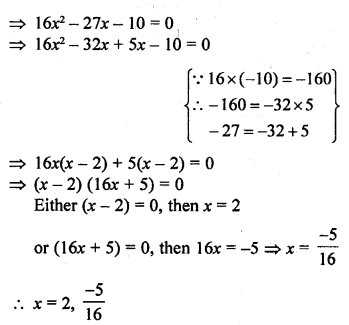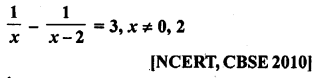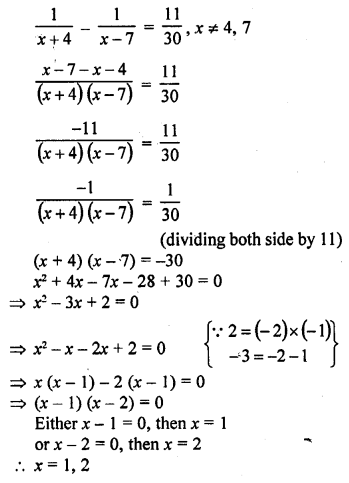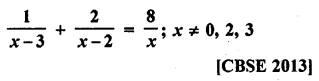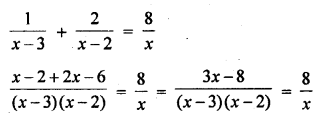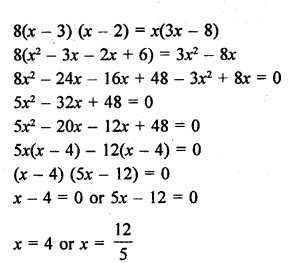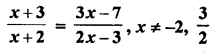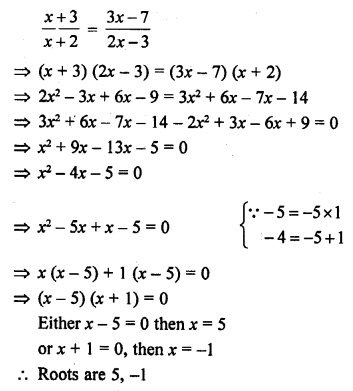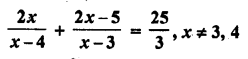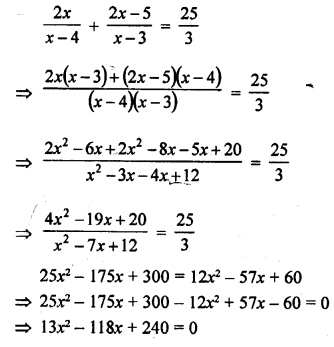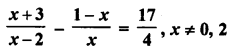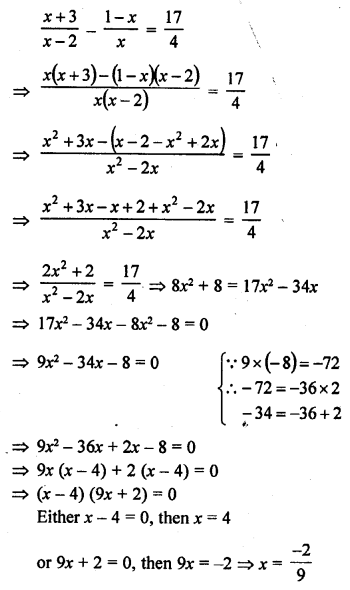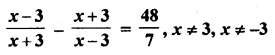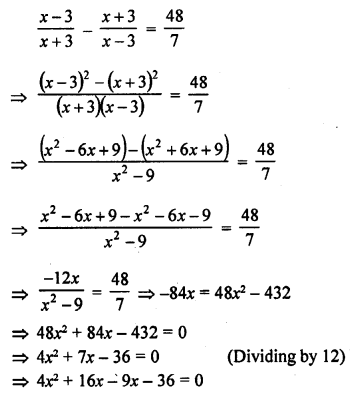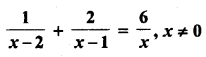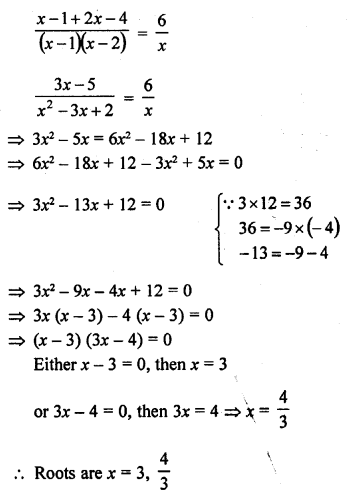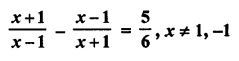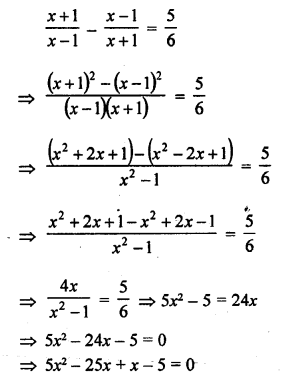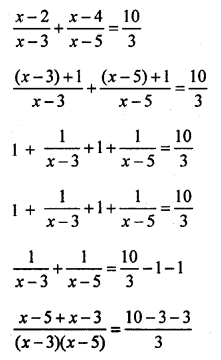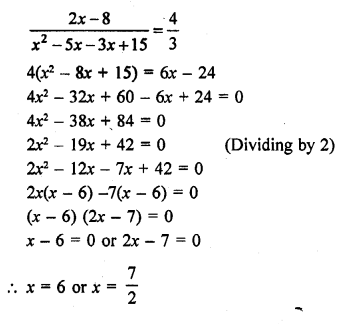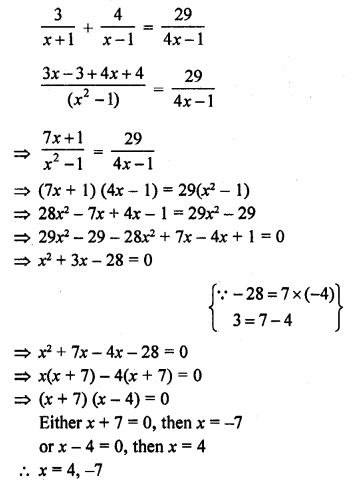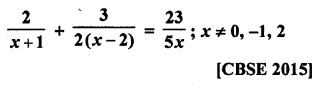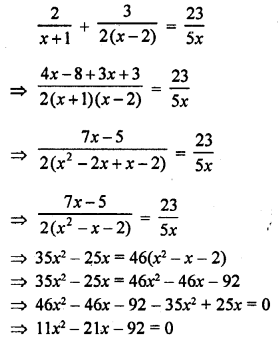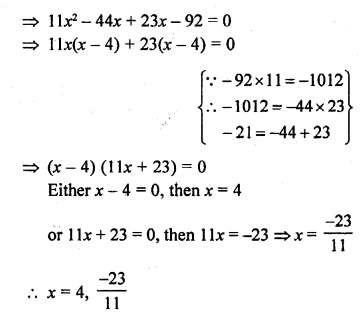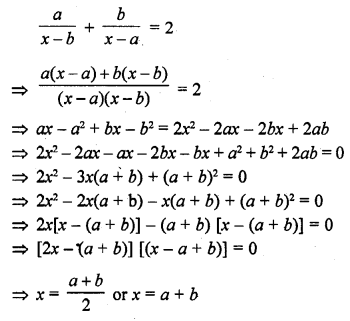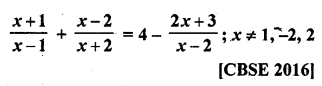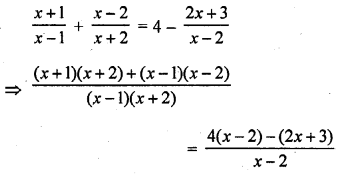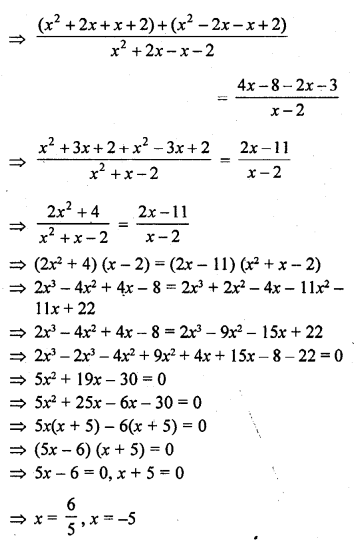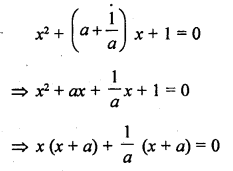Prasanna – Page 287

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9

January 6, 2023

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9

Other Exercises

Question 1.
Ashu is x years old while his mother Mrs. Veena is x² years old. Five years hence Mrs. Veena will be three times old as Ashu. Find their present ages.
Solution:
Present age of Ashu = x years
and age of his mother = x² years
5 years hence,
age of Ashu will be = (x + 5) years
and age of his mother = (x² + 5) years
According to the question,
x² + 5 = 3 (x + 5)
=> x² + 5 = 3x + 15
=> x² + 5 – 3x – 15 = 0
=> x² – 3x – 10 = 0
=> x² – 5x + 2x – 10 = 0
=> x (x – 5) + 2 (x – 5) = 0
=> (x – 5) (x + 2) = 0
Either x – 5 = 0, then x = 5
or x + 2 = 0, then x = -2 which is not possible being negative
Present age of Ashu = 5 years
and age of his mother = x² = (5)² = 25 years

Question 2.
The sum of the ages of a man and his son is 45 years. Five years ago, the product of their ages was four times the man’s age at that time. Find their present ages.
Solution:
Sum of ages of a man and his son = 45 years
Let the present age of the man = x years
Then age of his son = (45 – x) years
5 years ago,
Age of the man was = (x – 5) years
and age of his son = (45 – x – 5) years = (40 – x) years
According to the condition,
(x – 5) (40 – x) = 4 (x – 5)
=> 40 – x = 4 [Dividing by (x – 5)]
=> x = 40 – 4 = 36
Age of the man = 36 years
and age of his son = 45 – 36 = 9 years

Question 3.
The product of Shikha’s age five years ago and her age 8 years later is 30, her age at both times being given in years. Find her present age.
Solution:
Let present age of Shikha = x years
5 years ago, her age was = (x – 5) years
and 8 years later, her age will be = (x + 8) years
According to the condition,
(x – 5) (x + 8) = 30
=> x² + 3x – 40 = 30
=> x² + 3x – 40 – 30 = 0
=> x² + 3x – 70 = 0
=> x² + 10x – 7x – 70 = 0
=> x (x + 10) – 7 (x + 10) = 0
=> (x + 10)(x – 7) = 0
Either x + 10 = 0, then x = -10 which is not possible being negative
or x – 7 = 0, then x = 7
Her present age = 7 years

Question 4.
The product of Ramu’s age (in years) five years ago and his age (in years) nine years later is 15. Determine Ramu’s present age.
Solution:
Let present age of Ramu = x years
5 years ago his age was = (x – 5) years
and 9 years later his age will be = (x + 9) years
According to the condition,
(x – 5) (x + 9) = 15
=> x² + 9x – 5x – 45 = 15
=> x² + 4x – 45 – 15 = 0
=> x² + 4x – 60 = 0
=> x² + 10x – 6x – 60 = 0
=> x (x + 10) – 6 (x + 10) = 0
=> (x + 10) (x – 6) = 0
Either x + 10 = 0, then x = -10 but it is not possible being negative
or x – 6 = 0, then x = 6
Present age of Ramu = 6 years

Question 5.
Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution:
Sum of ages of two friends = 20 years
Let present age of one friend = x years
Age of second friend = (20 – x) years
4 years ago,
Age of first friend = x – 4
and age of second friend = 20 – x – 4 = 16 -x
According to the condition,
(x – 4) (16 – x) = 48
=> 16x – x² – 64 + 4x = 48
=> – x² + 20x – 64 – 48 = 0
=> – x² + 20x – 112 = 0
=> x² – 20x + 112 = 0
Here a = 1, b = – 20, c = 112
Discriminant(D) = b² – 4ac = (-20)² – 4 x 1 x 112
= 400 – 448 = – 48
∴ D < 0
Roots are not real
It is not possible

Question 6.
A girl is twice as old as her sister. Four years hence, the product of their ages (in years) will be 160. Find their present ages. [CBSE2010]
Solution:
Let age of sister = x years
Then age of girl = 2x years
4 years hence,
Girl’s age = 2x + 4
and sister’s age = x + 4
According to the condition,
(2x + 4) (x + 4) = 160
=> 2x² + 8x + 4x + 16 = 160
=> 2x² + 12x + 16 – 160 = 0
=> 2x²+ 12x – 144 = 0
=> x² + 6x – 12 = 0
=> x² + 12x – 6x – 72 = 0
=> x (x + 12) – 6 (x + 12) = 0
=> (x + 12) (x – 6) = 0
Either x + 12 = 0, then x = – 12 which is not possible being negative
or x – 6 = 0, then x = 6
Age of sister = 6 years
and age of girl = 2x = 2 x 6 = 12 years

Question 7.
The sum of the reciprocals of Rehman’s ages (in years) 3 years ago and 5 years from now is \(\frac { 1 }{ 3 }\). Find his present age. [NCERT]
Solution:
Let age of Rehman = x years
His age 3 years ago = x – 3
and age 5 years hence = x + 5
According to the condition,
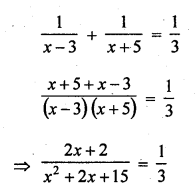
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9 1
=> x² + 2x – 15 = 6x + 6
=> x² + 2x – 15 – 6x – 6 = 0
=> x² – 4x – 21 =0
=> x² – 7x + 3x – 21 = 0
=> x (x – 7) + 3 (x – 7) = 0
=> (x – 7)(x + 3) = 0
Either x – 7 = 0, then x = 7
or x + 3 = 0 then x = – 3 which is not possible being negative
x = 7
His present age = 7 years

Question 8.
If Zeba were younger by 5 years than what she really is, then the square of her age (in years) would have been 11 more than 5 times her actual age. What is her age now? [NCERT Exemplar]
Solution:
Let the actual age of Zeba = x year .
Her age when she was 5 years younger = (x – 5) years
Now, by given condition,
Square of her age = 11 more than 5 times her actual age
(x – 5)² = 5 x actual age + 11
=> (x – 5)² = 5x + 11
=> x² + 25 – 10x = 5x + 11
=> x² – 15x + 14 = 0
=> x² – 14x – x + 14 = 0 [by splitting the middle term]
=> x (x – 14) – 1 (x – 14) = 0
=> (x – 1) (x – 14) = 0
=> x = 14
[Here, x ≠ 1 because her age is x – 5. So, x – 5 = 1 – 5= -4 i.e., age cannot be negative]
Hence, required Zeba’s age now is 14 years.

Question 9.
At present Asha’s age (in years) is 2 more than the square of her daughter Nisha’s age. When Nisha grows to her mother’s present age, Asha’s age would be one year less than 10 times the present age of Nisha. Find the present ages of both Asha and Nisha. [NCERT Exemplar]
Solution:
Let Nisha’s present age be x year.
Then, Asha’s present age = x² + 2 [by given condition]
Now, when Nisha grows to her mother’s present age i.e., after {(x² + 2) – x} years.
Then, Asha’s age also increased by [(x² + 2) – x] year.
Again by given condition,
Age of Asha = One years less than 10 times the present age of Nisha
(x² + 2) + {(x² + 2) – x} = 10x – 1
=> 2x² – x + 4 = 10x – 1
=> 2x² – 11x + 5 = 0
=> 2x² – 10x – x + 5 = 0
=> 2x (x – 5) – 1(x – 5) = 0
=> (x – 5) (2x – 1) = 0
∴ x = 5
[Here, x = \(\frac { 1 }{ 2 }\) cannot be possible, because at x = \(\frac { 1 }{ 2 }\), Asha’s age is 2\(\frac { 1 }{ 4 }\) years which is not possible]
Hence, required age of Nisha = 5 years
and required age of Asha = x² + 2 = (5)² + 2 = 25 + 2 = 27 years

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

CA Foundation Business & Commercial Knowledge Study Material – Other Business Terminology

January 6, 2023

CA Foundation Business & Commercial Knowledge Study Material – Other Business Terminology

Other Business Terminology

Acquisition: Takeover of one firm by another.
Administration: The process of determining and executing the policies and programmes of an organisation.
Allowance: A fixed sum allowed by an employer to an employee e.g. house rent allowance.
Bankruptcy: A situation when a firm’s assets are insufficient to pay its liabilities.
Bottom line: Net profits.
Business environment: All forces and factors external to the firm but influence its working and performance.
Business facilitators: The individuals, organisations/institutions and arrangement that ease the setting up, operating and exit of business firms.
By products: Products recovered from material discarded in a main process e.g. molasses in sugar industry.
Corporate: A business entity distinct from its members e.g. a company.
Corporate governance: The system that ensures that a company’s operations are conducted in an ethical manner and as per the law. It consists of board of directors, independent audit and financial reporting.
Drawings: Cash or goods taken by the owner of the firm for personal/family use.
Electronic commerce: Commercial transactions conduced over the Internet.
Electronic filing: Fifing documents online e.g. fifing tax returns online.
Franchise: The license given by one company to another to use the former name and sell its product/ service in a specified territory in exchange for payment of fee.
Globalisation: The process of removing barriers to flow of goods, services, labour, capital and technology from one country to another leading to the emergence of a global economy.
Goodwill: Money Value of a company’s reputation.
Infrastructure: The basic facilities necessary for the operation of a society and business firms. It consists of buildings, roads, railways, posts, power supply, etc.
Joint sector: Business enterprises owned jointly by Government and private sector.
Joint products: Two or more products separated in the same processing operation which usually require further processing. For example, gasoline, lubricant, paraffin and kerosene are joint products, all produced from crude oil.
Liberalisation: Systematic removal of restrictions on private business operations.
Logistics: Movement of supplies to the production facilities (inbound logistics) and movement of products from centres of production to markets (outbound logistics).
Merger: Combination of two or more independent firms into a single firm.
Mission Statement: A statement that defines the business scope (who we are and what we do) of an organisation.
Multinational: A company which has business operations in a country otherwise the country of its incorporation.
Patent: An exclusive legal right to the inventor for use of the invention.
Pestle: Political (P), Economic (E), Social (S), Technological (T), Legal (L) and Ecological (E) Environment.
Privatisation: Selling of public enterprises to public sector.
Private sector: All business enterprises owned and controlled by private persons.
Public sector: All enterprises owned and controlled by the Government.
Proprietorship: A business owned and controlled by an individual. Also known as sole proprietorship. Retained earnings: Undistributed profits of a company.
Return: Rate of earning on an investment.
Risk: Possibility of loss on an investment.
Secondary sector: Manufacturing and construction industries.
Subsidiary: A company owned and controlled by another company.
Sustainable development: Development that can be sustained over generations or development
without compromising ecology or environment.
Term insurance: Insurance for a specific time period with no defrayal to the insured person and which become null on its expiry.
Triple bottom line: Profit, people and planet i.e. simultaneous development of economy, society and ecology.
Turnaround: Financial recovery of a loss making firm.
Vision: The roadmap of a company’s future.
Whole life insurance: An insurance policy the sum of which is payable after the death of the insured to his nominee.

CA Foundation Business & Commercial Knowledge Study Material – Banking Terminology

January 6, 2023

CA Foundation Business & Commercial Knowledge Study Material Chapter 6 Common Business Terminologies – Banking Terminology

Banking Terminology

Acceptance: A signed acknowledgement indicating the acceptance of all the terms and conditions of an agreement.
Accepting house: A bank or financial institution engaged in acceptance and guarantee of bills of exchange.
Account balance: The net amount standing on the credit/debit side of the bank account of a customer.
Account payee cheque: A cheque the payment of which can only be credited to the bank account of the payee.
Accrued interest: Interest earned but not yet paid, also known as interest receivable.
Administered rates: Rates of interest which can be changed through a contract between the lender and the borrower, or by the Government.
American depository receipt (ADR): A receipt equal to the specific number of shares issued by a company in a foreign country. ADRs are traded only in the United States of America.
Annuities: Periodic payments in exchange for deposit of a sum of money.
Automated clearing house: A nationwide electronic clearing house that administers and monitors the cheque and fund clearance between banks. Through it debit and credit balances are distributed automatically.
Automated teller machine (ATM): An electronic machine through which money can be withdrawn and deposited at any time and on any day.
Balance transfer: Transfer of funds from one account to another or repayment of a loan with the help of another loan.
Bank account: An account with a bank.
Bank draft: A cheque drawn by a bank on its own branch or on another bank. It is payable on demand and also known as demand draft.
Bank passbook: A book containing data of transactions between a bank and its customer.
Bank rate: The rate of interest at which commercial banks can draw from the Reserve Bank of India for a long time period.
Bank reconciliation statement: A statement prepared to reconcile the difference between balances shown in cash book and passbook.
Bank statement: A Statement showing transactions between a bank and its customer during a specified time period.
Basis point: A measure in interest rate, stock market indices and market rates. It is 1 /100 of one per cent e.g. Rs. 0.001.
Bearer cheque: A cheque that can be encashed by its holder on the bank counter. It is transferable by mere delivery.
Bill discounting: Encashing a bill of exchange at a discount before the date of its maturity.
Bridge finance: Finance raised to fill up the time gap between a short term loan and long term loan also known as gap finance.
Bounced cheque: A cheque which the bank refuses to encash due to lack of adequate balance or for any other valid reason.
Cap: A limit to which rate of interest can be changed.
Cash credit: A revolving credit arrangement under which a bank allows the customer to borrow upto the specified amount, interest is charged only on the amount actually withdrawn.
Cash reserve: The total amount of cash available in the bank account and can be withdrawn immediately.
Cashier’s cheque: A cheque drawn by a bank to make payments to the banks or any other party.
Cheque: A negotiable instrument that instructs the bank to pay the specified amount from the drawer’s account to the payee.
Certificate of deposit: A certificate of making deposit premising to pay the depositor the deposited amount along with interest.
Chattel mortgage: Loan against the movable assets as collateral.
Clearing: The process of transferring the amount of a cheque from the payer’s account to the payee’s account.
Clearing house: Meeting of representatives of different banks to clear and confirm balances with each other. It is managed by the country’s Central Bank.
Compound interest: Calculating interest on the principal amount and accumulated interest.
Current account: A bank account from which money can be withdrawn as many times a day as needed and overdraft can be obtained.
Debit card: An instrument obtained after making payment and used to buy things by swiping it. Deposit slip: A slip containing details of money deposited in a bank account.
Depositor: The person who deposits, money into a bank account.
Debt recovery: The process of recovering money from a debtor by selling of collators and other assets.
Debt repayment: The repayment of debt along with interest.
Debt settlement: The process of negotiating the amount which a lender accepts repayment below the amount of debt and accrued interest.
E-cash: Use of electronic networks to transfer funds and execute transactions. Also known as electronic cash, digital cash.
Early withdrawal penalty: The penalty charged from a customer who withdraws his/her fixed deposit the due date.
Earnest money deposit: The deposit made by a buyer of real estate with the seller driving negotiation stage.
Education loan: A loan given for the education of the borrower at a concessional rate of interest.
Global depository receipt: A receipt specifying the number of shares issued by a company in a foreign country. The receipt is tradable in Europe.
Guarantor: One who promises to repay a loan in case the borrower fails to repay.
Interest: The charge which a borrower pays to the lender for use of money. It is the cost of credit.
Internet banking: Banking transfer done by the Internet. It is also known as online banking or electronic (e)banking.
Letter of credit: A written promise by a bank to an exporter to pay the specified amount on behalf of the importer for the goods sold.
Line of credit: An arrangement under which a bank allows a borrower to borrow money from time to time without further negotiations and upto the specified limit.
Lock-in-period: The time period during which no change in the quoted mortgage rates will be made by the lender.
Market value: The value at which consumers are willing to buy and sellers are willing to sell. Decided by demand and supply.
Maturity: The date on which an investment/loan becomes repayable.
Mortgage: A legal agreement between a lender and a borrower under which real estate is used as a collactral to ensure repayment of the loan.
Online banking: Same as internet banking.
Overdraft: Withdrawal of money in excess of the balance in the borrower’s current account. Payee: The person to whom money is to be paid.
Personal identification number (PIN): A secret code number given to customers to perform transactions through the ATM.
Repo rate: The rate at which banks borrow money from the Reserve Bank of India for short periods upto two weeks by pledging government securities.
Reverse repo rate: The rate of interest which the Reserve Bank of India pays to banks which deposit their surplus funds for short periods.
Smart card: A card with a computer slip used for storage, processing and transmission of data.
Syndicated loan: A large amount of loan given by a group of small banks to a single corporate borrower.
Time deposit: A bank deposit made for a specific time period, cannot be withdrawn before the expiry of the period.
Value at risk (VAR): A sum the value of which is subject to loss due to changes in the rate of interest. Wholesale banking: Banks which offer services to companies, financial and other institutions.
Zero balance accounts: A bank account in which no minimum balance is required e.g. Jan Dhan Account.
Zero-down-payment mortgage: A mortgage in which the borrower makes no loan payment. The mortgage buys below the amount at the entire purchase price.

CA Foundation Business & Commercial Knowledge Study Material – Marketing Terminology

January 5, 2023

CA Foundation Business & Commercial Knowledge Study Material Chapter 6 Common Business Terminologies – Marketing Terminology

Marketing Terminology

Advertising: Any paid form of non-personal presentation and promotion of ideas, goods and services through mass media such as newspapers, radio, TV, Internet by an identified sponsor.
Advertising agency: An organization consisting of experts who render advertising services for payment in terms of fee or commission or both.
Advertising campaign: An organization’s programme of advertising for a specific time period. Advertising copy The advertisement containing the message, photograph and other details. Advertising media The channels (e.g. print and electronic media) used to carry advertisements. Advice note A document sent by a seller informing the buyer of dispatch of goods.
Agent: A person authorised to act on behalf of another (principal, like buyer and seller and do not take ownership of goods.
Auction: An agent who sells goods through action on behalf of his principal.
After sale service: The services provided by the manufacturer/dealer to the buyers after selling the product/service.
Barrier to trade: Something that makes trade between two countries more difficult or expensive, e.g. a customs duty on imports.
Barriers to entry/exit: A barrier to entry/exit of new firms in the market, e.g. economies of scale, government policy.
Benchmarking: The process of comparing the products / services, or business processes of an enterprise against the best firm in the industry with the objective of improving quality and performance.
Brand: A name, symbol, design, logo or a combination thereof to identify a product and to differentiate it from competing products.
Brand equity: The estimated value of a brand on the basis of brand’s loyalty.
Brand recognition: Customers awareness of existence of a brand as an alternative for buying.
Brand loyalty: Commitment of customers to a brand.
Business-to-business (B2B): Marketing activities between two business firms carried through Internet. Business model: A company’s approach for converting its strategy into moneymaker.
Business portfolio: A company’s set of businesses or products.
Buying behaviour: The process used by buyers to decide whether or not to buy a product/service. It depends upon several internal and external factors.
Cash discount: A reduction in the price of products/services given to customers who buy on cash basis.
Competitive advantage: An advantage which a firm has over its competitors.
Competitive position: The position that a firm takes to face its competitors.
Conglomerate diversification: Starting or acquiring businesses which have no synergy with the firm’s exiting business. For example, ITC a tobacco company diversified into hotels, garments, foods and beverages, paper and paper board and agri business.
Consortium: A group of several firms which work together to buy something or to build something.
Consumer market: The market for products and services which people buy for their own/family’s use.
Corporate culture: The values beliefs, traditions, rituals, etc. shared by the members of an organization.
Cross-selling: Selling related products to buyers of a product. For example, selling handkerchief, ‘ Socks, ties to buyer of shirts/trousers.
Catalogue: A small booklet containing details about the products, their prices etc. of a firm.
Chain stores: A group of similar stores selling same products at the same prices, e.g. Bata Stores. Also known as multiple shops.
Channel of distribution: The route that a product takes to move from the manufacturer to consumers.
Clearing agent: An agent who takes care of customs formalities for imported goods.
Consumers’ cooperative store: A retail stored set up by consumers as a cooperative society to get 1 products of daily use at reasonable prices by eliminating middlemen.
Customer demand: A customer’s ability and willingness to buy a product/service.
Customer need: A basic requirement which a person wishes to satisfy.
Customer loyalty: A customer’s inclination to buy repeatedly from the same shop or store.
Customer satisfaction: The ability of a product/service to meet the customers expectations in terms of quality and performance in relation to the price paid.
Customer wants: The desire for a product/service to satisfy the underlying need. For example,
hunger the need whereas food is the want.
Departmental Store: A large retail store selling a wide range of goods under one roof, goods being
arranged in different departments.
Differentiation: Giving a unique identity to a product/service so that it stands out from rival
product/services.
Direct marketing: Selling products/services directly to consumers, e.g. telemarketing.
Diversify: Increasing the range of products /services which a firm produces and sells.
E-commerce: Business transactions made through electronic means e.g. Internet,
Economies of scale: Reduction in cost per unit due to large scale operations.
External environment: The forces and conditions that influence a company’s strategies and competitive position.
Factor: An agent who keeps the goods of others for sale on commission basis.
Fast moving consumer goods (FMCG): Products of duly use which are low priced, frequently purchased and sell in large volumes, e.g. biscuits, soaps, tooth pastes, packed juices, etc.
Forecasting: The process of estimating future demand on the basis of price levels, disposable incomes and other relevant factors.
Forwarding agent: The agent who attends to customs formalities on behalf of an exporter. Grading: Classifying agricultural products into different grades on the basis of their quality level.
Hire purchase: Buying goods and making payments in installments, goods considered on hire until the payment of the final installment.
Indent: A purchase order sent abroad for importing goods.
Innovators: Young and intelligent consumers who are the first to adopt new products.
Internal marketing: The process of earning support for a company and its activities from its employees.
Invoice: A written statement containing details of goods sold. It is sent by the seller to the buyer.
Itinerants: Retailers having no fixed place for selling. They move from place to place to sell their goods. Also known as mobile traders.
Joint venture: A new enterprise jointly established by two or more firms for some specific purpose and mutual benefit.
Labelling: Putting labels on products to indicate its name, contents, price date of manufacture and their necessary details.
Marketing: The process of discovering, creating and delivering value to satisfy the needs of a target market at a profit.
Market development: The process of offering existing or modified products to new groups of customers.
Market entry: Launching a new product into an existing market or a new market.
Market leader: A firm having control over a specific market.
Marketing Mix: A firm’s mix of product, price, place and promotion. In case of services it consists of three other elements people, process and physical evidence. ‘
Marketing plan: The plan covering the use of marketing mix to achieve the firm’s marketing objectives.
Market positioning: The marketing strategy for placing a firm’s products/services against competing products/services in the minds of consumers.
Market research: The process of systematically collecting, recording and analysing data about problems concerning the marketing of products and services.
Market segmentation: Dividing the total market into different parts on the basis of consumer’s characteristics to deliver tailor made offering to each part.
Market share: The sales of a product/brand or firm divided by total sales of similar products/ brands of firms in the industry.
Market targeting: The process of comparing all market segments and choosing the most attractive segment for a product/service.
Mass marketing: Delivering the same message through mass media to all consumers.
Merger: Combination of two or more firms into a single firm to expand business operations.
Mission: The unique purpose of a company that differentiates it from other companies in the industry, defines it scope of operations and reflects its values and priorities.
Niche marketing: Concentrating efforts on relatively small market segments e.g. herbal tea for health conscious consumers.
Opportunities: Favourable conditions in the external environment of business.
Packing: Designing and manufacturing suitable packages for various types of products.
Packing: Putting the product into its package.
Personal selling: Oral communication with prospective buyers to make a sale and develop relationships with them.
Physical distribution: Activities involved in physical movement of goods from producers to consumers e.g. transportation, warehousing, order processing and inventory control.
Pre-emptive pricing: Setting low prices to discourage entry of new suppliers in the market.
Price discrimination: Charging different prices from different customers for the same product service for reasons other than costs.
Price elasticity of demand: Change in demand due to change in price.
Price sensitivity: The effect of change in price on customers.
Price: The value of product/service expressed in terms of money.
Publicity: Promotion of an organisation and its products/services in mass media without payment. Retails Traders who sell directly to customers or ultimate users.
Penetration pricing: Charging a relatively low price to gain quick market acceptance of new product/service.
Salesmanship: The process of persuading people to buy a product/service through face-to-face interaction.
Sales promotion: Any activity used to boost the immediate sales of a product or service e.g. free samples, price off, etc.
Target marketing: Using appropriate advertisements to reach out to a group of consumers having similar characteristics.
Tele marketing: Using telephone to contact people and sell a product service.
Test marketing: Testing of a new product with a sample group of customers to judge their reactions.
Unique selling proposition (USP): A customer benefit that no other product/service can claim.

CA Foundation Business & Commercial Knowledge Study Material – Finance, Stock and Commodity Markets Terminology

January 5, 2023

CA Foundation Business & Commercial Knowledge Study Material Chapter 6 Common Business Terminologies – Finance, Stock and Commodity Markets Terminology

Terminology or vocabulary means a set of basic terms or concepts used in a particular field or discipline. Each and every subject (e.g. Economics, Accountancy, Law, Medicine, Management, etc.) has its own terminology. Good understanding of the correct meaning of the terms used is essential to gain conceptual clarity. A student or professional working in the concerned profession cannot be efficient without understanding the terminology used in the concerned profession. A Chartered Accountant is excepted to know and understand the terminology used not only in finance and accounts but also in related areas such as marketing banking, administration, etc. This is because a Chartered Accountant comes across these terminologies in course of audit.

Finance, Stock and Commodity Markets Terminology

Above par: Price of a security quoted higher than its face value.
Absorption or acquisition: Takeover of a firm by another firm.
Accommodation bill: A bill of exchange drawn and accepted without receiving value in exchange. It is means of lending money.
Account: A record of transactions relating to one head e.g. debtors.
Accountancy: The held of knowledge containing principles and techniques used in preparing accounts. Account current: A running account summarizing business transactions during a given time period.
Accounting: The process of measuring, and recording transactions in the books of account.
Agent: (broker): One who buys and sells securities on behalf of his clients.
Amortize: To charge regular portion of an expenditure over a fixed time period. For example an expenditure of Rs. 50,000 may be amortized over five years, charging Rs. 10,000 per year in the account books. Also called write off.
Annuity: An equal amount paid at fixed intervals (e.g. every three months) for a specified period (e.g. twenty years).
Appreciation: Increase in the value of an asset e.g. shares purchased for Rs. 1 lakh may be Rs. 5 lakh now. There is an appreciation of Rs. 4 lakh.
Arbitrage: Simultaneous purchase and sale of a security/commodity in different markets to take advantage of price differences.
Asset: An economic resource expected to give benefit in future. It may be tangible (e.g. a machine) or intangible (e.g. a patents). Assets are of three types:
- Current Assets: The assets which are likely to convert into cash within a year e.g. book debts and stock of finished goods.
- Fixed Assets: The assets which generate revenue and last more than one year e.g. building, vehicles, machinery.
- Intangible Assets: Assets having no physical shape e.g. patents, trademarks and copy-rights.
Ask/Offer: The lowest price at which the owner is willing to sell his securities.
Audit: The careful review of financial records to verify their accuracy.
Auditor: The qualified Chartered Accountant authorised and appointed to conduct an audit.
Authorised capital: The amount of share capital with which a company is registered. It is mentioned in the company’s Memorandum of Association.

Backwardation: The charge paid big a bear speculator to a bill for postponement of settlement of a transaction.
Bad debts: The debts which are not recoverable and are written off as a loss.
Badla: Carry forward of a transaction from one settlement period to the next without any payment or delivery.
Balance of payments: A statement of all money flows in and out of a country.
Balance of trade: A statement of a country’s exports and imports during the year.
Balance sheet: A statement containing the assets, liabilities and capital of an organisation. It shows the financial position on a specific date.
Base price: A security’s price at the beginning of a trading day. It is used to determine the day’s lowest/highest price and the price range.
Basket trading: The facility which enables investors to buy/sell in one go all the 30 scripts of Sensex in proportion of their current weights in the Sensex.
Bear: A pessimist who expects prices to fall and sells quickly before the value of his holding declines. Bear market: A market situation when share price are continuously falling.
Beta: A measurement of the relationship between the price of a security and the price movement of the whole market.
Bid: The highest price a buyer is willing to pay for a share. It is the opposite of ask/offer.
Blue chip: Shares of a large, well established and financially sound company. It can provide high capital gains.
Bond: A long-term promissory note issued by a company or government. It shows the amount of the debt, rate of interest and the due date.
Bonus shares: A free allotment of shares out of accumulated reserves to the existing shareholders in proportion to their current holding.
Book closure: The period during which a company keeps its register of members closed for updating prior to payment of dividend or issue of new shares/debentures.
Book value: The value of an asset recorded in the books of account. It also means the difference between total assets and total liabilities.
Brokerage: The commission charged by brokers.
Break even point: The number of units that must be sold to generate revenue equal to total expenses. Sale above this point create a profit and sales below it create loss.
Budget: A detailed plan expressed in quantitative terms for a specific future period.
Bull: One who expects prices to rise and buys in anticipation.
Bull market: A market situation in which share prices continuously rise.
Business days: The days on which stock markets are open – Monday to Friday, excluding public holidays.
Business risk: The risk inherent in the operations of a firm which uses no debt.
Buyer: The trading member who has placed on order for the purchase of securities.

Call: The demand for payment by the company which has issued shares.
Call option: The right (not obligation) to buy a particular share at a specified price within the specified time period.
Capital budgeting: The process of planning expenditure on fixed assets.
Capital gain: The increase in the value of a security.
Capital market: The financial market for shares, debentures and long-term debt.
Closing price: The price of a security at the end of a trading day.
Commercial paper: Short term and unsecured promissory note issued by a large firm with an interest rate below the prime lending rate of commercial banks.
Commodity: Products used for commerce and traded on authorized commodity platforms.
Convertible security: A preference share, debenture, a bond that can be converted into equity shares at the option of the holder.
Consolidation: Business combination of two or more firms.
Credit period: The length of time for which credit is granted.
Creditor: The individual/organization who owes money on a particular date.

Debenture: An instrument acknowledging debt raised by a company/corporation.
Debtor: An individual/enterprise who owes money, shown as an asset in the balance sheet. Defensive stock: A stock that provides constant dividends even during economic down turn. Depreciation: An expense allowance made for wear and tear of an asset over its estimated useful life.
Derivatives: A security whose price is derived from one or more underlying assets such as shares, bonds, commodities, currencies, etc.
Diversification: Spreading the investment risk by purchasing shares of different companies operating in different sectors. Also used to refer to a company investing in several related or unrelated business.
Dividend: A part of the company’s earning paid to shareholders.
Devaluation: Reducing the value of a currency in relation to other currencies, decided by the government.
Disinvestment: Selling a part of the share holding of a public enterprise to private sector.

E-commerce: Doing business transactions over the internet.
Economic activity: Any activity undertaken to earn money.
Equity capital: Funds provided by holders of equity shares.
Equity: Equity capital, free reserves, retained earnings and preference capital.
Exchange rate: The rate at which one currency can be purchased for another currency. Ex-dividend: Shares on which dividend declared after their purchase is not payable.

Foreign company: A company incorporated outside India but having business operations in India.
Forward trading: Buying and selling without the intention of delivery and payment, aim is to earn from fluctuations in price.
Futures: The right to buy or sell at a future date and at the specified price.
Face value: The price at which a share/bond/debenture is issued. Also known as par value.
Financial instrument: A written document sharing an agreement or a transaction e.g. share, debenture, cheque, etc.
Financial intermediary: One who acts as a link between buyers and sellers of securities, e.g. share brokers, banks.

Goodwill: The estimated money value of a firm’s reputation.
Government bonds: A security issued by a government to raise debt.
Government company: A Company in which government owns 51 per cent or more of the share capital.

Hedge: A strategy used to minimise the risk and maximize the return on investment.
Holding period: The time period during which an individual/corporation holds/owns an asset. This period is considered while pledging the asset as collateral.

Income stock: A security that offers dividend higher than that on common stock. It has a solid record of dividend payments.
Index: A statistical measure of change in the security market/economy. It is usually calculated as a percentage change in the base value overtime.
Initial public offer (IPO): A company’s first issue of shares to general public.
Internet trading: Buying and selling securities over the internet. SEBI approved it in January 2000. Interim dividend: A dividend declared prior to the close of the financial year.

Joint venture: A partnership between two or more independent firms resulting in the creation of a third enterprise.
Journal: Datewise records of transactions, a book of original entry.

Lame duck: A speculator struggling to honour his commitment due to unexpected fluctuations in the price of a security on the stock market.
Lease: A legal right for the use of an asset.
Ledger: A book of account in which entries are posted from the Journal into various accounts. Lien: A legal claim to property until repayment of debt.
Limit order: An order to buy or sell a share at a specified price. It specifies the minimum price the seller is willing to accept or a maximum price the buyer is willing to pay.
Liquidation: Piecemeal sale of the assets of a division of the company.
Listed stock: The shares of a company that are eligible for trading on the stock exchange.

Margin trading: Buying securities on a stock exchange after keeping a deposit with the broker. Market capitalization: The total market value of a company’s out standing shares.
Minimum subscription: The minimum amount of share capital a company must receive in cash before making allotment of shares. It is equal to 90 per cent of issued capital.
Money market: Market for raising short-term funds.
Mutual funds: A pool of money managed by experts for investing in shares, debentures and other securities. .

Nominee director: A director nominated by the financial institution from which the company has raised a loan.

Odd lot: Shares less than the trading lot and held by a small investor.
One sided market: A market having only potential buyers or only potential sellers.
Out-of-the money (OTM): In case of call options, it means the share price is below the strike price. In case of put options, it means the share price is above the strike price.

Par value: The value of a share printed on the share certificate.
Portfolio: Various types of securities of different companies held by an investor.
Preliminary expenses: Expenses incurred for the formation of a company.
Pre-opening session: Time duration from 9.00 am to 9.15 a.m. during which order entry, modification and cancellation are done before the start of trading on stock exchange.
Price earning (PIE) ratio: The market price of a share divided by the earning per share. Prospectus: A document issued by a Company to sell shares/debentures to the general public.
Proxy: A written authority given by a member of a company to some one to attend the meeting on his/her benefit.

Right shares: Equity shares issued by a company to the existing shareholders in proportion to their current holding.

Securities: A transferable certificate of ownership of shares, debentures, etc.
Share: A part in the share capital of a company.
Stock: Fully paid shares of a company.
Strike price: The price at which the shareholder can buy (in case of call option) or sell (in case of put option) a security.
Stock split: Splitting one share into several shares to increase the availability of existing shares e.g., splitting a share with face value of 100 into 10 shares with face value of Rs. 10 each.

Thin market: A market with a few bids to buy or offer to sell, the prices in such market vary highly. Trading session: The time period during which the stock market is open for trading.

Underwriting: Guarantee to subscribe to an issue of shares in case public does not subscribe to it.

Working capital: The capital used in day-to-day business activities, also called circulating capital.

Yield: Percentage return on investment in case of shares it is calculated by dividing the annual dividend with the current price of the share.
Yield-to-call: The rate of return earned on a bond when it is called before the date of maturity.

Zero coupon bond: A bond sold at a discount below par but paid back at face value. No interest is payable on it.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8

January 5, 2023

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8

Other Exercises

Question 1.
The speed of a boat in still water is 8 km/hr. It can go 15 km upstream and 22 km downstream in 5 hours. Find the speed of the stream.
Solution:
Let the speed of stream = x km/h
and speed of boat in still water = 8 km/h
Distance covered up stream = 15 km
and downstream = 22 km
Total time taken = 5 hours
According to the conditions,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 1

Question 2.
A train, travelling at a uniform speed for 360 km, would have taken 48 minutes less to travel the same distance if its speed were 5 km/hr more. Find the original speed of the train. [NCERT Exemplar]
Solution:
Let the original speed of the train = x km/h
Then, the increased speed of the train = (x + 5) km/h [by given condition]
and distance = 360 km
According to the question,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 3

Question 3.
A fast train takes one hour less than a slow train for a journey of 200 km. If the speed of the slow train is 10 km/hr less than that of the fast train, find the speed of the two trains.
Solution:
Total journey = 200 km
Let the speed of fast train = x km/hr
Then speed of slow train = (x – 10) km/hr
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 5
=> x (x – 50) + 40 (x – 50) = 0
=> (x – 50) (x + 40) = 0
Either x – 50 = 0, then x = 50
or x + 40 = 0, then x = -40 but it is not possible being negative
Speed of the fast train = 50 km/hr
and speed of the slow train = 50 – 40 = 10 km/hr

Question 4.
A passenger train takes one hour less for a journey of 150 km if its speed is increased by 5 km/hr from its usual speed. Find the usual speed of the train.
Solution:
Total journey = 150 km
Let the usual speed of the train = x km/hr
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 6
=> x (x + 30) – 25 (x + 30) = 0
=> (x + 30) (x – 25) = 0
Either x + 30 = 0, then x = -30 but it is not possible being negative
or x – 25 = 0, then x = 25
Usual speed of the train = 25 km/hr

Question 5.
The time taken by a person to cover 150 km was 2.5 hrs more than the time taken in the return journey. If he returned at a speed of 10 km/hr more than the speed of going, what was the speed per hour in each direction ?
Solution:
Distance = 150 km
Let the speed of the person while going = x km/hr
Then the speed while returning = (x + 10) km/hr
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 7

=> x (x + 30) – 20 (x + 30) = 0
=> (x + 30) (x – 20) = 0
Either x + 30 = 0, then x = -30 which is not possible being negative
or (x – 20) = 0 then x = 20
Usual speed of the man while going = 20 km/hr

Question 6.
A plane left 40 minutes late due to bad weather and in order to reach its destination, 1600 km away in time, it had to increase its speed by 400 km/hr from its usual speed. Find the usual speed of the plane.
Solution:
Distance = 1600 km
Let usual speed of the plane = x km/hr
Increased speed = (x + 400) km/hr
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 9
is not possible being negative or x – 800 = 0, then x = 800
Usual speed of the plane = 800 km/hr

Question 7.
An aeroplane takes 1 hour less for a journey of 1200 km if its speed is increased by 100 km/hr from its usual speed. Find its usual speed.
Solution:
Distance = 1200 km
Let usual speed of the aeroplane = x km/hr
Increased speed = (x + 100) km/hr
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 10
=> x (x + 400) – 300 (x + 400) = 0
=> (x + 400) (x – 300) = 0
Either x – 300 = 0, then x = 300
or x + 400 = 0, then x = -400 which is not possible being negative
Usual speed of the plane = 300 km/hr

Question 8.
A train travels at a certain average speed for a distance 63 km and then travels a distance of 72 km at an average speed of 6 km/hr more than the original speed. If it takes 3 hours to complete^total journey, what is its original average speed? [NCERT Exemplar]
Solution:
Let its original average speed be x km/h. Therefore
\(\frac { 63 }{ x }\) + \(\frac { 72 }{ x + 6 }\) = 3
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 11

Question 9.
A train covers a distance of 90 km at a uniform speed. Had the speed been 15 km/hr more, it would have taken 30 minutes less for the journey. Find the original speed of the train. [CBSE 2006C]
Solution:
Distance to be covered = 90 km
Let uniform-original speed = x km/h
Increased speed = (x + 15) km/hr
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 12
=> x² + 60x – 45x – 2700 = 0
=> x (x + 60) – 45 (x + 60) = 0
=> (x + 60)(x – 45) = 0
Either x + 60 = 0, then x = -60 which is not possible being negative
or x – 45 = 0, then x = 45
Original speed of the train = 45 km/hr

Question 10.
A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:
Total distance = 360 km
Let uniform speed of the train = x km/hr
Increased speed = (x + 5) km/hr
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 13
=> x (x + 45) – 40 (x + 45) = 0
=> (x + 45) (x – 40) = 0
Either x + 45 = 0, then x = -45 but it is not possible being negative
or x – 40 = 0, then x = 40
Speed of the train = 40 km/hr

Question 11.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/hr more than that of the passenger train, find the average speeds of the two trains.
Solution:
Distance between Mysore and Bangalore = 132 km
Let the speed of the passenger train=x km/hr
Then speed of express train = x + 11
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 14
Either x + 44 = 0, then x = -44 but it is not possible being negative
or x – 33 = 0, then x = 33
Speed of passenger train = 33 km/hr
and speed of express train = 33 + 11 = 44 km/hr

Question 12.
An aeroplane left 50 minutes later than its scheduled time, and in order to reach the destination, 1250 km away, in time, it had to increase its speed by 250 km/hr from its usual speed. Find its usual speed. (CBSE 2010)
Solution:
Distance = 1250 km
Usual speed = x km/hr
Increased speed = (x + 250) km/hr
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 15

Question 13.
While boarding an aeroplane, a passenger got hurt. The pilot showing promptness and concern, made arrangements to hospitalise the injured and so the plane started late by 30 minutes to reach the destination, 1500 km away, in time, the pilot increased the speed by 100 km/hr. Find the original speed / hour of the plane. [CBSE 2013]
Solution:
Distance = 1500 km
Let the original speed of the aeroplane = x km/hr
Then increased speed = (x + 100) km/hr
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 17
=> x² + 100x = 300000
=> x²+ 100x – 300000 = 0
=> x² + 600x – 500x – 300000 = 0
=> x (x + 600) – 500(x + 600) = 0
=> (x + 600) (x – 500) = 0
Either x + 600 = 0, then x = -600 which is not possible being negative
or x – 500 = 0, then x = 500
Original speed = 500 km/hr

Question 14.
A motorboat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream. [CBSE 2014]
Solution:
Let speed of the stream be x km/hr,
Speed of the boat upstream = (18 – x) km/hr
and Speed of the boat downstream = (18 + x) km/hr
Distance = 24 km
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 18
48x = 324 – x²
x² + 48x – 324 = 0
x² + 54x – 6x – 324 = 0
x(x + 54) – 6(x + 54) = 0
(x – 6) (x + 54) = 0
x – 6 = 0 or x + 54 = 0
x = 6 or x = – 54
Since speed cannot be negative
Speed of stream, x = 6 km/hr

Question 15.
A car moves a distance of 2592 km with uniform speed. The number of hours taken for the journey is one-half the number representing the speed, in km/ hour. Find the time taken to cover the distance. [CBSE 2017]
Solution:
Distance = 2592 km
Let the speed of the car = x km/hr
and time taken = \(\frac { x }{ 2 }\) hour
We have, Distance = Speed x Time
2592 = x x \(\frac { x }{ 2 }\)
=> 2592 = \(\frac { { x }^{ 2 } }{ 2 }\)
=> x² = 2592 x 2
=> x = √5184
=> x = 72 km/hr
and thus time taken = \(\frac { x }{ 2 }\) h = \(\frac { 72 }{ 2 }\) = 36 hour

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1

January 5, 2023

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1

Other Exercises

Question 1.
How many balls, each of radius 1 cm, can be made from a solid sphere of lead of radius 8 cm ?
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 1

Question 2.
How many spherical bullets each of 5 cm in diameter can be cast from a rectangular block of metal 11dm x 1m x 5 dm?
Solution:
Volume of reactangular block of metal
(V₁) = 11 dm x 1 m x 5 dm
= 11 dm x 10 dm x 5 dm = 550 dm³Diameter of spherical bullet = 5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 2

Question 3.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of the two balls are 1.5 cm and 2 cm respectively. Determine the diameter of the third ball.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 3

Question 4.
2.2 cubic dm of brass is to be drawn into a cylindrical wire 0.25 cm in diameter. Find the length of the wire.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 5

Question 5.
What length of a solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of length 16 cm, external diameter 20 cm and thickness 2.5 mm ?
Solution:
Length of hollow cylinder = 16 cm
External diameter = 20 cm
and thickness = 2.5 mm = 0.25 cm
∴External radius (R) = \(\frac { 20 }{ 2 }\) = 10 cm
and internal radius (r) = 10 – 0.25 = 9.75 cm
∴ Volume of the material used in hollow cylinder
= πh (R² – r²) = π x 16 (10² – 9.75²) cm²
= 16π (100.00 – 95.0625) = 16TC (4.9375) cm³
∴ Volume of solid cylinder = 16 x 4.93 75πcm3 Diameter = 2 cm
∴Radius (r) = \(\frac { 2 }{ 2 }\) = 1 cm
Let h be the height of the cylinder, then
πr²h = 16 x 4.9375π
⇒ π (1)² h = 16 x 4.93 75π
h = 16 x 4.9375 = 79
Hence height = 79 cm

Question 6.
A cylindrical vessel having diameter equal to its height is full of water which is poured into two identical cylindrical vessels with diameter 42 cm and jteight 21 cm which are filled completely. Find the diameter of the cylindrical vessel.
Solution:
Diameter of each small cylindrical vessels = 42 cm
∴Radius of each vessel (r) = \(\frac { 42 }{ 2 }\) = 21 cm
Height (h) = 21 cm
∴ Volume of each cylindrical vessal = πr²h = π (21 )2 (21) = 9261K cm³
and volume of both vessels = 2 x 9261π = 18522π cm³
Now volume of larger cylindrical vessel = 185 22π cm³
Let R be the radius of the vessel, then Height (H) = diameter = 2R,
∴Volume πR²H = πR² x 2R = 2πR²
∴ 2πR³ = 18522π
⇒ R³ = \(\frac { 18522 }{ 2 }\) = 9261
⇒ R³ = 9261 = (21 )³
∴ R = 21
∴Diameter = 2R = 2×21=42 cm

Question 7.
50 circular plates each of diameter 14 cm and thickness 0.5 cm are placed one above the other to form a right circular cylinder. Find its total surface area.
Solution:
Diameter of each circular plate = 14 cm
∴ Radius (r) = \(\frac { 14 }{ 2 }\) = 7 cm .
Thickness (h) = 0.5 cm
∴Height of 50 plates placing one above the other
= 0.5 x 50 = 25 cm
∴ Curved surface area of the cylinder so formed = 2πrh
= 2 x \(\frac { 2 }{ 7 }\) x 7 x 25 = 1100 cm2
and total surface area = curved surface area + 2 x base area
= 1100 + 2 x πr² =1100+ 2 x \(\frac { 22 }{ 2 }\) x 7 x 7
= 1100 + 308 = 1408 cm²

Question 8.
25 circular plates, each of radius 10.5 cm and thickness 1.6 cm, are placed one above the other to form a solid circular cylinder. Find the curved surface area and the volume of the cylinder so formed.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 6

Question 9.
Find the number of metallic circular discs with 1.5 cm base diameter and of height 0. 2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm. [NCERT Exemplar]
Solution:
Given that, lots of metallic circular disc to be melted to form a right circular cylinder. Here, a circular disc work as a circular cylinder.
Base diameter of metallic circular disc = 1.5 cm
∴Radius of metallic circular disc = \(\frac { 1.5 }{ 2 }\) cm [∵ diameter = 2 x radius]
and height of metallic circular disc i.e., = 0.2 cm
∴ Volume of a circular disc = π x (Radius)² x Height
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 7

Question 10.
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimensions 66 cm x 42 cm x 21 cm. [NCERT Exemplar]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 8

Question 11.
How many spherical lead shots of diameter 4 cm can be made out of a solid cube of lead whose edge measures 44 cm. [NCERT Exemplar]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 10
Hence, the required number of spherical lead shots is 2541.

Question 12.
Three cubes of a metal whose edges are in the ratio 3:4:5 are melted and converted into a single cube whose diagonal is 12 \(\sqrt { 3 } \) cm. Find the edges of the three cubes. [NCERT Exemplar]
Solution:
Let the edges of three cubes (in cm) be 3x, 4x and 5x, respectively.
Volume of the cubes after melting is = (3x)³ + (4x)³ + (5x)³ = 216×3 cm³
Let a be the side of new cube so formed after melting. Therefore, a³ = 216x³
So, a = 6x,
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 11

Question 13.
A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed. [NCERT Exemplar]
Solution:
The volume of the solid metallic sphere = \(\frac { 4 }{ 3 }\) π(10.5)³ cm³
Volume of a cone of radius 3.5 cm and height 3 cm = \(\frac { 1 }{ 3 }\) π (3.5)² x 3 cm³Number of cones so formed
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 12

Question 14.
The diameter of a metallic sphere is equal to 9 cm. It is melted and drawn into a long wire of diameter 2 mm having uniform cross-section. Find the length of the wire.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 13

Question 15.
An iron spherical ball has been melted and recast into smaller balls of equal size. If the radius of each of the smaller balls is \(\frac { 1 }{ 4 }\) of the radius of the original ball, how many such balls are made ? Compare the surface area, of all the smaller balls combined together with that of the original ball.
Solution:
Let R be the radius of the original ball, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 14

Question 16.
A copper sphere of radius 3 cm is melted and recast into a right circular cone of height 3 cm. Find the radius of the base of the cone.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 15

Question 17.
A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 16

Question 18.
The diameters of internal and external surfaces of a hollow spherical shell are 10 cm and 6 cm respectively. If it is melted and recast into a solid cylinder of length of 2 \(\frac { 2 }{ 3 }\) cm, find the diameter of the cylinder.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 17

Question 19.
How many coins 1.75 cm in diameter and 2 mm thick must be melted to form a cuboid 11 cm x 10 cm x 7 cm ?
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 18

Question 20.
The surface area of a solid metallic sphere is 616 cm². It is melted and recast into a cone of height 28 cm. Find the diameter of the base of the cone so formed. (Use π = 22/7). [CBSE 2010]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 19

Question 21.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied out on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap. [CBSE 2012]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 20

Question 22.
A solid metallic sphere of radius 5.6 cm is melted and solid cones each of radius 2.8 cm and height 3.2 cm are made. Find the number of such cones formed. [CBSE 2014]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 22

Question 23.
A solid cuboid of iron with dimensions 53 cm x 40 cm x 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe. [CBSE 2015]
Solution:
Length of cuboid (l) = 53 cm
Breadth (b) = 40 cm
Height (h) = 15 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 24

Volume =lbh= 53 x 40 x 15 cm³= 31800 cm³∴ Volume of cylindrical pipe = 31800 cm³Inner diameter of pipe = 7 cm
and outer diameter = 8 cm
∴ Outer radius (R) = \(\frac { 8 }{ 2 }\) = 4 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 25

Question 24.
The diameters of the internal and external surfaces of a holjow spherical shell are 6 cm and 10 cm respectively. If it is melted and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder. [CBSE 2001C]
Solution:
Outer diameter of hollow spherical shell = 10 cm
and inner diameter = 6 cm
Outer radius (R) = \(\frac { 10 }{ 2 }\) = 5 cm 6
and inner radius (r) = \(\frac { 6 }{ 2 }\) = 3 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 26

Question 25.
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Calculate the height of the cone.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 28

Question 26.
A hollow sphere of internal and external radii 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm. Find the height and slant height of the cone.
Solution:
Interval radius of hollow sphere (r) = 2m
and external radius (R) = 4m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 29

Question 27.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of the balls are 1.5 cm and 2 cm. Find the diameter of the third ball.
Solution:
Radius of big spherical ball (R) = 3 cm
∴ Volume = \(\frac { 4 }{ 3 }\) πR³ = \(\frac { 4 }{ 3 }\) n x (3)³ cm³
= \(\frac { 4 }{ 3 }\) π x 27 = 36π cm³Similarly volume of ball of radius (r₁) = 1.5 cm
∴ Volume = \(\frac { 4 }{ 3 }\) π( 1.5)³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 30

Question 28.
A path 2 m wide surrounds a circular pond of diameter 40 m. How many cubic metres of gravel are required to grave the path to a depth of 20 cm ?
Solution:
Diamter of pond = 40 m
∴ Radius (r) = \(\frac { 40 }{ 2 }\) =20 m
Width of path = 2 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 31

Question 29.
A 16 m deep well with diameter 3.5 m is dug up and the earth from it is spread evenly to form a platform 27.5 m by 7 m. Find the height of the platform.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 32
Volume of platform = Ibh = 27.5 x7 x h

Question 30.
A well of diameter 2 m is dug 14 m deep. The earth taken out of it is spread evenly all around it to form an embankment of height 40 cm. Find the width of the embankment.
Solution:
Diameter of well = 2 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 34

Question 31.
A well with inner radius 4 m is dug 14 m deep. Earth taken out of it has been spread evenly all around a width of 3 m it to form an embankment. Find the height of the embankment.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 36

Question 32.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has>been spread evenly all around it to a width of 4 m to form an embankment. Find the height of the embankment.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 37

Question 33.
Find the volume of the largest right circular cone that can be cut out of a cube whose edge is 9 cm.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 38

Question 34.
A cylindrical bucket, 32 cm high and 18 cm of radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 39

Question 35.
Rain water, which falls on a flat rectangular surface of length 6 m and breadth 4 m is transferred into a cylindrical vessel of internal radius 20 cm. What will be the height of water in the cylindrical vessel if a rainfall of 1 cm has fallen ? [Use π = 22/7]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 40

Question 36.
The rain water from a roof of dimensions 22 m x 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the rain water collected from the roof just fills the cylindrical vessel, then find the rain in cm. [NCERT Exemplar]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 41

Question 37.
A conical flask is full of water. The flask has base-radius r and height h. The water is poured into a cylindrical flafisk of base- radius mr. Find the height of water in the cylindrical flask.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 42

Question 38.
A rectangular tank 15 m long and 11 m broad is required to receive entire liquid contents from a full cylindrical tank of internal diameter 21m and length 5 m. Find the least height of the tank that will serve the purpose.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 43

Question 39.
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be fdled into cylindrical shaped small bottles each of diameter 3 cm and height 4 cm. How many bottles are necessary to empty the bowl ?
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 44

Question 40.
A cylindrical tub of radius 12 cm contains water to a depth of 20 cm. A spherical ball is dropped into the tub and the level of the water is raised by 6.75 cm. Find the radius of the ball.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 45

Question 41.
500 persons have to dip in a rectangular tank which is 80 m long and 50 m broad. What is the rise in the level of water inthe tank, if the average displacement of water by a person is 0.04 m3 ?
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 46

Question 42.
A cylindrical jar of radius 6 cm contains oil. Iron spheres each of radius 1.5 cm are immersed in the oil. How many spheres are necessary to raise the level of the oil by two centimetres ?
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 47

Question 43.
A cylindrical tub of radius 12 cm contains water to a depth of 20 cm. A spherical form ball of radius 9 cm is dropped into the tub and thus the level of water is raised by h cm. What is the value of h ?
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 48

Question 44.
Metal spheres, each of radius 2 cm, are packed into a rectangular box of internal dimension 16 cm x 8 cm x 8 cm when 16 spheres are packed the box is fdled with preservative liquid. Find the volume of this liquid. [Use π = 669/213]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 49

Question 45.
A vessel in the shape of a cuboid contains some water. If three identical spheres are immersed in the water, the level of water is increased by 2 cm. If the area of the base of the cuboid is 160 cm² and its height 12 cm, determine the radius of any of the spheres.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 50

Question 46.
150 spherical marbles, each of diameter 1.4 cm are dropped in a cylindrical vessel of diameter 7 cm contianing some water, which are completely immersed in water. Find the rise in the level of water in the vessel. [CBSE2014]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 51

Question 47.
Sushant has a vessel, of the form of an inverted cone, open at the top, of height 11 cm and radius of top as 2.5 cm and is full of water. Metallic spherical balls each of diameter 0.5 cm are put in the vessel due to which \((\frac { 2 }{ 5 } )\)² of the water in the vessel flows out. Find how many balls were put in the vessel. Sushant made the arrangement so that the water that flows out irrigates the flower beds. What value has been shown by Sushant? [CBSE 2014]
Solution:
Radius of vessel (R) = 2.5 cm
and height (h) = 11 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 52

Question 48.
16 glass spheres each of radius 2 cm are packed into a cuboidal box of internal dimensions 16 cm x 8 cm x 8 cm and then the box is filled with water. Find the volume of water fdled in the box. |NCERT Exemplar]
Solution:
Given, dimensions of the cuboidal
= 16 cm x 8 cm x 8 cm
∴ Volume of the cuboidal =16x8x8
= 1024 cm³Also, given radius of one glass sphere = 2cm
∴ Volume of one glass sphere = \((\frac { 4 }{ 3 } )\)πr³
= \((\frac { 4 }{ 3 } )\) x \((\frac { 22 }{ 7 } )\) x (2)³
= \((\frac { 704 }{ 21 } )\) = 33.523 cm³
Now, volume of 16 glass spheres = 16 x 33.523 = 536.37 cm³∴ Required volume of water = Volume of cuboidal – Volume of 16 glass spheres
= 1024 – 536.37 = 487.6 cm³

Question 49.
Water flows through a cylindrical pipe, whose inner radius is 1 cm, at the rate of 80 cm/sec in an empty cylindrical tank, the radius of whose base is 40 cm. What is the rise of water level in tank in half an hour? [NCERT Exemplar]
Solution:
Given, radius of tank, r₁ = 40 cm
Let height of water level in tank in half an hour = h₁Also, given internal radius of cylindrical pipe, r₁ = 1 cm
and speed of water = 80 cm/s /., in 1 water flow = 80 cm
∴In 30 (min) water flow = 80 x 60 x 30 = 144000 cm
According to the question,
Volume of water in cylindrical tank = Volume of water flow the circular pipe in half an hour
⇒ πr₁²h₁ = πr₂²h₂⇒ 40 x 40 x h₁ = 1 x 1 x 14400
∴ h₁ = \((\frac {144000 }{ 40 x 40 } )\) = 90 cm
Hence, the level of water in cylindrical tank rises 90 cm in half an hour.

Question 50.
Water in a canal 1.5 m wide and 6 m deep is flowing with a speed of 10km/hr. How much area will it irrigate in 30 minutes if 8 cm of standing water is desired ?
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 54

Question 51.
A famer runs a pipe of internal diameter 20 cm from the canal into a cylindrical tank in his field which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled ?
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 55

Question 52.
A cylindrical tank full of water is emptied by a pipe at the rate of 225 litres per minute. How much time will it take to empty half the tank, if the diameter of its base is 3 m and its height is 3.5 m? [Use π = 22/7] [ [CBSE 2014]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 56

Question 53.
A cylindrical tank full of water is emptied by a pipe at the rate of 225 litres per minute. How much time will it take to empty half the tank, if the diameter of its base is 3 m and its height is 3.5 m? [Use π = 22/7] [CBSE 2014]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 57

Question 54.
Water flows at the rate of 15 km/hr through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
[NCERT Exemplar]
Solution:
Given, length of the pond = 50 m and width of the pond = 44 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 58

Question 55.
A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/h. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired? [NCERT Exemplar]
Solution:
Volume of water flows in the canal in one hour = width of the canal x depth of the canal x speed of the canal water
= 3 x 1.2 x 20 x 1000 m³ = 72000 m³
In 20 minutes the volume of water
= \(\frac { 72000\times 20 }{ 60 }\) m³ = 24000 m³
Area irrigated in 20 minutes, if 8 cm,
i. e., 0.08 m standing water is required
= \((\frac { 2 }{ 5 } )\)
= \((\frac { 2 }{ 5 } )\) m²
= 300000 m²= 30 hectares.

Question 56.
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 cm2, find the volume of cylinder. (Use re = 22/7) [CBSE 2016]
Solution:
Let the radius and height of cylinder be r and h respectively.
r + h = 37 cm …(i) [given]
Total surface area of cylinder = 1628 cm²
2πr(r + h) = 1628
⇒ 2πr(37) = 1628
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 59

Question 57.
A tent of height 77 dm is in the form a right circular cylinder of diameter 36 m and height 44 dm surmounted by a right circular cone. Find the cost of the canvas at ₹3.50 per m². [Use π = 22/7]
Solution:
Total height of the tent = 77 dm
Height of the cylindrical part (h₁) = 44 dm = 4.4 m
Height of conical part (h₂) = 77 – 44 = 33 dm = 3.3 m
Diameter of the base of the tent = 36 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 60

Question 58.
The largest sphere is to be curved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
Solution:
Largest sphere to be curved must have its diameter = diameter of cylinder = height of cylinder
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 62

Question 59.
A right angled triangle whose sides are 3 cm, 4 cm and 5 cm is revolved about the sides containing the right angle in two ways. Find the difference in volumes of the two cones so formed. Also, find their curved surfaces.
Solution:
In ∆ABC, ∠B = 90°
and sides are 3 cm, 4 cm and 5 cm
Here diagonal is 5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 63

(i) When it is revolved along BC i.e., 4 cm side, then
Radius of the base of the cone (r₁) = 3 cm
and height (h₁) = 4 cm and slant height l = 5 cm
∴ Volume = \((\frac { 2 }{ 5 } )\) πr2h = \((\frac { 1 }{ 3 } )\) π x 3 x 3 x 4 cm³
= 12π cm³
and surface area = πrl = π x 3 x 5 cm2 = 157π cm2
(ii) When it is revolved along 3 cm side, then
r = 4 cm and h = 3 cm and l = 5 cm
∴ Volume = \((\frac { 1 }{ 3 } )\) πr2h =-\((\frac { 1 }{ 3 } )\) π x 4 x 4 x 3 cm3
= 16πcm³
and curved surface area = πrl
= π x 4 x 5 = 20n cm²
∴ Difference of their volumes = I6π- 12π = 4πcm³

Question 60.
A 5 m wide cloth is used to make a conical tent of base diameter 14 ir. and height 24 m. Find the cost of cloth used at the rate of ₹25 per metre. [Use π = 22/7] [CBSE 2014]
Solution:
Diameter of base of conical tent = 14 m
Radius (r) = \((\frac { 14 }{ 3 } )\)= 7 cm
Height (h) = 24 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 64

Question 61.
The volume of a hemi-sphere is 2425 \((\frac { 1 }{ 2 } )\) cm³, find its curved surface area. [2012]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 65

Question 62.
The difference between the outer and inner curved surface areas of a hollow right circular cylinder 14 cm long is 88 cm². If the volume of nretal used in making the cylinder is 176 cm³, find the outer and inner diameters of the cylinder. [CBSE 2010]
Solution:
Height of hollow right cylinder = 14 cm
Difference between outer and inner curved surface area = 88 cm²
and volume of metal used =176 cm³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 66

Question 63.
The internal and external diameters of a hollow hemispherical vessel are 21 cm and 25.2 cm respectively. The cost of painting 1 cm² of the surface is 10 paise. Find the total cost to paint the vessel ail over.
Solution:
Outer diameter of the hemispherical vessel = 25.2 cm
and inner diameter = 21 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 68

Question 64.
Prove that the surface area of a sphere is equal to the curved surface area of the circumscribed cylinder.
Solution:
Let r be the radius of the sphere, then surface area = 4πr² ….(i)
Then radius of the circumscribed cylinder = radius of the sphere = r
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 69

Question 65.
If the total surface area of a solid hemisphere is 462 cm², find its volume (Take π = 22/7).
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 70

Question 66.
Water flows at the rate of 10 m / minutes through a cylindrical pipe 5 mm in diameter. How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm? [NCERT Exemplar]
Solution:
Given, speed of water flow = 10 m min^-1 = 1000 cm/min
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 71

Question 67.
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius of the cone. [NCERT Exemplar]
Solution:
(i) Whenever we placed a solid right circular cone in a right circular cylinder with full of water, then volume of a solid right circular cone is equal to the volume of water failed from the cylinder.
(ii) Total volume of water in a cylinder is equal to the volume of the cylinder.
(iii) Volume of water left in the cylinder = Volume of the right circular cylinder – Volume of a right circular cone.
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 72
Now, given that
Height of a right circular cone = 120 cm
Radius of a right circular cone = 60 cm
∴Volume of a right circular cone = \((\frac { 1 }{ 3 } )\)πr² x h
= \((\frac { 1 }{ 3 } )\) x \((\frac { 22 }{ 7 } )\) x 60 x 60 x 120
=\((\frac { 22 }{ 7 } )\) x 20 x 60 x 120
= 144000π cm³
∴Volume of a right circular cone = Volume of water failed from the cylinder = 1440007c cm3 [from point (i)]
Given that, height of a right circular cylinder = 180 cm
and radius of a right circular cylinder = Radius of a right circular cone = 60 cm
∴Volume of a right circular cylinder = πr² x h
= π x 60 x 60 x 180 = 64800071 cm3 So, volume of a right circular cylinder = Total volume of water in a cylinder = 64800071 cm3 [from point (ii)]
From point (iii),
Volume of water left in the cylinder = Total volume of water in a cylinder – Volume of water failed from the cylinder when solid cone is placed in it
= 648000π- 144000π
= 504000π = 504000 x \((\frac { 22 }{ 7 } )\) = 1584000 cm³ 1584000
= \((\frac { 1584000 }{ (10)6 } )\) m³ = 1.584 m³
Hence, the required volume of water left in the cylinder is 1.584 m³.

Question 68.
A heap of rice in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of rice. How much canvas cloth is required to cover the heap? [NCERT Exemplar]
Solution:
Given that, a heap of rice is in the form of a cone.
Height of a heap of rice i.e., cone (h) = 3.5m
and diameter of a heap of rice i. e., cone = 9 m
Radius of a heap of rice i.e., cone (r) = \((\frac { 9 }{ 2 } )\) m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 73

Question 69.
A cylindrical bucket of height 32 cm and base radius 18 cm is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the concial heap is 24 cm, find the radius and slant height of the’ heap. [NCERT Exemplar]
Solution:
Given, radius of the base of the bucket = 18 cm
Height of the bucket = 32 cm
So, volume of the sand in cylindrical bucket
= πr²h = π (18)²x 32= 10368π
Also, given height of the conical heap (h) = 24 cm
Let radius of heap be r cm
Then, volume of the sand in the heap = \((\frac { 1 }{ 3 } )\) πr²h
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 74

Question 70.
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl? [NCERT Exemplar]
Solution:
Given, radius of hemispherical bowl, r = 9cm
and radius of cylindrical bottles, R = 1.5 cm
and height, h = 4 cm
∴Number of required cylindrical bottles
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 75

Question 71.
A factory manufactures 120,000 pencils daily. The pencils are cylindrical in shape each of length 25 cm and circumference of base as 1.5 cm. Determine the cost of colouring the curved surfaces of the pencils manufactured in one day at ₹0.05 per dm². [NCERT Exemplar]
Solution:
Given, pencils are cylindrical in shape.
Length of one pencil = 25 cm
and circumference of base = 1.5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 76
Now, cost of colouring 1 dm2 curved surface of the pencils manufactured in one day = ₹0.05
∴ Cost of colouring 45000 dm2 curved surface = ₹2250

Question 72.
The\((\frac { 3 }{ 4 } )\)th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
Solution:
Let height of water in cylindrical vessel = h cm
Volume of water (in cylinder) = \((\frac { 3 }{ 4 } )\) Volume of water (in come)
∵ Volume of cylinder = nr²h & Volume of cone = \((\frac { 1 }{ 3 } )\) πr²h
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 77
Hence, height of water in cylindrical vessel (h) = 1.5 cm

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5

January 5, 2023

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5

Other Exercises

Question 1.
Write the discriminant of the following quadratic equations :
(i) 2x² – 5x + 3 = 0
(ii) x² + 2x + 4 = 0
(iii) (x – 1) (2x – 1) = 0
(iv) x² – 2x + k = 0, k ∈ R
(v) √3 x² + 2√2 x – 2√3 = 0
(vi) x² – x + 1 = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5 1

Question 2.
In the following, determine whether the given quadratic equations have real roots and if so, And the roots :
(i) 16x² = 24x + 1
(ii) x² + x + 2 = 0
(iii) √3 x² + 10x – 8√3 = 0
(iv) 3x² – 2x + 2 = 0
(v) 2x² – 2√6 x + 3 = 0
(vi) 3a²x² + 8abx + 4b² = 0, a ≠ 0
(vii) 3x² + 2√5 x – 5 = 0
(viii) x² – 2x + 1 = 0
(ix) 2x² + 5√3 x + 6 = 0
(x) √2 x² + 7x + 5√2= 0 [NCERT]
(xi) 2x² – 2√2 x + 1 = 0 [NCERT]
(xii) 3x² – 5x + 2 = 0 [NCERT]
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5 4

Question 3.
Solve for x :
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5 14
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

January 5, 2023

RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Other Exercises

Mark the correct alternative in each of the following:
Question 1.
Which of the following is not a measure of central tendency :
(a) Mean
(b) Median
(c) Mode
(d) Standard deviation
Solution:
Standard deviation is not a measure of central tendency. Only mean, median and mode are measures. (d)

Question 2.
The algebraic sum of the deviations of a frequency distribution from its mean is
(a) always positive
(b) always negative
(c) 0
(d) a non-zero number
Solution:
The algebraic sum of the deviations of a frequency distribution from its mean is zero
Let x₁, x₂, x₃, …… x_n are observations and \(\overline { X }\) is the mean
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 1

Question 3.
The arithmetic mean of 1, 2, 3, ….. , n is
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 2
Solution:
Arithmetic mean of 1, 2, 3, …… n is

Question 4.
For a frequency distribution, mean, median and mode are connected by the relation
(a) Mode = 3 Mean – 2 Median
(b) Mode = 2 Median – 3 Mean
(c) Mode = 3 Median – 2 Mean
(d) Mode = 3 Median + 2 Mean
Solution:
The relation between mean, median and mode is: Mode = 3 Median – 2 Mean (c)

Question 5.
Which of the following cannot be determined graphically ?
(a) Mean
(b) Median
(c) Mode
(d) None of these
Solution:
Mean cannot be determind graphically, (a)

Question 6.
The median of a given frequency distribution is found graphically with the help of
(a) Histogram
(b) Frequency curve
(c) Frequency polygon
(d) Ogive
Solution:
Median of a given frequency can be found graphically by an ogive, (d)

Question 7.
The mode of a frequency distribution can be determined graphically from
(a) Histogram
(b) Frequency polygon
(c) Ogive
(d) Frequency curve
Solution:
Mode of frequency can be found graphically by an ogive, (c)

Question 8.
Mode is
(a) least frequent value
(b) middle most value
(c) most frequent value
(d) None of these
Solution:
Mode is the most frequency value of observation or a class, (c)

Question 9.
The mean of n observations is \(\overline { X }\) . If the first item is increased by 1, second by 2 and so on,
then the new mean is

Solution:
Mean of n observations = \(\overline { X }\)
By adding 1 to the first item, 2 to second item and so on, the new mean will be
Let x₁, x₂, x_3,….. x_n are the items whose mean is \(\overline { X }\) , then mean of
(x₁+ 1) + (x₂ + 2) + (x₃ + 3) + …… (x_n + n)
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 5

Question 10.
One of the methods of determining mode is
(a) Mode = 2 Median – 3 Mean
(b) Mode = 2 Median + 3 Mean
(c) Mode = 3 Median – 2 Mean
(d) Mode = 3 Median + 2 Mean
Solution:
Mode = 3 Median – 2 Mean (c)

Question 11.
If the mean of the following distribution is 2.6, then the value of y is
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 6
(a) 3
(b) 8
(c) 13
(d) 24
Solution:

Question 12.
The relationship between mean, median and mode for a moderately skewed distribution is
(a) Mode = 2 Median – 3 Mean
(b) Mode = Median – 2 Mean
(c) Mode = 2 Median – Mean
(d) Mode = 3 Median – 2 Mean
Solution:
The relationship between mean, median and mode is Mode = 3 Median – 2 Mean, (d)

Question 13.
The mean of a discrete frequency distribution x_i /f_i ; i= 1, 2, …… n is given by
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 8
Solution:

Question 14.
If the arithmetic mean of x, x + 3, x + 6, x + 9, and x + 12 is 10, then x =
(a) 1
(b) 2
(c) 6
(d) 4
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 10

Question 15.
If the median of the data : 24, 25, 26, x + 2, x + 3, 30, 31, 34 is 27.5, then x =
(a) 27
(b) 25
(c) 28
(d) 30
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 12

Question 16.
If the median of the data : 6, 7, x – 2, x, 17, 20, written in ascending order, is 16. Then x =
(a) 15
(b) 16
(c) 17
(d) 18
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 13

Question 17.
The median of first 10 prime numbers is
(a) 11
(b) 12
(c) 13
(d) 14
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 15

Question 18.
If the mode of the data : 64,60, 48, x, 43, 48, 43, 34 is 43, then x + 3 =
(a) 44
(b) 45
(c) 46
(d) 48
Solution:
Mode of 64, 60, 48, x, 43, 48, 43, 34 is 43
∵ By definition mode is a number which has maximum frequency which is 43
∴ x = 43
∴ x + 3 = 43 + 3 = 46 (c)

Question 19.
If the mode of the data : 16, 15, 17, 16, 15, x, 19, 17, 14 is 15, then x =
(a) 15
(b) 16
(c) 17
(d) 19
Solution:
Mode of 16, 15, 17, 16, 15, x, 19, 17, 14 is 15
∵By definition mode of a number which has maximum frequency which is 15
∴ x = 15 (a)

Question 20.
The mean of 1, 3, 4, 5, 7, 4 is m. The number 3, 2, 2, 4, 3, 3, p have mean m – 1 and median q. Then p + q =
(a) 4
(b) 5
(c) 6
(d) 7
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 16

Question 21.
If the mean of a frequency distribution is 8.1 and Σf_ix_i = 132 + 5k, Σf_i = 20, then k =
(a) 3
(b) 4
(c) 5
(d) 6
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 17

Question 22.
If the mean of 6, 7, x, 8, y, 14 is 9, then
(a)x+y = 21
(b)x+y = 19
(c) x -y = 19
(d) v -y = 21
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 18

Question 23.
The mean of n observations is \(\overline { x }\) If the first observation is increased by 1, the second by 2, the third by 3, and so on, then the new mean is
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 19
Solution:

Question 24.
If the mean of first n natural numbers is \(\frac { 5n }{ 9 }\) then n =
(a) 5
(b) 4
(c) 9
(d) 10
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 21

Question 25.
The arithmetic mean and mode of a data are 24 and 12 respectively, then its median is
(a) 25
(b) 18
(c) 20
(d) 22
Solution:
Arithmetic mean = 24
Mode = 12
∴ But mode = 3 median – 2 mean
⇒ 12 = 3 median – 2 x 24
⇒ 12 = 3 median =-48
⇒ 12 + 48 = 3 median
⇒ 3 median = 60
Median = \(\frac { 60 }{ 3 }\) = 20 (c)

Question 26.
The mean of first n odd natural number is
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 22
Solution:

Question 27.
The mean of first n odd natural numbers is \(\frac { n2 }{ 81 }\) , then n = 81
(a) 9
(b) 81
(c) 27
(d) 18
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 24

Question 28.
If the difference of mode and median of a data is 24, then the difference of median and mean is
(a) 12
(b) 24
(c) 8
(d) 36
Solution:
Difference of mode and median = 24
Mode = 3 median – 2 mean
⇒ Mode – median = 2 median – 2 mean
⇒ 24 = 2 (median – mean)
⇒ Median – mean = \(\frac { 24 }{ 2 }\) = 12 (a)

Question 29.
If the arithmetic mean of 7, 8, x, 11, 14 is x, then x =
(a) 9
(b) 9.5
(c) 10
(d) 10.5
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 25

Question 30.
If mode of a series exceeds its mean by 12, then mode exceeds the median by
(a) 4
(b) 8
(c) 6
(d) 10
Solution:
Mode of a series = Its mean + 12
Mean = mode – 12
Mode = 3 median – 2 mean
Mode = 3 median – 2 (mode -12)
⇒ Mode = 3 median – 2 mode + 24
⇒ Mode + 2 mode – 3 median = 24
⇒ 3 mode – 3 median = 24
⇒ 3 (mode – median) = 24
⇒ Mode – medain = \(\frac { 24 }{ 3 }\) = 8 (b)

Question 31.
If the mean of first n natural number is 15, then n =
(a) 15
(b) 30
(c) 14
(d) 29
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 26

Question 32.
If the mean of observations x₁, x₂, …, x_n is \(\overline { x }\) , then the mean of x₁ + a, x₂ + a,…, x_n + a is
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 28
Solution:

Question 33.
Mean of a certain number of observations is \(\overline { x }\) If each observation is divided by m (m ≠ 0) and increased by n, then the mean of new observation is
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 30
Solution:
Mean of some observations = \(\overline { x }\)
If each observation is divided by m and increased by n
Then mean will be = \(\frac { \overline { x } }{ m }\) +n

Question 34.
If u_i= \(\frac { xi-25\quad }{ 10 }\) Σf_iu_i = 20, Σf_i= 100, then \(\overline { x }\)
(a) 23
(b) 24
(c) 27
(d) 25
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 31

Question 35.
If 35 is removed from the data : 30, 34, 35, 36, 37, 38, 39, 40, then the median increases by
(a) 2
(b) 1.5
(c) 1
(d) 0.5
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 32

Question 36.
While computing mean of grouped data, we assume that the frequencies are
(a) evenly distributed over all the classes.
(b) centred at the class marks of the classes.
(c) centred at the upper limit of the classes.
(d) centred at the lower limit of the classes.
Solution:
In computing the mean of grouped data, the frequencies are centred at the class marks of the classes. (b)

Question 37.
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 33
Solution:

Question 38.
For the following distribution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 36
the sum of the lower limits of the median and modal class is
(a) 15
(b) 25
(c) 30
(d) 35
Solution:

Now, \(\frac { N }{ 2 }\) = \(\frac { 66 }{ 2 }\) = 33, which lies in the interval 10-15.
Therefore, lower limit of the median class is 10.
The highest frequency is 20, which lies in the interval 15-20.
Therefore, lower limit of modal class is 15.
Hence, required sum is 10 + 15 = 25. (b)

Question 39.
For the following distribution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 38
the modal class is
(a) 10-20
(b) 20-30
(c) 30-40
(d) 50-60
Solution:

Here, we see that the highest frequency is 30, which lies in the interval 30-40. (c)

Question 40.
Consider the following frequency distribution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 40
The difference of the upper limit of the median class and the lower limit of the modal class is
(a) 0
(b) 19
(c) 20
(d) 38
Solution:

Here, \(\frac { N }{ 2 }\) = \(\frac { 67 }{ 2 }\) = 33.5 which lies in the interval 125-145.
Hence, upper limit of median class is 145.
Here, we see that the highest frequency is 20 which lies in 125-145.
Hence, the lower limit of modal class is 125.
∴ Required difference = Upper limit of median class – Lower limit of modal class
= 145 – 125 = 2 (C)

Question 41.
In the formula \(\overline { X }\) = a + \(\frac { \Sigma fidi }{ \Sigma fi }\) for finding the mean of grouped data di’s are deviations from a of
(a) lower limits of classes
(b) upper limits of classes
(c) mid-points of classes
(d) frequency of the class marks
Solution:
We know that, d_i = x_i – a
i .e , d_i‘s are the deviation from a mid-points of the classes. (c)

Question 42.
The abscissa of the point of intersection of less than type and of the more than type cumulative frequency curves of a grouped data gives its
(a) mean
(b) median
(c) mode
(d) all the three above
Solution:
Since, the intersection point of less than ogive and more than ogive gives the median on the abscissa. (b)

Question 43.
Consider the following frequency distribution:
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 42
The upper limit of the median class is
(a) 17
(b) 17.5
(c) 18
(d) 18.5
Solution:
Given, classes are not continuous, so we make continuous by subtracting 0.5 from lower limit and adding 0.5 to upper limit of each class.
RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS 43
Here, \(\frac { N }{ 2 }\) = \(\frac { 57 }{ 2 }\) = 28.5, which lies in the interval 11.5-17.5.
Hence, the upper limit is 17.5.

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS

January 5, 2023

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics VSAQS

Other Exercises

Question 1.
Define Mean.
Solution:
The mean of a set of observations is equal to their sum divided by the total number of observations. Mean is also called an average.

Question 2.
What is the algebraic sum of deviations of a frequency distribution about its mean ?
Solution:
The algebraic sum of deviation of a frequency distribution about its mean is zero.

Question 3.
Which measure of central tendency is given by the x-coordinates of the point of intersection of the ‘more than’ ogive and ‘less than’ ogive ? (C.B.S.E. 2008)
Solution:
Median is given by the x-coordinate of the point of intersection of the more than ogive and less than ogive.

Question 4.
What is the value of the median of the data using the graph in the following figure of less than ogive and more than ogive ?

Solution:
Median = 4, because the coordinates of the point of intersection of two ogives at x-axis is 4.

Question 5.
Write the empirical relation between mean, mode and median.
Solution:
The empirical relation is Mode = 3
Median – 2 Mean

Question 6.
Which measure of central tendency can be determined graphically ?
Solution:
Median can be determinded graphically.

Question 7.
Write the modal class for the following frequency distribution:
RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS 2
Solution:
The modal class is 20-25 as it has the maximum frequency of 75 in the given distribution.

Question 8.
A student draws a cumulative frequency curve for the marks obtained by 40 students of a class as shown below. Find the median marks obtained by the students of the class.
RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS 3
Solution:
Median marks
Here N = 40, then \(\frac { N }{ 2 }\) = \(\frac { 40 }{ 2 }\) = 20
From 20 on y-axis, draw a line parallel to the x-axis meeting the curve at P and from P, draw a perpendicular on x-axis meeting it at M. Then M is the median which is 50.

Question 9.
Write the median class for the following frequency distribution:
RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS 4
Solution:

Here N = 100, then \(\frac { N }{ 2 }\) = 50
Which lies in the class 40-50 (∵32 < 50 < 60)
∴ Required class interval is 40-50

Question 10.
In the graphical representation of a frequency distribution, if the distance between mode and mean isk times the distance between median and mean, then write the value of k.
Solution:
We know that
Mode = 3 median – 2 mean ….(i)
Now mode – mean = k (median – mean) , ….(ii)
But mode – mean = 3 median – 2 mean [from (i)]
⇒ Mode – mean = 3 (median – mean) ….(iii)
Comparing (ii) and (iii)
k = 3

Question 11.
Find the class marks of classes 10-25 and 35-55. (C.B.S.E. 2008)
Solution:
RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS 6

Question 12.
Write the median class of the following distribution :
RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS 7
Solution:

Here n = 50
∴ Median = \(\frac { n + 1 }{ 2 }\) = \(\frac { 5 + 1 }{ 2 }\) = 25.5 which lies in the class 30-40
Hence median class = 30-40.

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3

January 5, 2023

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Other Exercises

Solve the following quadratic equations by factorization.
Question 1.
(x – 4) (x + 2) = 0
Solution:
(x – 4) (x + 2) = 0
Either x – 4 = 0, then x = 4
or x + 2, = 0, then x = -2
Roots are x = 4, -2

Question 2.
(2x + 3) (3x – 7) = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 1

Question 3.
3x² – 14x – 5 = 0 (C.B.S.E. 1999C)
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 2
Roots are x = 5, \(\frac { -1 }{ 3 }\)

Question 4.
9x² – 3x – 2 = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 3

Question 5.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 4
Solution:

Question 6.
6x² + 11x + 3 = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 6

Question 7.
5x² – 3x – 2 = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 7

Question 8.
48x² – 13x – 1 =0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 8
Roots are x = \(\frac { 1 }{ 3 }\) , \(\frac { -1 }{ 16 }\)

Question 9.
3x² = – 11x – 10
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 9

Question 10.
25x (x + 1) = -4
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 10

Question 11.
16x – \(\frac { 10 }{ x }\) = 27 [CBSE 2014]
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 11

Question 12.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 13
Solution:

Question 13.
x – \(\frac { 1 }{ x }\) = 3, x ≠ 0 [NCERT, CBSE 2010]
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 15

Question 14.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 17
Solution:

Question 15.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 19
Solution:

Question 16.
a²x² – 3abx + 2b² = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 22

Question 17.
9x² – 6b²x – (a⁴ – b⁴) = 0 [CBSE 2015]
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 23

Question 18.
4x² + 4bx – (a² – b²) = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 25

Question 19.
ax² + (4a² – 3b)x- 12ab = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 27

Question 20.
2x² + ax – a² = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 28

Question 21.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 29
Solution:

x² = 16
x = ±4

Question 22.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 31
Solution:

Question 23.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 33
Solution:

Question 24.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 36
Solution:

Roots are 4, \(\frac { -2 }{ 9 }\)

Question 25.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 38
Solution:

Question 26.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 41
Solution:

Question 27.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 43
Solution:

Question 28.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 46
Solution:

Question 29.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 48
Solution:

Question 30.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 50
Solution:

Question 31.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 52
Solution:

Question 32.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 55
Solution:

Question 33.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 58
Solution:

Question 34.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 60
Solution:

Question 35.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 62
Solution:

Question 36.

Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 66

Question 37.

Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 68

Question 38.

Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 71

Question 39.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 73
Solution:

Question 40.

Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 76

Question 41.
x² – (√2 + 1) x + √2 = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 77

Question 42.
3x² – 2√6x + 2 = 0 [NCERT, CBSE 2010]
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 79

Question 43.
√2 x² + 7x + 5√2 = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 80

Question 44.
\(\frac { m }{ n }\) x² + \(\frac { n }{ m }\) = 1 – 2x
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 81

Question 45.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 83
Solution:

Question 46.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 86
Solution:

Question 47.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 89
Solution:

Question 48.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 91
Solution:

Question 49.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 94
Solution:

Question 50.
x² + 2ab = (2a + b) x
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 97

Question 51.
(a + b)² x² – 4abx – (a – b)2 = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 98

Question 52.
a (x² + 1) – x (a² + 1) = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 100

Question 53.
x² – x – a (a + 1) = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 101

Question 54.
x² + (a + \(\frac { 1 }{ a }\)) x + 1 = 0
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 102

Question 55.
abx² + (b² – ac) x – bc = 0 (C.B.S.E. 2005)
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 104

Question 56.
a²b²x² + b²x – a²x – 1 = 0 (C.B.S.E. 2005)
Solution:
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 105

Question 57.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 106
Solution:

Question 58.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 109
Solution:

Question 59.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 112
Solution:

⇒ x = 0
x = 0, -7

Question 60.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 115
Solution:

Question 61.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 118
Solution:

Question 62.
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 122
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.